Appendix D.1.1. Case 1a: bX ≥ 0, aY + bY > 0
In this section, we consider a relaxed version of the class of coordination game as in
Section 4.3. We prove theorems presented in
Section 4.3, showing that these results can in fact be extended to the case where
, instead of requiring
and
.
First,
,
is an increasing function of
x, meaning
This implies that both players tend to agree to each other. Intuitively, if , then both players agree that the first action is the better one. For this case, we can show that, no matter what is, the principal branch lies on . In fact, this can be extended to the case whenever , which is the first part of Theorem 1.
Proof of Part 1 of Theorem 1. We can find that, for , for any according to Proposition A1. Since is monotonically increasing with x, for . This means that for any . Additionally, it is easy to see that . As a result, contains the principal branch. ☐
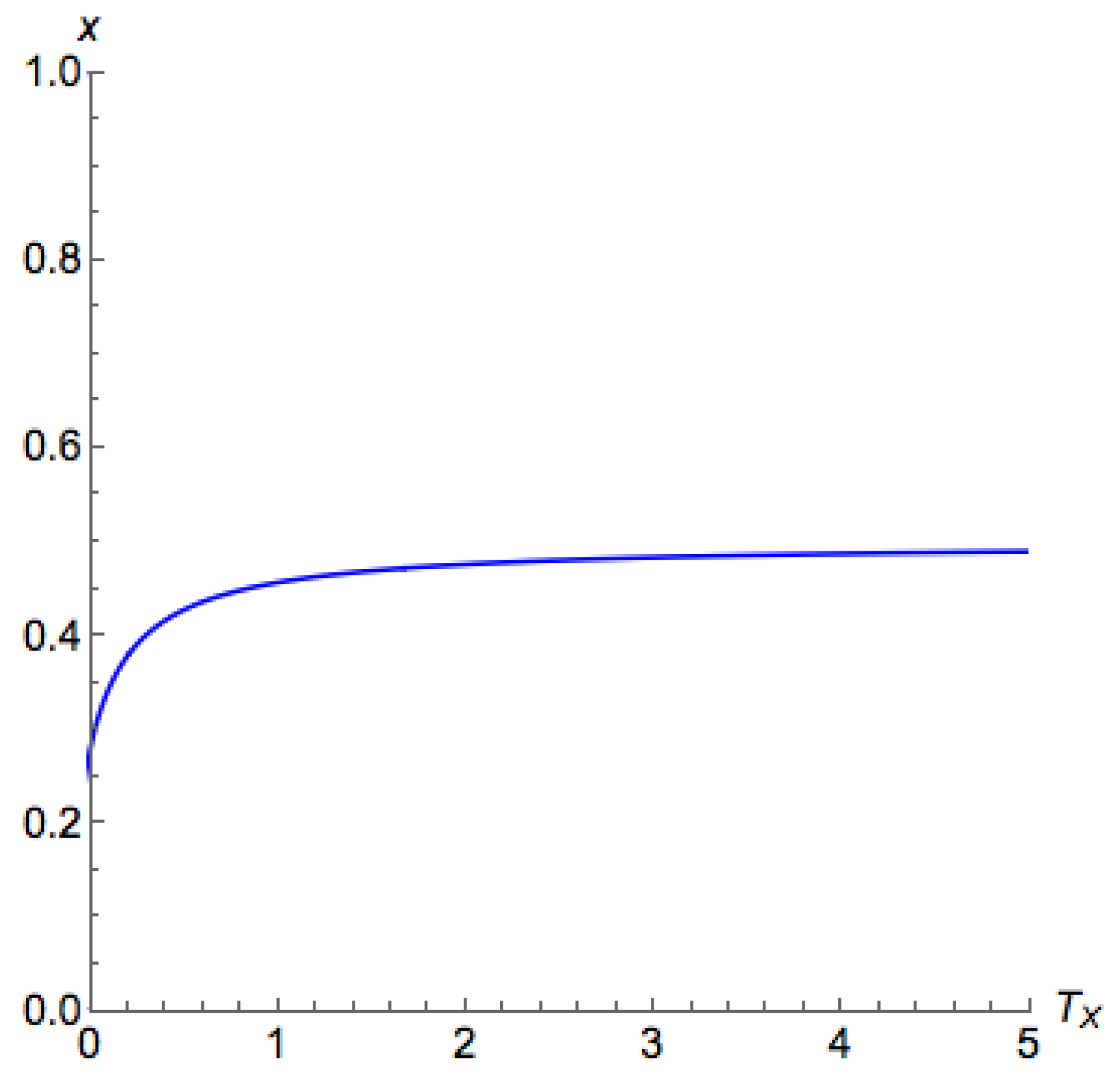
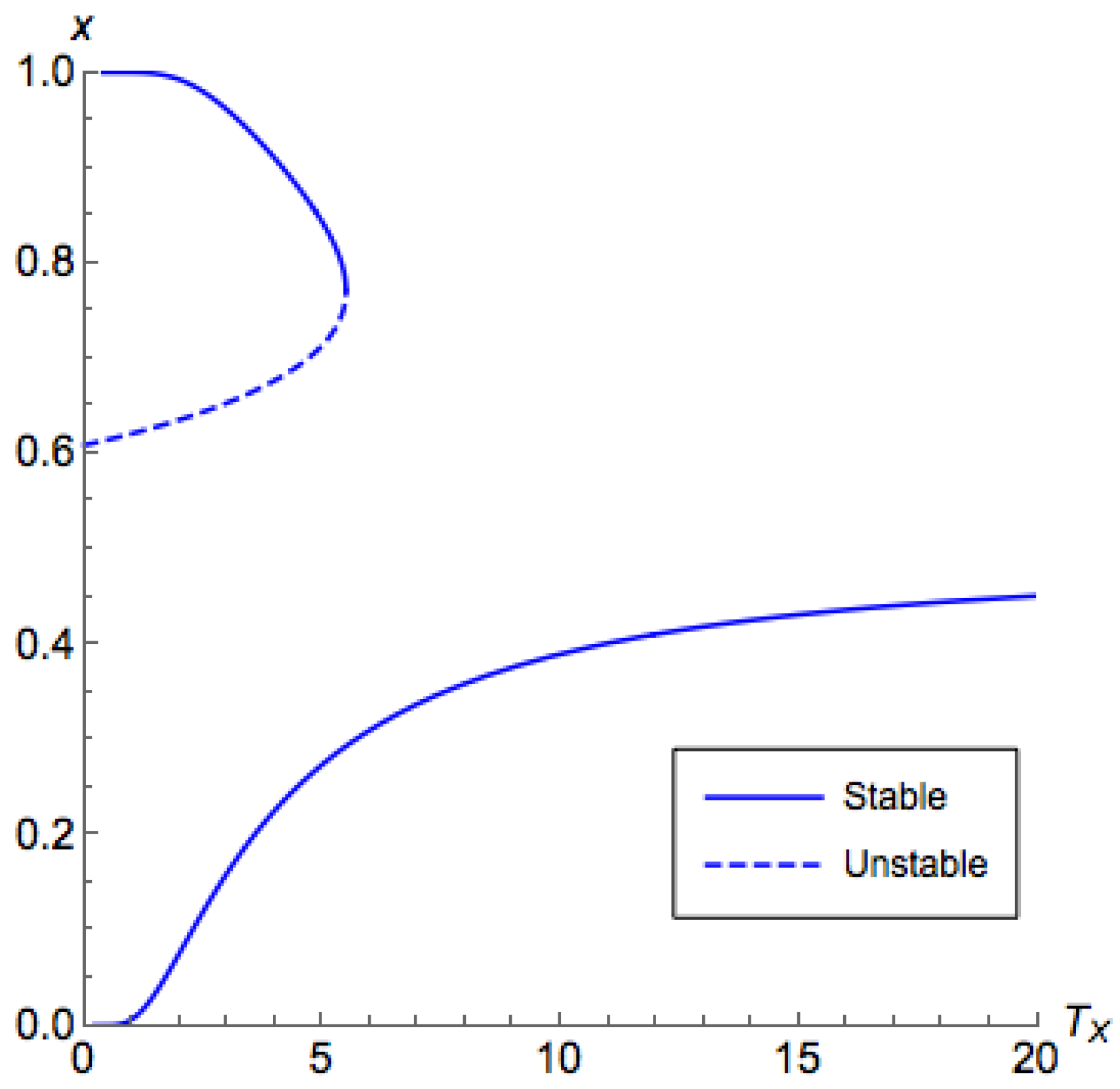
For Case 1a with , on the principal branch, the lower the , the closer x is to 1. We are able to show these monotonicity characteristics in Proposition A2, and they can be used to justify the stability owing to Lemma 1.
Proposition A2. In Case 1a, if , then for .
Proof. It suffices to show that
for
. Note that, according to Proposition A1, if
,
Since
is monotonically increasing when
,
for
. As a result,
; hence, we can see that, for
,
Consequently, for , ; hence, according to Lemma A2.
Proof of Part 1 of Theorem 3. According to Lemma 1, Proposition A2 implies that all is on the principal branch. This directly leads us to Part 1 of Theorem 3. ☐
Next, if we look into the region , we can find that, in this region, QREs appears only when and are low. This observation can be formalized in the proposition below. We can see that this proposition directly proves Parts 2 and 3 of Theorem 2, as well as Part 2 of Theorem 3.
Proposition A3. Consider Case 1a. Let and . The following statements are true for :
- 1.
If , then .
- 2.
If , then if and only if .
- 3.
for .
- 4.
If , then .
- 5.
If , then there is a nonnegative critical temperature such that for . If , then is given as , where is the unique solution to .
Proof. For the first and second part, consider any
and we can see that
Note that for , we have ; hence, .
From the above derivation, for all
such that
,
since
. Then
Further, when , . This implies that, for , . Since , and L is continuous, for . This implies the fourth part of the proposition.
Next, if we look at the derivative of
,
We can see that any critical point in must satisfy . When , , and . If , then . Hence, there is exactly one critical point for for , which is a local maximum for . If , then we can see that is always negative, in which case the critical temperature is zero. ☐
The results in Proposition A3 not only apply for the case but also general cases about the characteristics on . According to this proposition, we can conclude the following for the case , as well as the case when :
The temperature determines whether there is a branch appears in .
There is some critical temperature . If we raise above , then the system is always on the principal branch.
The critical temperature is given as the solution to the equality .
When there is a positive critical temperature, though it has no closed form solution, we can perform a binary search to look for that satisfies .
Another result we are able to obtain from Proposition A3 is that the principal branch for Case 1a when lies on .
Proof of Part 2 of Theorem 1. First, we note that is meaningful only when , for which case we always have . From Proposition A3, we can see that for , we have ; hence, for . From Proposition A1, we already have . Additionally, it is easy to see that . As a result, since is continuously differentiable over , for any , there exists such that . ☐
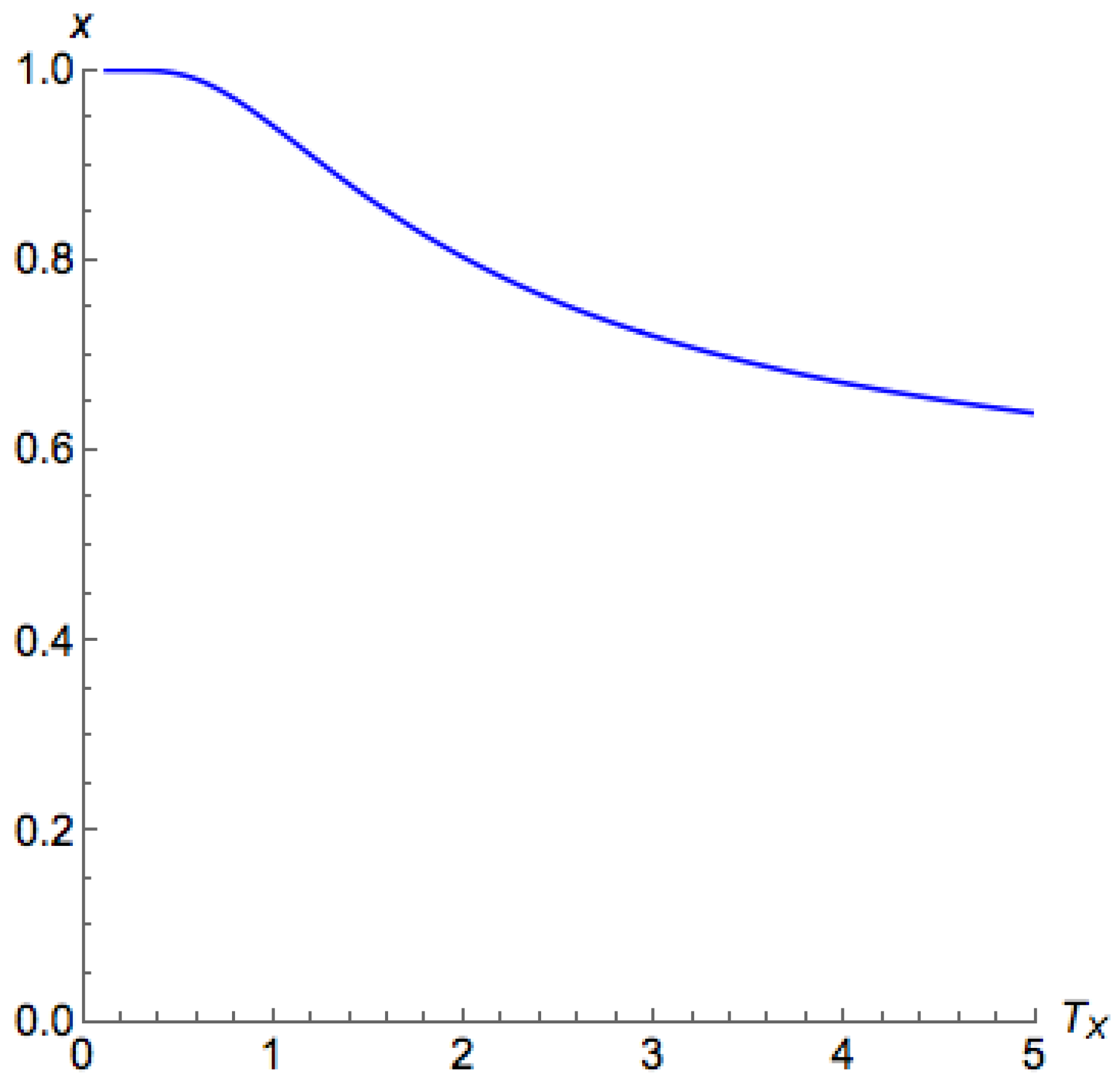
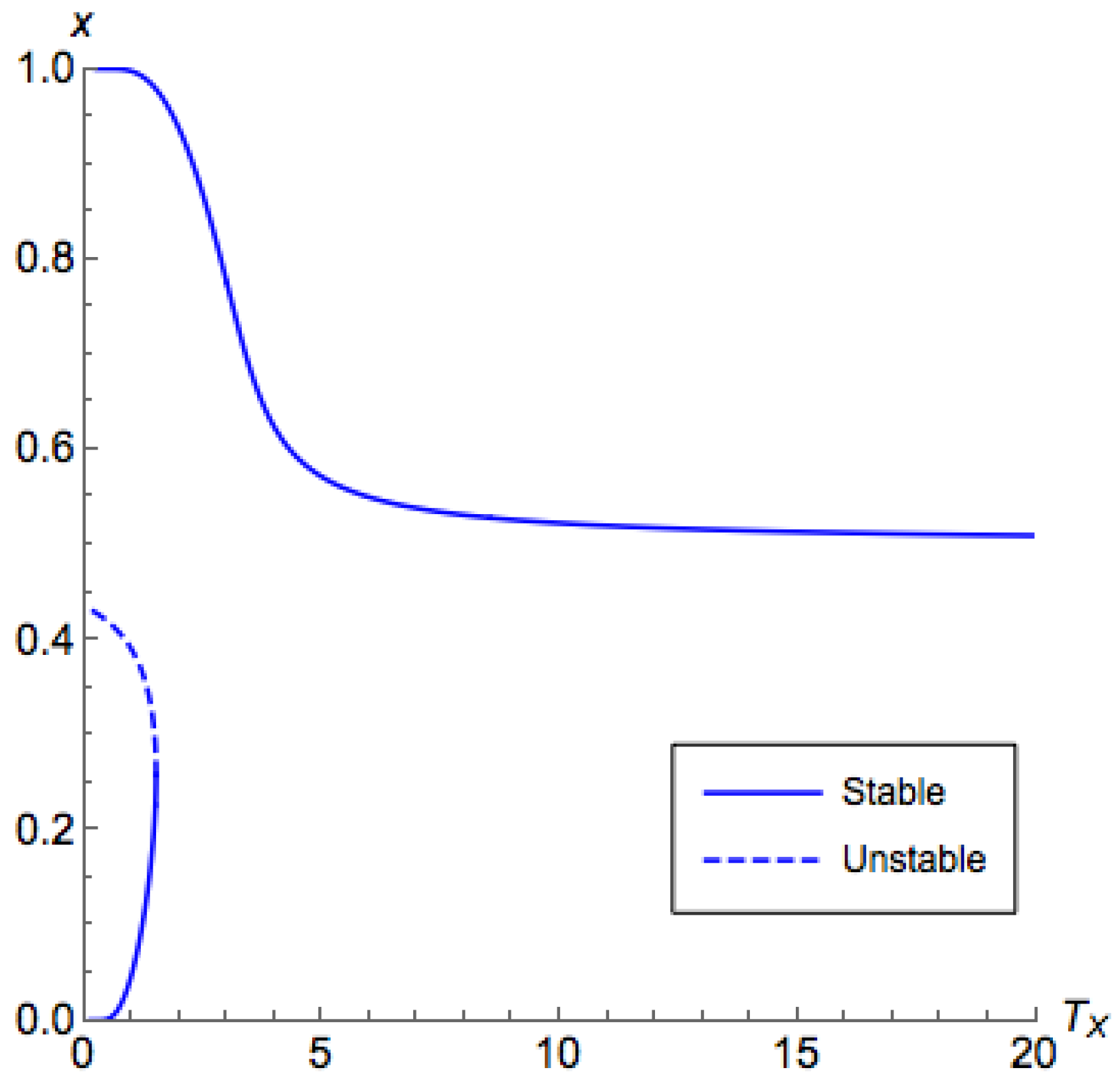
What remains to be shown is the characteristics on the side
when
. In
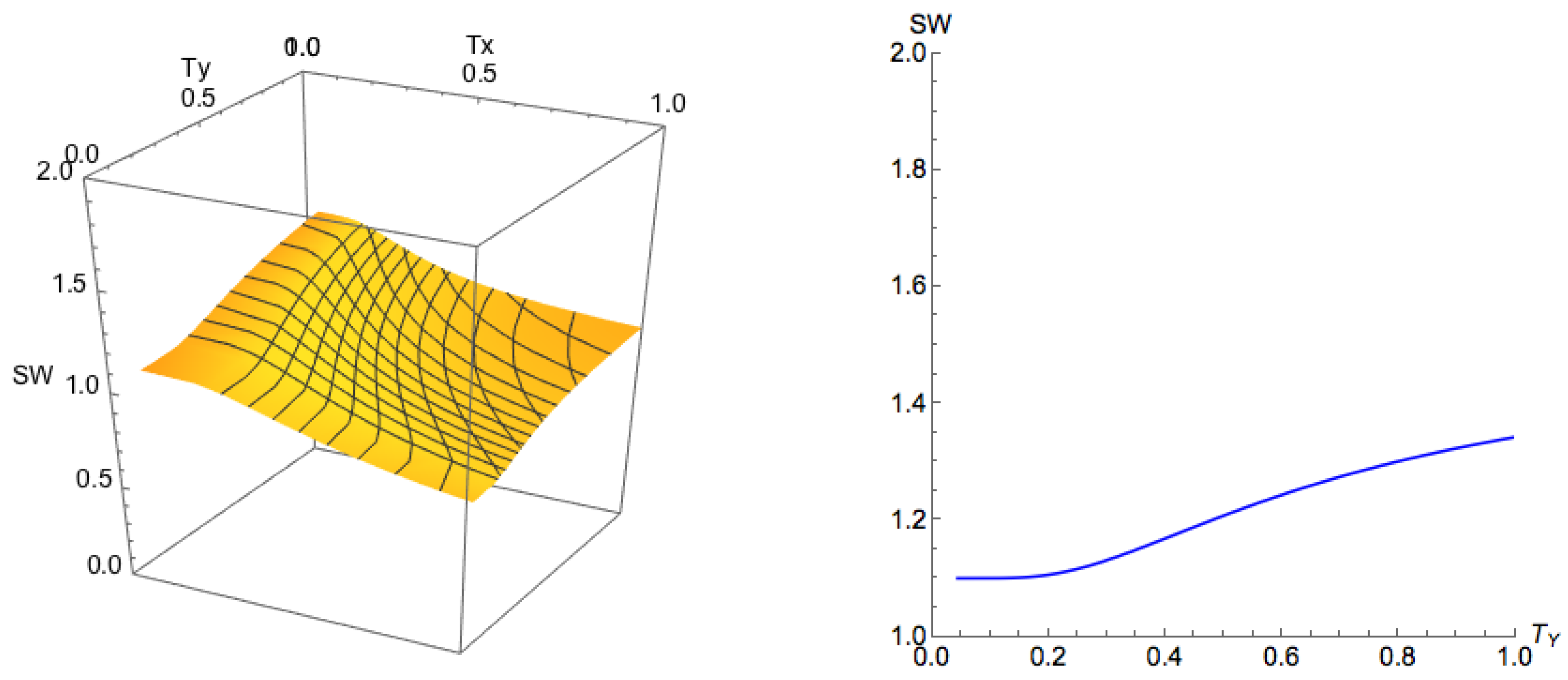
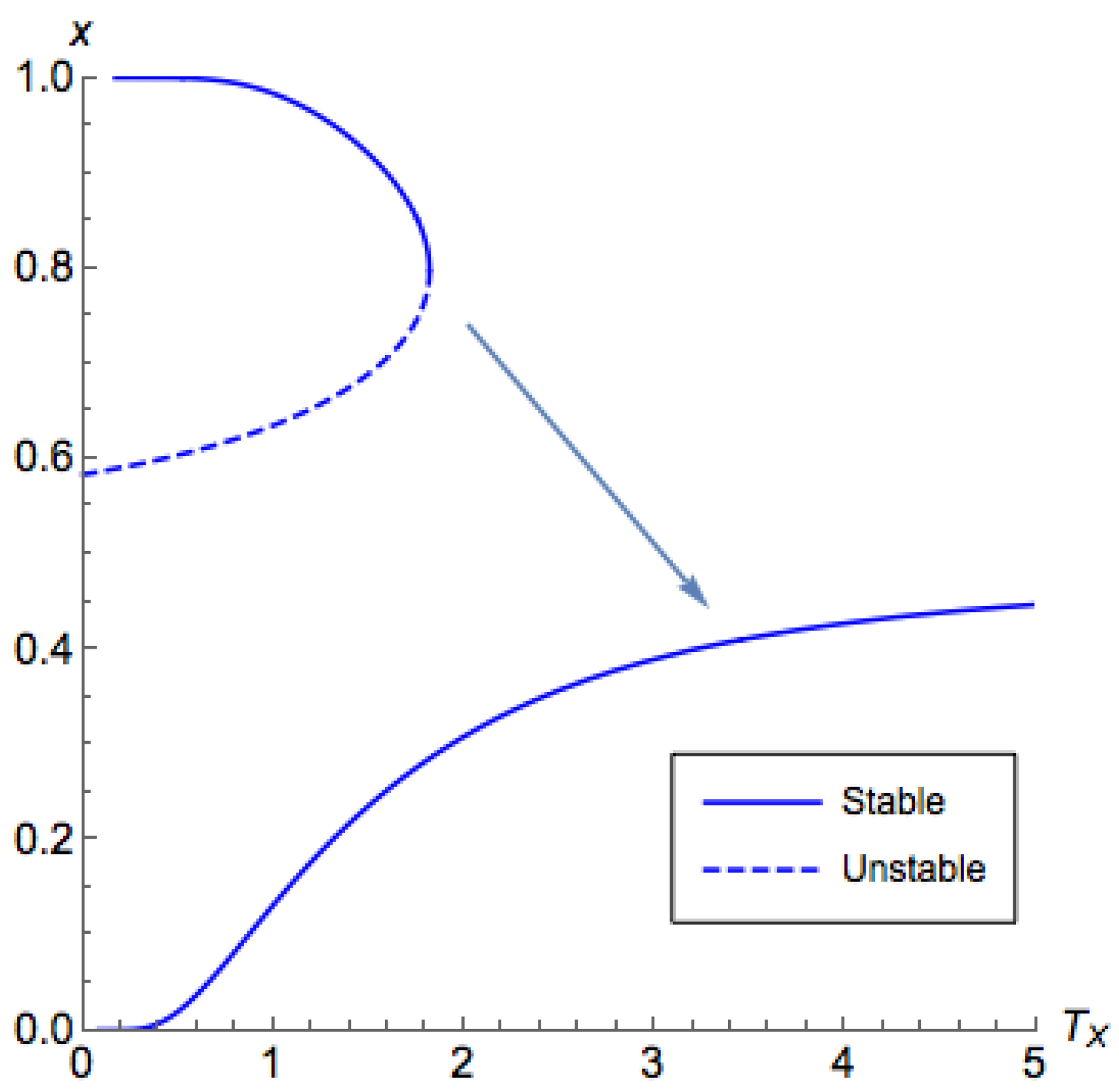
Figure 4 and
Figure 5, for low
, the branch on the side
demonstrated a similar behavior as what we have shown in Proposition A3 for the side
. However, for a high
, while we still can find that
contains the principal branch, the principal branch is not continuous. These observations are formalized in the following proposition. From this proposition, the proof of Part 4 of Theorem 2 directly follows.
Proposition A4. Consider Case 1a with . Let and . The following statements are true for .
If , then .
If , then if and only if .
For , we have .
If , then there is a positive critical temperature such that for , given as , where is the unique solution of .
Proof. For the first part and the second part, consider
, and we can find that
Note that, for , . Additionally, if , then for all .
For the third part,
for all
and
. Thus,
For the fourth part, we can find that any critical point of
in
must be either
or satisfies the following equation:
Consider
. For
,
is strictly less than
. Additionally,
. Now,
and
. Next, we can see that
is monotonically decreasing with respect to
x for
by looking at its derivative:
As a result, there is some such that . This implies that has exactly one critical point for . Additionally, if , ; if , then . Therefore, is a local minimum for L.
From the above arguments, we can conclude that the shape of for is as follows:
There is a local maximum at , where .
L is decreasing on the interval , where is the unique solution to Equation (A7).
L is increasing on the interval . If , then .
Finally, we can claim that there is a unique solution to , and such a point gives a local maximum to . ☐
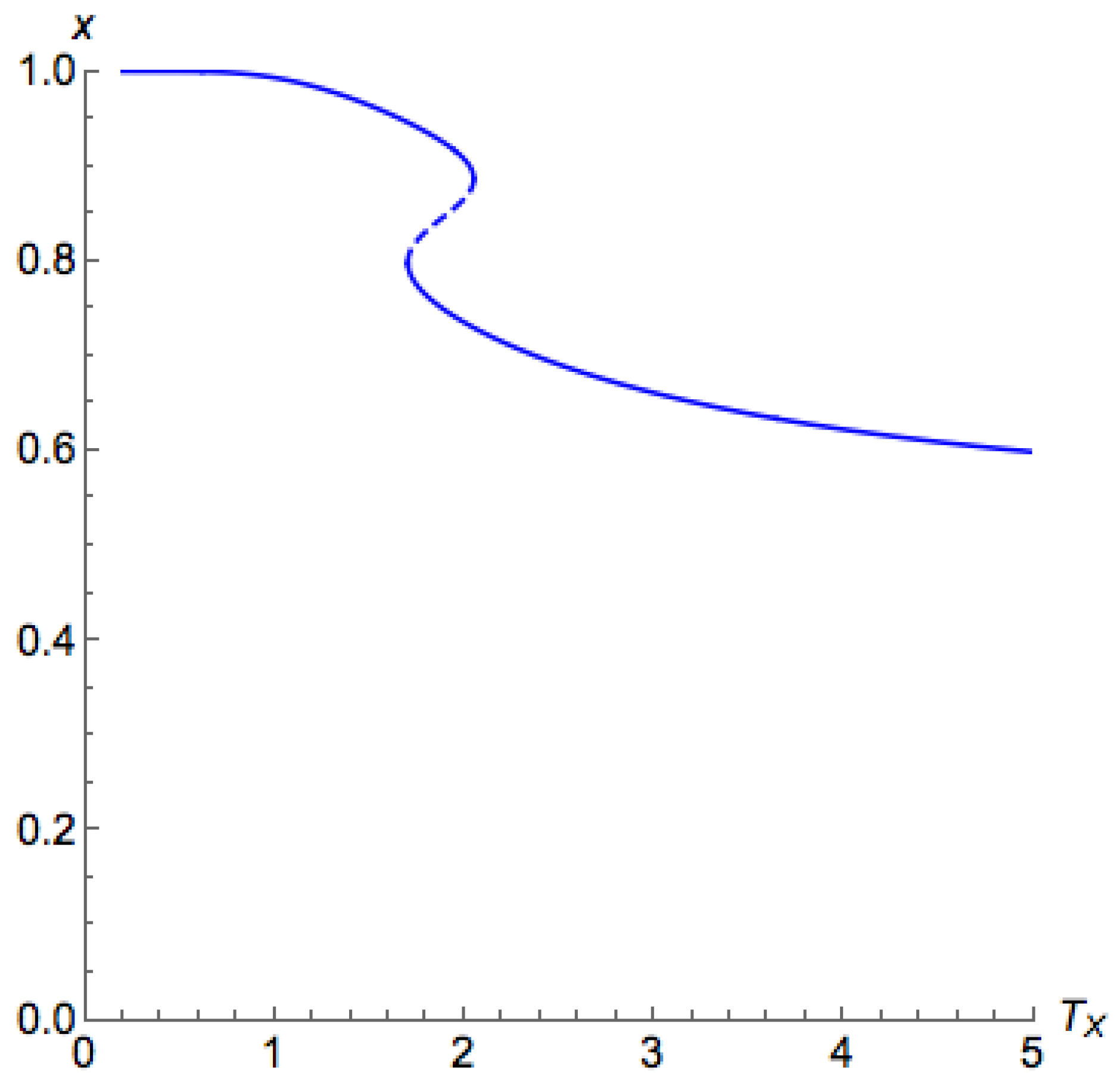
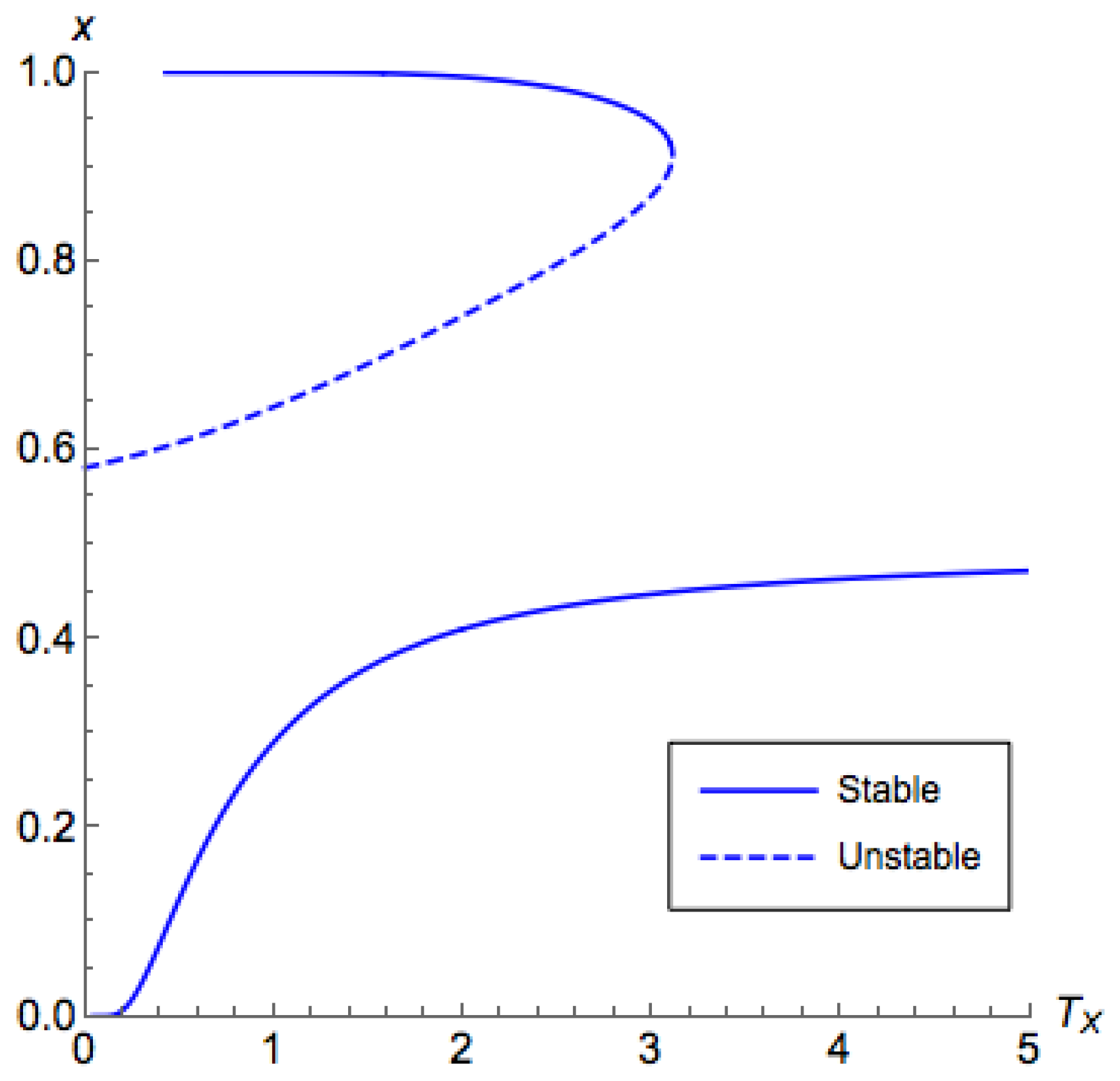
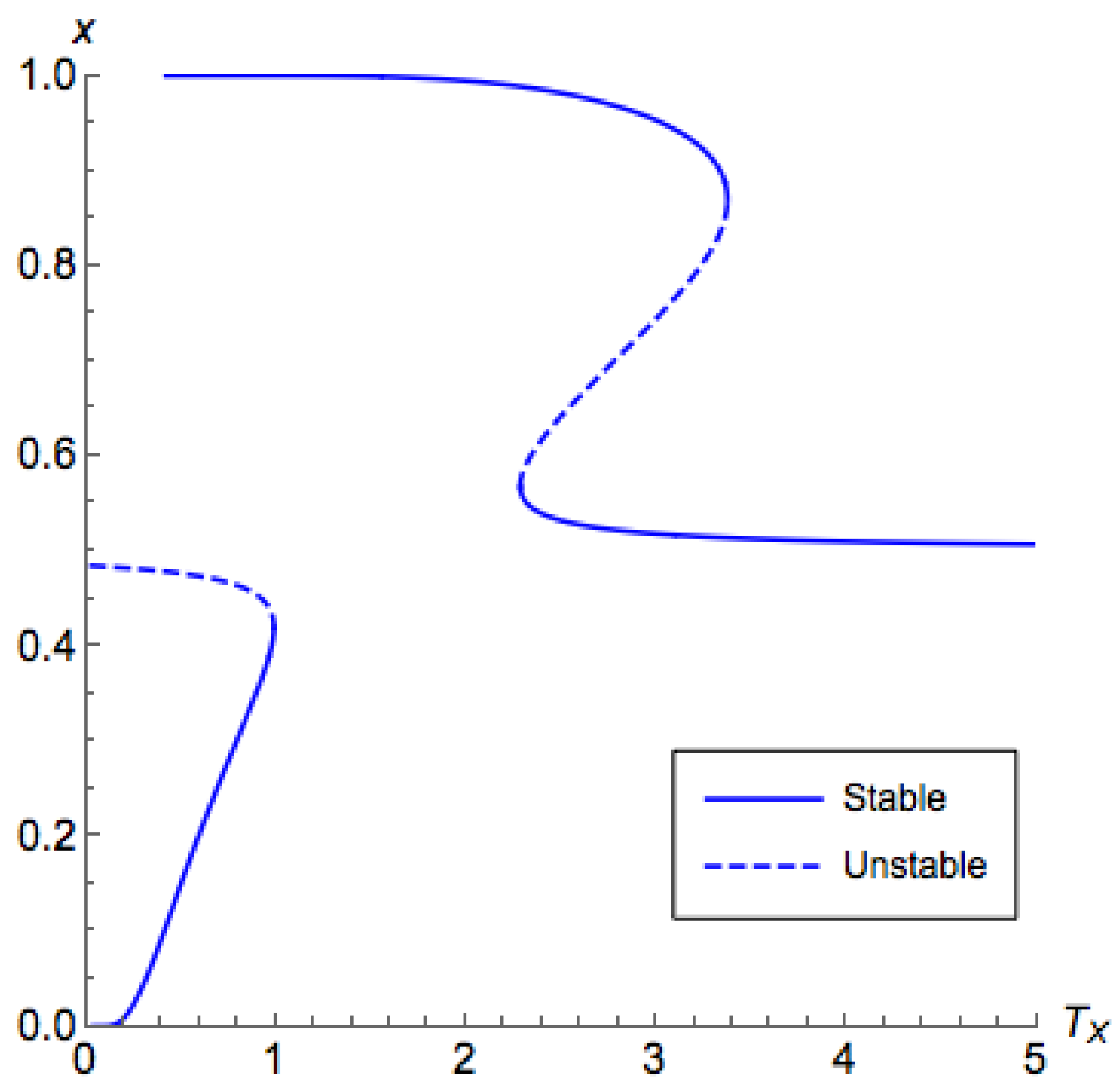
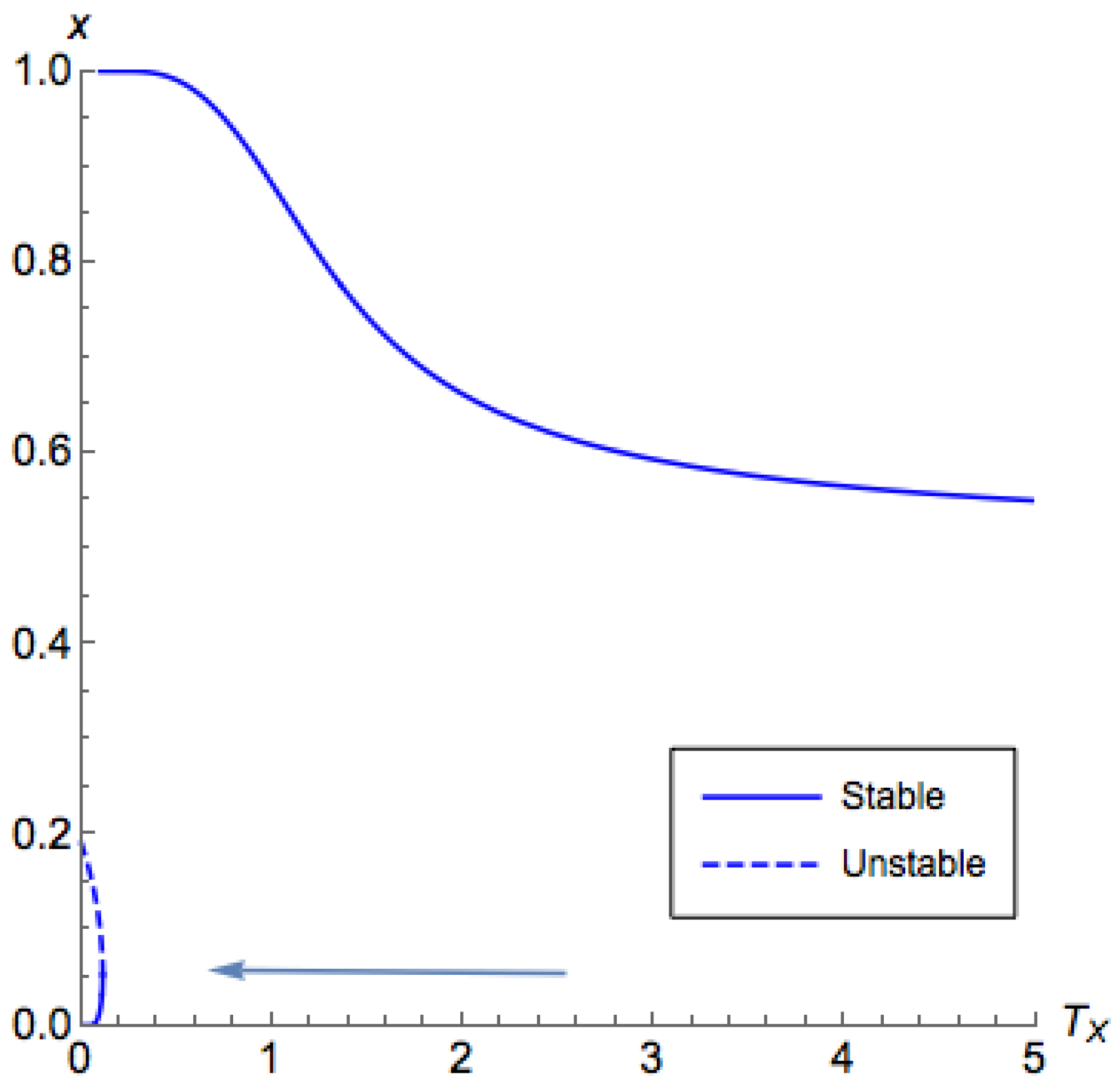
The above proposition suggests that, for
, we are able to use binary search to find the critical temperature. For
, unfortunately, with a similar argument of Proposition A4, we can find that there are potentially at most two critical points for
on
, as shown in
Figure 5, which may induce an unstable segment between two stable segments. This also proves Part 3 of Theorem 3.
Now, we have enough materials to prove the remaining statements in
Section 4.3.
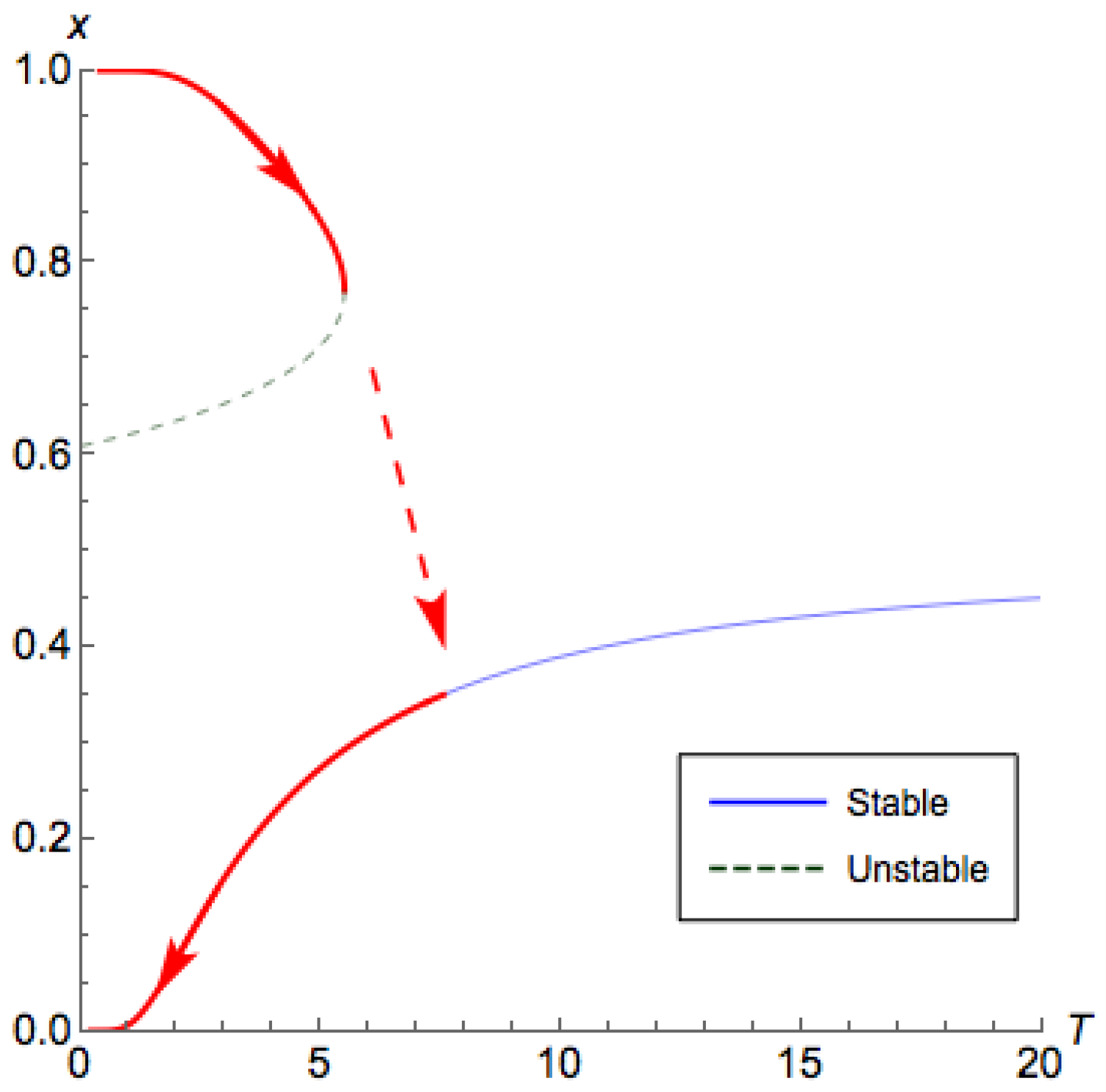
Proof of Parts 1, 5, and 6 of Theorem 2, Part 4 of Theorem 3. For , by Proposition A3, we can conclude that, for , we have , for which the QREs are stable by Lemma 1. With similar arguments, we can conclude that the QREs on are unstable. Additionally, given , the stable QRE and the unstable that satisfies appear in pairs. For , with the same technique and by Proposition A4, we can claim that the QREs in are unstable, while the QREs in are stable. This proves the first part of Theorem 2 and Part 4 of Theorem 3.
Parts 5 and 6 of Theorem 2 are corollaries of Part 5 of Proposition A3 and Part 4 of Proposition A4. ☐