Game Theory of Pollution: National Policies and Their International Effects
Abstract
1. Introduction
2. Models
2.1. Basics
- Nash game: Country i minimizes pollution costs (2) with respect to its investment at each time , where other countries are assumed to do the same (Section 2.2.1).
- Countries imitate behavior of their neighbors independently of the neighbors’ costs (Section 2.2.2).
- Countries imitate the investments of their neighbors dependent on the neighbors’ costs such that more profitable neighbors influence a country in a stronger way.
2.2. Different Variants of the Model
2.2.1. Nash Game: Optimizing Individual Costs
2.2.2. Basic Imitation Behavior
2.2.3. More Advanced Imitation Behavior
2.3. Stability Analysis
3. Case Studies
3.1. Implementation
- Nash game: When each country wants to minimize the present value of its own costs, the simulation starts with initial values for the pollution stock . Then, we use a fixed point approach to compute for each country such that the costs become minimal for each country . The optimization itself is done by a software implementation called jcobyla [48]. While for some specific scenarios we can calculate analytically, especially for larger problems, we cannot find analytically that easily. The software implementation is based on Powell’s numerical optimization implementation for constrained problems with unknown derivatives of the objective function [49]. We proceed with the next computation step by computing pollution , with discretization of the differential Equation (1) via a fourth-order Runge-Kutta approach with step size 0.01.
- Imitation game: Considering that the countries imitate other countries’ behavior, we start a computation step with values for and from the Nash game for the initial phase. Using those values, we can compute the investment into clean policies by applying either Formula (5) or (6). Then, we again use a fourth-order Runge-Kutta approach to compute the pollution stock. Afterwards, we continue with the next computation step until we reach the defined number of total computation steps corresponding to time T.
3.2. Settings of the Case Studies
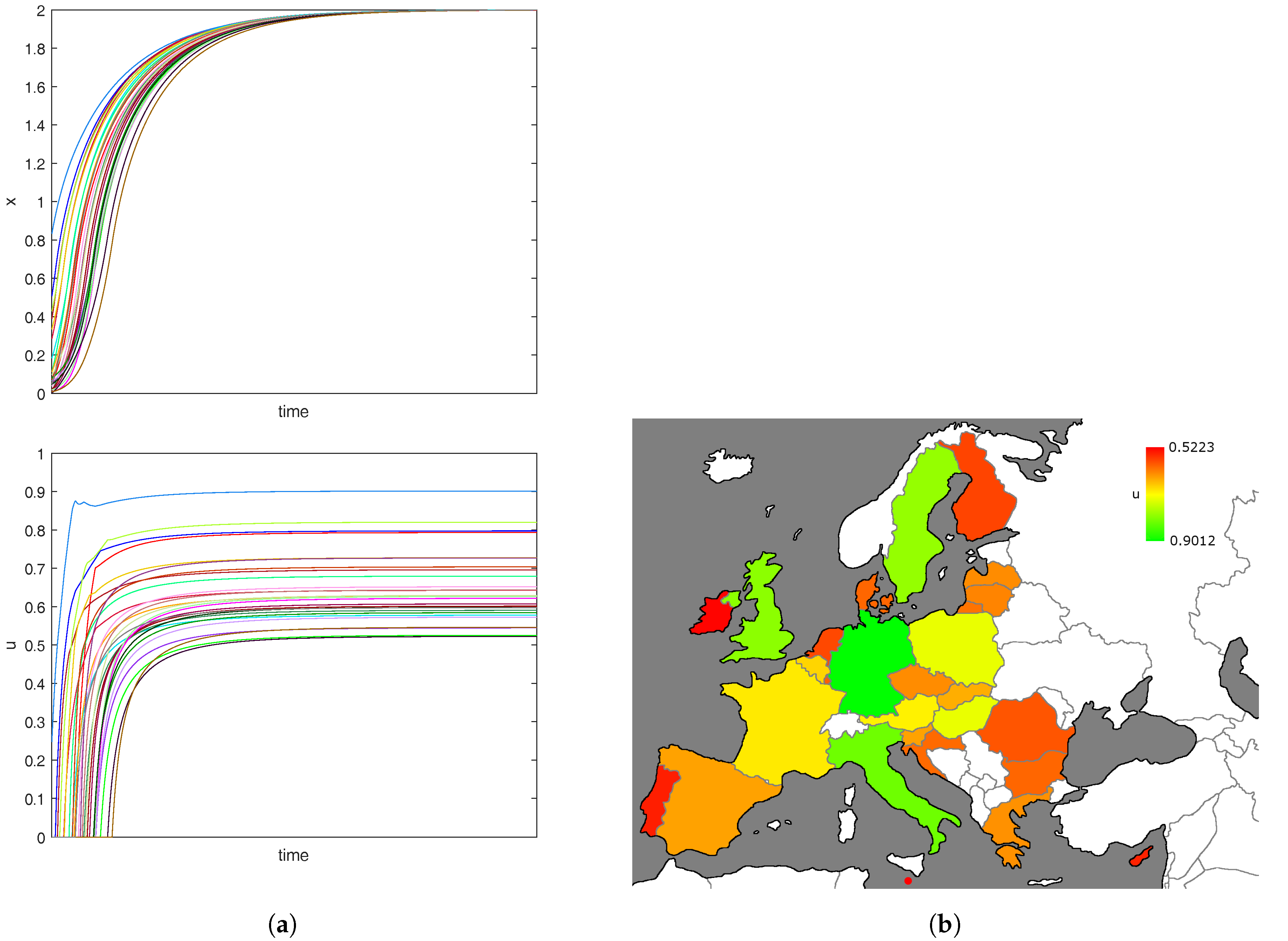
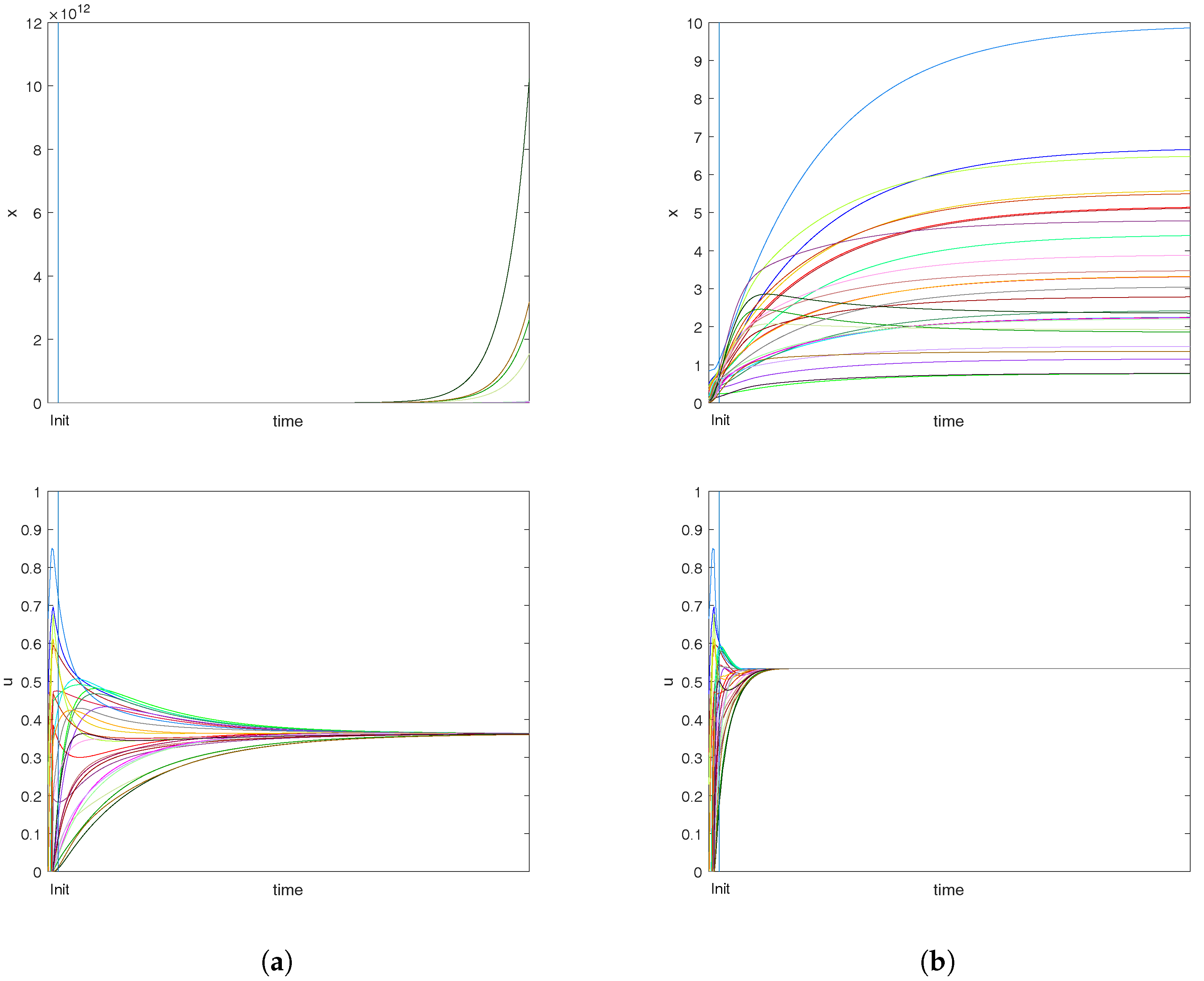
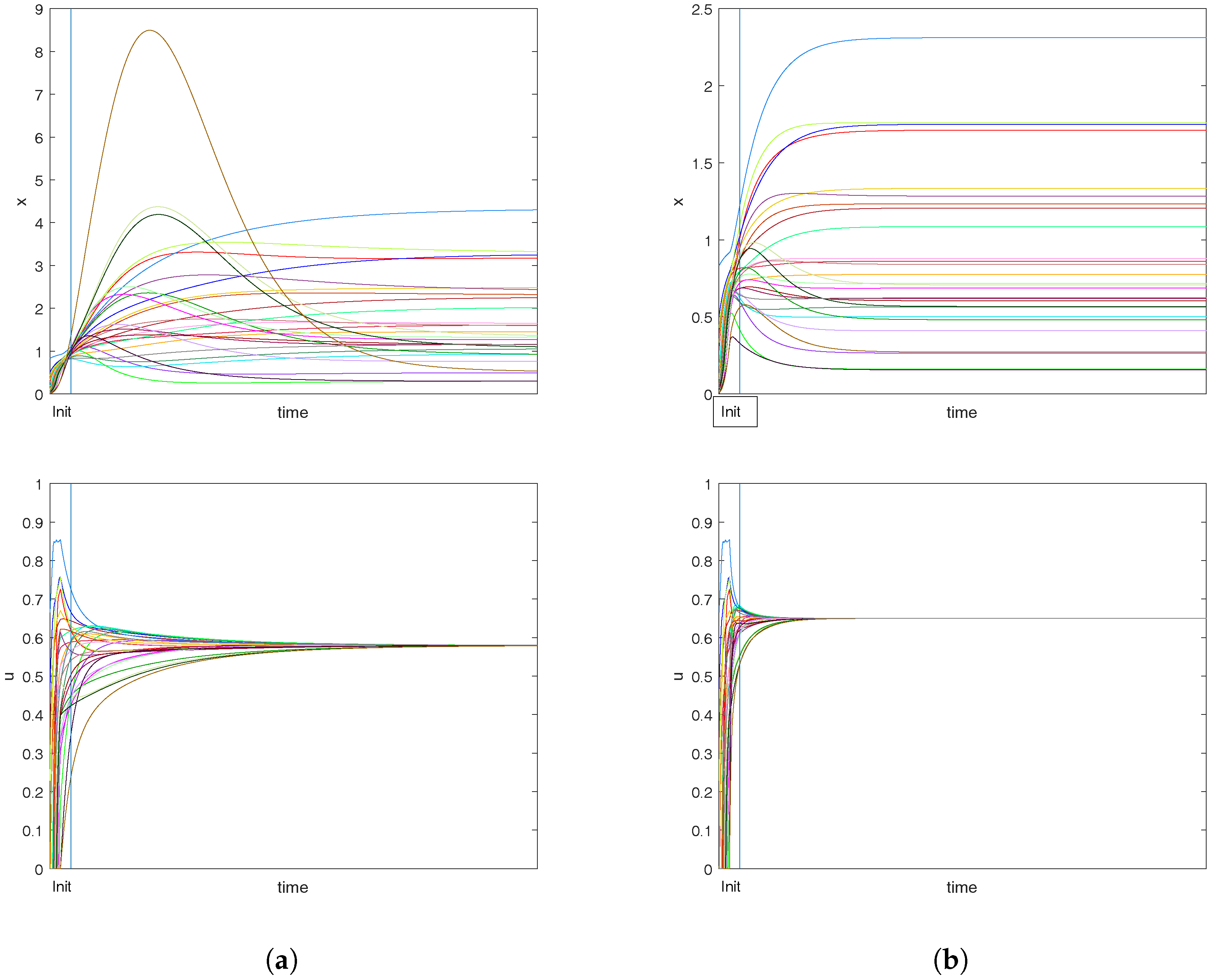
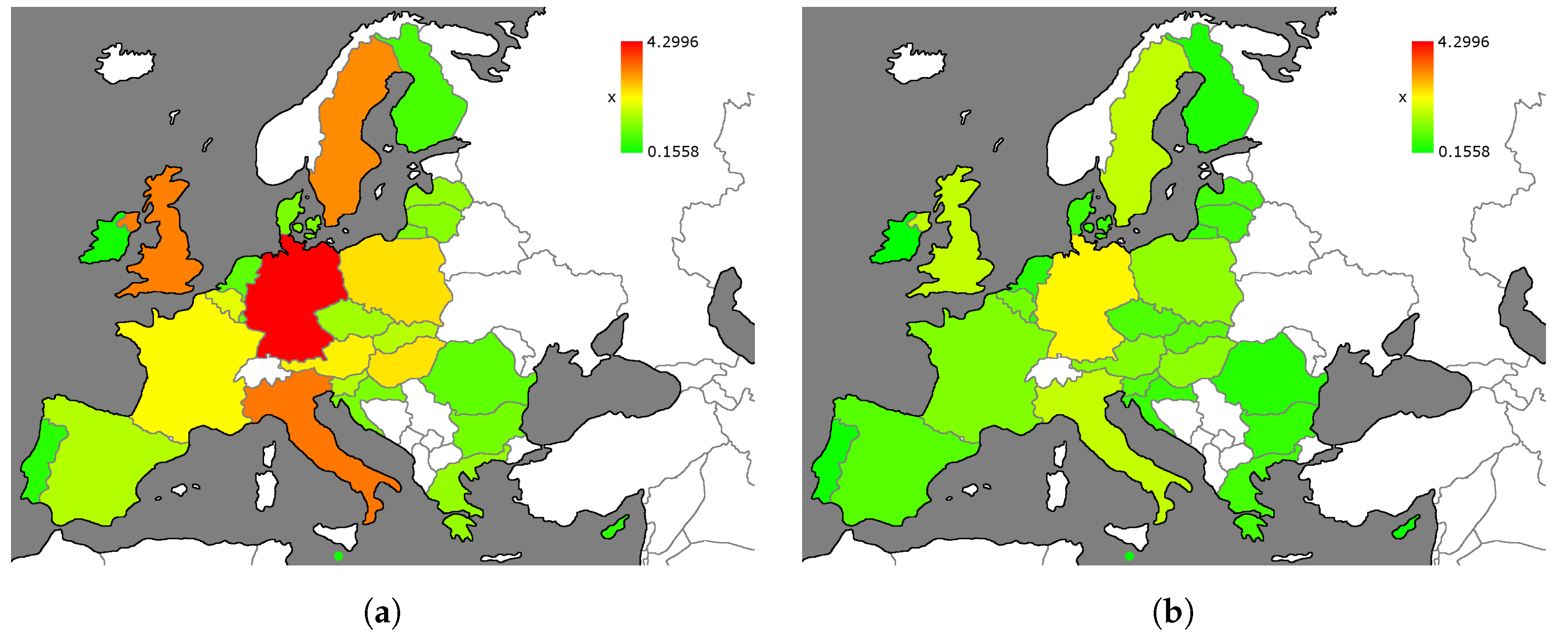
3.3. Optimizing Individual Costs
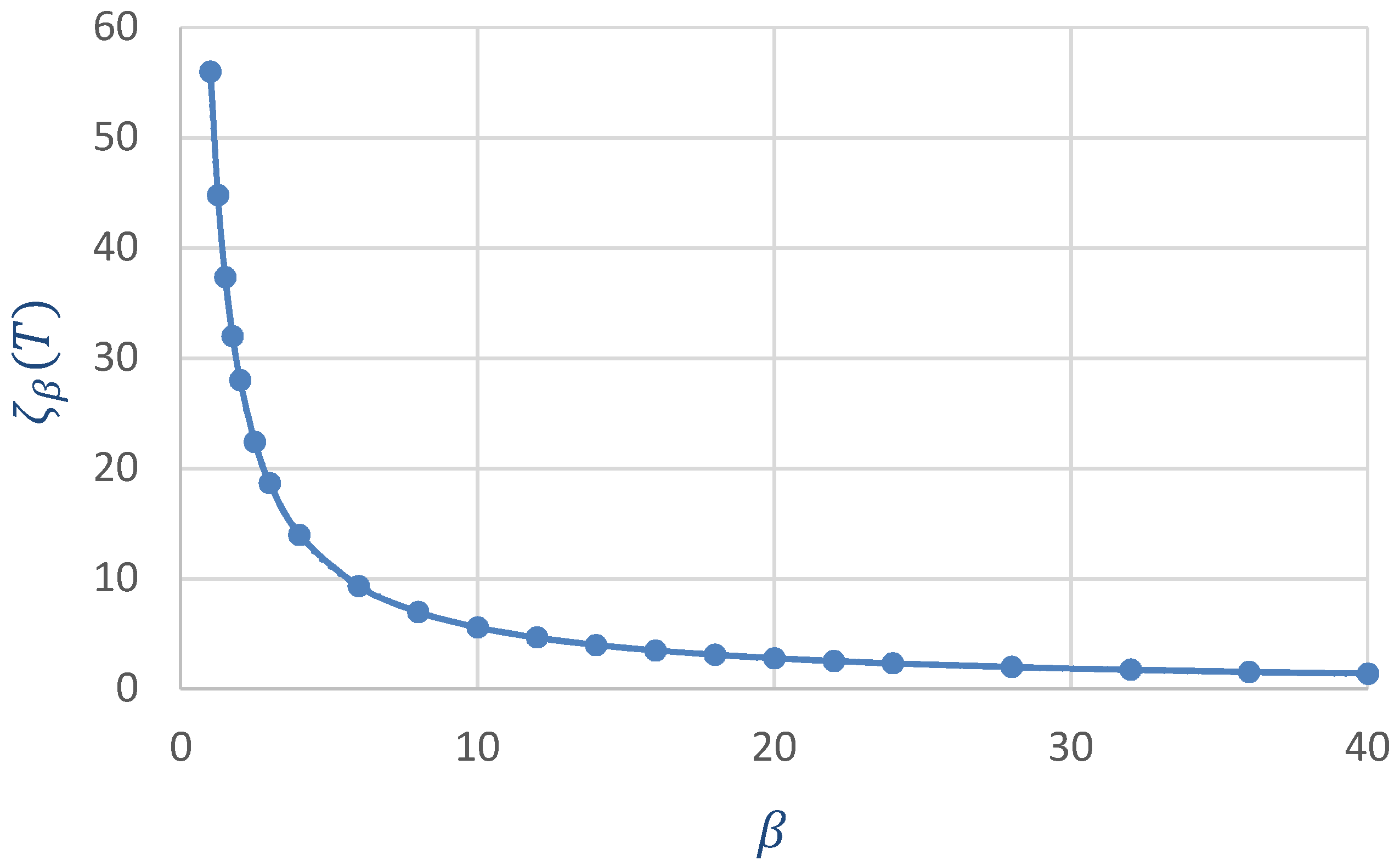
Influence of the External Control Parameter on Pollution Costs
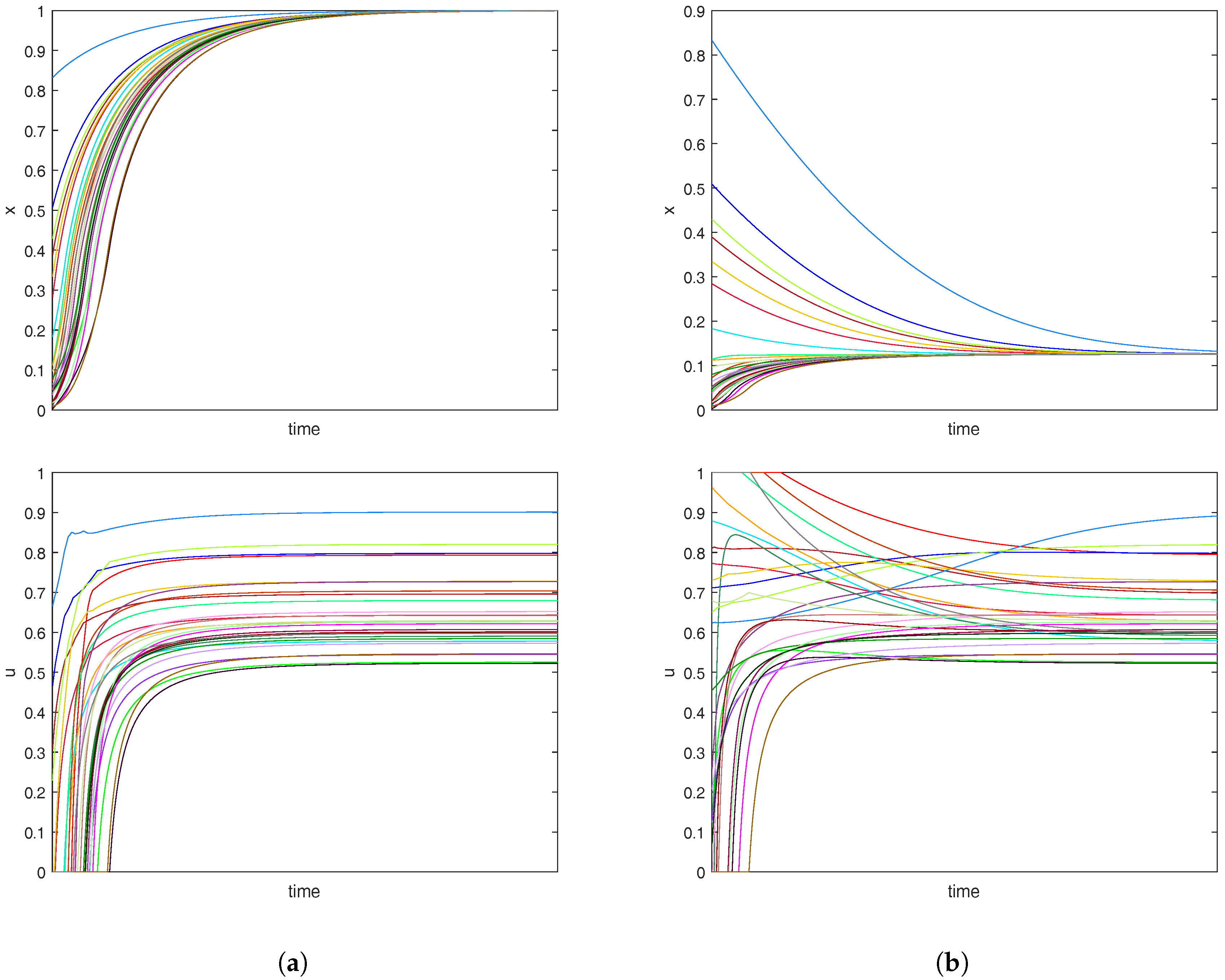
3.4. Imitation Behavior
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schandl, H.; Hatfield-Dodds, S.; Wiedmann, T.; Geschke, A.; Cai, Y.; West, J.; Newth, D.; Baynes, T.; Lenzen, M.; Owen, A. Decoupling global environmental pressure and economic growth: Scenarios for energy use, materials use and carbon emissions. J. Clean. Prod. 2016, 132, 45–56. [Google Scholar] [CrossRef]
- European Commission. Green Paper: A 2030 Framework for Climate and Energy Policies; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- Ferreira, H.L.; Staňková, K.; Lopes, J.; Slotweg, J.; Kling, W.L. Dual technology energy storage system applied to two complementary electricity markets using a weekly differentiated approach. J. Energy Storage 2017, 12, 226–242. [Google Scholar] [CrossRef]
- European Commission. Communication From the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions: Towards an EU Criminal Policy: Ensuring the Effective Implementation of EU Policies Through Criminal Law; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Ming, Z.; Kun, Z.; Daoxin, L. Overall review of pumped-hydro energy storage in China: Status quo operation mechanism and policy barriers. Renew. Sustain. Energy Rev. 2013, 17, 35–43. [Google Scholar] [CrossRef]
- Esteban, M.; Portugal-Pereira, J. Post-disaster resilience of a 100% renewableenergy system in Japan. Energy 2014, 68, 756–764. [Google Scholar] [CrossRef]
- Mason, I.G.; Page, S.C.; Williamson, A.G. Security of supply, energy spillage control and peaking options within a 100% renewable electricity system for New Zealand. Energy Policy 2013, 60, 324–333. [Google Scholar] [CrossRef]
- Eyer, J.; Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide; Sandia Report 2010–0815; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2010.
- Rastler, D.M. Electricity Energy Storage Technology Options—A White Paper Primer on Applications, Costs and Benefits; Technical Report; Eletric Power Research Institute: Palo Alto, CA, USA, 2010. [Google Scholar]
- Dursun, B.; Alboyaci, B. The contribution of wind-hydro pumped storage systems in meeting Turkey, selectric energy demand. Renew. Sustain. Energy Rev. 2010, 14, 1979–1988. [Google Scholar] [CrossRef]
- Lelieveld, J.; Berresheim, H.; Borrmann, S.; Crutzen, P.J.; Dentener, F.J.; Fischer, H.; Feichter, J.; Flatau, P.J.; Heland, J.; Holzinger, R.; et al. Global Air Pollution Crossroads over the Mediterranean. Science 2002, 298, 794–799. [Google Scholar] [CrossRef] [PubMed]
- Stohl, A.; Eckhardt, S.; Forster, C.; James, P.; Spichtinger, N. On the pathways and timescales of intercontinental air pollution transport. J. Geophys. Res. Atmos. 2002, 107, ACH 6-1–ACH 6-17. [Google Scholar] [CrossRef]
- Nkuiya, B. Transboundary pollution game with potential shift in damages. J. Environ. Econ. Manag. 2015, 72, 1–14. [Google Scholar] [CrossRef]
- United Nations. Kyoto Protocol to the United Nations Framework Convention on Climate Change; United Nations: New York, NY, USA, 1998. [Google Scholar]
- United Nations. United Nations Framework Convention on Climate Change; United Nations: New York, NY, USA, 1992. [Google Scholar]
- Jänicke, M. Trend-setters in environmental policy: The character and role of pioneer countries. Eur. Environ. 2005, 15, 129–142. [Google Scholar] [CrossRef]
- Liefferink, D.; Andersen, M.S. Strategies of the ’green’ member states in EU environmental policy-making. J. Eur. Public Policy 1998, 5, 254–270. [Google Scholar] [CrossRef]
- Andresen, S.; Agrawala, S. Leaders, pushers and laggards in the making of the climate regime. Glob. Environ. Chang. 2002, 12, 41–51. [Google Scholar] [CrossRef]
- US Environmental Protection Agency. Federal Implementation Plans: Interstate Transport of Fine Particulate Matter and Ozone and Correction of SIP Approvals; US Environmental Protection Agency: Washington, DC, USA, 2011.
- Bruvoll, A.; Larsen, B.M. Greenhouse gas emissions in Norway: Do carbon taxes work? Energy Policy 2004, 32, 493–505. [Google Scholar] [CrossRef]
- Wier, M.; Birr-Pedersen, K.; Jacobsen, H.K.; Klok, J. Are CO2 taxes regressive? Evidence from the Danish experience. Ecol. Econ. 2005, 52, 239–251. [Google Scholar] [CrossRef]
- European Parliament; Council of the European Union. Regulation (EU) No 333/2014 of the European Parliament and of the Council; European Parliament; Council of the European Union: Strasbourg, France, 2014. [Google Scholar]
- Boogaard, H.; Janssen, N.A.; Fischer, P.H.; Kos, G.P.; Weijers, E.P.; Cassee, F.R.; van der Zee, S.C.; de Hartog, J.J.; Meliefste, K.; Wang, M.; et al. Impact of low emission zones and local traffic policies on ambient air pollution concentrations. Sci. Total Environ. 2012, 435–436, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Ellison, R.B.; Greaves, S.P.; Hensher, D.A. Five years of London’s low emission zone: Effects on vehicle fleet composition and air quality. Transp. Res. Part D Transp. Environ. 2013, 23, 25–33. [Google Scholar] [CrossRef]
- Davis, L.W. The Effect of Driving Restrictions on Air Quality in Mexico City. J. Political Econ. 2008, 116, 38–81. [Google Scholar] [CrossRef]
- Akimoto, H. Global Air Quality and Pollution. Science 2003, 302, 1716–1719. [Google Scholar] [CrossRef] [PubMed]
- Long, N.V. Pollution control: A differential game approach. Ann. Oper. Res. 1992, 37, 283–296. [Google Scholar] [CrossRef]
- Dockner, E.J.; Long, N.V. International Pollution Control: Cooperative versus Noncooperative Strategies. J. Environ. Econ. Manag. 1993, 25, 13–29. [Google Scholar] [CrossRef]
- Jørgensen, S.; Zaccour, G. Incentive equilibrium strategies and welfare allocation in a dynamic game of pollution control. Automatica 2001, 37, 29–36. [Google Scholar] [CrossRef]
- Breton, M.; Sbragia, L.; Zaccour, G. A Dynamic Model for International Environmental Agreements. Environ. Resour. Econ. 2010, 45, 25–48. [Google Scholar] [CrossRef]
- Harford, J.D. Firm behavior under imperfectly enforceable pollution standards and taxes. J. Environ. Econ. Manag. 1978, 5, 26–43. [Google Scholar] [CrossRef]
- Krass, D.; Nedorezov, T.; Ovchinnikov, A. Environmental Taxes and the Choice of Green Technology. Prod. Oper. Manag. 2013, 22, 1035–1055. [Google Scholar] [CrossRef]
- Barrett, S. Self-Enforcing International Environmental Agreements. Oxf. Econ. Pap. 1994, 46, 878–894. [Google Scholar] [CrossRef]
- Nkuiya, B. The Effects of the Length of the Period of Commitment on the Size of Stable International Environmental Agreements. Dyn. Games Appl. 2012, 2, 411–430. [Google Scholar] [CrossRef]
- Nkuiya, B.; Marrouch, W.; Bahel, E. International Environmental Agreements under Endogenous Uncertainty. J. Public Econ. Theory 2015, 17, 752–772. [Google Scholar] [CrossRef]
- Miller, S.; Nkuiya, B. Coalition formation in fisheries with potential regime shift. J. Environ. Econ. Manag. 2016, 79, 189–207. [Google Scholar] [CrossRef]
- Lazkano, I.; Marrouch, W.; Nkuiya, B. Adaptation to climate change: How does heterogeneity in adaptation costs affect climate coalitions? Environ. Dev. Econ. 2016, 21, 812–838. [Google Scholar] [CrossRef]
- Garrab, S.; Breton, M. The impact of signatories’ leadership in environmental agreements. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–4. [Google Scholar]
- Amann, M.; Bertok, I.; Borken-Kleefeld, J.; Cofala, J.; Heyes, C.; Höglund-Isaksson, L.; Klimont, Z.; Nguyen, B.; Posch, M.; Rafaj, P.; et al. Cost-effective control of air quality and greenhouse gases in Europe: Modeling and policy applications. Environ. Model. Softw. 2011, 26, 1489–1501. [Google Scholar] [CrossRef]
- Turnock, S.T.; Butt, E.W.; Richardson, T.B.; Mann, G.W.; Reddington, C.L.; Forster, P.M.; Haywood, J.; Crippa, M.; Janssens-Maenhout, G.; Johnson, C.E.; et al. The impact of European legislative and technology measures to reduce air pollutants on air quality, human health and climate. Environ. Res. Lett. 2016, 11, 024010. [Google Scholar] [CrossRef]
- Björnerstedt, J.; Weibull, J. Nash Equilibrium and Evolution by Imitation; Working Paper Series 407; Research Institute of Industrial Economics: Stockholm, Sweden, 1994. [Google Scholar]
- Selten, R.; Ostmann, A. Imitation Equilibrium; Bonn Econ Discussion Papers 16/2000; Bonn Graduate School of Economics (BGSE), University of Bonn: Bonn, Germany, 2000. [Google Scholar]
- Apesteguia, J.; Huck, S.; Oechssler, J. Imitation—Theory and experimental evidence. J. Econ. Theory 2007, 136, 217–235. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. A survey of consensus problems in multi-agent coordination. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 1859–1864. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ranjbar-Sahraei, B.; Bou-Ammar, H.; Bloembergen, D.; Tuyls, K.; Weiss, G. Evolution of Cooperation in Arbitrary Complex Networks. In Proceedings of the 13th International Conference on Autonomous Agents and Multiagent Systems (AAMAS2014), Paris, France, 5–9 May 2014; pp. 677–684. [Google Scholar]
- Ranjbar-Sahraei, B.; Bou-Ammar, H.; Bloembergen, D.; Tuyls, K.; Weiss, G. Theory of Cooperation in Complex Social Networks. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Québec, Canada, 27–31 July 2014; pp. 1471–1477. [Google Scholar]
- Gustafsson, A. Jcobyla. Available online: https://github.com/cureos/jcobyla (accessed on 13 July 2017).
- Powell, M.J.D. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J.P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar]
- Charney, J.I.; Alexander, L.M.; Smith, R.W.; Colson, D.A. International Maritime Boundaries; Martinus Nijhoff Publishers: Dordrecht, The Netherlands; London, UK, 2011. [Google Scholar]
- Boden, T.A.; Andres, R.J.; Marland, G. Global, Regional, and National Fossil-Fuel CO2 Emissions. Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]
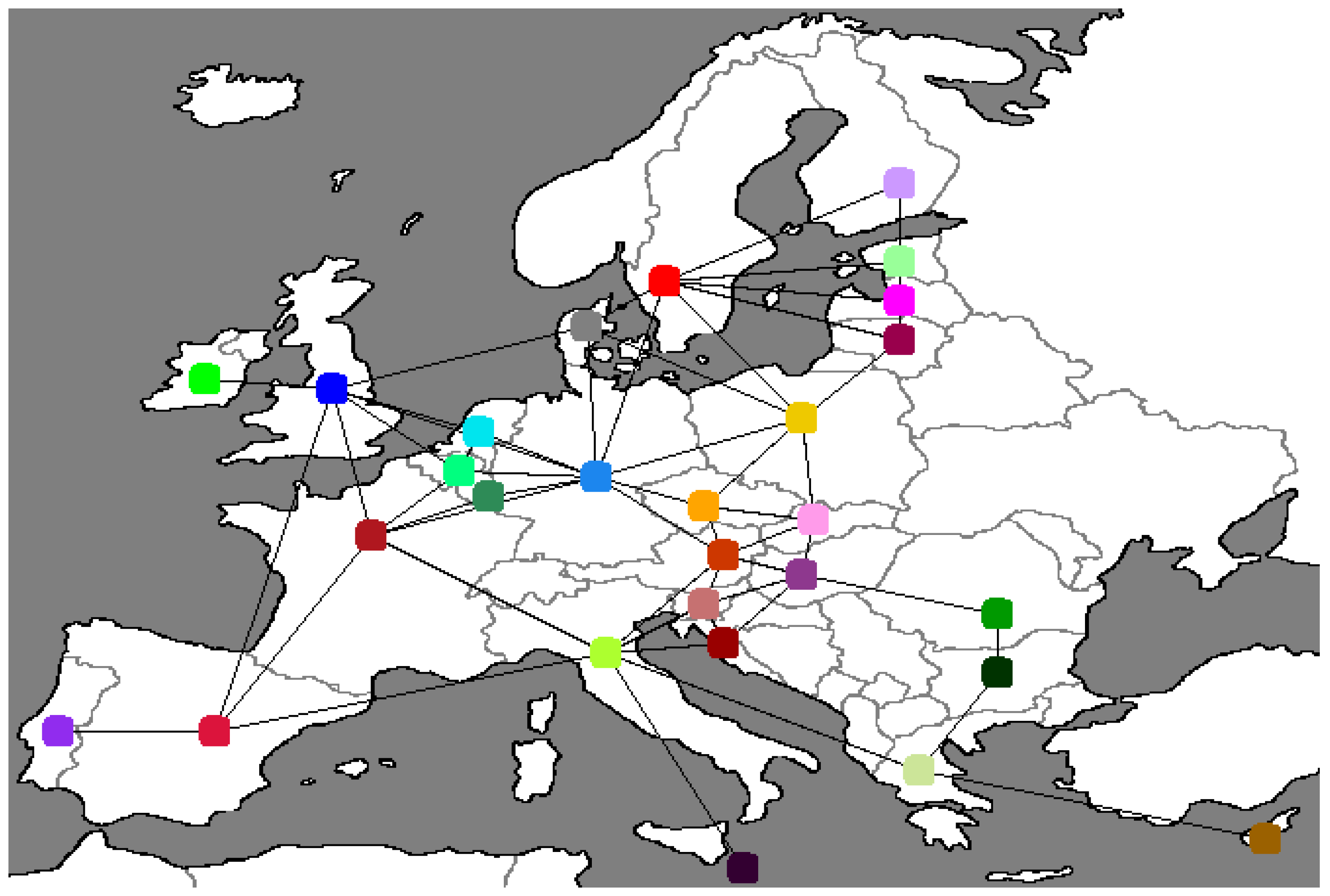
| Country | Neighbors |
|---|---|
| Sweden | Germany, Poland, Lithuania, Latvia, Estonia, Finland, Denmark |
| UK | Ireland, France, Spain, Germany, Netherlands, Belgium, Denmark |
| Ireland | UK |
| France | UK, Spain, Germany, Belgium, Luxembourg, Italy |
| Spain | UK, France, Portugal, Italy |
| Portugal | Spain |
| Germany | Sweden, UK, France, Netherlands, Belgium, Luxembourg, Poland, Czech Republic, Austria, Denmark |
| Netherlands | UK, Germany, Belgium |
| Belgium | UK, France, Germany, Netherlands, Luxembourg |
| Luxembourg | France, Germany, Belgium |
| Italy | France, Spain, Austria, Slovenia, Croatia, Greece, Malta |
| Poland | Sweden, Germany, Czech Republic, Slovakia, Lithuania, Denmark |
| Czech Republic | Germany, Poland, Austria, Slovakia |
| Austria | Germany, Italy Czech Republic, Slovakia, Hungary, Slovenia |
| Slovakia | Poland, Czech Republic, Austria, Hungary |
| Hungary | Austria, Slovakia, Slovenia, Croatia, Romania |
| Slovenia | Italy, Austria, Hungary, Croatia |
| Croatia | Italy, Hungary, Slovenia, |
| Greece | Italy, Bulgaria, Cyprus |
| Romania | Hungary, Bulgaria |
| Lithuania | Sweden, Poland, Latvia |
| Latvia | Sweden, Lithuania, Estonia |
| Estonia | Sweden, Latvia, Finland |
| Finland | Sweden, Estonia |
| Bulgaria | Greece, Romania |
| Malta | Italy |
| Cyprus | Greece |
| Denmark | Sweden, UK, Germany, Poland |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schüller, K.; Staňková, K.; Thuijsman, F. Game Theory of Pollution: National Policies and Their International Effects. Games 2017, 8, 30. https://doi.org/10.3390/g8030030
Schüller K, Staňková K, Thuijsman F. Game Theory of Pollution: National Policies and Their International Effects. Games. 2017; 8(3):30. https://doi.org/10.3390/g8030030
Chicago/Turabian StyleSchüller, Katharina, Kateřina Staňková, and Frank Thuijsman. 2017. "Game Theory of Pollution: National Policies and Their International Effects" Games 8, no. 3: 30. https://doi.org/10.3390/g8030030
APA StyleSchüller, K., Staňková, K., & Thuijsman, F. (2017). Game Theory of Pollution: National Policies and Their International Effects. Games, 8(3), 30. https://doi.org/10.3390/g8030030




