Abstract
Anticipated verbal feedback in a dictator game has been shown to induce altruistic behavior. However, in the ultimatum game which, apart from generosity, entails a strategic component since a proposer may (rightly) fear that the responder will reject a low offer, it remains an open question whether anticipated verbal communication can be effective in increasing offers. We implement a between-subjects experimental design in the ultimatum game with strategy method manipulating the form of anticipated verbal communication (no communication, one-sided communication from proposers and two-sided communication) and find that offers are significantly higher in the presence of anticipated two-sided communication. However, anticipated one-sided communication from proposers has no effect on offers, suggesting, as found in previous studies, that it is the anticipation of feedback that is relevant.
JEL Classification:
C78; C91; D03
1. Introduction
The effect of anticipated communication on altruistic behavior has become a focus of growing research interest in recent years. Participants in laboratory experiments involving the dictator game choose to donate higher amounts to recipients if they anticipate verbal feedback from those recipients. However, there is little research on whether anticipated communication can be effective in increasing offers in the ultimatum game. Unlike the dictator game which is exclusively one of generosity, the ultimatum game has components of both generosity and strategy. In choosing what amount to offer, the proposer in the ultimatum game may (rightly) fear that the responder will reject a low offer. We refer to such fears as strategic considerations. Therefore, an important research question that the present study addresses is whether strategic considerations crowd out impulses towards generosity that are triggered by anticipated communication. This not only is important in testing the robustness of the anticipated communication effect but additionally generates insights on the little-known role of anticipated communication in unrestricted bargaining settings.
Studies that have considered the role of anticipated verbal feedback on altruistic behavior include Xiao and Houser [1] and Ellingsen and Johannesson [2]. These studies find that in a dictator game where an allocator donates an amount of money to a recipient and the recipient sends an anonymous written message after learning of the amount, donations are significantly higher in relation to the standard (no-communication) condition. It is noted that there is a strong emotional response by recipients who receive what they perceive to be unfair donations (i.e., significantly below the 50:50 split), and this is expressed in terms of expressions of disapproval, including foul language. Ellingsen and Johannesson [2] argue that individuals are motivated by concerns for pride and blame which are prominent in the presence of anticipated verbal feedback whereas Xiao and Houser [1] similarly conclude that allocators in the dictator game have a preference for avoiding written expression of disapproval, or negative emotions. Brook and Servátka [3] further illustrate that this anticipated communication effect is not constrained to verbal communication by allowing recipients to convey approval and disapproval of allocations through sending pictorial representations of facial expressions (emoticons).
While empirical evidence clearly shows that offer levels are higher in the ultimatum game in comparison to donations in the dictator game, a few studies have compared behavior in both games to uncover the role that strategic considerations play in the ultimatum game.1 For example, Charness and Gneezy [4] experimentally investigate how anonymity and social distance affect behavior in these games and find contrasting effects. In the dictator game, reducing social distance significantly increases donations, whereas in the ultimatum game, there is no significant effect on offers. Such comparative studies highlight that behavioral insights obtained in one game do not naturally extend to the other.
Only a handful of experimental studies have considered the role of anticipated communication in the ultimatum game. In an earlier related paper, Xiao and Houser [5] allow one-sided communication from the responder to proposer in the ultimatum game in the form of a written message accompanying the “accept” or “reject” decision, occurring after the responder has learnt of the offer from the proposer. They find that proposer offers do not differ compared to the standard condition, but responders reject unfair offers significantly less frequently. In their assessment, the lower rejection rates imply that communication supplements costly punishment by providing a medium where an aggrieved responder can express her negative emotions. Andersson et al. [6] in turn allow one-sided communication from proposers to responders in the ultimatum game in the form of written messages. Proposers communicate before submitting an offer and responders view the messages either before making their acceptance decision or after. They find that average payoffs are significantly higher in the before condition and not in the after condition and attribute this to persuasion effects of anticipated communication, ruling out self-image effects.
Our paper contributes to this strand of literature by examining how anticipated verbal communication affects proposer and responder behavior in an unrestricted bargaining setting. It differs from the aforementioned studies in that the responder never learns of the proposer’s offer until the conclusion of play. This seemingly small difference results in a number of implications. First, in Xiao and Houser [5]’s study, it is likely that the proposer’s offer which is known to the responder is a focal point in the responder’s communication. For example, it is evident that expressions of negative emotions by a responder are triggered by knowledge of the proposer’s offer. Our design eliminates this focal point and therefore restricts the prevalence of emotional responses by responders that result from having direct knowledge of proposer choices. Second, in relation to Andersson et al. [6]’s study, a proposer in our study can choose to be persuasive in the messages or to convey a positive self-image through deception, for example, by claiming that she offered a higher amount than her actual offer. Gneezy [7] finds that in two-person interactions in which lying increases the payoffs to the liar in expense of her counterpart, the average person prefers not to lie if this only leads to a marginal increment in payoff but a significant reduction in the counterpart’s payoff. Therefore, our study provides a test of Gneezy [7]’s conjecture in a bargaining context. In addition, our paper contributes to the literature by studying the effect of anticipated two-sided communication which to the best of our knowledge has not been investigated before in the ultimatum game.
The content of the communication is not restricted in our experiment, but because identifiability may introduce nonpecuniary influences on preferences, participants are not allowed to divulge information in the written messages that can lead to them being identified. We find that impulses towards generosity still persist in the presence of strategic considerations with two-sided communication, with offers under two-sided communication being significantly higher to either one-sided communication from proposers to responders or no communication. Offers under one-sided communication and no communication do not differ, suggesting that the anticipation effect relates to the anticipation of feedback in the communication (and not anticipation of communication per se). In terms of responder behavior, we observe a significant amount of non-monotonicity in responder choices across all of our treatments, with higher conditional rejection frequencies for high (above equal-split) and low (below equal-split) offers. Rejection rates are higher under two-sided communication, relative to either one-sided communication or no communication. However, as was the case for offers, responder behavior does not differ between no communication and one-sided communication. A qualitative analysis of the informational content of communication in the communication treatments reveals that the vast majority of participants’ communication are statements or discussions of the ultimatum game being played (such as references to “offer”, “accept” and “reject”). We find support for Gneezy [7]’s conjecture, observing that proposers do not lie about their offers. However, we find evidence that proposers either avoid communication or use persuasion to justify lower offers under one-sided communication. They also restrict the content of communication to conversations that exclude references to fairness in this condition, which taken together may account for the observed behavioral differences.
2. Method
2.1. Experimental Design
We investigate behavior in the ultimatum game with strategy method [8]. In the ultimatum game, little is known about responder choices corresponding to especially high offers since such offers are rarely observed in practice, and previous studies have mostly elicited responses using the direct-response method. Considering a sample of 75 ultimatum game experiments, Oosterbeek et al. [9] find that less than a fifth elicited responses using the strategy method. Apart from this motivating factor, the strategy method enables us to obtain a larger number of observations from a single session.2
In our setting, the proposer (henceforth X) chooses an amount x to offer to the responder (henceforth Y) from a pie of 10 Euros, with the restriction that each player gets at least 1 Euro. This results in nine possible offers: . In turn, Y, without knowing the actual choice of X, indicates for each possible offer whether she accepts or rejects. We denote Y’s choice . A strategy of Y assigns to each x choice of X, and is a 9-element vector collected by having Y fill in a table similar to Table 1, with either “accept” or "reject" at each blank box.

Table 1.
Ultimatum game with strategy method: Y’s decision task.
An outcome of the game is a matched pair with the following payoffs:
where and denote the payoffs to X and Y respectively.
Before Y makes her choices, but after X has chosen a binding offer x, there is a three minute communication phase in each of the game experiments. We distinguish three treatments:
- No Communication: Standard condition where participants are anonymous and are not allowed to communicate, with a three minute time-gap during the communication phase.
- One-Sided Communication: X has the option to anonymously and unilaterally communicate in writing with Y during the communication phase.
- Two-Sided Communication: Both X and Y have the option to anonymously communicate with each other in writing during the communication phase.
2.2. Behavioral Predictions
A few ultimatum bargaining experiments have examined the effect of communication on bargaining outcomes, and have for the most part found that communication induces more egalitarian offers, and lower rates of disagreement between bargaining parties (see, for example [11,12]). Among the few standard ultimatum game studies that have looked at the effect of anticipated communication, there is weak evidence of communication increasing offers. The aforementioned one-sided communication findings of Xiao and Houser [5] suggest that strategic considerations crowd out impulses towards generosity. However, in comparison, our design allows for a stronger effect to be observed in Two-Sided Communication since, under this condition, the proposer participates in the communication as opposed to where she is passive and simply receives the accept or reject decision along with a written message from the responder. Participation of the proposer implies that the responder can ask directly about how much the proposer offered, and subsequently, the proposer is open to disapproval if the offer is judged to be unsatisfactory. Anticipating this, the proposer may simply choose to lie about a low offer to avoid disapproval from the responder. However, Gneezy [7] finds that in two-person interactions in which lying increases payoffs to the liar in expense of her counterpart, people do not like to lie. In his experiment, he observes that participants will be deceptive primarily if they stand to gain a lot from this or if it imposes little loss to the counterpart. Battigalli et al. [13] show that Gneezy [7]’s results can be explained by the theory of simple guilt [14]. Specifically, the monetary increase in the liar’s payoff may be offset by the guilt cost that she faces due to the increase in disappointment of the counterpart caused by the counterpart’s lower payoff. Therefore, due to guilt aversion, we hypothesize that the proposer will be more other-regarding.
Hypothesis 1.
X participants will make higher offers in Two-Sided Communication relative to No Communication.
Hypothesis 2.
X participants will make higher offers in Two-Sided Communication relative to One-Sided Communication.
A motivating factor for including the treatment One-Sided Communication is to investigate whether anticipated communication from proposers in the absence of feedback from responders can be effective in increasing offers in the ultimatum game. From the dictator game studies of Ellingsen and Johannesson [2] and Xiao and Houser [1], the crucial aspect is the feedback mechanism of anticipated communication where it emerges that higher donations signal a strong preference for avoiding written expressions of disapproval or negative emotions. In the absence of anticipated disapproval or any anticipated interaction with the responder in the ultimatum game, there is a very small likelihood that proposers will make higher offers. Moreover, in the dictator game, there is evidence that lack of feedback induces the allocator to act in a selfish manner. Andreoni and Rao [15], for example, find that the amount allocated is lowest when the allocator communicates unilaterally to the recipient in writing compared to no communication, one-sided communication from the recipient, and two-sided communication. It is observed that allocators primarily use the messages to express remorse for their lower donations which conceivably may reduce their feelings of guilt for the low donations. We therefore hypothesize that offers will be lowest under one-sided communication.
Hypothesis 3.
X participants will make lower offers in One-Sided Communication relative to No Communication.
2.3. Participants and Procedures
The experiment was conducted at the Cognitive and Experimental Economics Laboratory (CEEL) at the University of Trento. A total of 120 participants took part in six experimental sessions compromising two sessions per treatment. The participants were recruited from the undergraduate populations at the university. None of the participants had previously taken part in this series of experiments.
On their arrival, participants were allocated separate computer terminals, and given a copy of the instructions for the experiment. Time was allocated for private reading of these instructions. Thereafter, a member of the experimental staff read aloud the instructions in an attempt to make the rules and procedures of the experiment common knowledge.
Each participant was then randomly assigned either the role X or Y, and maintained that role for the remainder of the experiment. To ensure comprehension with the instructions, participants had to answer a set of control questions relating to the contents of the instructions prior to the actual start of the experiment.
The experiment consisted of five periods. At the start of each period, each participant with the role X was randomly paired with a participant with the role Y. No participant was paired with the same participant at a subsequent period, and this detail of the matching protocol was explicit in the instructions. At the end of each period, once the communication phase was complete and the final payoffs determined, a participant was informed of her actual choices and accruing payoff as well as those of her paired counterpart.
In the communication treatments, a member of the experimental staff monitored the contents of the messages to make sure that they complied with the instructions. Participants in these treatments were explicitly made aware of this fact prior to the actual start of the experiment. One period was randomly chosen for payment at the end of the experiment. The final monetary payment to a participant included an unconditional show-up fee and earnings from the randomly chosen period.3
3. Results
3.1. Descriptive Statistics
We begin with a summary of the choices of X participants across the three treatments. Table 2 provides a summary of individual-level mean offers over the five periods of the experiment.

Table 2.
Summary Statistics of Proposer and Responder Behavior.
Mean offers across periods are consistently highest under anticipated two-sided communication, ranging from 3.65 to 4.65 and do not differ much between no communication and anticipated one-sided communication where offers range between 3.25 and 3.85. A series of Mann Whitney U tests presented in Appendix B show that mean offers in the first period differ between Two-Sided Communication and No Communication (p-value = 0.039) and Two-Sided Communication and One-Sided Communication (p-value = 0.033). However, the tests do not reveal a statistically significant difference between first period offers in No Communication and One-Sided Communication (p-value = 0.845). Across the five periods, mean offers differ between Two-Sided Communication and No Communication (p-value = 0.010) and Two-Sided Communication and One-Sided Communication (p-value < 0.001). However, as was the case for first-period offers, overall mean offers do not differ between No Communication and One-Sided Communication (p-value = 0.197).
Observation 1.
Behavior of X participants under no communication and anticipated one-sided communication does not differ. However, offers are significantly higher under anticipated two-sided communication.
Figure 1 exhibits the distribution of the individual-level average offers over the five periods of the experiment. The results are consistent with our behavioral hypotheses 1 and 2 and show that anticipated two-sided communication induces higher offers from proposers. However, hypothesis 3 is not supported since anticipated one-sided communication does result in lower offers compared to no communication.
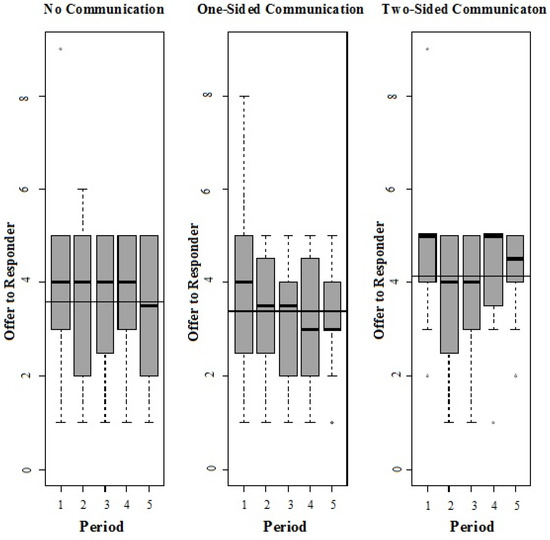
Figure 1.
Choices of X (average at the individual level).
Whether anticipated two-sided communication results in a more efficient allocation in general depends on the behavior of Y participants. Table 2 summarizes the mean acceptance rates across treatments over the five periods of the experiment. Acceptance rates are consistently lowest under anticipated two-sided communication ranging between 59% and 65%. For both anticipated one-sided communication and no communication, mean acceptance rates at each period exceed 70%. Figure 2 exhibits a grouped bar plot of conditional acceptance rates across the offer levels. What is immediately apparent from the bar plots is the non-monotonicity of Y choices across all treatments. A monotonic strategy of Y requires that if , then for all . Therefore, for example, if a participant accepts an offer , a monotonic strategy requires that she also accepts all offers .
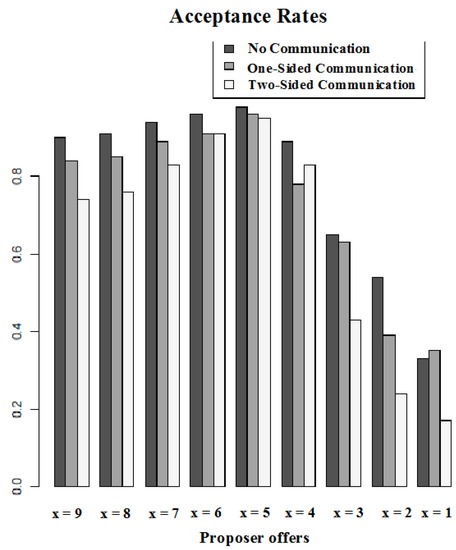
Figure 2.
Conditional choices of Y (comparison across treatments).
Mann Whitney U-tests show that for low offers, i.e., , acceptance rates differ between Two-Sided Communication and No Communication (p-value = 0.003), and Two-Sided Communication and One-Sided Communication (p-value = 0.007). However, the tests do not reveal a difference in acceptance rates between No Communication and One-Sided Communication (p-value = 0.767). Across all treatments, acceptance rates are highest for intermediate offers, i.e., . The maximum acceptance rate is observed at the equal split of the pie, , with nearly all such offers accepted by Y participants. For this range of offers, Mann Whitney U-tests do not highlight a significant difference in acceptance rates between treatments. For high offers, i.e., , acceptance rates differ only between Two-Sided Communication and No Communication (p-value = 0.024).
Observation 2.
Y participants in the presence of two-sided communication are more likely to reject unequal offers (either very low or very high). For intermediate offers, there are no behavioral differences between treatments.
Due to the non-monotonicity of a large number of participant Y strategy vectors, we observe that the frequency of rejection of high offers is high (relative to the expectation that no high offer is rejected). In No Communication, for example, 10 percent responder choices corresponding to the maximum offer of were “reject”, which is significantly different to the case where all choices are “accept” (Wilcoxon signed-rank test, p-value = 0.020). Apart from those that exclusively make use of first-period observations, the descriptive statistics reported in this section do not take into account the interdependence of individual choices across periods of the experiment. We address this shortcoming using regression analyses.
3.2. Regression Analyses
We specify regression and probability models in this section to gain an in-depth understanding of choices of X, and rejection behavior of Y. The models take into account dependencies that arise from the matching protocol implemented, feedback and repeated play across periods.
3.2.1. Analysis of Proposer Behavior
To analyze choices of X, we specify a random effects linear model. The dependent variable offer represents the value of the offer made by experimental participant i in period t, and takes on values in the range [1, 9]. The model takes the form:
where as explanatory variables, we include indicator variables for One-sided Communication and Two-Sided Communication and a period variable. is the time invariant experimental participant specific effect accounting for any such effect not included in the regression and is the disturbance term. In this case, and and are independent of . The explanatory variables in turn are independent of and for all experimental participants and periods. In addition to the linear model, we focus on what influences X participants to choose offers in the range [4, 6] which constitute 62% of actual offers. We therefore specify two random effects probit models denoted 1() and 1(), where is an indicator function that takes the value 1 if the condition holds, 0 otherwise. The baseline treatment in the regression analysis is No Communication. Table 3 summarizes the results of the regressions.4

Table 3.
Choices of X (Random Effects: linear and probit).
The results show that across all specifications, anticipated two-sided communication has a positive and significant effect on participant X’s offers relative to either no communication or anticipated one-sided communication. This effect is apparent even if we consider only observations from the first period or the last period. In general, anticipated one-sided communication has no effect on X offers relative to no communication, but significantly decreases the likelihood that participant X splits the endowment fifty−fifty. Experience has no effect on participant X offers.
Observation 3.
X participants offer more if they anticipate two-sided communication. Anticipated one-sided communication generally has no effect on X offers, but decreases the probability that X will split the endowment equally.
3.2.2. Analysis of Responder Behavior
To analyze the rejection behavior of Y, we specify a random intercept logit model. The dependent variable reject takes the value one if Y rejects an offer of X, and equals zero if she accepts. To account for the non-monotonicity of a significant proportion of participant Y strategies, we include in our set of explanatory variables dummies for the possible offer levels of X ( for , and for ).5 Other explanatory variables as previously defined are the indicator variables One-Sided Communication and Two-Sided Communication, and a period variable. The baseline offer level in the regression analysis is where , and the baseline treatment is No Communication. Modeling the binary response of responder i in period t as , the random intercept logit model takes the form:
where The model is estimated with GLLAMM (Stata), and we cluster standard errors at the experimental participant level to account for the interdependence of decisions made by a participant over the five periods of the experiment.6 Table 4 summarizes the results of the regressions.

Table 4.
Analysis of Responder Choices (GLLAMM: logit).
The results show that two-sided communication has a significant effect in increasing the likelihood that Y rejects an offer relative to either no communication or one-sided communication, whereas one-sided communication has no effect on the rejection behavior of Y relative to no communication. The non-monotonicity of Y choices exhibited in Figure 2 is confirmed by the probability model where it emerges that either low- or high-offers of X increase the likelihood of rejection by Y participants relative to the equal split (x = 5). In addition, low offers significantly increase the likelihood of rejection relative to high offers while rejection rates decline across periods. The reported effects remain even if we consider only observations from the first period or the last period.
Observation 4.
Y participants are more likely to reject X offers with two-sided communication, whereas one-sided communication has no effect on the rejection behavior of Y.
Observation 5.
Unequal offers (both above the equal split and below) are more likely to be rejected by Y participants, whereas experience makes it less likely that an offer is rejected.
3.3. Analysis of the Informational Content of Messages
In the behavioral predictions section, we argued that what appears to induce generosity in previous dictator game studies is the anticipation of verbal feedback from the recipient. However, our experimental design differs from those studies in the sense that the responder never learns of the offer amount until the end of the game. Therefore, there is no way to determine a priori what the content of communication will be. We therefore implement a qualitative analysis of the informational content of communication in One-Sided Communication and Two-Sided Communication to see whether existential differences in the content of communication between these treatments can explain observed behavioral differences. A shortcoming of this kind of analysis is that it does not account for the fact that communication is not independent across periods.
3.3.1. Game-Related Classification
Using the categorization implemented by Roth [11] and subsequently Zultan [12], we categorize the content of communication as either game-related or non-game-related. Specifically, we define game-related communication as any communication that includes reference to a parameter in the ultimatum game, such as, offer, accept, reject, payoff, and earning. Non-game-related communication on the other hand is any communication that does not fall into the defined category. The categorization was conducted using Stata, and Appendix D presents details of the procedure. Proposers in One-Sided Communication and proposer-responder pairs in Two-Sided Communication communicated over five periods. 84 percent of conversations in One-Sided Communication relative to 77 percent in Two-Sided Communication included game-related content. Only 9 percent of conversations were classified as non-game-related in One-Sided Communication, relative to 7 percent in Two-Sided Communication.
Observation 6.
The vast majority of proposer and proposer-responder pair conversations is game-related.
We further refine the game-related category and consider the proportion of conversations in which the proposer explicitly stated the offer amount. In One-Sided Communication, there was an explicit statement of the amount in 53 percent of cases, relative to 58 percent of cases in Two-Sided Communication. Out of this, less than 4 percent of cases in both One-Sided Communication and Two-Sided Communication involved deception, implying that most proposers who stated their offer amount were being truthful.
Observation 7.
Less than a tenth of proposers who stated their offer amounts under one-sided communication and two-sided communication were deceptive.
Therefore, Gneezy [7]’s conjecture is supported. Neither differences in the number of conversations using the game-related categorization nor differences in the rates of deception across treatments are significant in explaining behavioral differences in our experiment.
3.3.2. Persuasion, Apology, Information or Other Classification
Following the methodology in Houser and Xiao [16], 3 raters (undergraduate students) were invited to independently code 139 proposer messages into one of four categories: Persuasion, Information, Apology or Other. The raters were paid a fixed show up fee of 10 Euros and could earn an additional 15 Euros if their classification matched the modal classification for a randomly drawn message. The coders to a large extent agreed on the classification across all 4 categories. The interrater coefficient of agreement for rater 1 and rater 2 was , p-value < 0.001, for rater 1 and rater 3, , p-value < 0.001, and for rater 2 and rater 3, , p-value < 0.001. All three coefficients indicate a strong level of agreement. Table 5 presents rater 1’s classification across the two communication treatments.

Table 5.
Rater 1’s classification.
The results show that a significantly higher percentage of proposers in One-Sided Communication choose not to communicate relative to Two-Sided Communication. Additionally, for those proposers who choose to communicate, a significantly higher percentage under one-sided communication resort to persuasion. Under two-sided communication, proposers are more inclined to use communication as a means to communicate their offers to responders.
Observation 8.
A significantly higher number of proposers under one-sided communication choose not to communicate. For those who choose to communicate, a higher percentage resort to persuasion in comparison to two-sided communication.
Therefore, this classification explains behavioral differences between treatments to a large extent, showing that proposers either avoid communication or use persuasion to justify lower offers under one-sided communication.
3.3.3. Fairness Classification
A final criterion that we considered is based on the inequality aversion model of Fehr and Schmidt [17]. Communication can induce an expectation of fairness and if this this expectation is not met, then responders may be more willing to punish proposers, compared to absent the expectation. Proposers on the other hand may anticipate responders’ expectations and respond positively to them, thereby explaining behavioral differences in our experiment. We therefore categorized a message as fairness-oriented if it included a term referencing fairness such as fair, equal, equitable, even, half, fifty-fifty, same, and identical.7 Otherwise, we categorized the message as non-fairness oriented. As with game-related classification, we used Stata and Appendix D presents details of the procedure. In total, 32% of conversations in One-Sided Communication included fairness-oriented content relative to 53% in Two-Sided Communication. The mean offer for this category in One-Sided Communication and Two-Sided Communication was, respectively, ≈4.19 and ≈4.39. Conversely, 61% of conversations in One-Sided Communication, relative to 31% in Two-Sided Communication included non-fairness oriented content. The mean offer for this category in One-Sided Communication and Two-Sided Communication was, respectively, ≈2.90 and ≈3.55.
Observation 9.
A significantly higher proportion of conversations under two-sided communication include fairness-oriented content. Under both one-sided communication and two-sided communication, mean offers are significantly higher when the content of communication is fairness-oriented.
When the content of communication is fairness-oriented, there is no significant difference in the amounts offered under one-sided communication and two-sided communication, but there is a significant difference in the relative frequency of such conversations between the treatments. One, however, has to exercise caution when reading this result as it is possible that causality runs from offer to communication, in the sense that proposers who offer higher amounts are more likely to engage in fairness-oriented conversations. However, what is not in doubt is that there is a clear anticipation effect of communication in Two-Sided Communication. The inclusion of responders into the conversation results in a significantly larger number of fairness oriented conversations in comparison to one-sided communication, and proposers appear to anticipate such conversations, offering higher amounts on average. This result provides support for the view that communication in unrestricted bargaining enhances cooperation by focusing participants’ attention on a small number of fairness norms.
4. Conclusions
This paper has investigated whether the anticipated communication result of Xiao and Houser [1], Ellingsen and Johannesson [2] and Brook and Servátka [3] is robust to the presence of strategic considerations. In these studies, it is observed that donations in the dictator game are significantly higher in relation to the standard (no-communication) condition when the allocator knows that she will receive feedback in the form of an anonymous written message or nonverbal communication from the recipient. We show that generosity still persists in the ultimatum game if anticipated communication is two-sided. Thus, even though the expectation is that the proposer in the ultimatum game primarily focuses on whether the responder will reject a low offer (strategic considerations), it is also apparent that if the proposer knows that she will have to interact with the responder by exchanging anonymous written messages, then this has an additional effect on her allocation behavior. In other words, strategic considerations do not fully crowd out generosity in the ultimatum game with anticipated two-sided communication.
Eliciting choices using the strategy method allowed us to study responder behavior at offer levels that are rarely observed in the actual course of play. Interestingly, this revealed a great deal of non-monotonicity in responder choices both in the presence and absence of communication. Inequality aversion models such as that of Fehr and Schmidt [17] implicitly assume that individuals suffer a psychological cost if they are either better off or worse off than other individuals (i.e., they dislike inequality). We provide evidence that a significant number of responders are willing to sacrifice their own material payoff to avoid inequality, even if this inequality is in their favor.
Anticipated one-sided communication from the proposer does not result in behavior that differs with no communication, a result that mirrors Andreoni and Rao [15]’s result of one-sided communication from allocators to recipients in the dictator game.8 We find that proposers in this condition either avoid communication or use persuasion to justify lower offers. For allocators in the dictator game or proposers in the ultimatum game, it thus appears that the absence of anticipated feedback from the counterpart triggers selfish behavior. More studies are needed to confirm the robustness of this finding, however.
Acknowledgments
We thank four anonymous referees, Matteo Ploner, Jochen Jungeilges, Luca Corazzini, and seminar participants in Trento for helpful comments and suggestions. The experimental software was written by Marco Tecilla. Andrew Musau’s research was supported by the Competence Development Fund of Southern Norway through a grant to the Faculty of Economics and Social Sciences at the University of Agder, Norway.
Author Contributions
The authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Instructions (Translation from Italian)
[text corresponding to One-Sided Communication treatment is shown in square brackets]
{text corresponding to Two-Sided Communication treatment is shown in braces}
Thank you for taking the time to attend this session. If you have any question at any point before, during or at the end of the experiment, please raise your hand and one of the experimenters will assist you. You are not allowed to talk to anyone else in the room except for the experimenters.
You will receive a show-up fee of €2.50 for taking part in this session. In addition, you have the opportunity to earn more money depending on the decisions that you and others make during the session. At the end of the session, you will personally be paid the total sum of your show-up fee and earnings in private.
The experiment will take place on a computer where you will be paired with a different individual at each period. There will be a total of five periods. At no point during or after the experiment will any individual know the identities of individuals that he or she is paired with across the periods.
Decision Tasks
At the very beginning, the computer will randomly assign you either the role of X or Y. Once this assignment is complete, you will remain in that role for the remainder of the session. If you are assigned the role of X, you will be paired with an individual assigned the role of Y and vice-versa. Your earnings will depend on the decisions that you make in your pair.
On the computer screen, each individual X will select one of nine divisions of €10. These divisions are (€1, €9), (€2, €8), (€3, €7), (€4, €6), (€5, €5), (€6, €4), (€7, €3), (€8, €2), (€9, €1), where the Euro amounts within the parenthesis represent (Amount to X, Amount to Y) respectively.
Not knowing the choice of X, for each of the nine divisions, Y has to indicate whether he or she “accepts” or “rejects”. If Y accepts, then X and Y both receive the amounts as per the division. If Y rejects, then both X and Y receive €0. Note that there will be a three minute time-gap between the choice of X, which temporally comes first, and Y’s decision. At the end of each of the five periods, both X and Y participants are informed of the choice or choices made by their paired participant, and about their own payoff.
[A message
X has the option of sending a message(s) to Y prior to Y choosing whether to accept or reject the offers corresponding to each division. However, the message(s) will be after X has chosen one of the nine divisions. The following sequence illustrates the chronology of events:
There will be a message window on the computer screen where X can write a message(s) to Y within the three minute time-gap between X’s choice and Y’s decision. If X does not intend to send a message(s) to Y, then he or she can click on the button labeled "no message" at the bottom right hand corner of the screen. If this happens, then Y will be notified that X has chosen not to send any message(s). At any point within the allotted three minutes, X can send a message(s) to Y regardless of whether he or she had earlier opted not to.
In the message(s), X is not allowed to identify him or herself. Therefore, he or she cannot include personal details such as name, gender, appearance, age, address, phone number, and program or year of study. (Experimenters will monitor the message(s). Violations (to the discretion of the experimenters) will result in X forfeiting the €2.50 show-up fee and leaving the session with no earnings. The paired Y will receive the average amount received by other Y’s.) Apart from these restrictions, X may say anything that he or she wishes in the message(s).
{Messages
Both X and Y have the option of sending messages to each other prior to Y choosing whether to accept or reject the offers corresponding to each division. However, the messages will be after X has chosen one of the nine divisions. The following sequence illustrates the chronology of events:
There will be a message window on the computer screen and both X and Y can send messages to each other within the three minute time-gap between X’s choice and Y’s decision. If either X or Y does not intend to send a message(s) to the other, then he or she can click on the button labeled “no message” at the bottom right hand corner of the screen. If this happens, then the paired participant will be notified that either X or Y has chosen not to send any message and subsequently, he or she will decide whether to send a message(s) to him or her. At any point within the allotted three minutes, X and Y can send a message(s) to the paired participant regardless of whether they had earlier opted not to.
In the messages, both X and Y are not allowed to identify themselves. Therefore, they cannot include personal details such as name, gender, appearance, age, address, phone number, and program or year of study. (Experimenters will monitor the messages. Violations (to the discretion of the experimenters) will result in the violator forfeiting the €2.50 show-up fee and leaving the session with no earnings. The paired individual will receive the average amount received by other participants.) Apart from these restrictions, both X and Y may say anything that they wish in the messages.
Earnings
Out of the five periods, one period will be randomly selected for payment. Total earnings at the end of the experiment for both X and Y will be the sum of the show-up fee and earnings in the period that is randomly selected.
Appendix B. Comparisons of Individual Average Offers

Table A1.
Mann Whitney U tests: Comparisons of individual average offers across periods.
Table A1.
Mann Whitney U tests: Comparisons of individual average offers across periods.
| p-Value | |||
|---|---|---|---|
| No Communication | One-Sided Communication | Two-Sided Communication | |
| Period 1 vs. Period 2 | 0.8783 | 0.5782 | 0.0564 |
| Period 1 vs. Period 3 | 0.9443 | 0.4612 | 0.1116 |
| Period 1 vs. Period 4 | 0.9777 | 0.5150 | 0.4453 |
| Period 1 vs. Period 5 | 0.4535 | 0.4614 | 0.4901 |
| Period 2 vs. Period 3 | 0.7675 | 0.7924 | 0.6698 |
| Period 2 vs. Period 4 | 0.7575 | 0.8679 | 0.2148 |
| Period 2 vs. Period 5 | 0.4189 | 0.9113 | 0.1494 |
| Period 3 vs. Period 4 | 0.9888 | 0.9008 | 0.3879 |
| Period 3 vs. Period 5 | 0.5571 | 0.8351 | 0.2696 |
| Period 4 vs. Period 5 | 0.5204 | 0.9004 | 0.8818 |
; significance level.

Table A2.
Mann Whitney U tests: Comparisons of individual average offers across treatments.
Table A2.
Mann Whitney U tests: Comparisons of individual average offers across treatments.
| p-Value | ||||||
|---|---|---|---|---|---|---|
| Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Overall | |
| No Communication vs. One-Sided Communication | 0.8449 | 0.4203 | 0.4045 | 0.4040 | 0.9557 | 0.1970 |
| No Communication vs. Two-Sided Communication | 0.0388 | 0.8992 | 0.6286 | 0.1911 | 0.0248 | 0.0101 |
| One-Sided Communication vs. Two-Sided Communication | 0.0325 | 0.4437 | 0.1320 | 0.0246 | 0.0053 | 0.0000 |
; significance level.
Appendix C. Panel Regressions
In this section, we present results from estimating random intercept panel models that make use of individual-level data. Beginning from a very general model of the proposer in Equation (3) where we include interactions between the treatment indicator variables and the period variable, we eliminate insignificant interaction terms until we are left with the relatively simple models presented in Table 3.

Table A3.
Choices of X (Random Effects: linear and probit).
Table A3.
Choices of X (Random Effects: linear and probit).
| Offer∼ | 1() | |||||
|---|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | (1) | (2) | |
| (Intercept) | 3.935 | 3.775 | −0.519 | −0.476 | 0.381 | 0.332 |
| (0.327) | (0.234) | (0.352) | (0.262) | (0.239) | (0.239) | |
| One-Sided communication | −0.360 | −0.210 | −0.249 | −0.417 | −0.083 | −0.260 |
| (0.439) | (0.188) | (0.478) | (0.206) | (0.439) | (0.188) | |
| Two-Sided communication | 0.220 | 0.550 | 0.431 | 0.443 | 0.071 | 0.434 |
| (0.439) | (0.188) | (0.448) | (0.192) | (0.450) | (0.192) | |
| Period | −0.115 | −0.062 | 0.012 | −0.002 | −0.039 | −0.023 |
| (0.094) | (0.054) | (0.097) | (0.057) | (0.094) | (0.055) | |
| One-Sided communication*Period | 0.050 | −0.056 | −0.059 | |||
| (0.132) | (0.145) | (0.133) | ||||
| Two-Sided communication*Period | 0.110 | 0.004 | 0.123 | |||
| (0.132) | (0.136) | (0.138) | ||||
| W- | 1.74 | 16.42 | 2.09 | 17.30 | 0.12 | 13.01 |
| 1056.73 | 1053.43 | 360.53 | 356.74 | 385.65 | 383.45 | |
| No. of observations | 300 | 300 | 300 | 300 | 300 | 300 |
Standard errors in parenthesis. For the dependent variables in columns 4 through 7, is an indicator function that takes the value 1 if the condition holds, 0 otherwise. W- refers to the Wald test statistic for the null hypothesis H: One-Sided communication = Two-Sided communication against the alternative hypothesis H: One-Sided communication ≠ Two-Sided communication. refers to Akaike’s information criterion. ; ; significance level.
Similarly, for the responder, we begin with the model in Equation (4) where we include interactions between the levels of X offers, period and each of the treatment indicator variables. We in turn eliminate insignificant interaction terms until we are left with the relative simple model presented in Table 4.

Table A4.
Analysis of Responder Choices (GLLAMM: logit).
Table A4.
Analysis of Responder Choices (GLLAMM: logit).
| Reject ∼ | Coeff (Std. Err.) | ||
|---|---|---|---|
| (1) | (2) | (3) | |
| (Intercept) | −3.348 (0.824) | −3.240 (0.496) | −3.810 (0.565) |
| One-Sided communication | 0.593 (0.682) | 0.264 (0.423) | 0.408 (0.545) |
| Two-Sided communication | 1.027 (1.194) | 1.012 (0.443) | 0.945 (0.307) |
| x_LOW | 1.116 (0.973) | 1.193 (0.362) | 1.483 (0.531) |
| x_HIGH | 3.087 (1.020) | 2.887 (0.517) | 3.583 (0.576) |
| −0.325 (0.224) | −0.312 (0.216) | −0.098 (0.044) | |
| One-Sided communication*Period | 0.061 (0.120) | 0.049 (0.107) | |
| Two-Sided communication*Period | −0.013 (0.100) | −0.023 (0.100) | |
| x_LOW*Period | 0.117 (0.192) | 0.115 (0.190) | |
| x_HIGH*Period | 0.262 (0.235) | 0.257 (0.233) | |
| One-Sided communication*x_LOW | −0.076 (1.137) | ||
| Two-Sided communication*x_LOW | 0.226 (1.164) | ||
| One-Sided communication*x_HIGH | −0.474 (0.923) | ||
| Two-Sided communication*x_HIGH | −0.144 (1.149) | ||
| W- | 0.34 | 7.20 | 19.53 |
| W- | 38.33 | 45.18 | 331.50 |
| Log-likelihood | −1216.37 | −1217.60 | −1220.10 |
| 2462.74 | 2457.19 | 2454.21 | |
| No. of observations | 2700 | 2700 | 2700 |
GLLAMM refers to the Stata program to fit generalized linear latent and mixed models. W- refers to the Wald test statistic for the null hypothesis H: One-Sided communication = Two-Sided communication against the alternative hypothesis H: One-Sided communication ≠ Two-Sided communication. W- refers to the Wald test statistic for the null hypothesis H: = against the alternative hypothesis H: . refers to Akaike’s information criterion. Standard errors are clustered at the experimental participant level. ; significance level.
Appendix D. Categorization Procedure
All statistical analyses and categorization of messages in this paper was conducted using Stata version 14.2. Included in each observation, which is a row in Stata, was a string variable of maximum length 244 characters (Stata type str244). This variable contained the entire message of the proposer in One-Sided Communication, and proposer-responder pair in Two-Sided Communication in a given period. In instances where a participant(s) chose not to engage in communication, the variable had the entry “NO MESSAGE”. For the first category, we identified a list of key words that reference a parameter in the ultimatum game, including ultimatum, game, offer, accept, reject, payoff, euro, currency, period, earnings (and different combinations of these: in Italian), as well as numbers representing monetary amounts. Following listing of key words, we used Stata’s string function regexm() to identify occurrences of the key words within the strings, evaluating to 1 if a keyword is present and 0 otherwise.
The main challenges in the matching process were how to handle punctuation marks that delimit characters and the inclusion of both uppercase and lowercase letters in the written messages. However, as we will illustrate below, the regexm() function is able to handle both challenges.
For the sake of illustration, we translate three messages from the list of messages in the Two-Sided Communication and One-Sided Communication treatments and explain the procedure.
Example message from Two-Sided Communication:
X I decided to offer you 6, leaving me with 4.
Y You didn’t split half half?
X No, I chose a little bit less for myself.
This message exchange is entered into Stata without any alterations as follows:
I decided to offer you 6, leaving me with 4. You didn’t split half half? No, I chose a~little bit less for myself.’’
Example message from One-Sided Communication:
X HELLO, it’s hot outside today... isn’t it?
This message is entered into Stata without any alterations as follows:
"HELLO, it’s hot outside today... isn’t it?"
Example message from One-Sided Communication or Two-Sided Communication:
X or X-Y pair [No communication occurred]
This message is entered into Stata as follows:
"NO MESSAGE"
The commands below enter the text above into Stata:
input str244 message "I decided to offer you 6, leaving me with 4. You didn’t split half half? No, I chose a~little bit less for myself." "HELLO, it’s hot outside today... isn’t it?" "NO MESSAGE" end
The following commands utilizing the string function regexm() are combined to generate an indicator variable which we name "game_content" that tells us how many conversations included our defined keywords. First, we matched keywords delimited by spaces or punctuation marks:
gen indicator1 = regexm(" " + message + " ", "[,\. ](ultimatum|offer|accept|reject|
payoff|euro|currency|earn)[,\. ]")
Second, we matched keywords that did not include an uppercase letter
gen indicator2 = regexm(" " + message + " ", "[^A-Z] (ultimatum|offer|accept|reject|
payoff|euro|currency|earn)[^A-Z]")
Finally, we create our indicator variable which equals one if any of the indicators is equal to one, and zero otherwise.
egen game_content = rowmax(indicator*) list message game_content
The resulting Stata output is as shown in Figure A1. It is clear from the messages that only the first one has a game related content.
For the second category, we included all synonyms of the word “fair” that we could identify as keywords, including, reasonable, equal, half, and generous. The ensuing categorization followed the above description.

Figure A1.
Stata output.
References
- Xiao, E.; Houser, D. Avoiding the sharp tongue: Anticipated written messages promote fair economic exchange. J. Econ. Psychol. 2009, 30, 393–404. [Google Scholar] [CrossRef]
- Ellingsen, T.; Johannesson, M. Anticipated verbal feedback induces altrusitic behavior. Evol. Hum. Behav. 2007, 29, 100–105. [Google Scholar] [CrossRef]
- Brook, R.; Servátka, M. The anticipatory effect of nonverbal communication. Econ. Lett. 2016, 144, 45–48. [Google Scholar]
- Charness, G.; Gneezy, U. What’s in a name? Anonymity and social distance in dictator and ultimatum games. J. Econ. Behav. Organ. 2008, 68, 29–35. [Google Scholar] [CrossRef]
- Xiao, E.; Houser, D. Emotion expression in human punishment behavior. Proc. Natl. Acad. Sci. USA 2005, 102, 7398–7401. [Google Scholar] [CrossRef] [PubMed]
- Andersson, O.; Galizzi, M.M.; Hoppe, T.; Kranz, S.; van der Wiel, K.; Wengström, E. Persuasion in experimental ultimatum games. Econ. Lett. 2010, 108, 16–18. [Google Scholar] [CrossRef]
- Gneezy, U. Deception: The role of consequences. Am. Econ. Rev. 2005, 95, 384–394. [Google Scholar] [CrossRef]
- Selten, R. Die Strategiemethode zur Erforschung des eingeschränkt rationalen Verhaltens im Rahmen eines Oligopolexperimentes. In Beitraäge zur Experimentellen Wirtschaftsforschung; Sauermann, H., Ed.; Mohr Siebeck: Tübingen, Germany, 1967; pp. 136–168. [Google Scholar]
- Oosterbeek, H.; Sloof, R.; Van De Kuilen, G. Cultural differences in ultimatum game experiments: Evidence from a meta-analysis. Exp. Econ. 2004, 7, 171–188. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental comparisons. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef]
- Roth, A. Bargaining experiments. In The Handbook of Experimental Economics; Kagel, J., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 253–348. [Google Scholar]
- Zultan, R. Strategic and Social Pre-Play Communication in the Ultimatum Game. J. Econ. Psychol. 2012, 33, 425–434. [Google Scholar] [CrossRef]
- Battigalli, P.; Charness, G.; Dufwenberg, M. Deception: The role of guilt. J. Econ. Behav. Organ. 2013, 93, 227–232. [Google Scholar] [CrossRef]
- Battigalli, P.; Dufwenberg, M. Guilt in games. Am. Econ. Rev. 2007, 97, 170–176. [Google Scholar] [CrossRef]
- Andreoni, J.; Rao, J.M. The power of asking: How communication affects selfishness, empathy, and altruism. J. Public Econ. 2011, 95, 513–520. [Google Scholar]
- Houser, D.; Xiao, E. Classification of natural language messages using a coordination game. Exp. Econ. 2011, 14, 1–14. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
| 1. | By viewing the ultimatum game simply as the dictator game with the recipient having the option to veto the allocation, then one may attribute any behavioral differences between the games to the existence of this veto option in the ultimatum game. |
| 2. | Empirically, Brandts and Charness [10] conclude that both the strategy- and the direct response-method yield similar results in general, consistent with what game theory predicts. |
| 3. | Refer to the instructions in the Appendix A for details. |
| 4. | The random effects linear and probit models are estimated using the maximum likelihood estimation method. |
| 5. | A feasible estimation approach with monotonic strategy-vectors is to define a minimum acceptance threshold for a responder, i.e., the minimum amount that the responder is willing to accept, and then analyze how it changes across treatments (see, for example, Zultan [12]). |
| 6. | GLLAMM refers to the Stata program to fit generalized linear latent and mixed models. |
| 7. | As a disclaimer, we acknowledge that equal is not necessarily fair. However, for most participants in the ultimatum game, there is a high positive correlation between the two concepts. |
| 8. | In particular, for Andreoni and Rao [15], one sided communication results in lower contributions compared to no communication and all other communication conditions. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).