Probabilistic Unawareness
Abstract
:1. Introduction
2. Awareness and Unawareness
2.1. Some Intuitions
- there is “ignorance about the state space”
- “some of the facts that determine which state of nature occurs are not present in the subject’s mind”
- “the agent does not know, does not know that she does not know, does not know that she does not know that she does not know, and so on...”
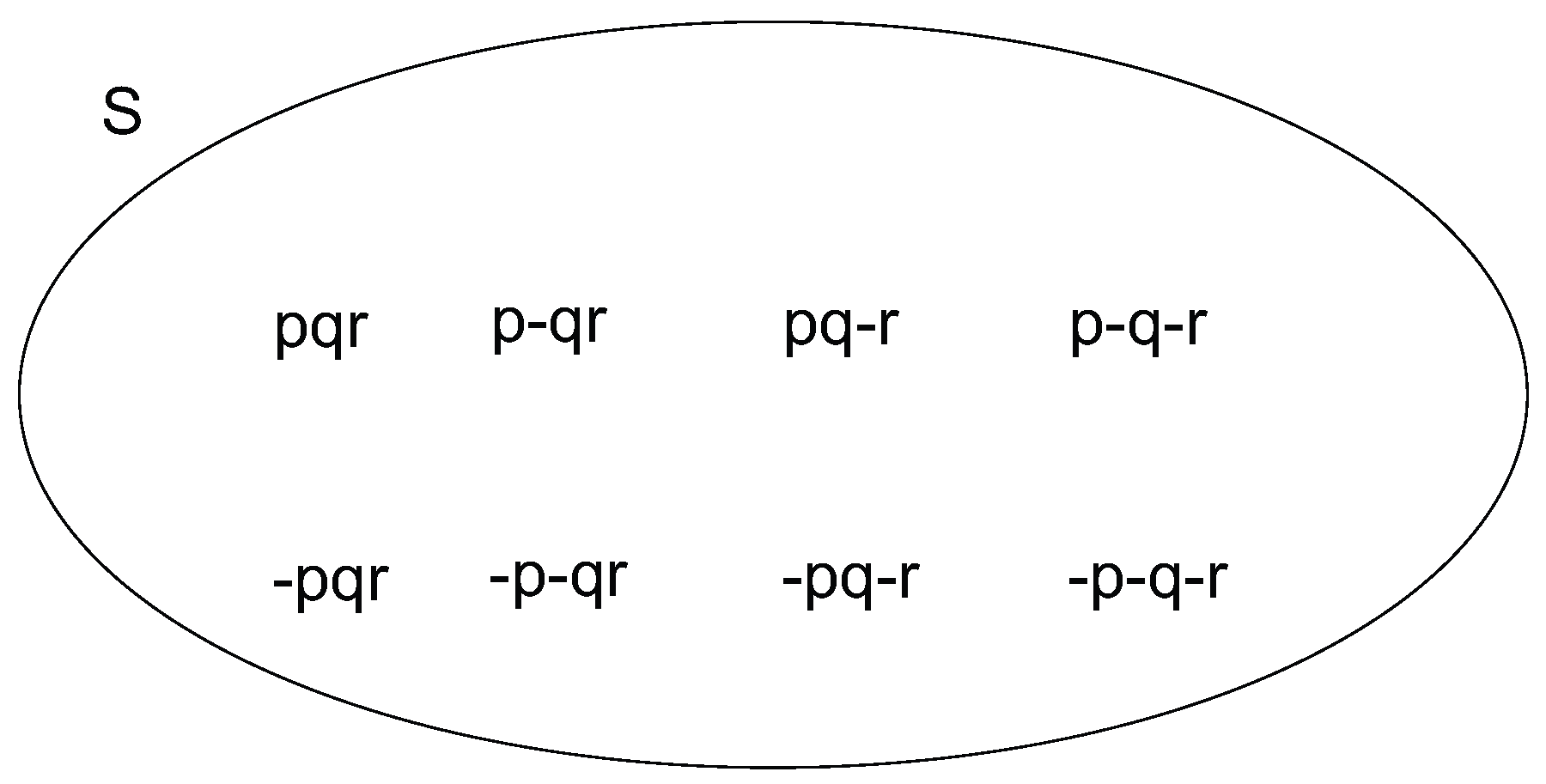
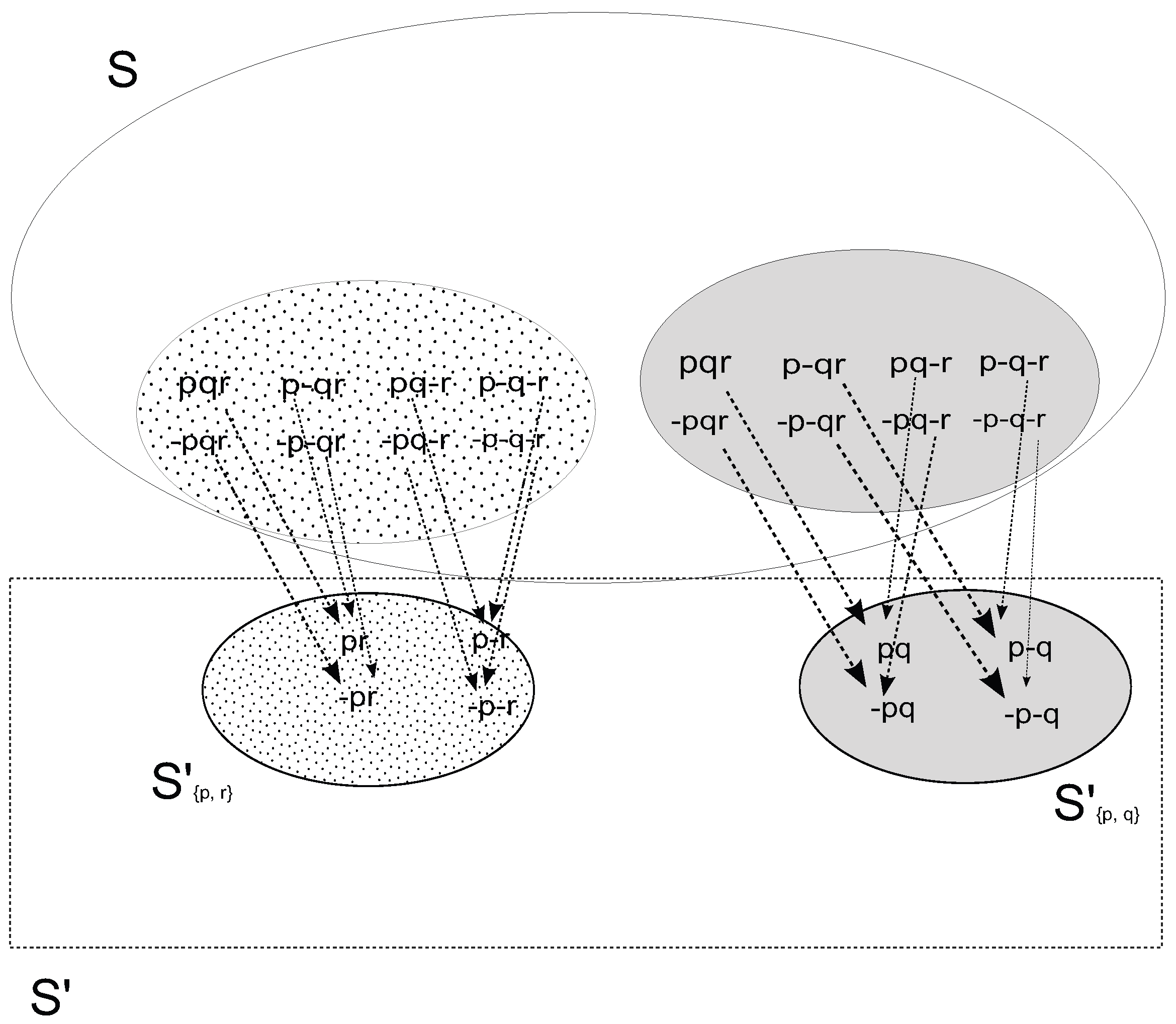
- p: the house is no more than 1 km far from the sea
- q: the house is no more than 1 km far from a bar
- r: the house is no more than 1 km far from an airport
- State (i): Pierre is undecided about r’s truth: he neither believes that r, nor believes that ; there are both r-states and -states that are epistemically accessible to him.
- State (ii): the possibility that r does not come up to Pierre’s mind. Pierre does not ask himself: ‘is there an airport no more than 1 km far from the house?”.
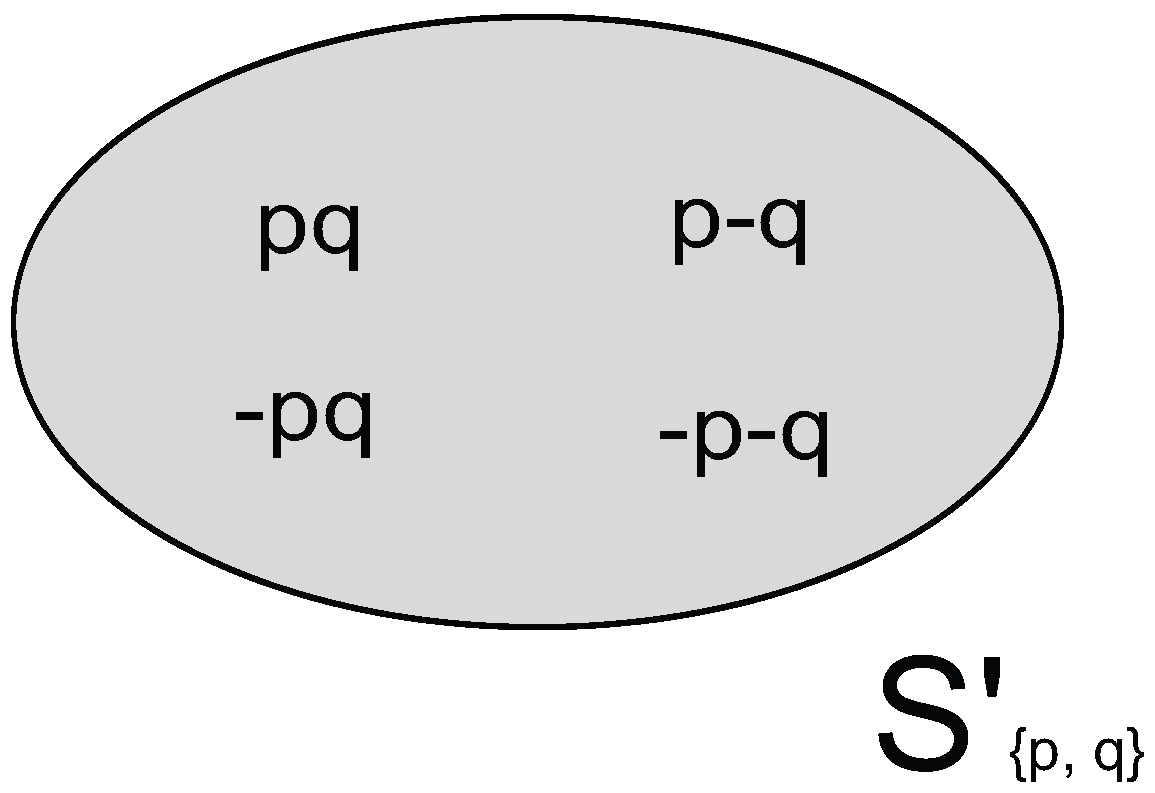
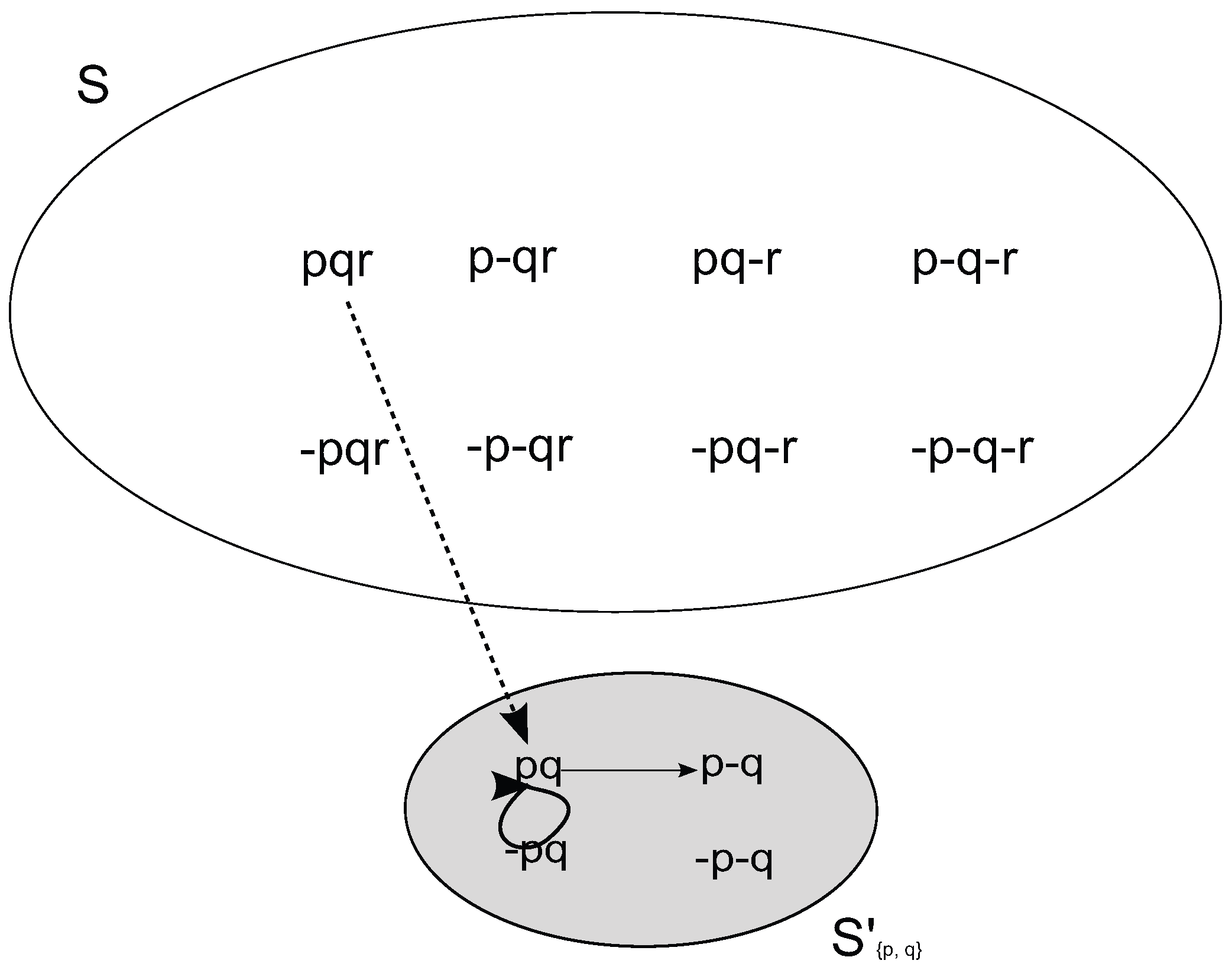
- where each state is labeled by the sequence of literals that are true in it. This state is also Pierre’s in doxastic State (i). The doxastic State (ii), on the other hand, is:
- Some states in the initial state space have been fused with each other; those that differ only in the truth value they assign to the formula the agent is unaware of, namely r.7
2.2. Some Principles in Epistemic Logic
- means “the agent believes that ϕ,
- means “the agent is aware that ϕ”.
| (symmetry) | |
| (distributivity over ∧) | |
| (self-reflection) | |
| (U-introspection) | |
| (plausibility) | |
| (strong plausibility) | |
| (BU-introspection) |
- (i)
- a non-trivial awareness operator that satisfies plausibility, U-introspection and BU-introspection and
- (ii)
- a belief operator that satisfies either necessitation or the rule of monotonicity8.
2.3. Some Principles in Probabilistic Logic
| (symmetry) | |
| (distributivity over ∧) | |
| (self-reflection) | |
| (U-introspection) | |
| (plausibility) | |
| (strong plausibility) | |
| (U-introspection) | |
| (minimality) |
3. Probabilistic (Modal) Logic
3.1. Language
- (the agent believes at most to degree a that ϕ)
3.2. Semantics
- (i)
- S is a state space
- (ii)
- Σ is a σ-field of subsets of S
- (iii)
- is a valuation for S s.t. is measurable for every
- (iv)
- is a measurable mapping from S to the set of probability measures on Σ endowed with the σ-field generated by the sets, .
- (i)
- iff
- (ii)
- iff and
- (iii)
- iff
- (iv)
- iff
3.3. Axiomatization
| System (PROP) Instances of propositional tautologies (MP) From ϕ and , infer ψ (L1) (L2) (L3) (L4) (DefM) (RE) From infer (B) From infer |
4. A Detour by Doxastic Logic without Full Awareness
4.1. Basic Heuristics
4.2. Generalized Standard Structures
- (i)
- S is a state space
- (ii)
- (where are disjoint) is a (non-standard) state space
- (iii)
- is a valuation for S
- (iv)
- is an accessibility relation for S
- (v)
- is an onto map s.t.
- (1) if , then (a) for each atomic formula , and (b) and
- (2) if , then
- (vi)
- is a valuation for s.t. for all for all , iff (a) and (b) for all . We note .
- (vii)
- is an accessibility relation for S s.t. for all for all , for some . We note .
- (i)
- iff
- (ii)
- iff and
- (iii)
- iff and either , or and
- (iv)
- iff for each ,
- (v)
4.3. Partial Generalized Standard Structures
5. Probabilistic Logic without Full Awareness
5.1. Language
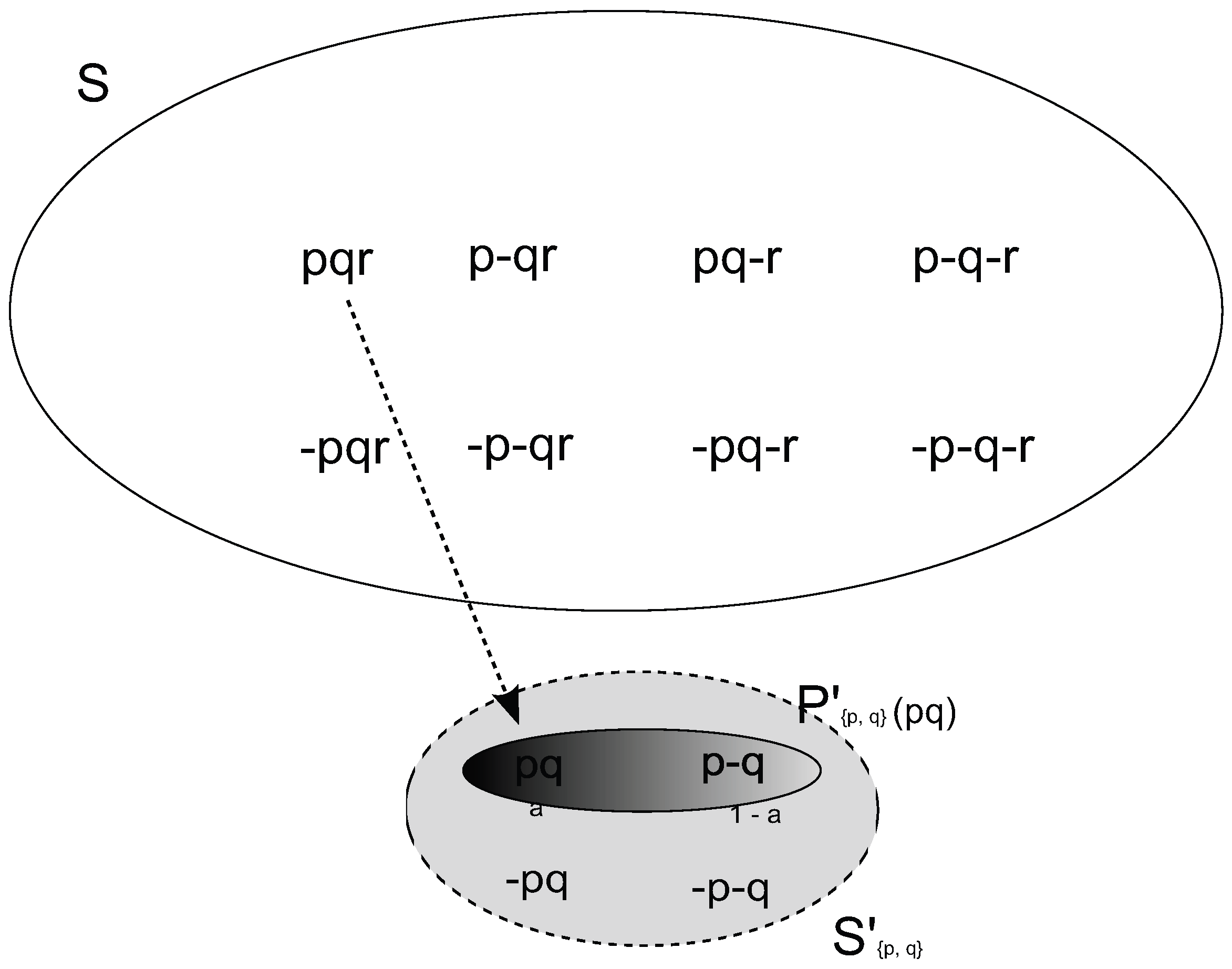
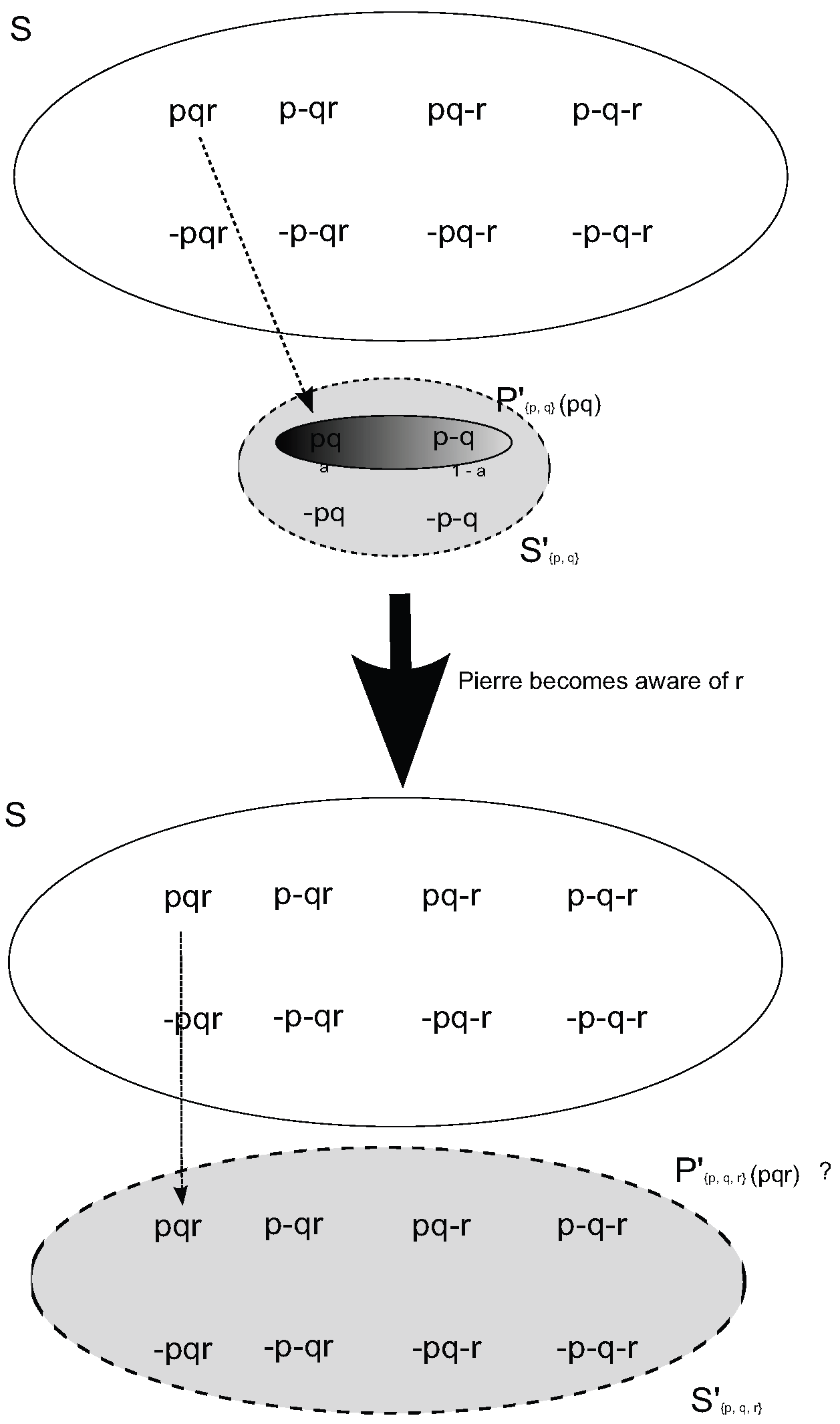
5.2. Generalized Standard Probabilistic Structures
- (i)
- S is a state space.
- (ii)
- where are disjoint “subjective” state spaces. Let .
- (ii)
- For each , is a σ-field of subsets of .
- (iii)
- is a valuation.
- (iv)
- is a measurable mapping from to the set of probability measures on endowed with the σ-field generated by the sets for all , .
- (v)
- is an onto map s.t. if , then for each atomic formula , . By definition, if and if .
- (vi)
- extends π to as follows: for all , iff and for all , 17. For every , , is measurable w.r.t. .
- (i)
- iff
- (ii)
- iff and
- (iii)
- iff and either , or and
- (iv)
- iff and
- (v)
- iff
| (symmetry) | |
| (distributivity over ∧) | |
| (self-reflection) | |
| (U-introspection) | |
| (plausibility) | |
| (strong plausibility) | |
| (U-introspection) | |
| (minimality) |
5.3. Axiomatization
| System (PROP) Instances of propositional tautologies (MP) From ϕ and , infer ψ (A1) (A2) (A3) (A4) (A5) (L1) (L2) (L3) (L4) (RE) From and , infer (B) From , infer: |
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Doxastic Logic: Proofs and Illustrations
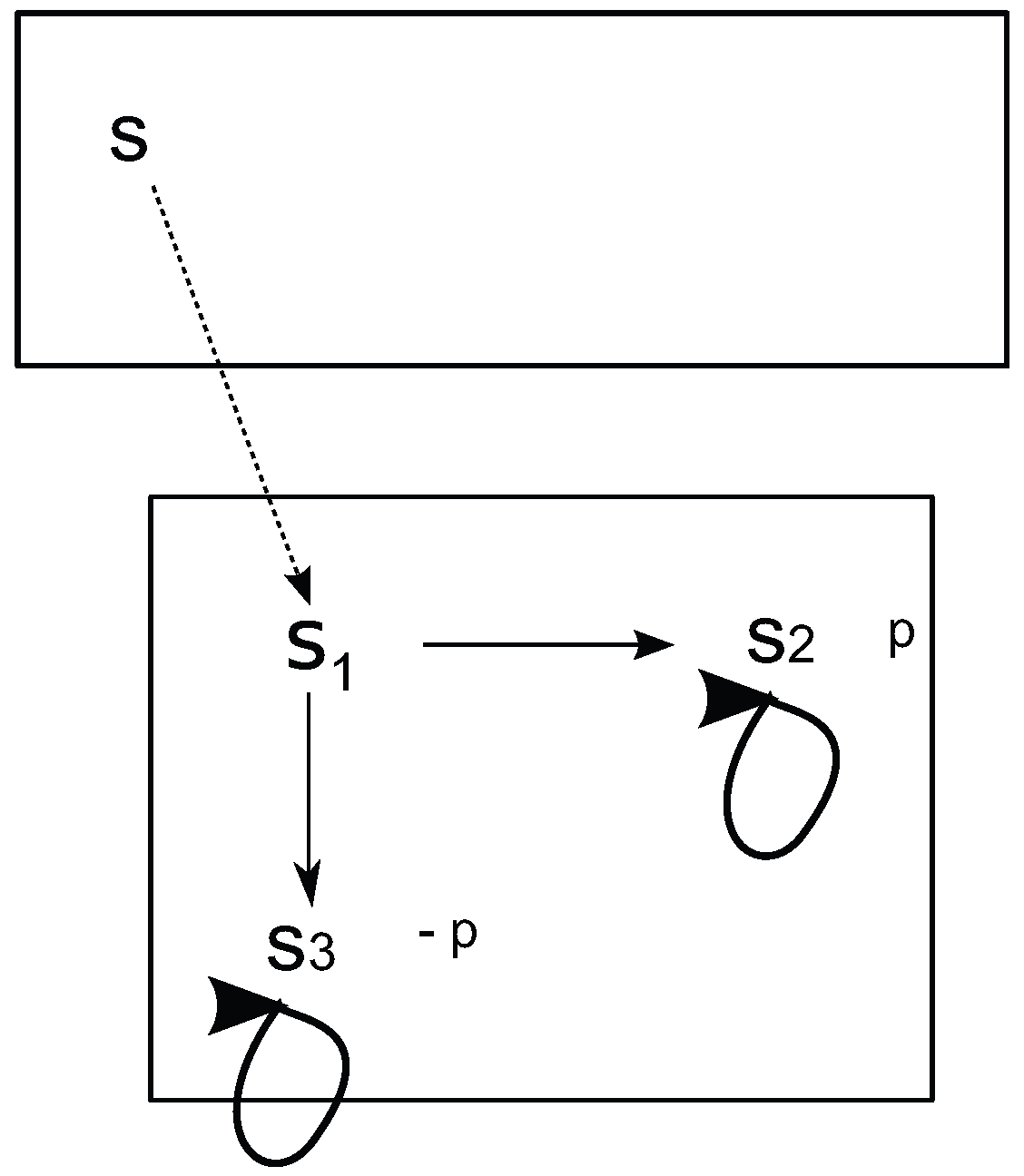
Appendix A.1. Illustration
- the actual state is
- s is projected in for some
- , and
- and
Appendix A.2. Proof of Fact 1
- if , then or iff ( and ) or ( and not ) iff .
- if , then or iff or iff ( and ) or ( and ) iff ( and ) or ( and ) iff iff
- if , then or iff ( and ) or ( and ( or )) iff by IH ( and and ) or ( and not ( and )) iff
- if , then or iff (for each , ) or ( and ) iff, by the induction hypothesis and since each belongs to - () or ( and ) iff
- if , then or iff or ( and ) iff (by Induction Hypothesis) or ( and ) iff (by the induction hypothesis) or ( and ) iff iff .
Appendix A.3. An Axiom System for Partial GSSs
- (i)
- S is a state space,
- (ii)
- is a valuation,
- (iii)
- is an accessibility relation,
- (iv)
- is a function that maps every state in a set of formulas (“awareness set”).
- 1.
- For every serial p.d. awareness structure , there exists a serial partial GSS based on the same state space S and the same valuation π s.t. for all formulas and each possible state siff
- 2.
- For every serial partial GSS , there exists a serial p.d. awareness structure based on the same state space S and the same valuation π s.t. for all formulas and each possible state siff
| System (PROP) Instances of propositional tautologies (MP) From ϕ and , infer ψ (K) (Gen)From ϕ, infer (D) (A1) (A2) (A3) (A4) (A5) (Irr)If no atomic formulas in ϕ appear in ψ, from , infer ψ |
Appendix B. Probabilistic Logic: Proof of the Completeness Theorem for HMU
- as atomic formulas, only , i.e., the atomic formulas occurring in ϕ,
- only probabilistic operators belonging to the finite set of rational numbers of the form , where q is the smallest common denominator of indexes occurring in ϕ and
- only formulas of epistemic depth smaller than or equal to that of ϕ (an important point is that we stipulate that the awareness operator A does not add any epistemic depth to a formula: ).
- (1)
- consider , the set of all the disjunctive normal forms built from , the set of propositional variables occurring in ϕ.
- (2)
- is the set of formulas for all where ψ is a disjunctive normal form built with “atoms” coming from to .
- (3)
- the construction has to be iterated up to the epistemic depth n of ϕ, hence to . The base is , i.e., the set of disjunctive normal forms built with “atoms” from to .
- (i)
- ( is the set of atomic components of epistemic depth 0)
- (i’)
- ( is the set of disjunctive normal forms based on )
- (ii)
- (ii’)
- .
- (i)
- , , .
- (ii)
- For each , in each , , there is a formula , which is equivalent to ψ
- (i)
- : ψ is obviously equivalent to some DNF in and .
- (ii)
- : by the induction hypothesis, there is equivalent to in and equivalent to in . Suppose w.l.o.g.that and, therefore, that . Then, can be expanded in . Obviously, the disjunction of the conjunctions occurring both in and is in and equivalent to ψ.
- (iii)
- : by IH, there is equivalent to χ in . Note that . By construction, . Consequently, there will be in a DNF equivalent to . Since , this DNF can be associated by expansion to a DNF in the base . Furthermore, since and , it follows by the rule of equivalence that .
- (i)
- (i’)
- (ii)
- and
- (ii’)
- .
- (i)
- , where , .
- (ii)
- , , , , there is a formula , which is equivalent to ψ.
- (iii)
- , if , then there is a formula , which is equivalent to ψ in .
- (iv)
- , , .
- (i)
- : ψ is obviously equivalent to some DNF in . Clearly, and .
- (ii)
- : by IH,- there is s.t. and and- there is s.t. and andLet us consider and suppose without loss of generality that . One may expand from to and expand the resulting DNF to . On the other hand, may be expanded to . is the disjunction of the conjunctions common to and . Obviously, and .
- (iii)
- : by IH, there is equivalent to χ in with . is equivalent to where . Each is in , so by expansion in , there is a DNF equivalent to it and, therefore, a DNF equivalent to .
- (iv)
- : by IH, there is equivalent to χ in with and . Note that . By construction, . Consequently, there will be in a DNF logically equivalent to . Since , there will be in the base a formula logically equivalent to . Furthermore, since and and , it follows that .
- (i)
- A formula ϕ is deducible from a set of formulas Γ, symbolized , if there exists some formulas in Γ s.t. .
- (ii)
- A set of formulas Γ is -consistent if it is false that
- (iii)
- A set of formulas Γ is maximally -consistent if (1) it is -consistent and (2) if it is not included in a -consistent set of formulas.
- (a)
- Let us say that two sets of formulas are Δ-equivalent if they agree on each formula that belongs to Δ. identifies the maximal -consistent sets of formulas that are -equivalent. is infinite iff there are infinitely many maximal -consistent sets of formulas that are not pairwise -equivalent.
- (b)
- If is a base for , then two sets of formulas are -equivalent iff they are -equivalent. Suppose that and are not -equivalent. This means w.l.o.g. that there is a formula ψ s.t. (i) , (ii) and (iii) . Let be a formula s.t. . Clearly, and and . Therefore, and are not -equivalent. The other direction is obvious.
- (c)
- Since is finite, there are only finitely many maximal -consistent sets of formulas that are not pairwise -equivalent. Therefore, is finite.
- (i)
- and
- (ii)
- and .
- (i)
- (ii)
- (i)
- For each , is finite.
- (ii)
- For each subset , there is s.t. where denotes the set of states of to which ψ belongs.
- (iii)
- For all , , iff
- (i)
- , implies , and implies
- (ii)
- There are only two cases: (i) either and while for , (ii) or and for any .
- (iii)
- (where q is the common denominator to the indexes)
- (i)
- is a maximal -consistent set}
- (ii)
- where is a maximal -consistent set, and
- (iii)
- for each ,
- (iv)
- for all state and atomic formula , iff
- (v)
- for , is a probability distribution on satisfying Condition (C)24.
- ; following directly from the definition of .
- . Since Γ is a standard state iff iff (by IH) . We shall show that iff . (⇒) Let us suppose that ; χ is in ; hence, given the properties of maximally-consistent sets, where is the extension of Γ to (the whole language). Additionally, since , . (⇐) Let us suppose that . Γ is coherent, therefore .
- . (⇒). Let us assume that . Then, and . By IH, this implies that and . Given the properties of maximally-consistent sets, this implies in turn that . (⇐). Let us assume that . Given the properties of maximally-consistent sets, this implies that and and, therefore, by IH, that and .
- . We know that in any GSPS , if for some , then iff . In our case, , and . Therefore, iff . However, given that , iff .
- . By definition iff and .(⇐) Let us suppose that and . Hence, is well defined. It is clear that given our definition of . It is easy to see that for . As a consequence, . (⇒) Let us suppose that . This implies that and, therefore, that . By construction, , and therefore, . Hence, .
- If , then oriff ( and ) or ( and )iff
- If , then oriff oriff ( and ) or ( and )iff ( and ) or ( and )iffiff
- If , then oriff ( and ) or ( and ( or ))iff by the induction hypothesis ( and and ) or ( and not ( and ))iff
- if , then oriff (for each , ) or ( and )iff, by the induction hypothesis and since each belongs to - () or ( and )iff
- If , then oriff () or ( and not , impossible given the induction hypothesis)iff ()iff (by the induction hypothesis)iff
References
- Fagin, R.; Halpern, J.; Moses, Y.; Vardi, M. Reasoning about Knowledge; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Hintikka, J. Impossible Worlds Vindicated. J. Philos. Log. 1975, 4, 475–484. [Google Scholar] [CrossRef]
- Wansing, H. A General Possible Worlds Framework for Reasoning about Knowledge and Belief. Stud. Log. 1990, 49, 523–539. [Google Scholar] [CrossRef]
- Fagin, R.; Halpern, J. Belief, Awareness, and Limited Reasoning. Artif. Intell. 1988, 34, 39–76. [Google Scholar] [CrossRef]
- Modica, S.; Rustichini, A. Unawareness and Partitional Information Structures. Games Econ. Behav. 1999, 27, 265–298. [Google Scholar] [CrossRef]
- Dekel, E.; Lipman, B.; Rustichini, A. Standard State-Space Models Preclude Unawareness. Econometrica 1998, 66, 159–173. [Google Scholar] [CrossRef]
- Halpern, J. Plausibility Measures : A General Approach for Representing Uncertainty. In Proceeddings of the 17th International Joint Conference on AI, Seattle, WA, USA, 4–10 August 2001; pp. 1474–1483.
- Heifetz, A.; Meier, M.; Schipper, B. Interactive Unawareness. J. Econ. Theory 2006, 130, 78–94. [Google Scholar] [CrossRef]
- Li, J. Information Structures with Unawareness. J. Econ. Theory 2009, 144, 977–993. [Google Scholar] [CrossRef]
- Galanis, S. Unawareness of theorems. Econ. Theory 2013, 52, 41–73. [Google Scholar] [CrossRef]
- Feinberg, Y. Games with Unawareness; Working paper; Stanford Graduate School of Business: Stanford, CA, USA, 2009. [Google Scholar]
- Heifetz, A.; Meier, M.; Schipper, B. Dynamic Unawareness and Rationalizable Behavior. Games Econ. Behav. 2013, 81, 50–68. [Google Scholar] [CrossRef]
- Rêgo, L.; Halpern, J. Generalized Solution Concepts in Games with Possibly Unaware Players. Int. J. Game Theory 2012, 41, 131–155. [Google Scholar] [CrossRef]
- Schipper, B. Awareness. In Handbook of Epistemic Logic; van Ditmarsch, H., Halpern, J.Y., van der Hoek, W., Kooi, B., Eds.; College Publications: London, UK, 2015; pp. 147–201. [Google Scholar]
- Aumann, R. Interactive Knowledge. Int. J. Game Theory 1999, 28, 263–300. [Google Scholar] [CrossRef]
- Harsanyi, J. Games with Incomplete Information Played by ‘Bayesian’ Players. Manag. Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- Fagin, R.; Halpern, J.; Megiddo, N. A Logic for Reasoning About Probabilities. Inf. Comput. 1990, 87, 78–128. [Google Scholar] [CrossRef]
- Lorenz, D.; Kooi, B. Logic and probabilistic update. In Johan van Benthem on Logic and Information Dynamics; Baltag, A., Smets, S., Eds.; Springer: Cham, Switzerland, 2014; pp. 381–404. [Google Scholar]
- Heifetz, A.; Mongin, P. Probability Logic for Type Spaces. Games Econ. Behav. 2001, 35, 34–53. [Google Scholar] [CrossRef]
- Cozic, M. Logical Omniscience and Rational Choice. In Cognitive Economics; Topol, R., Walliser, B., Eds.; Elsevier/North Holland: Amsterdam, Holland, 2007; pp. 47–68. [Google Scholar]
- Heifetz, A.; Meier, M.; Schipper, B. Unawareness, Beliefs and Speculative Trade. Games Econ. Behav. 2013, 77, 100–121. [Google Scholar] [CrossRef]
- Schipper, B.; University of California, Davis. Impossible Worlds Vindicated. Personal communication, 2013. [Google Scholar]
- Sadzik, T. Knowledge, Awareness and Probabilistic Beliefs; Stanford Graduate School of Business: Stanford, CA, USA, 2005. [Google Scholar]
- Savage, L. The Foundations of Statistics, 2nd ed.; Dover: New York, NY, USA, 1954. [Google Scholar]
- Board, O.; Chung, K. Object-Based Unawareness; Working Paper; University of Minnesota: Minneapolis, MN, USA, 2009. [Google Scholar]
- Board, O.; Chung, K.; Schipper, B. Two Models of Unawareness: Comparing the object-based and the subjective-state-space approaches. Synthese 2011, 179, 13–34. [Google Scholar] [CrossRef]
- Chen, Y.C.; Ely, J.; Luo, X. Note on Unawareness: Negative Introspection versus AU Introspection (and KU Introspection). Int. J. Game Theory 2012, 41, 325–329. [Google Scholar] [CrossRef]
- Fagin, R.; Halpern, J. Uncertainty, Belief and Probability. Comput. Intell. 1991, 7, 160–173. [Google Scholar] [CrossRef]
- Halpern, J. Reasoning about Uncertainty; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Vickers, J.M. Belief and Probability; Synthese Library, Reidel: Dordrecht, Holland, 1976; Volume 104. [Google Scholar]
- Aumann, R.; Heifetz, A. Incomplete Information. In Handbook of Game Theory; Aumann, R., Hart, S., Eds.; Elsevier/North Holland: New York, NY, USA, 2002; Volume 3, pp. 1665–1686. [Google Scholar]
- Kraft, C.; Pratt, J.; Seidenberg, A. Intuitive Probability on Finite Set. Ann. Math. Stat. 1959, 30, 408–419. [Google Scholar] [CrossRef]
- Gärdenfors, P. Qualitative Probability as an Intensional Logic. J. Philos. Log. 1975, 4, 171–185. [Google Scholar] [CrossRef]
- Van Benthem, J.; Velazquez-Quesada, F. The Dynamics of Awareness. Synthese 2010, 177, 5–27. [Google Scholar] [CrossRef]
- Velazquez-Quesada, F. Dynamic Epistemic Logic for Implicit and Explicit Beliefs. J. Log. Lang. Inf. 2014, 23, 107–140. [Google Scholar] [CrossRef]
- Hill, B. Awareness Dynamics. J. Philos. Log. 2010, 39, 113–137. [Google Scholar] [CrossRef]
- Halpern, J. Alternative Semantics for Unawareness. Games Econ. Behav. 2001, 37, 321–339. [Google Scholar] [CrossRef]
- Blackburn, P.; de Rijke, M.; Venema, Y. Modal Logic; Cambridge UP: Cambridge, UK, 2001. [Google Scholar]
- 2.In the whole paper we use “awareness” to denote the model of [4], to be distinguished from the attitude of awareness.
- 6.This is close to the “small world” concept of [24]. In Savage’s language, “world” means the state space or set of possible worlds, itself.
- 7.Once again, the idea is already present in [24]: “...a smaller world is derived from a larger by neglecting some distinctions between states”. The idea of capturing unawareness with the help of coarse-grained or subjective state spaces is widely shared in the literature; see, for instance, [8] or [9]. By contrast, in the framework of first-order epistemic logic, unawareness is construed as unawareness of some objects in the domain of interpretation by [25]. This approach is compared with those based on subjective state spaces in [26].
- 10.For a philosophical elaboration on this distinction, see [30].
- 11.A similar list of properties is proven in [21].
- 13.Since a is a rational number and the structures will typically include real-valued probability distributions, it may happen in some state that for no a, it is true that . It happens when the probability assigned to ϕ is a real, but non-rational number.
- 14.The work in [19] calls this system Σ+.
- 15.In an objective state space, the set of states need not reflect the set of possible truth-value assignments to propositional variables (as is the case in our example).
- 16.Intuitively: if the agent does not believe that ϕ, this means that not every state of the relevant partition’s cell makes ϕ true. If ϕ belonged to the sub-language associated with the relevant subjective state space, since the accessibility relation is partitional, this would imply that would be true in every state of the cell. However, by hypothesis, the agent does not believe that she/he does not believe that ϕ. We have therefore to conclude that ϕ does not belong to the sub-language of the subjective state space (see Fact 1 below). Hence, no formula can be true.
- 17.It follows from Clause (v) above that this extension is well defined.
- 18.In what follows, denotes the set of propositional variables occurring in ϕ.
- 19.I thank an anonymous referee for suggesting to me to clarify this point.
- 20.This restricted rule is reminiscent of the rule in [5].
- 21.Note that he/she could become unaware of some possibilities as well, but we will not say anything about that.
- 23.The work in [19] leaves the construction implicit.
- 24.In the particular case where , the probability assigns maximal weight to the only state of .
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cozic, M. Probabilistic Unawareness. Games 2016, 7, 38. https://doi.org/10.3390/g7040038
Cozic M. Probabilistic Unawareness. Games. 2016; 7(4):38. https://doi.org/10.3390/g7040038
Chicago/Turabian StyleCozic, Mikaël. 2016. "Probabilistic Unawareness" Games 7, no. 4: 38. https://doi.org/10.3390/g7040038
APA StyleCozic, M. (2016). Probabilistic Unawareness. Games, 7(4), 38. https://doi.org/10.3390/g7040038




