1. Introduction
In the summer of 2015, when the full scale of Europe’s refugee crisis became apparent to many, Hungarian prime minister Viktor Orbán proposed to give Syria’s neighboring countries three billion euros in financial aid. Hungary’s recent political course is often characterized as “anything but left”—see for example Szikra’s review [
1]—therefore, this apparent altruistic gesture was surprising. But Orbán’s proposal did not reveal pure altruism; it signaled clear Hungarian self-interest: an increased welfare could help Syria’s neighbors absorb more refugees; less inequality between Europe and the Middle East could make Europe a comparatively less attractive destination; and less inequality
within and
between Middle Eastern societies could even mitigate existing conflicts. Orbán’s proposals alone will, arguably, not solve the refugee crisis; but his statements do exemplify that overt distributional considerations can serve one’s ultimate self-interest.
Deviations from pure material self-interest have received much scholarly attention. The Dictator Game (DG) has become the prototypical tool to study the motives behind such non-selfish behavior. In the DG a decision-maker—the Dictator—is asked to choose between options that differ in the amount of monetary payoffs allocated to self and one or more other players. The game is one-shot, choices are made anonymously, and the other players must accept the Dictator’s decision [
2]. This eliminates the need for strategic considerations [
3]: Dictators can maximize selfish outcomes without having to fear future retaliation. Nevertheless, countless experiments have shown that non-selfish DG-choices are frequent [
4,
5]. Many individuals thus appear to have a
baseline-level of social motives [
3,
6,
7,
8].
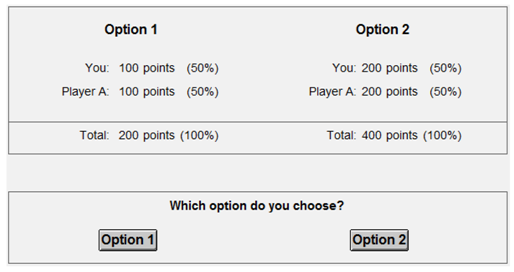
Much research has focused on social motives in two-player DGs. To explain the frequent deviations from selfishness, non-selfish utility functions have been introduced to capture how the other player’s material payoffs enter the utility of ego [
8,
9,
10]. A summary of Schulz and May [
11] showed that two-player models typically contain combinations of motives regarding own material payoffs (
selfishness), joint payoffs for self and other (
efficiency), payoffs received by the other player (
social efficiency), and the inequality between payoffs for self and payoffs for the other (
self-centered inequality). Multiplayer DGs have been studied increasingly in the last decades, and attempts have been made to generalize dyadic motives to the multiplayer setting [
12,
13,
14]. But such generalizations are not straightforward. First, an extensive comparison [
5] showed that Dictators shared significantly more in games with multiple recipients. Group size may thus influence the strength of social motives
1. Secondly, recent four-player experiments showed that the amount of sharing varied according to the decision-maker’s (earned) economic status [
13,
15]. The mechanisms that drive non-selfish choices may thus be considerably more complex in multiplayer games.
A distinctive feature of the multiplayer setting is that decision-makers can face dilemmas regarding the distribution of payoffs
between others, irrespective of (social) efficiency and self-centered inequality. Multiplayer DGs can be used to assess the comparative importance of such a
non-self-centered inequality motive, but studies on this matter have been scarce. Some prominent models have simply assumed that the non-self-centered inequality motive is negligible, or reduces to more basic types of motives
2. For example, decision-makers in the ERC model of Bolton and Ockenfels [
19] can consider their own payoffs and their relative position with respect to the group average (
i.e., the social reference point), but not the inequality that may exist within the group. Similarly, the inequality-aversion model of Fehr and Schmidt [
20] distinguishes different types of self-centered inequality motives (envy and guilt), but the model also assumes that individuals ignore the inequality
between other players.
The
social welfare model of Charness and Rabin [
14] and the
efficiency-maximin model of Engelmann and Strobel [
21]
do allow considerations for the distribution of goods between others. However, empirical tests have been limited to three-player games, which have inherent confounds. According to the social welfare model, individuals are motivated to increase the total amount of payoffs for all others, and favor distributions that progressively improve the conditions of the worst-off. Charness and Rabin [
14] tested the model in three-player DGs in which decision-makers could choose between an egalitarian option where self and two others received 575 points each, and an unequal option, where self received 900 points, and the two other players received 300 and 600 points respectively. Self-interested decision-makers would choose the second option, yet results showed that the majority (54%) chose the first option. But as the authors noted themselves: these results do not prove the existence of social welfare motives: considerations for social efficiency, self-centered inequality, or non-self-centered inequality could explain these choices as well. The model of Engelmann and Strobel [
21] assumes that decision-makers want to increase social efficiency and minimize the largest payoff-inequality between self and others (
i.e., a maximin motive). The model was tested on a number of three-player taxation DGs. In these games, decision-makers had middle-class positions, and were asked to choose between options with different allocations of payoffs between the other players. Results showed that many effectively transferred payoffs from rich to poor, which suggests a maximin motive; but these results are again troubled by confounds.
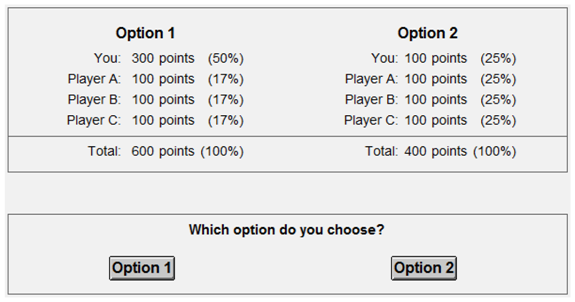
This research aims to study social motives in the multiplayer DG, and in particular to assess whether choices can be explained better with models that take non-self-centered inequality motives into account. Our review of previous studies showed that three-player DGs have inherit confounds, therefore we focus on the four-player DG—the added recipient allows us to better disentangle multiple types of motives. Confounds can be eliminated by holding certain (irrelevant) selfish or social consequences constant, but this should be done with care. Engelmann and Strobel [
21] for example eliminated selfish motives by fixing the material payoffs allocated to the decision-maker across the DG’s options. This allowed them to show the existence of the inequality-aversion motive in isolation, but their games lost their resemblance to real-world taxation problems (which generally involve at least some immediate efficiency-loss in the form of administrative costs). Moreover, if games allow decision-makers to influence social outcomes “for free”, it becomes impossible to quantify a motive’s strength. We strive to compare the relative importance of different types of selfish and social motives; this requires DGs with
trade-offs between selfish and social outcomes.
Our study is structured as follows. First, we theorize why it is relevant to model non-self-centered inequality motives. Secondly, we present a utility function that incorporates this motive in addition to motives regarding social efficiency and self-centered inequality. This model can be applied to two-player and multiplayer games, and contains a number of the aforementioned models as special cases. Thirdly, we estimate the model on data from two controlled experiments. We assess its comparative performance and interpret its parameters. Fourthly, we conduct exploratory analyses to assess whether our findings are robust to violations of our modeling assumptions; specifically, we consider non-linearities and alternative comparison mechanisms in the evaluation of inequalities. Finally, we discuss the implications of our findings, and suggest directions for further research.
3. Model
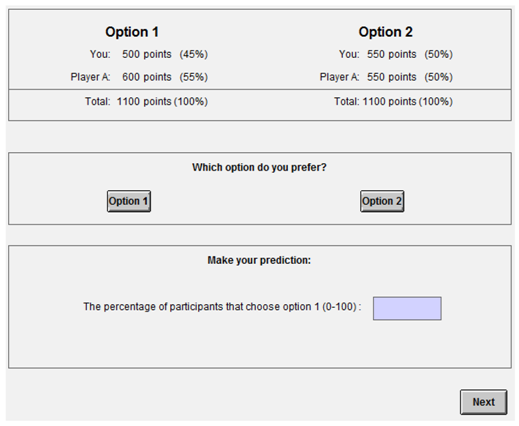
In multiplayer DGs, Dictators choose between options that vary in the amount of virtual tokens (
x) assigned to self (
i) and other players (
j,
k,
etc.). A rational Dictator evaluates the options according to a personal function that converts material payoffs to effective utilities, and then chooses the option that maximizes utility [
7]. We define utility as a linear combination of the option’s selfish and social consequences (
X), weighed by the decision-maker’s motives (
):
What selfish and social consequences should be included in our model? Previous research has shown that decision-makers in small-scale DGs consider social efficiency [
21,
38], as well as advantageous and disadvantageous inequality [
20,
22]. Our theory suggests that for the multiplayer setting, inequalities between others matter as well. It seems straightforward to construe a four-parameter model with corresponding terms for all aforementioned motives, but such
ad-hoc combinations can create identification problems. Engelmann [
39] showed that this already happens if one were to combine social efficiency motives and the two inequality aversion motives from the Fehr and Schmidt-model (
i.e., even
without introducing a term for non-self-centered inequality). The resulting three-parameter model is not identified, and reduces to a two-parameter model without the efficiency motive, or an equivalent two-parameter model with an efficiency-motive and a term that combines advantageous and disadvantageous inequality motives into one term.
We used the latter type as our reference model to expand with a term for non-self-centered inequality, but we acknowledge that this was an entirely arbitrary choice between two equivalent models.
Table 1 summarizes how we conceptualized
4 selfish and social consequences.
Selfish outcomes reflect the tokens allocated to self;
social efficiency refers to the average amount received by the other players;
self-centered inequality refers to the average pairwise distance between self and others;
non-self-centered inequality refers to the average distance between all pairs of others.
Qualitatively, the parameters in our model can be interpreted as follows: if a subject has , she is indifferent to social efficiency; if she has , she dislikes it; and if she has , she prefers it. The parameters and are interpretable in a similar manner: implies aversion to self-centered inequality, etc. Quantitatively, the parameters are interpretable as follows. First, we note that in our models, the weight of selfish outcomes is always fixed to 1. This causes social outcomes to be scaled relative to selfish outcomes. Suppose that a rational decision-maker is averse to non-self-centered inequality and has = −0.2. Suppose now that she is asked to play a DG that contains a dilemma between selfishness and social outcomes. The two DG-options yield positive payoffs for all players, and are construed such that they differ only in the amount of selfish payoffs and the amount of non-self-centered inequality . Option 1 has high selfish payoffs, but also a high degree of inequality between receivers; Option 2 has low selfish payoffs, but also a low degree of inequality between receivers. According to the DG’s definition, , and . Our decision-maker chooses the selfish option (Option 1) only if the option yields the highest utility, that is, if or, equivalently, if She chooses the non-selfish option (Option 2) only if the social gains outweigh the incurred selfish losses by a factor of five or more.
5. Results
Estimations were performed with
Just Another Gibbs Sampler (
JAGS) [
51] via its
RJAGS-plugin (version 3.4.0) for
R [
52]. Two chains were run from randomly generated initial values. A
burn-in period of 50,000 iterations was used, and samples were thinned at five iterations to minimize serial autocorrelation. A visual inspection showed stable trace plots for all parameters (see the supplementary materials), and the Markov Chain Monte Carlo (MCMC) errors were sufficiently small compared to the parameter estimates (
i.e., less than 5% of the posterior standard deviation). There were no signs of non-convergence, hence an additional 50,000 samples were drawn. Density plots showed that all parameters had symmetric and approximately normal posteriors. Results are presented as summaries of the parameters’ respective posterior distributions. Posterior means can be interpreted analogous to frequentist point estimates; posterior standard deviations are analogous to standard errors; and Bayesian
credible intervals are provided instead of frequentist
confidence intervals.
5.1. Model Selection
The main model is compared against a number of notable restricted models. The baseline model
M0 represents a
selfish model, in which decision-makers are only motived by selfish concerns, although they may make occasional evaluation errors;
M1 expands the baseline model with a term to capture motives for social efficiency;
M2 then adds a term for self-centered inequality motives, and is similar to the Fehr and Schmidt [
39] model. Our main model of interest is
M3; this model expands
M2 with a term for non-self-centered inequality. Note that by restricting the appropriate parameters in
M3 to zero, the models
M0,
M1, and
M2 can be acquired.
Table 6 summarizes the fit of the aforementioned models against our experimental data.
For the data from the first experiment, M3 showed a better fit than the restricted models. However, in comparison to M2 the improvement was only marginal: the incremental improvement in the DIC was small, ΔDIC(M2, M3) = 12, and only a 0.8% increase in predictive accuracy was achieved. This can be explained by the fact that the experiment contained 10 two-player DGs: for these games, the multiplayer model M3 by definition cannot improve predictions. If we consider only the four-player DGs, M3 did show a more pronounced improvement: for these games, the predictive accuracy increased by 2.3% compared to M2. For the second experiment, results were more straightforward. Again, M3 fitted better than the restricted models, and the improvement over M2 was larger: ΔDIC(M2, M3) = 555; the increase in predictive accuracy of M2 over M3 was 4.2%.
5.2. Parameter Interpretation
The posterior densities of the parameters from
M3 are summarized in
Table 7; estimates for
M2 are reported for reference. We note that for our particular scaled probit regression models it
is valid to compare raw coefficients across models: the constrained weight of selfish outcomes ensures that the models’ coefficients have the same scale. Both experiments showed that the terms shared by
M2 and
M3 are of similar magnitude; adding non-self-centered inequality motives only marginally affected estimates for social efficiency and self-centered inequality motives, we can therefore conclude that non-self-centered inequality has a separate contribution to utility.
We now evaluate the estimated distribution of social motives in our experimental populations, according to the estimates of M3. First, we interpret the motives’ means. These estimates quantify the average weight of the associated outcome on a decision-maker’s utility function. In the first experiment, the posterior estimate for mean( did not differ credibly from zero, since the 95% credible interval (95%-CI) was [−0.118; 0.078]. This indicates that decision-makers were, on average, indifferent to social efficiency. In the second experiment, mean( was credibly positive, 95%-CI [0.073; 0.150]. This indicates an average motive to improve social efficiency. In both experiments, mean() was credibly smaller than zero (i.e., the 95%-CIs are [−0.340; −0.260] and [−0.116; −0.068] respectively). This indicates an average distaste for self-centered inequality. In the first experiment, mean() did not differ credibly from zero, 95%-CI [−0.020; 0.113]; this indicates indifference to non-self-centered inequality. The second experiment showed that mean() was credibly smaller than zero, 95%-CI [−0.135; −0.086], which indicates a distaste for non-self-centered inequality. We note that the average motives differed markedly across experiments; possible explanations for this are presented in the discussion.
In a heterogeneous population, the means of social motives are relatively meaningless quantities on their own (i.e., the average person may not even exist in the data). Therefore we also assessed the level of heterogeneity in motives via the estimated standard deviations sd(), sd(), and sd(). A first observation is that these estimates were large compared to the estimated population means; this is in accordance with our expectation that populations comprise individuals with a large variety of motives. Interestingly, the estimated heterogeneity followed a similar pattern across experiments: sd() was approximately twice the size of both sd( and sd(), and sd() was approximately equal to sd(). We have no explanation for this regularity, and suggest that further research be conducted on the matter.
The estimated correlations quantify the degree of association between social motives. Results showed a negative association between motives for social efficiency and motives regarding self-centered inequality, cor(,) < 0; this negative association is not surprising: the more a decision-maker wants to increase social efficiency (, the more she wants to decrease self-centered inequality (i.e., ). For the first experiment this association was not credibly different from zero, 95%-CI [−0.322; 0.217]; for the second experiment the association was credibly negative, 95%-CI [−0.590; −0.327]. Both experiments showed a credibly negative association between social efficiency motives and motives regarding non-self-centered inequality, 95%-CIs for cor(,) are [−0.617; −0.217] and [−0.425; −0.133] respectively; thus preferences for social efficiency coincide with aversion to non-self-centered inequality. Finally, positive associations were found between motives regarding self-centered and non-self-centered inequality. This association was not credibly different from zero in the first experiment, since the 95%-CI for cor(,) was estimated as [−0.044; 0.490]; but for the second experiment, a credibly positive association was found: the 95%-CI for cor(,) was [0.344; 0.587].
It is observed that the posterior estimates for the correlations between motives were qualitatively similar across experiments, but their posterior uncertainty was considerably larger for the first experiment. This is likely due to a lack of statistical power – the first experiment had too few multiplayer observations. Bayesian procedures could mitigate this via the use of more-informative priors, but this is undesirable, for subsequent results can be unduly influenced by the choice of priors. This may hold especially for random effects, whose covariances have been known to be quite sensitive to the choice of priors [
49].
Appendix 3 presents a sensitivity analysis on this matter. We found that the magnitude of correlations did depend on how the
Wishart-prior was specified. But across investigated priors, posterior estimates of the correlations did not change sign. Qualitatively, our findings hold under many different priors for
.
5.3. Predictions Given Model M3
The estimated means, standard deviations and correlations are sufficient statistics for the
MVN-distribution of social motives in our experimental populations. We use this property to derive point estimates for the prevalence of certain theoretically relevant
combinations of motives. For this we used the R-package
mvtnorm [
53]. All calculations were done
conditional on the estimates from
M3. First, we estimated the percentage of
purely pro-social decision-makers; these are individuals with a combination of social efficiency-preferences (
, aversion to self-centered inequality aversion (
), and aversion to non-self-centered inequality
. In the first experiment, 16.10% qualified as purely pro-social; in the second experiment, this percentage was considerably higher, namely 43.07%. Secondly, we estimated the percentage of
purely competitive decision-makers; these are individuals with (
, (
), and (
). In the first experiment, approximately zero players were
pure competitors; in the second experiment this percentage was 8.67%. Finally, we estimated the percentage of individuals with aversion to inequality between others (
). For the first experiment, 43.28% were averse to non-self-centered inequality. In the second experiment, this percentage was again considerably higher, namely 74.00%.
7. Discussion
Our analyses of multiplayer DG choices suggest that motives regarding the inequality between others matter. We found that these motives could not be explained away by simpler dyadic motives such as social efficiency motives or concerns for self-centered inequality. Explorative analyses showed that our findings were robust under a number of potential model misspecifications: non-self-centered inequality motives also mattered in utility functions that included non-linear terms, and in models with alternative comparison mechanisms. Next, we discuss some methodological and substantive issues that warrant further scrutiny.
Our experiments showed the relevance of modeling a variety of motives to describe choices in multiplayer DGs, but the estimated strength of motives differed considerably across the two experiments. Compared to subjects from the first experiment, subjects in the second experiment appeared more “pro-socially” oriented. This is surprising, since subjects and procedures were highly similar across experiments: participants in both experiments were of similar backgrounds (e.g., there were no substantive differences in characteristics such as age and gender). It is thus improbable that two entirely different populations were sampled. In addition, the two experiments presented the DGs in the same manner: despite some cosmetic differences, the experimental instructions were nearly identical; experiments were conducted via similar Z-tree treatments, and in the same laboratory room. It is therefore unlikely that differences in experimental treatments could have produced these large differences in displayed social motives.
It is possible that systematic differences in the DG batteries caused the observed differences in motives. The first experiment contained a large battery of two-player games, whereas the second experiment contained mainly four-player games (the exception being a two-player game that was administered by accident to a small fraction of players). Group size differences may have affected the magnitude of displayed social motives: with more actors, the probability that at least one individual experiences envy towards at least one other player increases progressively; thus, larger groups have progressively more potential for conflict. A conflict perspective suggests that social consequences matter more in larger groups. But group size effects are likely more complicated: as group size increases, calculations in the DG become more difficult. We can speculate that limits to cognitive capacity place a hard limit on the number of recipients whose relative standing can be considered. In addition, common sense dictates that motives cannot be a linear or convex function of group size: most individuals want to prevent a complete depletion of their own material resources (we refer to Engelmann’s research note on this matter [
39]). The conjecture we make, then, is that when social adversities become too large to mitigate, individuals might give up altogether. Europe’s current refugee crisis clearly exemplifies this mechanism: as the influx of refugees increased, so did the protests of concerned citizens. Further research should be conducted to investigate the multiple ways in which group size can affect social motives.
Another explanation for the differences in motives across experiments is that subjects in our treatments differed systematically in their prior experiences. Spillover effects have been found in both strategic [
54] and nonstrategic experiments [
37], thus, such an explanation is at least plausible. In both experiments, our DGs were embedded in larger experimental sessions that included treatments unrelated to our study. In the first experiment, our DGs were preceded by a series of public good games designed to study the effect of punishment on cooperation. In the second experiment, our DGs were preceded by a series of trust and network formation games. At face value, these differential prior treatments coincide with our observed differences in the average distribution of motives (
i.e., more pro-social motives were found in the second experiment); but a more systematic investigation is needed to assess spill-over effects on elicited social motives. The differences between sessions do not negate our main conclusions: our study’s aim was (merely) to show the general relevance of modeling non-self-centered inequality motives, and that there can be differences across populations. However, we do note that if the aim is to acquire a representative population estimate of motives, care should be taken to standardize prior experiences across subjects, and to use a representative sample.
The main implication of our study is that choices in multiplayer games should be described via utility functions that take the complexities of the multiplayer setting into account. A particularly interesting question is whether our findings apply to other types of games. Future studies should investigate whether non-self-centered inequality motives also matter in strategic multiplayer games. This is not a trivial task: to derive predictions of behavior in strategic games requires knowledge of the game’s payoffs, the players’ own motives, the players’ beliefs about the motives of others, and any relevant higher-order beliefs. We know that individuals are heterogeneous in their social motives, but we still know very little about the expectations of individuals regarding the motives of others (although some notable advances have been made on two-player settings [
16,
17]).