Time-Preference Heterogeneity and Multiplicity of Equilibria in Two-Group Bargaining

Abstract

We consider a multilateral bargaining game in which the agents can be classified into two groups according to their instantaneous preferences. In one of these groups there is one agent with a different discount factor. We analyze how this time-preference heterogeneity may generate multiplicity of equilibria. When such an agent is sufficiently more patient than the rest, there is an equilibrium in which her group-mates make the same proposal as the members of the other group. Thus, in heterogeneous groups the presence of more patient members may reduce the utility of its members.

1. Introduction

In this note we consider a non-cooperative multilateral bargaining game in which agents can be classified into two groups according to their instantaneous preferences over a one-dimensional policy. As an example, one may consider negotiations involving political parties, trading blocks or lobbying groups composed by individuals with the same goals. In this setting, we show that heterogeneous time preferences in one of the groups may lead to multiple equilibrium expected outcomes. We characterize these equilibria, and show that this heterogeneity may induce the impatient members of the heterogeneous group to concede more than what is minimally required to obtain the acceptance of the agents in the opposite group. In those cases, the utility of the members of the heterogeneous group is affected negatively by the number of its impatient members and non-monotonically by the discount factor of its patient members.

Bargaining among groups of agents with aligned preferences has usually been modeled by considering these groups acting coordinately as single individuals. These models study how the internal decision rules affect the bargaining outcome in bilateral negotiations between groups, including the choice of a delegate or a ratification requirement ([1,2]), or other rules that specify how groups/alliances submit offers to the opponent, as in [3]. These papers conclude that groups will commit to internal rules that make “strong” members decisive, as this would improve the equilibrium outcome for the group. In the distributive setting where multilateral negotiations proceed recursively by sequentially allocating the share to each agent (as in [4,5,6,7]), aligned preferences are also present. In these cases, when agents have the same time preferences, a unique bargaining outcome is obtained at any stage where negotiations involve the choice of an individual’s share. This allows us to obtain, using an inductive argument, a unique equilibrium bargaining allocation. Although in such models one group is formed by just one agent, [7] also studies the general case where two homogeneous groups may have different sizes.1 In this work, we introduce time-preference heterogeneity into a symmetric two-group bargaining game that distorts the sharp alignment of preferences of the above-mentioned papers. Moreover, we consider a deliberation protocol in which any agent might be selected as the proposer. Thus, there are no internal decision rules, as in the literature on multilateral bargaining.

We study a multilateral bargaining game over a one-dimensional public policy in which (1) there are two groups of agents according to their instantaneous preferences, and (2) all agents except one have the same time preference. Negotiations proceed over discrete time and they are modeled using the standard random proposers protocol: At the beginning of each round, an agent is selected at random to make a proposal. Then, according to an orderly voting sequence, the rest of the agents respond to the offer by either accepting or rejecting it. If it obtains the favorable vote of all agents then the selected alternative is implemented and the game ends. Otherwise, a new round of bargaining begins in the following period. This setting is analyzed in [7], where it is shown that when agents are characterized by at most two types of preferences (both instantaneous and time preferences) a unique equilibrium is attained. In this case, the bargaining game is isomorphic to a two-player bargaining game in which the number of players in each group determines only the distribution of proposal rights. Consequently, a unique bargaining (stationary) equilibrium is attained, where both the size of a group and the degree of patience of its members affect positively the equilibrium utilities of the agents in that group. Nevertheless, as we show, introducing some (time-preference) heterogeneity into the symmetric two-group bargaining game might induce multiplicity of equilibria. The reason for his lies in the fact that the heterogeneity of discount factors makes the continuation utility space multidimensional.

The role of unequal discounting has been explored in the literature on repeated games (see, e.g., [8,9,10]). In these settings, heterogeneous time preferences have been shown to allow agents to trade payoffs across time. This possibility has been also exploited in [11] by introducing a normal form disagreement game in a bilateral distributive bargaining setting, to show that multiple bargaining equilibria are attained. Apart from these trading opportunities, time preference has been shown to be an important ingredient of any non-cooperative bargaining process since the seminal paper of Rubinstein [12]. Even though being more patient may represent a drawback in majority bargaining, as shown by [13,14], it is a standard result that in unanimity bargaining games the more patient players obtain greater payoffs, as (in contrast to majority bargaining) all responders must belong to the winning coalition. In our setting with two groups, where unanimity is required and the single-period payoff space is one-dimensional, intuition would suggest that the bargaining would be finally determined by the most patient agents.2 Although this logic applies when negotiations yield a unique bargaining outcome, we highlight that heterogeneity of time preferences within a group is a source of multiplicity, and this may involve that in some equilibrium the utility of all its members is affected negatively by the presence of a more patient agent in their group.3

We show that time preference heterogeneity does not alter the uniqueness result when considering stationary equilibria. In these cases, both the size of the group and the time preference of the heterogeneous agent in the group monotonically affect the utility of its members. However, without imposing stationarity, a unique (stationary) no-delay subgame perfect equilibrium (SPE) is attained only when such heterogeneity is relatively small. Otherwise, there are multiple no-delay equilibria. Rather than the multiplicity result (which is generally attained when the policy space is multidimensional), our contribution relates to the analysis of the (uncoordinated) behavior of the agents on the equilibrium path: multiplicity appears because the presence of more patient agents in a group may push their co-partisans to make proposals less favorable to them than what is minimally required to get the acceptance of the other group members. This happens because if their proposals were ‘nicer’ for the more patient agents then the latter would become ‘greedier’ and would reject the offer, since their continuation value following such nice proposals would be higher than the continuation value following the equilibrium proposal. Remarkably, when the extra-patience of these agents is sufficiently high there is an equilibrium (the least preferred for the members of the heterogeneous group) in which the most impatient agents make the same proposal as the agents in the opposite group. This will negatively affect the equilibrium utility of the members of the heterogeneous group, and the size of this effect depends on the number of impatient agents in this group. Moreover, in such an equilibrium, this negative effect is not monotone with respect to the time impatience of the most patient agent(s). Thus, the members in that group may either benefit or not from heterogeneity. Although there are no special reasons to suspect that such an equilibrium will be prominently played instead of others (for instance the stationary SPE), we just argue that this is a possibility, and that in those cases large groups with a more demanding partner may perform worse than smaller homogeneous groups. Thus, the “power in numbers” (a property that can be regarded as desirable in processes of collective decision) does not necessarily hold when there are no internal rules “coordinating” the strategies of their members, so the size may act against the interests of the group.

In the next section, we present the model and characterize the set of expected outcomes that can be attained in no-delay SPE in the presence of a more patient agent. In Section 3, we provide a numerical example that clarifies how heterogeneity alters the bargaining equilibria. In Section 4, we characterize the set of no-delay SPE when the heterogeneous agent is more impatient than the rest; and Section 5 concludes.

2. The Model and the Results

A set of agents $N=\left\{1,2...,n\right\}$ must select an alternative $x\in \left[0,1\right]$. The instantaneous preferences of each agent $i\in$ N are represented by a utility function $u_i\in \left\{u_A,u_B\right\}$ where

$$\begin{array}{c}{u}_A\left(x\right)=x,\\ u_B\left(x\right)=1-x\end{array}$$

The negotiations among agents begin at period $t=0$ and proceed by the random proposer’s version of the Rubinstein [12] alternating offer bargaining game: At each period $t\ge 0$, a player $i\in N$ is selected at random (all with equal probability) to make a proposal $x_i\in \left[0,1\right]$. Then, all other players, sequentially, reply with acceptance or rejection. The proposal is approved if it is unanimously accepted. Upon approval, the agreement is implemented and the game ends. Otherwise, the game moves to $t+1$, a new proposer is selected, and so on. The players are impatient and each $i\in N$ evaluates an agreement x at period t according to ${\delta }_i^t{u}_i\left(x\right)$, where ${\delta }_i\in \left(0,1\right)$ denotes the discount factor of agent i. We assume that there is a unique agent a with ${\delta }_a=\mu$ and that ${\delta }_i=\delta$ for all $i\in N-\left\{a\right\}$. Let $\overline{A}=A\cup \left\{a\right\}$ and B denote the set of agents with $A-type$ and $B-type$ utilities, respectively, and let $n_A+1$ and $n_B$ denote their respective cardinalities.

As in [7], we restrict the sequencing of responses.4

Definition 1. 

A bargaining game satisfies orderly voting if the players in B (respectively, $\overline{A}$) respond first to proposals made by agents in B (respectively, $\overline{A}$).

Given a bargaining game $G\left(N,\delta ,\mu \right)$, let H denote the set of histories (nodes) at which nature selects a proposer; $H_i$ the set of histories where i makes a proposal; $H_i^j=H_i\times \left[0,1\right]$ the set of histories where i responds to an offer made by j, and $H_i^i={\cup }_{j\in N\backslash \left\{i\right\}}{H}_i^j$, $j\ne i$, the set of histories where i must respond. A strategy ${\sigma }_i=\left(x_i,v_i\right)$ of player $i\in N$ specifies her actions at each subgame: A proposal rule $x_i:H_i\to \left[0,1\right]$ and an acceptance/rejection rule $v_i:H_i^i\to \{yes,no\}$. A subgame perfect equilibrium (SPE) is a profile of strategies $\sigma =\left({\sigma }_1,...,{\sigma }_n\right)$ that are mutually best responses at each subgame. An SPE is a no-delay equilibrium if any equilibrium proposal receives unanimous approval. We denote by E the set of such equilibria. With abuse of notation, $h_i\in H_i$ refers to the history that follows from $h\in H$ where i has been selected as the proposer; $\left(h_i,x^{\prime }\right)\in H_j^i$ denotes a generic history where j responds to an offer of $x^{\prime }$ made by agent i at $h_i\in H_i$ (so, it can only follow from previous responders accepting the proposal); and $\left(h_i,x^{\prime },j\right)\in H$ is the history that follows from agent j rejecting an offer $x^{\prime }$ made by agent i at $h_i\in H_i$. We also denote by $H^t\subset H$ the history starting at period t and by $h^t$ a generic element of $H^t$. Hence, $h^0=H^0$ denotes the initial node.

Given a no-delay SPE ${\sigma }^{*}=\left({\sigma }_1^{*},...,{\sigma }_n^{*}\right)$ where ${\sigma }_i^{*}=\left(x_i^{*},v_i^{*}\right)$ for all $i\in N$, let $x\left(h|{\sigma }^{*}\right)$ denote the (equilibrium) expected policy at $h\in H$; that is, $x\left(h|{\sigma }^{*}\right)={\sum }_{i\in N}{x}_i^{*}\left(h_i\right)/n$. Also, let $\underline{x}\left(N,\delta ,\mu \right)=arg{min}_{h\in H,{\sigma }^{*}\in E}x\left(h|{\sigma }^{*}\right)$ and $\overline{x}\left(N,\delta ,\mu \right)=arg{max}_{h\in H,{\sigma }^{*}\in E}x\left(h|{\sigma }^{*}\right)$; i.e., the minimum and maximum no-delay SPE expected outcomes that can be attained in any subgame. For any σ, we will denote by $\sigma \left(h\right)$ the profile of strategies that start at node $h\in H$. Note that if ${\sigma }^{*}\in E$ then ${\sigma }^{*}\left(h\right)$ also constitutes a no-delay SPE of the game starting at $h\in H$. Moreover, as we consider an infinite horizon bargaining game, $x\left(h|{\sigma }^{*}\right)$ must be itself a no-delay SPE expected outcome. That is, there exists ${\sigma }^{**}\in E$ with $x\left(h^0|{\sigma }^{**}\right)=x\left(h|{\sigma }^{*}\right)$.

For any $x\in \left[0,1\right]$, let

$$z_B^{+}\left(x\right)=max\{z\in \left[0,1\right]:u_B\left(z\right)\ge \delta u_B\left(x\right)\}$$

and

$$z_A^{-}\left(x\right)=min\{z\in \left[0,1\right]:u_A\left(z\right)\ge max\{\delta ,\mu \}{u}_A\left(x\right)\}$$

That is, $z_B^{+}\left(x\right)=1-\delta \left(1-x\right)$ and $z_A^{-}\left(x\right)=max\{\delta ,\mu \}x.$ We interpret these values as the worst outcome that an agent in B (resp. $\overline{A})$ would accept when rejection is followed by a (discounted) expected outcome of x. Using these definitions and adapting Sutton’s [18] formulation to our environment, we next derive some properties of the acceptance rules in any no-delay SPE.5

Lemma 1. 

Let ${\sigma }^{*}\in E$. Then, the following holds:

• For all $i\in B$ and all $h_j\in H_j$, $j\in N$,$v_i\left(h_j,x^{\prime }\right)=no$ if $x^{\prime }>z_B^{+}\left(\overline{x}\right)$; and for all $h_j\in H_j$, $j\in N$, and $x^{\prime }<z_A^{+}\left(\underline{x}\right)$ there is some $i\in \overline{A}$ such that $v_i^{*}\left(h_j,x^{\prime }\right)=no$.
• For all $i\in B$, $j\in \overline{A}$ and $h_j\in H_j$, $v_i^{*}\left(h_j,x^{\prime }\right)=yes$ for all $x^{\prime }<z_B^{+}\left(\underline{x}\right)$.
• For all $i\in \overline{A}$, $j\in B$ and $h_j\in H_j$, $v_i^{*}\left(h_j,x^{\prime }\right)=yes$ for all $x^{\prime }>z_A^{-}\left(\overline{x}\right)$.

Proof. 

Statement (1) follows directly from the definitions of $\underline{x}$, $\overline{x}$, $z_A^{-}\left(\underline{x}\right)$ and $z_B^{+}\left(\overline{x}\right)$. To prove Statements (2) and (3) we need to use the “orderly voting” assumption.

Let $j\in \overline{A}$, $x_j\left(h_j\right)=x^{\prime }<z_B^{-}\left(\underline{x}\right)$ for some $h_j\in H_j$ and suppose $v_i^{*}\left(h_j,x^{\prime }\right)=no$ for some $i\in B$. Let $R_B=\{1,...,r\}$ denote the ordered set of agents that reject such an offer, and consider the strategy of agent r. Because of orderly voting, this agent is pivotal in the sense that her action would determine if the proposal is accepted or not: By rejecting the offer she may obtain at most $\delta \left(1-\underline{x}\right)=1-z_B^{+}\left(\underline{x}\right)=u_B\left(z_B^{+}\left(\underline{x}\right)\right)$, whereas acceptance implies $u_B\left(x^{\prime }\right)=1-x^{\prime }>1-z_B^{+}\left(\underline{x}\right)$. This contradicts ${\sigma }^{*}\in E$, thus proves Statement (2). Statement (3) can be proved similarly. ☐

Lemma 1 provides some necessary conditions on the acceptance rules in any no-delay SPE. The next lemma specifies properties of the equilibrium proposals, that reflect the heterogeneity in $\overline{A}$.

Lemma 2. 

Let ${\sigma }^{*}\in E$. Then, the following holds:

• If $\delta \ge \mu$ then $x_i^{*}\left(h_i\right)\ge z_B^{+}\left(\underline{x}\right)$ for all $i\in A$ and any $h_i\in H_i$.
• If $\delta \le \mu$ then $x_a^{*}\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)$ for all $h_a\in H_a$.
• $x_i^{*}\left(h_i\right)\le z_A^{-}\left(\overline{x}\right)$ for all $i\in B$ and any $h_i\in H_i$.

Proof. 

We next prove Statement (1). Statements (2) and (3) can be proved similarly.

Let $\delta \ge \mu$ and assume $x_i^{*}\left(h_i\right)<z_B^{+}\left(\underline{x}\right)$ for some $i\in A$ at some $h_i\in H_i$. Consider a strategy ${\sigma }_i$ that is equal to ${\sigma }_i^{*}$ except for $x_i\left(h_i\right)\equiv x^{\prime }\in \left(x_i^{*}\left(h_i\right),z_B^{+}\left(\underline{x}\right)\right)$. We next argue that either this proposal must be unanimously approved or else agent i would prefer to delay the agreement, a contradiction in any case.

If $v_j^{*}\left(h_i,x^{\prime }\right)=yes$ for all $j\in N-\left\{i\right\}$ then it is immediate that $x_i^{*}\left(h_i\right)$ is not optimal, contradicting ${\sigma }^{*}\in E$. Let $R=\{1,...,r\}$ denote the ordered set of players such that $v_j^{*}\left(h_i,x^{\prime }\right)=no$. From Lemma 1.2 we know that $R\subset \overline{A}$.6 Consider agent $r\in R$: Action $v_r^{*}\left(h_i,x^{\prime }\right)=no$ is optimal if $x^{\prime }\le {\delta }_{r}x\left(h^{\left(r\right)}|{\sigma }^{*}\right)$ where $h^{\left(r\right)}=\left(h_i,x^{\prime },r\right)\in H$ refers to the history that follows from this rejection. As ${\delta }_{i}x\left(h^{\left(r\right)}|{\sigma }^{*}\right)\ge {\delta }_{r}x\left(h^{\left(r\right)}|{\sigma }^{*}\right)\ge x^{\prime }>x_i^{*}\left(h_i\right)$, this contradicts ${\sigma }^{*}\in E$ when $r=1$. Otherwise, if $r>1$, we next show that ${\delta }_{i}x\left(h^{\left(j+1\right)}|{\sigma }^{*}\right)>x_i^{*}\left(h_i\right)$ implies ${\delta }_{i}x\left(h^{\left(j\right)}|{\sigma }^{*}\right)>x_i^{*}\left(h_i\right)$ for all $j,j+1\in R$. This is immediate, because $v_j^{*}\left(h_i,x^{\prime }\right)=no$ is optimal if ${\delta }_{j}x\left(h^{\left(j\right)}|{\sigma }^{*}\right)\ge {\delta }_{j}x\left(h^{\left(j+1\right)}|{\sigma }^{*}\right)$. Hence, as ${\delta }_i\ge {\delta }_j$ for all $j\in R$ we obtain ${\delta }_{i}x\left(h^{\left(1\right)}|{\sigma }^{*}\right)\ge {\delta }_{1}x\left(h^{\left(1\right)}|{\sigma }^{*}\right)\ge ...\ge {\delta }_{1}x\left(h^{\left(r\right)}|{\sigma }^{*}\right)>x_i^{*}\left(h_i\right)$, contradicting ${\sigma }^{*}\in E$.  ☐

The previous lemmata allows to conclude that in any ${\sigma }^{*}\in E$ the most patient agents in $\overline{A}$ make proposals greater than or equal to $z_B^{+}\left(\underline{x}\right)$. Also, agents in B would propose policies lower than or equal to $z_A^{-}\left(\overline{x}\right)$. This allows to delimit the set of expected outcomes that can be attained in any no-delay SPE. To simplify the exposition, we focus our analysis on the case in which agent a is more patient than the rest of the population. So, we assume $\mu \ge \delta$ henceforth.7

Lemma 3. 

In any no-delay SPE ${\sigma }^{*}$, we have that $x\left(h^0|{\sigma }^{*}\right)\in \left[x_s,x^s\right]$, where

$$x_s=\frac{\left(1-\delta \right)}{\left(1-\delta \right)+\left(n_A+n_B\right)\left(1-\mu \right)}\mathit{\text{and}}{x}^s=\frac{\left(n_A+1\right)\left(1-\delta \right)}{\left(n_A+1\right)\left(1-\delta \right)+n_B\left(1-\mu \right)}$$

Proof. 

From Lemma 1.1 and Lemma 2.3, we know that $x_i^{*}\left(h_i\right)\le z_B^{+}\left(\overline{x}\right)$ for all $i\in \overline{A}$, and $x_j^{*}\left(h_j\right)\le z_A^{-}\left(\overline{x}\right)$ for all $j\in B$. Hence,

$$x\left(h^0|{\sigma }^{*}\right)\le \frac{\left(n_A+1\right)z_B^{+}\left(\overline{x}\right)+n_B{z}_A^{-}\left(\overline{x}\right)}{n}$$

From Lemma 1.1 and Lemma 2.2, we also obtain that $x_i^{*}\left(h_i\right)\ge z_B^{-}\left(\underline{x}\right)$ for all $i\ne a$ and $x_a^{*}\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)$ so that

$$x\left(h^0|{\sigma }^{*}\right)\ge \frac{\left(n_A+n_B\right)z_B^{-}\left(\underline{x}\right)+z_B^{+}\left(\underline{x}\right)}{n}$$

As $\overline{x}=max\{x\left(h^0|\sigma \right):\sigma \in E\}$ and $\underline{x}=min\{x\left(h^0|\sigma \right):\sigma \in E\}$, using the definitions of $z_A^{-}\left(x\right)$ and $z_B^{+}\left(x\right)$, the statement follows. ☐

Note that both $x_s$ and $x^s$ are increasing in μ with ${lim}_{\mu \to 1}{x}_s={lim}_{\mu \to 1}{x}^s=1$. Thus, for any given δ, the set of no-delay SPE expected outcomes collapses to a unique outcome as μ goes to 1.8

Lemmata 1 and 2 do not exclude the possibility of no-delay SPE where some player $i\in A$ (the most impatient) proposes $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$. This fact would open the possibility of multiple no-delay SPE expected outcomes, which is the point we address in this work. Otherwise, as shown next, a unique no-delay SPE is obtained.

Lemma 4. 

If ${\sum }_{i\in A}{x}_i^{*}\left(h_i^0\right)\ge n_A{z}_B^{+}\left(\underline{x}\right)$ for all ${\sigma }^{*}\in E$ then $\underline{x}=x^s$. Hence, there is a unique no-delay SPE expected outcome. This condition is satisfied both in any stationary no-delay SPE and in a symmetric setting with $\delta =\mu$.

Proof. 

As $\mu \ge \delta$, by Lemma 2.2, we have that $x_a^{*}\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)=1-\delta \left(1-\underline{x}\right)$ for all $h_a\in H_a$; and by Lemma 2.3, $x_j^{*}\left(h_j\right)\le z_A^{-}\left(\overline{x}\right)=\mu \overline{x}$ for all $j\in B$ and any $h_j\in H_j$. Hence,

$$x\left(h^0\right|{\sigma }^{*})=\frac{{\sum }_{i\in N}{x}_i^{*}\left(h_i^0\right)}{n}\ge \frac{\left(n_A+1\right)\left(1-\delta \left(1-\underline{x}\right)\right)+n_B\mu \overline{x}}{n}\ge \frac{\left(n_A+1\right)\left(1-\delta \left(1-\underline{x}\right)\right)+n_B\mu \underline{x}}{n}$$

As $\underline{x}=min\{x\left(h^0|\sigma \right):\sigma \in E\}$, we obtain

$$\underline{x}\ge \frac{\left(n_A+1\right)\left(1-\delta \right)}{\left(n_A+1\right)\left(1-\delta \right)+n_B\left(1-\mu \right)}=x^s$$

Therefore, by Lemma 3 the no-delay SPE expected outcome is unique.

Existence is also immediate. Just consider the following strategies: $x_i\left(h_i\right)=z_B^{+}\left(x^s\right)$ for all $i\in \overline{A}$ and any $h_i\in H_i$; $v_i\left(h_j,x^{\prime }\right)=yes$ iff $x^{\prime }\ge {\delta }_i{x}^s$ for all $i\in \overline{A}$ and any $h_j\in H_j$, $j\in N$; $x_i\left(h_i\right)=z_A^{-}\left(x^s\right)$ for all $i\in B$ and any $h_i\in H_i$; and $v_i\left(h_j,x^{\prime }\right)=yes$ iff $x^{\prime }\le z_B^{+}\left(x^s\right)$ for all $i\in B$ and any $h_j\in H_j$, $j\in N$.

In any stationary no-delay SPE yielding (time-independent) expected outcome $x^E\in \left[\underline{x},\overline{x}\right]$, using a reasoning similar to that in the proof of Lemma 2, it is immediate that a proposal $x^{\prime }$ would be accepted if $x^{\prime }\in \left(z_A^{-}\left(x^E\right),z_B^{+}\left(x^E\right)\right)$ and rejected when $x^{\prime }\notin \left[z_A^{-}\left(x^E\right),z_B^{+}\left(x^E\right)\right]$. Hence, at any such equilibrium $x_i^{*}\left(h_i^0\right)=z_B^{+}\left(x^E\right)$ for all $i\in \overline{A}$ and $x_i^{*}\left(h_i^0\right)=z_A^{-}\left(x^E\right)$ for all $i\in B$. Thus, it is immediate that $x^E=x^s$. In a symmetric setting with $\delta =\mu$, the statement follows directly from statements 1 and 2 in Lemma 2. ☐

Summarizing, as $x_a^{*}\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)$ for all $h_a\in H_a$ (Lemma 2.2), multiplicity might arise only when there is a no-delay SPE in which some agent $i\in A$ proposes $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$. Moreover, as by Lemma 1.2 agents in B would accept any proposal $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$, this might happen only if for any $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$, there is some $j\in \overline{A}$ such that $v_j\left(h_i^0,x^{\prime }\right)=no$. Next, we informally present an example in which this possibility generates multiple no-delay SPE.

Example 1. 

Suppose $\left|B\right|=2$ and $\left|\overline{A}\right|=2$, $\delta =0.9$ and $\mu =0.98$. Using Lemma 4 it is immediate that the stationary equilibrium yields the expected outcome $\overline{x}=x^s=0.833$.

Consider the following strategy proposals: $x_a\left(h_a^0\right)=z_B^{+}\left(x^1\right)=1-\delta \left(1-x^1\right)$ and $x_i\left(h_i^0\right)=z_A^{-}\left(x^1\right)=\mu x^1$ for all $i\in A\cup B$, where

$$\begin{array}{c}\hfill x^1=\frac{1}{4}\left(1-\delta \left(1-x^1\right)+3\mu x^1\right)\end{array}$$

so that $x^1=0.625$ and, hence, $x_i\left(h_i^0\right)=0.6125$ for all $i\in A\cup B$ and $x_a\left(h_a^0\right)=0.6625.$

We next show informally that strategies where the previous proposals are accepted by all agents, constitute a no-delay SPE. Suppose that the continuation expected outcome remains at $x^1=0.625$ unless some agent $i\in A$ proposes $x_i\left(h_i^0\right)\in \left[0.6125,0.6625\right)$, in which case the continuation expected outcome (after any rejection) is $x^2=0.677$. We derived $x^2$ as a policy satisfying $\mu x^2>0.6625$, so that it is optimal for agent a to reject any offer $x_i\left(h_i^0\right)\in \left[0.6125,0.6625\right)$ made by some $i\in A$.

It is obvious that both agents in B and agent a make their best proposal taking into account how their proposals would affect continuation expected outcomes. Moreover, $0.6125>0.6093=0.677\delta$. Hence, for any $i\in A$, $x_i\left(h_i^0\right)=0.6125$ and $v_i\left(h_j,x^{\prime }\right)=yes$ for all $h_j\in H_j$, $j\in N$ iff $x^{\prime }\ge 0.625\delta =0.5625$ for any $i\in A$ are optimal, as far as $x^2=0.676$ is a credible threat.

How can this threat be sustained? Consider the strategy proposals $x_i\left(h_i\right)\equiv x^2=0.677$ for all $i\in N$ such that: (i) If any of these proposals is rejected then the expected outcome remains; (ii) if $i\in B$ makes a different proposal then any rejection yields expected outcome $x^s=0.833$, which we know is a no-delay SPE expected outcome; and (iii) if $i\in \overline{A}$ makes a different proposal then any rejection yields expected outcome $x^1$. Since $u_B\left(0.677\right)=0.323>0.15=\delta u_B\left(0.833\right)$ and $u_A\left(0.677\right)=0.677\ge \mu u_A\left(0.625\right)=0.612\ge \delta u_A\left(0.625\right)=0.562$, the previous strategies are optimally consistent. Thus, there exist a no-delay SPE in which agents in A and B make the same proposals, yielding expected outcome $x_s=0.625<0.833=x^s$.

Next, we formally develop the arguments used in the previous example to characterize the set of no-delay SPE expected outcomes. Before, some notation and some preliminary results are presented. For any $x\in \left[0,1\right]$ let $y_a\left(x\right)$ and $y_i\left(x\right)$ for all $i\in A$ satisfy

$$\mu y_a=1-\delta \left(1-x\right)=z_B^{+}\left(x\right)\text{and}\delta y_i=x$$

(1)

That is, $y_a\left(x\right)$ is the (expected) outcome that makes agent a indifferent between obtaining $z_B^{+}\left(x\right)$ today or receiving $y_a\left(x\right)$ next period. Similarly, $y_i\left(x\right)$ is the expected outcome that makes agent $i\in A$ indifferent between obtaining x today or receiving $y_i\left(x\right)$ at the next period.

As noted previously, to attain multiple no-delay SPE it is required that $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$ for some $i\in A$, which might happen whenever for all $x^{\prime }\in \left(x_i^{*}\left(h_i\right),z_B^{+}\left(\underline{x}\right)\right)$ there is some $j\in \overline{A}$ with $v_j\left(h_i^0,x^{\prime }\right)=no$. The next lemma specifies some implications of this possibility.

Lemma 5. 

Let ${\sigma }^{*}\in E$ with $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$ for some $i\in A$ yielding $x\left(h^0|{\sigma }^{*}\right)=\underline{x}<x^s$. Then,

• $v_a^{*}\left(h_i^0,x^{\prime }\right)=no$ for all $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$
• There is some $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$ such that $x\left(h^{\left(j\right)}|{\sigma }^{*}\right)\in \left[y_a\left(\underline{x}\right),min\left\{y_i\left(x_i^{*}\left(h_i^0\right)\right),x^s\right\}\right]$, where $h^{\left(j\right)}=\left(h_i^0,x^{\prime },j\right)\in H^1$ is the history that follows when some player $j\in N$ rejects $x^{\prime }$.

Proof. 

Suppose $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$ for some $i\in A$ and there is $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$ such that $v_a^{*}\left(h_i^0,x^{\prime }\right)=yes$. Consider a proposal $x_i\left(h_i^0\right)=x^{\prime }$. By assumption agent a accepts the proposal, and by Lemma 1.2 agents in B also accept it. Thus $x^{\prime }$ must be rejected by some agent $j\in A$. Let $R=\{1,..,r\}\subset A$ denote the ordered set of agents $j\in A$ with $v_j\left(h_i^0,x^{\prime }\right)=no$. As $v_r\left(h_i^0,x^{\prime }\right)=yes$ would yield agreement on $x^{\prime }$, $v_r^{*}\left(h_i^0,x^{\prime }\right)=no$ is optimal iff $\delta x\left(h^{\left(r\right)}|{\sigma }^{*}\right)\ge x^{\prime }>x_i^{*}\left(h_i^0\right)$, where $h^{\left(r\right)}=\left(h_i,x^{\prime },r\right)\in H^1$. When $r>1$, it is also immediate that $\delta x\left(h^{(j+1)}|{\sigma }^{*}\right)\ge x^{\prime }$ implies that $\delta x\left(h^{\left(j\right)}|{\sigma }^{*}\right)\ge \delta x\left(h^{(j+1)}|{\sigma }^{*}\right)\ge x^{\prime }$ since otherwise $v_j\left(h_i^0,x^{\prime }\right)=no$ would not be optimal. As ${\delta }_i=\delta$, ${\delta }_{i}x\left(h^{\left(1\right)}|{\sigma }^{*}\right)\ge \delta x\left(h^{\left(1\right)}|{\sigma }^{*}\right)\ge ...\ge \delta x\left(h^{\left(r\right)}|{\sigma }^{*}\right)>x_i^{*}\left(h_i\right)$, contradicting $x_i^{*}\left(h_i^0\right)$ being an optimal proposal. This proves Statement 1.

We know that agent a must reject any offer $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$. Let $R\left(x^{\prime }\right)=\{1,...,r\}$ denote the ordered set of agents who reject $x_i\left(h_i^0\right)=x^{\prime }$, which we know must be a subset of $\overline{A}$. Consider the acceptance rule of agent r. In order to be optimal, it is required that ${\delta }_{r}x\left(h^{\left(r\right)}|{\sigma }^{*}\right)\ge x^{\prime }>x_i^{*}\left(h_i^0\right)$. If $r=1=a$ then this implies $\mu x\left(h^{\left(r\right)}|{\sigma }^{*}\right)\ge x^{\prime }$. In case that $r>1$, it is immediate that ${\delta }_{j+1}x\left(h^{(j+1)}|\sigma \right)\ge x^{\prime }$ implies ${\delta }_{j}x\left(h^{\left(j\right)}|\sigma \right)\ge {\delta }_{j}x\left(h^{(j+1)}|\sigma \right)$, since otherwise $v_j^{*}\left(h_i^0,x^{\prime }\right)=no$ might not be optimal. Hence, as $a\in R\left(x^{\prime }\right)$ for all $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$, we can conclude that if $x^{\prime }$ is rejected then $\mu x\left(h^{\left(1\right)}|\sigma \right)\ge x^{\prime }$. Since this must happen for all $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$ there must be some $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$ such that $x\left(h^{\left(1\right)}|{\sigma }^{*}\right)\ge y_a\left(\underline{x}\right)$: Suppose otherwise; that is, $x\left(h^{\left(1\right)}|{\sigma }^{*}\right)<y_a\left(\underline{x}\right)$, so that $\mu y_a\left(\underline{x}\right)=z_B^{+}\left(\underline{x}\right)>\mu$$x\left(h^{\left(1\right)}|{\sigma }^{*}\right)$, for all $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$. Let $x_i\left(h_i^0\right)=x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$ satisfying $x^{\prime }>\mu x\left(h^{\left(j\right)}|{\sigma }^{*}\right)$, which do exist by continuity. We next show that this proposal must be accepted, contradicting ${\sigma }^{*}\in E$. By Lemma 1.2, we know that for any $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$, $v_j\left(h_i,x^{\prime }\right)=yes$ for all $j\in B$. Hence, there is an ordered set of responders $R=\{1,...,r\}\subset \overline{A}$, $r\ge 1$, with $v_j\left(h_i,x^{\prime }\right)=no$ for all $j\in R$. In order to be optimal, we must have ${\delta }_{r}x\left(h^{\left(r\right)}|\sigma \right)\ge x^{\prime }$. When $r=1=a$ this contradicts $x^{\prime }>\mu x\left(h^{\left(r\right)}|\sigma \right)$. Following the previous argumentation for cases in which $r>1$, it is immediate that ${\delta }_{j}x\left(h^{\left(j\right)}|{\sigma }^{*}\right)\ge {\delta }_{j}x\left(h^{(j+1)}|{\sigma }^{*}\right)$ for all $j,j+1\in R$, so that $a\in R$ implies $\mu x\left(h^{\left(1\right)}|\sigma \right)\ge x^{\prime }$, contradicting $x^{\prime }>\mu x\left(h^{\left(1\right)}|\sigma \right)$.

As for all $x^{\prime }\in \left(x_i^{*}\left(h_i^0\right),z_B^{+}\left(\underline{x}\right)\right)$, $x\left(h^{\left(1\right)}|\sigma \right)$ must be also the expected outcome attained at some no-delay SPE, it is immediate that $x\left(h^{\left(1\right)}|\sigma \right)\le x^s$. Additionally, $x_i^{*}\left(h_i^0\right)$ is optimal only if $\delta x\left(h^{\left(1\right)}|\sigma \right)\le x_i^{*}\left(h_i^0\right)$. i.e., $x\left(h^{\left(1\right)}|\sigma \right)\le y_i\left(x_i^{*}\left(h_i^0\right)\right)$. This completes the proof of Statement 2.  ☐

The previous lemma gives some necessary conditions to attain multiple no-delay SPE. Before providing the sufficient conditions and thus characterize the set of no-delay SPE, the following lemma establishes a symmetry property that will facilitate the exposition.

Lemma 6. 

If there is a no-delay SPE ${\sigma }^{*}$ yielding expected outcome $x\left(h^0|{\sigma }^{*}\right)=\underline{x}<x^s$, then there is a no-delay SPE σ in which $x_i\left(h_i^0\right)=x_j\left(h_j^0\right)$ for all $i,j\in A$ yielding expected outcome $x\left(h^0|\sigma \right)=\underline{x}$.

Proof. 

Consider ${\sigma }^{*}\in E$ yielding (the minimum) expected outcome $\underline{x}<x^s$. We know that $x_a^{*}\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)$ and $x_i^{*}\left(h_i\right)\le z_A^{-}\left(\overline{x}\right)$ for all $i\in B$. Moreover, by Lemma 4 we know ${\sum }_{i\in A}{x}_i^{*}\left(h_i^0\right)<n_A{z}_B^{+}\left(\underline{x}\right)$ so that there is at least some $i\in A$ with $x_i^{*}\left(h_i^0\right)<z_B^{+}\left(\underline{x}\right)$. Let $i\in A$ satisfy $x_i^{*}\left(h_i^0\right)\le x_j^{*}\left(h_j^0\right)$ for all $j\in A$.

Let $\tilde{x}={\sum }_{j\in A}{x}_j^{*}\left(h_j^0\right)/n_A<z_B^{+}\left(\underline{x}\right)$; and define the following subsets of $H^1$:

• ${\widehat{H}}^1=\{\left(h_j^0,x^{\prime },k\right):j\in A,x^{\prime }\in \left(\tilde{x},z_B^{+}\left(\underline{x}\right)\right],k\in N\}$
• ${\tilde{H}}^1=\{\left(h_j^0,x^{\prime },k\right):j\in A,x^{\prime }\notin \left(\tilde{x},z_B^{+}\left(\underline{x}\right)\right],k\in N\}$

Consider the following strategy profile σ:

• $x_j\left(h_j^0\right)=\tilde{x}$ for all $j\in A$; $x_j\left(h_j^0\right)=x_j^{*}\left(h_j^0\right)$ for all $j\in B$; and $x_a\left(h_a^0\right)=x_a^{*}\left(h_a^0\right)$.
• $v_j\left(h_k^0,x^{\prime }\right)=v_j^{*}\left(h_k^0,x^{\prime }\right)$ for all $j\in N$ and $k\notin A$; $v_j\left(h_k^0,x^{\prime }\right)=yes$ iff $x^{\prime }\le z_B^{+}\left(\underline{x}\right)$ for all $j\in B$ and $k\in A$; $v_j\left(h_k^0,x^{\prime }\right)=yes$ iff $x^{\prime }\ge \delta \underline{x}$ for all $j\in A$, $k\in A$; and $v_a\left(h_k^0,x^{\prime }\right)=yes$ iff $x^{\prime }\in \left[z_A^{-}\left(\underline{x}\right),\tilde{x}\right]\cup \left(z_B^{+}\left(\underline{x}\right),1\right]$ for all $k\in A$.
• $\sigma \left(h^1\right)$ is a strategy profile of mutually best responses starting at some $h^1\in H^1$ such that:

  −

  $x\left(h^1|\sigma \right)=x^E\in \left[y_a\left(\underline{x}\right),y_i\left(x_i^{*}\left(h_i^0\right)\right)\right]$ if $h^1\in {\widehat{H}}^1$

  −

  $x\left(h^1|\sigma \right)=\underline{x}$ if $h^1\in {\tilde{H}}^1$

  −

  $x\left(h^1|\sigma \right)=x\left(h^1|{\sigma }^{*}\right)$ for all $h^1\in H^1\backslash \left({\widehat{H}}^1\cup {\tilde{H}}^1\right).$9

As $\delta x^E\le x_i^{*}\left(h_i^0\right)<\tilde{x}$, it can be easily checked that given $\sigma \left(h^1\right)$, proposals and acceptance rules are optimal at period 0. Hence, $\sigma \in E$. Moreover, by construction $x\left(h^0|\sigma \right)=\underline{x}$. ☐

From the previous result, in order to characterize the set of no-delay SPE expected outcomes, it suffices to consider no-delay SPE where $x_i\left(h_i^0\right)=x_j\left(h_j^0\right)$ for all $i,j\in A$. We define $y_A\left(x\right)$ as the value that solves

$$\delta y_A=\frac{nx-\left(1-\delta \left(1-x\right)\right)-n_B\mu x}{n_A}$$

That is, $y_A$ is such that $\delta u_A\left(y_A\right)=u_A\left(x_i\right)$ where $x_i$ satisfies

$$x=\frac{n_A{x}_i+1-\delta \left(1-x\right)+n_B\mu x}{n}$$

So far, we know that $\overline{x}=x^s$. The next result provides necessary and sufficient conditions for multiplicity; i.e., the existence of a no-delay SPE expected outcome $\underline{x}\in \left[x_s,x^s\right)$.

Proposition 1. 

There exists a no-delay SPE yielding $\underline{x}\in \left[x_s,x^s\right)$ iff $y_a\left(\underline{x}\right)\le min\left\{y_A\left(\underline{x}\right),x^s\right\}$. Thus, in these cases, $\underline{x}=min\{z\in \left[x_s,x^s\right):y_a\left(z\right)\le min\left\{y_A\left(z\right),x^s\right\}\}.$

Proof. 

We proof the statement by showing first that $y_a\left(\underline{x}\right)>min\left\{y_A\left(\underline{x}\right),x^s\right\}$ yields uniqueness, thus $y_a\left(\underline{x}\right)\le max\left\{y_A\left(\underline{x}\right),x^s\right\}$ is necessary; and second, that $y_a\left(\underline{x}\right)\le min\left\{y_A\left(\underline{x}\right),x^s\right\}$ is sufficient, obtaining the characterization of $\underline{x}$.

$\left(\Rightarrow \right)$ Suppose that $\underline{x}\in \left[x_s,x^s\right)$ is a no-delay equilibrium expected outcome and $y_a\left(\underline{x}\right)>min\left\{y_A\left(\underline{x}\right),x^s\right\}$. From Lemma 5, $\left[y_a\left(\underline{x}\right),min\{y_A\left(\underline{x}\right),x^s\}\right]\ne \varnothing$, which contradicts $y_a\left(\underline{x}\right)>min\left\{y_A\left(\underline{x}\right),x^s\right\}$.

$\left(\Leftarrow \right)$ Let $\underline{x}=min\{z\in \left[x_s,x^s\right):y_a\left(z\right)\le min\left\{y_A\left(z\right),x^s\right\}\}$. Denote by $\widehat{H}$ and $\tilde{H}$ two disjoint subsets of H and consider the following strategies:

• For all $h\in \widehat{H}\subset H$

  (a)

  $x_i\left(h_i\right)\equiv x_A\in \left[z_A^{-}\left(\underline{x}\right),z_B^{+}\left(\underline{x}\right)\right)$ for $i\in A$; $x_i\left(h_i\right)=z_A^{-}\left(\underline{x}\right)$ for $i\in B$, and $x_a\left(h_a\right)=z_B^{+}\left(\underline{x}\right)$, such that

  $$\underline{x}=\frac{n_B{z}_A^{-}\left(\underline{x}\right)+n_A{x}_A+z_B^{+}\left(\underline{x}\right)}{n}$$

  (b)

  For all $i\in B$ and any $j\in N$, $v_i\left(h_j,x^{\prime }\right)=yes$ iff $x^{\prime }\le z_B^{+}\left(\underline{x}\right)$. For all $i\in A$ and any $j\in N$, $v_i\left(h_j,x^{\prime }\right)=yes$ iff $x\ge \delta \underline{x}$. For agent a, $a_a\left(h_j,x\right)=yes$ iff $x^{\prime }\ge z_A^{-}\left(\underline{x}\right)$ and $j\in B$, and $v_a\left(h_j,x^{\prime }\right)=yes$ iff $x^{\prime }\in \left[z_A^{-}\left(\underline{x}\right),x_A\right]\cup \left(z_B^{+}\left(\underline{x}\right),1\right]$ and $j\in A$.

  (c)

  $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \tilde{H}$, for all $j\in N$ if $i\in A$ and $x^{\prime }\in \left(x_A,z_B^{+}\left(\underline{x}\right)\right]$; and $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \widehat{H}$ otherwise.

• For all $h\in \tilde{H}=H\backslash \widehat{H}$

  (a)

  $x_i\left(h_i\right)=z_A^{-}\left(z\right)=\mu z$ for all $i\in B$ and $x_i\left(h_i\right)\equiv x_A^{\prime }$ for all $i\in \overline{A}$, such that

  $$z=\frac{n_B\mu z+\left(n_A+1\right)x_A^{\prime }}{n}\in \left[y_a\left(\underline{x}\right),min\{y_A\left(\underline{x}\right),x^s\}\right]$$

  which by assumption exists. Moreover, as $z\le x^s$, it is easy to check that $z<x_A^{\prime }\le z_B^{+}\left(z\right)$.

  (b)

  For all $i\in \overline{A}$, $v_i\left(h_j,x^{\prime }\right)=yes$ for all $j\in N$ iff $x^{\prime }\ge {\delta }_{i}z$; and for all $i\in B$, $v_i\left(h_j,x^{\prime }\right)=yes$ iff either $j\in \overline{A}$ and $x^{\prime }\le x_A^{\prime }$ or $j\in B$ and $x^{\prime }\le z_B^{+}\left(z\right)$.

  (c)

  $h^{\prime }\left(h_i,x^{\prime },j\right)\in \widehat{H}$ for all $j\in N$ if $i\in \overline{A}$ and $x^{\prime }>x_A^{\prime }$; $h^{\prime }\left(h_i,x^{\prime },j\right)\in \tilde{H}$ for all $j\in N$ if $i\in \overline{A}$ and $x^{\prime }\le x_A^{\prime }$; and $h^{\prime }\left(h_i,x^{\prime },j\right)\in \tilde{H}$ for all $j\in N$ if $i\in B$ and for all $x^{\prime }$.

Next, we show that these strategies constitute a no-delay SPE that yields an expected outcome smaller than $\overline{x}=x^s$ when $h^0\in \widehat{H}$.

It is immediate that, when $h\in \widehat{H}$, agents in B cannot do better by accepting any proposal $x^{\prime }$ iff $x^{\prime }\le z_B^{+}\left(\underline{x}\right)$. Also, $z_A^{-}\left(\underline{x}\right)$ is the best proposal that can be accepted. Player a is also proposing optimally, as any $x^{\prime }>z_B^{+}\left(\underline{x}\right)$ is rejected and $h^{\prime }=\left(h_a,x^{\prime },r\right)\in \widehat{H}$, so that $x\left(h^{\prime }|\sigma \right)=\underline{x}<z_B^{+}\left(\underline{x}\right)$. Likewise, her acceptance rule is also optimal: she will never accept less than $z_A^{-}\left(\underline{x}\right)$ and rejecting $x^{\prime }\in \left(x_A,z_B^{+}\left(\underline{x}\right)\right)$ made by some agent $i\in A$ is also optimal, as $h^{\prime }=\left(h_i,x^{\prime },r\right)\in \tilde{H}$ and $x\left(h^{\prime }|\sigma \right)=z\ge y_a\left(\underline{x}\right)$. Agents in A are also making optimal proposals: Any proposal $x^{\prime }\in \left[0,z_A^{-}\left(\underline{x}\right)\right)\cup \left[z_B^{+}\left(\underline{x}\right),1\right]$ would be rejected and $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \widehat{H}$ so that $\delta x\left(h^{\prime }|\sigma \right)=\delta \underline{x}<z_A^{-}\left(\underline{x}\right)\le x_A$. Also, any proposal $x^{\prime }\in \left(x_A,z_B^{+}\left(\underline{x}\right)\right)$ would be rejected and $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \tilde{H}$, meaning that $x\left(h^{\prime }|\sigma \right)=z\le y_A\left(\underline{x}\right)$. So, their best proposal is $x_A$. It is also immediate that their acceptance rules are optimal as $h^{\prime }\in \widehat{H}$ follows from any rejection.

Hence, given the actions played at any $h\in \tilde{H}$, actions played at $h\in \widehat{H}$ are mutually optimal. Similarly, it can be shown that the actions played at $h\in \tilde{H}$ are mutually optimal, given actions played at any $h\in \widehat{H}$:

For agents in B, any proposal smaller than $z_A^{-}\left(z\right)$ is rejected by a and the continuation history is such that $h^{\prime }\in \tilde{H}$, implying $x\left(h^{\prime }|\sigma \right)=z>z_A^{-}\left(\underline{x}\right)$, and therefore $1-z_A^{-}\left(z\right)>\delta \left(1-z\right)$; and any proposal greater than or equal to $z_A^{-}\left(z\right)$ is accepted. Thus, $z_A^{-}\left(z\right)$ is optimal. To see that $x_i\left(h_i\right)=x_A^{\prime }$ for all $i\in \overline{A}$ is optimal, note that any smaller proposal would be either accepted or rejected, in which case the continuation history $h^{\prime }=\left(h_i,x^{\prime },k\right)\in \tilde{H}$ with $x\left(h^{\prime }|\sigma \right)=z$. Moreover, any proposal $x^{\prime }>x_A^{\prime }$ is rejected by some agents in B and $\left(h_i,x^{\prime },r\right)\in \widehat{H}$ so that $x\left(h^{\prime }|\sigma \right)=\underline{x}$. Hence, as $x_A^{\prime }$ is accepted, this is clearly optimal. Regarding the acceptance rules of agents in B they are also optimal: Rejecting a proposal any proposal $x^{\prime }$ made by another agent in B would yield $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \tilde{H}$ and therefore, $x\left(h^{\prime }|\sigma \right)=z$ satisfying $\delta u_B\left(x\left(h^{\prime }|\sigma \right)\right)=u_B\left(z_B^{+}\left(z\right)\right)$. Hence accepting $x^{\prime }$ would be optimal iff $x^{\prime }\le z_B^{+}\left(z\right)$. If the proposer is some agent $i\in \overline{A}$ and $x^{\prime }\le x_A^{\prime }$ rejection yields $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \tilde{H}$ so that $x\left(h^{\prime }|\sigma \right)=z$, too. Hence, acceptance is optimal. When an agent $i\in \overline{A}$ proposes $x^{\prime }>x_A^{\prime }$ then $h^{\prime }=\left(h_i,x^{\prime },j\right)\in \widehat{H}$ and therefore $x\left(h^{\prime }|\sigma \right)=\underline{x}$. Since $z\ge y_a\left(\underline{x}\right)$ so that $\mu z\ge z_B^{+}\left(\underline{x}\right)=1-\delta \left(1-\underline{x}\right)$, we obtain $\delta \left(1-\underline{x}\right)\ge 1-\mu z>1-z>1-x_A^{\prime }$ and therefore rejection is clearly optimal. The acceptance rule of agents in $\overline{A}$ are also optimal, as any rejection yields either $x\left(h^{\prime }|\sigma \right)=z$ or $x\left(h^{\prime }|\sigma \right)=\underline{x}$ so that ${\delta }_{i}z\ge x\left(h^{\prime }|\sigma \right)$ in any case. ☐

Having derived the necessary and sufficient conditions for multiplicity in terms of $y_A\left(\underline{x}\right)$ and $y_a\left(\underline{x}\right)$ , we next specify these conditions (and the minimal expected outcome that can be attained in any no-delay SPE) in terms of time preferences.

Proposition 2. 

If $\delta >\frac{1}{n-n_B}$ then there exists a discount factor $\overline{\mu }\left(\delta ,n,n_B\right)\in \left(\delta ,1\right)$ such that, when $\mu \ge \overline{\mu }\left(\delta ,n,n_B\right)$ there are multiple no-delay SPE expected outcomes given by

$$x^{*}\in \left[max\left\{x_s,\widehat{x}\right\},x^s\right]$$

where

$$\widehat{x}=\frac{\left(1-\delta \right)\left(\mu +n_A\delta \right)}{\left(n-\delta \right)\mu -n_A{\delta }^2-n_B{\mu }^2}$$

Otherwise, when either $\delta \le \frac{1}{n-n_B}$ or $\mu <\overline{\mu }\left(\delta ,n,n_B\right)$, there is a unique no-delay SPE yielding expected outcome $x^{*}=x^s$.

Proof. 

We know that the necessary and sufficient conditions to obtain a minimal expected outcome $\underline{x}\in \left[x_s,x^s\right)$ are $y_a\left(\underline{x}\right)\le y_A\left(\underline{x}\right)$ and $y_a\left(\underline{x}\right)\le x^s$, where

$$y_a\left(x\right)=\frac{1-\delta \left(1-x\right)}{\mu }\text{and}{y}_A\left(x\right)=\frac{nx-\left(1-\delta \left(1-x\right)\right)-n_B\mu x}{\delta n_A}$$

Note that

$$y_a^{\prime }\left(x\right)=\frac{\delta }{\mu }\text{and}{y}_A^{\prime }\left(x\right)=\frac{\left(n-\delta \right)-n_B\mu }{\delta n_A}$$

so that, as $n-\delta >n-1=n_A+n_B$ we have that

$$y_a^{\prime }\left(x\right)-y_A^{\prime }\left(x\right)=\frac{\delta }{\mu }-\frac{\left(n-\delta \right)-n_B\mu }{\delta n_A}=\frac{n_A{\delta }^2+n_B{\mu }^2-\left(n-\delta \right)\mu }{\mu \delta n_A}<0$$

Thus $y_a\left(x\right)=y_A\left(x\right)$ has at most one solution $\widehat{x}$, given by

$$\widehat{x}=\frac{\left(1-\delta \right)\left(\mu +n_A\delta \right)}{\left(n-\delta \right)\mu -n_A{\delta }^2-n_B{\mu }^2}$$

Moreover, as $y_a^{\prime }\left(x\right)-y_A^{\prime }\left(x\right)<0$, we have that $y_a\left(x\right)\le y_A\left(x\right)⟺x\ge \widehat{x}$. Thus, as $\underline{x}\ge x_s$, the minimal expected outcome that can be attained is

$$\underline{x}=max\left\{\widehat{x},x_s\right\}$$

as far as the other (necessary) condition $y_a\left(\underline{x}\right)\le x^s$ is satisfied. That is,

$$y_a\left(\underline{x}\right)=\frac{1-\delta \left(1-\underline{x}\right)}{\mu }\le \frac{\left(n_A+1\right)\left(1-\delta \right)}{\left(n_A+1\right)\left(1-\delta \right)+n_B\left(1-\mu \right)}⟺\underline{x}\le \tilde{x}=\frac{1-\delta }{\delta }\frac{\left(n_A+1\right)\delta -n\left(1-\mu \right)}{n-\left(n_A+1\right)\delta -n_B\mu }$$

Hence, $\underline{x}<x^s$ can be attained if $\left[max\{\widehat{x},x_s\},\tilde{x}\right]\ne \varnothing$.

After some algebra, we find that $\tilde{x}\ge \widehat{x}$ iff

$$\begin{array}{c}\hfill Z_1\left(\mu ;\delta ,n,n_B\right)=n{n}_B{\mu }^2+\left(n\delta -n{n}_B-\delta n_B-\delta n_B^2-n^2+n\delta n_B\right)\mu +\\ \hfill +\left(n^2{\delta }^2-n^2\delta +n^2-2n{\delta }^2{n}_B-n{\delta }^2+n\delta n_B+{\delta }^2{n}_B^2+{\delta }^2{n}_B\right)\le 0\end{array}$$

and $\tilde{x}\ge x_s$ whenever

$$\begin{array}{c}\hfill \mu \ge {\mu }_2=\frac{n\left(1-\delta \right)+\delta n_B}{n-1}\end{array}$$

It is immediate that $Z_1\left(\mu ;\delta ,n,n_B\right)$ is a convex function in μ, with

$$\begin{array}{cc}\hfill Z_1\left(0;\delta ,n,n_B\right)& =\delta \left(n-n_B\right)\left(-n-\delta +n\delta -\delta n_B\right)+n^2>0,\text{and}\hfill \\ \hfill Z_1\left(1;\delta ,n,n_B\right)& =\delta \left(\delta -1\right)\left(n-n_B-1\right)\left(n-n_B\right)<0,\hfill \end{array}$$

where $n_B\le n-2$ has been used to prove the first inequality. Thus, $Z_1\left(\mu ;\delta ,n,n_B\right)=0$ has a unique root ${\mu }_1\left(\delta ,n,n_B\right)\in \left(0,1\right)$ and $Z_1\left(\mu ;\delta ,n,n_B\right)\le 0$ for all $\mu \ge {\mu }_1\left(\delta ,n,n_B\right)$. Hence, $\underline{x}<x^s$ might be attained whenever $\mu \ge \overline{\mu }\left(\delta ,n,n_B\right)=max\left\{{\mu }_1\left(\delta ,n,n_B\right),{\mu }_2\left(\delta ,n,n_B\right)\right\}$.

Since ${\mu }_2\left(\delta ,n,n_B\right)<1⟺\delta >\frac{1}{n-n_B}$, uniqueness is obtained when $\delta \le \frac{1}{n-n_B}$, as this implies $\left[max\{\widehat{x},x_s\},\tilde{x}\right]=\varnothing$ for all $\mu <1$. Otherwise, as ${\mu }_1\left(\delta ,n,n_B\right)<1$, multiple no-delay SPE are attained when $\delta >\frac{1}{n-n_B}$.

Once we know that both $\underline{x}\left(N,\delta ,\mu \right)$ and $\overline{x}\left(N,\delta ,\mu \right)$ are SPE expected outcomes, it can be shown (see Lemma A1 in the Appendix) that any $x\in \left[\underline{x}\left(N,\delta ,\mu \right),\overline{x}\left(N,\delta ,\mu \right)\right]$ is a no-delay SPE expected outcome. ☐

The previous proposition provides necessary and sufficient conditions for multiplicity. Nevertheless, it does not specify the minimal no-delay SPE outcome. The next corollary addresses this issue and provides the sufficient conditions to obtain a no-delay SPE where agents in A make the same proposal as agents in B; i.e., $\underline{x}=x_s$.

Corollary 1. 

There exist $\overline{\delta }\in \left(\delta ,1\right)$, ${\mu }_2\left(\delta ,n,n_B\right)\in \left(\delta ,1\right)$ and ${\mu }_3\left(\delta ,n,n_B\right)\in \left(\delta ,1\right)$ such that $\underline{x}\left(N,\delta ,\mu \right)=x_s$ is a no-delay SPE expected outcome whenever

• $\delta \in \left(\frac{1}{n-n_B},\overline{\delta }\right]$ and $\mu \ge {\mu }_2\left(\delta ,n,n_B\right)$, or
• $\delta >\overline{\delta }$ and $\mu \ge {\mu }_3\left(\delta ,n,n_B\right).$

Proof. 

From Proposition 2, multiple no-delay SPE are attained iff $\delta >\frac{1}{n-n_B}$ and $\mu \ge \overline{\mu }\left(\delta ,n,n_B\right)\in \left(\delta ,1\right)$. In these cases, $\underline{x}\left(N,\delta ,\mu \right)=x_s$ whenever $\widehat{x}\le x_s$. In the proof of that proposition, $\overline{\mu }\left(\delta ,n,n_B\right)=max\left\{{\mu }_1\left(\delta ,n,n_B\right),{\mu }_2\left(\delta ,n,n_B\right)\right\}$, where ${\mu }_1\left(\delta ,n,n_B\right)\in \left(0,1\right)$ is the unique positive root of $Z_1\left(\mu ;\delta ,n,n_B\right)$ and ${\mu }_2=\frac{n\left(1-\delta \right)+\delta n_B}{n-1}$. It can be checked that ${\mu }_1\left(\delta ,n,n_B\right)\le {\mu }_2\left(\delta ,n,n_B\right)$ iff $Z_1\left({\mu }_2;\delta ,n,n_B\right)\le 0$, which turns out to be the case when

$$\begin{array}{c}\hfill \delta \le \overline{\delta }=n\frac{\left(n-1\right)\sqrt{n-n_B}-\left(n-n_B\right)}{\left({\left(n-1\right)}^2-\left(n-n_B\right)\right)\left(n-n_B\right)}\end{array}$$

That is, $\overline{\mu }\left(\delta ,n,n_B\right)={\mu }_2\left(\delta ,n,n_B\right)$ iff $\delta \le \overline{\delta }$.

Using the definitions, it is immediate that $x_s\ge \widehat{x}$ whenever

$${\mu }^2+\left(n-1\right)\delta \mu -n\delta \ge 0⟺\mu \ge {\mu }_3\left(\delta ,n,n_B\right)=\frac{1}{2}\left[\sqrt{{\delta }^2{\left(n-1\right)}^2+4n\delta }-\left(n-1\right)\delta \right]$$

Moreover, it can be checked that ${\mu }_3\left(\delta ,n,n_B\right)\le {\mu }_1\left(\delta ,n,n_B\right)\le {\mu }_2\left(\delta ,n,n_B\right)$ for all $\delta \le \overline{\delta }$ and that ${\mu }_3\left(\delta ,n,n_B\right)>{\mu }_1\left(\delta ,n,n_B\right)\ge {\mu }_2\left(\delta ,n,n_B\right)$ for all $\delta \in \left(\overline{\delta },1\right)$. So, the result follows. ☐

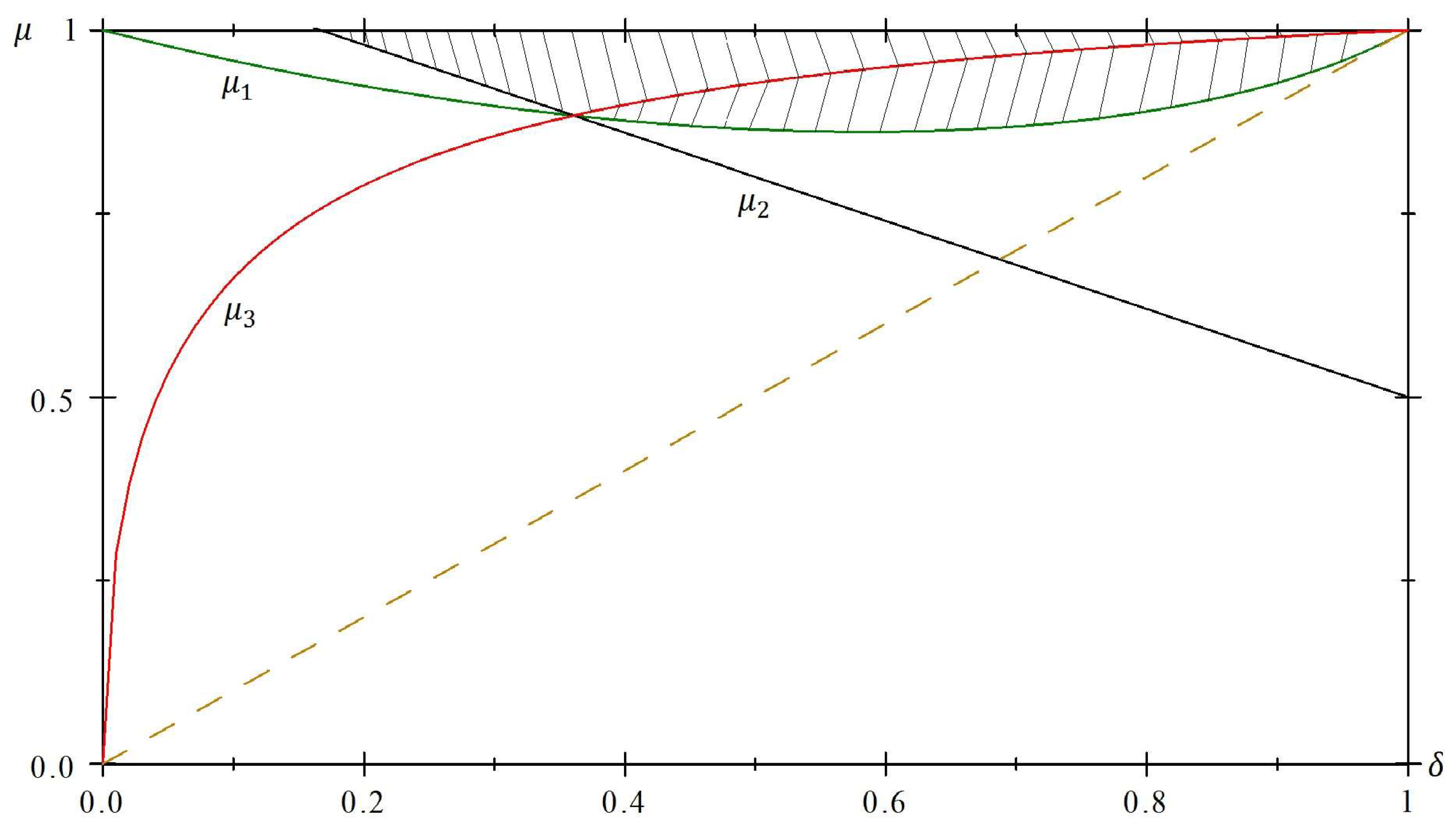
Figure 1 displays the set of parameters in which multiple no-delay SPE are attained when $n=11$ and $n_B=5$. The shaded areas determine the cases where the minimal no-delay SPE expected outcome is $\underline{x}=x_s$ (negative slope lines), and those where $\underline{x}=\widehat{x}>x_s$ is obtained (positive slope lines). For all other pairs $\left(\delta ,\mu \right)$ with $\mu \ge$δ the no-delay SPE yields expected outcome $x^s$.

When $\left(\delta ,\mu \right)$ belong to the sets specified in the previous corollary then $\underline{x}=x_s$, which is increasing in μ. However, when $\delta >\overline{\delta }$ and $\mu \in \left({\mu }_1,{\mu }_3\right)$ then $\underline{x}=\widehat{x}>x_s$, where

$$\widehat{x}=\frac{\left(1-\delta \right)\left(\mu +n_A\delta \right)}{\left(n-\delta \right)\mu -n_A{\delta }^2-n_B{\mu }^2}$$

as specified in Proposition 2. This function might be either increasing or decreasing in μ, depending on the relative sizes of groups $\overline{A}$ and B. When $n_B$ is sufficiently high relatively to $n_A$, $\underline{x}=\widehat{x}$ increases in μ whereas it decreases otherwise, which might seem counter-intuitive.10 The intuition behind this dependence relates to how μ alters the equilibrium proposals of agents in $A\cup B$. When $\sigma \in E$ yields $x\left(h^0|\sigma \right)=\underline{x}=\widehat{x}$, an increase in μ alters the equilibrium proposal of agents in A and B in opposite directions. While agents in B must increase their proposals, as $z_A^{-}\left(\underline{x}\right)$ increases in μ, agents in A decrease them, because now the minimal expected outcome required at the next period which makes a to reject their offer is smaller, as she is more patient. Thus, depending on the sizes of these effects, which clearly depend on $n_A$ and $n_B$, the overall effect of an increase in μ might be either positive or negative.

3. An Illustrative Example

The presence of agent a with time preference $\mu >\delta$ in group $\overline{A}$ generates a positive effects on its members in the unique stationary no-delay SPE: It induces the agents in the opposite group (B) to propose larger policies (and thus more favorable to $\overline{A}$ members) in order to satisfy the demands of a (the importance of this effect is increasing in both μ and the size of B). Nevertheless, such heterogeneity might generate a negative effect. As shown, when the discount factor of a is (relatively) large enough, there are no-delay SPE in which the co-partisans of a propose a policy less favorable to $\overline{A}$ members than the policy that is minimally required to get the acceptance of B members. This is because, when a is sufficiently patient she is willing to delay the agreement to a more favorable policy, which would made impatient agents in A worse-off. This threat forces A members to propose less preferred policies (the importance of this negative impact is increasing in the size of A). Hence, depending on the relative sizes of these two opposite effects, having a more patient agent in a group might be beneficial or detrimental for its members. In this section, we present an example that illustrates how heterogeneity affects the set of no-delay SPE expected outcomes.11

Let $n=11$ and $n_B=3$ so that $\overline{\delta }=0.30316$. Suppose also that $\delta =0.95>\overline{\delta }$. Direct calculations yield

$$x_s=\frac{0.05}{10.05-10\mu },x^s=\frac{0.4}{3.4-3\mu },\widehat{x}=\frac{0.05\mu +0.3325}{10.05\mu -6.3175-3{\mu }^2}$$

and

$${\mu }_1=0.95498,{\mu }_2=0.34\text{and}{\mu }_3=0.99565$$

The minimum no-delay SPE expected outcome is

$$\underline{x}=\left\{\begin{array}{cc}\frac{0.4}{3.4-3\mu }& 0.95\le \mu \le 0.95498\\ \frac{0.05\mu +0.3325}{10.05\mu -6.3175-3{\mu }^2}& 0.95498\le \mu \le 0.99565\\ \frac{0.05}{10.05-10\mu }& \mu \ge 0.99565\end{array}\right.$$

Figure 2 displays all no-delay SPE expected outcomes $x^{*}\in \left[\underline{x},\overline{x}\right]$ as a function of $\mu \ge \delta =0.95$. Solid lines represent $\underline{x}$ (the smallest expected outcome that can be obtained in any no-delay SPE, thus the least preferred for the members of $\overline{A}$) and $\overline{x}=x^s$ (the expected outcome in the any no-delay stationary SPE, which is also the largest expected outcome that can be attained in any no-delay SPE, thus the most preferred for the members of $\overline{A}$). Dashed lines represent the unique no-delay SPE expected outcomes when a is not included into negotiations and when ${\delta }_a=\delta$ (so that they do not depend on μ), given by $n_A/\left(n-1\right)$ and $\left(n_A+1\right)/n$, respectively.

After minor calculations, some observations are worth:

• The minimal no-delay SPE expected outcome $\underline{x}$ is not monotone in μ. For low values of μ such a relationship is negative, which might seem counter-intuitive. As noted in the previous section, this happens because when the costs of delaying an agreement for player a are reduced, their impatient partners make smaller proposals in order to prevent a delayed agreement induced from a’s rejection. Hence, although the proposals of agents in B increase in μ, those of agents in A are reduced. Since, in this example, $n_B$ is low relatively to $n_A$, the second effect dominates the first one.12 For large values of μ, agents in A make the same proposal as agents in B. Hence, only the first effect appears and therefore $\underline{x}=x_s$ increases in μ. Worthy, as $\mu \to 1$ the minimal no-delay SPE expected outcome converges to the maximal no-delay SPE expected outcome.
• There is a discontinuity at $\mu ={\mu }_1$. The reason for this lies in the fact that in order to get multiplicity there must exist $\underline{x}\in \left[x_s,x^s\right)$ with $y_a\left(\underline{x}\right)\le min\left\{y_A\left(\underline{x}\right),x^s\right\}$, which happens only when $\mu \ge {\mu }_1>\delta$. Moreover, when such an outcome exists then there is a (equilibrium) threat by agent a to reject proposals in $\left[z_A^{-}\left(\underline{x}\right),z_B^{+}\left(\underline{x}\right)\right]$, inducing a jump in the equilibrium proposals of agents in A, which is reflected in such a discontinuity.
• If $\mu \in \left[0.95498,0.99786\right)$ then $\underline{x}<n_A/\left(n-1\right)$, which is the unique no-delay SPE expected outcome when a is not included into negotiations. So, within this parameter range the members of A would prefer not to include agent a into negotiations rather than their least favorable equilibrium when a is added. This does not happen when $\mu >0.99786$ where including a makes all agents in A better off even in their least preferred no-delay SPE.
• If $\mu >0.99813$ then $\underline{x}>\left(n_A+1\right)/n$, which is the unique no-delay SPE expected outcome when $\mu =\delta$. So, even if agents in A anticipate that their worst equilibrium will be played, they all benefit from such heterogeneity.

4. When a Is more Impatient

We derived our multiplicity/uniqueness result for cases where $\mu \ge \delta$. Similar results can be obtained when $\mu <\delta$. The difference is that now, according to Lemma 2.1 in any no-delay SPE $x_i\left(h_i\right)\ge z_B^{+}\left(\underline{x}\right)$ for all $i\in A$ and any $h_i\in H_i$, whereas Lemma 2.2 does not guarantee $x_a\left(h_a\right)\ge z_B^{+}\left(\underline{x}\right)$ for any $i\in A$. In fact, using a similar argument as in Section 2, now multiple SPE are attained when there is some $\sigma \in E$ where $x_a\left(h_a^0\right)<z_B^{+}\left(\underline{x}\right)$. Although in these cases, the presence of an heterogeneous agent $a\in \overline{A}$ would have a small impact on the set of no-delay SPE expected outcomes, it might also be a source of multiplicity. The next Proposition summarizes these situations. We omit the proof, as it is similar to those presented in Section 2.

Proposition 3. 

For any N and $\delta >\tilde{\delta }=n/\left(n+1\right)$ there exists $\tilde{\mu }\left(\delta ,N\right)<\delta$ such that for all $\mu \le \tilde{\mu }\left(\delta ,N\right)$ the bargaining game $G\left(N,\delta ,\mu \right)$ exhibits multiple SPE expected outcomes given by

$$x^{*}\in \left[max\left\{\underline{s}\left(N,\delta ,\mu \right),\tilde{x}\left(N,\delta ,\mu \right)\right\},\overline{s}\left(N,\delta ,\mu \right)\right]$$

where

$$\underline{s}\left(N,\delta ,\mu \right)=\frac{n_A}{n},\overline{s}\left(N,\delta ,\mu \right)=\frac{n_A+1}{n}\text{and}\tilde{x}\left(N,\delta ,\mu \right)=\frac{1-\delta }{\delta }\frac{n_A\delta +\mu }{n-\left(n-1\right)\delta -\mu }$$

5. Final Remarks

In a two-group multilateral (unanimity) bargaining game, we highlighted the importance of the homogeneity (or relatively low heterogeneity) withing groups in order to obtain a unique no-delay SPE. The uniqueness result is not robust when there is one agent with a sufficiently different discount factor. In those cases, multiple equilibria are attained. Such indeterminacy is built on the conflict that appears among agents having the same instantaneous preferences over the collective decision. Interestingly, when the heterogeneous agent is sufficiently patient, there is an equilibrium in which her group-mates make the same proposal as the members of the opposite group. Nevertheless, we showed that this does not necessarily imply that group-mates are worse-off, as the acceptance requirement of such a player might be very demanding.

We introduced heterogeneity in one group in the form of different time preferences. One might think that, as we can always find a value of μ so close to δ such that there is a unique no-delay subgame perfect equilibrium, when impatience of all agents vanishes then uniqueness is restored. In this respect, we must remark that multiplicity is attained when $\mu -\delta$ exceeds a bound, which is decreasing in δ, so that multiple equilibria can be also attained when δ approaches 1. Moreover, the same qualitative results would obtain by considering heterogeneity in the cardinality of the instantaneous preferences. For instance, assuming $\mu =\delta$ and $u_a\left(x\right)=\alpha x$ with $\alpha <1$ would lead to the same qualitative results than those we obtained with $\mu >\delta$ and $u_a\left(x\right)=x$.