From Bargaining Solutions to Claims Rules: A Proportional Approach

Abstract

Agents involved in a conflicting claims problem may be concerned with the proportion of their claims that is satisfied, or with the total amount they get. In order to relate both perspectives, we associate to each conflicting claims problem a bargaining-in-proportions set. Then, we obtain a correspondence between classical bargaining solutions and usual claims rules. In particular, we show that the constrained equal losses, the truncated constrained equal losses and the contested garment (Babylonian Talmud) rules can be obtained throughout the Nash bargaining solution.

1. Introduction

As pointed out by [1,2,3], although the literature about conflicting claims problems, which originates in a fundamental paper by [4], proposes a vast number of rules, “the proportional solution is the most widely used”. The main reason is the fact that a proportional sharing allows individuals to compare the treatment afforded to each one, in terms of the proportion of the claim that is honored. Moreover, the principle behind this proportional point of view is that the obtained amount per unit of individual claim (or other proportion defining variable) is the same for all.

An interesting interpretation of proportionality, when analyzing conflicting claims problems, can be found in [5]: “(...) A few years ago I developed what appears to be a new viewpoint which leads to the proportional solution. Since the amount E is not enough to pay off the bankruptcy, one might adopt the following point of view: Instead of giving the claimants less than they are entitled to now, one can postpone paying them off and wait until the available money E grows, by investing it at the current interest rate until the invested amount plus interest totals the amount being claimed. The judge at this future point in time would pay off each claimant his/her full amount. Using the well-known accounting principle of computing the present value of this future asset we can see what amount of money this approach would yield each claimant today. If one does the algebra involved, one sees that the solution is the same as the proportional solution. (...)"

According to this proportional concern, we transform a conflicting claims problem $(E,c)$ into a claims-in-proportions bargaining problem $\left(S\right(E,c),d),$ by associating to each allocation $x,$ a new variable $p\in S(E,c),$ where $p_i$ is the proportion of the claim $c_i$ that agent i receives, $x_i=p_i{c}_i.$ Then, we define the associated bargaining-in-proportions approach. It turns out that well known claims rules can, in this fashion, be described by classical bargaining solutions. For instance, if we apply the Nash bargaining solution [6], we observe that (i) it provides the same allocation when applied to the problem $\left(S\right(E,c),d)$, and when applied directly to the conflicting claims problem $(E,c)$; and (ii) it coincides with the constrained equal awards rule [7]. Nevertheless, in general bargaining solutions do not coincide when applied to problems $\left(S\right(E,c),d)$ and $(E,c).$ Then, we analyze how a claims rule φ and a bargaining solution F in the following diagram are related.

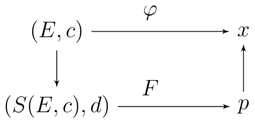
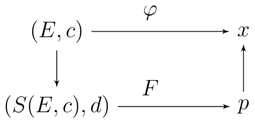
In particular, we show that the egalitarian [8] bargaining solution corresponds with the proportional rule, whereas when considering different reference points r the Nash solution provides the constrained equal losses, the truncated constrained equal losses, and the contested garment (Babylonian Talmud) rules in conflicting claims problems.

The paper is organized as follows. Section 2 contains the main definitions on conflicting claims and bargaining problems. Section 3 defines our model and presents the results about the correspondence between claims rules and bargaining solutions. Finally, Section 4 closes the paper with some remarks.

2. Preliminaries

2.1. Conflicting Claims Problems and Rules

Consider a set of individuals $N=\left\{1,2,...,n\right\}$. Each individual is identified by her claim, $c_i,$ $i\in N$, on some endowment $E.$ A conflicting claims problem appears whenever the endowment is not enough to satisfy all the individuals’ claims; that is, ${\displaystyle \sum _{i=1}^n}{c}_i>E.$ The pair $(E,c)\in \mathbb{R}\times {\mathbb{R}}^n$ represents the conflicting claims problem, and we will denote by $\mathcal{B}$ the set of all conflicting claims problems. A claims rule is a single valued function $\phi :\mathcal{B}\to {\mathbb{R}}_{+}^n$ such that: $0\le {\phi }_i(E,c)\le c_i,\forall i\in N$ (non-negativity and claim-boundedness); and ${\displaystyle \sum _{i=1}^n}{\phi }_i(E,c)=E$ (efficiency). We now present briefly the rules used throughout the paper. The reader is referred to [2,9] for reviews of this literature.

The proportional rule recommends a distribution of the endowment which is proportional to the claims, $P_i(E,c)\equiv \lambda c_i,$ where $\lambda ={\displaystyle \frac{E}{{\sum }_{i\in N}{c}_i}}.$

The constrained equal awards rule (Maimonides, 12th century) proposes equal awards to all agents subject to no one receives more than her claim, $CE{A}_i(E,c)\equiv min\left\{c_i,\mu \right\},$ where μ is such that ${\sum }_{i\in N}min\left\{c_i,\mu \right\}=E.$

The constrained equal losses rule (discussed by Maimonides [10]) proposes equal losses to all agents subject to no one receives a negative amount, $CE{L}_i(E,c)\equiv max\left\{0,c_i-\mu \right\},$ where μ is such that ${\sum }_{i\in N}max\left\{0,c_i-\mu \right\}=E.$

Given a claims rule $\phi ,$ the associated truncated by the endowment claims rule ${\phi }^T$ is defined by ${\phi }^T(E,c)\equiv \phi (E,c^T),$ where $c_i^T=min\{c_i,E\}.$

The adjusted proportional rule [11], which a generalization of the contested garment principle (Babylonian Talmud), recommends the allocation $A{P}_i(E,c)\equiv v_i+$$\left(E-{\sum }_{j=1}^n{v}_j\right)$ ${\displaystyle \frac{c_i^T-v_i}{{\sum }_{j=1}^n(c_j^T-v_j)}},$ where $v_i=max\{0,E-{\sum }_{k\ne i}{c}_k\}.$

2.2. Bargaining Problems and Solutions

A bargaining problem is a pair $(S,d)$, such that $S\subseteq {\mathbb{R}}_{+}^n$ is a subset in the $n-$dimensional Euclidean space, and d is a point in $int\left(S\right)$, which is called disagreement point. Furthermore, we consider the set S is convex, bounded, closed from above and comprehensive. Note that S is comprehensive in ${\mathbb{R}}_{+}^n$ if $x\in S,$$0\le y\le x,$ implies $y\in S.$ Given a bargaining problem $(S,d)$ its individually rational Pareto boundary is defined by ${\partial }_P(S,d)=\{x^{*}\in S:x_i\ge d_i\text{and}{y}_i>x_i\forall i\Rightarrow y\notin S\}.$ The ideal point a represents the maximum amount that each agent can achieve in such a problem: ${\mathit{a}}_{\mathit{i}}\left(\mathit{S}\right)\equiv max\left\{x_i\right|x\in S\},$ for each $i\in N.$ A bargaining solution F assigns to each bargaining problem $(S,d)$ a unique element $F(S,d)\in S.$ For additional information, the interested reader is referred to [12].

The Nash solution [6] $N(S,d)$ is the point maximizing the product of utility gains from the disagreement point $u\left(x\right)={\prod }_{i=1}^n(x_i-d_i)$ in ${\partial }_P(S,d).$

The Egalitarian solution [8] $E(S,d)$ selects the maximal point of S at which all agents’ utility gains are equal, i.e., the intersection point of the line throughout d with gradient 1 and ${\partial }_P(S,d).$

The Kalai-Smorodinsky solution [13] $KS(S,d)$ selects the point in ${\partial }_P(S,d)$ at which the agents’ gains are proportional to their ideal situation, i.e., the intersection point of the line throughout a and d and ${\partial }_P(S,d).$

The Nash α-asymmetric solution, $\alpha =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)$ ([14,15] ) $A{N}^{\alpha }(S,d)$ is the point that maximizes the function $u\left(x\right)={\prod }_{i=1}^n{(x_i-d_i)}^{{\alpha }_i}$ in ${\partial }_P\left(S\right).$

Given a point r $=(r_1,r_2,\dots ,r_n)$ such that r ≥ a, the Nash from the reference point r solution [16] $N^r(S,d)$ is the point that maximizes the function $u\left(x\right)={\prod }_{i=1}^n(r_i-x_i)$ in ${\partial }_P(S,d).$

3. Bargaining-In-Proportions: Correspondence between Bargaining Solutions and Claims Rules

The bargaining-in-proportions problem $\left(S\right(E,c),\mathbf{0})$ associated to a conflicting claims problem $(E,c)$ is defined by considering the proportion of the claim that each agent is willing to disclaim. So, if we name $p_i$ the proportion of her claim that individual i receives, the set of feasible claims can be written as:

$$S(E,c)=\{(p_1,p_2,\dots ,p_n):p_i\in [0,1],\sum _{i=1}^n{c}_i{p}_i\le E\}.$$

when there is no confusion, we will denote this set simply by $S.$ Observe that if $(p_1^{*},p_2^{*},...,p_n^{*})$ is a solution in the bargaining-in-proportions problem $\left(S\right(E,c),\mathbf{0}),$ then it induces a solution in the claims problem $(E,c),$$x_i^{*}=p_i^{*}{c}_i$.

We name utopia point the ideal point in this transformed problem; that is, the point $\mathit{u}=(u_1,u_2,\dots ,u_n)\in {\mathbb{R}}^n$ such that for each $i\in N,$$u_i=min\left\{1,E/c_i\right\}.$ Furthermore, we call maximum point to the unitary vector 1$=(1,1,\dots ,1)\in {\mathbb{R}}^n$ that represents the maximum proportion of the claim that an individual may expect to obtain before knowing the actual endowment $E.$

The next example provides an illustration, and relates the $CEA$ rule with the Nash solution.

Example 1. 

Consider the three person conflicting claims problem defined by $(E,c)=(100,(20,70,110\left)\right)$. Then, $CEA(E,c)=(20,40,40)$. The associated bargaining-in-proportions set is defined by $S=\{(p_1,p_2,p_3)\in {\mathbb{R}}^3:p_i\in [0,1],20p_1+70p_2+110p_3\le 100\}.$ The Nash bargaining solution in $(S,\mathbf{0})$ is, $N(S,\mathbf{0})=(1,4/7,4/11)$ that induces the proposal $(20,40,40).$ Therefore, the Nash bargaining solution corresponds with the one given by the $CEA$ rule.

Proposition 1. 

The following correspondences between solutions and rules hold:

• $N(S,\mathbf{0})$ and $CEA(E,c).$
• $A{N}^{\alpha =c}(S,\mathbf{0})$ and $P(E,c).$
• $E(S,\mathbf{0})$ and $P(E,c).$
• $KS(S,\mathbf{0})$ and $P^T(E,c).$
• $KS(S,\mathit{w})$ and $AP(E,c),$ for $w_i={\displaystyle \frac{v_i}{c_i}},$ and $v_i=max\{0,E-{\sum }_{k\ne i}{c}_k\}.$

Proof. See Appendix.

The $AP$ rule is a generalization of the $CG$ principle (Babylonian Talmud). This particular case, that involves just two individuals, can also be obtained throughout the Nash solution from point $w.$

Proposition 2. 

For $n=2$, $N(S,\mathit{w})$ corresponds with $CG(E,c).$

Proof. See Appendix.

Finally, the next result shows that the Nash bargaining solution (i) from the maximum point corresponds to $CEL$ rule, and (ii) from the utopia point provides the $CE{L}^T$ rule.

Proposition 3. 

The following correspondences between Nash solutions and claims rules hold:

• $N^{r=1}(S,\mathbf{0})$ and $CEL(E,c).$
• $N^{r=u}(S,\mathbf{0})$ and $CE{L}^T(E,c).$

The proof runs parallel to the one in Proposition 1 part (1).

4. Final remarks

In this work we build a connection between bargaining solutions and claims rules in a new scenario where the relevant notions about what the involved individuals discuss are the proportions of their claims that are (or are not) satisfied. Moreover, this new approach would allow to define new claims rules by using well known bargaining solutions.