1. Introduction
When John von Neumann and Oscar Morgenstern began working on
Theory of Games and Economic Behavior almost a century ago, they were motivated by the observation that most received theory pertained to price-based interactions in large markets, whereas a large fraction of economic activity involves bargaining in small group settings. The only economics class that John Nash took at Carnegie-Mellon as an undergraduate was International Trade, and he was intrigued by the absence of a widely accepted model for negotiations between countries over trade issues. The seminal work of these game theorists and others has generated a large bargaining literature, involving both theory and applications to specific social sciences.
1 Over the past two decades, for example, students of world politics have increasingly thought of interstate war as a bargaining problem. Drawing heavily on the literature of economics, bargaining models have become commonplace and have provided a number of significant insights regarding when and why states resort to arms. An analysis of strategic bargaining has been used to explain how wars begin and end, and how long they last. In addition, bargaining models have been adapted to explain the durability of peace agreements, extended deterrence, and the relation between trade and conflict. This paradigm also extends to other issues of importance to social scientists, e.g., the incidence of costly strikes that follow breakdowns in labor negotiations, or costly delays in the adjudication of tort claims. In all of these examples, bargaining is conducted in the “shadow of power” [
14].
2 In particular, a failure to reach an agreement in these settings produces a crisis or trial that is settled by a contest with an uncertain outcome.
An alternative perspective on conflict is that stable situations are sometimes disrupted by “exogenous” demands that arise from overconfidence, perceived or actual inequities, and the personalities of leaders that come to power. Bargaining models, in contrast, are focused on structural factors, e.g., power asymmetries, that determine strategic demands and the conflicts that arise endogenously in this framework [
5,
14,
15,
19]. These scholars claim that parties evaluate the distribution of benefits in light of the distribution of power, and decide whether to make demands about reallocating benefits to better represent the realities of power, as represented by the probabilities of winning in a conflict. So states of equal power, who also have equal shares in the benefits of the international system, are less likely to fight than are equally powerful states with decidedly unequal benefits. Similarly, the relative probabilities of winning in a labor dispute should affect strike decisions made by employees. Both the amount of the challenger’s demand and the probability of bargaining failure arise from the imbalance between the probability of winning in a conflict and the distribution of benefits
ex ante (Reed, Clark, Nordstrom, Hwang 2008).
Despite the theoretical appeal of the basic insights from bargaining theory, empirical evaluation of the claims that arise from these models has lagged behind. The lack of empirical work is not for lack of effort. Instead, the gap is due to the simple fact that many elements of the basic bargaining model are either difficult to measure or are unobservable. For example, in international bargaining and in labor negotiations alike, neither the probability of success nor the costs of bargaining failure are as explicitly known as models would suggest. Experimental analysis offers a unique opportunity to observe how power imbalances and other factors affect behavior in the context of models with clear theoretical predictions.
A common modeling approach is to constrain the timing and nature of decisions in a manner that makes it possible to derive clear theoretical predictions. The structure of a bargaining process can be simplified by designating one person as a decision maker in each discrete stage of the game, e.g., with alternating offers or a randomly determined decision order. The standard Stahl-Rubinstein model of alternating-offer bargaining has an infinite horizon, with no conflict, but effects of discounting and delay are sufficient to induce an immediate agreement that is shaped by the potential costs of delay. Finite versions of this model that are convenient for laboratory experiments typically impose exogenous payoffs in the final stage.
3 For example, the single-stage ultimatum game that has been used in hundreds of laboratory experiments has zero payoffs for each player if the ultimatum demand by one is rejected by the other. A zero payoff is sensible if a monopolist walks away from a deal, leaving both parties with no trade, or if conflict involves a total destruction of the potential surplus. Conflict, whether it is legal, economic, or military, can involve significant costs, but in the absence of nuclear escalation, these costs are unlikely to eradicate the value of the rights being contested. Moreover, conflict involves additional uncertainty about who will ultimately prevail.
In a laboratory experiment, conflict risk can be implemented by having the outcome of an impasse be determined by a random lottery. The predictions of this conflict bargaining model with a lottery depend on relative power, as measured by the probabilities that each side would prevail. In theory, demands and counter-offers should be shaped by power asymmetries, along with delay and conflict costs, but the subgame-perfect Nash prediction is similar to that of other models: (1) no delay; (2) nothing left on the table (in an expected payoff sense); and (3) no conflict. Un-modeled “exogenous” factors like overconfidence, overweighting of low probabilities, or differences in risk aversion and perceptions of fairness can generate conflict in laboratory bargaining games.
Our goal in this paper is to evaluate the extent to which bargaining outcomes and conflict rates are shaped by structural factors like power asymmetries. Even though the theory is straightforward, there is good reason to be skeptical of predictions that rely on backward induction reasoning. Our analysis therefore, is based on a laboratory experiment with financially motivated human subjects. In short, we find a significant relationship between players’ known winning probabilities and their initial demands and counteroffers. The effects of power asymmetries, however, are not as strong as predicted, and conflict occurs in about a quarter of the interactions, irrespective of whether or not differences in the probabilities of winning are high or low. Some behavioral explanations of the observed deviations from game-theoretic predictions are analyzed.
2. A Simple Model of Conflict Bargaining
We begin with a standard analysis of a two-stage model, which is followed by a derivation of the predictions for the particular setup parameters used in the experiment. In the model, two risk neutral players bargain over the division of surplus of size S, e.g., a parcel of territory or the surplus available in a trade agreement. The status quo division is (q, S − q), where q is the initial allocation for the first player, who begins by demanding an amount x1 and offering S − x1 to the other player. The responder can either accept the offer, in which case it is implemented, or make a counteroffer to divide the discounted value of the second-stage “pie,” δS, where δ ≤1. Thus the counteroffer is a split of δS – x2 for the first player and x2 for the second. If the initial demand is rejected and a counteroffer is made, then the first player must decide whether to accept the counteroffer or to engage in a costly conflict, which the first player wins with probability P. The conflict costs for the first player (“proposer”) and the second player (“responder”) are denoted by cp and cr respectively.
Assuming that both the players are fully informed of the payoffs and the win probabilities, the game is solved through backward induction. In the second stage, the responder’s demand would be an amount
x2 for which the residual available to the proposer, δ
S –
x2, is equal to the proposer’s expected payoff in a conflict after incurring the conflict cost,
Pδ
S −
cp, assuming that indifference will result in acceptance.
4 This equation determines the responder’s second stage demand:
x2 = (1 −
P)δ
S +
cp, which is a decreasing linear function of the proposer’s win probability. This value of
x2 is what the responder can expect to earn if play goes to the second stage, so the proposer makes a minimal offer of this amount to the responder in the first stage:
which is an increasing linear function of
P. For example, if conflict costs are 2,
S = 10, and δ
S = 9, then the initial and final demands would be:
x1 = 9
P − 1, and
x2 = 11 − 9
P. The effects of the payoff parameters are intuitive. For example, as delay costs increase (via a reduction in δ) the initial demand in Equation (1) is predicted to increase to take advantage of the strategic first-mover advantage. One interesting asymmetry for this two-stage game is that the equilibrium demands depend only on the conflict cost for the proposer, and that a higher proposer conflict cost increases the predicted spread between
x1 and
x2.
3. Experimental Design
The laboratory experiment is based on the two-stage bargaining model, with a pie size of $10 and a second stage (discounted) pie size of $9. The initial allocation was unbalanced at $3 for the proposer and $7 for the responder. Conflict costs were set at $2 for each player, and the proposer win probabilities were set at one of four levels: 0.2, 0.4, 0.6, and 0.8, where the probabilities were explained in terms of the roll of a 10-sided die.
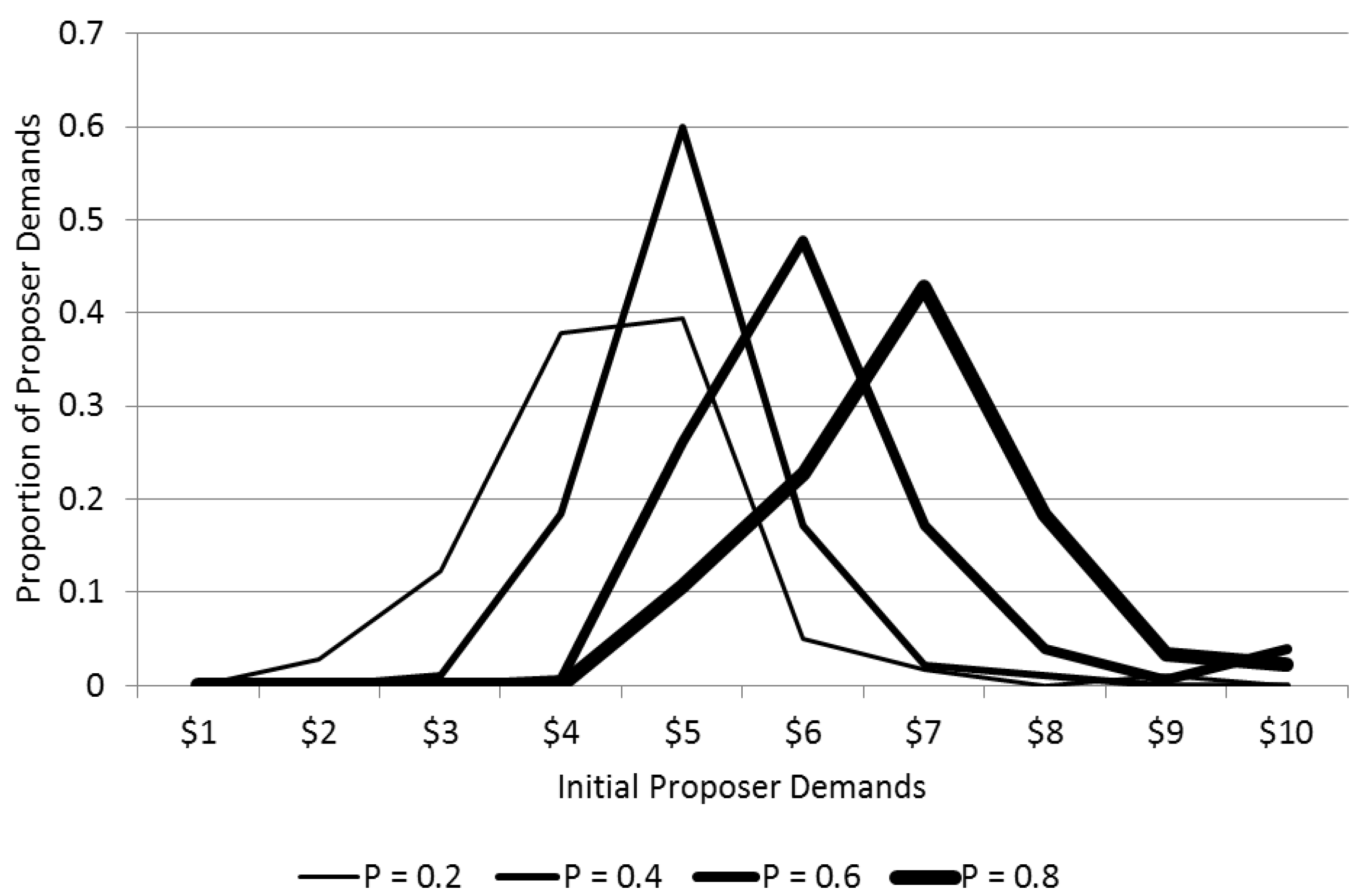
Subjects in the experiment were constrained to make discrete integer dollar demands, rather than continuous amounts. In this case, the backward induction arguments still yield a pattern of initial demands that is an increasing function of proposer win probabilities. The calculations may be illustrated for the case of a proposer win probability 0.8, for which the proposer’s expected payoff from conflict is 0.8(9) − 2 = $5.20, so a second-stage offer of $6 would be accepted, leaving the responder with $3. Given this knowledge, the proposer can demand $7 in the first stage and offer $3 to the responder. The other three sets of equilibrium demands can be derived analogously. For win probabilities of 0.2, 0.4, 0.6, and 0.8, the first stage demands are $1, $3, $5, and $7, and the second stage demands are $9, $7, $5, and $3 respectively.
The experiment was conducted using the Political Conflict option for the web-based Veconlab Bargaining Game.
5 This option implements a two-stage dispute model with an array of parameter choices. The instructions are configured automatically to match the setup parameters selected.
6 Each bargaining game implemented the two-stage model described in the previous section. For the parameters used, conflict is risky since the winner receives $9 and the loser receives nothing. After conflict costs were subtracted, conflict payments are $7 for the winner and −$2 for the loser.
Each session consisted of 12 subjects being randomly matched for 10 rounds, with one value of
P used in the first five rounds, and a switch to another value of
P in the final five rounds. We ran 12 sessions that used all possible treatment orders. The random pairing was chosen to avoid complications arising from repeated play with the same opponent.
7 The change in the win probability treatment in the second half of each session permits a within-subjects analysis of changes in relative power. Data from the second treatment, however, could be biased by “order effects,” a possibility that we will consider later. Order effects can also be interesting, since the impact of changes in power asymmetries may alter conflict rates.
The 144 subjects were University of Virginia students who were paid $6 for participating, plus half of accumulated earnings. Earnings were in the $18–$25 range, for a one-hour session, and were paid immediately after each session.
5. Experimental Implications
The experimental results show some evidence for the imperfect use of subgame perfect Nash equilibrium strategies. Although the demands and counteroffers fail to match game theoretic predictions, they do indicate that subjects involved in a bargaining game with a conflict stage take relative power into account when making demands. Although the qualitative features of some of the Nash predictions are apparent in the data, the systematic directional biases we observe are hardly surprising, given the results of prior laboratory studies (without the conflict stage).
11 For example, Neelin, Sonnenschein, and Spiegel [
13] ran experiments using multi-stage bargaining games. Their results for two-stage games reflect a certain regularity, subjects who are disadvantaged in the sense that they are predicted to demand less than half of the pie tend to be more aggressive, and subjects who are predicted to obtain a large share of the pie tend to demand less than they “should,” which is in line with ultimatum game experiments.
Anomalous results in bargaining experiments are typically thought to reflect concerns for fairness, rather than straightforward self-interested strategic behavior [
9]. Goeree and Holt [
7] exaggerated fairness considerations by providing subjects in two-stage bargaining games with unequal and known outside income payments. These “outside income” payments changed the equal final payoff locus, and exogenously induced inequities seemed to have a more prominent effect than delay cost changes that altered selfish Nash predictions. In many legal and political settings, however, it is hard to imagine that the actors have much concern for others’ payoffs. Instead of enhancing equity considerations, it may be instructive to move in the other direction. In particular, equity considerations in the lab can be dampened by providing unequal private incomes that are
not common knowledge, which would make equal-payoff outcomes difficult to ascertain. We conjecture that the effect of having a contest at the end of each game in our experiment is to create a competitive atmosphere that dampens concerns for fairness.
The addition of the random conflict lottery can introduce another source of potential bias, since anomalous results for risky choices are quite common. For example, probabilities might be overweighted if they are small. For early evidence supporting the notion of nonlinear probability weighting, see Cohen, Jaffray and Said [
3], who report results from an experiment with choices between a sure option and a lottery and observe less sensitivity to probabilities in their subjects’ choices than would be expected. In particular, subjects seemed to overweight low probabilities of gains and underweight high probabilities of gains, with the result being a relative insensitivity to intermediate probabilities. Similar patterns are reported by Kahneman and Tversky [
11]. Our data are consistent with these results in the sense that an overweighting of low proposer win probabilities might cause them to think that they can demand more and that responders would accept less than would be predicted on the basis of expected value calculations.
12 Nevertheless, the biases away from risk-neutral Nash predictions in
Figure 1,
Figure 4,
Figure 5 are not concentrated at the extremes of 0.2 and 0.8, which suggests another explanation.
Finally, it is well known from “centipede” and other multi-stage games that backward induction does not come easily to subjects. Binmore, Shaked, and Sutton [
2] dismiss the notion that we should expect to see subgame-perfect behavior in the laboratory, because even they, as designers, had to work to come up with the game theoretic results for their ultimatum bargaining game.
13 Even in the absence of the need for backward induction and probability assessments, e.g., a 1-stage bargaining game with no conflict, the Nash predictions are based on a perfect rationality assumption that a gain of only a penny would be enough to induce the other person to accept a final offer. A small amount of irrationality could produce random responses, and the effects of such randomness should be magnified in the presence of multiple stages and the exogenous uncertainty of a conflict. The next section presents a quantal response model of conflict bargaining in which “irrational” rejections or acceptances become more likely as expected payoff differences diminish, which provides an incentive for responders to be cautious with final counter-offers that are too near the “edge.” The converse of this is that proposers may be more aggressive with initial demands knowing that responders may accept a smaller share if they anticipate being cautious with counteroffers. By construction, a model with errors will produce conflicts. The interesting question, however, is whether such a model (without inequity aversion and probability misperception) can produce (1) proposer demands that are above Nash levels and too flat; (2) responder demands that are below Nash levels and too flat; and (3) conflict proportions that are significant and relatively invariant to power asymmetries.
6. Estimation of a Quantal Response Model of Two-Stage Bargaining
Consider a proposer who receives a counter offer of 9 –
x2 in the final stage and must decide whether to accept or reject. A conflict with a win probability of
p yields an expected payoff of 9
p −
cp. Given a logit precision parameter of λ, the probability that the counteroffer is accepted is calculated as a ratio of exponentials of precision-adjusted expected payoffs for accepting and rejecting:
which converges to 0.5 as λ→0 (pure noise) and which converges to 1 only if the payoff for accepting, 9 –
x2, is higher than the expected conflict payoff (perfect rationality). Also, note that equal expected payoffs result in choice probabilities of 1/2 in this case.
14Given λ, which is assumed to be the same for the responder, the model is solved by backward induction by letting the responder probabilities for each demand
x be determined analogously as ratios of precision-adjusted expected payoffs. The responder’s payoff for making a demand of
x2 depends on the acceptance probability from Equation (2) and the expected conflict payoff:Pr(
accept|
x2,
p)*
x2 + (1−Pr(
accept|
x2,
p))*(9(1−
p) −
cr). Let this expected payoff for a responder counter demand of
x2 be denoted by π(
x2|
p). In a quantal response equilibrium (McKelvey and Palfrey, 1995), the assumption is that the proposer choice probability in Equation (2) is equal to the responder’s belief probability used to construct the expected payoff for each possible responder counter-offer. Then the responder’s choice probabilities for each possible counter-demand are calculated:
for
x2 = 1, … 9, where the denominator ensures that the choice probabilities for each of the 9 possible counter demands sum to 1. As before, a very high value of the precision parameter will putprobability 1 on the expected-payoff-maximizing demand.
Proposer demands and acceptance probabilities for the first stage are calculated analogously by computing a “value” for optimal continuation for each player. The value of continuation would be the proposer’s expected payoff associated with a vector of possible responses from Equation (3) and an assumption that the proposer’s final decisions about whether to accept or reject will be in accordance with the acceptance probabilities from Equation (2).
15 In this manner, the single precision parameter enters all of the various acceptance and rejection probabilities and demand probabilities for proposers and responders. Estimation involves finding the value of λ that maximizes the probability of seeing the data pattern that was actually observed. The likelihood function is a product of terms, each involving a probability for a particular category raised to a power representing the number of observations in that category. The data consist of the numbers of accepted and rejected demands for each of the four proposer win probabilities (0.2, 0.4, 0.6, 0.8) for each of the 10 possible initial demands and each of the 9 possible counter-offers.
This model is a one-parameter generalization of the Nash equilibrium determined by λ, which for each value of
p generates 9 proposer acceptance probabilities from Equation (2), 10 responder acceptance probabilities for each value of
p, and the probabilities associated with each possible initial proposer demand and each possible responder counter offer. All of these probabilities are functions of the proposer win probability
p. Using data from the second half (rounds 6–10), we obtained a maximum likelihood estimate of λ = 1.110, with a standard error of 0.031.
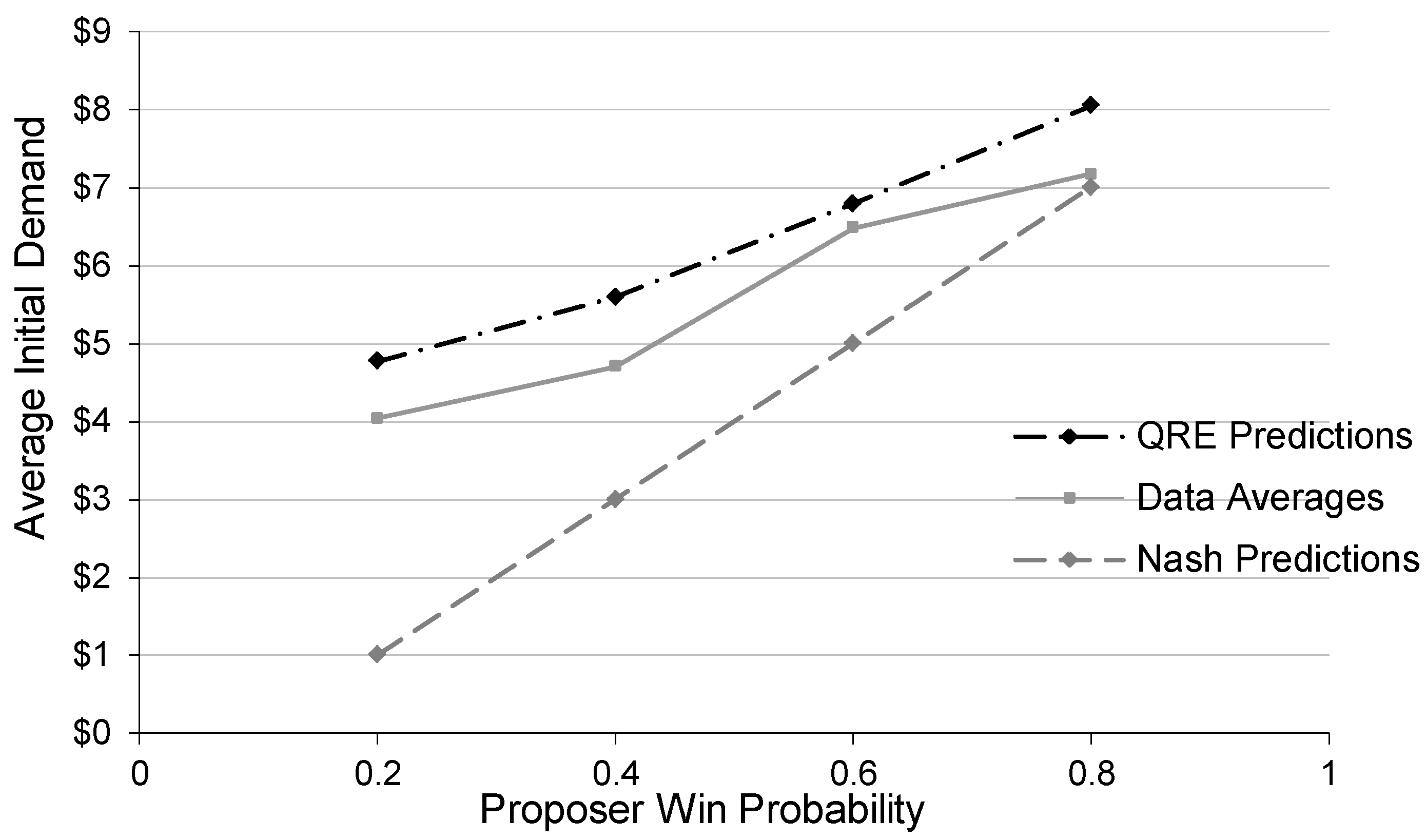
16 The maximized likelihood function was: −2,857. The vectors of initial proposal probabilities were used to calculate QRE predictions for average proposer demands for each proposer win probability, as shown by the dark dot-dash line in
Figure 6. As is the case for the second half data averages (gray line), these QRE predictions lie above the Nash prediction and are too flat relative to the Nash prediction. The proposers in the experiment, however, are making demands that are not quite as high as predicted by the QRE estimates.
Figure 6.
Average Proposer Demands (Second Part) and QRE Predictions.
Figure 6.
Average Proposer Demands (Second Part) and QRE Predictions.
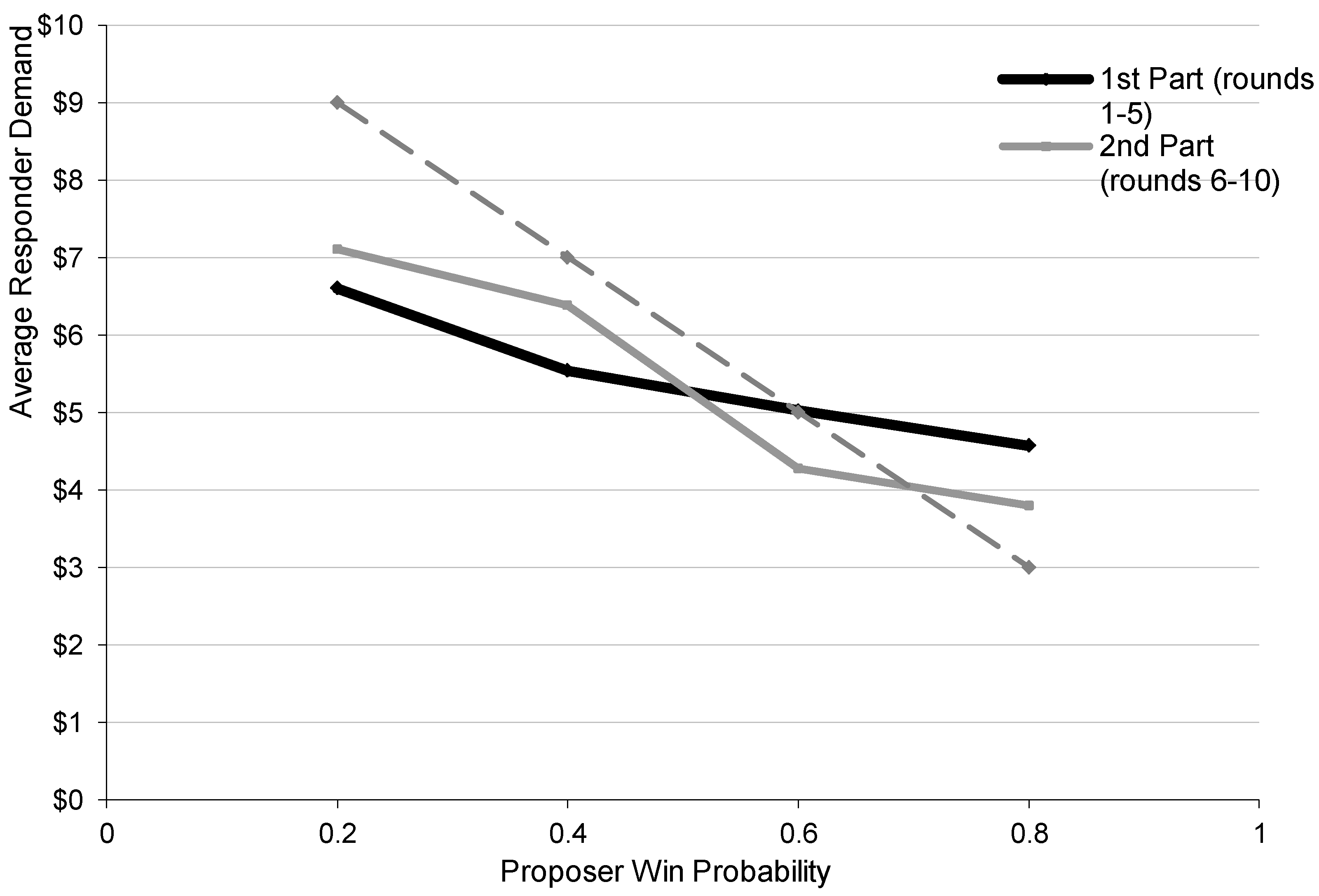
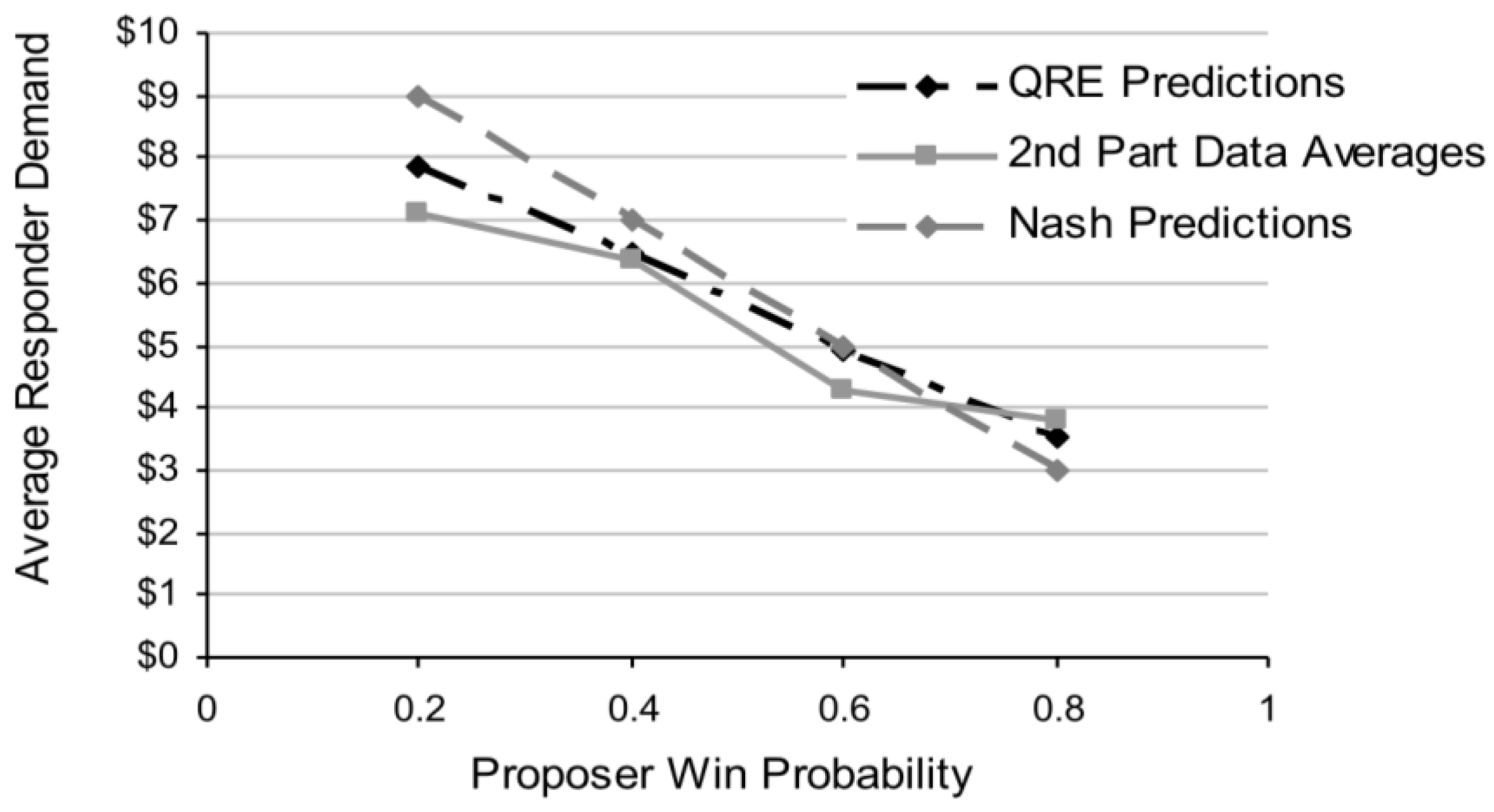
Similarly, the QRE predictions for the responder demands trace out a line that begins below the dashed Nash prediction line in
Figure 7 and is too flat relative to the that line. This feature of the QRE predictions matches the second half data (gray line).
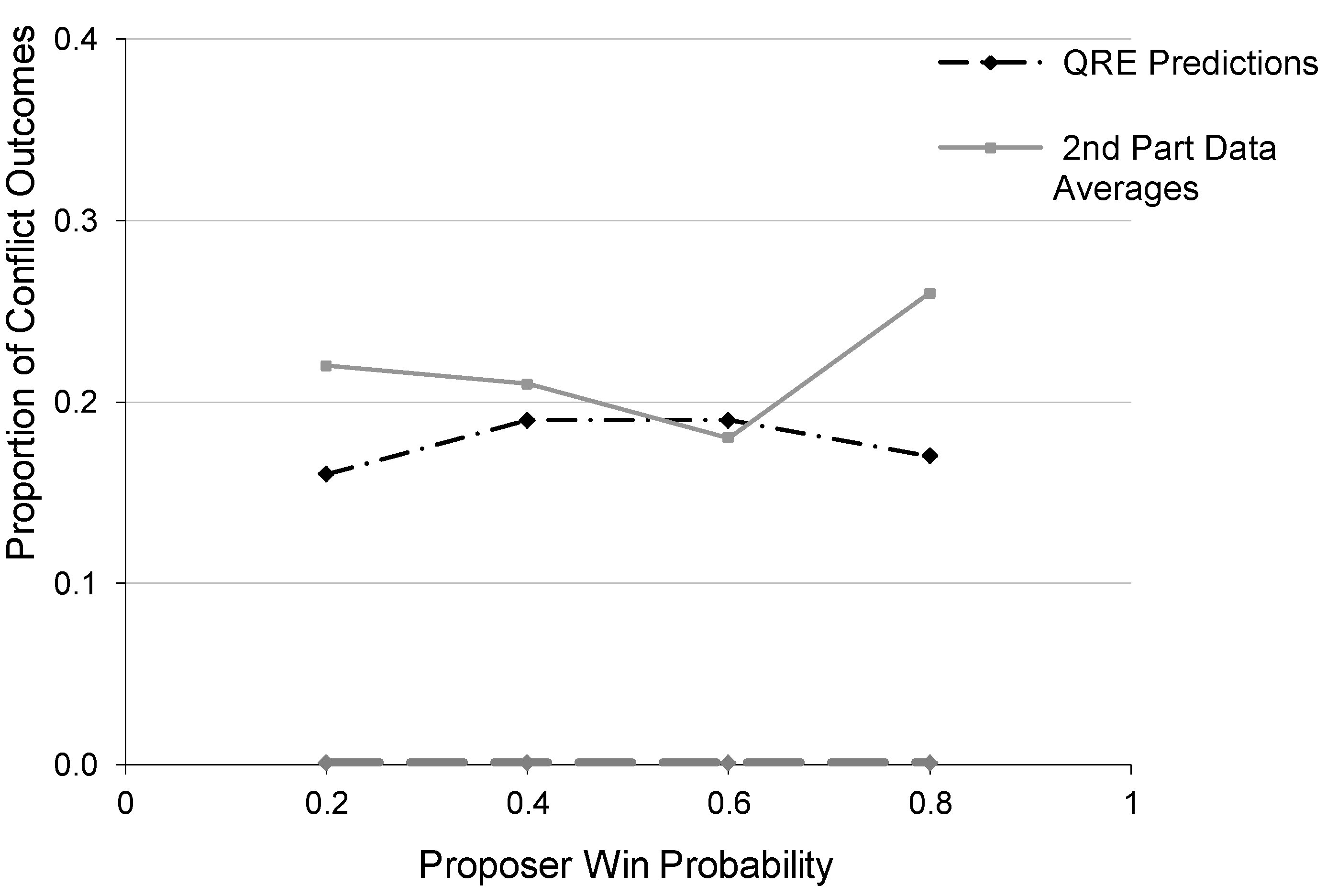
Finally, note that the QRE predictions for conflict rates shown in
Figure 8 are at about the level observed in the second-half data, but without the upward spike for the highest proposer win probability. These predictions are a major improvement over the Nash prediction of zero conflict rates for all power treatments.
Figure 7.
Average Responder Demands (Second Part) and QRE Predictions.
Figure 7.
Average Responder Demands (Second Part) and QRE Predictions.
Figure 8.
Conflict Rates (Second Part) and QRE Predictions.
Figure 8.
Conflict Rates (Second Part) and QRE Predictions.
An analysis of the proposer “continuation values” provides an interesting insight as to why initial proposer demands might be too high and too flat relative to Nash predictions. The proposer continuation values implied by the QRE choice probabilities are shown in the top row of
Table 3. For example, a proposer with a win probability of 0.2 (and who has an initial demand rejected) can expect to earn $0.99 in the final stage, largely because responders are less aggressive than predicted in this stage in anticipation of “irrational” rejections. The Nash continuation value after a rejected initial proposal would be 0 for this proposer, since the 0.2 chance of winning $9 in a conflict is less than the $2 conflict cost, so a responder second-stage counter-offer of $0 “should” be accepted by a perfectly rational proposer. The other proposer continuation values in the top row are also greater than the Nash continuation values in the second row, although the difference goes away for the highest proposer win probability of 0.8. The important point is that the higher the proposer’s continuation value from rejection, the higher the optimal initial demand, which explains why proposer demands lie above Nash levels for win probabilities below 0.8.
The bottom part of
Table 5 also shows the inferred continuation values for responders following their rejection of an initial proposer demand. For example, with a proposer win probability of 0.2, the responder continuation value is $9 since the proposer has no power when the conflict cost exceeds the proposer’s expected gain from conflict. Note that the inferred responder QRE continuation values in the third row are below their Nash continuation values in the bottom row, presumably because of the possibility that proposers will sometimes reject aggressive responder demands and force the responder into a costly conflict. This possibility reduces the optimal responder demand, which helps explain the qualitative direction of deviations from Nash predictions in
Figure 7.
Table 5.
Continuation Values Inferred From Quantal Response (QRE) and Nash Models.
Table 5.
Continuation Values Inferred From Quantal Response (QRE) and Nash Models.
| Proposer Win Probabilities: | p = 0.2 | p = 0.4 | p = 0.6 | p = 0.8 |
|---|
| Proposer Continuation Values (QRE): | $0.99 | $2.54 | $4.25 | $5.89 |
| Proposer Continuation Values (Nash) | $0 | $2 | $4 | $6 |
| Responder Continuation Values (QRE) | $7.05 | $5.15 | $3.28 | $1.47 |
| Responder Continuation Values (Nash) | $9 | $7 | $5 | $3 |
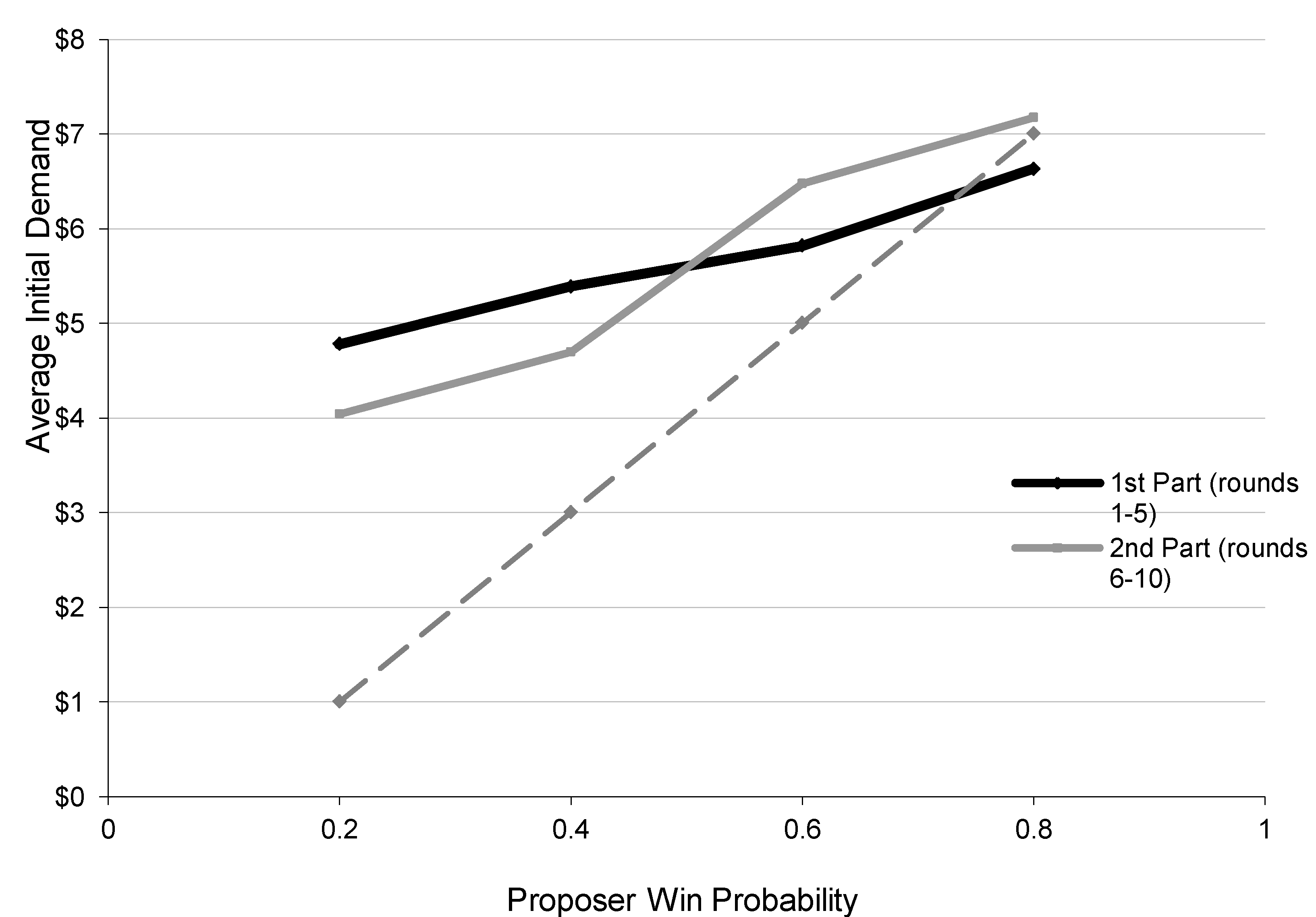
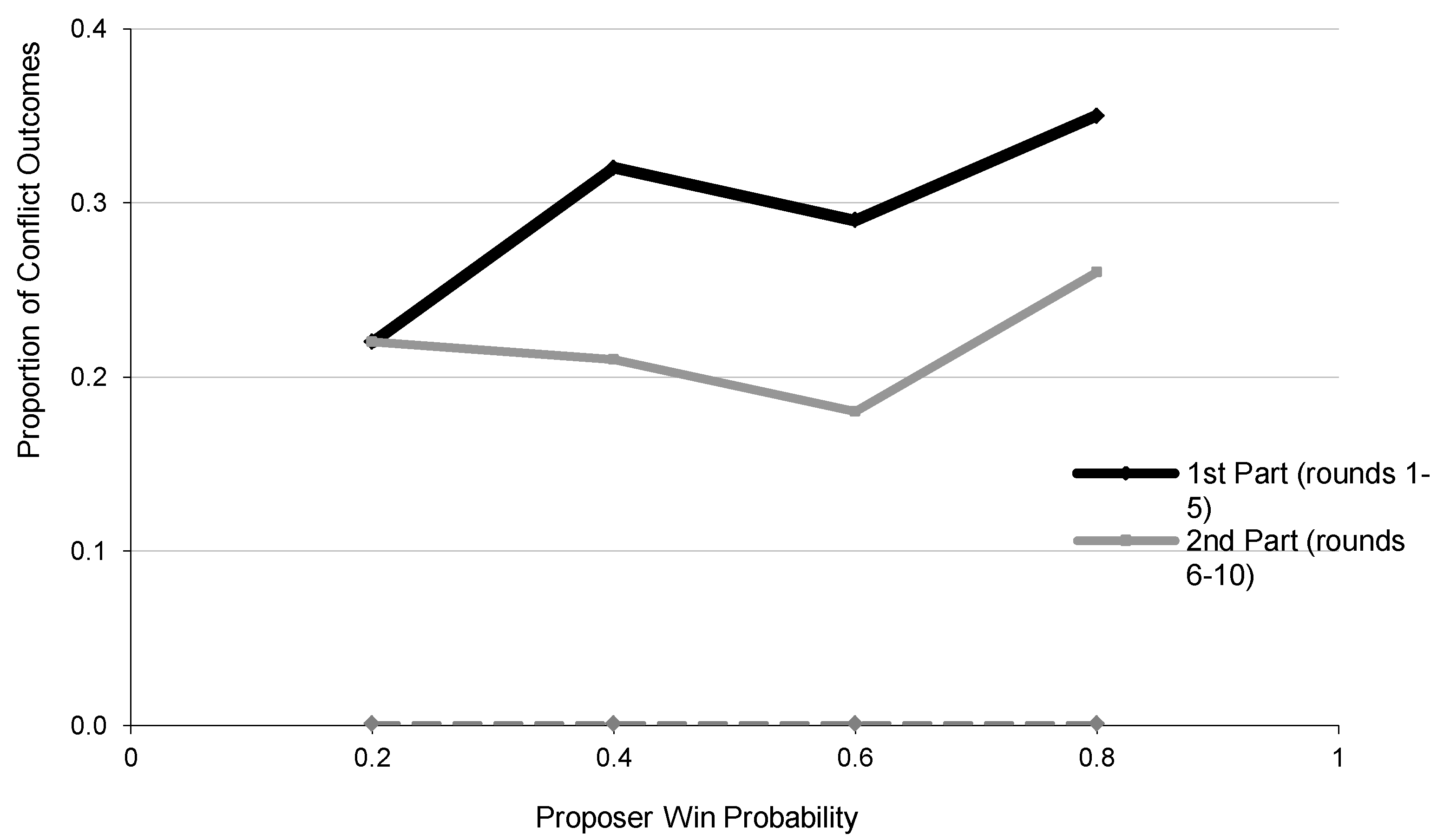
One unresolved issue that came up in the earlier discussion of experimental results is the observation that both proposer and responder demand patterns are “flatter” (less responsive to proposer win probabilities) in the first five rounds than was the case in the last five rounds. We do not believe that this difference was caused by the treatment change, as discussed previously, since the steepness of demand patterns continued to increase from round 6 to round 10. /This observation suggests some kind of learning or other change in attitudes. Note that the steeper demand lines for part 2 in
Figure 1 (for proposers) and
Figure 4 (for responders) are closer to the dotted line Nash predictions, which suggests an increase in the precision parameter λ. Estimation of the QRE model using only data from the first five rounds yields an estimate of λ = 0.76 (standard error = 0.025), which is in fact lower than the estimate of λ = 1.11 (standard error = 0.031) using data from the final five rounds. These different parameter estimates can be used to generate “predictions” for the patterns of average proposer and responder demands for each part. The lower precision estimate for part 1 (more noise) does yield a flatter predicted response of proposer and responder demands to changes in the proposer win probability,
P, as shown in
Table 6. The top part of the table indicates that predicted proposer demands are less responsive to increases in
P in part 1 than in part 2. The bottom half of the table shows a similar pattern for responder demands (more flatness in predictions for the first part). In terms of levels and crossover points, these predictions do deviate somewhat from the actual data patterns shown in
Figure 1 and
Figure 4, but the general qualitative differences in relative flatness are present in the QRE predictions.
Table 6.
Quantal Response Predictions for Proposer and Responder Demands Using Separate Precision Estimates for Part 1 (Rounds 1–5) and Part 2 (Rounds 6–10).
Table 6.
Quantal Response Predictions for Proposer and Responder Demands Using Separate Precision Estimates for Part 1 (Rounds 1–5) and Part 2 (Rounds 6–10).
| | P = 0.2 | P = 0.4 | P = 0.6 | P = 0.8 |
|---|
| Predicted Proposer Demands, Part 1 | $5.19 | $5.87 | $6.90 | $7.92 |
| Predicted Proposer Demands, Part 2 | $4.77 | $5.59 | $6.80 | $8.05 |
| Predicted Responder Demands, Part 1 | $7.50 | $6.47 | $5.24 | $4.14 |
| Predicted Responder Demands, Part 2 | $7.85 | $6.46 | $4.92 | $3.51 |
To summarize, maximum likelihood estimation of a simple model that adds a “noise” dimension to the standard game-theoretic analysis provides a logit precision parameter that, in turn, generates predicted decision patterns, which are similar to the patterns observed in the data:
- (1)
Proposer initial demands are increasing in proposer win probabilities, as expected, but are above Nash levels and are “too flat,”
- (2)
Responder final demands are decreasing in proposer win probabilities, but are below Nash levels and are also too flat.
- (3)
Conflict rates are significant and are roughly invariant to changes in proposer win probabilities.
Separate estimation for the part 1 and part 2 data suggests that noise declines in the final five rounds, which explains the reduced flatness in the proposer and responder demand patterns, and the reduction in conflict rates observed in the second part.
One interesting divergence between data and predictions of this one-parameter model is that conflict rates are under-predicted for both parts. In the first part, the predicted conflict rate (averaged over all four proposer win probabilities) is 0.21, whereas the observed conflict rate is close to 0.30. In the second part, the predicted conflict rate was 0.18, again below, but only slightly below, the observed rate of 0.22. As discussed earlier, it could be the case that subjects in the experiments derive some extra value from conflict, e.g., if there is some excitement in seeing a random outcome, or if there is a feeling of satisfaction from imposing a conflict cost on the other player after one’s offer has been rejected.
17 As a result, we do not think too much importance should be attached to the overall levels of observed conflict rates. An admittedly
ad hoc inclusion of a “conflict value” term in both proposer and responder conflict payoffs yields estimated values of about a dollar for each part.
18 7. Conclusion
This paper examines how the probability of winning in a conflict shapes the demands and counter-demands that are made in initial stages of the bargaining process. The experimental setup is novel in that it allows us to examine an important issue in the literature of international relations, i.e., how conflict rates are affected by power asymmetries that would come into play in the event of an impasse. The main results are intuitive, that demands and counter-demands are sensitive to relative power should a conflict arise, and that conflict does occur in a significant proportion of cases. Conflict rates seem to be unaffected by power asymmetries, since the players adjust their demands based on the asymmetries. What is observed is that proposers with power use their power to make aggressive demands. However, the aggressive demands by the proposers are received by responders who react with countervailing caution.
It is impractical to run experiments with real conflicts between political decision makers. We believe that the use of experimental methods provide a venue for testing expectations about bargaining and conflict and helps avoid problems of measurement and control that arise with field data, although there is clearly a cost in terms of external validity.
19 Our results are interesting in many ways given the prominence of the bargaining model in the recent literature on international conflict. Although the actual demands do not match the subgame-perfect Nash predictions, the results are qualitatively consistent with expectations from bargaining theory. Conflict outcomes are reduced but remain significant with repeated play. The implications of these results are interesting to consider. It appears that when subjects bargain, they are influenced by the structure of the game, the basic comparative-statics results derived from a Nash equilibrium are observed in the data and supported by appropriate nonparametric tests.
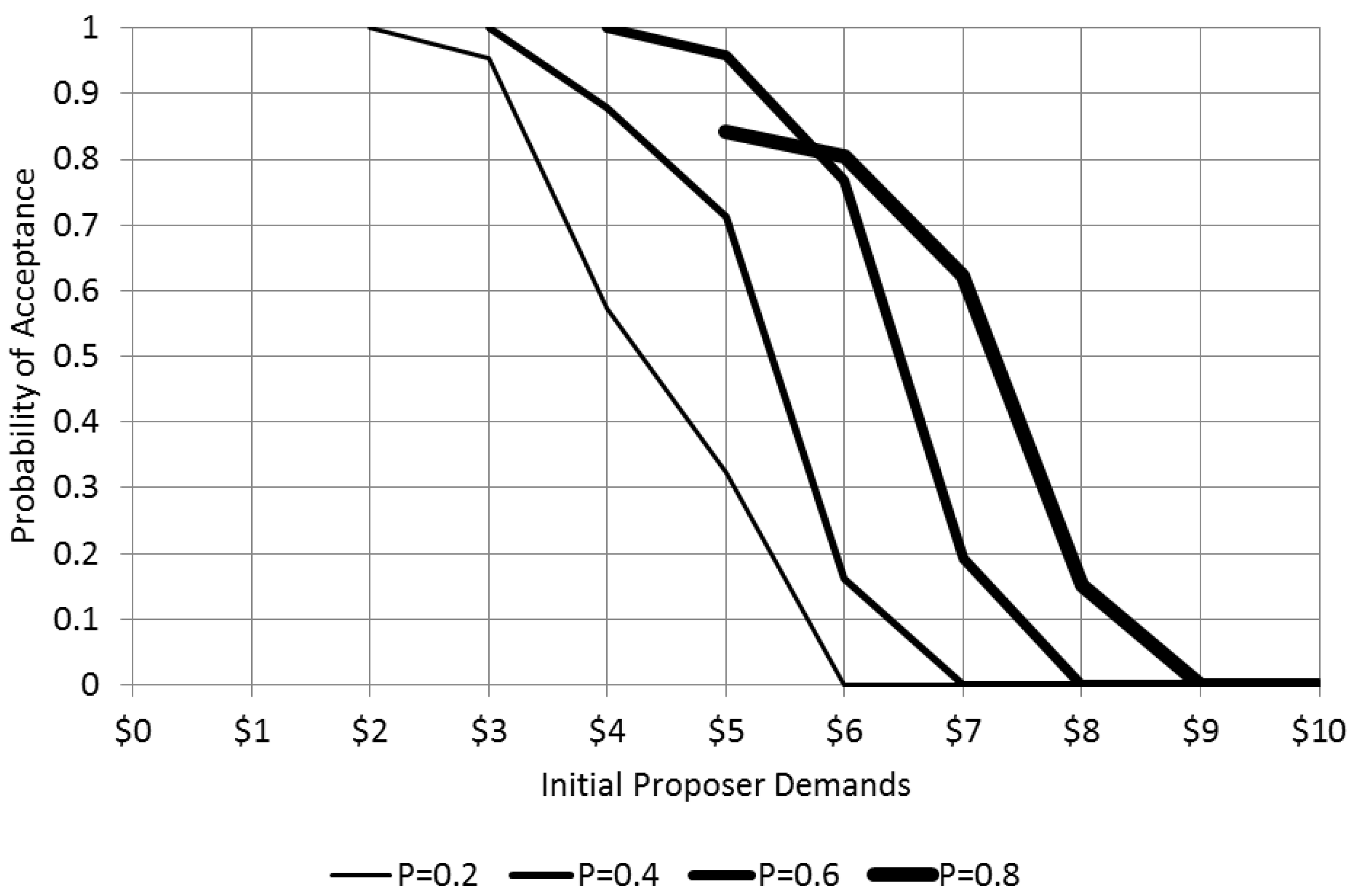
There are, however, systematic discrepancies between observed demands and subgame-perfect Nash predictions. These discrepancies could be a result of difficulties with backward induction reasoning that may inject behavioral “noise” into decision making. Probabilistic choice functions are typically used to relax the standard assumption of perfect rationality. This approach is especially helpful for the analysis of experimental data that show “smoothed” responses, as can be seen from the “inverse S” shapes of responder accept proportions in
Figure 3. The quantal response model imposes a fixed-point equilibrium condition that choice distributions match belief distributions; this approach is a simple generalization of Nash requirement that equilibrium strategies be best responses to other players’ strategies. For our experiment, the basic quantal response model provides a simple explanation of the overall pattern of deviations from Nash predictions, without the need to introduce preference parameters that pick up aversions to inequity or risk, although such additions might be useful in other contexts. Note that the introduction of additional unobserved parameters would necessitate estimation. Any estimation requires an error structure, which is precisely what a quantal response model provides, in an equilibrium setting that is appropriate for game theory. Moreover, an analysis of the continuation values inferred from the estimated logit precision parameter provides insights about why proposer demands are above Nash predictions, why responder demands are below Nash predictions, and why both demand patterns are less responsive to power asymmetries than predicted.
Given that risky conflict is a potential outcome of most bargaining procedures, especially those found in political and legal interactions, we believe that additional experimental investigation of this area could provide valuable insights that could later be validated with field experiments. For example, it is likely that the difficulties associated with backward induction can be reduced in a single-stage model or enhanced in games with more stages. Another interesting direction would be to explore the effects of ambiguity,
i.e., a situation in which the proposer win probabilities are not known, which is clearly a feature of most field applications. Subjects tend to exhibit more risk aversion in cases of ambiguity [
3], which can be implemented by not revealing the numbers of various colored marbles in urns used for random draws. Finally, the alternating-offer structure of these bargaining games could be generalized to allow endogenously or randomly determined decision sequences.