The keywords auctions in Yahoo! and Google are repeated games in which bidders gradually learn the value of their competitors and adjust their bids accordingly. The set of equilibria in repeated games can be very large and the strategies leading to such equilibria are complex. As Edelman
et al. [
6] note, it may not be reasonable to expect advertisers capable of executing such strategies, especially when they manage thousands of keywords. Edelman and Schwarz [
13] show that a static game with certain equilibrium strategy set is able to capture many important characteristics of the underlying dynamic game. Hence, we study a simultaneous-move one-shot auction assuming that (1) bidders are likely to learn all relevant information about each other’s value over time; (2) bidders submit their stable bids in equilibrium. A drawback of this simplification is it implies that the auction always begins with the same number of positions available prior to arrivals of bidders. In reality, the auction is continuous and the number of positions remaining for sale varies from time to time.
In practice, Google ranks advertisers based on the product of each advertiser’s bid and his “quality score”. The quality score is determined by a number of factors including the CTR, the keyword’s relevancy to the advertiser’s business and the quality of his web site. Varian [
7] and Edelman
et al. [
6] both show that incorporating quality score in the study does not provide much additional insight. Hence, in our paper both GSP and APR determine winners solely based on bid prices.
3.1. Equilibrium in GSP and APR
An exogenously given k ad positions are for sale through auction. There are n advertisers endogenously affected by the reserve price r. The expected CTR received by ad position i is . Since top positions receive higher CTR than lower positions, we have for and for . Advertisers are risk-neutral possessing independent private information. They may have distinct willingness to pay for one click, but for each advertiser, his per-click value stays the same even if his ad appears in different positions. Let , and denote the bid price, per-click value and identity of the ith highest bid, respectively. If is greater than the reserve price, both mechanisms allocate the ith position to the advertiser with the ith highest bid, , where . When the ith link is clicked by a user, advertiser pays the search engine an amount that equals the next highest bid, . If advertiser happens to be the winning bidder in the lowest ranking, he pays the posted reserve price in APR or the larger value between reserve price and the highest losing bid in GSP. The revenue received by the search engine from the ith sponsored link is and the surplus to advertiser is .
Definition 1 (Varian [7]) In a symmetric Nash equilibrium (SNE) bid prices satisfy
Varian shows that if a set of prices is an SNE, then it is a Nash equilibrium (NE). He further shows that if the state of advertiser
satisfies condition (
2) for position
and
, then it satisfies (
2) for all
j. Hence, one only needs to compare each advertiser’s current position with its two adjacent slots.
Since the advertiser in position
i does not want to move down, we have
On the other hand, the advertiser in position
has no incentive to move one slot up. Thus,
The above two inequalities lead to
Note that any
satisfying the above inequalities is an equilibrium bid. Hence, there is a range of such equilibrium strategies. From the practical point of view, this seems to make the equilibrium bids indeterminate. Varian [
7] examines the boundary cases by choosing the upper and lower bounds in (
5), which yields
It is easy to see that the bidding strategy at the lower bound belongs to the locally envy-free equilibrium (Edelman
et al. [
6]) and it is in fact the lowest-revenue envy-free equilibrium (Edelman and Schwarz [
13]). Equations based on such an equilibrium with various names can be found in several literatures including the self-selection condition in the priority pricing mechanism studied in Harris and Raviv [
18], and the indifference constraint in Wilson [
19] that considers the myopic incentive constrained pricing.
Questions that follow naturally are why advertisers are destined to the lower bound of SNE and how their bids converge to this particular point? Varian [
7] explains that it is more reasonable for the bidder to compare his current payoff with what he will end up if he outbids the advertiser one slot above him. He argues that among all SNE strategies, the lower bound strategy is the most appealing one to advertisers since it defines the lowest bid prices that render each agent the most advantageous position. Varian also shows that the lower bound strategy is closely related to the two-sided matching problem discussed in Roth and Sotomayor [
20]. Edelman
et al. [
6] show that if the dynamic game ever converges to a static vector of bids, that static equilibrium should correspond to a locally envy-free equilibrium of the static game induced by the GSP. In addition, both Edelman
et al. [
6] and Varian [
7] show that in the dominant-strategy Vickrey–Clarke–Groves equilibrium, the position and CPC of each advertiser coincide with those in the lower bound of the SNE, and the outcome is the best for advertisers but worst for the search engine. Hence, the lower bound strategy provides incentives to advertisers and it is most likely attainable. Edelman and Schwarz [
13] further show that the lower bound strategy in a GSP with complete information, capturing behaviors in an incomplete information game, can be viewed as a valid approximation. The empirical analysis conducted by Varian [
7] over a random sample of 2425 auctions at Google also shows that there is demonstrable evidence indicating that the actual bidding in Google’s ad auction converges to the neighborhood of the equilibrium strategy at the lower bound of SNE.
In the rest of the paper we use the term of (lowest-revenue) envy-free equilibrium and lower bound of the SNE interchangeably. Any equilibrium strategy examined will satisfy the lower bound constraint (
6).
3.2. Optimal Reserve Price in Sponsored Search Advertising
We consider n qualified advertisers whose per-click values are represented by an n-dimensional random vector (). The realization of these n values is (). Rearranging in an increasing order so that where , is the second smallest value in the n-tuple, and so on. The function of () that takes on the in each possible sequence () of values assumed by () is known as the ith order statistic.
Let
be identical and independent random variables with common probability density function
and distribution function
. We approximate the total number of advertisers by a Poisson random variable with a mean
λ. When the reserve price is equal to
r, the probability for each potential advertiser to participate in the auction is
and
is the average number of qualified bidders. One can regard
as the demand function for ad positions and
λ as the maximum arrival rate when the reserve price is set to zero. Hence, the probability of having
n eligible bidders per unit time is equal to
. Following Lariviere and Porteus [
21], we define
as the failure rate of
and
as the generalized failure rate. As
the generalized failure rate
is the absolute value of the price elasticity.
For a qualified bidder
j its per-click value satisfies the following conditional distribution function
Hence, the marginal probability density function of
is given by
and the expectation of
can be written as
Let
p be the CPC the advertiser at the last position pays,
i.e.,
, where
. Note that in GSP
p is the larger value between
r and the highest losing bid while
in APR. Equation (
6) enables us to derive
recursively. For
,
When there are
k positions offered and
n advertisers qualified, search engine’s revenue per unit time is given by
In view of (
10), for
, we have
which can be substituted into (
11) to form a linear function of order statistics:
As the true per-click values of advertisers are unknown to the search engine,
is uncertain and its expectation can be depicted as
Conditioning on the number of qualified bidders
n, the expected revenue rate is
The objective of the search engine is to maximize
by choosing an optimal reserve price
.
3.2.1. GSP
Lemma 1 In the lower bound of the locally envy-free equilibrium, the expected revenue rate to the search engine from the static generalized second-price auction (GSP) for sponsored search advertising is
The proof of Lemma 1 and all other proofs are placed in the
appendix.
In a GSP, the revenue contributions from
n bidders consist of two parts: the minimum amount to win a position, represented by
and the extra to secure each winning position, represented by
if
and
if
.
The standard regularity condition in the auction literature requires an increasing failure rate (IFR) (Maskin and Riley [
11]), while a milder condition is an increasing generalized failure rate (IGFR). The assumption that the distribution function has an IGFR is prevalent in pricing and revenue management literature (Ziya
et al. [
22] and Lariviere [
23]). It ensures either a unimodal or quasi-concave revenue function when selling a single product. Our model extends the result to the scenario with heterogeneous products.
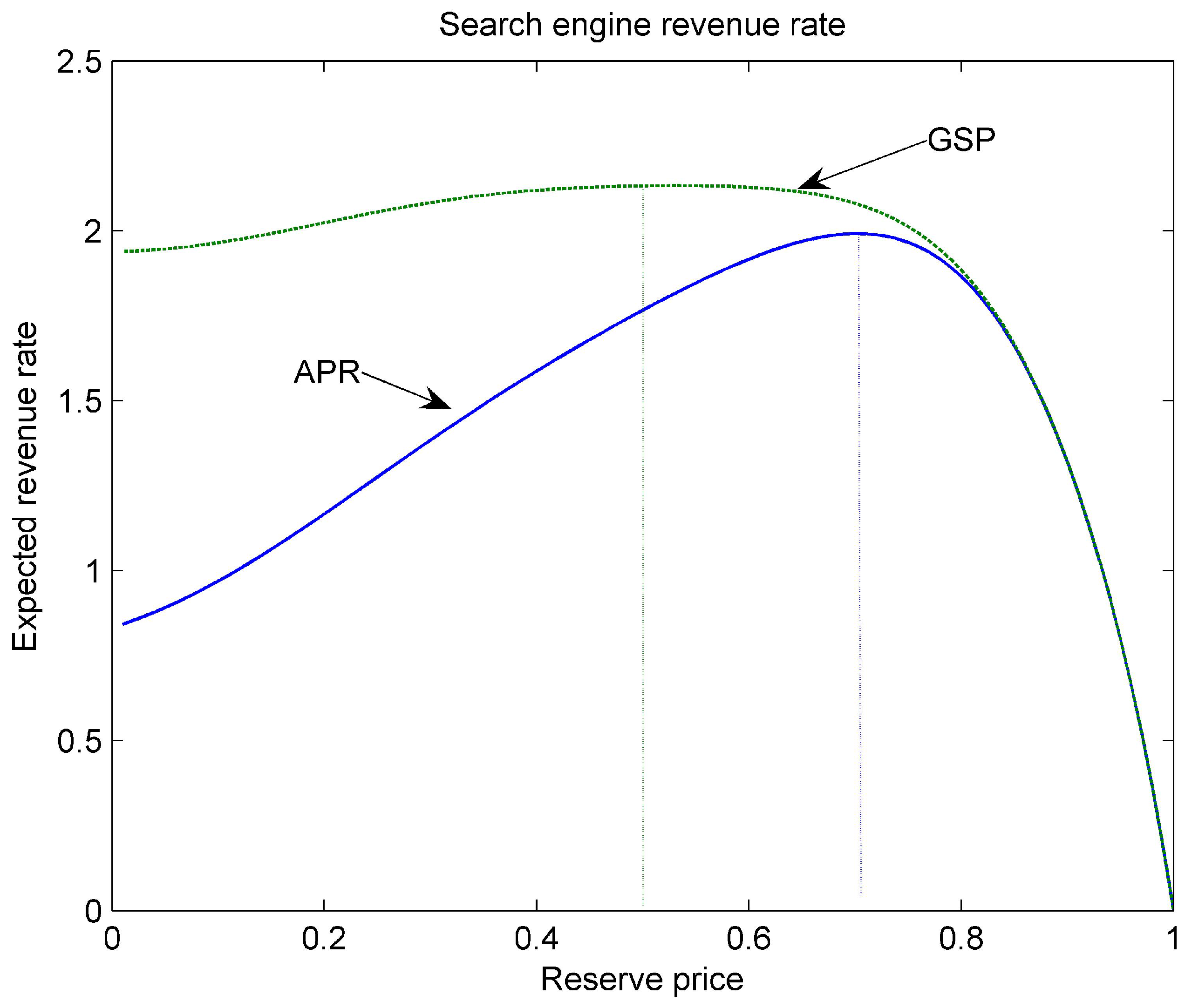
Theorem 1 If the value per click of each advertiser is a variable with IGFR, then (i) is a quasi-concave function; (ii) the optimal reserve price is given as the solution to the equation
Note that the generalized failure rate is the absolute value of price elasticity. IGFR implies that consumers respond to a price increase more negatively when the reserve price is high than when it is low. In sponsored search advertising, it means that the demand reduction in ad links resulted from a mark-up is increasing in the reserve price, which reflects the behavior of rational advertisers. Thus, the assumption of IGFR in Theorem 1 is minor and reasonable.
In auctions of selling a single item or multiple homogeneous items, the optimal reserve price solves Equation (
1) (Bulow and Roberts [
12]). Theorem 1 shows that it is also the optimality condition for the static GSP with heterogeneous items. Notice that condition (
15) is equivalent to
and
is the absolute value of price elasticity of demand. As
is an increasing function of
r, it makes perfect sense for (
15): increase the reserve price when demand is inelastic until the elasticity reaches unity; further increases will reduce the revenue.
Although English auctions with multiple heterogeneous items and endogenous entries have been studied in the literature, to our knowledge, there has not been theoretical development for an analytical solution of the optimal reserve price. The significance of Theorem 1, hence, is twofold. It provides the optimal reserve price for a static generalized English auction where the payment schedule for the last winning bidder is dependent on the number of bidders; second, it shows that heterogeneity among objects alone does not necessarily lead to a varied optimal reserve price.
3.2.2. APR
Lemma 2 In the locally envy-free equilibrium, the expected revenue rate to the search engine from APR for sponsored search advertising is When there are
n bidders in the auction, their contributions consist of two parts: the minimum amount they have to pay to win a position, represented by
and the premium paid for securing each winning position, represented by
For example, the advertiser taking the first position in the auction must pay
per unit time to pass the revenue threshold defined by the reserve price, and an extra amount
to be on top. In general, the heterogeneity among items for sale drives each consumer to select the most advantageous one for him. If all items are identical (with the same CTR or quality), no one will pay more than the reserve price.
The marginal revenue function can be verified as
Theorem 2 If each advertiser’s per-click value is a random variable with IGFR, then is quasi-concave and there exists a unique reserve price that maximizes the expected revenue rate. The optimal reserve price is given as the solution to the equationwhere The optimality condition (
17) of reserve price in APR clearly differs from (
15) in GSP, which can be written as
. The perturbation factor
shows that it is directly related to the bidder population
λ, the number of available ad positions
k, and the distribution of bidders’ valuation function
F. The proof of Theorem 2 shows that
is decreasing in
r. With the assumption of IGFR, there is an optimal reserve price that achieves the maximal expected revenue rate.