Non-Cooperative Representations of Cooperative Games
Abstract
1. Introduction
2. Preliminaries
2.1. Notation and Definitions for Non-Cooperative Games
2.2. Notation and Definitions for Cooperative Games
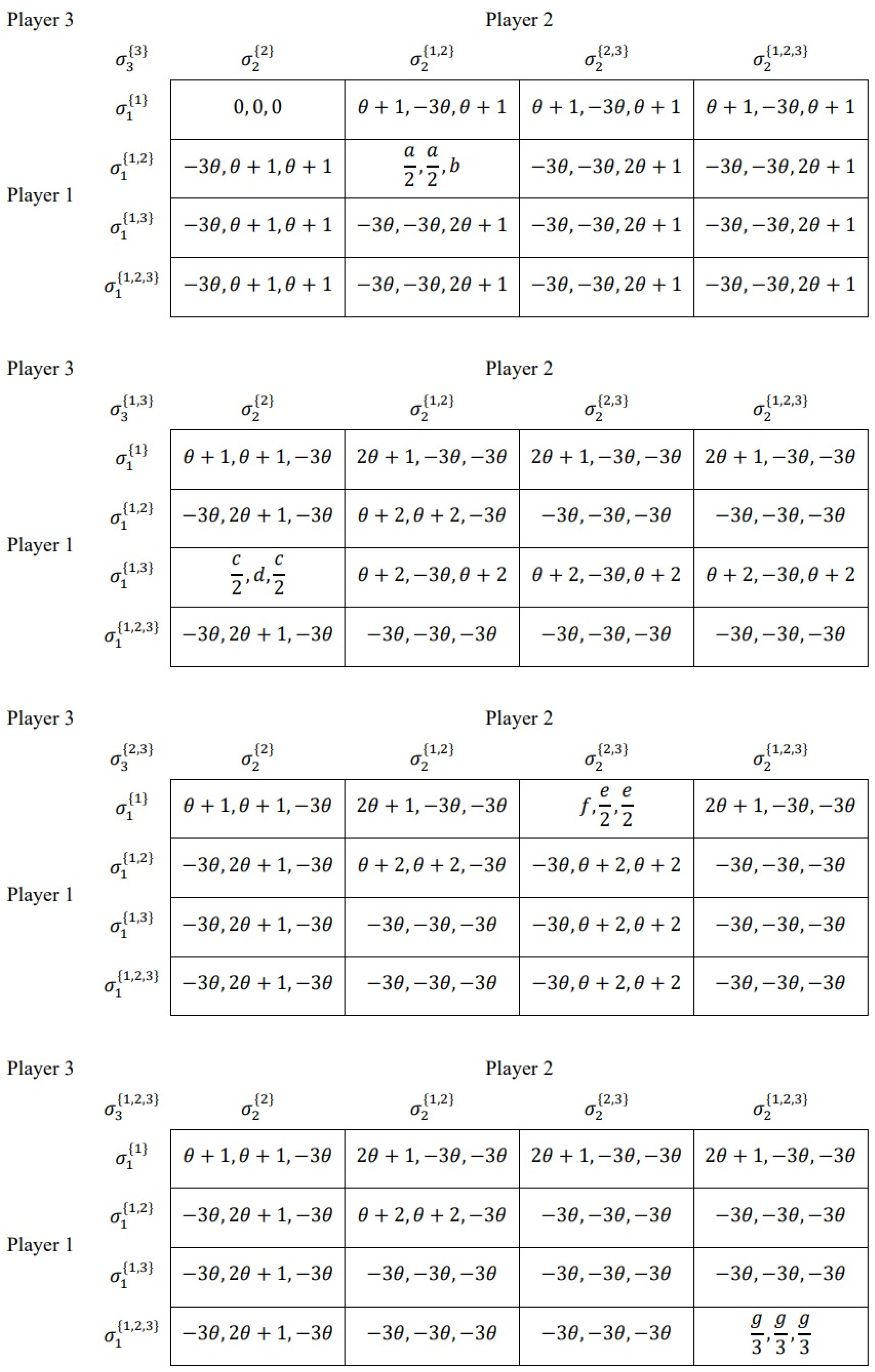
3. Example Representations Under NE
4. Theorems on the Existence of Representations of Cooperative Games
5. Discussion on the Construction of Representations
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CE | Composite equilibrium |
| CFF | Characteristic function form |
| NE | Nash equilibrium |
| PFF | Partition function form |
| PSD | Potentially strictly dominant |
| PWD | Potentially weakly dominant |
| THPE | Trembling hand perfect equilibrium |
| Mathematical Notation | |
| Normal-form game | |
| N | Player set |
| Partition of the player set | |
| S | Subset or coalition of the player set |
| i | Player of the player set |
| Composite game of for which the player set is (see Definition 1) | |
| Cardinality of | |
| Set of all partitions of N | |
| Set of all subsets of N | |
| The finest partition of N, i.e., the partition containing all singletons | |
| The coarsest partition of N, i.e., the partition containing the grand coalition | |
| Embedded coalition where S is in | |
| , | Strategy sets of player i/coalition S |
| , | Dominant strategies of player i/coalition S |
| x | Strategy profile for a given normal-form game |
| , | Returns the strategy that player i/coalition S plays in x respectively |
| , | Returns the number of PSD/PWD strategies in x played by players in S |
| , | Returns the corresponding coalition when i’s strategy is PSD/PWD in x |
| , | Payoff function of player i/coalition S |
| v | Worth function |
| Cooperative game (in either CFF or PFF depending on the context) |
References
- Abe, T. (2021). Cartel formation in cournot competition with asymmetric costs: A partition function approach. Games, 12(1), 14. [Google Scholar] [CrossRef]
- Abe, T., & Funaki, Y. (2021). The projective core of symmetric games with externalities. International Journal of Game Theory, 50(1), 167–183. [Google Scholar] [CrossRef]
- Aumann, R. J., & Peleg, B. (1960). Von Neumann-Morgenstern solutions to cooperative games without side payments. Bulletin of the American Mathematical Society, 66(3), 173–179. [Google Scholar] [CrossRef]
- Bloch, F., & Van den Nouweland, A. (2014). Expectation formation rules and the core of partition function games. Games and Economic Behavior, 88, 339–353. [Google Scholar] [CrossRef]
- Chander, P. (2020). Stability of the merger-to-monopoly and a core concept for partition function games. International Journal of Game Theory, 49(4), 953–973. [Google Scholar] [CrossRef]
- Chander, P., & Tulkens, H. (1997). The core of an economy with multilateral environmental externalities. International Journal of Game Theory, 26(3), 379–401. [Google Scholar] [CrossRef]
- Hart, S., & Kurz, M. (1983). Endogenous formation of coalitions. Econometrica: Journal of the Econometric Society, 51, 1047–1064. [Google Scholar]
- Ichiishi, T. (1981). A social coalitional equilibrium existence lemma. Econometrica: Journal of the Econometric Society, 49, 369–377. [Google Scholar]
- Kóczy, L. Á. (2018). Partition function form games. Springer International Publishing. [Google Scholar]
- Maskin, E. (2016). How can cooperative game theory be made more relevant to economics?: An open problem. In J. F. Nash, & M. T. Rassias (Eds.), Open problems in mathematics (pp. 347–350). Springer International Publishing. [Google Scholar]
- Ray, D. (2007). A game-theoretic perspective on coalition formation. Oxford University Press. [Google Scholar]
- Ray, D., & Vohra, R. (1999). A theory of endogenous coalition structures. Games and Economic Behavior, 26(2), 286–336. [Google Scholar] [CrossRef]
- Strantza, S., Sartzetakis, E., & Diamantoudi, E. (2020). International environmental agreements and trading blocks—Can issue linkage enhance cooperation? Strategic Behavior and the Environment, 8(3), 269–310. [Google Scholar]
- Thrall, R. M., & Lucas, W. F. (1963). N-person games in partition function form. Naval Research Logistics Quarterly, 10(1), 281–298. [Google Scholar] [CrossRef]
- Von Neumann, J., & Morgenstern, O. (1944). Theory of games and economic behavior. Princeton University Press. [Google Scholar]
- Yi, S. S. (1996). Endogenous formation of customs unions under imperfect competition: Open regionalism is good. Journal of International Economics, 41(1–2), 153–177. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, J. Non-Cooperative Representations of Cooperative Games. Games 2025, 16, 39. https://doi.org/10.3390/g16040039
Chan J. Non-Cooperative Representations of Cooperative Games. Games. 2025; 16(4):39. https://doi.org/10.3390/g16040039
Chicago/Turabian StyleChan, Justin. 2025. "Non-Cooperative Representations of Cooperative Games" Games 16, no. 4: 39. https://doi.org/10.3390/g16040039
APA StyleChan, J. (2025). Non-Cooperative Representations of Cooperative Games. Games, 16(4), 39. https://doi.org/10.3390/g16040039




