Abstract
The coexistence of the winner’s curse and cost overruns in the construction industry implies a cost pendulum in which the winning bid is undervalued, whereas the final payment to the contractor is overvalued. We posit that this results from a strategic interaction between three stakeholders: the public agency (PA), the project manager (PM), and the winning contractor, and we propose a game-theoretic framework to model this dynamic. In the current state of practice, the subgame between the contractor and the PM leads to opportunistic contractor behavior and lenient supervision, resulting in increased costs for the PA. We analyze how procedural and cultural interventions by the PA, specifically shifting from a low-bid to an average-bid auction and incentivizing stricter PM oversight, alter the strategic equilibrium. Our findings indicate that while each change alone provides limited improvement, implementing both significantly reduces cost overruns by aligning stakeholder incentives. The findings of this analysis provide insight into how public agencies can mitigate the widespread problem of cost overruns.
1. Introduction
Cost overruns in construction projects have long been recognized as a widespread global phenomenon that imposes significant costs on society Thijssen (2022). Estimates of how many projects experience cost overruns have ranged from 50% Love et al. (2019a) to almost 90% Flyvbjerg et al. (2002). Despite the many attempts to tackle this enormous burden on budgets, it appears that practical solutions were thus far ineffective in overcoming it, as Love et al. (2022) lament, “Hundreds of years of pain, with minimal gain”.
With budgets constrained by overwhelming project costs, policymakers are striving to reduce costs during earlier phases, such as the tendering phase. Indeed, low-bid tenders are the most common form of bidding for construction projects in the public sector, driven by the need for competition, transparency, and equal opportunity Coggins et al. (2016); El-Sayegh et al. (2021). A well-known outcome of low-bid tenders is the winner’s curse phenomenon Capen et al. (1971), where the winning contractor is cursed by being obligated to provide construction services at a sub-optimal price. Surprisingly, when examining empirical data, it is found that contractors are frequently able to recoup their costs during the construction phase, resulting in cost overruns. That is, one may infer a pendulum effect in which a low winning bid pendulates to a final inflated payment Giat and Mitelman (2023).
In this paper, we model the strategic interactions between stakeholders in the construction industry. These stakeholders are the public agency (PA), project managers (PMs), and construction contractors. By analyzing the payoff structure, our model shows that the pendulum dynamic is the equilibrium outcome. In this process, contractors engage in opportunistic behavior and defective strategies, whereas PMs adopt a lenient management style. The game between contractors and PMs, however, neglects the PA, which is perhaps the most important stakeholder of the construction project. The main thesis of this paper is that the PA can make cultural and operational changes that will affect the game between PMs and contractors. These changes, if designed correctly, are shown to be able to mitigate or even remediate the pendulum effect.
The extended game is a two-period game in which the PA acts in the first period, whereas the PM and the contractor participate in subsequent periods. Therefore, the PA’s optimal action is such that the outcome of the subsequent periods’ games results in the best value for the PA. To obtain this, the PA may institute procedural changes in the tendering process (that mainly affect the winning contractor’s outcome) and cultural changes in how the PM’s performance is measured. We compare how each of these changes affects the PA’s outcome and show that while each change separately hardly results in an improvement to the PA, the institution of both changes does have a profound positive effect. Thus, the game theory framework demonstrates that a robust strategy to overcome the pendulum effect must include multiple measures explaining the disappointing results of many attempts to overcome cost overruns. The insights from this study can, therefore, provide guidance for industry practitioners and policymakers in developing more effective strategies for construction project management.
2. Literature Review
2.1. Construction Tenders and Cost Overruns
Cost overruns in construction projects have been the subject of many studies, both theoretical and empirical, with little apparent gain Love et al. (2022). Researchers have employed different approaches in an attempt to understand the causes of cost overruns. One line of investigation is to observe a particular industry or managerial mechanism and glean the specific or technical aspects of that industry or mechanism that result in cost overruns. For example, in tunneling projects, Paraskevopoulou and Boutsis (2020) showed that final costs are strongly affected by preliminary ground investigations. In transit projects, Gao and Touran (2020) examined differences between heavy and light rail, finding that the former suffered considerably more cost overruns than the latter. Wasfy and Nassar (2021) discussed project delays and costs emanating from debatable issues between the contractor and the employer.
Another approach is a systematic observation of construction projects and enterprises through interviews, workshops, and questionnaire surveys. The product of this investigation was an inventory of possible causes. For example, Famiyeh et al. (2017) surveyed consultants and contractors from sixty government school projects in Ghana. Similarly, Rosenfeld (2014) analyzed responses from two hundred practitioners in the Israeli construction industry.
In parallel to these two approaches, another line of investigation has emerged, arguing that a more fundamental understanding of the forces at play is needed. This approach is more strategic in its nature, favoring intuitive reasoning and focusing on the strategic motivation of stakeholders over the tactical aspects of the project or the business environment. Two main theories have taken this course: the hiding hand hypothesis dating back to Hirschman (1967) and the planning fallacy, originally proposed by Tversky and Kahneman (1974) and later championed by Flyvbjerg (2016) in the context of capital projects as a counter to the Hiding Hand.
According to the hiding hand hypothesis, the planners’ ignorance in the very early stages of the project stimulates creativity and problem-solving in the later stages of the project. Thus, the hiding hand is a benevolent hand that allows us to reap benefits that would otherwise not be realized. In contrast, Flyvbjerg et al. (2002) argued that cost overruns in large capital projects are the result of intentional misrepresentation at the feasibility stage, which lies with which project promoters seek to convince decision-makers to obtain project approval. According to this explanation, the hiding hand is anything but malevolent and institutional checks and balances are needed to restrain it. In a similar pessimistic tone, Locatelli et al. (2017) argued that the construction management literature ignores the elephant in the room, i.e., corruption. Flyvbjerg (2016)’s criticism of the hiding hand itself was heavily criticized by Anheier (2016); Ika (2018); Love et al. (2019b). Although Love et al. (2019a) questioned whether either the hiding hand or the planning fallacy are testable, they are repeatedly used as foundational theories for improvement in project management Ika et al. (2020); Lovallo et al. (2023).
The strategic behavior (or misbehavior) in the planning stage is but a prelude to the strategic interaction in the tendering stage. Low-bid tenders, particularly in public projects, are traditionally the most widespread bidding method for infrastructure and construction projects, e.g., El-Sayegh et al. (2021); Onsarigo et al. (2020). The need to guarantee transparency, publicity, and equal opportunity in public procurement demands clear procedures to be followed by bidders, rendering the low-bid method optimal from a legal perspective Awwad and Ammoury (2019). The low-bid method may result in higher costs than the competitive price, such as when collusion happens Signor et al. (2023). However, this is true with almost any bidding mechanism, and with proper scrutiny, collusion attempts could be detected Signor et al. (2020a).
Notwithstanding illegal collusion, low-bid tenders have been criticized for failing to select the best value bid Ballesteros-Pérez et al. (2015). In particular, low-bid tenders frequently result in a phenomenon known as the winner’s curse. This was first reported by Capen et al. (1971), who found that auction winners in the oil industry consistently received lower returns on investment compared to their initial expectations. The winner’s curse has since been found in a very wide range of business settings, including construction contracts (see Giat and Mitelman (2023)).
Consequently, alternative tendering methods have been proposed. For example, additional criteria other than the best price have been adopted by various public agencies where a formula incorporating criteria concerning price, technical, and organizational considerations determines the best bid W. C. Wang et al. (2013). Another approach to qualifying the low-bid method is presnted by Signor et al. (2020b), who suggested that only bids above an “irresponsible bid threshold” should be accepted. Similarly, Chetan et al. (2018) proposed a two-stage auction process with multiple attributes that allows the client to design an appropriate bid-scoring formula. Other alternatives include the second low-bid method and the average-bid method. See, for example, Awwad and Ammoury (2019), who found that from the client’s perspective, the below-average-bid method is preferred for less competitive projects, whereas for highly competitive projects, the second low-bid method is preferred. Ballesteros-Pérez et al. (2015) candidly concluded that in the current state of practice, much is left to be desired as tendering methods are based more on intuition than on theoretical and empirical considerations.
2.2. Project Management in the Construction Industry
It is unfortunate that despite the great investment in improving project management, project managers frequently fail to deliver the project as requested J. Varajão and Cruz-Cunha (2013). Managing construction projects, in particular, is a challenge due to the ever-changing nature of the projects involved Ziemba and Obła̧k (2015). According to Das and Rahman (2010), “opportunism is defined as a behavior by a party that pursues self-interests with deceit at the expense of other parties”. Contractors’ opportunistic behavior resulting in losses to the client could be considerable, and many researchers and practitioners are advocating for a collaborative relationship between the client and the contractor Suprapto et al. (2015). Key factors that enable such cooperation are trust, commitment, and reliability Deep et al. (2021). Thus, better incentives and means of measuring successful performance are needed if clients wish to change project managers’ attitudes to strictly enforce the contract J. E. Varajão (2018).
Y. Wang et al. (2019) studied how contracts are used to curb opportunism and distinguished between “hard” and “weak” forms of opportunism. While many studies focus on the prevention of opportunism, there are much fewer that examine the enforcement of contracts after violations took place. A recent study of Chinese general contractors by Yao et al. (2023) examined three types of violations: letter violations, mutually agreed spirit violations, and unilaterally assumed spirit violations.
2.3. Game Theory Models
The bidding process has been frequently modeled using game theory, e.g., by Budde and Minner (2015); Lorentziadis (2016). In particular, the winner’s curse phenomenon is explained and analyzed using game theory techniques (see Kagel and Levin (2002)). For construction projects, Ahmed et al. (2016) considered the competition in multistage bidding, where the general contractor who submits the bids employs subcontractors for the actual construction. Barough et al. (2012) used the prisoner’s dilemma and the chicken game to facilitate the resolution of conflicts in construction projects. The prisoner’s dilemma was similarly utilized by Ho and Hsu (2014) to explain how to improve construction tenders that are characterized by high bid preparation costs. Kembłowski et al. (2017) used normal-form noncooperative games to model the bidding process for a highway construction project from the bidder’s perspective.
Cost overruns were investigated by Cantarelli et al. (2013) using a game theory signaling model. They demonstrated that misguided signaling leads to cost overruns. Peldschus et al. (2010) used game theory to select an optimal construction site. San Cristóbal (2015) used a model based on game theory in order to identify the activities that are responsible for the delays in construction projects and to help guide PMs in dealing with project delays. All these papers used single-period games. In contrast, Shang and Abdel Aziz (2020) developed a two-period game to assist public agencies in designing payment mechanisms for public–private partnership transportation projects.
The ubiquity of cost overruns in construction projects suggests that these outcomes are systemic and rooted in differing incentives and payoffs of the different stakeholders (the public agency, project managers, and the winning contractor). Therefore, game theory is an ideal tool for the analysis of this interaction. Notwithstanding the game theory studies described above, it appears that the potential of game theory to explain cost overruns in the construction industry is yet to be realized. Indeed, a review by Piraveenan (2019) of game theory applications concluded that theoretic game analyses for construction project management have great potential but are currently nascent. Even more recently, Eissa et al. (2021) conducted a review of game theory applications in the field of construction engineering and concluded that “even though the construction industry is rich with encounters among its stakeholders, construction engineering and management research lacks a thorough investigation of game-theoretic applications”. Similarly, Narbaev et al. (2022) conducted a thorough review of game theory models in project management and found that the literature “is not as rich as the ones in the other areas of business management, such as finance, operations management, and supply chain management”. Furthermore, not one of the studies they reviewed considered the multi-level strategic relationship between the public agency, project managers, and the contractor. This gap study attempts to fill that gap.
3. Model Background
Our model builds on a case study by Giat and Mitelman (2023) conducted in the Department of Engineering and Construction (DEC), a large public organization in Israel. The DEC employs PMs who oversee the construction of projects by contractors after a low-bid tendering process. They analyzed a data set of 148 low-bid construction projects and confirmed the pendulum effect described above: on average, the winning bid was 8% lower than the expert cost estimate, whereas the final payment to the contractor was 16% greater than the cost estimate.
Depending on project complexity, managerial structures in DEC can differ significantly, encompassing a range of diverse members, positions, responsibilities, and hierarchies. Nevertheless, the pendulum effect remained consistent across different project complexities. Therefore, it is argued that the strategic interaction can be simplified to three members: PMs, contractors, and the PA. Ultimately, the PM’s approval is necessary for the contractor to be rewarded beyond their binding offer. Arguably, such decisions are shaped by the regulations and norms established by the PA, the pressures imposed by the contractor, and the incentives and personality of the PM.
Löwstedt and Räisänen (2012) emphasized the importance of qualitative studies and subjective narratives in understanding organizational behavior. Therefore, we complement the background of our model with informal subjective narratives from experienced senior-level PMs from DEC. Via a social app, we sent the following question:
In the construction industry, the following global phenomenon has been identified: contractors win tenders with offers that are below market value but, at the completion of the project, are rewarded above market value. How do you explain this phenomenon?
Below are excerpts from answers that we received:
- “In the beginning of a project, all involved in the project are aware of the reality that the winning bid is well below market value. This understanding makes it easier for PMs and their supervisors to approve additional claims. This dynamic results in the contractor being overpaid”.
- “Contractors are trained to find loopholes in tenders, and will bid low assuming that they will be able to exploit these to their favor during project execution. The problem is, even when the design is optimal and rigorous, changes in projects are unavoidable. Ultimately, at least some of the claims are just, or in the grey area. Most PMs will yield to the contractors’ pressures and approve their claims”.
- “The construction industry has informally accepted cost overruns as a reality, and higher management is focused on getting projects completed. In some cases, usually with young PMs with little experience, they will play tough with the contractor. However, at some point, they will conform to the norm and approve special claims made by the contractor. Either because they understand that otherwise they will fail to deliver the project, or because higher management will overrule their decisions”.
- “The private sector selects contractors according to their previous reputation. Public tenders use the low bid method and therefore contractors are obliged to submit unrealistic bids. If the PM will be strict in terms of budget, then either the project quality would be compromised, or the schedule would be delayed. The contractor will not pay out-of-pocket under any scenario”.
- “This reality exists not only in the construction industry. Every three years, catering contractors in our organizations are also hired via low bid tenders. We noticed a pattern were the winning contractor gradually compromised the quality of the meals served. I imagine this is the same type of trick that building contractors use”.
PMs were then asked to respond to a second and final question:
What is the influence of a lenient versus strict approach when managing a contractor in a project?
The following are excerpts from responses to this question:
- “A strict approach can be beneficial in situations where the contractor has a history of underperforming or taking advantage of lenient PMs. It can serve as a deterrent against cost overruns and ensure that the project adheres to the initial plan. However, in some cases the PMs approach has a limited impact on project outcomes”.
- “A lenient approach may foster better collaboration between the PM and the contractor, leading to a more positive working environment. However, it could also result in cost overruns and schedule delays, as the contractor might take advantage of the PM’s flexibility to request additional funds or time”.
- “A strict approach can help maintain control over the project budget and timeline, minimizing the risk of cost overruns and delays. However, an overly rigid approach may strain the relationship between the PM and the contractor, potentially leading to disputes, claims, and reduced overall project quality”.
- “A balance between leniency and strictness is crucial. A PM should be flexible enough to accommodate necessary changes or unexpected challenges, while still ensuring that the contractor is held accountable for delivering the project within the agreed-upon budget and timeline. This approach encourages collaboration and problem-solving while maintaining the integrity of the project”.
- “A lenient approach might result in a more adaptive and responsive project team that can quickly address unexpected issues or changes. However, it could also make it challenging for the PM to enforce contractual obligations, potentially jeopardizing the project’s success”.
To summarize, the senior managers’ responses suggest a strategic line of reasoning for the existence of the pendulum effect. Their responses show that they believe the PMs’ choice of approach, strict or lenient, has a substantial impact on PM–contractor interaction. Overall, this qualitative study contributed to our understanding of the project dynamics from the PMs’ perspective and facilitated the development of the game theory model.
4. Game Theory Framework
4.1. Basic Model: The Current State
The events following the contractor’s winning of the low bid tender can be modeled as a simultaneous noncooperative game between two players: the contractor and the PM. In the simplest form, each player has exactly two possible actions with respect to their commitment to the contract between the PA and the contractor. The pendulum effect that was described in the previous sections is argued to be the result of a strategic interaction between the two players.
For the contractor’s actions, we used the terminology of the classical prisoner’s dilemma game: commit (C) and defect (D). The contractor may choose to “commit”, i.e., to honor all the contract’s stipulations and satisfactorily address all the issues raised by the PM. Alternatively, the contractor may choose to “defect”, meaning that the contractor will use various tactics that will minimize their costs and maximize their revenue Das and Rahman (2010); Liu et al. (2016); Y. Wang et al. (2019). Examples of such opportunistic behavior include the following:
- Compromising quality, safety, and/or schedule.
- Searching for loopholes in the binding contract.
- Engaging in disputes (e.g., making false claims, filing lawsuits, etc.).
- Using corrupt means to avoid fulfilling obligations.
The PM is charged by their employer (i.e., the PA) to represent the department and ensure that the project is executed in strict compliance with the contract’s terms. Therefore, it is the duty of the PM to confront the contractor whenever needed. However, being confrontational does not come without costs to the PM. First, a strict approach takes an emotional toll on the PM. Second, strictness is usually met with confrontation. Since the PA’s cultural workplace climate is confrontation-averse, managers do not reward PMs for strictness. Indeed, it has been acknowledged in the literature that there are efforts in the construction industry to shift from adversarial relationships to more collaborative ones Patrucco et al. (2021). Finally, since cost overruns are so common, the PM bears no reputation costs when the project under their management exceeds its budget. Accordingly, the PM’s possible actions are to be “strict” (S) or to be “lenient” (L). Leniency implies that the PM does not confront the contractor when the latter behaves unscrupulously. Furthermore, leniency also implies negligence that adversely affects compliance with the contract terms even when the contractor does generally follow the contract (i.e., the contractor acts towards C).
Figure 1 describes the simultaneous game between the PM and the contractor in normal form. We assumed that the players are risk-neutral and, therefore, payoffs can be viewed as the means of the outcomes. The payoffs for the contractor are presented as a percentage of the true cost. By true cost, we mean the operational costs (e.g. materials, labor, etc.) plus the industry’s typical margin of profit.

Figure 1.
The game between the contractor and the PM in the current situation.
We let denote the relative difference between the winning bid and the true cost and let denote the relative difference between the payment to the contractor and the estimated cost. The variable reflects the underpayment to the contractor and the savings to the PA, whereas reflects the cost overrun rate. For example, in the case study by Giat and Mitelman (2023) described in the previous section, the winning bid was 92% of the estimated cost, and accordingly, . The payments to the contractor were 116% of the estimated cost and, therefore, in that case, .
Notice that when we refer to the contract being underpaid or overpaid, it is relative to the true cost and not the winning bid. This tacitly assumes that the contractor’s profit expectations are similar to the typical industry profit margin. However, this assumption is made mainly for convenience, and the ensuing analysis will not materially change if the contractor’s profit expectations do not differ significantly from the industry-accepted profit margins.
Payoffs to the PM are ordinal and are denoted by , where . We now explain the payoffs to the contractor and the PM for each outcome of the game, where outcome (X,Y) denotes the contractor playing X and the PM playing Y.
- Outcome (C,S)—the contractor commits and the PM is strict: Since the contract terms are followed, the contractor ends up with a underpayment. Since the commitment was obtained without confrontation, the PM’s payoff is high (h).
- Outcome (C,L)—the contractor commits and the PM is lenient: Although the contractor is committed to the contract, the PM’s leniency results in greater payments to the contractor than when (C,S) is played. We assume that the difference between a lenient and strict PM amounts to a difference of percentage points. That is, represents how much the payment to the contractor increases if a strict PM changes their behavior to lenient. The PM’s payoff is slightly lower than in the previous case () since the extra to the contractor is at the expense of the PA and is attributed to the PM’s slack behavior.
- Outcome (D,L)—the contractor defects and the PM is lenient: The contractor’s unscrupulous antics are left unchecked by the PM; therefore, the contractor is overpaid . Due to the organization’s culture, the PM’s payoff is medium (m) since, although there are considerable project overruns, these are somewhat tolerated when there are no PM–contractor conflicts.
- Outcome (D,S)—the contractor defects and the PM is strict: The PM’s strictness decreases the payments to the contractor by . In addition, the contractor has expenses that are beyond normal construction-related costs (e.g., additional managerial and legal costs). These are assumed to be x percentage points. Therefore, the contractor’s net overpayment is . These external costs are never too large to deter defection, namely that and, therefore, . The PM’s payoff is low (l) because of the organization’s culture that does not reward strictness if it leads to confrontations.
Note that represents the added payments to the contractor as a result of the PM’s leniency. We reasonably assumed that it could not be more than the maximal overruns, i.e., .
Outcome (D,L) is the unique Nash equilibrium of the game. That is, the contractor is deceitful, and the PM yields to the contractor. Therefore, in equilibrium, the contractor is overpaid . The contractor’s overpayment is a manifestation of the pendulum effect. It does not only eliminate the anticipated underpayment to the low bid but even reverses the final outcome to result in an overpaid contractor.
4.2. Public Utility
From the PA’s (i.e., the public) perspective, the equilibrium outcome is the worst possible outcome. Empirical evidence suggests that this is frequently the de facto result in public agencies Giat and Mitelman (2023). The underlying force driving this result is that the contractor is always motivated to defect. Consequently, it is better for the PM to be lenient and avoid confrontation.
The current situation appears to benefit the contractor at the expense of the PA. This is because the PA’s net gain from the project is generally the additive inverse of the contractor’s overpayment. For example, if the contractor is overpaid (such as for (D,L)), then the PA’s losses are . The only exception is the (D,S) outcome. Here, the PA’s loss is only whereas the contractor’s net overpayment is because x represents external costs to the contractor that are not at the expense of the PA.
5. The Extended Model: Mitigating Cost Overruns
The analysis of the current state reveals that while the PM is the PA’s agent, their interests are not aligned. Therefore, we need to broaden the game to include the PA as a third player. We propose that the PA considers cultural and procedural changes to its operations that will strategically affect the other players’ actions and improve the public’s utility.
- Cultural change: The current workplace culture is confrontation-adverse; therefore, it is unrewarding to strict PMs. An alternative approach is to implement ways to measure PMs’ performance and reward them based on the actual project outcome Giebe and Gürtler (2012); J. E. Varajão (2018). A successful implementation of such a system is expected to encourage PMs to stand their ground whenever they sense that contractors are defecting.
- Procedural change: The current tendering method designates the winner as the contractor with the lowest valid bid. Due to the winner’s curse, a commitment strategy is unsustainable to the contractor. Their a priori loss makes them hard-pressed to resist the defecting strategy. An alternative approach is to change the tendering method to the average-bid method. In this method, the contract is awarded to the bidder whose offer is closest to the average of all submitted bids (see Chang et al. (2015)). As demonstrated in Giat and Mitelman (2023), the average bid tends to align closely with the estimated project cost, making this approach a viable means of reducing the financial pressures that drive opportunistic behavior. Importantly, Chang et al. (2015)’s empirical finding that “bidding behavior remains similar between the average bid and low price auctions” promises that even after implementing this change, the average bid is still expected to be a good approximation of the estimated project cost.
Accordingly, there are four feasible actions for the PA. The first (“current situation”) is to remain with the current tendering method and cultural climate. The second (“procedural change”) is to change only its procedural approach and change the tender rules such that the winner is paid the average bid. The third (“cultural change”) is to change only its cultural approach and transform the organization’s culture to one that rewards strictness even if it is confrontational. The fourth (“both actions”) is implementing both procedural and cultural change.
The game between the three players is played in two periods. The PA is the first mover and chooses its action in the first period, which can then be viewed by the other players. If the PA makes no changes, then the second period’s sub-game between the contractor and the PM is described in Figure 1. We note that the equilibrium outcome of this sub-game results in a payoff to the PA. For each of the PA’s three other possible actions, the subsequent sub-games are described in Figure 2, Figure 3 and Figure 4. In each rubric, the payoff is a three-tuple describing, by order, the payoffs of the contractor, the PM, and the PA.
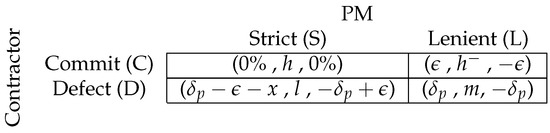
Figure 2.
The PM–contractor’s second-period game when the PA’s action in the first period was procedural change.
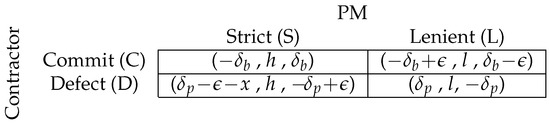
Figure 3.
The PM–contractor’s second-period game when the PA’s action in the first period was cultural change.

Figure 4.
The PM–contractor’s second-period game when the PA’s action in the first period was procedural and cultural changes.
- The PA’s action is procedural change: When the PA plays the procedural change in the first period, the second period is affected only through the change to the contractor’s payoff function. Because the average bid is equal to the true cost of the project, if the contractor plays C, they are overpaid 0% or when the PM is lenient or strict, respectively. However, when the contractor plays D, there will be no change compared to the current situation since the change in the contract terms plays a small role for a deceitful contractor. The second period’s sub-game is given in normal form in Figure 2. Equilibrium depends on the contractor’s externalities (i.e., the external cost x). If , then D is a dominant strategy for the contractor, and the outcome (D,L) remains equilibrium with no improvement to the current situation. If , then there are two pure-strategy equilibria, (C,S) and (D,L), for which the public’s loss is 0% and , respectively (for brevity, the mixed-strategy equilibrium is ignored). Therefore, when , implementing a procedural change poses a benefit to the public interest through the projects that will settle on the (C,S) equilibrium.
- The PA’s action is cultural change: A cultural change in the first period by the PA affects only the payoff to the PM in the second period. The second period’s sub-game for this situation is given in Figure 3. By playing S, the PM is rewarded (h), whereas by playing L, the PM is penalized (l). As a result, S is a dominant strategy for the PM, and D is a dominant strategy for the contractor. Thus, (D,S) is equilibrium, and the public’s loss is compared to the current state’s loss of .
- The PA’s action is both changes: If both changes are made by the PA in the first period, then the two previously discussed changes to the payoff functions will happen (see Figure 4). Due to the cultural change, S is the dominant strategy for the PM. If , then D is the dominant strategy for the contractor, and (D,S) is equilibrium with a public loss of , an improvement from the current loss of . If , then (C,S) is equilibrium, and the public loss decreases to zero.
We summarized in Table 1 the equilibrium outcomes and payoffs to the PA. These are provided for the current situation and each of the changes.

Table 1.
The second period’s outcome following the PA’s first-period decision.
6. Discussion
Implementing just one of the changes could result in a better payoff to the PA. If only cultural change is implemented, then the losses decrease to . If only procedural changes are adopted and , then the losses for some of the projects will reduce to zero. Implementing both the procedural and cultural changes will reduce its loss from the current to zero (if ) or (if ). Thus, regardless of the value of x, the public’s benefit is maximized by making the two changes; therefore, the PA’s optimal strategy is to do so.
Changing from a low-bid method to an average-bid method may lead to a change in the contractors’ bidding behavior. One may expect that contractors raise their bidding price since they now wish to meet the average bid. This, in turn, may result in an average bid that is above the true project value, resulting in a loss to the PA. However, empirical and theoretical evidence suggests this is not the case, and bids do not increase after such a procedural change (see Chang et al. (2015)). However, as our results show, procedural change alone is only partly beneficial to the PA. It must be coupled with cultural change to ensure the best outcome.
The framework’s underlying assumption is that trying to prevent any particular deceitful behavior by contractors is parallel to treating the symptoms instead of the cause. This approach will only result in contractors devising new questionable methods to increase their income. It is more effective and beneficial to create a business environment in which contractors themselves will opt against these behaviors. The proposal to make both procedural and cultural changes achieves exactly that.
Another issue that must be considered is the tension between contractors and PMs. In the current state, there is little conflict between the two groups because PMs capitulate to contractors’ pressure. While a lack of discord is supposedly a blessing, in this setting, it results in cost overruns and public losses. Depending on the external costs of the contractors, the proposed changes may lead to two results. If these costs are high (), then the equilibrium outcome is (C,S), implying two benefits: there are no cost overruns, and there is no contention between the contractors and the PM. It is only when the external costs of the contractors are low () that the outcome will be contentious (D,S). Possibly, the PA can create an environment in which the external costs to the contractor are sufficiently high to ensure the equilibrium outcome is the more constructive outcome (C,S).
7. Conclusions and Limitations
In this paper, we developed a two-period game to explain cost overruns in the construction industry and to analyze possible ways to overcome them. Our game theory model attempts to rise above specific reasons for each project and capture the strategic relationship between the contractor and the PM in general. In this noncooperative game, the dominant strategy of the contractor is to struggle to increase revenues, even if these are inconsistent with the contract clauses. The PM does not have a dominant strategy upfront; however, given that the contractor is expected to act according to their dominant strategy, the PM also aligns with the defective strategy of the contractor, and the outcome of the game is an increase in the payment to the contractor.
The current outcome is detrimental to the public’s interest. Therefore, we broadened our view and considered strategic actions that the PA can take so that the subsequent game between the contractor and the PM results in a more favorable outcome for the PA. We proposed two corrective measures for the PA: modifying the tendering method and changing the PMs’ work culture. Together, they are expected to improve public welfare and reduce cost overruns. The results of public organizations that have implemented measures aimed at changing the incentives of the PM and the contractor may corroborate or refine the proposed framework.
Our work has several limitations that should be considered. We did not incorporate risk into the payoffs of the contractor by assuming that the contractors are risk neutral. This assumption is not valid for contractors that are not sufficiently diversified. The models that we proposed considered only two possible actions for the PM and the contractor, whereas the reality is reasonably more complex. There may be other organizational changes that the PA can undertake to the given problem that we have not considered. Admittedly, it is highly challenging to implement changes in large public organizations with long-standing practices and rigid frameworks. However, these additional actions and measures for the given problem can be assessed using the proposed framework. We hope that additional research and validation will corroborate and further develop the current model.
Author Contributions
Conceptualization, Y.G. and A.M.; Methodology, Y.G. and A.M.; Formal analysis, Y.G. and A.M.; Writing—original draft, Y.G. and A.M.; Writing—review & editing, Y.G. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ahmed, M. O., El-Adaway, I. H., Coatney, K. T., & Eid, M. S. (2016). Construction bidding and the winner’s curse: Game theory approach. Journal of Construction Engineering and Management, 142(2), 04015076. [Google Scholar] [CrossRef]
- Anheier, H. K. (2016). Of Hiding Hands and other ways of coping with uncertainty: A commentary. Social Research, 83(4), 1005–1010. [Google Scholar] [CrossRef]
- Awwad, R., & Ammoury, M. (2019). Owner’s perspective on evolution of bid prices under various price-driven bid selection methods. Journal of Computing in Civil Engineering, 33(2), 04018061. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P., Skitmore, M., Pellicer, E., & González-Cruz, M. C. (2015). Scoring rules and abnormally low bids criteria in construction tenders: A taxonomic review. Construction Management and Economics, 33(4), 259–278. [Google Scholar] [CrossRef]
- Barough, A. S., Shoubi, M. V., & Skardi, M. J. E. (2012). Application of game theory approach in solving the construction project conflicts. Procedia-Social and Behavioral Sciences, 58, 1586–1593. [Google Scholar] [CrossRef]
- Budde, M., & Minner, S. (2015). Optimal capacity provision for service providers with subsequent auctioning of projects. International Journal of Production Economics, 170, 652–662. [Google Scholar] [CrossRef]
- Cantarelli, C. C., Chorus, C. G., & Cunningham, S. W. (2013). Explaining cost overruns of large-scale transportation infrastructure projects using a signalling game. Transportmetrica A: Transport Science, 9(3), 239–258. [Google Scholar] [CrossRef]
- Capen, E. C., Clapp, R. V., & Campbell, W. M. (1971). Competitive bidding in high-risk situations. Journal of Petroleum Technology, 23(06), 641–653. [Google Scholar] [CrossRef]
- Chang, W.-S., Chen, B., & Salmon, T. C. (2015). An investigation of the average bid mechanism for procurement auctions. Management Science, 61(6), 1237–1254. [Google Scholar] [CrossRef]
- Chetan, T., Jenamani, M., & Sarmah, S. P. (2018). Two-stage multi-attribute auction mechanism for price discovery and winner determination. IEEE Transactions on Engineering Management, 66(1), 112–126. [Google Scholar] [CrossRef]
- Coggins, J., Teng, B., & Rameezdeen, R. (2016). Construction insolvency in Australia: Reining in the beast. Construction Economics and Building, 16(3), 38–56. [Google Scholar] [CrossRef]
- Das, T., & Rahman, N. (2010). Determinants of partner opportunism in strategic alliances: A conceptual framework. Journal of Business and Psychology, 25(1), 55–74. [Google Scholar] [CrossRef]
- Deep, S., Gajendran, T., & Jefferies, M. (2021). A systematic review of ‘enablers of collaboration’ among the participants in construction projects. International Journal of Construction Management, 21(9), 919–931. [Google Scholar] [CrossRef]
- Eissa, R., Eid, M. S., & Elbeltagi, E. (2021). Current applications of game theory in construction engineering and management research: A social network analysis approach. Journal of Construction Engineering and Management, 147(7), 04021066. [Google Scholar] [CrossRef]
- El-Sayegh, S. M., Basamji, M., Haj Ahmad, A., & Zarif, N. (2021). Key contractor selection criteria for green construction projects in the UAE. International Journal of Construction Management, 21(12), 1240–1250. [Google Scholar] [CrossRef]
- Famiyeh, S., Amoatey, C. T., Adaku, E., & Agbenohevi, C. S. (2017). Major causes of construction time and cost overruns. Journal of Engineering, Design and Technology, 15(2), 181–198. [Google Scholar] [CrossRef]
- Flyvbjerg, B. (2016). The fallacy of beneficial ignorance: A test of Hirschman’s hiding hand. World Development, 84, 176–189. [Google Scholar] [CrossRef]
- Flyvbjerg, B., Holm, M. S., & Buhl, S. (2002). Underestimating costs in public works projects: Error or lie? Journal of the American Planning Association, 68(3), 279–295. [Google Scholar] [CrossRef]
- Gao, N., & Touran, A. (2020). Cost Overruns in US Rail transit projects: A statistical analysis. In Construction research congress 2020: Project management and controls, materials, and contracts (pp. 593–601). American Society of Civil Engineers. [Google Scholar]
- Giat, Y., & Mitelman, A. (2023). Cost overruns, winner’s curse, wisdom of the crowd and a pendulum effect in public construction tenders. IEEE Engineering Management Review, 51(2), 141–151. [Google Scholar] [CrossRef]
- Giebe, T., & Gürtler, O. (2012). Optimal contracts for lenient supervisors. Journal of Economic Behavior & Organization, 81(2), 403–420. [Google Scholar]
- Hirschman, A. O. (1967). The principle of the hiding hand. The Public Interest, 6, 10–23. [Google Scholar]
- Ho, S. P., & Hsu, Y. (2014). Bid compensation theory and strategies for projects with heterogeneous bidders: A game theoretic analysis. Journal of Management in Engineering, 30(5), 04014022. [Google Scholar] [CrossRef]
- Ika, L. A. (2018). Beneficial or detrimental ignorance: The straw man fallacy of Flyvbjerg’s test of Hirschman’s hiding hand. World Development, 103, 369–382. [Google Scholar] [CrossRef]
- Ika, L. A., Love, P. E., & Pinto, J. K. (2020). Moving beyond the planning fallacy: The emergence of a new principle of project behavior. IEEE Transactions on Engineering Management, 69(6), 3310–3325. [Google Scholar] [CrossRef]
- Kagel, J. H., & Levin, D. (2002). Common value auctions and the winner’s curse. Princeton University Press. [Google Scholar]
- Kembłowski, M. W., Grzyl, B., & Siemaszko, A. (2017). Game theory analysis of bidding for a construction contract. In IOP conference series: Materials science and engineering (Vol. 245, p. 062047). IOPScience. [Google Scholar]
- Liu, J., Gao, R., Cheah, C. Y., & Luo, J. (2016). Incentive mechanism for inhibiting investors’ opportunistic behavior in PPP projects. International Journal of Project Management, 34(7), 1102–1111. [Google Scholar] [CrossRef]
- Locatelli, G., Mariani, G., Sainati, T., & Greco, M. (2017). Corruption in public projects and megaprojects: There is an elephant in the room! International Journal of Project Management, 35(3), 252–268. [Google Scholar] [CrossRef]
- Lorentziadis, P. L. (2016). Optimal bidding in auctions from a game theory perspective. European Journal of Operational Research, 248(2), 347–371. [Google Scholar] [CrossRef]
- Lovallo, D., Cristofaro, M., & Flyvbjerg, B. (2023). Governing large projects: A three-stage process to get it right. Academy of Management Perspectives, 37(2). [Google Scholar] [CrossRef]
- Love, P. E., Ika, L. A., & Ahiaga-Dagbui, D. D. (2019a). On de-bunking ‘fake news’ in a post truth era: Why does the planning fallacy explanation for cost overruns fall short? Transportation Research Part A: Policy and Practice, 126, 397–408. [Google Scholar] [CrossRef]
- Love, P. E., Ika, L. A., & Sing, M. C. (2019b). Does the planning fallacy prevail in social infrastructure projects? Empirical evidence and competing explanations. IEEE Transactions on Engineering Management, 69(6), 2588–2602. [Google Scholar] [CrossRef]
- Love, P. E., Pinto, J. K., & Ika, L. A. (2022). Hundreds of years of pain, with minimal gain: Capital project cost overruns, the past, present and optimistic future. IEEE Engineering Management Review, 5(4), 56–70. [Google Scholar] [CrossRef]
- Löwstedt, M., & Räisänen, C. (2012). ‘Playing back-spin balls’: Narrating organizational change in construction. Construction Management and Economics, 30(9), 795–806. [Google Scholar] [CrossRef]
- Narbaev, T., Hazır, Ö., & Agi, M. (2022). A review of the use of game theory in project management. Journal of Management in Engineering, 38(6), 03122002. [Google Scholar] [CrossRef]
- Onsarigo, L., Duncan, K., & Atalah, A. (2020). The effect of prevailing wages on building costs, bid competition, and bidder behaviour: Evidence from ohio school construction. Construction Management and Economics, 38(10), 917–933. [Google Scholar] [CrossRef]
- Paraskevopoulou, C., & Boutsis, G. (2020). Cost overruns in tunnelling projects: Investigating the impact of geological and geotechnical uncertainty using case studies. Infrastructures, 5(9), 73. [Google Scholar] [CrossRef]
- Patrucco, A. S., Moretto, A., & Knight, L. (2021). Does relationship control hinder relationship commitment? The role of supplier performance measurement systems in construction infrastructure projects. International Journal of Production Economics, 233, 108000. [Google Scholar] [CrossRef]
- Peldschus, F., Zavadskas, E. K., Turskis, Z., & Tamosaitiene, J. (2010). Sustainable assessment of construction site by applying game the. Engineering Economics, 21(3), 223–237. [Google Scholar]
- Piraveenan, M. (2019). Applications of game theory in project management: A structured review and analysis. Mathematics, 7(9), 858. [Google Scholar] [CrossRef]
- Rosenfeld, Y. (2014). Root-cause analysis of construction-cost overruns. Journal of Construction Engineering and Management, 140(1), 04013039. [Google Scholar] [CrossRef]
- San Cristóbal, J. R. (2015). The use of game theory to solve conflicts in the project management and construction industry. International Journal of Information Systems and Project Management, 3(2), 43–58. [Google Scholar] [CrossRef]
- Shang, L., & Abdel Aziz, A. M. (2020). Stackelberg game theory-based optimization model for design of payment mechanism in performance-based PPPs. Journal of Construction Engineering and Management, 146(4), 04020029. [Google Scholar] [CrossRef]
- Signor, R., Ballesteros-Pérez, P., & Love, P. E. D. (2023). Collusion detection in infrastructure procurement: A modified order statistic method for uncapped auctions. IEEE Transactions on Engineering Management, 70(2), 464–477. [Google Scholar] [CrossRef]
- Signor, R., Love, P. E., & Ika, L. A. (2020a). White collar crime: Unearthing collusion in the procurement of infrastructure projects. IEEE Transactions on Engineering Management, 69(5), 1932–1943. [Google Scholar] [CrossRef]
- Signor, R., Love, P. E. D., Marchiori, F. F., & Felisberto, A. D. (2020b). Underpricing in social infrastructure projects: Combating the institutionalization of the winner’s curse. Journal of Construction Engineering and Management, 146(12), 05020018. [Google Scholar] [CrossRef]
- Suprapto, M., Bakker, H. L., Mooi, H. G., & Moree, W. (2015). Sorting out the essence of owner—Contractor collaboration in capital project delivery. International Journal of Project Management, 33(3), 664–683. [Google Scholar] [CrossRef]
- Thijssen, J. J. (2022). Optimal investment and abandonment decisions for projects with construction uncertainty. European Journal of Operational Research, 298(1), 368–379. [Google Scholar] [CrossRef]
- Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases: Biases in judgments reveal some heuristics of thinking under uncertainty. Science, 185(4157), 1124–1131. [Google Scholar] [CrossRef]
- Varajão, J., & Cruz-Cunha, M. M. (2013). Using AHP and the IPMA competence baseline in the project managers selection process. International Journal of Production Research, 51(11), 3342–3354. [Google Scholar] [CrossRef]
- Varajão, J. E. (2018). A new process for success management–bringing order to a typically ad-hoc area. The Journal of Modern Project Management, 5(3), 92–99. [Google Scholar]
- Wang, W. C., Yu, W. D., Yang, I. T., Lin, C. C., Lee, M. T., & Cheng, Y. Y. (2013). Applying the AHP to support the best-value contractor selection—Lessons learned from two case studies in Taiwan. Journal of Civil Engineering and Management, 19(1), 24–36. [Google Scholar] [CrossRef]
- Wang, Y., Chen, Y., Wang, W., Chen, Y., & Jin, M. (2019). Revisiting the relationship between contract governance and contractors’ opportunistic behavior in construction projects. IEEE Transactions on Engineering Management, 69(6), 2517–2529. [Google Scholar] [CrossRef]
- Wasfy, A., & Nassar, A. H. (2021). Delay analysis statements in the presence of debatable concerns in construction projects. IEEE Engineering Management Review, 49(4), 123–135. [Google Scholar] [CrossRef]
- Yao, H., Chen, Y., & Tang, Y. (2023). Contract violations in the construction projects: How contractual obligations are reached affects contractual and reputational enforcement. IEEE Transactions on Engineering Management, 71, 7160–7172. [Google Scholar] [CrossRef]
- Ziemba, E., & Obła̧k, I. (2015). Change management in information systems projects for public organizations in Poland. Interdisciplinary Journal of Information, Knowledge, and Management, 10, 47–62. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).