Abstract
The computational complexity of large-scale networked evolutionary games has become a challenging problem. Based on network aggregation and pinning control methods, this paper investigates the problem of control design for strategy consensus of large-scale networked evolutionary games. The large-size network is divided into several small subnetworks by the aggregation method, and a pinning control algorithm is proposed to achieve the strategy consensus of small subnetworks. Then, the matchable condition between the small subnetworks is realized by the input–output control. Finally, some sufficient conditions as well as an algorithm are proposed for the strategy consensus of large-scale networked evolutionary games.
1. Introduction
Evolutionary games were first proposed by biologists to study social behaviors in nature Smith and Price (1973) and have been widely applied in natural, social and economic systems in the past few decades (Fan et al., 2021; Zhang et al., 2021). Classical evolutionary games often assume that each player interacts with all other players or randomly selected players. However, due to the impact of complex network environments, the ability of each player to obtain information is limited, which is dependent of the local information among players and the network topology. Accordingly, evolutionary games on the network have been proposed and called networked evolutionary games (NEGs) Nowak and May (1992). In NEGs, nodes represent players and edges represent the interactions between players. Therefore, nodes and edges play an important role in the study of NEGs. In recent years, the state feedback control, incentive-based control and robustness of NEGs have been well studied (Jia et al., 2024; Sun et al., 2023; Wang et al., 2023; Ye, 2022) and have become popular problems in biology, sociology, system science and other disciplines (Fowler & Christakis, 2010; Iyer & Killingback, 2016).
With the development of logical dynamical systems and finite games, researchers need to adopt effective control methods to optimize the performance of systems and promote the evolution towards the expected goal in practical application scenarios such as biology, sociology and economics. However, traditional methods have difficulties dealing with complex logical relations. The semi-tensor product of matrices Cheng et al. (2011) provides an effective way to solve this problem by transforming elements of a finite set into logical vectors and then converting complex logical expressions into simple algebraic state-space representations. Based on this method, a series of important results have been obtained on the observability Y. Li et al. (2024), controllability X. Yang and Li (2023) and stability Guo et al. (2019) of Boolean networks. These studies are helpful to predict the network behavior of gene regulation and optimize the spread of social behavior. Additionally, the semi-tensor product method has been introduced in game theory (W. Liu et al., 2023; G. Zhao et al., 2024; R. Zhu et al., 2022), particularly playing a key role in the study of strategy consensus in NEGs Jia et al. (2024).
It is worth pointing out that the network topology of NEGs often consists of a large number of nodes and edges. However, the computational complexity of methods in (Jia et al., 2024; W. Liu et al., 2023; G. Zhao et al., 2024; R. Zhu et al., 2022) grows exponentially with the increase in number of nodes. As a result, it is necessary to develop some new methods to reduce the complexity of studying NEGs. Some useful techniques were proposed to study large-scale logical networks, including logical matrix factorization H. Li and Wang (2015), compositional method H. Li and Pang (2024), network aggregation Y. Zhao et al. (2013) and pinning control Zhong et al. (2021). These methods can effectively reduce the computational complexity and improve the efficiency of network analysis and control, especially for handling complex logical dynamical systems.
In recent years, the network aggregation method has been widely used in the analysis and control of logical networks, such as stabilization H. Li et al. (2021), reachability Y. Zhao et al. (2016) and observability Y. Liu et al. (2020). Particularly, the problem of controlling the strategy choices of players of a large-scale NEG in order to achieve consensus was solved using network aggregation techniques. Based on the strategy profile reachability of each control sub-game, the network aggregation was used to study the large-size networked evolutionary matrix games with a general network structure H. Li et al. (2024). The basic idea of network aggregation is to divide a network into several subnetworks and derive the behavior of the whole network by studying the properties of the subnetworks J. Yang and Cho (2016). In addition, an important method called pinning control was introduced to study logical networks Lu et al. (2016), and several interesting results were obtained (H. Li & Wang, 2015; Lin et al., 2022; S. Zhu et al., 2023, 2022). The main idea of pinning control is to achieve the control objective by controlling only a small subset of nodes Zhong et al. (2020), thereby reducing the computational complexity. The strategy consensus of large-scale NEGs was also solved through pinning control, and the strategy consensus problem of NEGs was considered in Jiang et al. (2024) via the degree-based pinning control. To our best knowledge, there are no results on combining network aggregation and pinning control to study the strategy consensus of NEGs. Therefore, it is meaningful to combine these two methods for the purpose of reducing both the computational complexity and target players of NEGs.
In this paper, we study the strategy consensus of large-scale NEGs via network aggregation and pinning control. The contributions of this article are mainly summarized below. On one hand, by partitioning the whole network, we give the algebraic form of NEGs with pinning control and obtain a sufficient condition for subnetworks to achieve a strategy consensus. On the other hand, based on the network aggregation, we give a sufficient condition for a strategy consensus of large-scale NEGs by selecting a small number of control players in subnetworks.
The remainder of this paper is organized as follows. Section 2 gives some preliminaries. Section 3 presents the algebraic representations of strategy profile dynamics’ equations of the subnetworks via network aggregation. Section 4 provides the main results of this paper. Section 5 is a brief conclusion.
At the end of this section, we present some useful notations.
- is the set of natural numbers, and is the set of real numbers.
- denotes the ith column of matrix A.
- .
- .
- , where is the -dimensional identity matrix.
- A logical matrix is simply denoted as .
- and denote the sets of -dimensional real matrices and logical matrices, respectively.
2. Preliminaries
In this section, we briefly recall some preliminaries on the semi-tensor product of matrices and the model of NEGs.
The main tool used in this paper is the semi-tensor product of matrices. This is a new multiplication that can be used for matrices with different dimensions. For more details, please refer to Cheng et al. (2011).
Definition 1.
Let and be given. The semi-tensor product of two matrices X and Y, denoted by , is defined as
where is the least common multiple of n and p, and ⊗ denotes the Kronecker product.
Remark 1.
When , the semi-tensor product of matrices X and Y is consistent with the conventional matrix product. In the following text, the symbol ⋉ will be omitted.
The semi-tensor product of matrices has many useful properties, one of which is shown below. Let be an n-dimensional pseudo-logical function. Using the semi-tensor product method, there exists a unique matrix , such that
where M is called the structural matrix of f.
In the following, we present some necessary preliminaries on NEGs.
Definition 2.
An NEG with n players is composed of the following three elements:
- (i)
- An undirected network graph , where represents the set of n players, and represents the set of edges;
- (ii)
- A fundamental network game, where denotes the strategy set, denotes the strategy of player i at time t, denotes the strategy profile at time t, and denotes the payoff matrix;
- (iii)
- A strategy updating rule (SUR)
Remark 2.
represents the set of all neighbors of player i within l steps (including l), and N represents the set of all neighbors of player i within one step. represents the average payoff of player j at time t, expressed as
Remark 3.
There are several common SURs, such as unconditional imitation, myopic best response adjustment, and the Fermi rule.
Remark 4.
According to the SUR in Definition 2, we can derive the fundamental evolutionary equations below:
Using the semi-tensor product of matrices, we can obtain the following strategy profile dynamics (SPDs):
where .
Definition 3.
Given an NEG , assume that is a partition of V, where . If the strategies of the players in U can be fixed, then is called a control networked evolutionary game, where is called the state player, and is called the control player.
Definition 4.
Given two sets of players and , where , the mapping is defined as
Definition 5.
If there exists an integer , such that , is satisfied for any integer and any initial strategy profile , then an NEG is said to achieve strategy consensus at .
3. Problem Formulation
We divide the set V of a large-scale NEG into k subsets:
where holds for any two different , and each set represents a set of players in a subnetworked evolutionary game . Define and as the sets of input players and output players corresponding to , respectively, where
and .
We assume and define
where , , and . The degree of players in satisfies the following conditions:
and if there exist two nodes that have equal degree, then we keep the order of these two nodes in V.
We assume that the network graph of the considered NEG is connected, and after partitioning the set V into k subsets, the network graph of each subnetwork is also connected, where . Consider the ith subnetworked evolutionary game below:
where and . Then, the SPDs are constructed from (4) as follows:
where , and .
This paper aims to achieve the strategy consensus in subnetworked evolutionary games and eventually achieve the strategy consensus in whole NEGs by network aggregation. In the next section, we focus on how to choose control players in order to achieve the strategy consensus in the subnetworks.
4. Main Results
Firstly, we establish a criterion for achieving the strategy consensus in subnetworked evolutionary games and present a control design procedure based on this criterion.
In order to facilitate the analysis, we need to give some basic assumptions. Let the target strategy profile of an NEG with n players be . Then, define the target strategy profile of the ith subnetwork as , the target strategy profile of the input players as , and the target strategy profile of the output players as .
In the SPDs (5) of subnetworked evolutionary game , we fix the strategies of input and output players in as the target strategy . Then, (5) can be written as
where , and . Thus, we have
Since , we derive that
Then, we have the following result.
Theorem 1.
Let be the set of input and output control players of . Then, the subnetworked evolutionary game achieves strategy consensus to , if and only if
where .
Proof.
(Necessity) Suppose that the subnetworked evolutionary game achieves the strategy consensus to . By Definition 5, there exists such that is satisfied for any integer and any initial strategy profile , that is, holds for any .
Since is the set of input and output players of , we can derive that
is satisfied for any and any . Then, according to (6) and (8), we obtain that
holds for any integer and any . Based on and the arbitrariness of , we have
Next, we prove that there exists a positive integer satisfying (9). Let be the smallest positive integer satisfying (9), and assume that . Then, there must exist a such that , and .
When the strategy of the input and output players of are fixed to the target strategy , there exists such that . Then, the trajectory of from constitutes a cycle, which has the form of . This contradicts the definition of a strategy consensus. Thus, (7) is satisfied.
(Sufficiency) Assume that (7) is satisfied. Then, we have
Based on (6), for any integer and any , we obtain
Then, according to (10), we derive that
Thus, for any initial state and any integer , it holds that . Notice that is the set of input and output control players, that is, for any , we have , . Then, we obtain , . Hence, we conclude that achieves the strategy consensus to . □
From Theorem 1, if (7) holds, then the control players set of is the set of input and output players, that is, . If (7) does not hold, we need to add the control players of by fixing the strategy of as and is called the control player with the largest degree. Therefore, (6) can be written as
where . Then, we have . According to , we obtain
where .
In the following, we continue to verify whether
holds, where . Denote as the set of input and output players of , that is, , and define as the set of control players with the largest degree. If (12) holds, then we derive that . Otherwise, we control several players with larger degrees at the same time, in which we control the first players belonging to the set , where , fixing their strategies to . Similarly, we can obtain
where . Then, we have . According to , we obtain that
where .
When , we need to consider whether
holds, respectively, where = . Denote the minimum value of that makes (14) hold as , that is, . Thus, the control players set of is
such that achieves the strategy consensus to .
Based on the above analysis, we present Algorithm 1 that briefly summarizes how to design the set of control players for .
| Algorithm 1 Calculate the set of control players for |
| Input: , , |
| Output: |
| if then |
| else |
| for do |
| if then |
| end if |
| end for |
| end if |
In what follows, based on the control design procedure for achieving strategy consensus of subnetworked evolutionary games, we give a sufficient condition for achieving the strategy consensus of large-scale NEGs.
Denote , where is the set of control players of derived from the above algorithm. Then, a sufficient condition is given below for the strategy consensus of large-scale NEGs.
Theorem 2.
An NEG achieves strategy consensus to if the strategies of all players in the set C are fixed to .
Proof.
Consider any initial state of . If the strategies of the players in the set are fixed to , then, based on Theorem 1 and Definition 5, it follows that will achieve strategy consensus to at time . Let . Define as the -step strategy trajectory of and as the ordered set of states corresponding to , where , . Since the strategies of all players in the set C are fixed to , for each , the corresponding input sequence is fixed. Then, we obtain that
is satisfied for any , , that is, there exists a corresponding -matching input sequence such that for any and any initial state , we have . Hence, we derive the -step strategy trajectory , where , . In other words, can reach at the th step. Then, for any , we have , . Thus, holds for any integer . Therefore, the NEG reaches the strategy consensus to . □
Remark 5.
By the above algorithm, we can calculate the set of control players for each . Therefore, we obtain that the set of control players for the large-scale network is .
Remark 6.
Different partitions of a network will result in different subnetworks, and the final set of control players C may also be different.
Finally, we use two examples to illustrate Theorem 2.
Example 1.
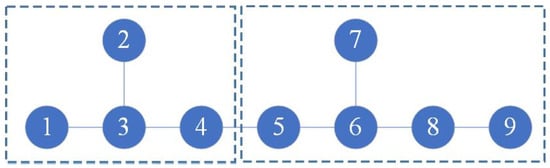
Consider an NEG whose network graph is shown in Figure 1. Select control players to guarantee that the considered NEG achieves strategy consensus to , where the strategy set , the payoff matrix , and the SUR is an unconditional imitation with fixed priority (Cheng et al., 2015).

Figure 1.
Network graph of the NEG in Example 1.
As shown in Figure 1, we divide the whole network into two subnetworks and . For subnetwork , we have
Fixing the strategy of the players in the set to be , the SPDs of are obtained as
where , and . Thus, we have
where .
According to the unconditional imitation with fixed priority, the average payoffs of players 1, 2, 3 and the strategy update dynamics of player 1 and player 2 in subnetwork are obtained, as shown in Table 1.

Table 1.
From average payoffs to dynamics in .
By a simple calculation, we have . Since
we derive that achieves strategy consensus to at , and the set of control players of is .
Similarly, for subnetwork , we have
Fixing the strategy of the players in the set to be , the SPDs of are obtained as
where and . Thus, we have . Since and , we need to control such that holds for any . Then, we obtain
where . By a simple calculation, we have .
It is verified that holds, and thus achieves strategy consensus to at . Moreover, the set of control players of is .
Therefore, the set of control players for the whole network is . Controlling the players in C with a fixed strategy allows the above NEG to achieve strategy consensus to at (see Figure 2).
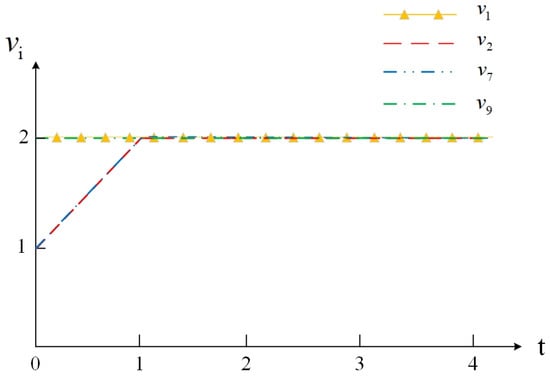
Figure 2.
State trajectory of player with the initial state , where .
Remark 7.
When we define the strategy “1” as “non-confession” and the strategy “2” as “confession”, the game of Example 1 can be regarded as a special case of the prisoner’s dilemma.
Example 2.
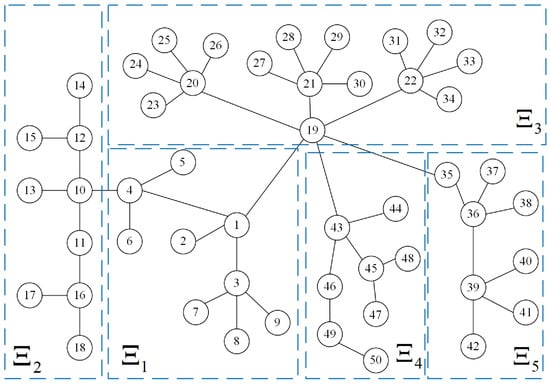
Consider an NEG whose network graph is shown in Figure 3. The policy set, payment matrix and SUR are the same as those in Example 1. Select control players to guarantee that the considered NEG achieves strategy consensus to .

Figure 3.
Network graph of the NEG in Example 2.
As shown in Figure 3, we divide the network into five parts. For subnetwork , we have
Fixing the strategy of the players in the set to be , the SPD of is obtained as
where , and . Thus, we have
where . By a simple calculation, we have . Since
according to Theorem 1, we derive that the set of control players of is
For , , the calculation process is similar to that of . To avoid redundancy, the detailed calculations are not presented here. Finally, the set of control players for the whole network is
5. Conclusions
In this paper, we analyzed the strategy consensus of large-scale NEGs via network aggregation and pinning control. Based on the semi-tensor product of matrices, we gave the algebraic form of the subnetworked evolutionary games. Then, we established a criterion for achieving strategy consensus in subnetworks and presented a control design procedure based on that criterion. Finally, by using network aggregation, we provided a sufficient condition for NEGs to achieve strategy consensus. Through the network aggregation method, the control set of a larger network can be identified by studying the properties of subnetworks, which can effectively reduce the computational complexity. In future studies, we can focus on finding the optimal aggregation method such that the number of control players in the large network is minimized.
Author Contributions
Investigation, H.L.; Writing—original draft, Z.G. and M.Q.; Supervision, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the National Natural Science Foundation of China under grants 62473239 and 62073202, and the Major Basic Research Project of Natural Science Foundation of Shandong Province under grant ZR2024ZD41.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cheng, D., He, F., Qi, H., & Xu, T. (2015). Modeling, analysis and control of networked evolutionary games. IEEE Transactions on Automatic Control, 60(9), 2402–2415. [Google Scholar] [CrossRef]
- Cheng, D., Qi, H., & Li, Z. (2011). Analysis and control of Boolean networks: A semi-tensor product approach. Springer. [Google Scholar]
- Fan, W., Wang, S., Gu, X., Zhou, Z., Zhao, Y., & Huo, W. (2021). Evolutionary game analysis on industrial pollution control of local government in China. Journal of Environmental Management, 298, 113499. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J. H., & Christakis, N. A. (2010). Cooperative behavior cascades in human social networks. Proceedings of the National Academy of Sciences of the United States of America, 107(12), 5334–5338. [Google Scholar] [CrossRef]
- Guo, Y., Zhou, R., Wu, Y., Gui, W., & Yang, C. (2019). Stability and set stability in distribution of probabilistic Boolean networks. IEEE Transactions on Automatic Control, 64(2), 736–742. [Google Scholar] [CrossRef]
- Iyer, S., & Killingback, T. (2016). Evolution of cooperation in social dilemmas on complex networks. PLoS Computational Biology, 12(2), e1004779. [Google Scholar] [CrossRef]
- Jia, Y., Li, Y., & Feng, J. (2024). Networked evolutionary game-based demand response via feedback controls. IEEE Transactions on Automation Science and Engineering, 21(2), 1638–1646. [Google Scholar] [CrossRef]
- Jiang, M., Yu, S., Yan, Y., & Zhao, Y. (2024, July 18–20). Networked evolutionary game analysis on strategy consensus under pinning control based on degree. The 2024 International Conference on Automation, Control and Robotics Engineering (pp. 17–21), Jeju Island, Republic of Korea. [Google Scholar]
- Li, H., Liu, Y., Wang, S., & Niu, B. (2021). State feedback stabilization of large scale logical control networks via network aggregation. IEEE Transactions on Automatic Control, 66(12), 6033–6040. [Google Scholar] [CrossRef]
- Li, H., & Pang, X. (2024). Stability analysis of large-scale Boolean networks via compositional method. Automatica, 159, 111397. [Google Scholar] [CrossRef]
- Li, H., & Wang, Y. (2015). Logical matrix factorization with application to topological structure analysis of Boolean network. IEEE Transactions on Automatic Control, 60(5), 1380–1385. [Google Scholar] [CrossRef]
- Li, H., Wang, S., & Li, W. (2024). Aggregation method to strategy consensus of large-size networked evolutionary matrix games. IEEE Transactions on Automatic Control, 69(6), 3975–3981. [Google Scholar] [CrossRef]
- Li, Y., Feng, J., Cheng, D., & Jia, Y. (2024). Observability decomposition of Boolean control networks under several kinds of observability. IEEE Transactions on Automatic Control, 69(2), 1340–1347. [Google Scholar] [CrossRef]
- Lin, L., Cao, J., Lu, J., Zhong, J., & Zhu, S. (2022). Stabilizing large-scale probabilistic Boolean networks by pinning control. IEEE Transactions on Cybernetics, 52(12), 12929–12941. [Google Scholar] [CrossRef]
- Liu, W., Li, C., Fu, S., & Zhao, J. (2023). Set stability of probabilistic logical networks and its application to state-based games. IEEE Transactions on Control of Network Systems, 10(3), 1581–1589. [Google Scholar] [CrossRef]
- Liu, Y., Wang, S., & Li, H. (2020, October 9–11). Two methods of dealing with largescale logical networks. The 2020 IEEE International Conference on Control and Automation (pp. 813–818), Singapore. [Google Scholar]
- Lu, J., Zhong, J., Huang, C., & Cao, J. (2016). On pinning controllability of Boolean control networks. IEEE Transactions on Automatic Control, 61(6), 1658–1663. [Google Scholar] [CrossRef]
- Nowak, M. A., & May, R. A. (1992). Evolutionary games and spatial chaos. Nature, 359(6398), 826–829. [Google Scholar] [CrossRef]
- Smith, J. M., & Price, G. R. (1973). The logic of animal conflict. Nature, 246, 15–18. [Google Scholar] [CrossRef]
- Sun, Z., Chen, X., & Szolnoki, A. (2023). State-dependent optimal incentive allocation protocols for cooperation in public goods games on regular networks. IEEE Transactions on Network Science and Engineering, 10(6), 3975–3988. [Google Scholar] [CrossRef]
- Wang, S., Chen, X., Xiao, Z., Szolnoki, A., & Vasconcelos, V. V. (2023). Optimization of institutional incentives for cooperation in structured populations. Journal of the Royal Society Interface, 20(199), 20220653. [Google Scholar] [CrossRef] [PubMed]
- Yang, X., & Li, H. (2023). Reachability, controllability, and stabilization of Boolean control networks with stochastic function perturbations. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 53(2), 1198–1208. [Google Scholar] [CrossRef]
- Yang, J., & Cho, K. H. (2016). Control of a class of large-scale Boolean networks for biological systems using constant inputs. IFAC PapersOnLine, 49(26), 300–305. [Google Scholar] [CrossRef]
- Ye, M. (2022). Distributed robust seeking of Nash equilibrium for networked games: An extended state observer-based approach. IEEE Transactions on Cybernetics, 52(3), 1527–1538. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J., Lou, J., Qiu, J., & Lu, J. (2021). Dynamics and convergence of hyper-networked evolutionary games with time delay in strategies. Information Sciences, 563, 166–182. [Google Scholar] [CrossRef]
- Zhao, G., Ma, X., & Li, H. (2024). Construction of quasi-potential games based on topological structures. IEEE Transactions on Circuits and Systems II: Express Briefs, 71(8), 3825–3829. [Google Scholar] [CrossRef]
- Zhao, Y., Kim, J., & Filippone, M. (2013). Aggregation algorithm towards large-scale Boolean network analysis. IEEE Transactions on Automatic Control, 58(8), 1976–1985. [Google Scholar] [CrossRef]
- Zhao, Y., Ghosh, B. K., & Cheng, D. (2016). Control of large-scale Boolean networks via network aggregation. IEEE Transactions on Neural Networks and Learning Systems, 27(7), 1527–1536. [Google Scholar] [CrossRef]
- Zhong, J., Ho, D. W. C., Lu, J., & Jiao, Q. (2020). Pinning controllers for activation output tracking of Boolean network under one-bit perturbation. IEEE Transactions on Cybernetics, 49(9), 3398–3408. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J., Li, B., Liu, Y., Lu, J., & Gui, W. (2021). Steady-state design of large-dimensional Boolean networks. IEEE Transactions on Neural Networks and Learning Systems, 32(3), 1149–1161. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R., Chen, Z., Zhang, Z., Liu, Z., & Zhang, J. (2022). Event-triggered control for weighted networked evolutionary games with threshold. IEEE Transactions on Circuits and Systems II: Express Briefs, 69(8), 3515–3519. [Google Scholar] [CrossRef]
- Zhu, S., Lu, J., Azuma, S., & Zheng, W. X. (2023). Strong structural controllability of Boolean networks: Polynomial-time criteria, minimal node control and distributed pinning strategies. IEEE Transactions on Automatic Control, 68(9), 5461–5476. [Google Scholar] [CrossRef]
- Zhu, S., Lu, J., Zhong, J., Liu, Y., & Cao, J. (2022). Sensors design for large-scale Boolean networks via pinning observability. IEEE Transactions on Automatic Control, 67(8), 4162–4169. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).