A Controlled Discrete-Time Queueing System as a Model for the Orders of Two Competing Companies

Abstract

We consider two companies that are competing for orders. Let $X_1\left(n\right)$ denote the number of orders processed by the first company at time n, and let $\tau \left(k\right)$ be the first time that $X_1\left(n\right)<j$ or $X_1\left(n\right)=r$, given that $X_1\left(0\right)=k$. We assume that $\{X_1\left(n\right),n=0,1,\dots \}$ is a controlled discrete-time queueing system. Each company is using some control to increase its share of orders. The aim of the first company is to maximize the expected value of $\tau \left(k\right)$, while its competitor tries to minimize this expected value. The optimal solution is obtained by making use of dynamic programming. Particular problems are solved explicitly.

1. Introduction

Many papers have been published on the optimal control of queueing systems. Often the authors assume that it is possible to control the service rate; see, for example, Laxmi et al. [1], Chen et al. [2] and Tian et al. [3]. In other papers, the aim is to control the arrival of customers into the system; see Wu et al. [4]. Sometimes, it is assumed that there are different types of customers; see Wen et al. [5] and Dudin et al. [6]. Another problem that is often considered is to determine the optimal number of servers in the system; see Asadzadeh et al. [7].

In this paper, we consider a single-server queueing model in discrete time. Orders arrive one at a time. We assume that the time needed for an order to arrive is a random variable A that follows a geometric distribution with parameter $2p_A$, so that

$$P[A=n]={(1-2p_A)}^{n-1}2p_A\mathrm{for}n=1,2,\dots$$

(1)

Moreover, the service time is a random variable S having a geometric distribution with parameter $p_S$.

There are two competing companies. In equilibrium, orders arrive at each company according to a random variable $A_i$ having a geometric distribution with parameter $p_A$, for $i=1,2$.

Instead of solving an optimal control problem, our aim in this paper is to present a stochastic dynamic game that can serve as a model for the behavior of companies competing for orders. We must, of course, make simplifying assumptions in order to obtain a mathematically tractable problem. However, we believe that the model is realistic enough to be useful.

Let $X_1\left(n\right)$ be the number of orders being processed by the first company at time n, and let

$$\tau \left(k\right)[=\tau (k,j,r)]:=inf\{n\ge 0:X_1\left(n\right)<j\mathrm{or}{X}_1\left(n\right)=r\mid X_1\left(0\right)=k\},$$

(2)

where $j\le k\le r$ and $j,k,r\in \mathbb{N}$.

Now, suppose that each company can try to use some form of control in order to increase its share of the orders. More precisely, we assume that the first company uses the control $u_n\in \{0,p_A\}$ at time n to increase the arrival rate of its orders. Similarly, the second company uses $v_n\in \{-p_A,0\}$ at time n to decrease the order arrival rate of its competitor.

Remark 1.

Writing that $v_n=-p_A$ means that Company 2 is making some efforts (for instance, by lowering its prices) in order to reduce to zero the rate at which Company 1 receives orders, unless this company also tries to increase or at least keep its share of the orders.

Let

$$p_A\left(n\right):=p_A+u_n+v_n\mathrm{for}n=1,2,\dots$$

(3)

We define the cost function

$$J\left(k\right)=\sum _{n=0}^{\tau \left(k\right)-1}\left\{q_1{u}_n^2+q_2{v}_n^2+\lambda (v_n-u_n)\right\},$$

(4)

where $q_1$, $q_2$ and $\lambda$ are positive constants. We look for the values $u_n^{*}$ and $v_n^{*}$ of the control variables that are such that the expected value of $J\left(k\right)$ is minimized.

The idea behind the cost function is as follows: since the parameter $\lambda$ is positive, if r is large, then Company 1 wants to maximize the time it stays in business. To do this, it would like to use the control $u_n=p_A$; however, this leads to quadratic control costs. Company 2, for its part, would like to use $v_n=-p_A$ in order to bankrupt Company 1 as quickly as possible, but this also entails quadratic control costs.

Problems in which the optimizers try to minimize or maximize the expected value of a certain cost function until a given random event occurs are known as homing problems. Whittle [8] considered the case when the optimizer controls an n-dimensional diffusion process until it leaves a given subset of ${\mathbb{R}}^n$. Rishel [9] also treated the homing problems for n-dimensional diffusion processes; these processes were more realistic models for the wear of devices than those proposed by various authors.

The author has recently extended homing problems to the optimal control of queueing systems in continuous time; see [10,11,12]. In these three papers, the aim was to determine the optimal number of servers working at time t. He also published a paper ([13]) on a homing problem for a controlled random walk with two optimizers.

Next, we define the value function

$$F\left(k\right)=\underset{\begin{array}{c}(u_n,v_n)\\ 0\le n\le \tau \left(k\right)-1\end{array}}{min}E\left[J\left(k\right)\right].$$

(5)

The function $F\left(k\right)$ is the expected cost incurred (which can sometimes be a reward) if both optimizers choose the optimal value of $u_n$ and $v_n$ between the initial time $n=0$ and time $\tau \left(k\right)-1$.

In Section 2, the dynamic programming equation satisfied by the value function $F\left(k\right)$ will be derived, and a particular problem will be solved explicitly. In Section 3, the problem formulation will be modified. We will then assume that the value of $u_n$ is known, and we will look for the value of $v_n$ that maximizes the expected value of a certain cost function. Concluding remarks will be made in Section 4.

2. Dynamic Programmic Equation

We will derive the dynamic programming equation satisfied by $F\left(k\right)$. We have

$$\begin{array}{ccc}\hfill F\left(k\right)& =& \underset{\begin{array}{c}(u_n,v_n)\\ 0\le n\le \tau \left(k\right)-1\end{array}}{min}\{q_1{u}_0^2+q_2{v}_0^2+\lambda (v_0-u_0)\hfill \\ & & +E\left[\sum _{n=1}^{\tau \left(k\right)-1}\left\{q_1{u}_n^2+q_2{v}_n^2+\lambda (v_n-u_n)\right\}\right]\}.\hfill \end{array}$$

(6)

Then, making use of Bellman’s principle of optimality (see [14]), we can write that

$$F\left(k\right)=\underset{(u_0,v_0)}{min}\left\{q_1{u}_0^2+q_2{v}_0^2+\lambda (v_0-u_0)+E\left[F\left(X_1\left(1\right)\right)\right]\right\}.$$

(7)

Indeed, whatever the two optimizers decide to do at time $n=0$, the decisions they make from time $n=1$ to time $\tau \left(k\right)-1$ must be optimal.

Remark 2.

Equation (7) is valid because of our assumptions that $A_i$, for $i=1,2$, and S have a geometric distribution. Indeed, as is well known, this distribution possesses the memoryless property. If we assume instead that these random variables have any other (discrete) distribution, then we will have to take the past into account, rendering the optimization problem almost intractable.

Furthermore, we have

$$\begin{array}{ccc}\hfill E\left[F\left(X_1\left(1\right)\right)\right]& =& F(k+1)p_A\left(0\right)(1-p_S)+F(k-1)[1-p_A\left(0\right)]p_S\hfill \\ & & +F\left(k\right)\left[p_A\left(0\right)p_S+[1-p_A\left(0\right)](1-p_S)\right].\hfill \end{array}$$

(8)

Hence, we can state the following proposition.

Proposition 1.

The value function $F\left(k\right)$ satisfies the dynamic programming equation (DPE)

$$\begin{array}{ccc}\hfill F\left(k\right)& =& \underset{(u_0,v_0)}{min}\{q_1{u}_0^2+q_2{v}_0^2+\lambda (v_0-u_0)\hfill \\ & & +F(k+1)p_A\left(0\right)(1-p_S)+F(k-1)[1-p_A\left(0\right)]p_S\hfill \\ & & +F\left(k\right)\left[p_A\left(0\right)p_S+[1-p_A\left(0\right)](1-p_S)\right]\}.\hfill \end{array}$$

(9)

Moreover, we have the boundary condition $F\left(k\right)=0$ if $k<j$ or $k=r$.

Remark 3.

(i) 

We take for granted that each optimizer does not know what the other has decided to do. In Section 3, we will assume that Company 2 knows the decision made by Company 1.

(ii) 

There are four possibilities for $(u_0,v_0)$: $(0,0)$, $(0,-p_A)$, $(p_A,0)$ and $(p_A,-p_A)$. If we solve the difference equation corresponding to each possible value of $(u_0,v_0)$, we actually obtain the value of the function $F\left(k\right)$ if the optimizers choose the same value of $(u_0,v_0)$ for any k. Hence, we cannot obtain the value function and/or the optimal controls for any value of k by comparing the four expressions for $F\left(k\right)$ obtained by solving the four difference equations.

(iii) 

We can write that $(u_n,v_n)=(u_n\left(k\right),v_n\left(k\right))$. The number of possible pairs $(u_0\left(k\right),v_0\left(k\right))$ for $j\le k<r$ is equal to $4^{r-j}$. If we have the values of $(u_0\left(k\right),v_0\left(k\right))$ for $k=j,\dots ,r-1$, we can solve a system of $r-j$ linear equations to obtain the corresponding values of $F\left(k\right)$ for any k. If $r-j$ is small, it is a simple matter to consider all the possible values of $(u_0\left(k\right),v_0\left(k\right))$ and compute the function $F\left(k\right)$ for $k=j,\dots ,r-1$. We can then determine the optimal controls and the associated value function.

In the following subsection, a particular problem will be solved explicitly.

An Example

Suppose that $q_1=q_2=\lambda =1$, $j=1$ and $r=3$. Moreover, we take $p_A=1/4$ and $p_S=1/2$. The values of $F\left(1\right)$ and $F\left(2\right)$ for the $4^2=16$ possible choices for $(u_0\left(1\right),v_0\left(1\right))$ and $(u_0\left(2\right),v_0\left(2\right))$ are presented in Table 1.

Table 1. Values of $F\left(1\right)$ and $F\left(2\right)$ for the 16 possible choices for the control variables.

No.	${\mathit{u}}_0\left(1\right)$	${\mathit{v}}_0\left(1\right)$	${\mathit{u}}_0\left(2\right)$	${\mathit{v}}_0\left(2\right)$	$\mathit{F}\left(1\right)$	$\mathit{F}\left(2\right)$
1	0	0	0	0	0	0
2	$p_A$	0	0	0	$-0.6$	$-0.45$
3	0	$-p_A$	0	0	$-0.375$	$-0.28125$
4	0	0	$p_A$	0	$-0.107$	$-0.4286$
5	0	0	0	$-p_A$	$-0.125$	$-0.5$
6	$p_A$	$-p_A$	0	0	$-0.923$	$-0.692$
7	$p_A$	0	$p_A$	0	$-0.75$	$-0.75$
8	$p_A$	0	0	$-p_A$	$-1.125$	$-1.5$
9	0	$-p_A$	$p_A$	0	$-0.375$	$-0.5625$
10	0	$-p_A$	0	$-p_A$	$-0.375$	$-0.75$
11	0	0	$p_A$	$-p_A$	$-0.231$	$-0.923$
12	$p_A$	$-p_A$	$p_A$	0	$-0.964$	$-0.857$
13	$p_A$	$-p_A$	0	$-p_A$	$-1.125$	$-1.5$
14	$p_A$	0	$p_A$	$-p_A$	$-1.2$	$-1.65$
15	0	$-p_A$	$p_A$	$-p_A$	$-0.375$	$-1.03125$
16	$p_A$	$-p_A$	$p_A$	$-p_A$	$-1.154$	$-1.615$

For example, if $(u_0\left(1\right),v_0\left(1\right))=(0,0)$ and $(u_0\left(2\right),v_0\left(2\right))=(0,-p_A)$ (Case no. 5), then we have $p_A\left(0\right)=p_A$ if $k=1$ and $p_A\left(0\right)=0$ if $k=2$. We must solve the system of linear equations

$$\begin{array}{}\mathrm{(10)}& \hfill F\left(1\right)& =& \frac{1}{8}F\left(2\right)+\frac{1}{2}F\left(1\right)\hfill \mathrm{(11)}& \hfill F\left(2\right)& =& -\frac{3}{16}+\frac{1}{2}F\left(2\right)+\frac{1}{2}F\left(1\right),\hfill \end{array}$$

whose solution is $F\left(1\right)=-1/8$ and $F\left(2\right)=-1/2$.

We see that the optimal strategy is to choose Case no. 14; that is, we take $(u_0\left(1\right),v_0\left(1\right))$ = $(p_A,0)$ and $(u_0\left(2\right),v_0\left(2\right))$ = $(p_A,-p_A)$.

Remark 4.

The four difference equations that must be solved, subject to the boundary conditions $F\left(0\right)=F\left(3\right)=0$, are given below. We denote their solutions by $F_i\left(k\right)$, for $i=1,2,3,4$.

(1)

$(u_0,v_0)=(0,0)$:

$$F\left(k\right)=\frac{1}{8}F(k+1)+\frac{3}{8}F(k-1)+\frac{1}{2}F\left(k\right).$$

(12)

We easily find that the solution is $F_1\left(k\right)\equiv 0$.

(2)

$(u_0,v_0)=(p_A,0)$:

$$F\left(k\right)=-\frac{3}{8}+\frac{1}{4}F(k+1)+\frac{1}{4}F(k-1)+\frac{1}{2}F\left(k\right).$$

(13)

We find that

$$F_2\left(k\right)=\frac{3}{8}k(-3+k).$$

(14)

(3)

$(u_0,v_0)=(0,-p_A)$:

$$F\left(k\right)=-\frac{3}{8}+\frac{1}{2}F(k-1)+\frac{1}{2}F\left(k\right).$$

(15)

Because $p_A\left(0\right)=0$, $X_1\left(n\right)$ cannot reach the value 3 if $k=1$ or 2. The solution that satisfies the boundary condition $F\left(0\right)=0$ is

$$F_3\left(k\right)=-\frac{3}{8}k.$$

(16)

(4)

$(u_0,v_0)=(p_A,-p_A)$:

$$F\left(k\right)=-\frac{3}{8}+\frac{1}{8}F(k+1)+\frac{3}{8}F(k-1)+\frac{1}{2}F\left(k\right).$$

(17)

We have

$$F_4\left(k\right)=\frac{3}{52}(-3+3^{k+1}-26k).$$

(18)

The functions $F_i\left(k\right)$, for $i=2,3,4$, are shown in Figure 1. Moreover, the values of $F_i\left(k\right)$ for $k=1,2$ and $i=1,2,3,4$ are presented in Table 2.

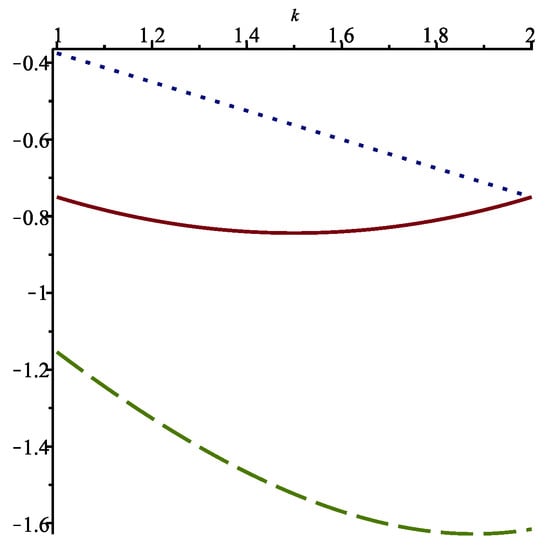
Figure 1. Functions $F_2\left(k\right)$ (solid line), $F_3\left(k\right)$ (dotted line) and $F_4\left(k\right)$ (dashed line) for $k\in [1,2]$.

Table 2. Values of $F_i\left(k\right)$ for $k=1,2$ and $i=1,2,3,4$.

i	${\mathit{F}}_{\mathit{i}}\left(1\right)$	${\mathit{F}}_{\mathit{i}}\left(2\right)$
1	0	0
2	$-0.375$	$-0.75$
3	$-0.75$	$-0.75$
4	$-1.154$	$-1.615$

Notice that $F_1\left(k\right)$ corresponds to Case no. 1, while $F_4\left(k\right)$ corresponds to Case no. 16. We observe that none of the functions $F_1\left(k\right),\dots F_4\left(k\right)$ is the value function. However, $F_4\left(k\right)$ yields values which are quite close to those obtained with the value function. Therefore, if $r-j$ is large, so that the number of equations to consider is also large, then a suboptimal solution can be obtained by assuming that $(u_0\left(k\right),v_0\left(k\right))$ will be the same for any k.

3. Optimal Control When ${\mathit{u}}_{\mathit{n}}$ Is Known

In this section, we assume that Company 2 knows the strategy of Company 1, and tries to maximize the expected value of the following cost function:

$$C\left(k\right)=\sum _{n=0}^{\tau \left(k\right)-1}\left\{q_1{u}_n+q_2{v}_n\right\}+K\left[X_1\left(\tau \left(k\right)\right)\right].$$

(19)

The terminal cost function $K(·)$ is defined by

$$K\left[X_1\left(\tau \left(k\right)\right)\right]=\left\{\begin{array}{cc}{K}_1& \mathrm{if}{X}_1\left(\tau \left(k\right)\right)=r,\hfill \\ K_2& \mathrm{if}{X}_1\left(\tau \left(k\right)\right)=j-1,\hfill \end{array}\right.$$

(20)

where $K_1<0$ and $K_2>0$. The constant $r\in \mathbb{N}$ could be the maximum number of orders that Company 1 can process at the same time.

Suppose that Company 1 uses the control $u_n\left(k\right)=p_A$ for any n and any k. Company 2 must decide whether to choose $v_n\left(k\right)=0$ or $-p_A$. We define the value function

$$V\left(k\right)=\underset{v_n,0\le n\le \tau \left(k\right)-1}{max}E\left[C\left(k\right)\right].$$

(21)

Proceeding as in the previous section, we can prove the following proposition.

Proposition 2.

The value function $V\left(k\right)$ satisfies the dynamic programming equation

$$\begin{array}{ccc}\hfill V\left(k\right)& =& \underset{v_0\in \{-p_A,0\}}{max}\{q_1{p}_A+q_2{v}_0+V(k+1)p_A\left(0\right)(1-p_S)\hfill \\ & & +V(k-1)[1-p_A\left(0\right)]p_S\hfill \\ & & +V\left(k\right)\left[p_A\left(0\right)p_S+[1-p_A\left(0\right)](1-p_S)\right]\},\hfill \end{array}$$

where $p_A\left(0\right)=2p_A+v_0$. Furthermore, the function $V\left(k\right)$ is such that $V\left(r\right)=K_1$ and $V(j-1)=K_2$.

There are now $2^{r-j}$ possible strategies for Company 2. If $r-j$ is small, we can proceed as in the previous section and calculate the expected value of $C\left(k\right)$ for each possible strategy.

Assume that $q_1=q_2=1$, $p_A=1/4$, $p_S=1/2$, $K_1=-10$, $K_2=10$, $r=5$ and $j=1$. We present in Table 3 the value of $V\left(1\right),\dots ,V\left(4\right)$ for each of the 16 possible strategies that Company 2 can choose. These values are obtained by solving the system of four linear equations

$$\begin{array}{ccc}\hfill V\left(k\right)& =& \frac{1}{4}+v_0\left(k\right)+V(k+1)\left(\frac{1}{2}+v_0\left(k\right)\right)\frac{1}{2}\hfill \\ & & +V(k-1)\left(\frac{1}{2}-v_0\left(k\right)\right)\frac{1}{2}+V\left(k\right)\frac{1}{2},\hfill \end{array}$$

(22)

for $k=1,2,3,4$, together with the boundary conditions $V\left(0\right)=-10$ and $V\left(5\right)=10$. We conclude that the optimal strategy is the one that corresponds to Case no. 15; that is, $v_0\left(1\right)=0$ and $v_0\left(k\right)=-p_A$ for $k=2,3,4$.

Table 3. Values of $V\left(1\right),\dots V\left(4\right)$ for the 16 possible choices for the control variables $v_0\left(1\right),\dots ,v_0\left(4\right)$.

No.	${\mathit{v}}_0\left(1\right)$	${\mathit{v}}_0\left(2\right)$	${\mathit{v}}_0\left(3\right)$	${\mathit{v}}_0\left(4\right)$	$\mathit{V}\left(1\right)$	$\mathit{V}\left(2\right)$	$\mathit{V}\left(3\right)$	$\mathit{V}\left(4\right)$
1	0	0	0	0	8	5	1	$-4$
2	$-p_A$	0	0	0	$8.92$	$5.69$	1.46	$-3.77$
3	0	$-p_A$	0	0	$9.36$	$7.73$	$2.82$	$-3.09$
4	0	0	$-p_A$	0	$9.56$	$8.11$	$5.67$	$-1.67$
5	0	0	0	$-p_A$	$9.29$	$7.57$	$4.86$	$1.14$
6	$-p_A$	$-p_A$	0	0	$9.45$	$7.81$	$2.81$	$-3.06$
7	$-p_A$	0	$-p_A$	0	$9.52$	$8.08$	$5.64$	$-1.68$
8	$-p_A$	0	0	$-p_A$	$9.42$	$7.68$	$4.95$	$1.21$
9	0	$-p_A$	$-p_A$	0	$10.13$	$9.26$	$6.65$	$-1.17$
10	0	$-p_A$	0	$-p_A$	10	9	6	2
11	0	0	$-p_A$	$-p_A$	$10.47$	$9.93$	$8.40$	$3.80$
12	$-p_A$	$-p_A$	$-p_A$	0	$9.72$	$8.87$	$6.31$	$-1.34$
13	$-p_A$	$-p_A$	0	$-p_A$	$9.67$	$8.69$	$5.76$	$1.82$
14	$-p_A$	0	$-p_A$	$-p_A$	$9.84$	$9.35$	$7.86$	$3.40$
15	0	$-p_A$	$-p_A$	$-p_A$	$10.49$	$9.98$	$8.44$	$3.83$
16	$-p_A$	$-p_A$	$-p_A$	$-p_A$	$9.83$	$9.34$	$7.85$	$3.39$

Remark 5.

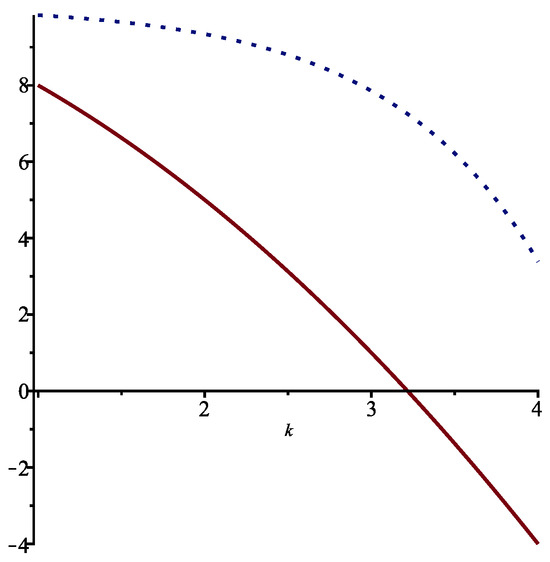
As in the previous section, we can obtain at least a suboptimal solution which is close the optimal one by solving the difference equations obtained by assuming first that $v_0\left(k\right)\equiv 0$, namely

$$\begin{array}{ccc}\hfill V\left(k\right)& =& q_1{p}_A+V(k+1)2p_A(1-p_S)+V(k-1)(1-2p_A)p_S\hfill \\ & & +V\left(k\right)\left[2p_A{p}_S+(1-2p_A)(1-p_S)\right],\hfill \end{array}$$

(23)

and then that $v_0\left(k\right)\equiv -p_A$:

$$\begin{array}{ccc}\hfill V\left(k\right)& =& q_1{p}_A-q_2{p}_A+V(k+1)p_A(1-p_S)+V(k-1)(1-p_A)p_S\hfill \\ & & +V\left(k\right)\left[p_A{p}_S+(1-p_A)(1-p_S)\right].\hfill \end{array}$$

(24)

The first equation corresponds to Case no. 1, and the second one to Case no. 16. We find that the solutions to these equations in the particular case considered above are, respectively,

$$V_1\left(k\right)=10-\frac{3}{2}k-\frac{1}{2}{k}^2$$

(25)

and

$$V_{16}\left(k\right)=\frac{1220}{121}-\frac{10}{121}{3}^k.$$

(26)

See Figure 2.

Figure 2. Functions $V_1\left(k\right)$ (solid line) and $V_{16}\left(k\right)$ (dotted line) for $k\in [1,4]$.

Notice that the solution obtained when $v_0\left(k\right)\equiv 0$ (Case no. 1) actually gives the minimum of the expected value of the cost function $C\left(k\right)$. Moreover, we see in Table 3 that the choice that corresponds to Case no. 11 almost yields the optimal solution that we are looking for.

4. Conclusions

In this paper, a homing problem for a queueing model in discrete time has been considered. The problem can be seen as a dynamic game because there are two optimizers with opposing objectives.

In Section 2, dynamic programming was used to derive the equation satisfied by the value function. From this equation, one can deduce the optimal values of the control variables. However, we have seen that, in order to do this, one has to solve a possibly large number of systems of linear equations, subject to the appropriate boundary conditions. Although solving each system is straightforward, repeating this procedure a large number of times can become tedious. We have also seen that it is possible to obtain a good suboptimal solution to our problem fairly quickly.

In Section 3, the problem formulation was modified. We assumed that the strategy of Company 1 was known, and we looked for the strategy that Company 2 should adopt to maximize the expected value of a certain cost function. We treated the case when the control variable $u_n$ is always equal to $p_A$. However, the same type of analysis could be carried out for any choice of $u_n$. In particular, we could find the optimal strategy of Company 2 if $u_n\equiv 0$.

In theory, we could easily extend the problems considered to the case when each optimizer can choose between more than two possible values for the variable it controls. The calculations would, however, become quite complex. One could possibly use numerical simulations to determine the optimal solutions. Indeed, instead of solving a large number of difference equations, simulating the proposed model can enable us to determine the optimal solution by computing the value function for each simulation. Simulating geometric random variables is not a difficult task.

Finally, it is also possible to consider optimal control problems for queueing models in continuous time with two optimizers.