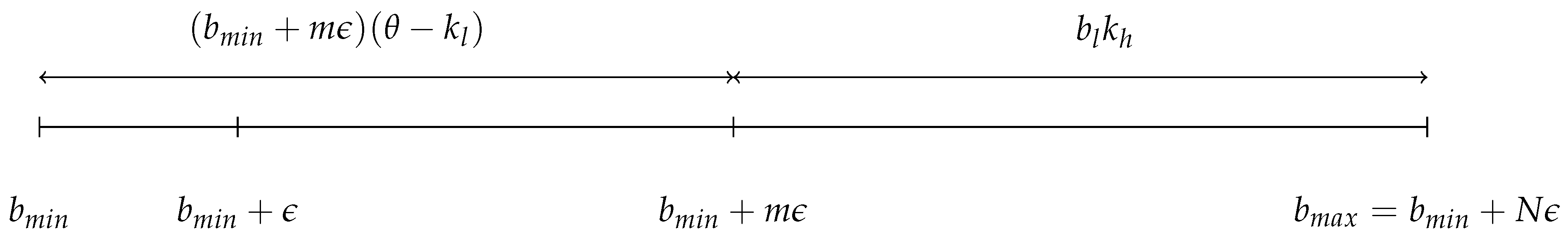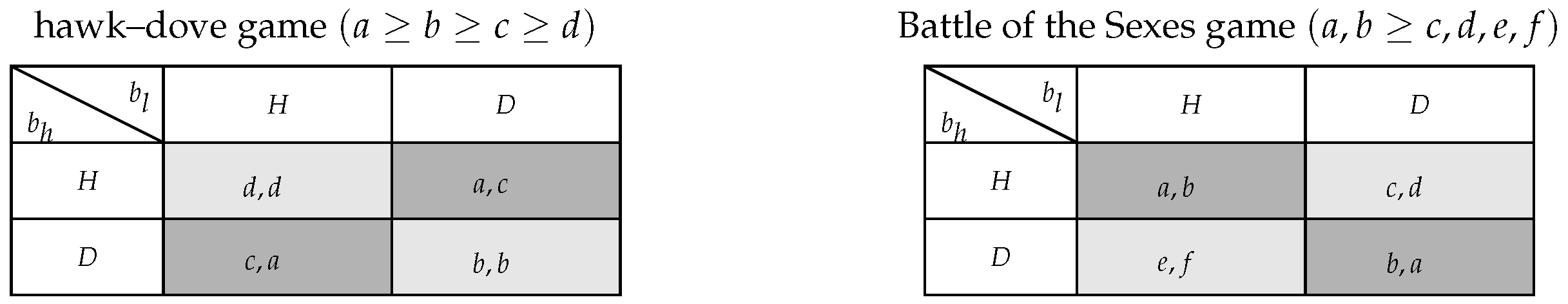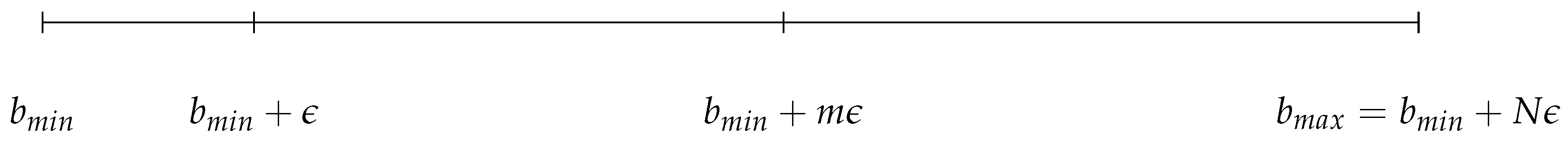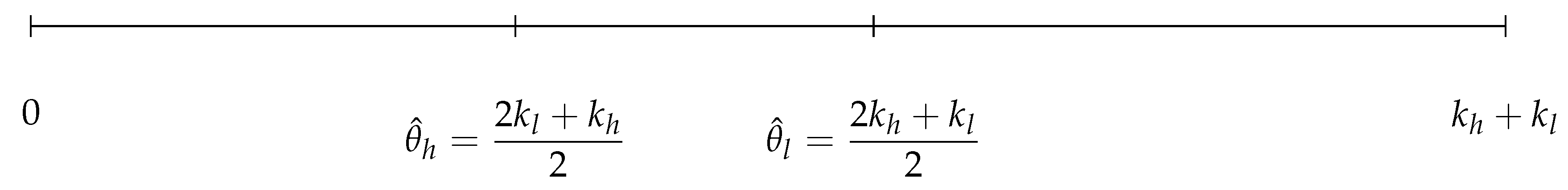1. Introduction
The hawk–dove game is one of the salient models used to study a wide range of questions in the industrial organization literature. In the classical representation of the game, players compete by using two strategies—hawk and dove. In this case, the hawk–dove game has two possible Nash equilibria in pure strategies—one of the players behaves as a hawk and the other as a dove. As both players prefer the equilibrium in which they select the hawk strategy and the opposing player selects the dove strategy, which equilibrium emerges between two individuals in any given iteration of the game is ambiguous—either of the two pure-strategy Nash equilibria could be played. To break the ambiguity associated with a multiplicity of equilibria, numerous equilibrium selection methods have been proposed.
We analyze in detail the outcome of three different equilibrium selection methods applied to a hawk–dove game in which we extend the set of strategies and consequently, the set of possible Nash equilibria. The extension of the set of strategies helps us to capture many real-world situations where the players can choose among a large strategy set. In each of those equilibria, as in the basic two-strategy hawk–dove game, one of the players behaves as a dove, the other as a hawk, and both prefer the equilibrium in which the other player selects the dove strategy. We apply the tracing procedure method of Harsanyi and Selten (1988) [
1], the robustness to strategic uncertainty method of Andersson, Argenton and Weibull (2014) [
2], and the quantal response method of McKelvey and Palfrey (1998) [
3] to predict which equilibrium is selected by the players.
We frame the hawk–dove game as a uniform-price auction
1 in which two players with asymmetric production capacities
2 compete to satisfy an inelastic demand.
3 Having observed the demand, the players simultaneously and independently submit a bid for their entire production capacity, assumed to be lower than the total demand. That is, each player faces a positive residual demand when it is dispatched last in the auction. The auctioneer establishes the maximum and the minimum bids that can be submitted in the auction. The player that submits the higher bid sets the price and satisfies the residual demand, while the player that submits the lower bid is dispatched first and satisfies the total demand at the price set by the other player. In the case of a tie, the players are dispatched in proportion to their production capacity
4.
The game described above has multiple pure-strategy Nash equilibria in which one of the players submits the maximum bid allowed by the auctioneer (dove strategy) and the opponent submits a bid that makes undercutting unprofitable (hawk strategy). As in the classic representation of the hawk–dove game, the players have opposing preferences for both sets of equilibria; each player prefers the set of equilibria in which the opposing player submits the maximum bid allowed by the auctioneer (dove strategy), since in that case the player dispatched first sells its entire production capacity at the maximum price allowed by the auctioneer.
When the demand is low or intermediate in the auction, the tracing procedure method of [
1] and the quantal response method of [
3] select the same equilibrium. When the demand is instead high, the tracing procedure method does not select any equilibrium, but the quantal response method still selects the same equilibrium as when the demand is low or intermediate. An increase in the minimum bid allowed by the auctioneer does not change the equilibrium selected, but it does worsen the coordination in the selected equilibrium when the tracing procedure is applied and makes coordination easier when the quantal response method is applied. The robustness to strategic uncertainty method proposed by [
2] selects two of the multiple equilibria irrespective of the demand size and the minimum bid allowed by the auctioneer.
In a similar setup, Boom 2008 Ref. [
8] applies the tracing procedure method to predict the equilibrium selected by the players in a uniform-price auction. The author also assumes uniform prior beliefs, but restricts the set of strategies that can be selected by the players to the strategies that are part of a Nash equilibria. By restricting the set of strategies, the author finds that with independence of the demand realization, the tracing procedure always selects the equilibrium in which the player with the higher production capacity submits the maximum bid (dove strategy), since the players always deviate to a pair of strategies that is a Nash equilibrium. In contrast, we do not restrict the set of strategies
5 and we find that the tracing procedure only selects the equilibrium in which the player with the higher production capacity submits the maximum bid (dove strategy) when the demand is low or intermediate, but when the demand is high, no equilibrium is selected by the tracing procedure. This is because the players deviate to a pair of strategies that are not a Nash equilibrium, and a miscoordination problem emerges.
Our paper is related to the industrial organization literature, which endogenizes the emergence of a price leader in duopoly models, in two respects. First, we endogenize the emergence of a price leader, in our case, in a uniform-price auction. Second, due to the multiplicity of equilibria, we also apply the tracing procedure to study which equilibrium is selected in the game. In particular, Ref. [
9] focus on a model with homogeneous products, linear demand, constant marginal cost, and with one firm being more efficient than the other. Using an endogenous timing game introduced by Hamilton and Slutksky (1990) [
10], the authors apply the tracing procedure method to show that the player with the lower production costs emerges as a leader in a Stackelberg model with a continuous set of strategies. Ref. [
11] focus on a model with price competition in a duopoly with differentiated substitutable products, linear and symmetric demand, and constant marginal cost. In contrast to the models of quantity competition, when the players compete in prices, the leadership role is not the most preferred one. This result is in line with other models of price competition with capacity constraints [
12,
13,
14].
The emergence of a price leader when applying the tracing procedure has also been studied in experimental settings. In particular, Ref. [
15] use a vertical product differentiation model with two asymmetric players, first choosing qualities and then choosing prices, in order to design an experiment with the structure of a Battle of the Sexes game. The tracing procedure method applied to their theoretical framework and their experimental results predict that the higher the degree of asymmetry of the game, the higher the predictive power of the tracing procedure method. These results are in line with our results, but in contrast to the experimental design proposed by [
15], where the players compete only by setting two prices, we provide a theoretical framework where the players compete using more than two strategies.
The hawk–dove game can also be analyzed using other approaches. Using behavioural economics, Ref. [
4] study coordination failures in a context of inequality. They study this relationship by running an experiment where the authors vary the degree of inequality and efficiency of an allocation problem. They frame the experiment as a hawk–dove game that illustrates a typical trade-off where two agents compete for the appropriation of a scarce resource, and each can choose whether to fight or accommodate. The authors find that an increase in inequality facilitates the coordination in one of the equilibria.
6 We complement their analysis using a game theoretical approach, where we apply the tracing procedure, the robustness to strategic uncertainty method, and the quantal response methods to a hawk–dove game. Following the quantum game theory approach applied to the 2008 financial crisis, Ref. [
16] finds that hawks “exhibit low entanglement with others and thus behave classically, whereas Doves exhibit higher, leading to more quantum behavior”. The analysis suggests that hawks could be induced to reduce risky, destructive trading practices by raising their entanglement.
The article proceeds as follows.
Section 2 describes the set-up, the timing, and the equilibrium of the game.
Section 3,
Section 4 and
Section 5 apply the tracing procedure method, the robustness to strategic uncertainty method, and the quantal response method, respectively, to the game and study the equilibrium selected by the players.
Section 6 concludes the paper. The proofs are in
Appendix A. In
Appendix B, we provide an example to illustrate the theoretical analysis. In
Appendix B, we also describe the algorithms that we apply in the computational simulations used in the paper. In
Appendix C, we provide a complete discussion of the tie-breaking rule and its importance in the paper.
2. Model
In this section, we present the set-up and the timing of a uniform-price auction, and we characterize the equilibrium.
Set-up: There are two players, h and l, with production capacity and , respectively, where . The level of demand, , is perfectly inelastic. Moreover, , i.e., the demand is large enough to guarantee that both players face a positive residual demand. We introduce this assumption because when the demand is very low , both players have enough production capacity to satisfy the demand individually. In that case, the resulting Nash equilibrium is unique, and selection methods are no longer useful.
Timing: Having observed the realization of demand
, each player simultaneously and independently submits a bid specifying the lowest price at which it is willing to supply up to its capacity,
,
, where
and
are determined by the auctioneer. The players can only submit bids higher than or equal to
and lower than or equal to
.
7 The number of bids in that interval (
N) is determined exogenously and it can be freely set. The minimum bid increment between one bid and the next is defined by
. Let
m be an integer between 1 and
N. The set of strategies is represented in
Figure 1.
Let
denote a bid profile. On the basis of this profile, the auctioneer calls players into operation. The output allocated to player
h (player
l’s output is symmetric), denoted by
, is given by:
8When player h submits the lower bid, it sells its entire production capacity . When both players submit the same bid, the demand is split among them in proportion to their production capacity . When player h submits the higher bid, it satisfies the residual demand .
Finally, the payments are worked out by the auctioneer. When the auctioneer runs a uniform-price auction, the price received by a player for any positive quantity dispatched by the auctioneer is equal to the higher offer price accepted in the auction. Hence, player
h’s payoffs
9 (in the paper, we write all the equations from the viewpoint of player
h; the equations for player
l follow the same structure), denoted by
, are given by:
10When player
h submits the lower bid, it sells its entire production capacity
, and player
l sets the price
. Therefore, player
h’s payoffs are
. When players
h and
l submit the same bid, the payoff is split among them in proportion to their production capacity
.
11 When player
h submits the higher bid, it satisfies the residual demand
, and it sets the price
. Therefore, player
h’s payoffs are
.
Equilibrium: The uniform-price auction described above has a multiplicity of pure-strategy equilibria defined by:
In each of the equilibria defined in Equation (
3), one player submits the maximum bid (dove strategy), and the other submits a bid that makes undercutting unprofitable (hawk strategy). When the players are asymmetric in production capacity, the set of equilibria in which the player with the higher production capacity submits the maximum bid is larger than the set of equilibria in which the player with the lower production capacity submits the maximum bid. To provide a better understanding of the uniform-price auction and the set of equilibria in that game, in
Appendix B (
Figure A4), we provide an illustrative example. That is the example that we use in all the numerical simulations in the paper.
The players have opposite preferences on both sets of equilibria. Both players prefer the set of equilibria in which the opposing player submits the maximum bid (dove strategy), since in that case the player that is dispatched first sells its entire production capacity at the highest possible price.
3. Tracing Procedure Method
In this section, we study which equilibrium is selected by the tracing procedure method when we apply it to the uniform-price auction presented in the model section [
1]. We also study the impact of an increase in the minimum bid allowed by the auctioneer on the selected equilibrium.
The tracing procedure method assumes that players’ payoffs
12 are a linear combination of the original payoff matrix and the expected payoff matrix based on players’ beliefs:
In Equation (
4),
represents the original payoff matrix for player
h (Equation (
2)), and
represents the expected payoff matrix based on player
h’s beliefs. In
,
is the probability that player
l assigns to each strategy based on player
h’s beliefs.
13 Therefore, when
, players’ payoffs are determined only by players’ expected payoff based on their prior beliefs. When
, players’ payoffs are determined only by the original payoff matrix.
In general, at
the players choose a pair of strategies that is not an equilibrium of the original game. When
t increases, the players change their strategies. At some
, the players chose a pair of strategies that is an equilibrium of the original game [
1]. That pair of strategies
) will be the equilibrium selected by the tracing procedure method. Therefore, the key point in the tracing procedure method is to find the player that first deviates to a Nash equilibrium in the original game, and to find the parameter
t for which the deviation occurs.
In Lemma 1, we analyse player h’s expected payoff when that player has uniform prior beliefs about player l’s strategies.
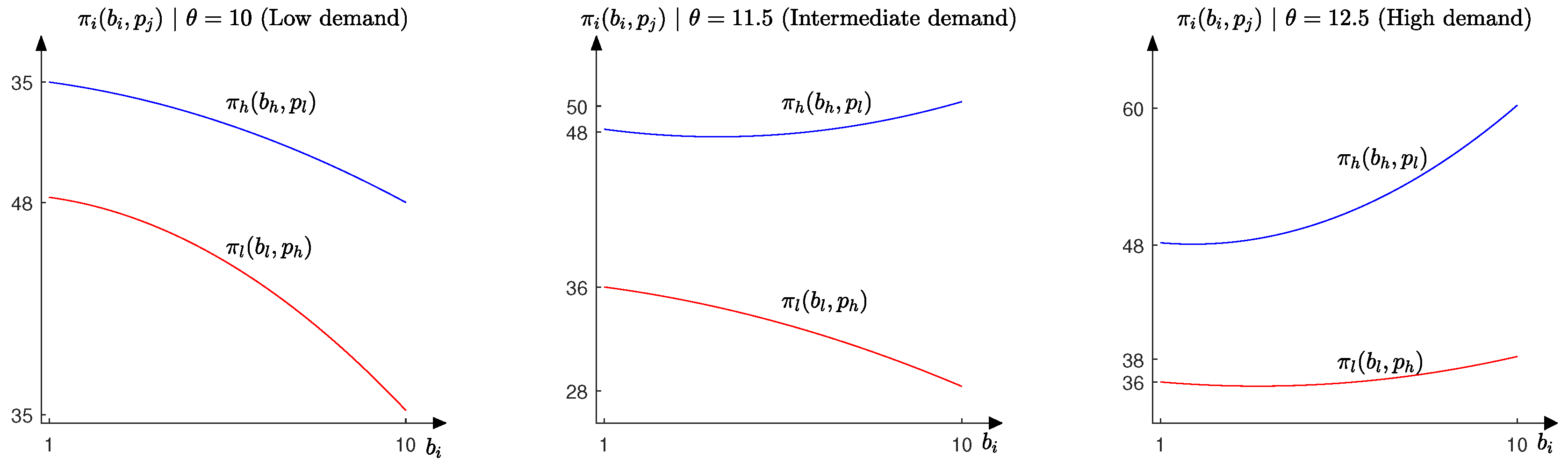
Lemma 1. When all players have uniform prior beliefs about the strategies played by other players, and when the demand is low , both players maximize their expected payoff by submitting the minimum bid. When the demand is intermediate , player h maximizes its expected payoff by submitting the maximum bid allowed by the auctioneer and player l maximizes its expected payoff by submitting the minimum bid allowed by the auctioneer. When the demand is high , both players maximize their expected payoff by submitting the maximum bid.
Lemma 1 determines the low, intermediate, and high demand thresholds (Equations (
A3)–(
A5),
Appendix A, and
Figure 2). When the demand is low
, both players maximize their expected payoff by submitting the minimum bid allowed by the auctioneer (left-hand panel,
Figure 3). When the demand is intermediate
, player
h maximizes its expected payoff by submitting the maximum bid allowed by the auctioneer and player
l maximizes its expcted payoff by submitting the minimum bid allowed by the auctioneer (central panel,
Figure 3). When the demand is high
, both players maximize their expected payoff by submitting the maximum bid allowed by the auctioneer (right-hand panel,
Figure 3). These two thresholds determine the demand for which the players prefer to submit the minimum or the maximum bid at the beginning of the tracing procedure method
. This result is formalized in Proposition 1.
Proposition 1. When , the tracing procedure method selects one of the three possible types of equilibria.
- i.
Low demand : Both players submit a bid equal to the minimum bid allowed by the auctioneer.
- ii.
Intermediate demand : The player with the higher production capacity submits the maximum bid, and the player with the lower production capacity submits the minimum bid allowed by the auctioneer.
- iii.
High demand : Both players submit a bid equal to the maximum bid.
When
, the players’ total payoffs are determined only by the expected payoffs. When the demand is low
, the players’ residual demand is very low, and it is very risky for them to submit a high bid. Therefore, both players maximize their expected payoffs by submitting the minimum bid allowed by the auctioneer (left-hand panel,
Figure 3). In this case, the equilibrium selected by the tracing procedure method when
is
. When the demand is intermediate
, the player with the higher production capacity faces a high residual demand and maximizes its expected payoff by submitting the maximum bid. In contrast, the player with the lower production capacity faces a low residual demand and maximizes its expected payoff by submitting the minimum bid allowed by the auctioneer (central panel,
Figure 3). In that case, the equilibrium selected by the tracing procedure method when
is (
). Finally, when the demand is high
, both players face a high residual demand and they maximize their expected payoff by submitting the maximum bid allowed by the auctioneer (right-hand panel,
Figure 3). In that case, the equilibrium selected by the tracing procedure method when
is
.
It is easy to check that when and the demand is intermediate, the tracing procedure method immediately selects one of the Nash equilibria in the original game. Therefore, it is not necessary to conduct further analysis. In contrast, when and the demand is low or high, the players do not select one of the Nash equilibria in the initial game, and it is necessary to determine which player deviates first to a Nash equilibrium in the original game and to find the parameter t for which that player deviates to the equilibrium. Proposition 2 formalizes this analysis.
Proposition 2. When the demand is low or intermediate , the tracing procedure method selects the equilibrium in which the player with the higher production capacity submits the maximum bid, and the player with the lower production capacity submits the minimum bid allowed by the auctioneer. When the demand is high , no equilibrium is selected by the tracing procedure method.
According to Proposition 1, when
and the demand is low, both players submit the minimum bid allowed by the auctioneer (left-hand panel,
Figure 3). When
, the players assign more weight to the original payoff matrix
, and one of the players has incentives to deviate by raising its bid. Given that for the same pair of strategies
,
, player
h deviates first. Once player
h raises its bid, player
l is better off for two reasons: first, because it maximizes its expected payoffs
, and second, because it sells its entire production capacity for a higher price. When
t increases, player
h continues raising its bid until the equilibrium
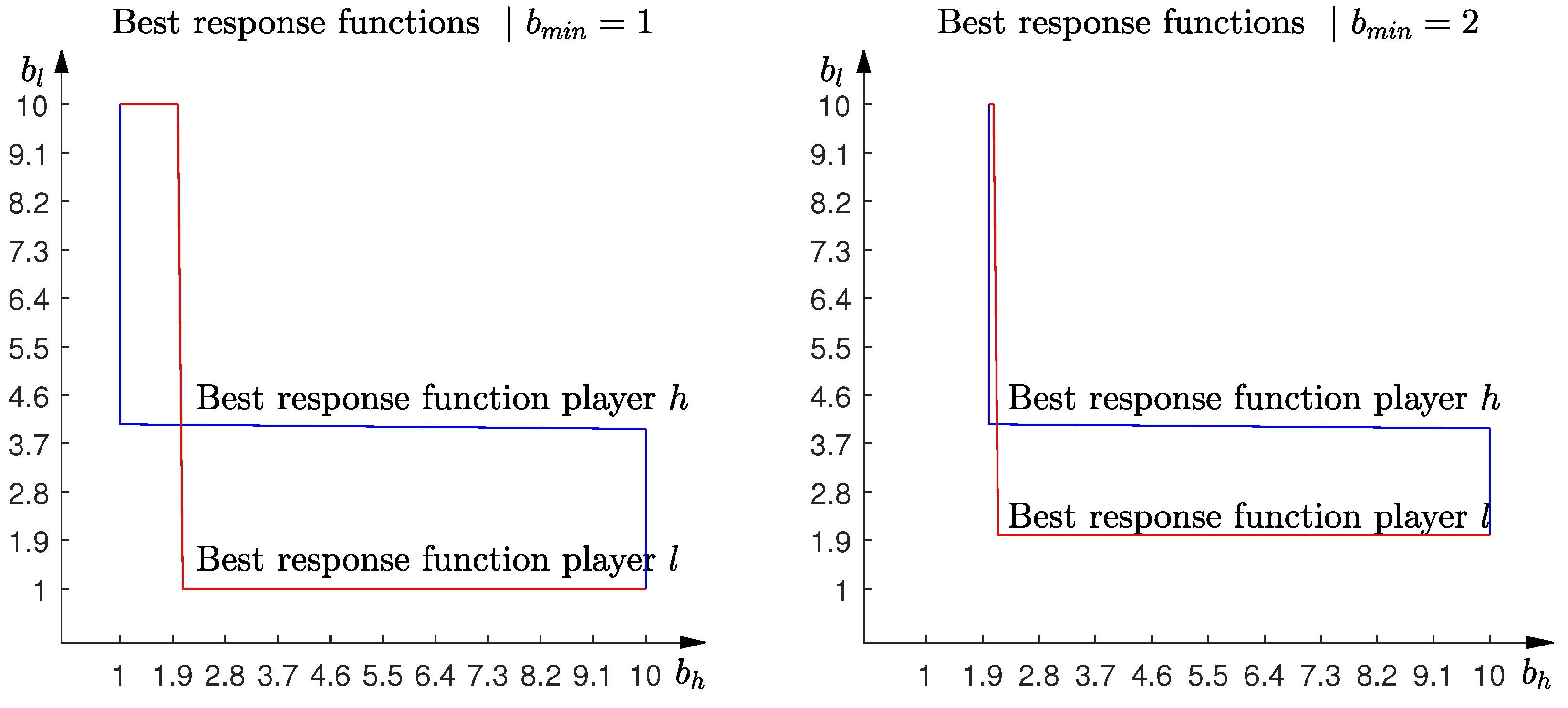
is selected (left-hand panel,
Figure 4).
According to Proposition 1, when
and when the demand is intermediate, the tracing procedure method selects the equilibrium
, i.e., it selects an equilibrium in the original game (central panel,
Figure 3). Therefore,
is the equilibrium selected by the tracing procedure, since the players do not deviate when
t increases.
According to Proposition 1, when
and the demand is high, both players submit the maximum bid allowed by the auctioneer (right-hand panel,
Figure 3). When
, the players assign more weight to the original payoff matrix
, and one of the players has incentives to deviate by decreasing its bid, since by doing so it will be dispatched first, selling its entire production capacity at the maximum bid allowed by the auctioneer. In contrast to the case when the demand is low, the player that does not deviate is worse off, since it will serve the residual demand. Therefore, it has incentives to undercut the other player, initiating a price war. It is important to note that the price war does not select any equilibrium, since at some
, one of the players has incentives to submit the maximum bid allowed by the auctioneer generating cycles and not selecting any equilibrium. This contrasts with [
8], where the players always deviate to one equilibrium, since in that paper, the set of strategies is restricted to the strategies that belong to the equilibrium.
We conclude this section by studying the impact that an increase in the minimum bid allowed by the auctioneer has on the equilibrium selected by the tracing procedure method.
Proposition 3. When the demand is low ,14 an increase in the minimum bid allowed by the auctioneer has two effects on the convergence to the equilibrium. - i.
The parameter t for which the players deviate from the equilibrium when increases.
- ii.
The parameter t for which the players coordinate in one of the Nash equilibria of the original game increases.
An increase in the minimum bid allowed by the auctioneer makes submitting a low bid more attractive, since in this case, both players split the demand in proportion to their production capacity at a higher price. Therefore, the parameter
t that makes them deviate from the equilibrium
in the tracing procedure method when
increases. As can be observed in the left-hand side of
Figure 4, when the minimum bid allowed by the auctioneer is low, the parameter
t for which the players coordinate in one of the equilibria of the game is
. However, as can be observed in the right-hand panel of that figure, when the minimum bid allowed by the auctioneer increases to
, the corresponding value of
t is
.
In the numerical simulations, we have also observed that the bid that makes players indifferent between submitting the minimum bid and deviating to a higher bid also increases. Therefore, when the players deviate from the original equilibrium in the tracing procedure method, they deviate by submitting a higher bid. As can be observed in the left-hand panel in
Figure 4, when the minimum bid allowed by the auctioneer is low
, the player with the higher production capacity deviates first by increasing its bid to
. However, as can be observed in the right-hand panel of that figure, when the minimum bid allowed by the auctioneer increases to
, the player with the higher production capacity deviates by increasing its bid to
.
The theoretical results in Proposition 3 have important welfare implications, since an increase in the minimum bid makes coordinating in one of the equilibria of the game more difficult for the players. Therefore, the expected equilibrium price can be lower, since the players do not coordinate in one of the equilibria in which the equilibrium price is equal to the maximum bid.
4. Robustness to Strategic Uncertainty Method
In this section, we study which equilibrium is selected by the robustness to strategic uncertainty method when we apply it to the uniform-price auction presented in the model section [
2]. We also study the impact of an increase in the minimum bid allowed by the auctioneer in the selected equilibrium.
The robustness to strategic uncertainty method proposes that players face some uncertainty about the strategies played by other players. Player
h’s uncertainty about player
l’s strategy is modeled as follows:
where the random variables
are statistically independent.
Equation (
5) can be interpreted as follows: player
h thinks that player
l will play strategy
plus some random perturbation. When the uncertainty parameter (
t-parameter) goes to zero, the players do not face any uncertainty.
For
, the random variable
has a probability density defined by:
In line with [
2], the profit function
15 is defined by:
A pair of strategies
is a t-equilibrium of the game if
and
maximize (
6). Therefore, to find the t-equilibrium of the game, it is enough to work out the best response functions and to find the intersection between them.
If we apply Equation (
6) to the payoff function in the uniform-price auction model defined by Equation (
2), we obtain:
where
is the cumulative distribution function of
. The first term in Equation (
7),
, represents player
h’s expected payoff when it submits the lower bid in the auction. With probability
, player
h submits the lower bid in the auction. In that case, player
l sets the price (
), and player
h sells its entire production capacity (
). The second term in Equation (
7),
, represents player
h’s expected payoff when it submits the higher bid in the auction. With probability
, player
h submits the higher bid in the auction. In that case, player
h sets the price (
) and satisfies the residual demand
.
Using Equation (
7), it is easy to work out one player’s expected payoff given the strategy of the other player. In particular, we set
and vary
between
and
. Knowing that the random variable
has a probability density defined by
, and if, as in [
2], we assume that
, we work out player
h’s expected payoff
, and we choose
that maximizes that payoff. Repeating that process for every
, we work out player
h’s best response function. Using the same approach, we work out player
l’s best response function. The intersection between both players’ best response functions determines the equilibrium selected by the robustness to strategic uncertainty method.
In
Figure 5, we plot the players’ best response functions. When one player submits a low bid, the best strategy for the other player is to submit a high bid. The players shift from low to high bids when the opponent player submits a bid around the threshold that determines the set of Nash equilibria (Equation (
3)). The intersection of the best response functions selects two of the Nash equilibria in the original game. In each of these two equilibria, one player submits the maximum bid and the other player submits the minimum bid allowed by the auctioneer.
We conclude this section studying the impact that an increase in the minimum bid allowed by the auctioneer has on the equilibrium selected by the robustness to strategic uncertainty method. An increase in the minimum bid allowed by the auctioneer reduces the set of Nash equilibria (right-hand panel,
Figure 5). However, the equilibrium selected by the robustness to strategic uncertainty method does not change. As in the case when the minimum bid allowed by the auctioneer is lower, the robustness to strategic uncertainty method selects the equilibria in which one player submits the minimum bid and the other player submits the maximum bid (right-hand panel,
Figure 5).
5. Quantal Response Method
In this section, we study which equilibrium is selected by the quantal response method when we apply it to the uniform-price auction presented in the model section [
3]. We also study the impact of an increase in the minimum bid allowed by the auctioneer in the selected equilibrium.
The quantal response method assumes that the players choose among the strategies in the game based on their relative expected payoff. The key idea is that when the players calculate their expected payoff, they make calculation errors according to some random process. Based on that random process, the players assign more probability to the strategies that give a higher expected payoff. The Nash equilibrium in the quantal response method is the set of probabilities for which none of the players wants to deviate. Formally, the Nash equilibrium in the quantal response method is defined as follows: Given , a sequence such that , and , a corresponding sequence with for all t such that , then is a Nash equilibrium.
In their seminal paper, [
3] use the logistic quantal response function. That specific function is a particular parametric class of quantal response functions that has a long tradition in the study of individual choice behaviour. The logit equilibrium correspondence is the correspondence
given by:
where the term in the numerator
is one of the players’ expected payoff when it selects strategy
i and the other player selects strategy
j.
16 The term in the denominator
is the sum of one of the players’ expected payoff when it selects strategy
i and the other player selects all the strategies in its set of strategies. Therefore, by using Equation (
8), each player assigns more probability to the strategies that give it a higher expected payoff.
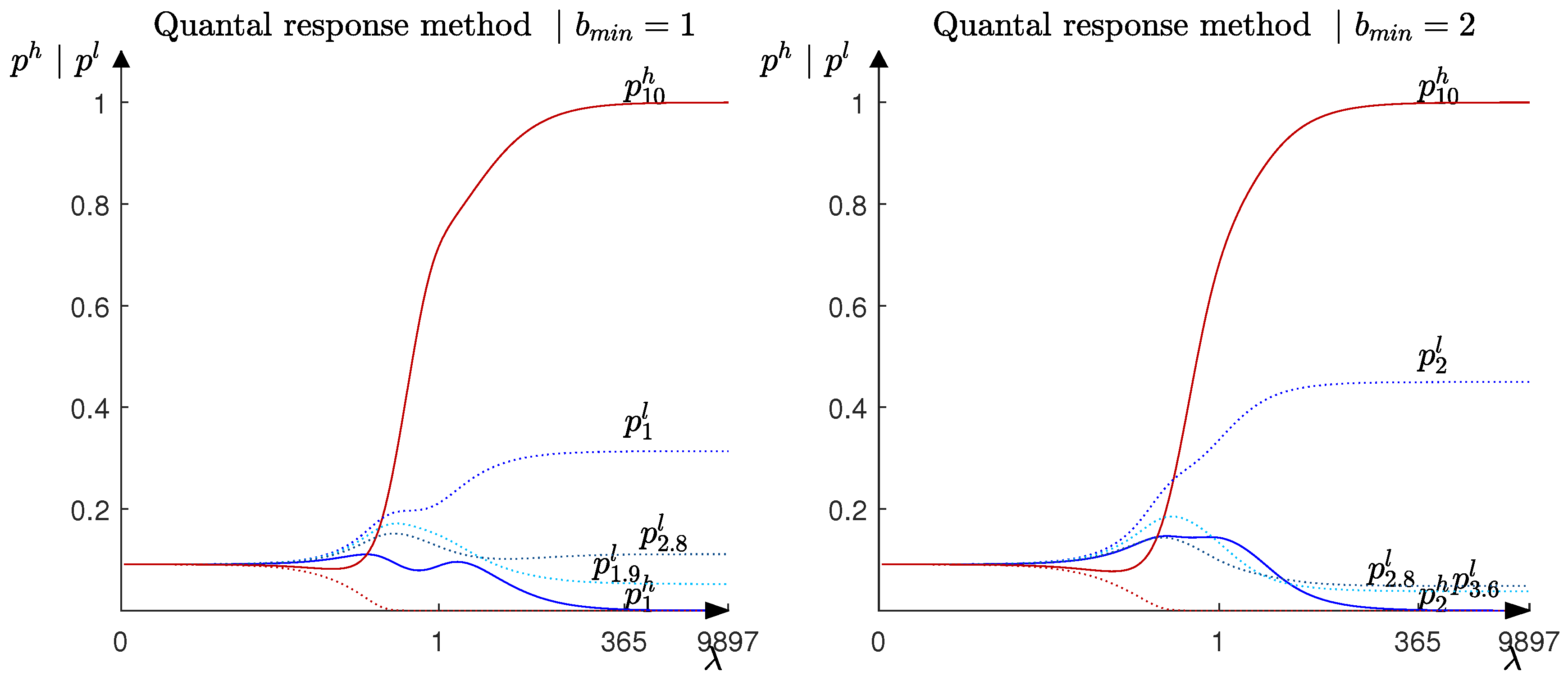
When we apply the quantal response method to the uniform-price auction presented in the model section, we observe that the player with the higher production capacity (player
h) plays the maximum bid with a probability close to one (continuous red line
) and the minimum bid with a probability close to zero (continuous blue line
). In contrast, the player with the lower production capacity (player
l) assigns higher probabilities to the lower bids (discontinuous blue line
,
,
) (left-hand panel,
Figure 6)
17.
The equilibrium selected by the quantal response method is in line with the equilibrium selected by the tracing and the robustness to strategic uncertainty methods. Moreover, the pattern that appears in the equilibrium selected by the quantal response method is very similar to the pattern that appears in the other two methods, since in the three methods the players tend to select extreme strategies. In particular, the player with the higher production capacity submits the maximum bid and the player with the lower production capacity submits the lower bids in the strategies supported with higher probabilities. Moreover, the quantal response method shows similarities to the tracing procedure method, since the quantal response method defines a unique selection from the set of Nash equilibria by “tracing” the graph of the logit equilibrium correspondence beginning at the centroid of the strategy simplex (the unique solution when ) and continuing for larger and larger values of .
We conclude this section by analyzing the effect that an increase in the minimum bid allowed by the auctioneer has on the equilibrium selected by the quantal response method. After an increase in the minimum bid allowed by the auctioneer, player
h assigns probability one to the maximum bid allowed by the auctioneer and player
l assigns higher probabilities to the lower bids in the strategies’ support (left-hand panel,
Figure 6). An increase in the minimum bid does not change the strategy of the player with the higher production capacity, since it still faces a high residual demand and does not change its strategy (continuous red line
), but makes it more attractive for the player with the lower production capacity to submit lower bids, since for that player, the expected payoff associated with low bids increases (discontinuous blue lines
,
,
).
18 Therefore, an increase in the minimum bid allowed in the auction facilitates the coordination in the equilibrium of the game where the player with the higher production capacity submits the maximum bid allowed by the auctioneer. This contrasts with the results that we obtain when we apply the tracing procedure method, where an increase in the minimum bid allowed by the auctioneer reduces the possibilities that the players coordinate in that equilibrium.
6. Conclusions
Hawk–dove games are widely used in the industrial organization literature. Such games have a multiplicity of Nash equilibria. In each of those equilibria, one of the players submits the maximum bid (dove strategy) and the other player submits a bid that makes undercutting unprofitable (hawk strategy). By framing the hawk–dove game as a uniform-price auction, we apply the tracing procedure method [
1], the robustness to strategic uncertainty method [
2], and the quantal response method [
3] to predict which equilibrium is selected by the players. We also analyze the impact of an increase in the minimum bid allowed by the auctioneer on the equilibrium selection.
The equilibrium selected by the tracing procedure method proposed by [
1] depends crucially on the realization of the demand. When the demand is low or intermediate, the tracing procedure method selects the equilibrium in which the player with the higher production capacity submits the maximum bid (dove strategy) and the player with the lower production capacity submits the minimum bid allowed by the auctioneer (hawk strategy). When the demand is high, the tracing procedure method does not select any equilibrium. This contrasts with [
8], where the tracing procedure method always selects the equilibrium in which the player with the higher production capacity submits the maximum bid (dove strategy). When the auctioneer increases the minimum bid allowed in the auction, the equilibrium selected by the players does not change, but the coordination in that equilibrium is more difficult.
The robustness to strategic uncertainty method proposed by [
2] selects the two equilibria in which one of the players submits the maximum bid (dove strategy) and the other player submits the minimum bid allowed by the auctioneer (hawk strategy). When the auctioneer increases the lower bid allowed in the auction, the equilibria selected by the players do not change.
The quantal response method proposed by [
3] predicts that the player with the higher production capacity submits the maximum bid (dove strategy) with probability one and the player with the lower production capacity submits the lower bids in the strategy set with higher probabilities (hawk strategy). An increase in the minimum bid allowed by the auctioneer does not change the strategy of the player with the higher production capacity, but increases the probability that the low-production-capacity player assigns to the minimum bid, and the coordination in one of the equilibria of the game is easier.
The theoretical results that we present in this paper contribute to the industrial organization literature that endogenize the emergence of a price leader in duopoly models. We also extend the literature of hawk–dove games, since, in our paper, the players can choose among a large set strategies.
The theoretical analysis that we have developed also gives us the opportunity to compare the equilibrium played in a uniform-price auction with the one played in a discriminatory-price auction. Therefore, the theoretical framework that we develop could be useful for comparing the results among different auction types.
We have discussed that there appears to be no clear consensus in the literature on the definition and the relationship between “hawk–dove” and “Battle-of-Sexes” games. In this paper, we assume that a game has the structure of a “hawk–dove” game when it follows the structure presented in [
7], and we applied three different equilibrium selection methods to it. The analysis in our paper is useful in fostering research into the relationship between the “hawk–dove” and “Battle-of-Sexes” games and the equilibrium that emerges in these games. We leave that analysis for future research.