Abstract
The Global Malmquist Productivity Index (GMPI) stands as an evolution of the Malmquist Productivity Index (MPI), emphasizing global technology to incorporate all-time versions of Decision-Making Units (DMUs). This paper introduces a novel approach, integrating the Nash Bargaining Game model with GMPI to establish a Cross-Productivity Index. Our primary objective is to develop a comprehensive framework utilizing the Nash Bargaining Game model to derive equitable common weights for different time versions of DMUs. These weights serve as a fundamental component for cross-evaluation based on GMPI, facilitating a holistic assessment of DMU performance over varying time periods. The proposed index is designed with essential properties: feasibility, non-arbitrariness concerning the base time period, technological consistency across periods, and weight uniformity for GMPI calculations between two-time versions of a unit. This research amalgamates cross-evaluation and global technology while employing geometric averages to derive a conclusive cross-productivity index. The core motivation behind this methodology is to establish a reliable and fair means of evaluating DMU performance, integrating insights from Nash Bargaining Game principles and GMPI. This paper elucidates the rationale behind merging the Nash Bargaining Game model with GMPI and outlines the objectives to provide a comprehensive Cross-Productivity Index, aiming to enhance the robustness and reliability of productivity assessments across varied time frames.
1. Introduction
Data Envelopment Analysis (DEA) has been introduced as a tool for evaluating the performance of homogeneous and similar Decision-Making Units (DMUs). Since then, numerous theoretical and practical developments have been presented for this mathematical programming-based technique, and various topics have been discussed in its scope. One of these topics in the context of evaluating the performance of DMUs is the development of performance appraisal indexes over time, such as the Malmquist, Laspeyres, Paasche, Fisher, Tornqvist, and Hicks-Moorsteen [1]. Among these indexes, the Malmquist Productivity Index (MPI) has received considerable attention and has been the subject of numerous studies in this area.
The MPI, proposed by Caves et al. [2], is based on the first-period technology for performance appraisal. By using the fixed period as the fundamental technology, the MPI maintains certain desirable properties such as consistency in calculating the MPI due to the same basis, transitivity, and circularity. However, the choice of the base time period is arbitrary, and other time periods are not taken into consideration. To address this issue, various suggestions have been proposed, such as using the geometric mean of the MPIs obtained by considering both time periods as the basis [3], and using global technology.
The concept of global technology as the benchmark technology for evaluating the performance of DMUs over time was first added to the MPI concepts at DEA by [4]. The use of this technology as a set of all time versions of all DMUs led to the introduction of the Global Malmquist Productivity Index (GMPI). This index has features such as feasibility, independence of results from different technologies, circularity, and consistency. Consistency means that the basis for calculating the index is the same for different DMUs, which makes the DMUs comparable based on the scores. But the consistency of [4]’s GMPI was only linked to the technology used. The authors of [5] pointed out a kind of inconsistency in this index, which is the possibility of using different weights to calculate the GMPIs of different DMUs. Geometrically, not only different DMUs, but even different time versions of a DMU, can use a different hyperplane of the global technology as the benchmark. To address such inconsistencies, ref. [5] proposed a method involving a Common Weight (CW) for all DMUs across all times, aiming to mitigate disparities arising from varied technologies and support hyperplanes. However, this method showed limitations, lacking peer evaluation and being heavily reliant on weight selection.
Cross-evaluation can also be chosen as an intermediary solution for dynamic evaluation of DMUs: between full weight freedom in [4], and full weight limitation of all DMUs to a CW in [5]. Ding et al. [6] used the concept of cross-evaluation in calculating MPI. However, this applies exclusively to global technology, and cross-evaluation is utilized solely for identifying efficiencies, not productivity indexes. In the conventional MPI formula, only Cross-Efficiency (CE) scores replace the efficiency scores of conventional DEA models. Additionally, the weights used in evaluations are not common, introducing a challenge of inconsistency. In addition, the function used to aggregate performance is of an arithmetic type that is not compatible with MPI studies in the use of geometric functions. Homayoni et al. [7] proposed a cross-productivity index to address the issues identified in [6], where the weights from self-evaluation and peer evaluation were used directly in the productivity index calculation. However, the problem of inconsistency still exists, as the efficiencies in their MPI ratio are calculated based on different weights.
In this paper, we introduce a methodology for calculating GMPIs that addresses the limitations of previous approaches. We consider the global technology set, comprised of all DMUs in two different time periods, as the benchmark. To ensure fair evaluation and account for DMUs’ preferred weights, we suggest using several CWs for self and peer evaluation, instead of relying on just one CW. For both time versions of a DMU, we obtain a CW and use it to calculate the GMPI of that DMU and others.
Due to the competitive nature of the DEA evaluation process, we employ the Nash bargaining game model with suitable breakdown points to establish fair CWs. This cooperative model is formulated to simultaneously maximize the utility of all participants. Additionally, it results in a Pareto-optimal solution, which motivates players to accept it. We create a cross-evaluation matrix containing values of self and peer productivity and aggregate the GMPIs using the geometric mean to maintain the multiplicative structure at the aggregate level. This approach overcomes the inconsistency issue of previous methods and provides a more acceptable evaluation of DMUs. Furthermore, our method accounts for DMUs’ preferences and ensures fairness in the evaluation process.
After examining the literature on CW and MPI in DEA, it is apparent that no attempt has been made to obtain a CW for the time versions of a DMU. Furthermore, no study has yet calculated a GMPI matrix. A review of the literature also suggests that game theory has not been used to generate productivity indexes in DEA.
The proposed integrated framework of GMPI, CW, Nash bargaining, and cross-evaluation allows the constructed GMPI to possess certain properties. The use of a CW in calculating the efficiencies of time versions of a DMU ensures that the GMPI fraction is well defined and consistent across all DMUs. The use of global technology ensures that the models used to estimate efficiencies are always feasible [4]. Additionally, both self-evaluation and peer evaluation are considered, resulting in an aggregated GMPI that inherits the desired cross-evaluation features. This includes reducing the dependence of results on a particular weight, increasing stability and reality, avoiding overestimation, being fair due to the use of desired weights of each unit, and reflecting reality more accurately.
The paper is structured as follows. The second section offers an overview of essential background information. In the third section, we introduce the proposed method along with its properties, and the fourth section presents an examination of the method through a numerical example. Finally, the last section presents our conclusions and suggestions for future research.
2. Preliminaries
In this section, we provide a brief overview of some fundamental concepts and principles of DEA and game theory that are necessary for understanding the proposed method. For ease of reference, all the symbols and abbreviations used throughout the paper are compiled in Table 1.

Table 1.
The abbreviations and nomenclatures used in this paper.
2.1. Cross-Efficiency
The cross-evaluation method, introduced by [8,9], utilizes peer evaluation in addition to self-evaluation, establishing various sets of input and output weights for each DMU and computing its efficiencies based on all these weight combinations. Consequently, each DMU will obtain multiple distinct efficiency scores, and the average portrays the comprehensive performance of the DMU. DMUs can then be compared and ranked based on average cross-efficiencies, that exhibit robust discrimination capabilities and adhere to reasonable logic. The DEA literature has extensively studied cross-efficiency, with recent studies including [10,11,12,13,14,15,16,17].
Employing the conventional notation in DEA, we consider a set of n DMUs to be evaluated based on m inputs and s outputs. Each DMU is denoted as DMUj = (Xj, Yj) (j = 1, …, n), where Xj = (x1j, …, xmj) and Yj = (y1j, …, ysj) represent the input and output vectors of DMUj, respectively.
The efficiency rating for any given DMUo can be computed using the following ratio form of the CCR model [18]:
uo and vo represent the vectors of output and input weights of DMUo, respectively. This problem is solved by sequentially evaluating the efficiency of each DMU, altering it as the unit under evaluation, resulting in n evaluations to determine the relative efficiency of all DMUs. The efficiency score ranges from 0 to 1, with DMUs scoring 1 considered efficient and those scoring less than 1 considered inefficient.
When the most preferred weights obtained by model (1) for a given DMUj (rating DMU) are employed to compare the efficiency score for another DMUo (rated), the so-called cross-efficiency value is:
The resulting cross values between each DMU can be collected and arranged in a Cross-Efficiency Matrix (CEM), as shown in Table 2. The entries in column ‘o’, which correspond to the rated DMUo, represent the evaluations obtained by using the preferred weights of all n DMUs. These evaluations include the self-evaluation (based on its own weights) and the evaluations based on the weights of n − 1 other DMUs (peer-evaluation). On the other hand, the entries in row j represent the evaluations of all DMUs based on the preferred weights of rating DMUj. The efficiency values evaluated for each DMU with respect to itself are positioned on the main diagonal of the CEM.

Table 2.
Cross-Efficiency Matrix.
The cross-efficiency score of DMU0 is typically computed as the average of its cross-efficiencies using (3):
2.2. Malmquist Productivity Index
The Malmquist Productivity Index (MPI) is a widely used tool in productivity analysis, particularly in DEA. The MPI evaluates and compares productivity changes across DMUs over time. Essentially, the MPI gauges productivity changes by examining shifts in the efficiency frontier or best practice technology across different time periods. It allows analysts to measure changes in productivity by considering both technological progress and efficiency improvements. This method compares the efficiency of DMUs between different time periods, reflecting alterations in technology or efficiency enhancements within DMUs.
Consider the performance evaluation and productivity change for n DMUs at two times, t and t + 1. Let and represent the efficiencies of unit o at time t relative to the technology frontier of time t and t + 1, respectively. Similarly, and denote the efficiencies of this unit at time t + 1 relative to the technological boundaries of time t and t + 1. The efficiencies are computed using model (1). The MPI is defined as follows:
Less, more, and equal MPI values of 1 indicate regress, progress, and zero productivity change over time t and t + 1, respectively.
The MPI has undergone numerous theoretical advancements since its inception, all geared toward refining its application and augmenting its analytical prowess within the realm of productivity analysis. Table 3 encapsulates a selection of these theoretical extensions of the MPI.

Table 3.
Theoretical extensions of MPI.
2.3. Game Theory
Game theory is a mathematical framework that helps analyze decision making and strategic interactions between different individuals or groups. Cooperative game theory, a subset of game theory, centers on scenarios in which players can unite and collaborate to attain their goals. In cooperative games, players can agree on how to distribute the payoff among themselves, which is the essence of the bargaining method. The bargaining method is a cooperative game theory solution concept that provides a way to allocate the gains from cooperation among the players.
The bargaining method assumes that players negotiate a cooperative solution that maximizes the sum of their payoffs. The solution must be feasible, meaning that it should lie within the players’ negotiation range. The negotiation range is determined by the players’ reservation values, which are the minimum payoffs they are willing to accept. The bargaining method provides different solutions depending on the negotiation process, such as the Nash bargaining solution, the Kalai-Smorodinsky solution, and the egalitarian solution.
Assuming n players, denoted as {1, …, n}, engage in a bargaining scenario, where the payoff vector is represented as an element in Rn. Here, Rn signifies the feasible set and serves as the breakdown point. According to [73], a reasonable solution in bargaining should adhere to fundamental properties in bargaining theory. These properties encompass: Pareto efficiency, ensuring that no participant can be made better off without making another participant worse off; invariance concerning affine transformations, implying the solution remains unchanged despite linear transformations; independence of irrelevant alternatives, asserting that the chosen solution remains consistent irrespective of irrelevant options; and symmetry, signifying the equitable treatment of all participants. The authors of [73] demonstrated the existence of a unique solution satisfying these four properties, referred to as the Nash solution. The Nash solution can be derived by maximizing where ui and bi are the elements of u and b, respectively. This involves selecting a vector from the feasible solutions of the game that maximizes the product of the differences between each player’s desired utility and their respective breakdown points, with the less desirable point serving as the breakdown.
The combination of game theory and DEA has been explored in various studies, which aim to evaluate the efficiency of decision-making units. The use of game theory models can help capture the strategic interactions between the units, while DEA can measure their efficiency. Table 4 summarizes the findings of some of these studies and their contributions to the field. Overall, the combination of game theory and DEA can provide a comprehensive framework to analyze decision-making processes in complex and dynamic environments.

Table 4.
A literature review on DEA-Game.
3. Cross Common Weights Global Malmquist Productivity Index Based on Bargaining Games
3.1. Motivation through a Numerical Example
In this section, our focus is on delineating the motivation behind the proposed method by utilizing a hypothetical example. Our aim is to explicate the methodology for computing the GMPI through the lens of a straightforward numerical illustration. To embark on this, we will delve into a dataset encompassing 8 DMUs, each characterized by two inputs and one output, assessed at two distinct time points: t and t + 1. At time t, these DMUs are denoted as A through G, while at time t + 1, they are represented as A’ through G’. The pertinent data concerning these DMUs is delineated in Table 5, laying the foundation for our illustrative example.

Table 5.
Data for numerical example.
The technology of the 8 DMUs in two time periods and two-dimensional space is presented in Figure 1. The constant return to scale technology is depicted with the bold (black) border, which represents the t-time technology frontier. DMUs A, B, D, E, and F are located on this frontier. The faint (orange) frontier with points A’, D’, and E’ on it represents the technology boundary of time t + 1. Directional vectors are included in the figure to indicate the change in state of the DMUs from time t to t + 1.
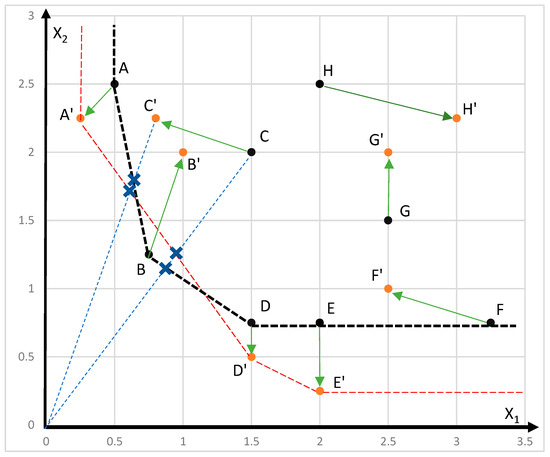
Figure 1.
Two-time technology comparison for numerical example DMUs.
To gauge the performance change of unit C, traditionally, analysts employ the geometric mean of efficiency between C’ and C at both time points, t and t + 1, within the framework of the MPI. The MPI serves as a customary measure for assessing productivity alterations over time. In this context, efficiencies are computed by measuring the radial distance between the under-evaluated DMU and its radial projection onto the frontiers, to the origin. In Figure 1, the cross signs mark the projections of point C and C’ on the frontiers of times t and t + 1. The projection points on the time t frontier lie on the line segments AB and BD, while the projection points on the time t + 1 frontier lie on the segment A’D’. There are four projection points and three different faces, which means that the performance of unit C is calculated based on the distance to different bases or different supporting hyper-planes of the two-time technologies. This leads to the use of different normal vectors and different input and output weights for calculating the corresponding performance of a DMU, resulting in inconsistency in evaluating the performance of the under-evaluated unit.
To overcome inconsistencies resulting from the use of different technologies and time bases, Pastor and Lovell [4] proposed the use of a global technology that includes all DMUs from both time periods. Figure 2 displays the global technology and its corresponding global frontier, where efficient DMUs A’, D’, and E’ are for time t + 1, and efficient unit B is for time t. To calculate the efficiencies used in MPI, we now examine the projections of points C and C’ on this global frontier, resulting in only two projection points: one on the A’B line segment, and the other on the BD line segment. Although the number of bases has been reduced, the point of concern is that the efficiencies of C and C’ are still calculated relative to different line segments and, therefore, different bases.
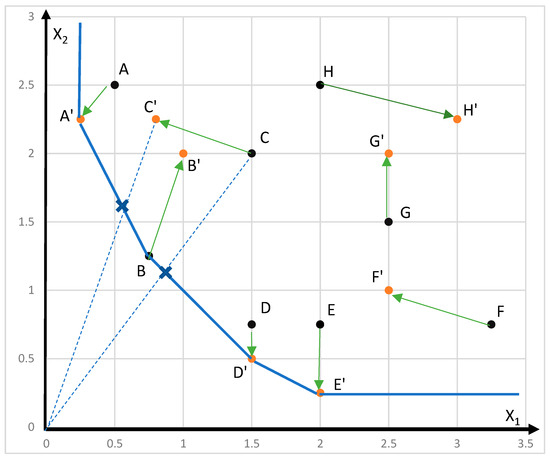
Figure 2.
Global technology for numerical example data.
Due to the inconsistencies highlighted, [5] proposed a method involving a CW applied uniformly across all DMUs and time periods. This aimed to mitigate disparities arising from disparate technologies and supporting hyperplanes. However, this approach lacked the capacity for peer evaluation and showed a high reliance on the weight selection, posing limitations.
In the upcoming section, we propose an alternative method centered on employing a global frontier, ensuring consistency in the underlying technology for efficiency calculations. By using a shared weight across two versions of a DMU, our approach maintains uniformity in efficiency calculations, leveraging the normal vector of a hyperplane derived from the global frontier. This obviates inconsistencies seen in previous methods. Furthermore, the common weight we introduce adheres to the Pareto property, facilitating cross-comparisons among DMUs, thus enabling peer evaluation—a feature lacking in the [5] method. Unlike [5], our approach’s analytical output is not reliant on a singular weight, enhancing confidence in the evaluation while embracing additional favorable characteristics.
3.2. Method Description
In this section, we outline the steps of our proposed method to calculate a Cross Global Malmquist productivity index. We will consider a set of 10 DMUs, aiming to analyze how their productivity changes across different time periods.
For the first time, the global technology and its boundary, i.e., the global frontier, was used by [4] to calculate GMPI. Following [4], we consider a global technology constructed from data encompassing all DMUs over two distinct time periods (all periods in the case in which we may have more periods). The efficiency of for k = t, t + 1 relative to the global frontier, can be obtained using model (5).
so that is the weight vector for inputs and outputs, and Xj = (x1j,…,xmj) and Yj = (y1j, …, ysj) are input and output vectors of DMUj, respectively. Ref. [4] defined the GMPI for DMUo as follows:
As indicated by [4], the GMPI is circular and, in contrast to the super-efficiency case, the associated linear programming is always feasible under any conditions [106,107]. As mentioned in the previous section, our approach is to use the same weights to calculate such that this common weight (CW) is used to calculate the fractional efficiencies of . The efficiencies of this fraction are related to two-time versions of a DMU. Obviously, these two DMUs tend to have a CW in such a way that their performance is maximized, and therefore they have a kind of conflict based on the choice of the CW. This situation brings to mind the concepts of game theory, in which these two DMUs play the role of players in a two-person cooperative game in that they do a kind of bargaining to reach a CW with each other.
In cooperative game theory, a Nash bargaining game models the negotiation process between players to reach a mutually beneficial outcome. In the context of efficiency evaluation for DMUs, this game reflects the bargaining process to determine the CW that maximizes the joint efficiency gains. In this context, the concept of a “breakdown point” becomes essential. The breakdown point signifies a threshold or critical value beyond which further enhancements in efficiency become challenging or less feasible. Given the objective of enhancing efficiency, the breakdown point in this scenario should indeed relate to efficiency. It could represent the maximum level of joint efficiency achievable, or a point where the gains from further improvements are significantly diminished or impractical. Determining this point is crucial for understanding the limitations or challenges in striving for higher efficiencies among the DMUs.
There are several options for selecting the bargaining breakdown point or bargaining lower bound of a DMU, and the literature on DEA bargaining games has proposed various methods [79,87,96,104,108,109,110]. One approach is based on the leader-follower model [108,109], where one DMU is assumed to be a leader and its optimistic efficiency is computed first. Then, the other DMU acts as a follower, whose efficiency is calculated without changing the leader’s efficiency score. Another method involves adding a virtual DMU with the maximum number of inputs while producing the least amount of output values to estimate the breakdown points [79,87,104]. The CCR input-oriented and cross-efficiency evaluation models have also been used to determine breakdown points [95,110]. Yet, cross-efficiency scores may lack uniqueness, introducing non-uniqueness to the Nash bargaining efficiency for a DMU. This can diminish the theoretical value and practical utility of the Nash bargaining game DEA model. Therefore, we propose that the possible minimum efficiency of DMUs are good choices for the breakdown points. Employing an aggressive perspective based on the leader-follower strategy, we determine the breakdown point (with minimum efficiency) of each DMU with respect to the global frontier.
To do that, let us at first consider as the leader, and the as the follower DMU. We use model (7) to obtain the minimum efficiency for the follower .
In this model, is the efficiency of (maximum efficiency) relative to the global frontier, which is obtained using model (7). The third constraint is related to maintaining the efficiency at its maximum value. Similarly, we consider as the leader DMU, and the unit as the follower DMU (model (8)):
We now use the following bargaining model (9) to obtain a fair CW between and :
In this model, and are players who bargain together to achieve a fair CW, and and , obtained from models (7) and (8), are the breaking points.
To ensure Pareto optimality, symmetry, scale invariance, and contraction independence, it is necessary for the Nash bargaining feasible set to be convex. By performing basic calculations, we can express model (10) in the following form:
It is worth noting that all the constraints in model (10) are linear, which means that the feasible set S is continuous, compact, and convex. As a result, the conditions of the bargaining game are satisfied in model (10), making it suitable for our intended purpose.
The optimal solution of (10), which is the CW between the two-time versions of DMUo in the global technology, are denoted by . Since these CWs are derived from a bargaining game, they can be considered a fair and acceptable solution for players to calculate efficiencies. The Nash bargaining efficiencies for and using these common optimal weights are and , respectively. The rate of change in the performance of and , which we call the Self-Evaluation Nash Common Weight Global Malmquist Productivity Index (SGMPI), is given by:
which indicates progress in the performance of unit o from time t to t + 1. Similarly, we can obtain the CW and SGMPI values for all DMUs. Now, considering the peer evaluation strategy, we use the weights of each DMU to evaluate the productivity change of other DMUs. As a result, considering the common weights between the time versions of DMUj obtained based on model (10), we calculate the Peer Evaluation Nash Common Weight Global Malmquist Productivity Index (PGMPI) for DMUo as follows:
Then we form a Cross-GMPI matrix, whose elements are SGMPI and PGMPI of all units. See Table 6.

Table 6.
Cross-GMPI matrix.
Each row displays the rating values of the other DMUs based on the weights associated with the DMUs in that row. The SGMPI values are on the main diagonal, whereas the other matrix numbers represent the PGMPI values. To aggregate the (S/P) GMPI values, we employed the geometric mean function. The mean values, i.e., Cross Evaluation Nash Common Weight Global Malmquist Productivity Index (CGMPI) for DMUo is:
These values are based on the use of more than one common weight, which is shared to evaluate all DMUs, unlike the GMPI proposed by [5] and other GMPIs which use only one weight vector to calculate the GMPI. In general, we propose the following algorithm to estimate the MPI based on an integrated framework of cross evaluations, bargaining games, common weights, and global technology.
Phase One: Using the bargaining game.
- Solving model (5) to obtain the favorite weight and maximum efficiency of each unit relative to the global frontier.
- Solving models (7) and (8) to get the game’s breakdowns for each player and .
- Solving the Nash bargaining game model (10) to obtain the CW between and .
- Obtaining Nash bargaining efficiencies using common optimal weights, i.e., and .
Phase Two: Using cross evaluation.
- Calculating the self and peer values
- 2.
- Forming a Cross-GMPI matrix (Table 6) with elements (S/P) GMPIjo.
- 3.
- Aggregating the scores of column ‘o’ of the Cross-GMPI matrix by using geometric mean to obtain CGMPIo (13).
In the forthcoming numerical analysis, the proposed methodology will be elaborated upon, highlighting its distinctive features and advantages.
4. Application of Proposed Method to the Example
In this section, we delve into a comprehensive numerical example using the dataset previously introduced in the motivation section. Our aim is to showcase the functionality of our proposed integrated approach in computing the GMPI in detail. The primary focus here is to elucidate the methodology introduced in this study, outlining its intricacies, steps, and distinctive features. Employing the dataset, we provide a detailed, step-by-step breakdown of how our method is applied and its functionalities, emphasizing its unique attributes and advantages. Towards the end, we conduct a brief comparison between our method and existing methodologies, specifically the GMPI and CWGMPI, to highlight the distinct advantages observed in our proposed method through the numerical illustration.
Describing the proposed method involves revisiting the numerical example outlined in Section 3, and focusing on DMU C. The maximum efficiency of C, using model (5), is 0.571429. With this efficiency held constant for DMU C, we use model (7) to obtain the minimum efficiency for C’, which is the bargaining breakdown point for C’, at 0.666667. Similarly, considering as the leader DMU, and the unit as the follower DMU, and solving model (8), the breakdown value for the C unit will be 0.55. By employing these values in bargaining model (10), the optimal CW between DMUs C and C’ is (v1*, v2*, u*) = (0.34476397, 0.24142703, 0.56035676), and the value of the game is 0.0003337. Using this common weight, the efficiencies of DMUs C and C’ are 0.560357 and 0.571429, respectively. The SGMPI for C is equal to (0.698888)/(0.560357) =1.247219, which indicates progress in the performance of unit C from time t to t + 1. Similarly, we can obtain the CW and SGMPI values for all DMUs (A,A’), (B,B’), …, (H,H’). Table 7 shows the minimum and maximum efficiency values of the models (7)/(8) and (5).

Table 7.
The lower and upper bounds of efficiencies.
Table 8 displays the outcomes of the implementation of the bargaining model (10). The optimal values of CW are presented in columns 2 to 4, while the fifth column shows the value of the game.

Table 8.
Bargaining model results.
We utilized the weights obtained earlier to evaluate the productivity of other DMUs and determine their corresponding productivity ratios. Table 9 presents the Cross- GMPI matrix. As mentioned before, each row exhibits the rating values of the other DMUs according to the weights linked with the DMUs listed in that respective row. For instance, in the second row, the corresponding line of A and A’, the values for the other DMUs are derived from the CW of the bargaining game between A and A’. The three numbers in each cell denote the efficiencies in time 1, time 2, and the performance change index (efficiency of time 2/efficiency of time 1) from top to bottom, respectively. The CGMPI values are listed in the last row of Table 9.

Table 9.
Cross-evaluation matrix, SGMPI and PGMPI and CGMPI values of numerical example.
Based on the CGMPI values in the last row of Table 9, DMUs B, G, and H have experienced regression in productivity, while other units show improvement, as can be seen in Figure 1 and Figure 2.
Upon careful examination of the game values, it has been observed that for DMUs whose lower efficiency is 1, the value of the game will always be zero. In such cases, we can avoid the computation of the game model (10) by considering the optimal weight of the other unit as a common weight. For instance, let us consider DMUs A and A’. Since A’ is located on the global frontier, its optimal weight is (0.61538462, 0.30769231, 0.84615385) (line segment parallel to the vertical axis), and the optimal weight of A is (0.61538462, 0.30769231, 0.84615385) (line segment A’B). As the optimal value of A’ does not change, we can use the weight vector related to A as the common weight for both DMUs. This reduces the computational burden significantly.
In what follows, we compare the proposed Cross-GMPI method with two other methods, namely the GMPI method proposed by [4] and the CWGMPI method proposed by [5]. The reason for this choice is that these two indexes are based on the consideration of global technology.
First, we consider the GMPI model. In this method, each of the two-time versions of the 8 DMUs are compared to the global boundary separately, and as a result, 16 separate weights are obtained. Table 10 shows these weights. In the last column, the value of GMPI is given. Since the output orientation of the CCR model (1) is used in the evaluation of units relative to the frontier, and considering that the output of all units is equal to the constant number one, then the optimal value of the objective function of the CCR model is equal to the optimal weight of U*. So, the numbers in the fourth column of Table 10, in addition to the optimal value for the output weight of the units at any time, indicate the efficiency value of the DMU of that row. For example, the efficiency of unit A in the first time is equal to 0.846154, and in the second time is equal to 1. To calculate GMPI, the division of two efficiencies is used. The optimal weights corresponding to these two efficiency vectors are (0.615385, 0.307692, 0.846154) and (4, 0, 1), respectively. As can be seen, the weight vectors are not the same. As a result, two efficiency values are divided for calculating the GMPI, which are based on different weights. Apart from this, the index calculated for the units is based on self-evaluation strategy, not peer evaluation. In the proposed cross-MPI method, instead of 16 different weight vectors, eight weight vectors were used (Table 8); that is, for both time versions of a DMU, a common weight vector is used, so the basis for calculating the efficiency of two DMUs is the same. Also, these vectors were used to calculate the efficiencies, and as a result the GMPI, of other units in the form of peer evaluation.

Table 10.
The optimal weights and value for GMPI.
Now we consider the CWGMPI model. If we use this model to evaluate the 8 DMUs of the numerical example, only one common weight vector is generated for all units, and all the efficiencies used to calculate the CWGMPI are based on this one vector. In Table 11, GMPI values based on this vector for units are given. As you can see, not only is this index not based on peer evaluation, but it is not even based on self-evaluation, and all calculations and rankings depend on this common weight.

Table 11.
The optimal weights and value for CWGMPI.
Now let us review the CGMPI values obtained by the proposed method which can be seen in Table 9. For a better visual understanding, we use a radar chart (Figure 3).
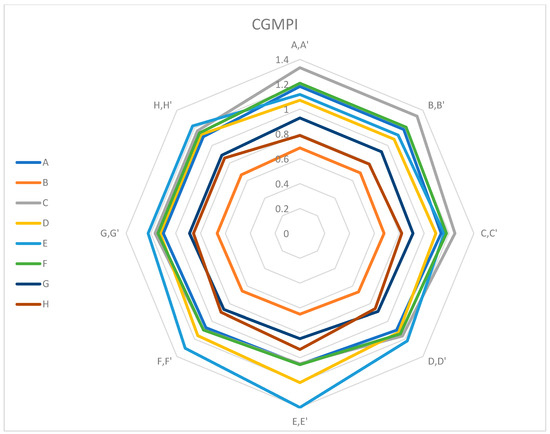
Figure 3.
Cross-GMPI matrix radar diagram of the proposed method for the numerical example.
In a radar chart, the different levels, or concentric polygons (from inside to outside), represent the values or scales of the dimensions being measured. The distance of a point from the center of the chart to a specific level on each axis corresponds to the value of the variable for that particular entity. The interpretation of levels in the radar chart based on the data provided enables a quick assessment of the relative performance of DMUs (A to H) across multiple weights (Common weights between DMUs A,A’ to H,H’ in Table 7). DMUs A, B, G, and H seem to have nearly identical performance across all weights. They maintain consistent values across the radar chart, indicating similar strengths and weaknesses in the measured weights. DMUs C, D, E, and F exhibit more variation in their performance across different weights. The third numbers in the columns of Table 8 are the vertices of the octagons of Figure 3. When one level is inside another level, it suggests that the DMU corresponding to the outer level performs better compared to the DMU associated with the inner level. Briefly, we notice that DMU B is at the innermost level of the graph, and this means that this unit undoubtedly has the least change in performance compared to other units. After that unit, G and H units are located. On the other hand, units E and C are the largest octagons, i.e., polygons with the greatest distance from the center of the radar. These results are consistent with the CGMPI values obtained by the proposed method in the last row of Table 8. Therefore, it can be inferred that the conclusion regarding the state of change in the performance of the units is based on an average value as represented by an octagon. It is obvious that the inference and analysis of the situation based on such a process is much more reliable than the analysis based on only one of its values.
The proposed integrated framework of GMPI, CW, Nash bargaining, and cross-evaluation allows the constructed GMPI to possess certain properties. The use of a CW in calculating the efficiencies of time versions of a DMU ensures that the GMPI fraction is well defined and consistent across all DMUs. This means that the basis of comparison is the same for performance appraisal. That is, not only is the efficiency used in calculating the Malmquist index based on common boundaries, but also on common weights or common supporting hyperplanes of boundaries [5]. Since a common weight is employed in the computation of productivity indexes for all units each time, the base for comparison remains consistent, ensuring the consistency and comparability of results.
The Malmquist index measures productivity change by comparing a unit’s efficiency at time t + 1 to time t. In DEA, these efficiencies are relative and reliant on a frontier comparison. Malmquist indexes are categorized based on single or multiple technology use: reference-based (using only one technology, e.g., time t or global technology) or adjacent-based (employing more than one time technology). Adjacent-based indexes may encounter infeasibility issues due to some units’ super-efficiency in one period relative to another. Employing global technology ensures feasibility in efficiency estimation models [4]. By utilizing global technology, our proposed index avoids potential inefficiency concerns in efficiency calculations.
DEA’s notable functionality lies in its ability to assist each DMU in selecting the most advantageous weights or multipliers for inputs and outputs during efficiency calculations. However, traditional DEA models, particularly in measuring MPI, tend to overstate efficiency due to the flexibility in weight selection for inputs and outputs. Consequently, this overestimation affects the rationality of derived MPI values. Various strategies address this issue, notably the common set of weights and the cross-evaluation process. Cross-evaluation, a significant component of DEA theory, surpasses the common set of weight method in applications [111]. It presents clear benefits, including personalized DMU ordering and the avoidance of unrealistic weight schemes without necessitating expert weight restrictions [112].
Utilizing a self-evaluation and peer evaluation methodology akin to cross-evaluation to compute cross GMPI, our approach yields realistic values for judgment. Cross GMPI, derived from the mean of productivity scores, represents an average productivity change, ensuring stability and reliability in assessment.
5. Conclusions
This study presents an innovative, integrated approach to compute the MPI through a combination of global technology, Common Weights, Nash bargaining, and cross-evaluation techniques. Our proposition advocates for obtaining CWs for two-time versions of a DMU based on global technology, facilitating efficiency calculations in tandem with a singular frontier, and ensuring consistency and comparability in results across different evaluations.
By employing the Nash bargaining game model, these CWs satisfy desirable properties, ensuring incentive alignment among DMUs and yielding Pareto-efficient solutions. Additionally, the novelty of incorporating CWs for peer and cross-sectional evaluations stands out as a novel contribution, enhancing the method’s robustness and applicability.
This integrated framework yields a proposed index boasting several desirable properties: feasibility, non-arbitrariness in base time period selection, technological and weight consistency, result stability and reliability, and equitable assessments. The comparison of our Cross-GMPI method with existing models, namely the GMPI and CWGMPI, underscores its superiority in offering a holistic evaluation while maintaining fairness and reliability across evaluations.
The numerical example showcases the effectiveness of our proposed method. Utilizing radar charts for visual representation allows for a swift yet comprehensive assessment of DMU performance across various weights. This visual depiction highlights consistent performances among certain DMUs and variations in others, providing nuanced insights into their relative strengths and weaknesses.
In essence, our integrated approach not only resolves efficiency overestimation concerns prevalent in traditional DEA models, but also ensures a more equitable and reliable assessment. Its distinct advantages, such as avoidance of unrealistic weight schemes, and enhanced stability, underline its superiority in performance evaluation.
The present study could be improved or expanded in several ways. This research discussed a methodology for determining a CW vector of DEA based on the Nash bargaining solution. In general, the resulting Nash bargaining game model is non-linear, given the nature of ratio forms of DEA efficiency. Converting the nonlinear model into a parametric linear programming problem with one parameter whose lower and upper bounds can be determined, and using a heuristic search on the single parameter employing the Kalai-Smorodinsky solution (which is the unique allocation rule for two-player bargaining problems with linear programming), or using Egoist’s dilemma for this purpose, could be considered for future research. Developing the present study for more than two time periods using the Extended Nash bargaining game, using more advanced and newer indexes in the literature to calculate cross-sectional MPI values, and considering the effects of return to scale and of internal structures for DMUs, could also be guidelines for future research. It is recommended that studying the effects of common inputs, merging and decomposition of DMUs, and decision-making in a centralized scenario and in uncertainty conditions, be considered for future research.
Author Contributions
Conceptualization, R.F., M.R.M., P.F.W. and Y.T.; Methodology, R.F.; Software, M.R.M.; Formal analysis, R.F., P.F.W. and Y.T.; Data curation, R.F.; Writing—original draft, R.F. and M.R.M.; Writing—review & editing, R.F., P.F.W. and Y.T.; Project administration, P.F.W. and Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Walheer, B. Malmquist Productivity Index for Multi-Output Producers: An Application to Electricity Generation Plants. Socioecon. Plann Sci. 2019, 65, 76–88. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity. Econometrica 1982, 50, 1393. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Pastor, J.T.; Lovell, C.A.K. A Global Malmquist Productivity Index. Econ. Lett. 2005, 88, 266–271. [Google Scholar] [CrossRef]
- Kao, C. Malmquist Productivity Index Based on Common-Weights DEA: The Case of Taiwan Forests after Reorganization. Omega 2010, 38, 484–491. [Google Scholar] [CrossRef]
- Ding, L.; Yang, Y.; Wang, W.; Calin, A.C. Regional Carbon Emission Efficiency and Its Dynamic Evolution in China: A Novel Cross Efficiency-Malmquist Productivity Index. J. Clean. Prod. 2019, 241, 118260. [Google Scholar] [CrossRef]
- Homayoni, A.; Fallahnejad, R.; Hosseinzadeh Lotfi, F. Cross Malmquist Productivity Index in Data Envelopment Analysis. 4OR 2021, 20, 567–602. [Google Scholar] [CrossRef]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data Envelopment Analysis: Critique and Extensions. New Dir. Program Eval. 1986, 1986, 73–105. [Google Scholar] [CrossRef]
- Doyle, J.; Green, R. Efficiency and Cross-Efficiency in DEA: Derivations, Meanings and Uses. J. Oper. Res. Soc. 1994, 45, 567. [Google Scholar] [CrossRef]
- Abolghasem, S.; Toloo, M.; Amézquita, S. Cross-Efficiency Evaluation in the Presence of Flexible Measures with an Application to Healthcare Systems. Health Care Manag. Sci. 2019, 22, 512–533. [Google Scholar] [CrossRef]
- Seyedalizadeh Ganji, S.R.; Rassafi, A.A.; Xu, D.L. A Double Frontier DEA Cross Efficiency Method Aggregated by Evidential Reasoning Approach for Measuring Road Safety Performance. Measurement 2019, 136, 668–688. [Google Scholar] [CrossRef]
- Deng, X.; Fang, W. A Novel Mean-Variance-Maverick DEA Prospect Cross-Efficiency Approach for Fuzzy Portfolio Selection. J. Intell. Fuzzy Syst. 2019, 37, 8113–8130. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.M.; Huang, Y. Cross-Efficiency Aggregation Method Based on Prospect Consensus Process. Ann. Oper. Res. 2020, 288, 115–135. [Google Scholar] [CrossRef]
- Fang, L.; Yang, J. An Integrated Ranking Approach Using Cross-Efficiency Intervals and the Cumulative Prospect Theory. Comput. Ind. Eng. 2019, 136, 556–574. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.T. Cross Efficiency Measurement and Decomposition in Two Basic Network Systems. Omega 2019, 83, 70–79. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.M. DEA Target Setting Approach within the Cross Efficiency Framework. Omega 2020, 96, 102072. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y.; Li, M.J.; Wang, Y.M. Meta-Frontier Analysis Using Cross-Efficiency Method for Performance Evaluation. Eur. J. Oper. Res. 2020, 280, 219–229. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Maniadakis, N.; Thanassoulis, E. A Cost Malmquist Productivity Index. Eur. J. Oper. Res. 2004, 154, 396–409. [Google Scholar] [CrossRef]
- Tohidi, G.; Razavyan, S.; Tohidnia, S. A Global Cost Malmquist Productivity Index Using Data Envelopment Analysis. J. Oper. Res. Soc. 2012, 63, 72–78. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Shiraz, R.K.; Maniadakis, N. A Cost Malmquist Productivity Index Capturing Group Performance. Eur. J. Oper. Res. 2015, 241, 796–805. [Google Scholar] [CrossRef]
- Huang, M.Y.; Juo, J.C.; Fu, T. tan Metafrontier Cost Malmquist Productivity Index: An Application to Taiwanese and Chinese Commercial Banks. J. Product. Anal. 2015, 44, 321–335. [Google Scholar] [CrossRef]
- Walheer, B. Cost Malmquist Productivity Index: An Output-Specific Approach for Group Comparison. J. Product. Anal. 2018, 49, 79–94. [Google Scholar] [CrossRef]
- Mirzaeian, F.; Fallahnejad, R. Cost Malmquist Productivity Index Based on Piecewise Linear Cost Function in Data Envelopment Analysis. Ind. Manag. J. 2015, 13, 300–328. [Google Scholar]
- Asmild, M.; Tam, F. Estimating Global Frontier Shifts and Global Malmquist Indices. J. Product. Anal. 2007, 27, 137–148. [Google Scholar] [CrossRef]
- Pastor, J.T.; Asmild, M.; Lovell, C.A.K. The Biennial Malmquist Productivity Change Index. Socio-Econ. Plan. Sci. 2011, 45, 10–15. [Google Scholar] [CrossRef]
- Afsharian, M.; Ahn, H. The Overall Malmquist Index: A New Approach for Measuring Productivity Changes over Time. Ann. Oper. Res. 2014, 226, 1–27. [Google Scholar] [CrossRef]
- O’Donnell, C.J.; Fallah-Fini, S.; Triantis, K. Measuring and Analysing Productivity Change in a Metafrontier Framework. J. Product. Anal. 2017, 47, 117–128. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S.N. Multi-Period Efficiency and Malmquist Productivity Index in Two-Stage Production Systems. Eur. J. Oper. Res. 2014, 232, 512–521. [Google Scholar] [CrossRef]
- Kao, C. Measurement and Decomposition of the Malmquist Productivity Index for Parallel Production Systems. Omega 2017, 67, 54–59. [Google Scholar] [CrossRef]
- Yu, M.-M.; Chen, L.-H. A Meta-Frontier Network Data Envelopment Analysis Approach for the Measurement of Technological Bias with Network Production Structure. Ann. Oper. Res. 2019, 287, 495–514. [Google Scholar] [CrossRef]
- Tavana, M.; Khalili-Damghani, K.; Santos Arteaga, F.J.; Hashemi, A. A Malmquist Productivity Index for Network Production Systems in the Energy Sector. Ann. Oper. Res. 2019, 284, 415–445. [Google Scholar] [CrossRef]
- Oh, D. hyun A Global Malmquist-Luenberger Productivity Index. J. Product. Anal. 2010, 34, 183–197. [Google Scholar] [CrossRef]
- Aparicio, J.; Pastor, J.T.; Zofio, J.L. On the Inconsistency of the Malmquist-Luenberger Index. Eur. J. Oper. Res. 2013, 229, 738–742. [Google Scholar] [CrossRef]
- Kerstens, K.; Van De Woestyne, I. Comparing Malmquist and Hicks-Moorsteen Productivity Indices: Exploring the Impact of Unbalanced vs. Balanced Panel Data. Eur. J. Oper. Res. 2014, 233, 749–758. [Google Scholar] [CrossRef]
- Arabi, B.; Munisamy, S.; Emrouznejad, A. A New Slacks-Based Measure of Malmquist-Luenberger Index in the Presence of Undesirable Outputs. Omega 2015, 51, 29–37. [Google Scholar] [CrossRef]
- Du, J.; Duan, Y.; Xu, J. The Infeasible Problem of Malmquist–Luenberger Index and Its Application on China’s Environmental Total Factor Productivity. Ann. Oper. Res. 2017, 278, 235–253. [Google Scholar] [CrossRef]
- Du, J.; Chen, Y.; Huang, Y. A Modified Malmquist-Luenberger Productivity Index: Assessing Environmental Productivity Performance in China. Eur. J. Oper. Res. 2018, 269, 171–187. [Google Scholar] [CrossRef]
- Lambert, D.K. Productivity Measurement from a Reference Technology: A Distance Function Approach. J. Product. Anal. 1998, 10, 289–304. [Google Scholar] [CrossRef]
- Fuentes, H.J.; Grifell-Tatjé, E.; Perelman, S. A Parametric Distance Function Approach for Malmquist Productivity Index Estimation. J. Product. Anal. 2001, 15, 79–94. [Google Scholar] [CrossRef]
- Pastor, J.T.; Lovell, C.A.K.; Aparicio, J. Defining a New Graph Inefficiency Measure for the Proportional Directional Distance Function and Introducing a New Malmquist Productivity Index. Eur. J. Oper. Res. 2019, 281, 222–230. [Google Scholar] [CrossRef]
- Asmild, M.; Baležentis, T.; Hougaard, J.L. Multi-Directional Productivity Change: MEA-Malmquist. J. Product. Anal. 2016, 46, 109–119. [Google Scholar] [CrossRef]
- Kevork, I.S.; Pange, J.; Tzeremes, P.; Tzeremes, N.G. Estimating Malmquist Productivity Indexes Using Probabilistic Directional Distances: An Application to the European Banking Sector. Eur. J. Oper. Res. 2017, 261, 1125–1140. [Google Scholar] [CrossRef]
- Grifell-Tatjé, E.; Lovell, C.A.K. A Generalized Malmquist Productivity Index. TOP 1999, 7, 81–101. [Google Scholar] [CrossRef]
- Orea, L. Parametric Decomposition of a Generalized Malmquist Productivity Index. J. Product. Anal. 2002, 18, 5–22. [Google Scholar] [CrossRef]
- Lovell, C.A.K. The Decomposition of Malmquist Productivity Indexes. J. Product. Anal. 2003, 20, 437–458. [Google Scholar] [CrossRef]
- Zelenyuk, V. Aggregation of Malmquist Productivity Indexes. Eur. J. Oper. Res. 2006, 174, 1076–1086. [Google Scholar] [CrossRef]
- Camanho, A.S.; Dyson, R.G. Data Envelopment Analysis and Malmquist Indices for Measuring Group Performance. J. Product. Anal. 2006, 26, 35–49. [Google Scholar] [CrossRef]
- Yu, M.M. The Capacity Productivity Change and the Variable Input Productivity Change: A New Decomposition of the Malmquist Productivity Index. Appl. Math. Comput. 2007, 185, 375–381. [Google Scholar] [CrossRef]
- Wang, Y.M.; Lan, Y.X. Measuring Malmquist Productivity Index: A New Approach Based on Double Frontiers Data Envelopment Analysis. Math. Comput. Model. 2011, 54, 2760–2771. [Google Scholar] [CrossRef]
- Chen, K.H.; Yang, H.Y. A Cross-Country Comparison of Productivity Growth Using the Generalised Metafrontier Malmquist Productivity Index: With Application to Banking Industries in Taiwan and China. J. Product. Anal. 2011, 35, 197–212. [Google Scholar] [CrossRef]
- Pantzios, C.J.; Karagiannis, G.; Tzouvelekas, V. Parametric Decomposition of the Input-Oriented Malmquist Productivity Index: With an Application to Greek Aquaculture. J. Product. Anal. 2011, 36, 21–31. [Google Scholar] [CrossRef]
- Mayer, A.; Zelenyuk, V. Aggregation of Malmquist Productivity Indexes Allowing for Reallocation of Resources. Eur. J. Oper. Res. 2014, 238, 774–785. [Google Scholar] [CrossRef]
- Afsharian, M.; Ahn, H. Multi-Period Productivity Measurement under Centralized Management with an Empirical Illustration to German Saving Banks. OR Spectr. 2017, 39, 881–911. [Google Scholar] [CrossRef]
- Diewert, W.E.; Fox, K.J. Decomposing Productivity Indexes into Explanatory Factors. Eur. J. Oper. Res. 2017, 256, 275–291. [Google Scholar] [CrossRef]
- Walheer, B. Disaggregation of the Cost Malmquist Productivity Index with Joint and Output-Specific Inputs. Omega 2018, 75, 1339–1351. [Google Scholar] [CrossRef]
- Arocena, P.; Saal, D.S.; Urakami, T.; Zschille, M. Measuring and Decomposing Productivity Change in the Presence of Mergers. Eur. J. Oper. Res. 2019, 282, 319–333. [Google Scholar] [CrossRef]
- Afsharian, M.; Ahn, H.; Harms, S.G. Performance Comparison of Management Groups under Centralised Management. Eur. J. Oper. Res. 2019, 278, 845–854. [Google Scholar] [CrossRef]
- Balk, B.M.; Althin, R. A New, Transitive Productivity Index. J. Product. Anal. 1996, 7, 19–27. [Google Scholar] [CrossRef]
- Grifell-Tatjé, E.; Lovell, C.A.K.; Pastor, J.T. A Quasi-Malmquist Productivity Index. J. Product. Anal. 1998, 10, 7–20. [Google Scholar] [CrossRef]
- Førsund, F.R. The Rise and Fall of Slacks: Comments on Quasi-Malmquist Productivity Indices. J. Product. Anal. 1998, 10, 21–34. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimating and Bootstrapping Malmquist Indices. Eur. J. Oper. Res. 1999, 115, 459–471. [Google Scholar] [CrossRef]
- Althin, R. Measurement of Productivity Changes: Two Malmquist Index Approaches. J. Product. Anal. 2001, 16, 107–128. [Google Scholar] [CrossRef]
- Chen, Y. A Non-Radial Malmquist Productivity Index with an Illustrative Application to Chinese Major Industries. Int. J. Prod. Econ. 2003, 83, 27–35. [Google Scholar] [CrossRef]
- Shestalova, V. Sequential Malmquist Indices of Productivity Growth: An Application to OECD Industrial Activities. J. Product. Anal. 2003, 19, 211–226. [Google Scholar] [CrossRef]
- Asmild, M.; Paradi, J.C.; Aggarwall, V.; Schaffnit, C. Combining DEA Window Analysis with the Malmquist Index Approach in a Study of the Canadian Banking Industry. J. Product. Anal. 2004, 21, 67–89. [Google Scholar] [CrossRef]
- Daskovska, A.; Simar, L.; van Bellegem, S. Forecasting the Malmquist Productivity Index. J. Product. Anal. 2010, 33, 97–107. [Google Scholar] [CrossRef]
- Fuentes, R.; Lillo-Bañuls, A. Smoothed Bootstrap Malmquist Index Based on DEA Model to Compute Productivity of Tax Offices. Expert Syst. Appl. 2015, 42, 2442–2450. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Zhang, H.; Zhang, R.; Xu, B. Factor-Specific Malmquist Productivity Index Based on Common Weights DEA. Oper. Res. 2016, 16, 51–70. [Google Scholar] [CrossRef]
- Karagiannis, G.; Knox Lovell, C.A. Productivity Measurement in Radial DEA Models with a Single Constant Input. Eur. J. Oper. Res. 2016, 251, 323–328. [Google Scholar] [CrossRef]
- Li, Z.; Crook, J.; Andreeva, G. Dynamic Prediction of Financial Distress Using Malmquist DEA. Expert Syst. Appl. 2017, 80, 94–106. [Google Scholar] [CrossRef]
- Zhu, N.; Liu, Y.; Emrouznejad, A.; Huang, Q. An Allocation Malmquist Index with an Application in the China Securities Industry. Oper. Res. 2017, 17, 669–691. [Google Scholar] [CrossRef]
- Nash, J.F.; Nash, J. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Banker, R.D. A Game Theoretic Approach to Measuring Efficiency. Eur. J. Oper. Res. 1980, 5, 262–266. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W.; Clarke, R. Constrained Game Formulations and Interpretations for Data Envelopment Analysis. Eur. J. Oper. Res. 1989, 40, 299–308. [Google Scholar] [CrossRef]
- Rousseau, J.J.; Semple, J.H. Two-Person Ratio Efficiency Games. Manag. Sci. 1995, 41, 435–441. [Google Scholar] [CrossRef]
- Hao, G.; Wei, Q.; Yan, H. Generalized DEA Model and the Convex Cone Constrained Game. Eur. J. Oper. Res. 2000, 126, 515–525. [Google Scholar] [CrossRef]
- Zhou, Z.; Sun, L.; Yang, W.; Liu, W.; Ma, C. A Bargaining Game Model for Efficiency Decomposition in the Centralized Model of Two-Stage Systems. Comput. Ind. Eng. 2013, 64, 103–108. [Google Scholar] [CrossRef]
- Du, J.; Liang, L.; Chen, Y.; Cook, W.D.; Zhu, J. A Bargaining Game Model for Measuring Performance of Two-Stage Network Structures. Eur. J. Oper. Res. 2011, 210, 390–397. [Google Scholar] [CrossRef]
- An, Q.; Chen, H.; Xiong, B.; Wu, J.; Liang, L. Target Intermediate Products Setting in a Two-Stage System with Fairness Concern. Omega 2017, 73, 49–59. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Izadbakhsh, H.; Yousefi, S. An Improvement Approach Based on DEA-Game Theory for Comparison of Operational and Spatial Efficiencies in Urban Transportation Systems. KSCE J. Civ. Eng. 2016, 20, 1526–1531. [Google Scholar] [CrossRef]
- Jalali Naini, S.G.; Moini, A.; Jahangoshai Rezaee, M. Nash Bargaining Game Model for Two Parallel Stages Process Evaluation with Shared Inputs. Int. J. Adv. Manuf. Technol. 2013, 67, 475–484. [Google Scholar] [CrossRef]
- Borrero, D.V.; Hinojosa, M.A.; Mármol, A.M. DEA Production Games and Owen Allocations. Eur. J. Oper. Res. 2016, 252, 921–930. [Google Scholar] [CrossRef]
- Wu, H.; Lv, K.; Liang, L.; Hu, H. Measuring Performance of Sustainable Manufacturing with Recyclable Wastes: A Case from China’s Iron and Steel Industry. Omega 2017, 66, 38–47. [Google Scholar] [CrossRef]
- Du, J.; Chen, Y.; Cook, W.D.; Liang, L.; Zhu, J. Evaluating Two-Stage Network Structures: Bargaining Game Approach. In International Series in Operations Research and Management Science; Springer New York LLC: New York, NY, USA, 2014; Volume 208, pp. 165–187. [Google Scholar]
- Jahangoshai Rezaee, M.; Moini, A.; Haji-Ali Asgari, F. Unified Performance Evaluation of Health Centers with Integrated Model of Data Envelopment Analysis and Bargaining Game. J. Med. Syst. 2012, 36, 3805–3815. [Google Scholar] [CrossRef] [PubMed]
- Jahangoshai Rezaee, M.; Moini, A.; Makui, A. Operational and Non-Operational Performance Evaluation of Thermal Power Plants in Iran: A Game Theory Approach. Energy 2012, 38, 96–103. [Google Scholar] [CrossRef]
- Yang, X.; Morita, H. Efficiency Improvement from Multiple Perspectives: An Application to Japanese Banking Industry. Omega 2013, 41, 501–509. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Tone, K. Egoist’s Dilemma: A DEA Game. Omega 2006, 34, 135–148. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Sahoo, B.K.; Tone, K. Fair allocation based on two criteria: A dea game view of “add them up and divide by two”(<Special Issue>Operations Research for Performance Evaluation). J. Oper. Res. Soc. Jpn. 2009, 52, 131–146. [Google Scholar] [CrossRef]
- Jahanshahloo, G.R.; Hosseinzadeh Lotfi, F.; Sohraiee, S. Egoist’s Dilemma with Interval Data. Appl. Math. Comput. 2006, 183, 94–105. [Google Scholar] [CrossRef]
- Sohraiee, S. Evaluation of Egoist’s Dilemma with Fuzzy Data. Appl. Math. Sci. 2009, 3, 1219–1233. [Google Scholar]
- Daneshvar, S. Egoists Dilemma with Fuzzy Data. Afr. J. Math. Comput. Sci. Res. 2012, 5, 9–16. [Google Scholar] [CrossRef]
- Sekine, S.; Fu, J.; Muto, S. Game Theoretic Approaches to Weight Assignments in Data Envelopment Analysis Problems. Math. Probl. Eng. 2014, 2014, 434252. [Google Scholar] [CrossRef]
- Wu, J.; Liang, L.; Zha, Y.C. Determination of the Weights of Ultimate Cross Efficiency Based on the Solution of Nucleolus. Xitong Gongcheng Lilun Yu Shijian/Syst. Eng. Theory Pract. 2008, 28, 92–97. [Google Scholar] [CrossRef]
- Wu, J.; Liang, L.; Yang, F.; Yan, H. Bargaining Game Model in the Evaluation of Decision Making Units. Expert Syst. Appl. 2009, 36, 4357–4362. [Google Scholar] [CrossRef]
- Lozano, S. Information Sharing in DEA: A Cooperative Game Theory Approach. Eur. J. Oper. Res. 2012, 222, 558–565. [Google Scholar] [CrossRef]
- Lozano, S. Using DEA to Find the Best Partner for a Horizontal Cooperation. Comput. Ind. Eng. 2013, 66, 286–292. [Google Scholar] [CrossRef]
- Lozano, S. DEA Production Games. Eur. J. Oper. Res. 2013, 231, 405–413. [Google Scholar] [CrossRef]
- Lozano, S.; Hinojosa, M.A.; Mármol, A.M. Set-Valued DEA Production Games. Omega 2015, 52, 92–100. [Google Scholar] [CrossRef]
- Hinojosa, M.A.; Lozano, S.; Mármol, A.M. DEA Production Games with Fuzzy Output Prices. Fuzzy Optim. Decis. Mak. 2018, 17, 401–419. [Google Scholar] [CrossRef]
- Wu, H.; Du, S.; Liang, L.; Zhou, Y. A DEA-Based Approach for Fair Reduction and Reallocation of Emission Permits. Math. Comput. Model. 2013, 58, 1095–1101. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y. Supplier Evaluation Based on Nash Bargaining Game Model. Expert Syst. Appl. 2014, 41, 4181–4185. [Google Scholar] [CrossRef]
- Omrani, H.; Gharizadeh Beiragh, R.; Shafiei Kaleibari, S. Performance Assessment of Iranian Electricity Distribution Companies by an Integrated Cooperative Game Data Envelopment Analysis Principal Component Analysis Approach. Int. J. Electr. Power Energy Syst. 2015, 64, 617–625. [Google Scholar] [CrossRef]
- Sugiyama, M.; Sueyoshi, T. Finding a Common Weight Vector of Data Envelopment Analysis Based upon Bargaining Game. Stud. Eng. Technol. 2014, 1, 13–21. [Google Scholar] [CrossRef][Green Version]
- Zhu, J. Robustness of the Efficient DMUs in Data Envelopment Analysis. Eur. J. Oper. Res. 1996, 90, 451–460. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Infeasibility of Super-Efficiency Data Envelopment Analysis Models. INFOR J. 1999, 37, 174–187. [Google Scholar] [CrossRef]
- Lundberg, S.; Pollak, R.A. Separate Spheres Bargaining and the Marriage Market. J. Political Econ. 1993, 101, 988–1010. [Google Scholar] [CrossRef]
- Liang, L.; Cook, W.D.; Zhu, J. DEA Models for Two-Stage Processes: Game Approach and Efficiency Decomposition. Nav. Res. Logist. 2008, 55, 643–653. [Google Scholar] [CrossRef]
- Wu, J.; Liang, L.; Yang, F. Determination of the Weights for the Ultimate Cross Efficiency Using Shapley Value in Cooperative Game. Expert. Syst. Appl. 2009, 36, 872–876. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.Y.; Lu, W.M. Research Fronts in Data Envelopment Analysis. Omega 2016, 58, 33–45. [Google Scholar] [CrossRef]
- Anderson, T.R.; Hollingsworth, K.; Inman, L. The Fixed Weighting Nature of a Cross-Evaluation Model. J. Product. Anal. 2002, 17, 249–255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).