Generalized Hyperbolic Discounting in Security Games of Timing

Abstract

In recent years, several high-profile incidents have spurred research into games of timing. A framework emanating from the FlipIt model features two covert agents competing to control a single contested resource. In its basic form, the resource exists forever while generating value at a constant rate. As this research area evolves, attempts to introduce more economically realistic models have led to the application of various forms of economic discounting to the contested resource. This paper investigates the application of a two-parameter economic discounting method, called generalized hyperbolic discounting, and characterizes the game’s Nash equilibrium conditions. We prove that for agents discounting such that accumulated value generated by the resource diverges, equilibrium conditions are identical to those of non-discounting agents. The methodology presented in this paper generalizes the findings of several other studies and may be of independent interest when applying economic discounting to other models.

1. Introduction

Game theory’s great promise is to predict the evolution of a multi-agent interaction from agents’ preferences. Unfortunately, the particulars of scenarios tend to complicate the derivation of these predictions, and accurately describing a real scenario requires progressively more advanced models of agent behavior. This is markedly true for interactions that persist over time.

Research on games of timing dates back to the Cold War period, and various scenarios have by now motivated a sizable body of literature (see, for example, [1]). One effort is a series of papers centered around the so-called FlipIt model [2], which attempts to capture the dynamics of a persistent two-agent interaction involving a single contested resource. This resource is an abstract representation of, e.g., knowledge of cryptographic keys or passwords or ownership of cloud resources [3].

FlipIt models capture scenarios taken in part from a series of high-profile (cyber) attacks against supposedly well-protected targets—the Iranian industrial control systems [4], the U.S. Office of Personnel Management [5,6], large telecommunication providers [7,8], major health care insurance companies [9], and, recently, critical infrastructure companies in Ukraine [10]. An essential property shared by these threats is that against them, perfectly effective preventative investments are nearly impossible [11,12]. Mitigation strategies such as in-depth security audits or longer-term investments to reorganize existing IT infrastructures are therefore weighed against the economic incentives of would-be attackers.

While this line of work has explored diverse facets of security decision-making, a limitation in most studies on games of timing in general and on FlipIt-like games in particular is that they do not consider economic discounting in the valuation of the contested resource—so although the environment changes over time, the value of the resource and the costs of attacking or defending it do not. A few more recent efforts have attempted to bridge this deficiency by considering the effect of exponential discounting on the valuation and defense costs over time [13,14,15]. Such studies have found new predictions of optimal defense investments due mainly to the fact that an exponentially discounted investment has a finite cumulative valuation over time. Although mathematically appealing, exponential discounting is known to have low descriptive accuracy in most contexts. It remains to consider a more comprehensive approach to time-based discounting.

Our work meets this need by analyzing a FlipIt-like contested resource scenario under a more generic present-focused discounting framework using a two-parameter family of generalized hyperbolic discounting functions. These well-studied functions, introduced by Loewenstein and Prelec in 1992 [16], smoothly interpolate an agent’s temporal valuation between an arbitrary rate of exponential discounting and a constant valuation, nesting exponential and hyperbolic discounting as special cases. As we cover the entire space of generalized hyperbolic discounting functions, our conclusions subsume those of earlier research efforts involving persistent resource control—including some that do not involve discounting and work on exponential discounting [13,14].

Our primary technical contribution is to show that for a wide range of agent discounting preferences, the agent’s strategic considerations and equilibrium conditions are the same as if they were not discounting. We also provide a complete characterization of player utilities and (Nash) equilibrium conditions for the FlipIt model in which both agents are interacting using the same strategic class out of periodic or exponential (defined in Section 4.5) and when both agents are applying a form of discounting with parameters from the same class out of sub-hyperbolic or super-hyperbolic (defined in Section 3). We show that generalized hyperbolic discounting unlocks the possibility of equilibria in which neither player moves and prove that periodic strategies no longer always strictly dominate the class of so-called renewal strategies, as they do for the model without discounting, a result first stated by van Dijk et al. [2]. Beyond these new discoveries, and because some of the derivations developed for this work can be used to extend results from less generic models, we believe that our framework would likely be helpful in other timing-based games besides FlipIt.

We organized the rest of the paper as follows. In Section 2, we discuss related work. Then, we describe our model, which builds on FlipIt, in Section 4. We present our analysis of the model in Section 5, and we discuss some interesting aspects of our findings in Section 6. Finally, we conclude in Section 7. Following the main document are appendices containing formal proofs and derivations to support the claims made in Section 5 and Section 6.

2. Related Work

Many interactions, including security interactions and especially those dealing with Advanced Persistent Threats (APTs), have an important temporal dimension. Studying such interactions necessitates comparing the value of present and future potential gains or losses. It is here that discounting models come into play, offering precise explanations for the valuations of economic resources, including privacy and security, by individuals, institutions, or societies over time.

Within the field of economics, the exponential discounted-utility model pioneered by Samuelson [17] and Ramsey [18] has become the predominant approach to discounting. The exponential model posits that the rate at which assets depreciate remains constant, allowing a single discount factor, $\beta$, to encapsulate all individuals’ disparate perceptions and behaviors at different times. Specifically, it discounts utility flows with the function ${\mathrm{e}}^{-\beta t}$, where t is the horizon of the utility flow and $\beta$ is a free parameter representing the discounting rate.

The exponential model is popular because it is relatively easy to understand and reason about and mathematically tractable. There are also solid theoretical arguments for exponential discounting. Strotz [19] was the first one to derive exponential discounting as the only approach to intertemporal choice available to decision-makers whose choices are always consistent, in the sense that they are never in conflict with themselves at later points in time. This theoretical effort was later repeated by others in different settings [20,21]. The consistency property has established exponential discounting as the dominant model that is often considered to be normatively correct [22].

However, we know that the exponential discounting utility model is only very rarely descriptively accurate—it does not do well predicting the behaviors of agents in the real world. Numerous behavioral research works have uncovered facets of human and animal behavior that cannot be captured by the exponential discounting framework [23]. This includes present-focused preferences, preference reversals, self-control problems [16,24], effects of temptation [25], psychometric distortions such as subjective time [26] and probability perception [27], magnitude effects, and myopic decision-making on account of our limited cognitive faculties [28]. The search for more descriptive accuracy has resulted in many other discounting models, including present-biased or quasi-hyperbolic discounting [29] and the hyperbolic and generalized hyperbolic models discussed below. Ericson and Laibson [30] present an excellent overview of theories on intertemporal choice.

Within the wealth of existing models, the model studied most by psychologists is the hyperbolic discounting function, first implied by Herrnstein [31]. It is a mathematically uncomplicated one-parameter model that has been shown to greatly outperform exponential discounting in terms of descriptive accuracy and incorporates present-focused preferences and preference reversals. Hyperbolic discounting scales utility with the function ${(1+\alpha t)}^{-1}$, where t is again the horizon of the utility flow, and where $\alpha$ is a free parameter related to the discounting rate. Hyperbolic discounting preserves the proportion between the ratio of future valuations and the corresponding future times—e.g., the relative drop in valuation between times 10 and 20 is (almost) the same as the relative drop in valuation between times 100 and 200. This implements a strictly decreasing discount rate; when compared with exponential discounting, hyperbolic discounting depreciates faster near $t=0$ and slower for large t.

The hyperbolic model is often extended with an additional parameter $\beta$ to ${(1+\alpha t)}^{-\beta /\alpha }$. It is then called generalized hyperbolic discounting or hyperboloid discounting. Here, the ratio $\beta /\alpha$ reflects the nonlinear scaling of the amount and delay [32,33]. Parameter $\alpha$ can also be interpreted as how much the function departs from constant-rate (exponential) discounting [16], with lower values of $\alpha$ corresponding to more (traditional) “rational” behavior.

The generalized hyperbolic discounting function has many desirable properties making it an excellent choice for study. For one, it embeds several other major models: classical exponential discounting, hyperbolic discounting, and constant or no discounting, for $\alpha \to \infty$, $\alpha =\beta$, and $\alpha \to 0$, respectively. Generalized hyperbolic discounting can be shown to have quantitatively higher predictive accuracy beyond that which can be accounted for simply by the addition of an additional parameter to the hyperbolic model [33,34]. The additional parameter allows the modeling of very different agent types. For example, many studies have shown that humans, in many contexts, tend to exhibit behavior in accordance with $\alpha \gg \beta$, while animals such as pigeons exhibit behavior where $\alpha \approx \beta$; we refer to Vanderveldt et al. [23] for a review of these studies. Lastly, in addition to expressing delay discounting behavior of agents with present-focused preferences, generalized hyperbolic discounting can be rationalized as a result of risk and probability discounting [35]. The underlying idea is that the value of a future reward should be discounted because there is a risk that rewards will not be realized. Generalized hyperbolic discounting can arise both when the hazard rate is horizon-dependent and when it is uncertain [36,37,38].

Our work builds on these behavioral and economic insights to advance the literature on games of timing [1] through the adoption of generalized hyperbolic discounting in the framework of a FlipIt-like game [2,39]. As such, our work contributes also to the overall space of security economics and, in particular, the application of game theory to security and privacy challenges [40,41].

FlipIt is a game motivated by persistent, stealthy, sophisticated attacks by an advanced persistent threat (APT) and models a situation where two players compete for the ownership of a resource generating value over time [2,39]. Apart from the inclusion of discounting, the interaction we investigate is exactly that of FlipIt described by van Dijk et al. [2], although our mathematical description of it is significantly different and more streamlined.

The interesting strategic aspects of FlipIt have led to numerous follow-up studies. Most closely related to our work are studies on the impact of exponential discounting in the framework of the FlipIt game [13,14,15]. These have found new predictions of optimal defense investments due largely to the fact that an exponentially discounted investment has a finite cumulative valuation over time. Throughout the paper, we will discuss the relationship of model variations with generalized hyperbolic discounting, exponential discounting, and no discounting in detail.

To the best of our knowledge, there is no comprehensive review article about the FlipIt game. Most of the literature has centered on the study of variations of the game’s structure, such as the types of involved players [42,43], the speed and efficacy of moves [42,43,44,45], the game’s time horizon [45,46], the structure of the resource and partial control [47,48,49], variations on the assumption of perfect stealthiness [42,43,44,46], discretization [45], the effects of budget constraints [46], and more sophisticated strategies involving machine learning [50]. FlipIt can also be embedded as a stage into other games [51]. More recently, Banik and Bopardikar [52] have formulated a variation of FlipIt as a zero-sum discrete control game, where the defender aims to stabilize a dynamical system. Miura et al. [53] have formulated a FlipIt-like game, augmented by an epidemic model, where defender and attacker compete to control as many computing resources as possible over a set period of time.

Although the concept of time forms the very core of the FlipIt game, van Dijk et al. [2] and most follow-up work consider many aspects of the interaction to remain unchanged as time progresses. This includes the value of the resource, as well as the costs to attack it. This presents some conceptual challenges, as nothing is everlasting, and also results in some questionable predictions, such as every resource being attacked by attackers at non-zero rates. In [13,14], Merlevede et al. introduced exponential discounting of future gains and costs, addressing some of these concerns. In [15], these authors also introduce a novel class of “discounted strategies” to the exponentially discounted game in which players move less frequently as the resource loses value. We are unaware of further studies considering discounting in the context of the FlipIt game.

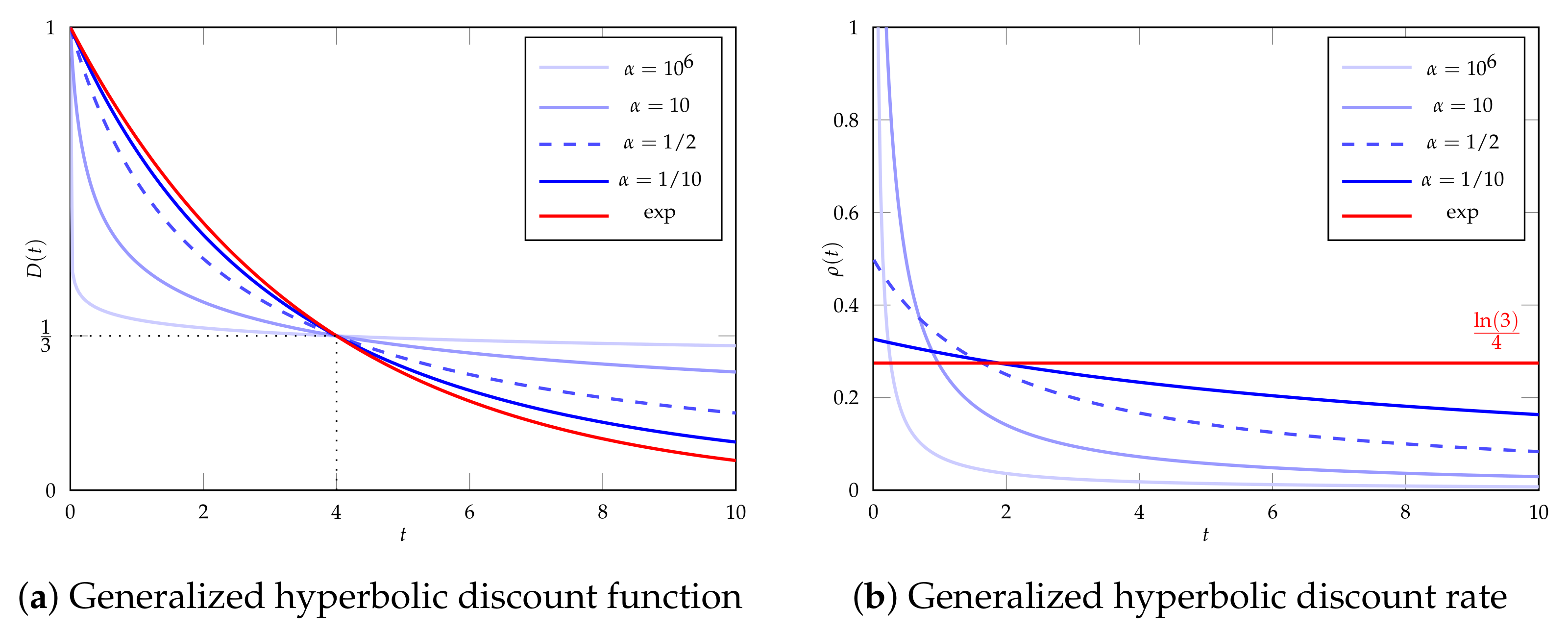
3. Discounting

The term discounting implies that the future value of a measurable quantity is less than its present value. The effect of this value decrease can be formalized by a discount function $D\left(t\right)$. $D\left(t\right)$ gives a multiplicative factor expressing the value at future time $t>0$ relative to its present value (at time $t=0$).

An intuitive measure of the behavior of the discount function is the discount rate:

$$\begin{array}{c}\hfill \rho \left(t\right)=-\frac{D^{\prime }\left(t\right)}{D\left(t\right)}.\end{array}$$

The discount rate indicates how fast the value decreases at any time $t\ge 0$.

Our model discounts player gains and player costs along a member of the family of generalized hyperbolic discounting functions, introduced by Loewenstein and Prelec [16]1, which have the form

$$\begin{array}{c}\hfill \left\{D\left(t\right)=\frac{1}{{(1+\alpha t)}^{\beta /\alpha }}\mid \alpha >0,\beta >0\right\}.\end{array}$$

Figure 1a illustrates the hyperbolic discount function, while Figure 1b displays the corresponding discount rates. For generalized hyperbolic discounting, discount rates are always strictly decreasing:

$$\rho \left(t\right)=\frac{\beta }{1+\alpha t}.$$

Parameter $\alpha$ determines how much the function resembles the exponential function. For varying $\alpha$, the family of generalized hyperbolic discounting functions spans a wide variety of discounting behaviors, including exponential discounting for $\alpha \to 0$, true hyperbolic discounting for $\alpha =\beta$, and no discounting for $\alpha \to \infty$.

$$\begin{array}{ccc}\hfill \underset{\alpha \to 0}{lim}\frac{1}{{(1+\alpha t)}^{\beta /\alpha }}& ={\mathrm{e}}^{-\beta t}\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(\mathrm{exponential}\right)\end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\left.\frac{1}{{(1+\alpha t)}^{\beta /\alpha }}\right|}_{\alpha =\beta }& =\frac{1}{1+\beta t}\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(\mathrm{hyperbolic}\right)\end{array}$$

(2)

$$\begin{array}{ccc}\hfill \underset{\alpha \to \infty }{lim}\frac{1}{{(1+\alpha t)}^{\beta /\alpha }}& =1\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\mathrm{no} \mathrm{discounting}).\end{array}$$

(3)

Note that for exponential discounting ($D\left(t\right)=e^{-\beta t}$), the discount rate is equal to a constant value ($\rho \left(t\right)=\beta$).

The case of “true” hyperbolic discounting ($\alpha =\beta$) corresponds to a boundary condition separating two qualitatively distinct classes of discounting functions. We will refer to generalized hyperbolic discounting with $\alpha <\beta$ as super-hyperbolic discounting, and to discounting with $\alpha \ge \beta$ as sub-hyperbolic discounting. We include hyperbolic discounting ($\alpha =\beta$) as a member of the class of sub-hyperbolic discounting functions. The following observations largely explain the behavioral differences between these two classes of functions.

• For $\alpha <\beta$ (super-hyperbolic discounting), the area under $D\left(t\right)$’s curve is finite and given by:

  $$\begin{array}{c}\hfill {\int }_{\tau =0}^{+\infty }D\left(\tau \right)\mathrm{d}\tau =\frac{1}{\beta -\alpha }.\end{array}$$

  (4)
• For $\alpha \ge \beta$ (sub-hyperbolic discounting), ${\int }_{\tau =0}^{T}D\left(\tau \right)\mathrm{d}\tau$ does not converge for $T\to +\infty$.

4. Model

This section introduces our model for stealthy timing-based security games with generalized hyperbolic-discounted costs and resource valuations. We model the same interaction first presented in van Dijk et al. [2] but present a simplified, more streamlined mathematical characterization and include discounting. Our model subsumes models without discounting [2] and with exponential discounting [14] as special cases (

Table 1. Discounting models used with FlipIt-like games with their discounting parameters and relation to the other models.

Class of Discounting	No Discounting [2]	Exponential Discounting [14]	Generalized Hyperbolic Discounting
Discounting parameters	∅	$\{{\beta }_A,{\beta }_A^c,{\beta }_D,{\beta }_D^c\}$2	$\{{\alpha }_D,{\beta }_D,{\alpha }_D^c,{\beta }_D^c,{\alpha }_A,{\beta }_A,{\alpha }_A^c,{\beta }_A^c\}$
Relation to other models	n.a.	$lim\lambda \to 0$ is None	$lim\alpha \to 0$ is Exponential

). Although adding generalized hyperbolic discounting is a small technical change, it has a large conceptual impact as a model for risk, ephemerality, or bounded rationality. It also necessitates an entirely different mathematical approach to model analysis.

4.1. Overview

In our two-player game, a defender (D) and an attacker (A) vie for control over a central resource. To obtain control, either player $i\in \{A,D\}$ can choose to pay a fixed instantaneous cost $c_i$ to ‘flip’ or immediately assume control of the resource. The last player to execute a move always controls the resource.

The controlling player accrues utility at a rate that decreases over time along a generalized hyperbolic function. The cost to execute a move is also time-discounted along a (possibly different) generalized hyperbolic function. Control is stealthy in the sense that neither player knows who controls the resource until the moment that they initiate an instantaneous flip. The remainder of this section formalizes the game.

4.2. Player Strategies

For player $i\in \{D,A\}$, define

$$\begin{array}{c}\hfill {\overrightarrow{t}}_i=(t_{i,0},t_{i,1},t_{i,2},\dots )\end{array}$$

to be a strictly increasing sequence of real times at which player i moves.3 The length of ${\overrightarrow{t}}_i$ can be finite or infinite. A player strategy in this game is defined completely by a probability distribution over a set of possible ${\overrightarrow{t}}_i$.

4.3. Player Control

The player control function indicates, for a given pair of move sequences $({\overrightarrow{t}}_D,{\overrightarrow{t}}_A)$, whether the defender or the attacker is deriving utility from the resource at any given moment in time. In the particular case where different players’ moves collide in time, we define the outcome as a no-op, meaning that resource ownership remains unchanged. Thus, removing any such collisions if necessary, we may assume without loss of generality that ${\overrightarrow{t}}_D\cap {\overrightarrow{t}}_A=\varnothing$.

Let

$$\begin{array}{c}\hfill \overrightarrow{t}={\overrightarrow{t}}_D\cup {\overrightarrow{t}}_A=(t_0,t_1,t_2,\dots )\end{array}$$

be the strictly increasing sequence of player move times. Then, for any time $t\ge t_0$, we define the latest flip time function by

$$\begin{array}{c}\hfill LFT:t\mapsto max\{t_k\in \overrightarrow{t}:t_k\le t\}.\end{array}$$

From time $t=0$ until the time of the first flip $t_0$, the defender has control of the resource. The player control function can, therefore, be expressed as

$$\begin{array}{c}\hfill PC:t\mapsto \left\{\begin{array}{cc}D\hfill & \mathrm{if}t<t_0\mathrm{or}LFT\left(t\right)\in {\overrightarrow{t}}_D\hfill \\ A\hfill & \mathrm{if}LFT\left(t\right)\in {\overrightarrow{t}}_A.\hfill \end{array}\right.\end{array}$$

(5)

The asymmetry of the player control function shows that the defender has an advantage due to starting the game in control of the resource.

We also define a player control indicator function

$${PC}_i:t\mapsto {\overrightarrow{1}}_{PC\left(t\right)=i},$$

(6)

which can be useful for integration. The player control indicator function tells us, for a given player $i\in \{D,A\}$ and time $t>0$, whether that player controls the resource at that time.

4.4. Player Utilities

Each player’s utility is defined to be the difference between the player’s gains and the player’s costs:

$$\begin{array}{c}\hfill u_i=G_i-C_i.\end{array}$$

Both gains and costs are subject to generalized hyperbolic discounting. We define generalized hyperbolic discounting, player gains, and then player costs in the following subsections.

4.4.1. Gains

Players achieve gains when in control of the resource. Gains initially accrue value at some rate of V units of value per unit of time. Gains decrease over time according to a player-dependent generalized hyperbolic discount function

$$D_i:\left\{\begin{array}{c}[0,+\infty [\to ]0,1]\hfill \\ {\displaystyle t\mapsto \frac{1}{{(1+{\alpha }_{i}t)}^{{\beta }_i/{\alpha }_i}},}\hfill \end{array}\right.$$

(7)

where ${\alpha }_i$ and ${\beta }_i$ are parameters characterizing player i’s (im)patience. We use reversed brackets to indicate open interval boundaries to avoid confusing intervals for ordered tuples, notably strategy profiles.

The discounted gain rate of player i up to time t may be determined by computing the expected weighted integral of ${PC}_i\left(t\right)$ up to t, normalized with respect to the total (discounted) value of the resource up to t:

$$\begin{array}{cc}\hfill G_i\left(t\right)& =\frac{\mathbb{E}\left[{\int }_{\tau =0}^t{PC}_i\left(\tau \right)·V·D_i\left(\tau \right)\mathrm{d}\tau \right]}{{\int }_{\tau =0}^{t}V·D_i\left(\tau \right)\mathrm{d}\tau }.\hfill \end{array}$$

(8)

The expectation is taken over possible game outcomes resulting from the player’s strategies, represented by stochastic process ${PC}_i$. Normalization allows comparing player gains for different discount rates and interpreting gain as a fraction of total achievable gain.

The gain of player i is the maximum limit of her discounted gain rate as time t moves to infinity:

$$G_i=\underset{t\to \infty }{lim\; sup}{G}_i\left(t\right).$$

(9)

Note that $G_i\left(t\right)\in [0,1]$ for every t, and so $G_i\in [0,1]$ as well. When the strategies are restricted to periodic or exponential, as described in Section 4.5, then ${lim}_{t\to \infty }{G}_i\left(t\right)$ exists for each player $i\in \{D,A\}$, so that we can replace lim sup with limit. If we would further assume that players have the same discounting factors so that $({\alpha }_D,{\beta }_D)=({\alpha }_A,{\beta }_A)$, then we would obtain $G_D+G_A=1$ by the linearity of expectation.

4.4.2. Costs

When players perform a move, this comes at a fixed instantaneous cost of $c_i>0$. As with gains, we discount costs according to a player-dependent generalized hyperbolic discount function

$$D_i^c:\left\{\begin{array}{c}[0,+\infty [\to ]0,1]\hfill \\ {\displaystyle t\mapsto \frac{1}{{(1+{\alpha }_i^{c}t)}^{{\beta }_i^c/{\alpha }_i^c}},}\hfill \end{array}\right.$$

(10)

where ${\alpha }_i^c$ and ${\beta }_i^c$ characterize i’s (im)patience, this time with respect to costs. Note that ${\alpha }_i^c$ and ${\beta }_i^c$ do not have to equal ${\alpha }_i$ and ${\beta }_i$, meaning that costs may be discounted at different rates from gains. This results in four discounting parameters per player and eight discounting parameters in total.

The discounted spending rate of player i up to time t may be determined by computing the expected weighted sum of instantaneous costs of the moves made by i up to time t, normalized with respect to the total (discounted) value of the resource:

$$C_i\left(t\right)=\frac{\mathbb{E}\left[{\sum }_{\tau \in {\overrightarrow{t}}_i,\tau \le t}{c}_i{D}_i^c\left(\tau \right)\right]}{{\int }_{\tau =0}^{t}V·D_i\left(\tau \right)\mathrm{d}\tau }.$$

(11)

As with gains, the expectation is taken with respect to the distribution used to define ${\overrightarrow{t}}_i$. Scaling gains and costs by the same factor (${\int }_{\tau =0}^{t}V·D_i\left(\tau \right)\mathrm{d}\tau$) makes the normalization operation neutral with respect to the behavior of utility-maximizing players. Finally, since we only deal with normalized costs and gains and since $c_i$ and V are both free parameters, we can, without loss of generality, assume that

$$V=1.$$

(12)

This assumption allows us to consider the instantaneous cost $c_i=c_i/V$ as a unitless value, expressing a fraction of the initial rate at which the resource accrues value per unit of time.

A player’s (total) cost is defined as the limit of her spending rate as time t moves to infinity:

$$C_i=\underset{t\to \infty }{lim}{C}_i\left(t\right).$$

(13)

4.5. Restricted Strategies

The description of all possible player strategies given in Section 4.2 is the most general class of strategies to which we can define a definite outcome according to our discounted FlipIt model. However, to exhibit an effective strategy and facilitate analysis, it is necessary to introduce additional constraints that reduce the number of free parameters in a strategy specification.

Each of the two strategy classes we consider in this paper—the class of exponential and the class of periodic strategies—has been studied extensively in prior work. Both classes are described by a single real parameter corresponding to the expected number of moves per unit of time, which we will refer to as flip rate or move rate throughout the paper. Both classes are also motivated by real-world examples of mitigation strategies in the context of advanced persistent threats.

4.5.1. Exponential Strategies

An exponential strategy is characterized by having the time of its first flip as well as its flip inter-arrival times (the time between subsequent flips) drawn from the same exponential distribution, described by probability density function

$$\begin{array}{c}\hfill f\left(t\right)=\nu e^{-\nu t}.\end{array}$$

If player i adopts an exponential strategy, we refer to the exponential distribution’s rate parameter ${\nu }_i$ as her flip rate, move rate, or play rate. The expected time between two of her moves then equals $1/{\nu }_i$.

Exponential strategies are fully characterized by the single parameter ${\nu }_i$ and are robust to information leakage due to their memorylessness properties. These properties make them a straightforward choice when the timing of moves might be observable.

4.5.2. Periodic Strategies with Random Phase

A strategy is a periodic strategy iff the time between consecutive moves is constant. If player i adopts a periodic strategy, the time between her moves is the period of her strategy, and we denote it by ${\delta }_i$. The inverse of the period, ${\nu }_i=1/{\delta }_i$, is her strategy’s play rate. In the context of periodic strategies, we refer to the time of the first flip, $t_{i,0}$, as the phase and denote it as ${\phi }_i$. Periodic strategies with random phase are those periodic strategies whose phase is drawn uniformly random from the positive values smaller than its period. A periodic strategy with random phase is fully characterized by the single real number ${\delta }_i$, or equivalently ${\nu }_i$. Formally,

$$\begin{array}{cc}\hfill t_{i,0}={\phi }_i\sim U[0,\delta ]& \mathrm{and}\hfill \\ \hfill t_{i,n+1}-t_{i,n}=\Delta t_{i,n}=\delta & \mathrm{for}\mathrm{all}n\ge 0,\hfill \end{array}$$

where $U[0,\delta ]$ denotes the uniform distribution between 0 and $\delta$.

As with exponential strategies, periodic strategies are specified by a single real parameter. They are of even more practical importance because decision-makers commonly implement them in real-world systems (e.g., Microsoft’s “Patch Tuesday” and secret rotation policies). An additional reason for looking into periodic strategies is that, when not discounting, they tend to perform outstandingly in the sense that they strictly dominate a wide class of strategies, including the exponential ones. This result was formalized in van Dijk et al. [2], and we revisit it in Section 6, where we state the property more precisely and show that it no longer applies in our discounted setting.

5. Analysis

In this section, we mathematically analyze our game and the behavior of participating rational players.

We begin by considering the case of sub-hyperbolic discounting ($\alpha \ge \beta$), where we state our principal result and show that the analysis of outcomes fundamentally reduces to that of the original FlipIt model without discounting as presented by van Dijk et al. [2]. For the case of super-hyperbolic discounting ($\alpha <\beta$), our analysis requires many new investigations. We begin by addressing structural aspects of our game model that apply to both the exponential and the periodic strategy classes. We then proceed through a sequence of analyses involving successively more advanced notions of model outcomes, considering both strategy classes at each stage. The first stage addresses player utilities. The following stages continue the analyses addressing incentives, best responses, and, finally, Nash equilibria.

5.1. Sub-Hyperbolic Discounting

This section characterizes player behavior of hyperbolic and sub-hyperbolic discounters, i.e., player behavior when $\alpha \ge \beta$.

Theorem 1 (Player utilities for (sub-)hyperbolic discounters).

For any strategy profile producing convergent utilities when not discounting, the utilities of players discounting with $\alpha \ge \beta$ are the same as when not discounting. Specifically, discounted gains equal non-discounted gains

$$\underset{t\to \infty }{lim}\frac{\mathbb{E}\left[{\int }_{\tau =0}^t{PC}_i\left(\tau \right)\mathrm{d}\tau \right]}{t}=\underset{t\to \infty }{lim}\frac{\mathbb{E}\left[{\int }_{\tau =0}^t{PC}_i\left(\tau \right)D_i\left(\tau \right)\mathrm{d}\tau \right]}{{\int }_{\tau =0}^t{D}_i\left(\tau \right)\mathrm{d}\tau },$$

(14)

and discounted costs equal non-discounted costs

$$\underset{t\to \infty }{lim}\frac{\mathbb{E}\left[{\sum }_{\tau \in {\overrightarrow{t}}_i,\tau \le t}{c}_i\right]}{t}=\underset{t\to \infty }{lim}\frac{\mathbb{E}\left[{\sum }_{\tau \in {\overrightarrow{t}}_i,\tau \le t}{c}_i{D}_i^c\left(\tau \right)\right]}{{\int }_{\tau =0}^t{D}_i^c\left(\tau \right)\mathrm{d}\tau }.$$

(15)

Proof Outline.

To start, we show that the running average functional form with an unbounded denominator has the property that restarting the game at any fixed future point in time gives a new functional form with the same limit. Given a number $\epsilon >0$, we construct a tracking mechanism on the functional form’s behavior, verifying that it adheres to the required convergence properties. The construction deterministically factors time into an infinite sequence of intervals $[s_k,s_{k+1}]$, where $s_k$ is the kth restart time, and $s_{k+1}$ is the infimum over the set of absolute times, which are required to exist by applying the limit definition to the kth functional form and $\epsilon$.

A key property of this construction is that in the limit as $k\to \infty$, the absolute restart times $s_k$ dominate the interval durations $(s_{k+1}-s_k)$. We do not assume this. We prove that it has to be true of our construction for each fixed $\epsilon$, or else there is a direct contradiction to our original limit assumption.

Now, we come to the discounted functional form. The only real attachment we have to the original functional form is a simple bounding relationship due to $D\left(\tau \right)$ decreasing in $\tau$, which can be applied to finite integration intervals. Therefore, we use that to show that for all sufficiently large k, the discounted functional form on the interval $[s_k,s_{k+1}]$ has to be close to the same limit as the non-discounted functional form. To wrap things up, for every sufficiently large time t, the well-defined representation of the discounted functional form in terms of the interval construction has three parts: a finite part early in time, an unbounded middle part, which is close to the correct running average value, and the present moment part, which is dominated by the restart time, and hence by the middle part.

The conclusion is that the limit value of the discounted functional form must be within $4\epsilon$ of the non-discounted limit value, and since $\epsilon$ was chosen arbitrarily at the beginning of the construction, the two limit values are the same. Due to notational differences between the functional form representations for gains and costs, the formal proofs are provided in different subsections, but the outline above is the same for both forms.

Appendix A gives the detailed proof.    □

Although we state and prove Theorem 1 for (sub-)hyperbolic discounting, the theorem and proof generalize to a much larger class of discounting functions (or other decreasing functions), the most crucial restriction being that the total discounted value accrued over time must diverge. Note that we impose no restrictions on the player’s strategy spaces except that player strategies must result in outcomes such that the limit expression for undiscounted utility exists, that is, ${lim}_{t\to \infty }\frac{\mathbb{E}\left[{\int }_{\tau =0}^t{PC}_i\left(\tau \right)\mathrm{d}\tau \right]}{t}$ must be defined. This is the case for the exponential and periodic strategy regimes.

Corollary 1.

When ${\alpha }_i\ge {\beta }_i$, ${\alpha }_j\ge {\beta }_j$, our model of discounted security games of timing is strategically equivalent to that of FlipIt-like games without discounting.

Proof. 

Each player evaluates the benefit of a periodic or exponential strategy based on the outcome. The theorem states that discounting (sub-)hyperbolically does not change this outcome, irrespective of the strategy that produced that outcome. Therefore, discounting does not change the computation of the optimal strategy.    □

5.2. Super-Hyperbolic Discounting

When discounting super-hyperbolically (${\alpha }_i<{\beta }_i$), player i’s calculated resource valuation is finite, even when accumulated over all of time.

With a finite total valuation, splitting the game into two parts turns out to be helpful for the derivation of player utilities: one typically finitely long part spanning from the start of the game until the first move by either player and another part spanning the remainder of time. We refer to the gain accrued by the defender, who starts in control, over the first part as the defender advantage ${\overline{D}}_D$. The gain obtained by players during the second part is independent of their identity as attacker or defender, and we refer to player i’s gain over this part as i’s anonymous gain ${\overline{G}}_i$. Appendix B.1 formally defines the concepts of defender advantage and anonymous gain, presents some of their properties, and uses them to present generic close-to-analytic expressions for $G_D$, $C_D$, $G_A$, and $C_A$.

5.3. Player Utilities for Super-Hyperbolic Discounting

For super-hyperbolic discounting behavior, i.e., when $\alpha <\beta$, player utilities depend on the specific values of parameters $\alpha$ and $\beta$. This section lists analytical expressions for player utilities for exponential and periodic play.

5.3.1. For Exponential Play

The expression for player gain is not an elementary function but can be expressed in terms of the exponential integral function.

Definition 1 (Exponential integral function).

Define the exponential integral function as:

$$\begin{array}{c}\hfill E_r\left(x\right)={\int }_{s=1}^{+\infty }\frac{\mathrm{d}s}{e^{sx}{s}^r}.\end{array}$$

(16)

To ease notation, we also introduce a helper function.

Definition 2 (Helper function for exponential play).

Define the helper function for exponential play as:

$$\begin{array}{c}\hfill f:\left\{\begin{array}{c}{\mathbb{R}}_0^{+}\times {\mathbb{R}}_0^{+}\to ]0,1[\hfill \\ (r,x)\mapsto e^x·x·E_r\left(x\right).\hfill \end{array}\right.\end{array}$$

(17)

The anonymous gain for exponential play has an elegant description through this helper function.

Lemma 1 (Anonymous gains for exponential play).

If both players are playing exponentially, then player i’s anonymous gain is given by:

$$\begin{array}{c}\hfill {\overline{G}}_i=\frac{{\nu }_i}{{\nu }_i+{\nu }_j}·f\left(\frac{{\beta }_i-{\alpha }_i}{{\alpha }_i},\frac{{\nu }_i+{\nu }_j}{{\alpha }_i}\right).\end{array}$$

(18)

Proof Outline.

The total anonymous gain is the expected gain generated by the resource after the first move by either player is made. Player i moves at a rate or expected frequency of ${\nu }_i$, and her probability of having moved last, and therefore being in control, equals ${\nu }_i/({\nu }_i+{\nu }_j)$ at any point in time following the first move. We also show that the point in time at which the first move arrives is distributed according to an exponential distribution with rate parameter ${\nu }_i+{\nu }_j$. Finally, we derive a formula for the total anonymous gain by taking expectations over the time of the first move.

The full proof is in Appendix B.2.    □

Lemma 2 (Costs for exponential play).

The cost of an exponential strategy with play rate ${\nu }_i$ is given by:

$$C_i=c_i·\frac{{\alpha }_i+{\beta }_i}{{\alpha }_i^c+{\beta }_i^c}·{\nu }_i.$$

(19)

Proof. 

The probability density of flipping at any time is constant and equal to the play rate ${\nu }_i$. The discounted instantaneous cost of performing a flip at time t is $c_i·D_i^c\left(t\right)$. Obtain the stated result by evaluating

$$\begin{array}{c}\hfill C_i=({\alpha }_i+{\beta }_i){\int }_{t=0}^{+\infty }{\nu }_i·c_i·D_i^c\left(t\right)\mathrm{d}t.\end{array}$$

   □

The structure of the cost expression Equation (19) reveals that the presence of different discounting factors for costs and gains complicates notation without impacting the results. We obtain the same range of behaviors by assuming costs and gains are discounted by the same parameters and varying only the instantaneous cost of a move $c_i$. We will assume that the discounting parameters for costs and gains are equal (${\alpha }_i^c={\alpha }_i,{\beta }_i^c={\beta }_i$), essentially re-defining instantaneous cost as

$$\begin{array}{c}\hfill c_i·\frac{{\alpha }_i+{\beta }_i}{{\alpha }_i^c+{\beta }_i^c}.\end{array}$$

(20)

The utility functions for exponential play follow from Lemmas 1 and 2.

Theorem 2 (Utilities for exponential play).

If both players are playing exponentially and have ${\alpha }_i<{\beta }_i$, their utilities are given by:

$$\begin{array}{cc}\hfill u_D& =-c_D{\nu }_D-\frac{{\nu }_A}{{\nu }_D+{\nu }_A}·f\left(\frac{{\beta }_D-{\alpha }_D}{{\alpha }_D},\frac{{\nu }_D+{\nu }_A}{{\alpha }_D}\right)+1\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill u_A& =-c_A{\nu }_A+\frac{{\nu }_A}{{\nu }_D+{\nu }_A}·f\left(\frac{{\beta }_A-{\alpha }_A}{{\alpha }_A},\frac{{\nu }_D+{\nu }_A}{{\alpha }_A}\right).\hfill \end{array}$$

(22)

Proof. 

The attacker never obtains any utility before his first move. Therefore, his gain is equal to his anonymous gain. Subtracting costs from gains yields Equation (21).

To obtain the defender’s gain, we use the fact that if ${\alpha }_D={\alpha }_A$ and ${\beta }_D={\beta }_A$, then the players’ gains sum to one. This relation is discussed in Appendix B as Equation (A43). Writing the defender’s gain as one minus the expression for the anonymous gain and subtracting costs yields Equation (22).    □

Figure 2 illustrates gains and utilities for exponential play. The defender has a notable advantage over the attacker because she starts in control of the resource. The gain curves show this advantage decreasing as players move more often. Higher play rates by i (right for $i=D$, up for $i=D$) correspond to i moving and taking control of the resource more often, increasing i’s gain. Similarly, higher play rates by her opponent j (up for $i=D$, right for $i=A$) decrease i’s gain.

Higher play rates by i always increase her cost. The utility curves illustrate that these flip costs always, at some point, offset the increase in gain. We can also see where players’ utilities are maximal. The defender’s utility is always highest at the origin, where it equals one. The attacker’s utility reaches a maximum for some point along the abscissa (where it depends on ${\alpha }_A$, ${\beta }_A$, and $c_A$).

5.3.2. For Periodic Play

As for exponential play, we introduce a helper function to ease notation.

Definition 3 (Helper function for periodic play).

Define the helper function for periodic play as:

$$\begin{array}{c}\hfill h_i\left(\nu \right)=\frac{\nu }{(2{\alpha }_i-{\beta }_i)(3{\alpha }_i-{\beta }_i)}\left({\left(1+\frac{{\alpha }_i}{\nu }\right)}^{\frac{3{\alpha }_i-{\beta }_i}{{\alpha }_i}}-1\right).\end{array}$$

(23)

We use the notation $h_i^{\prime }\left(\nu \right)$ to refer to the helper function’s derivative, $\frac{\mathrm{d}{h}_i\left(\nu \right)}{\mathrm{d}\nu }$.

Unlike for exponential play, the expression for anonymous player gain depends on whether the player is faster or slower.

Lemma 3 (Anonymous gains for periodic play).

If both players play periodically and have${\alpha }_i<{\beta }_i$, then the anonymous gain of the slower player is given by:

$$\begin{array}{c}{\overline{G}}_i{|}_{{\nu }_i\le {\nu }_j}={\nu }_i·\left(h_i\left({\nu }_j\right)-\frac{1}{2{\alpha }_i-{\beta }_i}\right).\end{array}$$

(24)

The anonymous gain of the faster player is given by:

$$\begin{array}{c}\hfill {\overline{G}}_i{|}_{{\nu }_i\ge {\nu }_j}={\nu }_i·\left(h_i\left({\nu }_i\right)-\frac{1}{2{\alpha }_i-{\beta }_i}+({\nu }_j-{\nu }_i)h_i^{\prime }\left({\nu }_i\right)\right).\end{array}$$

(25)

The derivation of these non-trivial expressions can be found in Appendix B.3.

We can derive the costs and utilities for periodic play in the same way as for exponential play.

Lemma 4 (Costs for periodic play).

The cost of a periodic strategy with play rate ${\nu }_i$ is given by:

$$\begin{array}{c}\hfill C_i=c_i·\frac{{\beta }_i-{\alpha }_i}{{\beta }_i^c-{\alpha }_i^c}·{\nu }_i.\end{array}$$

(26)

Proof. 

The proof is the same as the proof for exponential play (Lemma 2).    □

The cost formulas for exponential and periodic play are identical, allowing us to redefine the instantaneous costs using Equation (20) as for exponential play. In the remainder of this paper, we will always assume that ${\alpha }_i^c={\alpha }_i$ and ${\beta }_i^c={\beta }_i$.

Theorem 3 (Utilities for periodic play).

If the defender is the faster player (${\nu }_D\ge {\nu }_A$), player utilities are given by:

$$\begin{array}{c}{\left.u_D\right|}_{{\nu }_D\ge {\nu }_A}=-c_D{\nu }_D-{\nu }_A·\left(h_D\left({\nu }_D\right)-\frac{1}{2{\alpha }_D-{\beta }_D}\right)+1\end{array}$$

(27)

$$\begin{array}{c}{\left.u_A\right|}_{{\nu }_D\ge {\nu }_A}=-c_A{\nu }_A+{\nu }_A·\left(h_A\left({\nu }_D\right)-\frac{1}{2{\alpha }_A-{\beta }_A}\right).\end{array}$$

(28)

If the defender is the slower player (${\nu }_D\le {\nu }_A$), player utilities are given by:

$$\begin{array}{c}{\left.u_D\right|}_{{\nu }_D\le {\nu }_A}=-c_D{\nu }_D-{\nu }_A·\left(h_D\left({\nu }_A\right)-\frac{1}{2{\alpha }_D-{\beta }_D}+({\nu }_D-{\nu }_A)h_D^{\prime }\left({\nu }_A\right)\right)+1\end{array}$$

(29)

$$\begin{array}{c}{\left.u_A\right|}_{{\nu }_D\le {\nu }_A}=-c_A{\nu }_A+{\nu }_A·\left(h_A\left({\nu }_A\right)-\frac{1}{2{\alpha }_A-{\beta }_A}+({\nu }_D-{\nu }_A)h_A^{\prime }\left({\nu }_A\right)\right).\end{array}$$

(30)

Note that although it is not possible to evaluate the formulae in Theorem 3 for ${\beta }_i=2{\alpha }_i$ or ${\beta }_i=3{\alpha }_i$, these gaps in the function’s domain are removable singularities. To deal with these, we re-define $u_i$ as the continuous extension of the formulae above; Appendix B.3 lists the full definition.

Figure 3 illustrates gains and utilities for periodic play. A comparison of periodic to exponential gains (Figure 2) shows that they are similar but that the rate of change of players’ gains with respect to their move rates is higher for periodic play. Since the costs for periodic and exponential play are the same, this is also reflected in players’ utilities. The defender’s advantage decreases faster for periodic play as players start moving more quickly.

The super-hyperbolically discounted utility functions look and exhibit behavior that is very similar to the exponentially discounted utility functions derived in Merlevede et al. [14], both for periodic and exponential play. The generalized hyperbolic model interpolates between the exponentially discounted and the undiscounted utilities, and we can observe that this interpolation results in very “smoothly” changing utilities, where small changes to ${\alpha }_i$ and ${\beta }_i$ result in small changes to the player utilities and, ultimately, even in the behavior of rational players. As we will see in the coming sections and discuss in Section 6, discounting parameters for which $2{\alpha }_i<{\beta }_D$ result in a function with mostly the same characteristics as the (simpler) exponentially discounted utility functions, while the game with ${\alpha }_i<{\beta }_i<2{\alpha }_i$ exhibits some new characteristics.

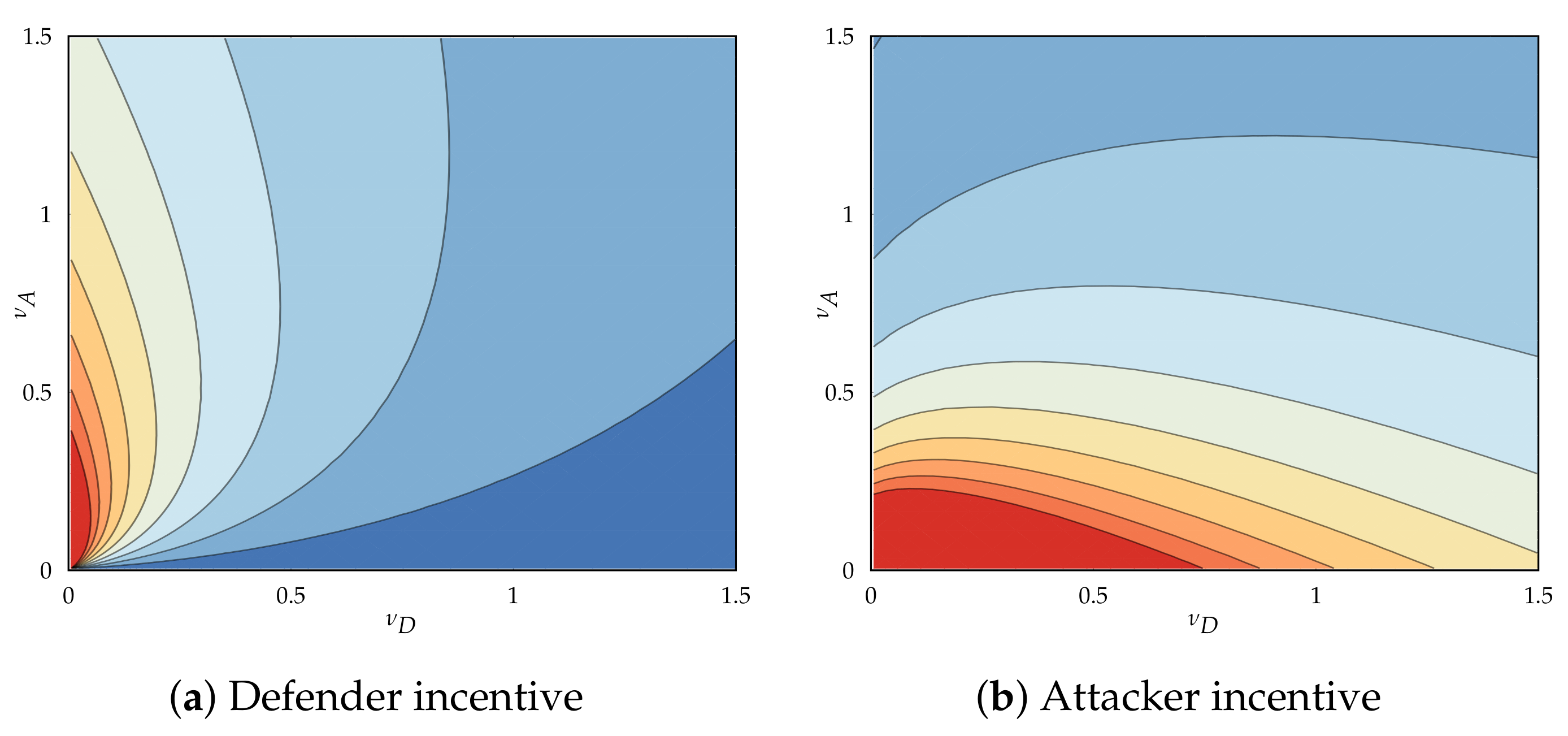
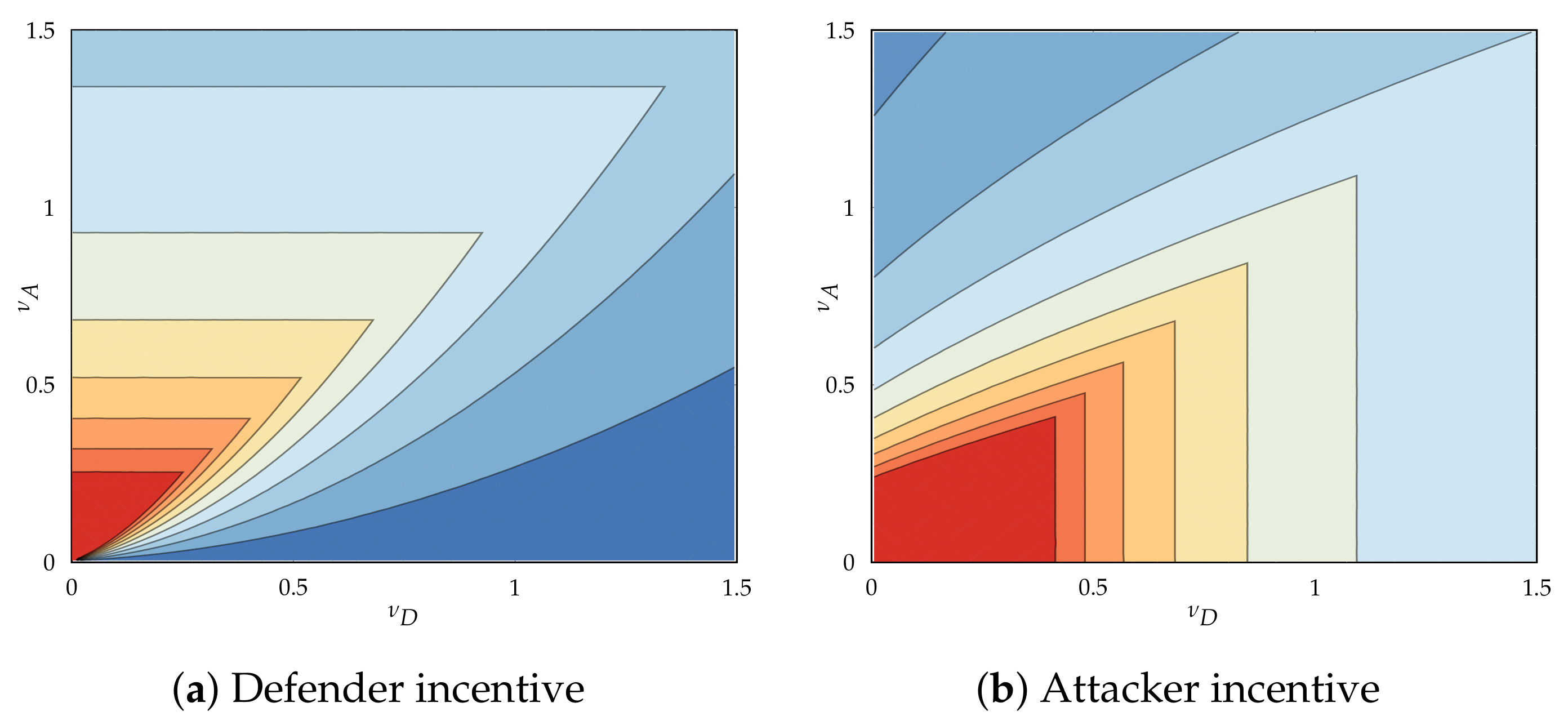
5.4. Player Incentives and Best Responses

Knowing players’ utility functions, our attention turns to how players behave as they try to optimize their utility. The first step involves player incentives.

Definition 4 (Player incentive).

Player i’s incentive is the partial derivative of her utility to her play rate, expressed in standard mathematical notation as

$$\frac{\partial u_i}{\partial {\nu }_i}.$$

Player incentives are closely related to player best responses because the roots of a player’s incentive function point to the local optima of her utility function.

A player’s incentive is generally a function of both her own play rate and her opponent’s play rate. Appendix C.1 states expressions for the player incentives for exponential and periodic play.

Figure 4 and Figure 5 display players’ incentive functions for exponential and periodic play. The defender’s incentive to play is low when the attacker moves slowly. She generally has less motivation to move than the attacker, as she is always in control while the resource is the most valuable. Note that the graphs assume that executing a move is free ($c_D=c_A=0$), causing incentives to always be positive. Increasing the cost of a move does not change the shape of the incentive function but shifts it downwards (by an amount $c_i$). Other properties of these graphs are discussed in the following sections.

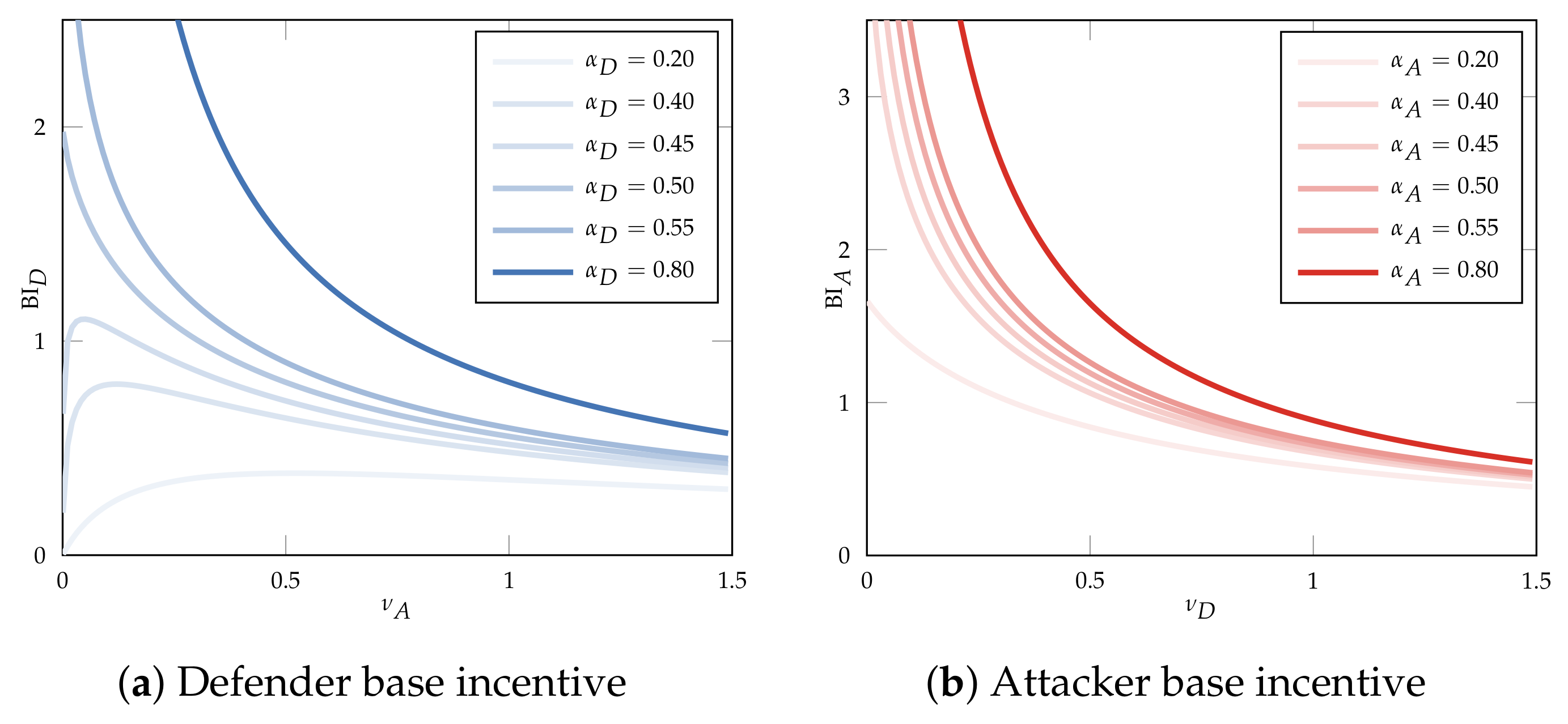
5.4.1. Directionality of Incentives and Base Incentive

Using standard analytical techniques, we can show that incentives are decreasing for both exponential and periodic play (see Appendix C.2). Specifically, for exponential play, a player’s incentive is always strictly decreasing in her own play rate. For periodic play, the direction of a player’s incentive depends on whether she is the faster or slower-moving player. If she is the slower-moving player, her incentive is independent of her play rate, while her incentive is strictly decreasing in her play rate if she is the faster-moving player. We state this more precisely in Lemmas A18 and A22. The independence of incentive is clearly visible in Figure 5 as perfectly horizontal and vertical contour lines.

As players’ incentives are always decreasing, their incentive is maximal when they are not playing $({\nu }_i=0)$, and the existence of a non-zero best response depends on their incentive when they do not play. This observation motivates the definition of base incentive.

Definition 5 (Base incentive).

Player i’s base incentive when playing against a player who moves at rate ${\overline{\nu }}_j$ is her incentive when not playing (${\nu }_i=0$). Define player i’s base incentive functionas:

$$\begin{array}{c}\hfill {BI}_i\left(\nu \right)={\left.\frac{\partial u_i}{\partial {\nu }_i}\right|}_{\genfrac{}{}{0ex}{}{{\nu }_i=0}{{\nu }_j=\nu }}.\end{array}$$

(31)

Note that a player’s base incentive function is a function of her opponent’s play rate. Figure 6 displays base incentive functions for exponential play. Graphs of the base incentive for periodic play look very similar.

Using the concept of base incentive and leveraging what we know of the directionality of the incentive function, we can state the following.

Corollary 2 (Best responses for exponential play).

For exponential play, each player has a unique, single-valued best response determined by her base incentive and incentive as follows:

• If her base incentive is negative, her best response is not to play.
• If her base incentive is strictly positive, then her incentive function has a single root at ${\nu }_i^{★}>0$, and her best response is to play at rate ${\nu }_i^{★}$.

Corollary 3 (Best responses for periodic play).

Player i’s best response to her opponent playing at rate ${\overline{\nu }}_j$ can be characterized in terms of her base incentive as follows:

• If her base incentive is strictly negative, then her unique best response is not to play.
• If her base incentive is zero, then any play rate ${\nu }_i\in [0,{\overline{\nu }}_j]$ is a best response.
• If her base incentive is strictly positive, then her incentive function has a single root at ${\nu }_i^{★}>0$, and her best response is to play at rate ${\nu }_i^{★}$.

Corollaries 2 and 3 imply that each of the contour lines in Figure 4 and Figure 5 corresponds to a best-response curve for a specific flip cost ($c_i$). The properties of the incentive functions stated above allow finding best responses as the roots of the incentive function using straightforward numerical procedures.

5.4.2. Directionality and Origin of Base Incentive

We can analyze the behavior of the base incentive function using standard analytical techniques (see Appendix C.3). The attacker’s base incentive is always strictly decreasing. The behavior of the defender’s base incentive function is discontinuous at ${\nu }_A=0$ and depends on the relative size of $2{\alpha }_D$ and ${\beta }_D$ and ${\nu }_A=0$. If $2{\alpha }_D\ge {\beta }_D$, then her base incentive function is strictly decreasing, similar to the attacker’s. If $2{\alpha }_D<{\beta }_D$, then her base incentive is first strictly increasing, then strictly decreasing. We state this more precisely in Lemma A23.

As players’ base incentives are usually maximal when their opponents are barely moving at all, whether or not players choose to participate in the game is related to the sign of the base incentive near the origin. We can again analyze the behavior of base incentives near the origin using standard analytical techniques. For both exponential and periodic play, the base incentive of the defender is equal to $-c_D$ at the origin. The value of the right limit of the base incentive of the defender at zero (${\nu }_A\downarrow 0)$, and the value of the base incentive of the attacker at zero (${\nu }_D=0$), depends on the relative size of $2{\alpha }_i$ and ${\beta }_i$. The origin base incentive becomes unboundedly large if $2{\alpha }_i>{\beta }_i$ and converges to specific values for $2{\alpha }_i<{\beta }_i$. We state this precisely in Lemmas A28 and A29.

The properties of the base incentive function, together with their values at the origin, allow us to state the following results on best responses to non-participatory players.

Corollary 4 (Defender best response to non-participatory attacker).

For exponential and periodic play, the defender’s best response to a non-participatory attacker is not to play.

Corollary 5 (Attacker best response to non-participatory defender).

For exponential and periodic play, the attacker’s best response to a non-participatory defender is as follows:

• If $2{\alpha }_A\ge {\beta }_A$, move at non-zero rates, regardless of cost ($c_i$).
• If $2{\alpha }_A<{\beta }_A$, move at non-zero rates iff $c_A<\frac{1}{{\beta }_A-2{\alpha }_A}$ and at the zero rate otherwise.

5.5. Equilibria for Super-Hyperbolic Discounting

This section characterizes and presents numerical procedures for finding Nash equilibria when both players discount super-hyperbolically.4 It starts with an investigation of equilibria in which at least one player does not move for both the periodic and the exponential regimes and to which we will refer as non-participatory equilibria (Section 5.5.1). It then discusses participatory equilibria for the exponential regimes (Section 5.5.2) and the periodic regimes (Section 5.5.3).

5.5.1. Non-Participatory Equilibria

Non-participatory equilibria are (Nash) equilibria in which at least one player never moves. The following can be stated as a corollary of Corollaries 4 and 5 and Lemma A28.

Corollary 6

For both exponential and periodic play, characterize the set of non-participatory equilibria as follows:

• If $2{\alpha }_A<{\beta }_A$ and $c_A\ge \frac{1}{2{\alpha }_A-{\beta }_A}$, then there is a non-participatory equilibrium in which neither player moves.
• Otherwise, there may be an equilibrium in which only the attacker plays if $2{\alpha }_D<{\beta }_D$ or if $2{\alpha }_D={\beta }_D$ and $c_D\ge \frac{1}{{\alpha }_D}$.

There are no other non-participatory equilibria.

Algorithm 1 presents a way to numerically determine the set of non-participatory strategy profiles.

Algorithm 1 Procedure for finding the set of non-participatory equilibria for exponential and periodic play

1: if $2{\alpha }_A<{\beta }_A$ and $c_A\ge \frac{1}{2{\alpha }_A-{\beta }_A}$ then 2:     return $\left\{\right(0,0\left)\right\}$ // Neither player moves 3: end if 4: if $2{\alpha }_D={\beta }_D$ and $c_D\ge \frac{1}{{\alpha }_D}$ then 5:     return $\left\{(0,{\nu }_A^{★})\right\}$ // Only attacker moves 6: end if 7: if $2{\alpha }_D<{\beta }_D$ then    // Compute best response of attacker to non-participatory defender 8:     ${\nu }_A^{★}\to Bisect({\left.\frac{\partial u_A}{\partial {\nu }_A}\right|}_{\genfrac{}{}{0ex}{}{{\nu }_A=x}{{\nu }_D=0}}, X_{\min }=0, X_{\max }=\frac{1}{c_A})$ // Strictly decreasing    // Inspect defender’s base incentive at ${\nu }_A^{★}$ 9:     if ${\mathrm{BI}}_D\left({\nu }_A^{★}\right)$ ≤ 0 then 10:         return $\left\{(0,{\nu }_A^{★})\right\}$ // Only attacker moves 11:    end if 12: end if 13: return ∅ // No non-participatory equilibria

5.5.2. Participatory Equilibria for Exponential Play

We now focus on equilibria in which both players move at non-zero rates, beginning with equilibria for the exponential strategy regime.

From our characterization of best responses for exponential play in terms of the base incentive function (Corollary 2) and the direction and the roots of this base incentive function (Lemma A23), we can bound the domain in which to look for participatory equilibria $({\nu }_D^{★},{\nu }_A^{★})$.

• ${\nu }_D^{★}\in ]0,{\overline{\nu }}_D[$, where ${\overline{\nu }}_D>0$ is the (unique) root of the attacker’s base incentive function.
• If $2{\alpha }_D\ge {\beta }_D$, then ${\nu }_A^{★}\in ]0,{\overline{\nu }}_A[$, where ${\overline{\nu }}_A>0$ is the root of the defender’s base incentive function.
• If $2{\alpha }_D<{\beta }_D$, then ${\nu }_A^{★}\in ]{\overline{\nu }}_A^{\left(1\right)},{\overline{\nu }}_A^{\left(2\right)}[$, where ${\overline{\nu }}_A^{\left(1\right)}$ and ${\overline{\nu }}_A^{\left(2\right)}$ are the roots of the defender’s base incentive function with ${\overline{\nu }}_A^{\left(2\right)}\ge {\overline{\nu }}_A^{\left(1\right)}>0$.

If the mentioned roots do not exist, there is no participatory equilibrium.

We can use a numerical procedure to find the participatory roots for exponential play. We find equilibria by searching through the domain $]0,{\overline{\nu }}_D[$ for the stable points ${\nu }_D^{★}$ of the function ${\nu }_D\mapsto {BR}_D\left({BR}_A\left({\nu }_D\right)\right)$, equivalently the roots of the function

$$r:\left\{\begin{array}{cc}]0,{\overline{\nu }}_D[\hfill & \to ]-\infty ,{\nu }_D]\hfill \\ {\nu }_D\hfill & \mapsto {\nu }_D-{BR}_D\left({BR}_A\left({\nu }_D\right)\right).\end{array}\right.$$

(32)

The strategy profile $({\nu }_D^{★},{BR}_A\left({\nu }_D^{★}\right))$ is then an equilibrium.

We can obtain the same results by looking for stable points of the function ${\nu }_A\mapsto {BR}_A\left({BR}_D\left({\nu }_A\right)\right)$.

5.5.3. Participatory Equilibria for Periodic Play

For periodic play, the insight that a players’ incentives are independent of their play rates when they are the slower player allows us to restrict the set of equilibria immediately. The following can be stated as a corollary of Corollary 3.

Corollary 7 (Faster play rate in participatory equilibrium).

In any participatory equilibrium, the faster-moving player moves at a rate corresponding to a root of the slower player’s base incentive function.

When the faster player moves at a rate ${\overline{\nu }}_f$ that is a root of the slower player’s base incentive, any rate ${\nu }_s\in ]0,{\overline{\nu }}_f]$ is a best response for the slower player. Whether there exists an equilibrium involving ${\overline{\nu }}_f$ depends on whether one of these play rates makes playing ${\overline{\nu }}_f$ a best response for the faster player (${\overline{\nu }}_f={BR}_f\left({\nu }_s\right)$).

We analyze the direction of the faster player’s incentive to see if such a ${\nu }_s$ exists. It turns out that we can define the direction of player incentives in terms of the base incentive function.

Lemma 5.

For periodic play, the direction of the incentive of the faster player playing at rate ${\overline{\nu }}_f$ with respect to the slower player’s play rate is opposite to the direction of the slower player’s base incentive in ${\overline{\nu }}_f$:

$$\begin{array}{c}\hfill {\left.\frac{{\partial }^2{u}_f}{\partial {\nu }_s\partial {\nu }_f}\right|}_{{\nu }_s\le {\nu }_f}=-\frac{\mathrm{d}{BI}_{s,f}\left({\nu }_f\right)}{\mathrm{d}{\nu }_f}=-{BI}_{s,f}^{\prime }\left({\nu }_f\right),\end{array}$$

where ${BI}_{s,f}$ is the base incentive function of the slower player evaluated using the faster player’s discounting parameters ${\alpha }_f$ and ${\beta }_f$.

Proof. 

For equal discounting parameters, the sum of player gains is constant (Equation (A43)). For exponential and periodic play, the impact of cost on incentive is constant, so the change of the faster player’s incentive with respect to the slower player’s move rate is opposite to the change of the slower player’s incentive with respect to the faster player’s move rate:

$$\begin{array}{c}\hfill \frac{\partial }{\partial {\nu }_s}\left(\frac{\partial u_f}{\partial {\nu }_f}\right)=\frac{\partial }{\partial {\nu }_s}\left(-\frac{\partial u_s}{\partial {\nu }_f}-c_f-c_s\right)=-\frac{\partial }{\partial {\nu }_f}\left(\frac{\partial u_s}{\partial {\nu }_s}\right).\end{array}$$

The slower player’s incentive equals her base incentive (Lemma A22).    □

This gives us an elegant description of the faster player’s incentive.

Lemma 6.

For periodic play, the faster player’s incentive is given by

$$\begin{array}{c}\hfill \frac{\partial u_f}{\partial {\nu }_f}={BI}_f\left({\nu }_f\right)+({\nu }_f-{\nu }_s){BI}_{s,f}^{\prime }\left({\nu }_f\right).\end{array}$$

(33)

Proof. 

Lemma 5 implies that the faster player’s incentive changes linearly as a function of the slower player’s move rate, with the slope given by $-{BI}_{s,f}^{\prime }\left({\nu }_f\right)$. The functions for incentive for slower and faster players are equal to each other when play rates are equal; therefore, when ${\nu }_s={\nu }_f$, player f has an incentive of ${BI}_f\left({\nu }_f\right)$.    □

Corollary 6 and Equation (33) reveal that the faster player’s incentive behaves linearly with respect to the slower player’s move rate. We leverage this to determine the play rates by the slower player for which the faster player’s move rate is a best response. We can state the following as a corollary of Corollary 3 and Lemma 6.

Corollary 8 (Slower play rate in participatory equilibrium for periodic play).

Let ${\overline{\nu }}_f>0$ be the play rate of the faster-moving player. Move rates for the slower player to which move ${\overline{\nu }}_f$ is a best response for the faster player can be characterized as follows:

$$S_s\left({\overline{\nu }}_f\right)=\left\{\begin{array}{cc}[0,{\overline{\nu }}_f]\hfill & if{BI}_{s,f}^{\prime }\left({\overline{\nu }}_f\right)=0and{BI}_f\left({\overline{\nu }}_f\right)=0\hfill \\ \varnothing \hfill & if{BI}_{s,f}^{\prime }\left({\overline{\nu }}_f\right)=0and{BI}_f\left({\overline{\nu }}_f\right)\ne 0\hfill \\ \left\{\frac{{BI}_f\left({\overline{\nu }}_f\right)}{{BI}_{s,f}^{\prime }\left({\overline{\nu }}_f\right)}-{\overline{\nu }}_f\right\}\cap [0,{\overline{\nu }}_f]\hfill & otherwise.\hfill \end{array}\right.$$

Corollaries 7 and 8 and our knowledge of the base incentive function allow us to finally characterize the Nash equilibria for periodic play.

Theorem 4 (Participatory equilibria).

The set of equilibria where the defender moves faster than the attacker (${\nu }_D^{★}\ge {\nu }_A^{★}$) is given by:

$$\left\{({\nu }_D^{★},{\nu }_A^{★})\mid {\nu }_D^{★}\in \{{\nu }_D\mid {BI}_A\left({\nu }_D\right)=0\},{\nu }_A^{★}\in S_A\left({\nu }_D^{★}\right)\right\},$$

where $S_A$ is as in Lemma 8. If $2{\alpha }_A\ge {\beta }_A$ or $c_A$ is $<\frac{1}{{\beta }_A-2{\alpha }_A}$, this set has zero or one element(s). Otherwise, it is empty.

Proof. 

Because the attacker’s base incentive is always strictly decreasing (${BI}_{A,D}^{\prime }<0$), we can disregard the case where ${BI}_{A,D}^{\prime }=0$, so $S_A\left({\nu }_D^{★}\right)$ contains at most one element regardless of the value of ${\nu }_D^{★}$. The set $\{{\nu }_D\mid {BI}_A\left({\nu }_D\right)=0\}$ contains at most one element. This is because the attacker’s base incentive function is strictly decreasing (Lemma A23). Therefore, there is at most one ${\nu }_D^{★}$. It exists if and only if the attacker’s base incentive is strictly positive, which is the case if $2{\alpha }_A<{\beta }_A$ and $c_A<\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\beta }_A-2{\alpha }_A$}\right.$ or if $2{\alpha }_A\ge {\beta }_A$ (Lemma A29). Whether a corresponding ${\nu }_A^{★}$ exists is easily verified by evaluating $S_A\left({\nu }_D^{★}\right)$, that is, by evaluatiing ${BI}_D\left({\nu }_D^{★}\right)/{BI}_{A,D}^{\prime }\left({\nu }_D^{★}\right)-{\nu }_D^{★}$.    □

Theorem 5 (Participatory equilibria with faster attacker for periodic play).

The set of equilibria where the attacker moves faster than the defender (${\nu }_A^{★}\ge {\nu }_D^{★}$) is given by:

$$\left\{({\nu }_D^{★},{\nu }_A^{★})\mid {\nu }_A^{★}\in \{{\nu }_A\mid {BI}_D\left({\nu }_A\right)=0\},{\nu }_D^{★}\in S_D\left({\nu }_A^{★}\right)\right\},$$

where $S_A$ is as in Lemma 8. This set has zero or one element(s) if $2{\alpha }_D>{\beta }_D$. If $2{\alpha }_D\ge {\beta }_D=0$, it has zero or one element(s) if $2{\alpha }_D>{\beta }_D$ and is empty otherwise. If $2{\alpha }_D<{\beta }_D$, this set can have zero, one, two, or a continuum of elements.

Proof. 

The proof of Theorem 5 is identical to that of Theorem 4, except that if $2{\alpha }_A<{\beta }_A$, then the defender’s base incentive function is first increasing then decreasing (Lemma A23). This results in up to two elements in $\{{\nu }_A\mid {BI}_D\left({\nu }_A\right)=0\}$ and introduces the possibility for ${BI}_{D,A}^{\prime }\left({\nu }_A^{*}\right)$ to be equal to zero, resulting in infinite roots if ${BI}_A\left({\nu }_A\right)=0$.    □

We can derive all periodic Nash equilibria algorithmically. Algorithm 2 gives an algorithm for deriving the equilibria with faster defender play. A similar but slightly longer algorithm yields the equilibria for faster attacker play.

Algorithm 2 Algorithm for finding the set of participatory equilibria with faster-moving defender for periodic play

// Check if the attacker’s base incentive has a root 1: if $2{\alpha }_A<{\beta }_A$ and $c_A\ge \frac{1}{{\beta }_A-2·{\alpha }_A}$ then return ∅ end if    // Determine the defender’s equilibrium play rate 2: ${\nu }_D^{★}\leftarrow Bisect\left({BI}_A\left(x\right),x_{\min }=0,x_{\max }=1/c_A\right)$// Strictly decreasing    // Determine attacker’s equilibrium play rate 3: ${\nu }_A^{★}\leftarrow {BI}_D\left({\nu }_D^{★}\right)/{BI}_{A,D}^{\prime }\left({\nu }_D^{★}\right)-{\nu }_D^{★}$ 4: if ${\nu }_A^{★}\notin ]0,{\nu }_D^{★}]$ then return ∅ end if 5: return $\left\{({\nu }_D^{★},{\nu }_A^{★})\right\}$

6. Discussion

In this section, we interpret our results further and look closely at how generalized hyperbolic discounting qualitatively impacts player utilities and utility-maximizing player behavior.

6.1. Degenerated Discounting Behavior

Our principal result is that complex discounted behavior often degenerates into non-discounting behavior (Theorem 1). There is a mathematical component to this result and a practical component. We begin with the mathematical component and shed some light on how it was established.

Mathematically, our result falls into the space of games involving infinite time horizons. In the original FlipIt paper, a significant part was dedicated to proving that if players are using renewal strategies, then the formalism that defines the game’s outcome in terms of very long-term (until infinity) running averages is valid. The important point was to show that if we define a game with an infinite time horizon, then there is some way to calculate the outcome from a class of strategies that can be specified finitely. Specifically, an initial result was that the formalism works for renewal strategies.

Because of this background, earlier versions of our result about sub-hyperbolic discounting assumed that the strategies were renewal. This gave us the additional property that restarting the game at a later point in time yields essentially the same outcome pattern. However, we could not find any counterexample to the discounting equivalence even while violating the renewal assumption.

One key example function helped to provide insight:

$$PC\left(t\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\exists m,\frac{m(m+1)}{2}\le t<\frac{{(m+1)}^2}{2}\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(34)

This example satisfies

$$\underset{t\to \infty }{lim}\frac{{\int }_0^{t}PC\left(\tau \right)\mathrm{d}\tau }{t}=\frac{1}{2}.$$

(35)

However, for every integer m, there is a point in time s such that if we restart the game at time s, then the value of the functional form remains bounded away from its correct limit value for duration m. Well-behaved functions generated from renewal strategies essentially cannot depend on absolute time, so they do not have this property. Nevertheless, for this same example, the discounted limit value is also $\frac{1}{2}$.

If we perform our windowing construction using this example, we see that the restart time is quadratic in the window size. Iterating on this example, we see very quickly that whenever the restart time always dominates the next window size, then the discounted limit will converge. However, when we try to exemplify a window size that is about the same as the restart time, the original functional form does not converge. This gives us enough information to imagine the current proof structure.

The narrative we now follow does not assume that the function is well behaved but rather starts from a worst-case scenario in which the player control function is “optimized” to make the discounted limit deviate from the non-discounted one. In this framing, our tactic is to use the limit definition to construct, for each fixed $\epsilon >0$, and as a function of t, a monitor on the function’s tail until the end of time. We use the properties of this monitor to show that whatever the function is doing, there is, at most, a finite amount of time after which it can no longer deviate from the truth of the original limit’s definition by more than $4\epsilon$. From this, we show that discounting (sub-)hyperbolically results in the same outcome as not discounting at all.

The main intuition here is that discounting hyperbolically or sub-hyperbolically still assigns an infinite value to future gains and costs. Therefore, whatever happens in the now is not as important as the long-term future, which, independent of any (sub-)hyperbolic discounting parameters, always tends toward the same thing. The source of gravity for this sameness is that, if we wait long enough, the discount rate drops over time for all possible parameter values until it becomes essentially flat. In any case, the result is both moderately philosophical and mathematically precise, which makes it interesting.

There are also interesting behaviorally grounded aspects. Experimental research suggests that humans do temporally discount the future but tend to do so sub-hyperbolically [30,56].5 We have shown that the behavior of rational actors who do not discount, the behavior of those who discount sub-hyperbolically, and the behavior of those who discount hyperbolically is identical. Additionally, we observed that the behavior of super-hyperbolic discounters ($\alpha <\beta$) remains similar as long as α and β are close to each other; there is no major jump or discontinuity in behavior. Consequently, the impact of discounting is absent or small for what appears to be the most relevant part of the parameter space. Our result seemingly has some implications that are perhaps counter-intuitive:

• All existing research and results on FlipIt-like timing games without discounting carry over to the most commonly observed discounting behavior. This includes the results presented in van Dijk et al. [2] and follow-up work without discounting.
• The players’ utilities, incentives, best responses, and the game’s equilibria are not impacted by the fact that the defender starts the game in control of the resource. Differences between defender and attacker emerge only when discounting super-hyperbolically.

Upon encountering a surprising result, we must evaluate if it represents a significant finding or if it is an unintended artifact of model imperfections. We discern some caveats that may temper some of the implications of Theorem 1: one related to commitment and two arguments for super-hyperbolic discounting in our context.

Commitment

Consider a choice between the following two options: a reward at time T or a somewhat larger reward a fixed duration later. For sufficiently large T, a hyperbolic discounter always prefers to wait for the larger reward, as her discount rate is lower for times further removed from the present. However, unless she somehow commits to her choice, she might choose to claim the smaller reward anyway when the time T actually comes because her discount rate is high for times close to the present. This is known as “preference reversal” or “time-inconsistent preferences”.

A utility-maximizing hyperbolic discounter knows that preference reversal can happen and, in the absence of commitments, has to take her own time-inconsistent preferences into account when making decisions. This can change her best response; for example, she could opt for a third option of claiming an even smaller reward sometime before T, even if she would prefer the larger reward after T when she opts for it.

Our model assumes that the decision on which strategy to execute is made at the start of the game. We, therefore, implicitly assume that players can (and, in fact, must) commit to this strategy and cannot change it later on if their preferences were to change. Setting fixed strategies at the start of the game is common in games of timing where no new information becomes available as the game progresses, but for discounters with time-inconsistent preferences, it takes away any tension that may exist between players’ desired long-run strategies today and what their future selves would choose to do.

Since we model instantaneous rewards and costs as constant over time, it appears somewhat unlikely that such tension exists, as agents are not rewarded for patience. Nevertheless, the role of commitment is something to take into account, and it could be interesting to extend the game with multiple decision-making points, e.g., in the style of extensive form games.

Organizational Actors

Experimental research suggests that individuals tend to discount sub-hyperbolically, but the actors in the modeled interaction typically represent highly sophisticated (adversarial) organizations. Little research exists on appropriate values for α and β in this context. Presumably, organizational actors tend to act more rationally in an economic sense, which might mean they do discount super-hyperbolically—for example, exponentially or close to exponentially (small α).

Rationalization of Risk

Sub-hyperbolic discounting appears to be a more appropriate model for present-focused preferences and delay discounting. However, super-hyperbolic discounting can arise naturally as a result of rationalizing risk. We can, instead of discounting the generated value, consider the risk that the resource might stop generating value at some point in time. Assigning a constant probability of disappearance to any fixed-length time interval results in an exponentially discounted model—an extreme form of super-hyperbolic discounting. However, the entire family of (generalized) hyperbolic discount functions can appear if we consider resources that have been around for longer to be less likely to disappear or by introducing uncertainty over the probability of disappearance.

6.2. Short-Horizon and Long-Horizon Discounting

For both exponential and periodic play, our description of incentives often resulted in two separate cases based on whether α was more or less than half the value of β. It turns out that the behavioral shift around this point is similarly significant to that between super- and sub-hyperbolic discounters. The result is a partitioning of the parameter space in three zones, with ${\alpha }_i>{\beta }_i$ being equivalent to that of FlipIt-like games without discounting [2], $2{\alpha }_i<{\beta }_i$ resulting in games that exhibit mostly the same characteristics as the exponentially discounted model presented in Merlevede et al. [13,14], and a “new” space for ${\alpha }_i<{\beta }_i<2{\alpha }_i$ exhibiting part of the behavior of exponential discounters but not all (e.g., no decreasing attacker best-response curves or the possibility for three equilibria).

In the remainder of this section, we refer to super-hyperbolic discounters with $2\alpha <\beta$ as short-horizon discounters and to super-hyperbolic discounters with $2\alpha \ge \beta$ as long-horizon discounters.

Figure 7 and Figure 8 illustrate player behavior through best-response graphs for periodic play and varying costs for defenders and attackers. In all figures, α and β are chosen such that the value of the resource is halved over the course of the first unit of time.6 We discuss some features of these graphs over the course of the following sections.

6.3. Player Indifference for Periodic Play

A remarkable property of periodic strategies is that the incentive of the slower player is independent of her own play rate. This is visible as the vertical lines on Figure 7 and Figure 8. This independence resulted in a set-valued best-response function, an interesting mathematical analysis, and, sometimes, many Nash equilibria. It appears for all values of α and β and could, therefore, also be observed in related work that did not include discounting [2] or that modeled exponential discounting [14]. However, where does the player indifference come from, and does it hold up in a real-world setting?

To reason about this, we only need to concern ourselves with gains, as the impact of cost on incentives is constant irrespective of discounting parameters (Lemma 4). Careful thought7 reveals that irrespective of the precise play rate of the slower player, every move she makes remains guaranteed to be successful, resulting in an unchanged incentive. In contrast, for faster periodic or exponential play, moving more frequently increases the probability of moving while already in control.

In any real-life scenario, the assumptions made by our model are unlikely to hold exactly. As the qualitative analysis above shows, changing either the assumption of perfect stealthiness or perfect periodic-ness would disrupt the perfectly vertical or horizontal lines on our best-response curves, especially near their edges. However, the indifference is “stable” in the sense that the slope changes only slightly if assumptions are changed only slightly; Nash equilibria induced by indifference do not appear particularly brittle. It is interesting to see that the slower player’s indifference can be observed regardless of discounting method, and for all discounting values α and β, for both players and despite the importance of resource ownership at the start of the game.

6.4. Effective Move Cost and Motivation

Comparing the graphs in Figure 7 and Figure 8 from left to right reveals that both long- and short-horizon defenders always play at significantly reduced rates compared to non-discounters, while the behavior of attackers is more nuanced. We discern two distinct effects of discounting on player incentives. Note that these effects were previously observed by Merlevede et al. [14], as exponential discounting is essentially an extreme form of super-hyperbolic, short-horizon discounting.

• Increased effective cost. Players must pay for the instantaneous cost of a move “up front”. They first pay for the move and accrue benefits from this move later, resulting in the benefits being discounted at a higher rate than the costs. For both players, this effect results in a slightly higher “effective cost” of a move and reduces their incentive.
• Relevance of starting position. Another behavioral change is caused by the defender starting out in control of the resource. This envigorates the attacker—he will attack at reasonably high rates to reduce the time before the first move to obtain the resource before its value has been discounted away, even in the absence of a defender. In contrast, this demotivates the defender, as she is sure to be in control of the resource when it is at its most valuable.

Higher effective costs cause both players to always drop out of the game in response to high opponent play rates more quickly and cause their maximal best response to be lower. However, the invigoration of the attacker more than offsets this effect at low move rates, while the defender’s comfortable starting position causes the defender’s best responses to drop even lower.

The effects of the starting position on player behavior are stronger for short-horizon players. For short-horizon attackers, eagerness to obtain the resource quickly can become such that their best responses become decreasing in the defender’s move rate, reaching a maximum when the defender does not move at all. Defenders can become demotivated enough not to respond at all to attacks as long as they happen infrequently.

Interestingly, more present-oriented defenders will tend to defend their resources less, while more present-oriented attackers will attack poorly defended targets more frequently than their more future-oriented counterparts.

Taking a step back, it is not hugely surprising that the identity of the player starting out in control is relevant only in the face of a finite (convergent) total valuation of the resource. However, in real interactions, it seems to make sense for the starting ownership to matter. This can be because of how we discount, or because we intuitively realize that no interaction will ever go on forever. In this context, discounting as the rationalization of risk again comes to mind.

6.5. Equilibrium Selection

Our analysis shows that, for periodic and exponential play, the discounted model allows for a single equilibrium for (sub-)hyperbolic discounting, two equilibria for long-horizon discounting, and possibly infinitely many equilibria for short-horizon discounting. Inspection of Figure 7 and Figure 8 and our theoretical results show that if two or three equilibria exist, they always map onto two or three of the following situations:

• The attacker moves infrequently, and the defender does not respond.
• Both players move at a low, non-zero rate.
• Both players move at a higher, non-zero rate.

In fact, if multiple equilibria exist, the defender always does not play in one of them.

Distinct equilibria result in distinct outcomes, and in games of timing, which are generally not zero-sum games, some outcomes may be objectively inferior to others in the sense that they are not Pareto-optimal. Upon examining the equilibrium situations described, it becomes clear that both players always fare better in the outcome where the defender refrains from playing. Intriguingly, this suggests that defenders should avoid making regular defensive moves in certain scenarios to prevent an arms race from harming both parties. This is a particularly poignant observation because such outcomes cannot be equilibrium outcomes when not discounting or when discounting sub-hyperbolically.

6.6. Perfectly Secure Systems

One of the foundational assumptions in the interaction with APTs that we model is the capability of advanced threat actors to execute indefensible attacks. Nevertheless, timing game analysis shows that defenders, through high-frequency maneuvering, can completely avoid system compromise by causing the attacker to drop out, effectively achieving “perfectly secure” systems. Unfortunately, such a strategy entails significant costs and is not an equilibrium solution. In the absence of attacks, defensive vigilance is likely to lapse.

When factoring in discounting, structural measures that make it harder to breach the system provide an alternative path to secure systems. Games with a super-hyperbolic discounting attacker invariably have a Nash equilibrium in which neither player moves provided that the (instantaneous) cost of attacks is high enough, that is, if

$$c_A\ge \frac{1}{{\beta }_A-2·{\alpha }_A}.$$

In fact, as $c_A$ is a unitless number that expresses the cost of an attack in relation to the worth of the resource to the attacker, it is possible to increase $c_A$ and achieve perfect security not only by security hardening but also by decreasing the resource’s worth to attackers—for example, by not storing sensitive data for longer than is absolutely necessary.

In our opinion, the presence of a Nash equilibrium at $(0,0)$ is a strong argument for super-hyperbolic discounting, as, practically speaking, most real systems are never attacked by most attackers, an outcome that is not an equilibrium outcome in the absence of discounting for the attacker.

An interesting path for future research to explore would be to define a two-stage game in which the defender (and, possibly, the attacker) could choose to invest before the game of timing starts, increasing the value of $c_A$. This presents defenders with an alternative way of increasing the security of their system that may prevent the disastrous “arms race” scenario of Section 6.5.

6.7. Non-Optimality of Periodic Strategies

One of the major theoretical results holding in the non-discounted setting [2] that we touched on in Section 4.5.2 is that the class of periodic strategies strictly dominates the class of all renewal strategies. These are strategies that have the time of their first move as well as all inter-arrival times drawn from the same time-independent distribution.8 This theoretical result has been a major motivator for the interest in the class of periodic strategies.

In the context of super-hyperbolic discounting, too, we can show that a player playing an exponential strategy against a player with a periodic or exponential strategy can strictly increase her utility by playing a periodic strategy with the same rate parameter instead. Both strategies are equally costly, and the periodic strategy is optimal in the sense that it minimizes the probability of moving when already in control of the resource. Therefore, the set of periodic strategies strictly dominates the set of exponential strategies.

However, where the periodic strategy, when not discounting, ended up strictly dominating the class of not only the exponential strategies but that of all renewal strategies, we can show that this is not the case when discounting super-hyperbolically. This observation also applies to the exponentially discounted model [14] but is a novel result presented in this paper.

Theorem 6 (Non-optimality of periodic strategies).

For super-hyperbolic discounting defenders facing an attacker playing a periodic strategy, the class of periodic strategies with random phase does not dominate the class of renewal strategies.

Proof. 

We prove this by giving a counterexample. We define a class of strategies that are renewal strategies that outperform the periodic strategy under certain conditions. Specifically, we define a renewal strategy resembling the periodic strategy but with a lower probability of moving near the beginning of the game, when the defender is likely to still be in control of the resource. The formal proof is in Appendix D.    □

The periodic strategy and renewal strategies are “flawed” in the sense that they are incapable of fully exploiting the knowledge of resource ownership at the start of the game. The optimality of periodic strategies relies on a form of time independence that is no longer satisfied when discounting super-hyperbolically. The search for new classes of analytically tractable strategies that are more suited to contexts with super-hyperbolic discounting remains an interesting open avenue for future research.

7. Conclusions

The model presented in this paper introduces four parameters governing the preferences of two players discounting along a generalized hyperbolic discounting function (${\alpha }_A$, ${\alpha }_D$, ${\beta }_A$, and ${\beta }_D$) and is sufficiently general as to subsume several previously studied classes of such games, including exponential discounting [14,15] and the original FlipIt game [2], which does not involve discounting. The price of this generality is an increase in the complexity of derivations and formulae. The additional degrees of freedom also make it more difficult to clearly narrate our players’ expected behavior.

On the upside, we are able to provide a characterization of equilibrium configurations for the canonical regions of our parameter space, and our machinery brings together several different approaches into one unifying framework. Many of our generalized arguments subsume and even simplify the arguments and calculations from prior related work [2,14,15]. Examples include our notations surrounding anonymous gain and our focused usage of base incentives. Over the long run, these analysis techniques may prove more valuable than the current characterization results they produced here.

Two central markers roughly guide the equilibrium characterizations. If each player is discounting hyperbolically or slower, then the equilibrium conditions are exactly the same as when the players are not discounting [2]. On the other end of the discounting spectrum, where both players are discounting faster than hyperbolic, the equilibrium conditions are very similar to those obtained in earlier work where players discount exponentially [14,15].

The present work advances our collective understanding of games of timing in which control of a single resource flips back and forth between two time-based-discounting players, and it extends a series of discounting-centric investigations begun within the FlipIt framework. By showing that discounting (sub-)hyperbolically does not impact player utilities, we enable an extended interpretation of all existing results on the undiscounted model [2] and its variations. We have also proven that one of the principal results for this undiscounted model—the strict dominance of periodic over renewal strategies—no longer holds when discounting super-hyperbolically; this includes exponential discounting.

Our result stating that hyperbolically discounted, FlipIt-like security games of timing are strategically equivalent to those without discounting seems especially powerful. The proof that we present makes little assumptions about the game structure or discounting function and may have applications beyond the space of FlipIt-like games.

Future work can extend and apply the tools and techniques we have developed here to other applicable models. Additionally, there are interesting possible extensions starting from this paper, such as considering more general discounting-customized strategy classes, increasing the number of players, or adjusting the background context in different dimensions others have opened. Likewise, we can study our model in the context of a behavioral experiment [57,58].