Abstract
Poker is a game of skill, much like chess or go, but distinct as an incomplete information game. Substantial work has been done to understand human play in poker, as well as the optimal strategies in poker. Evolutionary game theory provides another avenue to study poker by considering overarching strategies, namely rational and random play. In this work, a population of poker playing agents is instantiated to play the preflop portion of Texas Hold’em poker, with learning and strategy revision occurring over the course of the simulation. This paper aims to investigate the influence of learning dynamics on dominant strategies in poker, an area that has yet to be investigated. Our findings show that rational play emerges as the dominant strategy when loss aversion is included in the learning model, not when winning and magnitude of win are of the only considerations. The implications of our findings extend to the modeling of sub-optimal human poker play and the development of optimal poker agents.
1. Introduction
The analysis of poker can be traced back to Von Neumann, whose great interest in the game led to the development of the field of game theory [1]. With elements of incomplete and unreliable information, risk management, opponent modeling, and deception, the challenges that arise in analyzing poker are distinct from those in complete information games such as chess or checkers. As a complex game, early research tackled simpler non-cooperative, zero-sum, incomplete information games that had computable optimal strategies [2,3,4,5]. Here, we organize poker research into three approaches with distinct, interrelated goals: understanding human poker play, engineering effective heuristics to increase wins in real (AI or human) players, and the analysis of optimal poker using game theory.
The field of human poker play models human decision-making in competitive incomplete information settings. This research focus is part of a strong body of literature on modeling human learning [6,7]. Many studies observed participants in laboratory experiments during which simplified versions of poker with tractable optimal solutions were played [2,3]. Researchers observed that players displayed tendencies to make suboptimal decisions (i.e., bluff, take risks, deceive) based on their emotional states and perceptions of their opponents [4,8,9]. Researchers also examined whether humans could improve after repeated play. Even with consistent feedback over many rounds, most failed to improve their strategies, that is to play more optimally [5,8,9]. Findings from human-decision making studies helps us understand the intricacies of the game of poker. These insights have implications for both the development of optimal poker playing agents as well as a theoretical modeling of the game.
A separate endeavor involves creating winning poker agents that can calculate the best response to every move, paralleling the abilities of chess and checkers agents. These agents efficiently traverse an enormous constructed game state space to achieve this [10,11,12]. As an incomplete information game, constructing the state-space for poker is an impressive undertaking requiring: (1) a massive database of poker hands (2) methods that allow an optimal decision to be made in every situation. The goal of these solutions is that they are game-theoretically optimal such that no money is lost in the long run, regardless of the opponent’s strategy. Groups have employed machine learning and artificial intelligence methodologies to where agents can compete with the best human players [13,14] with some even claiming to have weakly solved the game of Texas Hold’em poker [10]. Successful gameplay, while of great value, fails to expand our understanding of decision-making and strengths of strategies (e.g., rational play, bluffing). Investigating the relative advantage of different strategies from a game theoretic perspective gives deeper insights into poker play that a myopic state-space parsing cannot. Additionally, game theory can utilize insights from both human and AI modeling approaches depicted above and a more principled approach to the analysis of poker.
The game theoretic framework provides a systematic approach to the analysis of optimal strategies and near Nash equilibrium play in poker play [15,16] and evolutionary game theory provides an approach to learning dynamics [17,18]. Poker involves a significant element of strategic reasoning under uncertainty as well as rational play based on strength of the player’s hand. Game theory can provide insights into stable, balanced strategies that players can adopt and introduces the concept of mixed strategies [19] in which players can randomize their actions to make their strategies less exploitable [4,12]. Incorporating learning dynamics in conjunction with the game theoretic framework provides a foundation for understanding how players can learn and adapt their strategies over repeated play which can lead to the development of AI agents capable of playing poker at an expert level [15]. An advantage of evolutionary game theory is that no expert knowledge of poker is required. Instead, through continuous play adaptation of strategies occurs until an effective strategy is developed. The hands-off nature can also lead to the development of previously unthought-of strategies [15]. It was shown that even without the incorporation of expert knowledge, an evolutionary method can result in the development of strategies that are competitive with Poki and PSOpti [15].
Later evolutionary game theoretic efforts established poker as a game of skill by exhibiting the success of rational agents over irrational agents in tournament structure play [20] where agents had fixed strategies. Using simple imitation dynamics was enough for the rational strategy to dominate a population of rational and irrational adaptive poker agents [21]. These analyses did not rely on the use of data from human poker play or the traversal of a constructed state space to uncover optimal actions to take in any state of the game. Instead the focus is on the performance of strategies, their relative efficacy, and the learning processes that influence which dominant strategies emerge over the course of play. Here, we highlight two distinct but interactive components of modeling: the defined strategies of the agents and the learning dynamics by which the agents revise their strategies. While studying strategies is ultimately the primary concern of game theorists, how learning mechanisms influence the relative strength of strategies over each other is also of great—perhaps even equal—importance. More specifically, it is not clear how the design of a learning mechanism impacts the outcome of strategy learning and whether a strategy will remain dominant across all learning dynamics. It is not sufficient to assume that any “reasonable” learning dynamic will lead to the same optimal strategy emerging in the population.
This paper aims to investigate the interplay between learning dynamic design and dominant strategies in poker. We test strategies (i.e., rational and irrational) across a variety of appropriate learning dynamics and track the evolution of strategies in the population. The learning dynamics employed in this paper are designed in the family of Erev and Roth (ER) reinforcement learning (RL) dynamics [22]. Importantly, these dynamics do not require agents to be highly or even boundedly rational. Limiting the agents to low rationality is well established as it has been seen that human interactions often do not think with high rationality [23,24,25,26]. The manner in which the agents maintain their strategy allows them to play and learn mixed strategies, an important aspect of poker play [4,12]. Our analysis uncovers features inherent to poker through carefully studying strategies rather than action sequences. It also provides descriptive qualities somewhat akin to that of modeling human play. The systematic definition and exploration of dynamics and strategies provides a foundation for future exploration of more complicated components of strategies such as bluffing and risk. Our approach can also provide simple, communicable, and easily transferable advice to the poker players of any skill level. After establishing simple strategies one can use to decide one’s actions, one is able to model real world play as a composition or weighting of the different strategies. Further, various reinforcement learning dynamics are proposed that have descriptive power with regard to the change in a players’ strategy based on outcomes of repeated play.
1.1. Previous Work
Javarone established poker as a game of skill using tournaments between rational and random agents [20] before introducing population dynamics to enable agents to revise their strategy through play. By employing voter-model-like dynamics, it was shown that under various initial population compositions, the rational strategy is ultimately the one that is learned [27]. Acknowledging that a revision rule predicated on knowledge of the opponent’s strategy is unrealistic, most recently Javarone introduced a strategy revision rule that only depends on the payoff received. Under this revision rule, when agents play until one has all of the money, the rational strategy becomes the dominant strategy in the population. Meanwhile, in single hand challenges neither rational nor irrational is distinguished as the dominant strategy [21].
Others have applied evolutionary game models to real world data of online poker play [28,29]. The learning of the players in the data set was summarized using a handful of strategy descriptors, and the learning of agents over the course of play was analyzed. Evolutionary modeling has been a useful element with regard to the design of some poker AI [15,30,31].
1.2. Evolutionary Game Theory
Classical game theory involves studying optimal strategies for players that do not change their strategy over time. Evolutionary game theory extends this by introducing learning, updating, and population level dynamics. By defining dynamics for learning in an agent population, interactions not predicated upon the assumption of rational actors are possible [23]. Further, the dynamics themselves can be investigated, not just the equilibria of the game. Evolutionary game theory has become a valuable tool in the arsenal of many researchers, with papers in over one hundred research areas applying evolutionary game theory concepts as a part of their research [32,33,34,35].
1.3. Poker
Texas Hold’em is the most popular of many variants of poker. This paper follows Javarone in studying two person (heads-up) Texas Hold’em. When two players sit down at a table to play, they bring with them the stack of chips which they will wager. The goal is to increase this chip stack. On a hand, a player is first dealt two cards that are only visible to them (hidden cards). One player places a small portion of their stack into the pot, the small blind, and the other a small quantity twice that size (the big blind). The two bets are added to the pot which will accumulate as chips are bet over the course of the hand. These mandatory bets create an incentive for players with weak hands to play. Then play commences. During a player’s turn, there are three possible actions: fold, call, or raise. By folding, a player forfeits the hand, preventing them from winning any money but also preventing them from losing any more money. If the player opts to call, they bet the minimum stake required to stay in the hand, and the turn passes to the next player. The other option is to raise. By doing so, the player bets the minimum stake required to stay in the hand, along with an extra amount of chips. This now forces the other player to pay the increased amount or fold. In a betting round, the turn passes back and forth between the two players until both have called or folded. Between betting rounds, community cards are revealed that are available to both players, with there ultimately being five community cards available. After the final betting round, if neither player has folded, they each create their best possible combination of five cards from their two hidden cards and the five community cards. The player with the best combination wins the pot.
1.4. Erev and Roth Learning
The learning dynamics used in this paper follow the principles of Erev and Roth (ER) learning. ER learning is a model of reinforcement learning and decision-making used across a wide range of strategic environments [36,37]. It can characterize patterns of both human decision-making and learning in agent-based simulations, providing a realistic representation of how agents adapt their strategies in response to feedback with no a priori heuristics. In our dynamics, each agent learns using an urn of colored marbles. The colors correspond to strategies. At the start of a game of poker an agent picks a marble at random from the urn. This dictates their strategy. The urn for each agent is updated by adding marbles based on the outcome of the game and the payoff received. ER learning has the advantage of low rationality, as the determination of strategy depends only on accumulated payoffs [25]. Hence, the simple learning and agent decision making allows us to more confidently identify interplay between strategy and game elements that influence payoffs. To make it clear that the results are tied to the game and not just the learning model employed, additional justification is given for the choosing of ER learning, as it is a widely applied, simple, and well-analyzed learning model. On top of this, other papers (including [37,38]) are discussed to explain that the results in learning that come from the use of ER learning are what can be expected from other learning models. We also include an exhaustive list of all models developed during the research process in the Appendix B. These elements appear as follows: Erev and Roth put forth two basic principles with which one should start their search for a descriptive model for learning: the law of effect and the power law of practice. The law of effect dictates that actions that lead to favorable outcomes are more likely to be repeated than actions that lead to less favorable outcomes. Per the power law of practice, the learning curve for agents is steep early on but quickly flattens. This is accomplished by agents accumulating propensities for each strategy over the course of play. As the agents become more experienced, each individual round of play has less influence on their belief. Human psychology studies have noted this behavior [39,40]. Compared to dynamics that are not probabilistic, leading to deterministic selection of strategies [38], we opted for Roth-Erov learning. These other strategies are similar to Roth-Erev learning in their myopic nature, and perform at least as well [37]. For the first exploration of learning dynamics in poker, the ER learning model was chosen due to its prevalence in studying psychological phenomena, such as poker. This flexible and well-analyzed model enables the results of this paper to be put into context with other results with greater precision. The ER model was not the only one examined in the research process; the other dynamics are listed in Appendix B.
The goal of this paper is to develop an understanding of what drives the success of strategies under different learning dynamics. Poker has been established as a game of skill, but we show that not all feedback mechanisms result in skilled play being learned.
2. Materials and Methods
The experiments involve the simulation of a simplified poker game on top of which agents revise their belief on strategies through repeated play.
2.1. Rational and Random Strategies
There are two strategies available to the agents. These are a rational strategy and a random strategy. The only difference between the two strategies is how they determine the strength of their starting hand when dealt their two hidden cards. Agents playing the rational strategy look up the strength of their hand in a table that maps each starting hand to the probability that it is the best hand. The construction of this table involved running one hundred million hands to calculate the probability of each hand being the best hand. The random agents pick their win probability randomly from a uniform distribution on the range [0.2923, 0.8493], the range of possible hand win probabilities. From there, agents use the same method to determine their actions, regardless of strategy. When considering their action, an agent has a belief of their win probability o, knows the current size of the pot P, and is deciding b. As they are looking to maximize the expected value of their hands, they use the following equation as proposed in [41]:
The first term is the money that the agent stands to win by betting b and their opponent calling. They will win the pot, win back their own wager, and take the wager of their opponent, which the agent believes will happen with probability o (their win probability). The second term is the money the agent loses by betting. When the agent bets, they are separating themselves from those chips, which are then added to the pot with certainty. With a bit of algebra:
This clearly shows that if , the expected value increases with larger bet sizes so the agent will go all-in. If , the bet size does not matter, and the agent will go all-in. If , the expected value decreases with larger bets. Thus, they will see if betting the minimum stake required to stay in the hand has non-negative expected winnings. If it does, they place that bet. Otherwise they fold (which has expected winnings of zero). Either way the agent is maximizing their expected winnings under their belief about their hand strength. This decision making process is visualized in Figure 1. When the agent is considering their decision, they carry with them their believed win probability. The game state consists of the minimum stake required to stay in the hand as well as the current size of the pot. With that information, they use Equation (2) to calculate the expected winnings of a bet b, deciding to place the bet b which maximizes their expected winnings.
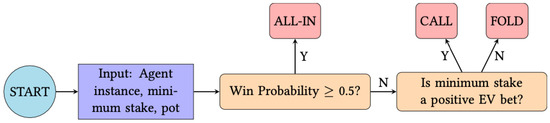
Figure 1.
Flowchart illustrating how agents determine their actions. The decision involves their believed hand strength (associated with agent attribute), the minimum stake required to stay in the pot, and the current pot size. The agents bet in a manner that maximizes their expected winnings given their limited reasoning capabilities (Equation (2)).
2.2. Relative Strengths of Strategies with No Learning
As a benchmark for comparison, we first consider the efficacy of the two strategies relative to one another by simulating one hundred million hands between a rational and random agent with no learning.
2.3. Learning Dynamics
To follow [42], take to be the propensity of agent a to play strategy k at time t. For each of the n agents and strategies , , meaning each agent starts off with the same propensity for each strategy and all agents start off with the same propensities in each strategy. This is the case for all dynamics. Further, the agents calculate their probability of playing strategy k at time t as:
This paper considers two possible strategies, rational and random, so agents will maintain propensities for these two strategies. Thus, k and j refer to rational and random strategies (not respectively). When discussing propensities, the strength of the initial belief should be considered. Agents that have large initial propensities relative to the average payoff received on each round will learn slowly (as they already have a strong belief), while those with small initial propensities relative to the average payoff received on each round are at risk of having highly varied learning at the start that relies on the outcomes of the first few hands. Below is the specification for each of the four learning dynamics implemented. We are interested in the converged composition of urns for the population.
2.3.1. Unweighted Learning
This first dynamic is a simple application of the law of effect and power law of practice. After a hand of poker, the winning agent adds one marble for the strategy they used. The losing agent does not reinforce their played strategy, and thus the learning for the winner can be specified as follows, given agent q won playing strategy j at time t:
2.3.2. Win Oriented Learning
To build on the unweighted learning, the reinforcement amount is now weighted by the amount of chips won. It is still the case that only the winning agent learns. For an agent q playing strategy j at time t:
In this case, where x is the change in stack for the agent on the hand. For the winning agents, , and for the losing agents, , so no marbles are added.
2.3.3. Holistic Learning
To go one step further, now losing is considered. Strategies are now rewarded not only for maximizing their wins but minimizing their losses. As a result, both the winning and losing agents experience meaningful learning after each hand. To achieve this, the minimum possible payoff is subtracted from the payoff of the hand for each agent, giving:
However, . Note that is the least possible payoff, which occurs when the agent loses their entire chip stack on the hand. Thus, 10,000 as each agent starts with 10,000 chips.
2.3.4. Holistic Learning with Recency
The final step is to incorporate recency by introducing a simulation parameter , an extension of basic ER learning [42,43]. When the agent learns, some proportion of their previous belief is discounted. Initially this does not have much of an effect as the propensities are small. Later on, a small fraction of the agents’ propensities will be about as much as is learned on an epoch. Thus, each time they play a hand, the agent will forget about as much as they are learning. The proportion forgotten, , is kept small to prevent the agents from only considering the most recent outcomes. For a detailed analysis of the value of , see (Appendix A). This modification of holistic learning can be specified as:
As in holistic learning, where 10,000.
2.4. Simplified Poker
The agents play a simplified version of heads-up Texas Hold’em poker (only involving two players). To begin, one player pays a fixed amount of chips called the small blind, and the other pays the big blind—a quantity of chips double the value of the small blind. These blinds create an initial pot. The two players are then dealt two cards each that are only visible to the player receiving the cards. Betting ensues. The betting process begins with the player that paid the small blind. They have the choice to fold, call, or raise. If the small blind player does not fold, the big blind has the choice to fold, call, or raise. The turn will then pass back and forth until one player folds or both have called. If a player folds at any time, the other is the winner by default. The winner adds the chips from the pot to their stack and the hand is finished. In the case of both players calling, the five community cards are dealt and each player creates their best five card combination from their two hidden cards and the five community cards. The player with the best combination wins the pot.
2.5. Simulation Structure
The simulation consists of multiple hands of simplified poker between two agents at a time. On each hand, two agents are randomly selected from the population, they play simplified poker, learn, and are then placed back into the population. Play is organized into epochs. An epoch consists of a number of hands such that on average each agent in the population has played one hand. The simulations involve a population of two hundred agents—one hundred agents of each strategy—playing for ten thousand epochs. Different population sizes and lengths of simulation were tested and our simulation setup was sufficient for analysis.
3. Results
In this paper, we assess the relative strength of rational and random strategies with no learning and across four ER learning dynamics. To assess strategy performance during the learning process, the number of each marble across the entire population is assessed at the end of the simulation. We present our findings in the following sections.
3.1. Relative Strength with No Learning
The plot for the relative strengths of strategies with no learning depicts the average difference in payoffs between the two strategies for different hand strengths. Here, one rational agent and one random agent are each dealt a hand. They play a round of simplified poker against each other, and their respective hands and payoffs are recorded. This process is repeated one hundred million times. The results indicate that on average, across all possible hand strengths, the rational strategy has a higher average payoff (Figure 2).
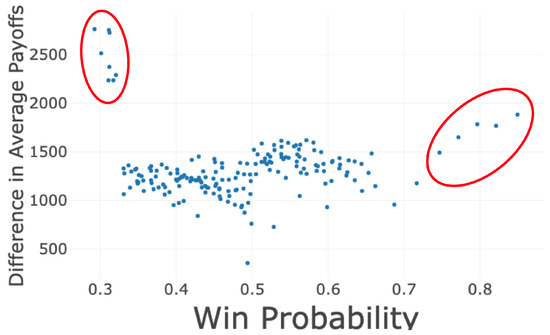
Figure 2.
Difference in Average Payoffs Across Hands for Rational and Random Strategies for every possible hand. Regions circled are hands where a rational agent wins considerably more than average against the random agent. The data is created by one hundred million hands played between a rational and random agent.
Observe that for all starting hands, the average payoff for the rational strategy is greater than the payoff for the random strategy when dealt the same starting hand. This corroborates the notion that poker is a game of skill as shown in earlier works [20]. The two regions where the rational agent has the greatest difference in payoffs are the weakest (upper left part of figure) and the strongest hands (right portion). In the case of the weakest hands, rational agents fold and minimize their losses while random agent do not and frequently lose more money as a result. For the strongest hands, the rational agent accurately assess their strength and play aggressively, with a small chance of folding. Random agents have a higher chance of folding as their hand strength is determined at random.
3.2. Unweighted Learning
To begin, learning is based on the outcome of winning or losing, with only winners learning. To analyze the results of learning, first the marbles accumulated by the population are considered. For this, at the end of each epoch the marble count for each strategy of all of the agents is tallied, plotted below for unweighted learning (Figure 3a).
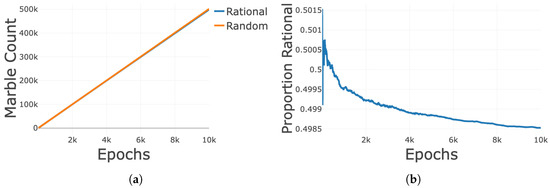
Figure 3.
All curves are the average of one hundred iterations of the simulation. (a) Sum of population marble count for each strategy over the epochs across one hundred iterations of the simulation for Unweighted learning. (b) The proportion of rational marbles in the population for unweighted learning. For each epoch, the total number of rational marbles is divided by the total number of marbles in the population, plotted for all epochs above for one hundred iterations of the simulation.
Note that the total marble count for the rational and random strategies stay close to one another over the ten thousand epochs (one million hands). In other words, agents are learning to play the rational and random strategies at the same rate. In terms of the convergence of learning, even after one million hands there is no meaningful convergence to the random or rational strategy (Figure 3a). For unweighted learning, only the winning or losing of a hand influences the marble count, so the win rate in a rational-random matchup drives convergence. According to the simulation, a rational agent wins about 49.8% of matchups, which is virtually a coin flip.
3.3. Win Oriented Learning
To build on unweighted learning, win oriented learning now takes into account the magnitude of a win. It is still the case that only the winning agent learns. In terms of population marble counts, the random strategy is now increasing faster than the rational strategy (Figure 4a).
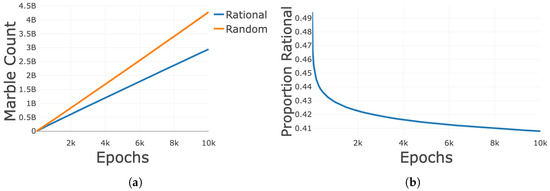
Figure 4.
All curves are the average of one hundred iterations of the simulation. (a) Sum of population marble count for each strategy over the epochs across one hundred iterations of the simulation for Win-Oriented learning. (b) The proportion of rational marbles in the population for Win-oriented learning. For each epoch, the total number of rational marbles is divided by the total number of marbles in the population, plotted for all epochs above across one hundred iterations of the simulation.
As evident from the graph above, [44] (Figure 4b) the population of agents will converge to the random strategy. This is unexpected and nontrivial. Under a reasonable learning dynamic the random strategy is the one that is learned, despite having been shown to have a lower average payoff for all hands relative to the rational strategy (see Section 3.1). The emergence of learning to play the random strategy occurs because only the amount won is considered. When the difference in losses is not considered, the random strategy outperforms the rational strategy for a considerable range of hands (Figure 5).

Figure 5.
Difference in Average Winnings of Rational and Random Strategies for every possible hand. The different regions are ranges of hands for which the rational agent plays differently, leading to different average winnings on those hands. The data is created by one hundred million hands played between a rational and random agent.
For the weakest hands, a rational agent will fold those hands while the random strategy will usually play them. The result is that even though the random agent will usually lose those hands, in the cases that they win, they will earn a considerably higher payoff than the rational agent. Since the losses, and the magnitude of them are not considered under this dynamic, the random strategy is not punished for losing most of the time and is only rewarded in the few cases in which they get lucky. For the hands with win probabilities ranging from 0.33 to 0.5, the rational agent will now call on many of those hands, giving themselves a chance to win some money. However, the random agent will frequently press further, raising and building the pot. Given that the hands have a win probability of less than 0.5, this will usually result in a lost hand if the random agent is called. In the cases in which the random agent wins, they will receive a greater payoff than the rational strategy would have for those same hands. The rational strategy reasserts itself as the optimal strategy for hands with a win probability greater than 0.5. For these hands, the rational agent will now play as aggressively as the random agents do, except from time to time the random agent will underestimate their hand and fold/call when it would be more advantageous to raise. This enables the rational strategy to win more on average than the random agent (Figure 5).
3.4. Holistic Learning
Holistic learning builds on win oriented learning by considering losses. More specifically, it rewards strategies that minimize losses along with maximizing wins. With this addition, the population marble count for the rational strategy now grows more rapidly than the population marble count for the random strategy (Figure 6a). In terms of a converged strategy, this will result in the rational strategy being the dominant strategy [44] (Figure 6b). When the magnitude of losses are considered, the random strategy is punished for their tendency to play hands more aggressively. This results from of the right skewed distribution of win probabilities for the rational strategy while the random strategy picks from a uniform distribution on the same interval.
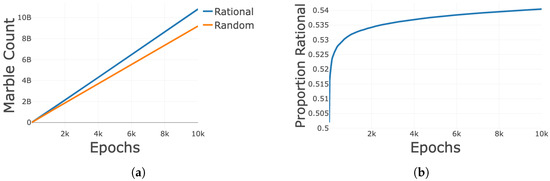
Figure 6.
All curves are the average of one hundred iterations of the simulation. (a) Sum of population marble count for each strategy over the epochs across one hundred iterations of the simulation for Holistic learning. (b) The proportion of rational marbles in the population for Holistic learning. For each epoch, the total number of rational marbles is divided by the total number of marbles in the population, plotted for all epochs above for one hundred iterations of the simulation.
3.5. Holistic Learning with Recency
Adding recency enables the learning to continue at a reasonable clip, as the amount the agent learns on a hand will start to be approximately the same amount as is forgotten. This prevents propensities from accumulating to a point where each individual hand does not have any discernible influence on the learned strategy. By designing agents to forget, if the amount of marbles added for a strategy on a hand is less than the amount forgotten, the agents will forget this strategy. This can be seen for the random strategy (Figure 7a). This does not change the strategy that is ultimately converged to [44], but it does lead the agents to learn at a faster rate, as is evident from the population marble count, which is 70% rational by the end of ten thousand epochs rather than 54% without recency (Figure 7b).
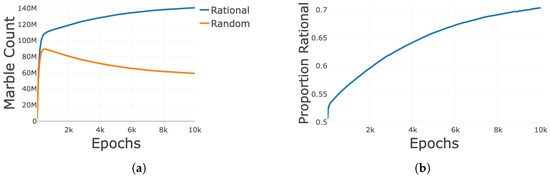
Figure 7.
All curves are the average of one hundred iterations of the simulation. (a) Sum of population marble count for each strategy over the epochs across one hundred iterations of the simulation for Recency Holistic learning.(b) The proportion of rational marbles in the population for Recency Holistic learning. For each epoch, the total number of rational marbles is divided by the total number of marbles in the population, plotted for all epochs above for one hundred iterations of the simulation.
4. Discussion and Conclusions
The study of poker and game theory has been intertwined since the field’s inception by Von Neumann in the 1920s. The analysis of poker owes much to game theory and evolutionary learning models. More recent work has established poker as a game of skill and shown the strength of rational play over random strategy [20,21]. Building on past efforts, in this paper we explore the influence of learning dynamics on the relative strengths of different strategies. The only difference between the rational and random strategies is how they determine the strength of their hidden cards at the beginning of the hand. The results indicate that rational play is not dominant across all learning dynamics. The features of learning dynamics can put rational agents at a disadvantage when loss is not taken into consideration. The dynamics we selected are well studied with desirable features to model poker. The learning dynamics begin with minimal features and build to include more aspects of game play. This allows for a principled investigation into the influence of dynamics and different learning specifications on strategies. Our approach had the added benefit of providing plausible models for sub-optimal human play as well.
The first type of learning dynamics only considers wins, while the second one includes the magnitude of the win. In the third specification, we also include the extent of the loss, and the fourth and final dynamic gives recent events more weight over past events. These dynamics build towards a more complete set of features of poker play. In many contexts, a win may be all that matters, but in gambling the magnitude of a win is also of interest. Given that poker involves chips to gamble with, minimizing the losses is also a core element of any effective strategy. The learning dynamic we employed reflect these considerations and show that in design dynamics, the context of the game must be taken into account.
When considering rational and random agents, our results highlight the influence of the learning specifications on which strategy will overtake in the population. The difference in outcomes for each dynamic gives valuable insights as to what makes each strategy effective. The efficacy of the rational strategy does not come from winning more hands. Surprisingly, in the cases where the rational agent wins, they do not receive a greater average payoff than a random agent. It is in fact that rational agent’s ability to minimize losses that leads to higher payoffs compared to random agents. This is only highlighted when the learning dynamics include loss aversion. As for random agents, the arbitrary hand strength that is selected does not inhibit winning and the magnitude of wins, but rather, leads to an increase in losses. Often when the random agent loses, they forfeit a large amount of their stack. In contrast, rational agents lose a smaller portion of their funds when facing a loss. This principled approach to building from simple dynamics to more sophisticated specifications has allowed for a deeper analysis of the strengths and drawbacks of each strategy.
The simple models in which the random strategy takes over the populations can provide insight into the sub-optimal play prevalent in real world poker play. The first dynamics can point to a bias or heuristic that players may have: more wins will result in higher gains. Similarly, many players may remember the exhilarating hands for which they won a large amount and ignore the times that also led to large losses. The second learning dynamics models such players where wins and the amount of winnings are considered and losses conveniently forgotten. The benefit of our approach is that it allows future learning dynamics to incorporate other factors in their analysis.
In addition to expanding on learning dynamics, we can explore other important strategies that are yet to be modeled. Bluffing is a key element of poker play that adds considerable complexity to the game. Future research plans will tackle bluffing in simple poker play by exploring a variety of bluffing techniques. Another area of interest is developing a mechanism for mixed strategies where agents randomize their choices based on certain probabilities. The game theory approach can also incorporate aspects of optimal play analysis in the form of situational play. Here, agents possess memory of games and recall the strength of a strategy when faced with a similar hand and depending on their past performance, adopt other strategies as a result. The ultimate goal of such research is to simulate a full poker game with a wide range of strategies and learning dynamics.
In this paper, we could not include an exhaustive analysis of all appropriate learning dynamics. While we considered other reinforcement learning mechanisms, the ER learning dynamics provided a sound foundation that later work can build upon.
Author Contributions
Model conceptualization, M.G. and N.A.; Methodology, A.F. and M.G. and N.A.; Mathematical specification, A.F.; Model implementation, A.F.; Writing—original draft preparation, A.F.; Writing—review and editing, M.G. and N.A.; Figures, A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Baker ’64 Collabria Fellowship in Data Analysis, The Hazel Quantitative Analysis Center, Wesleyan University.
Data Availability Statement
The code, results and supporting files for the project can be found at https://github.com/allunamesrtaken123/Collabria-Fellowship/ (accessed on 2 October 2023).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Investigation of ϕ
In the results, took the value of 0.01. This follows the literature, as it is suggested that a small value of is ideal [42,43]. Here, the results from other values of are considered to show that is a reasonable and justifiable choice. Other considered values were 0.1, 0.05, and 0.001. For each, the proportion of the total marbles in the population that are rational was calculated after each epoch, just as was done with the rest of the simulations.
The values of that result in the rational strategy being learned are 0.01, 0.001, and 0. When , there is hardly any forgetting, and thus the learning is similar to when there is no forgetting. The learning from values of 0.05 and 0.1 is distinct. The proportion of marbles in the population that are rational settles on values between 0.5 and 0.6. The population stops experiencing meaningful learning beyond the earliest epochs. It can be seen that early on, the population is moving towards rational for all values of . However, beyond about 150 epochs for and 750 epochs for , the change in proportion of marbles that are rational drops off. These curves do not indicate that the agent population converges to a mixed strategy. The stoppage of learning happens because for larger values of , the agents begin to weigh their recent experience too heavily relative to their overall experience. At first, the amount forgotten is not much compared to the amount learned, but once the amount learned equals the amount forgotten, the agents start to weigh their recent experiences too heavily. For , the agent will forget ten percent of their previous belief after each hand, meaning the result from fifty hands ago hardly influences their current belief. This opens the agents up to having their overall belief warped by variance in short term outcomes. Winning one hand will result in a large swing in belief, and that belief will reverberate through the decision making in the next rounds, ultimately leading them to lock themselves into one strategy or the other. The divide of the population between entirely rational or entirely random is what creates the appearance of a population level convergence to a mixed strategy (Figure A2).
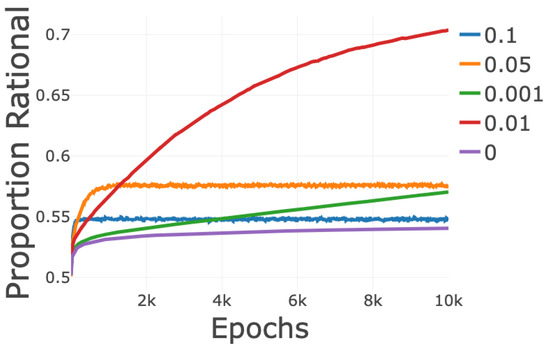
Figure A1.
All curves are the average of one hundred iterations of the simulation. The plot shows the proportion of population marbles that are rational, for different values of . The legend on the right indicates the value of that each color corresponds to. The simulation involved ten thousand epochs of play between two hundred agents.
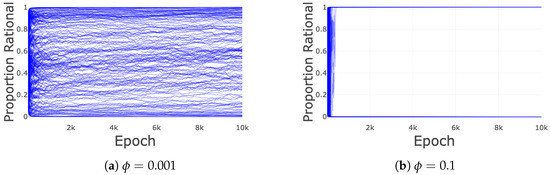
Figure A2.
(a) Each line represents one agent. The proportion of marbles that agent has in the rational strategy at each epoch is plotted here. For , the proportion of marbles the agents has in the rational category is changing over all ten thousand epochs. Meanwhile, for , the agents quickly settle into a strategy and then do not deviate from that strategy for the rest of the simulation, stopping any population level learning.
The choice of avoids the trap of emphasizing the most recent outcomes too heavily while also allowing the learning to continue at a fast clip throughout the simulation.
Appendix B. Other Tested Dynamics
Below are a list of other dynamics that were conceived, implemented, and analyzed during the reserarch process. Those presented in the paper are simple, well-analyzed, and provide valuable insights and are bolded in the table below.

Table A1.
Learning dynamics tested (bolded dynamics showcased in paper).
Table A1.
Learning dynamics tested (bolded dynamics showcased in paper).
| Dynamic | Description |
|---|---|
| Complete Information Weighted Learning | Agents learn to play like their opponent, and the extent to which they learn depends on the outcome. Each agent maintains a confidence level in the various playable strategies. On a loss the amount of confidence an agent will lose in the strategy they just used is proportional to the amount of money lost. That confidence is placed in the strategy played by the opponent. The winning agent does not learn. |
| Death | Agents that do not have the money required to play are removed from the population. Money is taken as an indicator of fitness, so when the agents run out of money they have effectively died. |
| Holistic Learning | Strategies are determine by sampling a marble at random from each urn. Upon the conclusion of the hand, both agents return their selected marble to their urn. Both agents then add marbles to their urn equal to their change in stack from the hand minus the minimum possible payoff (−10,000). |
| Holistic Learning with Recency | Strategies are determine by sampling a marble at random from their urn. Upon the conclusion of the hand, both agents return their selected marble to their urn. Before adding marbles, their previous propensities for each strategy is multiplied by where is small. Then, agents add marbles to their urn equal to their change in stack from the hand minus the minimum possible payoff (−10,000). |
| Incomplete Information Weighted Learning | Similar to complete information weighted learning, except the losing agent does not place their loss of confidence in the strategy played by their opponent. Instead, they uniformly distribute the confidence between the strategies they did not play. The winning agent does not learn. |
| Pólya Urn Complete Information Learning | Both winning and losing agent learn. Agent has propensities for each strategy. When choosing their strategy for a hand, they randomly select their strategy, weighted by propensities. The winner increments the propensity for the strategy used by one while the loser increments the strategy their opponent played by one. |
| Pólya Urn Incomplete Information Learning | Again, both the winning and losing agents update after the hand. Strategies are determined at the start of the hand in the same manner as for Pólya Urn complete information learning and the winner updates in the same manner. However, the losing agent randomly picks one of the propensities for a strategy they did not play and increments that propensity by one rather than the one their opponent played. |
| Unweighted Learning | Strategies are determine by sampling a marble at random from their urn. Upon the conclusion of the hand, both agents return their selected marble to each urn. Only the winning agent learns, and they do so by adding one marble for the strategy used. |
| Win Oriented Learning | Strategies are determine by sampling a marble at random from their urn. Upon the conlcusion of the hand, both agents return their selected marble to their urn. Only the wining agent learns, and they do so by adding a number of marbles equal to the chips won on the hand. |
References
- Leonard, R.J. From Parlor Games to Social Science: Von Neumann, Morgenstern, and the Creation of Game Theory 1928–1944. J. Econ. Lit. 1995, 33, 730–761. [Google Scholar]
- Kuhn, H.W.; Bohnenblust, H.F.; Brown, G.W.; Dresher, M.; Gale, D.; Karlin, S.; Kuhn, H.W.; Mckinsey, J.C.C.; Nash, J.F.; Neumann, J.V.; et al. A simplified two-person poker. In Contributions to the Theory of Games (AM-24), Volume I; Princeton University Press: Princeton, NJ, USA, 1952; pp. 97–104. [Google Scholar]
- Nash, J.F.; Shapley, L.S.; Bohnenblust, H.F.; Brown, G.W.; Dresher, M.; Gale, D.; Karlin, S.; Kuhn, H.W.; Mckinsey, J.C.C.; Nash, J.F.; et al. A simple three-person poker game. In Contributions to the Theory of Games (AM-24), Volume I; Princeton University Press: Princeton, NJ, USA, 1952; pp. 105–116. [Google Scholar]
- Rapoport, A.; Erev, I.; Abraham, E.V.; Olson, D.E. Randomization and Adaptive Learning in a Simplified Poker Game. Organ. Behav. Hum. Decis. Process. 1997, 69, 31–49. [Google Scholar] [CrossRef]
- Seale, D.A.; Phelan, S.E. Bluffing and betting behavior in a simplified poker game. J. Behav. Decis. Mak. 2010, 23, 335–352. [Google Scholar] [CrossRef]
- Hausken, K.; Moxnes, J.F. Behaviorist stochastic modeling of instrumental learning. Behav. Process. 2001, 56, 121–129. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D. Learning in games. Eur. Econ. Rev. 1998, 42, 631–639. [Google Scholar] [CrossRef]
- Findler, N.V. Studies in machine cognition using the game of poker. Commun. ACM 1977, 20, 230–245. [Google Scholar] [CrossRef]
- Findler, N.V. Computer Model of Gambling and Bluffing. IRE Trans. Electron. Comput. 1961, EC-10, 97–98. [Google Scholar] [CrossRef]
- Bowling, M.; Burch, N.; Johanson, M.; Tammelin, O. Heads-up limit hold’em poker is solved. Science 2015, 347, 145–149. [Google Scholar] [CrossRef]
- Billings, D.; Burch, N.; Davidson, A.; Holte, R.; Schaeffer, J.; Schauenberg, T.; Szafron, D. Approximating Game-Theoretic Optimal Strategies for Full-Scale Poker. In Proceedings of the 18th International Joint Conference on Artificial Intelligence, IJCAI’03, Acapulco, Mexico, 9–15 August 2003; pp. 661–668. [Google Scholar]
- Billings, D. Algorithms and Assessment in Computer Poker. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2006. [Google Scholar]
- Brown, N.; Sandholm, T. Libratus: The Superhuman AI for No-Limit Poker. In Proceedings of the Twenty-Sixth International Joint Conference onArtificial Intelligence, IJCAI-17, Melbourne, Australia, 19–25 August 2017; pp. 5226–5228. [Google Scholar] [CrossRef]
- Brown, N.; Sandholm, T.; Amos, B. Depth-Limited Solving for Imperfect-Information Games. arXiv 2018, arXiv:1805.08195. [Google Scholar]
- Quek, H.; Woo, C.; Tan, K.; Tay, A. Evolving Nash-optimal poker strategies using evolutionary computation. Front. Comput. Sci. China 2009, 3, 73–91. [Google Scholar] [CrossRef]
- Nash, J.F. Equilibrium Points in n-Person Games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Bankes, S.C. Agent-based modeling: A revolution? Proc. Natl. Acad. Sci. USA 2002, 99, 7199–7200. [Google Scholar] [CrossRef]
- Perc, M.; Grigolini, P. Collective behavior and evolutionary games—An introduction. Chaos Solitons Fractals 2013, 56, 1–5. [Google Scholar] [CrossRef]
- Oliehoek, F.; Vlassis, N.; de Jong, E. Coevolutionary Nash in poker games. BNAIC 2005, 1, 188–193. [Google Scholar]
- Javarone, M.A. Poker as a Skill Game: Rational versus Irrational Behaviors. J. Stat. Mech. 2015, 2015, P03018. [Google Scholar] [CrossRef]
- Javarone, M.A. Modeling Poker Challenges by Evolutionary Game Theory. Games 2016, 7, 39. [Google Scholar] [CrossRef]
- Roth, A.E.; Erev, I. Learning in extensive-form games: Experimental data and simple dynamic models in the intermediate term. Games Econ. Behav. 1995, 8, 164–212. [Google Scholar] [CrossRef]
- Conlisk, J. Why Bounded Rationality? J. Econ. Lit. 1996, 34, 669–700. [Google Scholar]
- Arthur, W.B. Designing Economic Agents that Act like Human Agents: A Behavioral Approach to Bounded Rationality. Am. Econ. Rev. 1991, 81, 353–359. [Google Scholar]
- Skyrms, B. Learning to Signal with Two Kinds of Trial and Error. In Foundations and Methods for Mathematics to Neuroscience: Essays Inspired by Patrick Suppes; Center for the Study of Language and Information: Stanford, CA, USA, 2014. [Google Scholar]
- Kalai, E.; Lehrer, E. Rational Learning Leads to Nash Equilibrium. Econometrica 1993, 61, 1019–1045. [Google Scholar] [CrossRef]
- Javarone, M.A. Is poker a skill game? New insights from statistical physics. Europhys. Lett. 2015, 110, 58003. [Google Scholar] [CrossRef]
- Ponsen, M.; Tuyls, K.; Jong, S.; Ramon, J.; Croonenborghs, T.; Driessens, K. The dynamics of human behaviour in poker. In Proceedings of the Belgian/Netherlands Artificial Intelligence Conference, Enschede, The Netherlands, 30–31 October 2008. [Google Scholar]
- Ponsen, M.; Tuyls, K.; Kaisers, M.; Ramon, J. An evolutionary game-theoretic analysis of poker strategies. Entertain. Comput. 2009, 1, 39–45. [Google Scholar] [CrossRef]
- Barone, L.; While, L. An adaptive learning model for simplified poker using evolutionary algorithms. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 1, pp. 153–160. [Google Scholar] [CrossRef]
- Kendall, G.; Willdig, M. An Investigation of an Adaptive Poker Player. In Proceedings of the AI 2001: Advances in Artificial Intelligence; Stumptner, M., Corbett, D., Brooks, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 189–200. [Google Scholar]
- Traulsen, A.; Glynatsi, N.E. The future of theoretical evolutionary game theory. Philos. Trans. R. Soc. B Biol. Sci. 2023, 378, 20210508. [Google Scholar] [CrossRef] [PubMed]
- Friedman, D. Evolutionary Games in Economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef]
- Hazra, T.; Anjaria, K. Applications of game theory in deep learning: A survey. Multimed. Tools Appl. 2022, 81, 8963–8994. [Google Scholar] [CrossRef] [PubMed]
- Keller, L.; Ross, K. Selfish genes: A green beard in the red fire ant. Nature 1998, 394, 573–575. [Google Scholar] [CrossRef]
- Weber, R.A. ‘Learning’ with no feedback in a competitive guessing game. Games Econ. Behav. 2003, 44, 134–144. [Google Scholar] [CrossRef]
- Sarin, R.; Vahid, F. Predicting How People Play Games: A Simple Dynamic Model of Choice. Games Econ. Behav. 2001, 34, 104–122. [Google Scholar] [CrossRef]
- Sarin, R.; Vahid, F. Payoff Assessments without Probabilities: A Simple Dynamic Model of Choice. Games Econ. Behav. 1999, 28, 294–309. [Google Scholar] [CrossRef]
- Blackburn, J.M. The Acquisition of Skill: An Analysis of Learning Curves; IHRB Report 73; H.M. Stationery Office: Singapore, 1936. [Google Scholar]
- Newell, A.; Rosenbloom, P. Mechanisms of skill acquisition and the law of practice. In Cognitive Skills and Their Acquisition; Psychology Press: New York, NY, USA, 1993; Volume 1. [Google Scholar]
- Li, J. Exploitability and Game Theory Optimal Play in Poker. Boletín De Matemáticas 2018, 1–11. Available online: https://math.mit.edu/~apost/courses/18.204_2018/Jingyu_Li_paper.pdf (accessed on 1 October 2023).
- Erev, I.; Roth, A.E. Predicting How People Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Barrett, J.; Zollman, K.J. The role of forgetting in the evolution and learning of language. J. Exp. Theor. Artif. Intell. 2009, 21, 293–309. [Google Scholar] [CrossRef]
- Beggs, A. On the convergence of reinforcement learning. J. Econ. Theory 2005, 122, 1–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).