Quantum Tapsilou—A Quantum Game Inspired by the Traditional Greek Coin Tossing Game Tapsilou

Abstract

This paper introduces a new quantum game called Quantum Tapsilou that is inspired by the classical traditional Greek coin tossing game tapsilou. The new quantum game, despite its increased complexity and scope, retains the most important characteristic of the traditional game. In the classical game, both players have $\frac{1}{4}$ probability to win. The quantum version retains this characteristic feature, which is that both players have the same probability to win, but only now this probability varies considerably and depends on previous moves and choices. The two most important novelties of Quantum Tapsilou can be attributed to its implementation of entanglement via the use of rotation gates instead of Hadamard gates, which generates Bell-like states with unequal probability amplitudes, and the integral use of groups. In Quantum Tapsilou both players agree on a specific cyclic rotation group of order n, for some sufficiently large n. The game is based on the chosen group, in the sense that both players will draw their moves from its elements. More specifically, both players will pick rotations from this group to realize their actions using the corresponding $R_y$ rotation gates. In the Quantum Tapsilou game, it is equally probable for both players to win. This fact is in accordance with a previous result in the literature showing that quantum games where both players choose their actions from the same group, exhibit perfect symmetry by providing each player with the possibility to pick the move that counteracts the other player’s action.

1. Introduction

Undoubtedly, game theory has established itself by now as a multifaceted framework that can readily and easily provide a multitude of tools that facilitate the analysis of complex situations, especially those concerning conflict, competition, or cooperation. The actors or agents involved in these situations are called players. The fundamental assumption of game theory is that players are always rational, and strive to maximize their profit or minimize their loss. Each player possesses their own set of objectives, and their actions can disrupt the plans of other players. At the conclusion of the game, each player assesses their gains or losses by employing a payoff function. The premise of rationality plays a crucial role in guaranteeing that each agent is motivated to maximize their own payoff. Game theory is particularly suited for tackling serious and difficult problems from a plethora of different fields, ranging from economics, political and social sciences, to computer science, biology, and psychology. It is instructive to mention as an example of social and legal significance the possibility to understand and detect criminal activities via the use of evolutionary game theory, as proposed in Ref. [1]. The interested reader in the study of similar critical social issues may consult Ref. [2] for more references. Evolutionary dynamics offers fresh and unconventional insights into classical games such as the famous Prisoners’ Dilemma (see Refs. [3,4] for more details). Additional references on the subject of evolutionary and coevolutionary games can be found in Refs. [5,6]. In this work we shall be employing only a few elementary concepts from game theory that can be found in standard textbooks such as Refs. [7,8,9].

The realm of quantum computation holds the promise of ushering us in a new era of computational capabilities. Despite its origins dating back to the early 1980s, it took some time for this field to fully develop and reach its current state. Presently, there are commercial quantum computers in existence, albeit with a rather modest number of qubits. However, it is anticipated that this situation will undergo significant transformation in the years ahead. If these predictions prove accurate, there will be a substantial increase in the number of available qubits. Consequently, this quantum leap will lead to a remarkable enhancement of our computational power, enabling us to address complex decision-making and optimization challenges effectively.

In this broader context, it appears inevitable that quantum games would emerge as a natural consequence. The emerging field of quantum game theory explores the integration of quantum principles and concepts into classical games, such as coin flipping, the Prisoner’s Dilemma, and various others.

1.1. Related Work

It would be historically accurate to say that the inception of the field of quantum games occurred in 1999 when Meyer introduced the PQ penny flip game in his influential paper [10]. This game serves as the quantum counterpart to the classical penny flip game. One of the notable features of Meyer’s formulation was the incorporation of two well-known fictional characters, Picard and Q, from the renowned television series Star Trek. In this game Picard embodies the classical player, while Q embodies the quantum player. This signifies that Picard follows the rules of the classical penny flip game while Q can utilize arbitrary unitary operators, a hallmark of the quantum realm. Meyer demonstrated that in this game Q can consistently emerge victorious by employing the venerable Hadamard transform.

Many researchers, inspired by Meyer’s concepts, extended this game pattern to n-dimensional quantum systems. This avenue of exploration was pursued in Refs. [11,12,13]. Later, a comprehensive mapping of every finite variation of the PQ penny flip game to easily constructed finite automata was provided in Ref. [14]. Recently, this same game underwent extensive analysis from the perspective of group theory, with its relation to dihedral groups being established in Ref. [15]. A general analysis of quantum games under the assumption that both players draw their move from groups and not just unstructured sets, coming to some interesting conclusions, can be found in Ref. [16]. While in many works, the quantum player appears to possess a distinct advantage over the classical player, the situation is not as straightforward, as demonstrated in Ref. [17]. Here, the authors cleverly altered the rules of the PQ penny flip game in order to allow the classical player to secure a victory. A broader and intriguing problem concerning quantum gambling based on Nash equilibrium has been explored recently in Ref. [18]. The connection between infinitely repeated games and finite automata was also studied by Refs. [19,20,21,22]. Later, Meyer used quantum lattice gas automata to study Parrondo games in Ref. [23]. Employing probabilistic automata to tackle the Prisoners’ Dilemma game was undertaken by Ref. [24], whereas Ref. [25] considered the advantages of different automata variants in game theory.

Another research direction of the utmost importance, involves quantum coin flipping as a critical component in numerous quantum cryptographic protocols. There, familiar figures such as Alice and Bob take on the roles of remote parties striving to reach a consensus on a random bit. For a comprehensive presentation, the seminal work in Ref. [26] is invaluable, and for more recent developments pertaining to state-of-the-art cryprographic protocols we refer to Refs. [27,28,29,30]. Some of these ideas have been extended in Ref. [31] to quantum dice rolling in scenarios involving multiple outcomes and more than two parties. Most of the papers mentioned above, rely in an integral way on the phenomenon of quantum entanglement, a trend that is also followed by the current work.

Another influential work, also from 1999, was presented by Eisert et al. in Ref. [32]. There they demonstrated for the first time the so called Eisert–Wilkens–Lewenstein protocol. This protocol has gained wide acceptance and is now extensively used in the literature [33]. Using their protocol, they defined a variant of the famous Prisoners’ Dilemma and demonstrated that there exists a quantum strategy that is better than any classical strategy. Subsequently, many researchers followed that line of research, obtaining interesting results. For some recent developments one may also consult Ref. [34], where the Eisert–Wilkens–Lewenstein protocol was generalized. Let us also point out that the inclination to employ unconventional approaches for improving outcomes in classical games extends beyond the realm of quantum mechanics. Even in the domain of well-known classical games, such as the Prisoners’ Dilemma, efforts have been made to interpret them in terms of biological concepts (for a comprehensive overview, refer to Ref. [35]).

Contribution: This paper introduces Quantum Tapsilou, which is a novel quantum game inspired by a traditional Greek coin tossing game called tapsilou. While the classical game has a simple probability distribution, with both players having a $\frac{1}{4}$ probability of winning, Quantum Tapsilou exhibits an additional level of complexity using quantum mechanics. In Quantum Tapsilou, both players still have equal chances of winning, but these probabilities are now influenced by their previous choices and the use of quantum principles. There are two key innovations in Quantum Tapsilou:

• Entanglement through Rotation Gates. Instead of using Hadamard gates, which are commonly associated with creating entangled states with equal probability amplitudes, Quantum Tapsilou employs rotation gates, specifically $R_y$ rotation gates. These gates generate Bell-like states with unequal probability amplitudes, which adds a new layer of complexity to the game dynamics;
• Integral Use of Groups. In Quantum Tapsilou, both players agree on a specific cyclic rotation group of order n, where n should be a sufficiently large integer in order to provide the players with extra choices and increase the suspense of the game. This group forms the basis of the game because both players select rotations from this group to perform their actions using the corresponding $R_y$ rotation gates. Agreeing on this group, and, subsequently, choosing the precise rotations within the group, significantly impact the outcome of the game, introducing a strategic element based on group theory.

By incorporating these quantum principles and group theory, Quantum Tapsilou retains the characteristic aspects of the classical tapsilou game while adding complexity and variability to the probabilities of winning. Players must consider their choices of rotations within the agreed-upon group, as well as the entangled states generated by the $R_y$ rotation gates, to maximize their chances of winning in this intriguing quantum adaptation of a traditional Greek game. This is another example of the critical role of groups in ensuring a symmetric correspondence of actions in quantum games in the sense that for each action of each player, the other player can come up with a move to counteract it, a fact that is in accordance with a previous result in Ref. [16].

1.2. Organization

This paper is organized as follows: Section 1 gives a concise introduction to the field of quantum games, along with some of the most relevant references. Section 2 presents the traditional Greek game tapsilou, while Section 3 explains why the original game is meaningful and well-conceived. Section 4 and Section 5 give an easygoing account of the intuition behind the quantization of the classical game and the formal presentation of the new quantum game, respectively. Section 6 contains an extensive and rigorous analysis of the main properties of the proposed game Finally, Section 7 summarizes the main conclusions of this work and contains some possible research directions for future work.

2. The Traditional Game “Tapsilou”

The Greek gambling game “tapsilou” is a coin tossing game that originates from the Greek island of Corfu. The name “tapsilou” is a local idiom meaning “up high”. This is a traditional game played in New Year’s Eve and New Year’s Day in Mantouki, Corfu. It is also known as “crosses and marks” (“stavri or markoi”) and goes back in the history of the island. It was extremely popular in the 1960s, 1970s and 1980s among the young people and it was tradition to play it around the New Year celebration. Although it is considered a game, for many of the participants it meant their economic ruin [36].

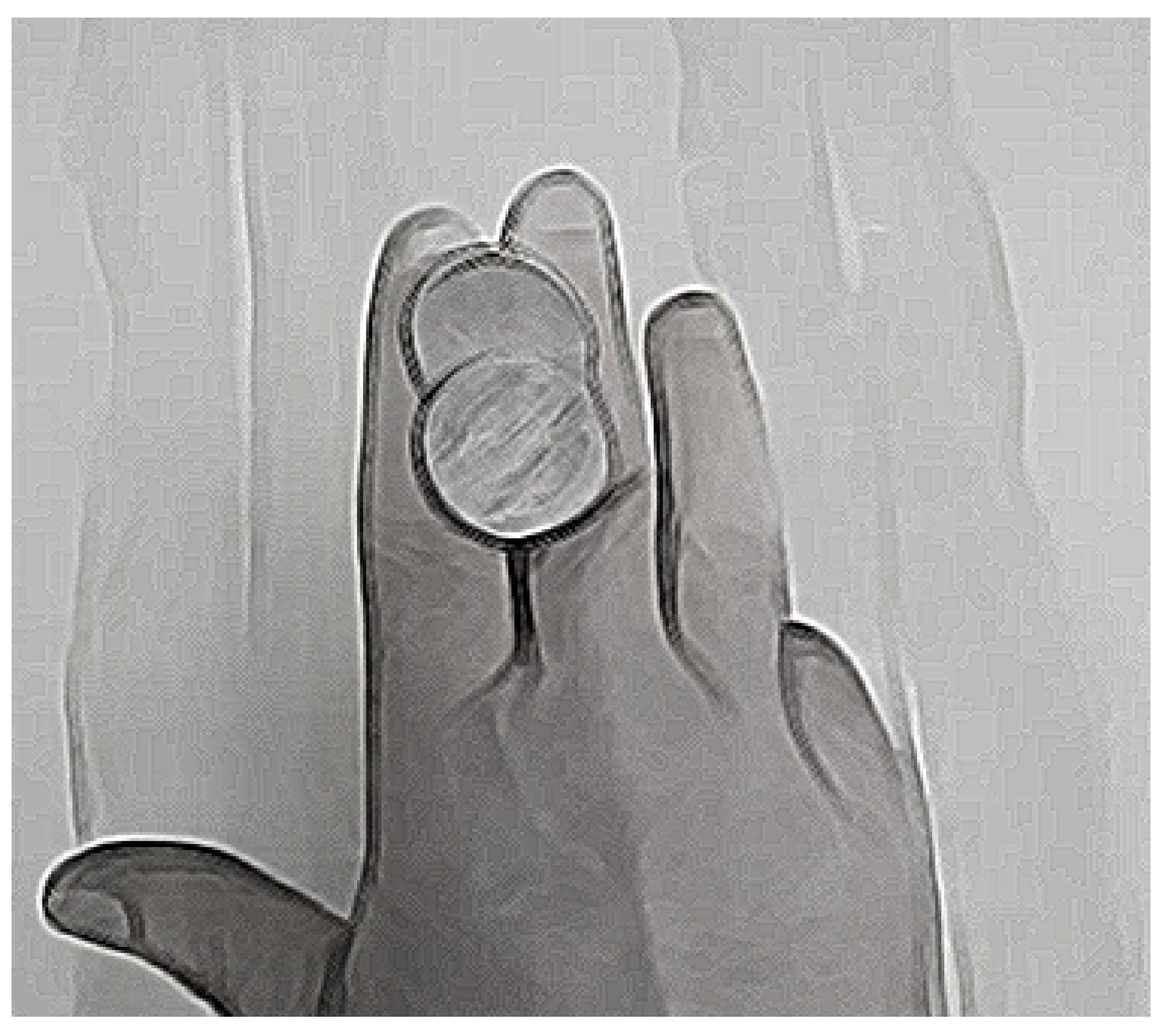
Tapsilou needs two coins. They used mostly Greek currency (drachmas), the so called 5-drachmas (“talara or talira”), like those depicted in Figure 1. It was the biggest in diameter coin of the days. The coin depicts a figure in one side, the heads side, and a number on the other, the tails side. Thus, the alternative name “crosses and marks”. As a terrain, the participants typically chose a sandlot. Two coins are placed in one of the player’s two-or-three fingers, as shown in Figure 2. This player is the tosser and from now on will also be referred to as player 1. The initial position of the coins on the fingers is one coin with the face up and one with the cross. The other players, usually more than one, are the gamblers, and, henceforth, will also be collectively referred to as player 2. The gamblers draw a circle around the tosser, who throws the coins high to the sky, thus the origin of the name “tapsilou”. After the flip, the coins end up on the ground. If the coins end up with two faces, the tosser wins. If the coins end up with crosses, the gamblers win, and in case the coins end up with one face and one cross, the tossing is repeated until there is a winner.

Although tapsilou requires at least two players, the tosser and at least one gambler, there is no limit as to what the maximum number of players is. It would not be unusual to have 15 or more players, as long as there is an amount of money that is large enough to bet. Before the tossing, the gamblers must announce their bet. If the two coins come up faces up, the tosser wins and takes all the bet money, whereas if they both come up crosses, the tosser pays each gambler twice the agreed bet. If the result is one coin face up and one coin cross, then the gamblers choose, individually, whether they will keep the same bet or raise it, and the tosser throws the coins again. This process is repeated, until the tosser or the gamblers win. The tosser loses when he has no more money left. If the tossers budget is running low, he may decide to take no more bets, or up to a certain amount, so as to not end up in debt. When the tosser loses all his money, another player takes his place.

Tapsilou is a forbidden game, so in many cases there may be lookout men. There are two common cheating strategies in this game The most tricky one is to crack the coin just a little bit, so as to always drop from one side. This, of course, makes the coins biased, but the crack has to be unnoticeable. The other cheating strategy is during the tossing to employ a technique where the two coins seem to flip in the air before they end up in the ground, but in fact only one flips, while the other does not flip at all. This is just an illusion that only the best trained cheaters can achieve. If a gambler recognizes a certain cheat strategy, he has the right to call it (using Greek idioms such as“den paei” or “ta kovo”) and the bet is cancelled.

3. Two Coins Seem to Be the Proper Choice

In this section, we give a precise quantitative description of the game and examine its possible generalizations.

Assuming that no cheating takes place, we see that the classical version of tapsilou is characterized by the following properties, where we use H and T to denote heads and tails, respectively.

(C₁)

The number of players is 2. Player 1 is the tosser, and player 2 is the gambler. Despite the fact that in real life many persons may play the gambler simultaneously, they can all be identified as one player in a theoretical analysis;

(C₂)

The number of coins is 2;

(C₃)

Viewing the two coins as comprising a system, we assume from now on that the initial state of this system is $(H,T)$;

(C₄)

If the final state is $(H,H)$, then player 1 wins. If the final state is $(T,T)$, then player 2 wins. In any other case, the game goes on to the next round;

(C₅)

The probability that player 1 wins is equal to the probability that player 2 wins, namely $\frac{1}{4}$;

(C₆)

The probability that neither player wins is $\frac{1}{2}$.

A question that comes to mind is whether it would be possible to generalize this game by tossing more than two coins. Under the plausible assumption that in such a generalization player 1 wins if all coins end up heads and player 2 wins if all coins end up tails, it is easy to calculate the probability for each player to win. If n coins are used, the condition for player 1 to win is that all n coins end up heads, an event that may happen with probability $\frac{1}{2^n}$. Symmetrically, for player 2 the probability that all n coins come up tails is also $\frac{1}{2^n}$. The next

Table 1. This table gives the probabilities of players 1 and 2 to win in a possible generalization of the game tapsilou.

Coins & Probability
# of Coins	P (Player 1 Wins)	P (Player 2 Wins)	P (Neither Wins)
3	0.125	0.125	0.750
4	0.0625	0.0625	0.875
5	0.0313	0.0313	0.938

gives the numerical values of these probabilities when the number of coins is 3, 4 and 5. If tapsilou were to use more than two coins, the game would not be very interesting because the probability of neither player winning and just spending most of the gaming tossing coins would be far greater, than having a winner. Therefore, using exactly two coins seems to be the best choice in order to have a game with suspense and symmetry.

In view of our previous analysis, it would seem that the classical world cannot offer a meaningful generalization of tapsilou. If one hopes to achieve an interesting variation of the classical game, turning to the quantum realm seems to be the most promising option.

4. The Intuition behind the Quantum Tapsilou

In this section we explain the rationale behind the proposed Quantum Tapsilou game (QTG from now), which captures the spirit of the classical tapsilou game. In the QTG, kets $|0\rangle$ and $|1\rangle$ correspond to the classical heads and tails states, respectively. Consequently, the initial state of the QTG is $|0\rangle |1\rangle$, and player 1 (player 2) wins if the final state of the system (after measurement) is $|0\rangle |0\rangle$ ($|1\rangle |1\rangle$). The following

Table 2. This table compares the characteristics of the classical tapsilou against the corresponding characteristics of the quantum tapsilou.

Classical vs. Quantum Tapsilou
	State	Initial State	Winning State for Player 1	Winning State for Player 2
Classical	H (Heads) T (Tails)	$(H,T)$	$(H,H)$	$(T,T)$
Quantum	|0〉 |1〉	$|0\rangle |1\rangle$	$|0\rangle |0\rangle$	$|1\rangle |1\rangle$

summarizes these facts.

Let us first assume that player 1 (the tosser) can employ quantum actions to his advantage. In order for him to win, both coins must end up heads. This is easily achievable in the quantum realm using entanglement. Thus, entanglement is the key for player 1 to ensure that both coins end up in the same state. The most well-known example of maximal entanglement for a two-qubit system, such as the system consisting of the coins in the QTG, is given by the Bell states, also called EPR pairs. There are four Bell states expressed, as shown below (see Ref. [39]).

$$\begin{array}{c}\hfill |{\Phi }^{+}\rangle =\frac{|0\rangle |0\rangle +|1\rangle |1\rangle }{\sqrt{2}}\end{array}$$

(1)

$$\begin{array}{c}\hfill |{\Phi }^{-}\rangle =\frac{|0\rangle |0\rangle -|1\rangle |1\rangle }{\sqrt{2}}\end{array}$$

(2)

$$\begin{array}{c}\hfill |{\Psi }^{+}\rangle =\frac{|0\rangle |1\rangle +|1\rangle |0\rangle }{\sqrt{2}}\end{array}$$

(3)

$$\begin{array}{c}\hfill |{\Psi }^{-}\rangle =\frac{|0\rangle |1\rangle -|1\rangle |0\rangle }{\sqrt{2}}\end{array}$$

(4)

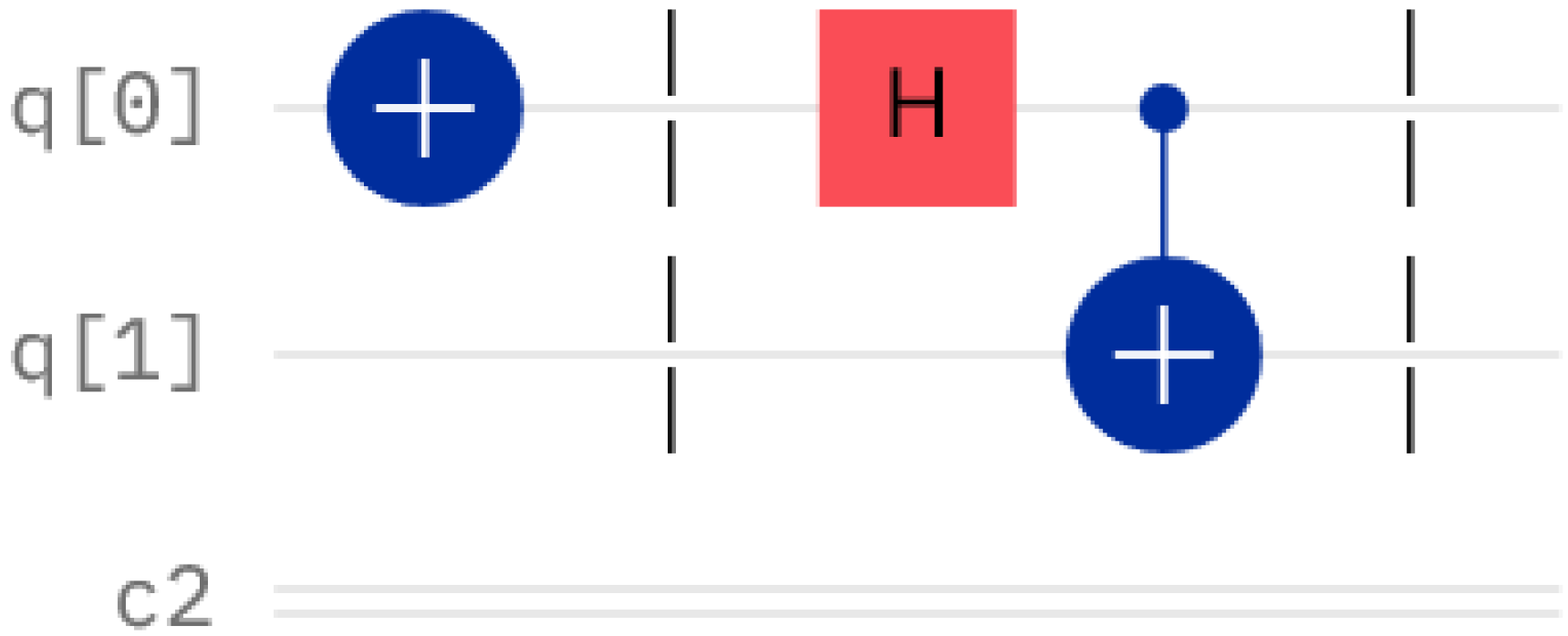
A typical quantum circuit used to generate entangled pairs, which is based on the Hadamard transform, is shown in Figure 3.

To avoid any possible confusion, we emphasize that the quantum circuit of Figure 3, as well as all quantum circuits in the forthcoming figures, are designed using the IBM Quantum Composer [40]. In the context of IBM Quantum Composer, the qubit numbering follows the “little-endian” convention, that is, the rightmost qubit is the least significant qubit (LSQ), and the leftmost qubit is the most significant qubit (MSQ). The same tool is used for the visualization of the state vector of the quantum system. 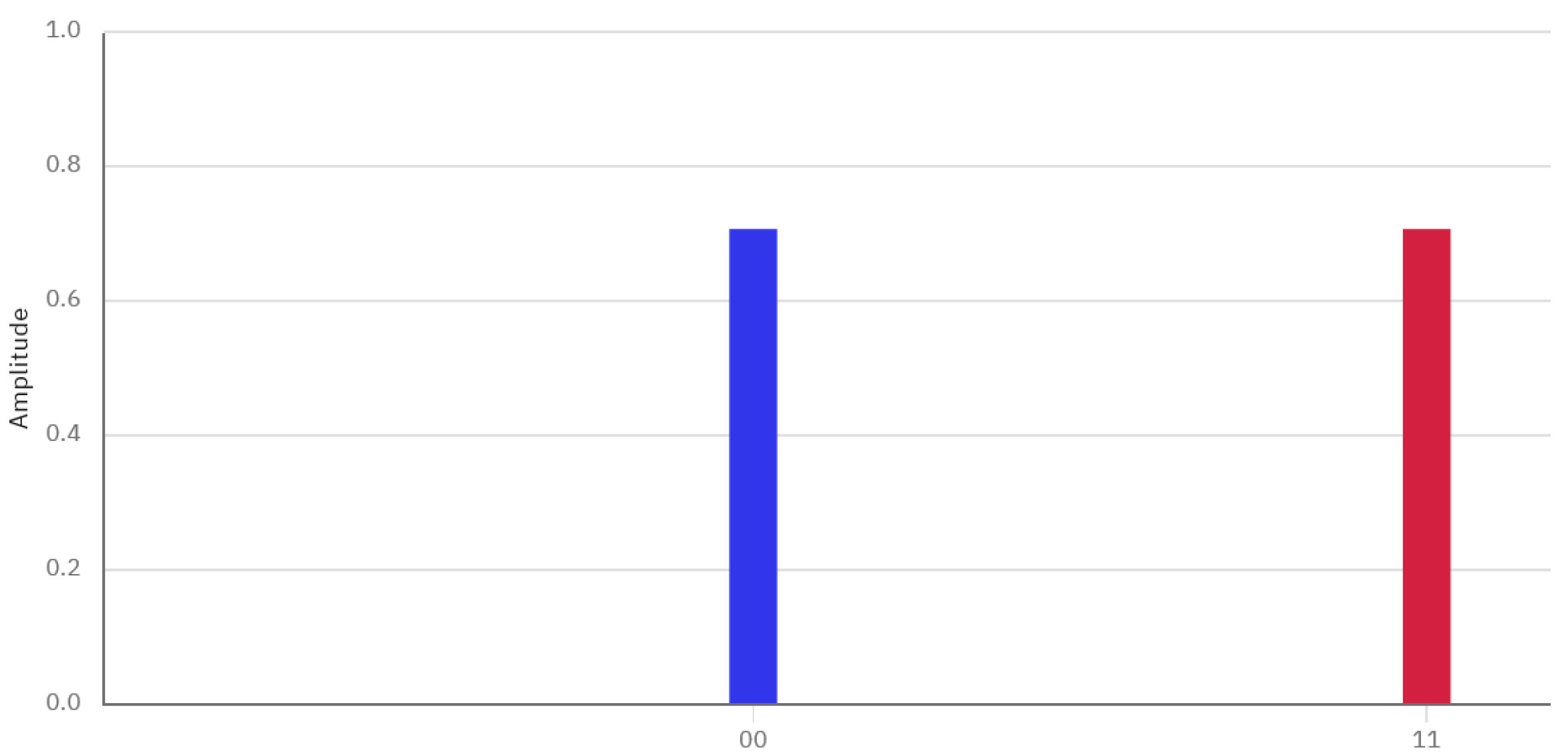The circuit in Figure 3 will prepare the system of the two coins in the $|{\Phi }^{-}\rangle$ state, which is characterized by the state vector depicted in Figure 4. However, if the coins are measured in the $|{\Phi }^{-}\rangle =\frac{|0\rangle |0\rangle -|1\rangle |1\rangle }{\sqrt{2}}$ state, the tosser does not have any real advantage because each player has equal probability $\frac{1}{2}$ to win.

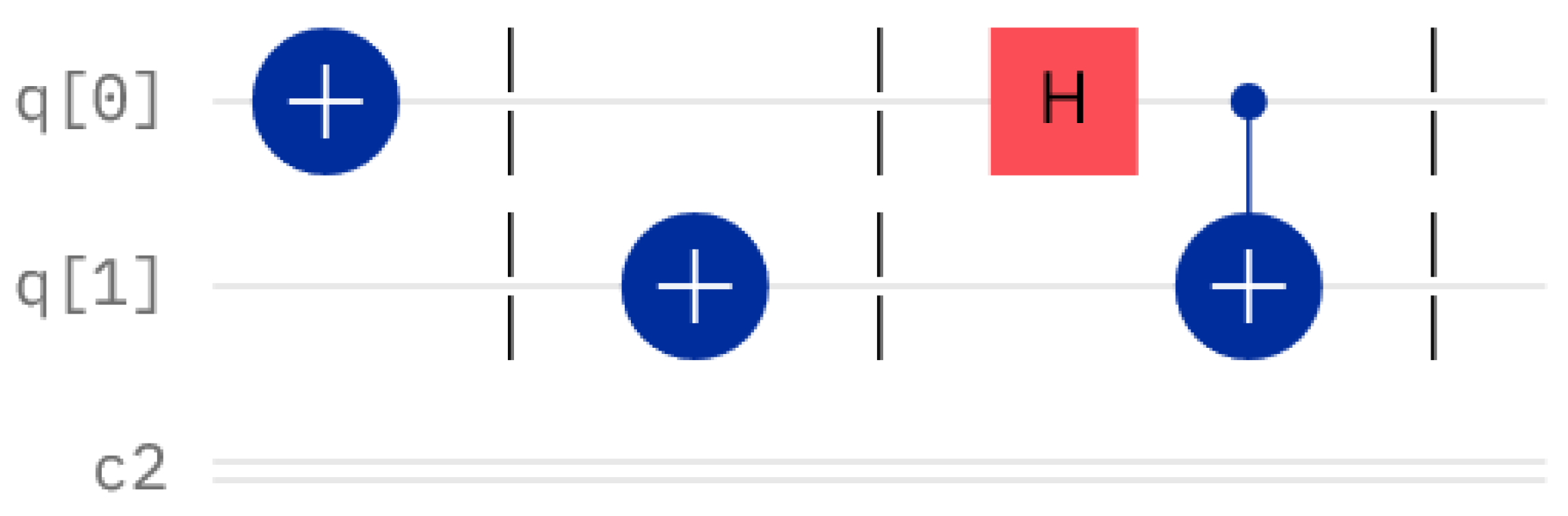
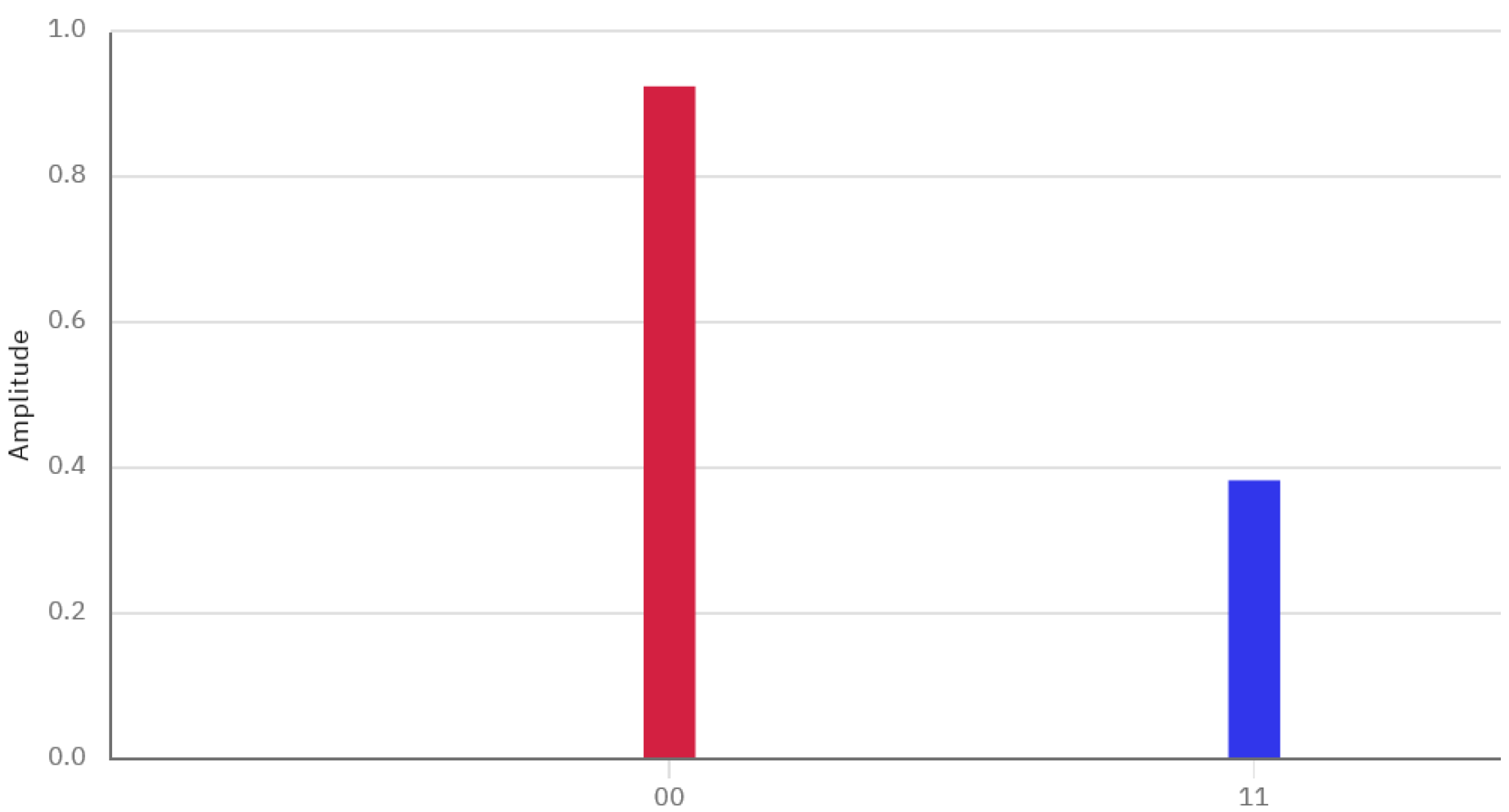
It is also plausible that player 1 drives the system to the $|{\Psi }^{-}\rangle$, via the circuit of Figure 5. The $|{\Psi }^{-}\rangle$ Bell state is defined as: $|{\Psi }^{-}\rangle =\frac{|0\rangle |1\rangle -|1\rangle |0\rangle }{\sqrt{2}}$. As shown in Figure 6, if the coins are measured in this state, it is certain that nobody wins, and the game keeps going on ad infinitum.

Therefore, from the perspective of player 1, it becomes evident that he must entangle the two coins in a more subtle way. Common sense suggests that player 1 should devise a kind of entanglement that satisfies the following requirements.

• Both coins end up in the same state with certainty, i.e., with probability 1;
• While it may still be possible that both coins may come up tails, the probability that both coins may end up heads must be significantly higher. In other words, the odds should favor player 1 decisively.

One way that player 1 may achieve such an effect is to use rotation gates in place of the Hadamard gate. Towards this end, the simplest choice would be to use the quantum gate $R_y\left(\theta \right)$ with the appropriate parameter $\theta \in \mathbb{R}$, which is defined as

$$\begin{array}{c}\hfill R_y\left(\theta \right)=\left[\begin{array}{cc}\hfill cos\frac{\theta }{2}& \hfill -sin\frac{\theta }{2}\\ \hfill sin\frac{\theta }{2}& \hfill \phantom{-}cos\frac{\theta }{2}\end{array}\right].\end{array}$$

(5)

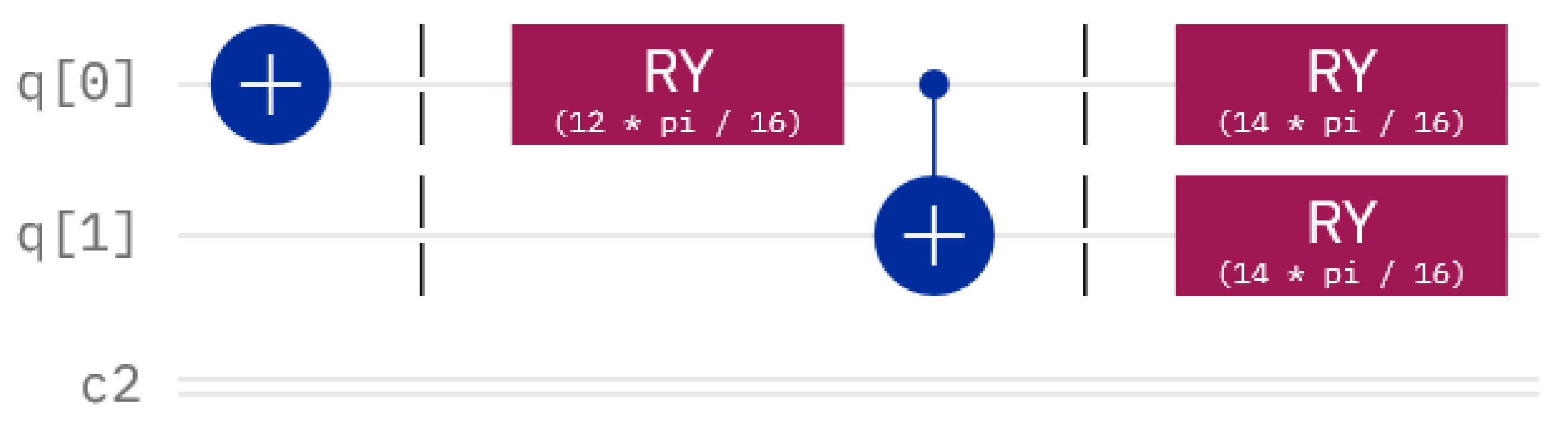
The gate $R_y$ rotates the state of the coin around the y axis of the Bloch sphere through an angle $\frac{\theta }{2}$ counterclockwise. Figure 7 illustrates a quantum circuit that employs the rotation gate $R_y\left(\frac{12\pi }{16}\right)$ to send the two coins to the state described by Figure 8.

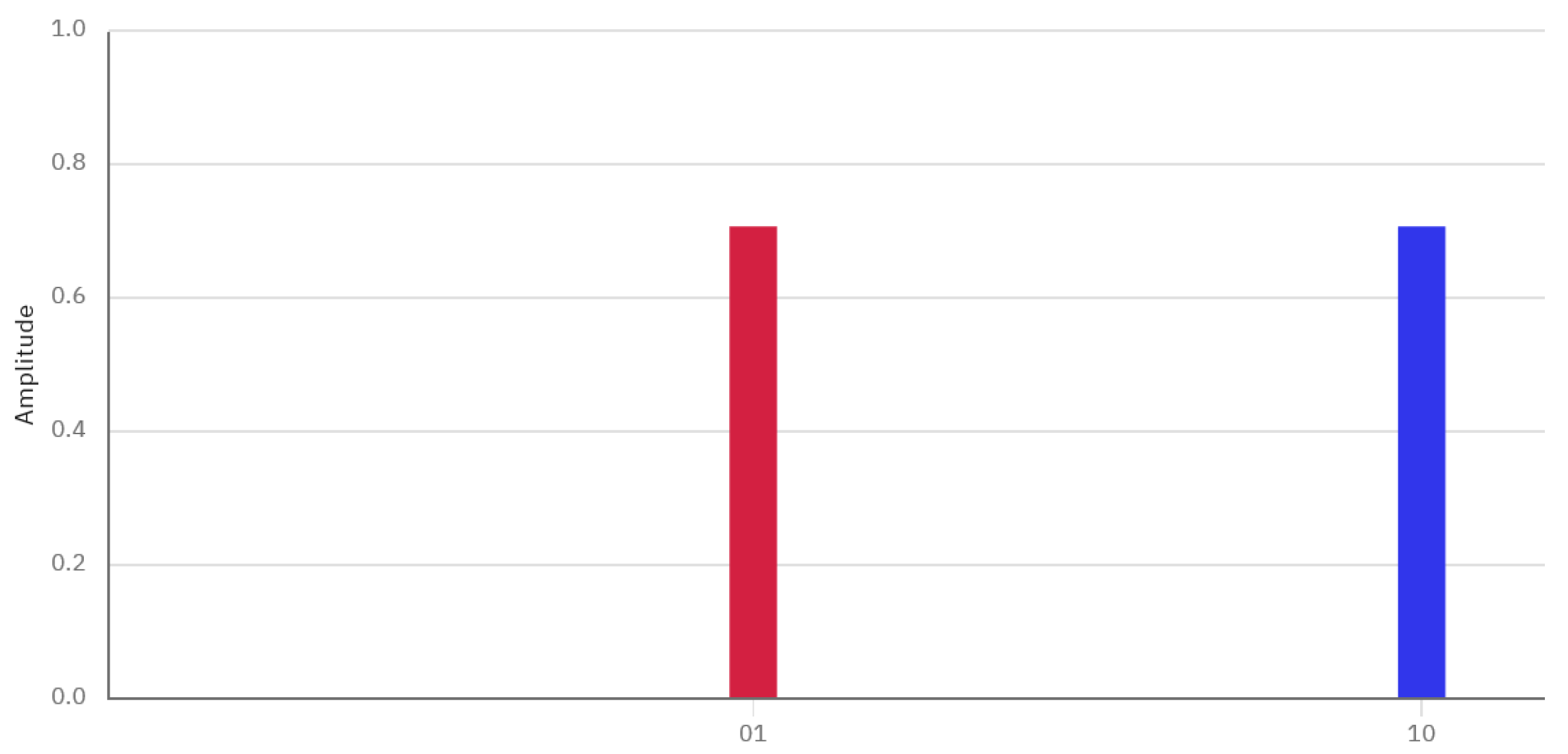
In this scenario, the final state of the two coins is determined by measurements in the computational basis $B=\{|0\rangle ,|1\rangle \}$. The outcome that stands out as particularly probable has player 1 emerging as the victor and player 2 experiencing a loss. These measurements and their associated probabilities determine the winner and the loser in the game. Obviously, in such a case, player 2, being rational, has no incentive whatsoever to participate in the game. There is, however, a way to make the game suspenseful again by letting player 2 choose the basis with respect to which the coins are measured.

As demonstrated by the above Figure 9 and Figure 10, if player 2 chooses the proper measurement basis, despite the rotation used by player 1, he can turn the tables and make sure that the odds of winning are now in his favor.

5. The Formal Presentation of the QTG

This section contains the precise description of the QTG, together with its comprehensive mathematical analysis. In our vision of the QTG, rotations play a decisive role, and, since rotations form groups, and groups are a prevalent theme in quantum mechanics, we shall employ some elementary concepts from the theory of groups, adhering to the notation and definitions found in standard textbooks such as Refs. [41,42,43]. Group theory was introduced to QM by Weyl [44] and Wigner [45] and has since remained an important tool. So, without further ado, we proceed to introduce the required machinery.

(N₁)

The general cyclic rotation group of order n, denoted by $\langle r\rangle$, contains the following n elements

$$\begin{array}{c}\hfill \langle r\rangle =\{\mathbb{1},r,r^2,\dots ,r^{n-1}\},\end{array}$$

(6)

where r is the rotation on the plane by $\frac{2\pi }{n}$. Its elements $\mathbb{1},r,r^2,\dots ,r^{n-1}$ are plane rotations. Specifically, $r^k$ is the rotation by $\frac{2\pi k}{n}$, $0\le k\le n-1$, and $\mathbb{1}=r^0$ is the identity element.

(N₂)

To each group element $r^k$, which represents the plane rotation by $\frac{2\pi k}{n}$, we associate the rotation gate $R_y\left(\frac{2\pi k}{n}\right)$

$$\begin{array}{c}\hfill R_y\left(\frac{2\pi k}{n}\right)=\left[\begin{array}{cc}\hfill cos\frac{\pi k}{n}& \hfill -sin\frac{\pi k}{n}\\ \hfill sin\frac{\pi k}{n}& \hfill \phantom{-}cos\frac{\pi k}{n}\end{array}\right],\end{array}$$

(7)

the two orthonormal kets

$$\begin{array}{c}\hfill {|0\rangle }_{\frac{2\pi k}{n}}=\left[\begin{array}{c}cos\frac{\pi k}{n}\\ sin\frac{\pi k}{n}\end{array}\right]\end{array}$$

(8)

$$\begin{array}{c}\hfill {|1\rangle }_{\frac{2\pi k}{n}}=\left[\begin{array}{c}\hfill -sin\frac{\pi k}{n}\\ \hfill \phantom{-}cos\frac{\pi k}{n}\end{array}\right],\end{array}$$

(9)

and the change of basis matrix

$$\begin{array}{c}\hfill B_{\frac{2\pi k}{n}}=\left[\begin{array}{cc}\hfill \phantom{-}cos\frac{\pi k}{n}& \hfill sin\frac{\pi k}{n}\\ \hfill -sin\frac{\pi k}{n}& \hfill cos\frac{\pi k}{n}\end{array}\right],\end{array}$$

(10)

which affects the change from the computational basis $B=\{|0\rangle ,|1\rangle \}$ to a new basis where the basis kets are ${|0\rangle }_{\frac{2\pi k}{n}}$ and ${|1\rangle }_{\frac{2\pi k}{n}}$. More details on the computation of the change of basis matrix can be found in Refs. [46,47,48].

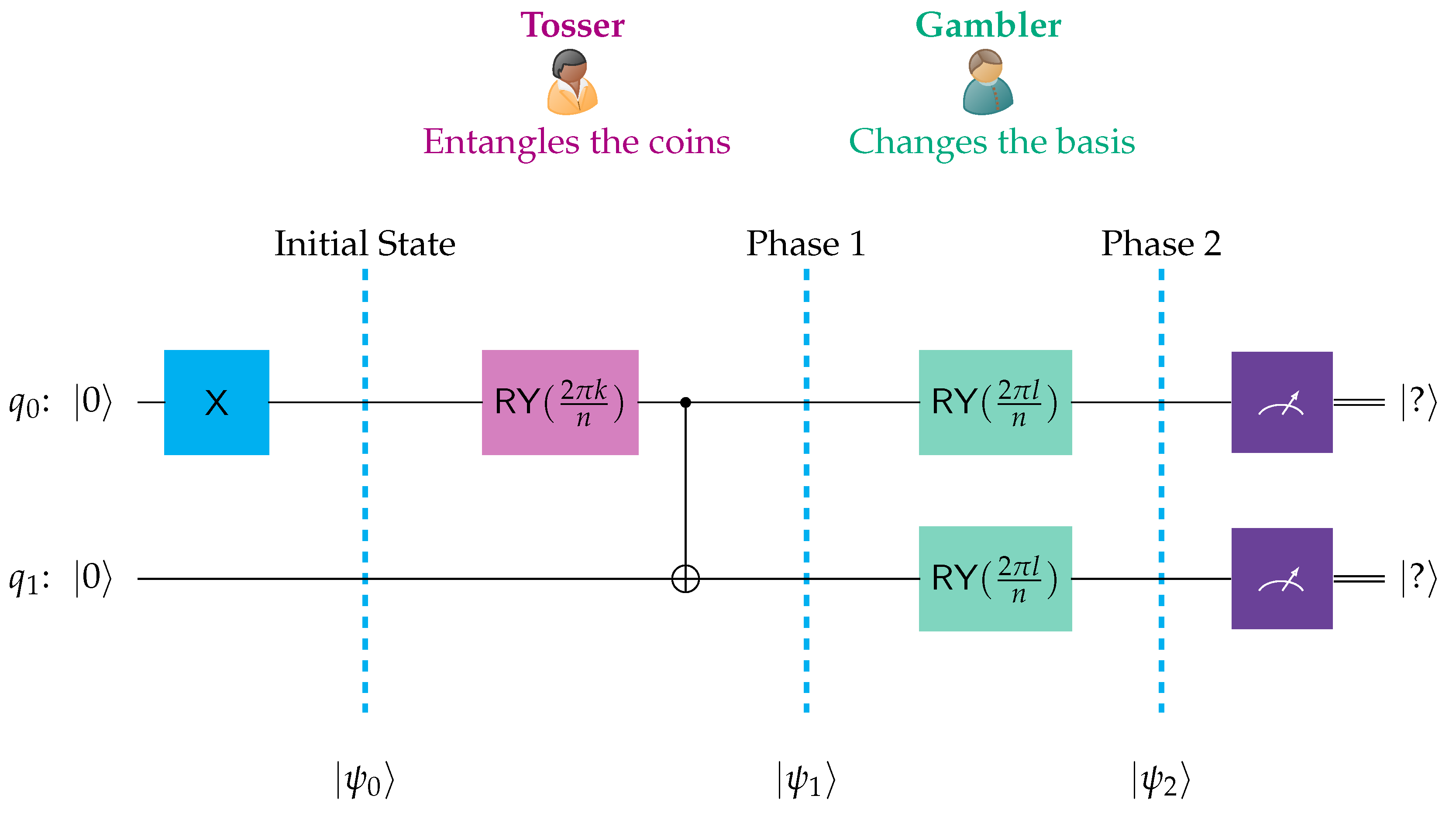
Before proceeding to formally state the rules of the QTG, let us recall that in all quantum circuits and in all figures of this work, the qubit numbering follows adheres to the IBM Quantum Composer and Qiskit convention, where the rightmost (or top) qubit is the least significant qubit and the leftmost (or bottom) qubit is the most significant qubit.

(R₁)

The initial state of the two coin system is $|0\rangle |1\rangle$. The winning state for player 1 (the tosser) is $|0\rangle |0\rangle$, and the winning state for player 2 (the gambler) is $|1\rangle |1\rangle$;

(R₂)

Both players agree on a specific cyclic rotation group $\langle r\rangle$ of order n, for some sufficiently large n. This will be the group upon which the QTG will be based. Both players will pick elements from this group to realize their actions;

(R₃)

Player 1 chooses an element $r^k\in \langle r\rangle$, $0\le k\le n-1$, and uses the rotation operator $R_y\left(\frac{2\pi k}{n}\right)$ (recall Equation (7)) to entangle the two coins. Formally, player 1’s action is described by

$$\begin{array}{c}\hfill CNOT·\left(I\otimes R_y\left(\frac{2\pi k}{n}\right)\right),\end{array}$$

(11)

where $CNOT$ and I are the controlled NOT and identity operators, respectively;

(R₄)

Player 2 chooses an element $r^l\in \langle r\rangle$, $0\le l\le n-1$, and measures the two coins with respect to the orthonormal basis $B_{\frac{2\pi l}{n}}$ (recall Formula (10)). Formally, player 2’s action is described by

$$\begin{array}{c}\hfill R_y\left(\frac{2\pi l}{n}\right)\otimes R_y\left(\frac{2\pi l}{n}\right).\end{array}$$

(12)

Although, for concreteness, we have set as $|0\rangle |1\rangle$ the initial state of the game, it is noteworthy to mention that the choice of the initial state does not really matter. Picking a different initial state, would not change the nature of the QTG and the forthcoming analysis.

The QTG is captured by the abstract quantum circuit shown below in Figure 11.

6. The Mathematical Analysis of the QTG

In this section we shall analyze the QTG from a rigorous mathematical viewpoint, in order to draw conclusions about the options of the two players and their odds of winning. We use the abstract quantum circuit of Figure 11 as a guide. In our exposition, we follow the Qiskit [49] way of ordering the qubits, which means that the bottom qubit is the most significant and the top the least significant.

By rule (R${}_1$), the initial state of the system, denoted by $|{\psi }_0\rangle$, is given by

$$\begin{array}{c}\hfill |{\psi }_0\rangle =|0\rangle |1\rangle =\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right].\end{array}$$

(13)

Player 1, the tosser, acts first on the system, using the action described by Equation (11) in rule (R${}_3$). In view of Formula (7), the matrix representation of the tensor product $(I\otimes R_y\left(\frac{2\pi k}{n}\right))$ is

$$\begin{array}{c}\hfill I\otimes R_y\left(\frac{2\pi k}{n}\right)\stackrel{\left(7\right)}{=}\left[\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1\end{array}\right]\otimes \left[\begin{array}{cc}\hfill cos\frac{\pi k}{n}& \hfill -sin\frac{\pi k}{n}\\ \hfill sin\frac{\pi k}{n}& \hfill \phantom{-}cos\frac{\pi k}{n}\end{array}\right]=\left[\begin{array}{cccc}\hfill cos\frac{\pi k}{n}& \hfill -sin\frac{\pi k}{n}& \hfill 0& 0\\ \hfill sin\frac{\pi k}{n}& \hfill \phantom{-}cos\frac{\pi k}{n}& \hfill 0& 0\\ \hfill 0& \hfill 0& \hfill cos\frac{\pi k}{n}& -sin\frac{\pi k}{n}\\ \hfill 0& \hfill 0& \hfill sin\frac{\pi k}{n}& \phantom{-}cos\frac{\pi k}{n}\end{array}\right].\end{array}$$

(14)

Since, we follow the IBM Quantum Composer and Qiskit convention in the numbering of qubits, the matrix representation of the CNOT, as applied to the circuit of Figure 11, is the one given below, according to the Qiskit documentation [50]. The permutation of the Controlled-NOT (CNOT) gate, also known as the CX gate in Qiskit, can appear different from the notation encountered in some textbooks, e.g., Ref. [39], due to differences in qubit indexing and conventions used in quantum computing libraries such as Qiskit. The difference in operation arises from the fact that Qiskit follows the little-endian qubit indexing convention, where the least significant qubit is on the right. This explains the difference in the mathematical representation of the CNOT gate.

$$\begin{array}{c}\hfill CNOT=\left[\begin{array}{cccc}\hfill 1& \hfill 0& \hfill 0& 0\\ \hfill 0& \hfill 0& \hfill 0& 1\\ \hfill 0& \hfill 0& \hfill 1& 0\\ \hfill 0& \hfill 1& \hfill 0& 0\end{array}\right]\end{array}$$

(15)

Using (14) and (15), we may derive the matrix representation of the action of player 1.

$$\begin{array}{cc}\hfill CNOT·\left(I\otimes R_y\left(\frac{2\pi k}{n}\right)\right)& \stackrel{\left(14\right),\left(15\right)}{=}\left[\begin{array}{cccc}\hfill 1& \hfill 0& \hfill 0& 0\\ \hfill 0& \hfill 0& \hfill 0& 1\\ \hfill 0& \hfill 0& \hfill 1& 0\\ \hfill 0& \hfill 1& \hfill 0& 0\end{array}\right]\left[\begin{array}{cccc}\hfill cos\frac{\pi k}{n}& \hfill -sin\frac{\pi k}{n}& \hfill 0& 0\\ \hfill sin\frac{\pi k}{n}& \hfill \phantom{-}cos\frac{\pi k}{n}& \hfill 0& 0\\ \hfill 0& \hfill 0& \hfill cos\frac{\pi k}{n}& -sin\frac{\pi k}{n}\\ \hfill 0& \hfill 0& \hfill sin\frac{\pi k}{n}& \phantom{-}cos\frac{\pi k}{n}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}\hfill cos\frac{\pi k}{n}& \hfill -sin\frac{\pi k}{n}& \hfill 0& 0\\ \hfill 0& \hfill 0& \hfill sin\frac{\pi k}{n}& \phantom{-}cos\frac{\pi k}{n}\\ \hfill 0& \hfill 0& \hfill cos\frac{\pi k}{n}& -sin\frac{\pi k}{n}\\ \hfill sin\frac{\pi k}{n}& \hfill \phantom{-}cos\frac{\pi k}{n}& \hfill 0& 0\end{array}\right]\hfill \end{array}$$

(16)

By combining (13) and (16), we conclude that the state of the two coins at the end of Phase 1, i.e., after the tosser’s action, which is denoted by $|{\psi }_1\rangle$, is given by

$$\begin{array}{c}\hfill |{\psi }_1\rangle =\left[\begin{array}{c}-sin\frac{\pi k}{n}\\ 0\\ 0\\ \phantom{-}cos\frac{\pi k}{n}\end{array}\right].\end{array}$$

(17)

Example 1

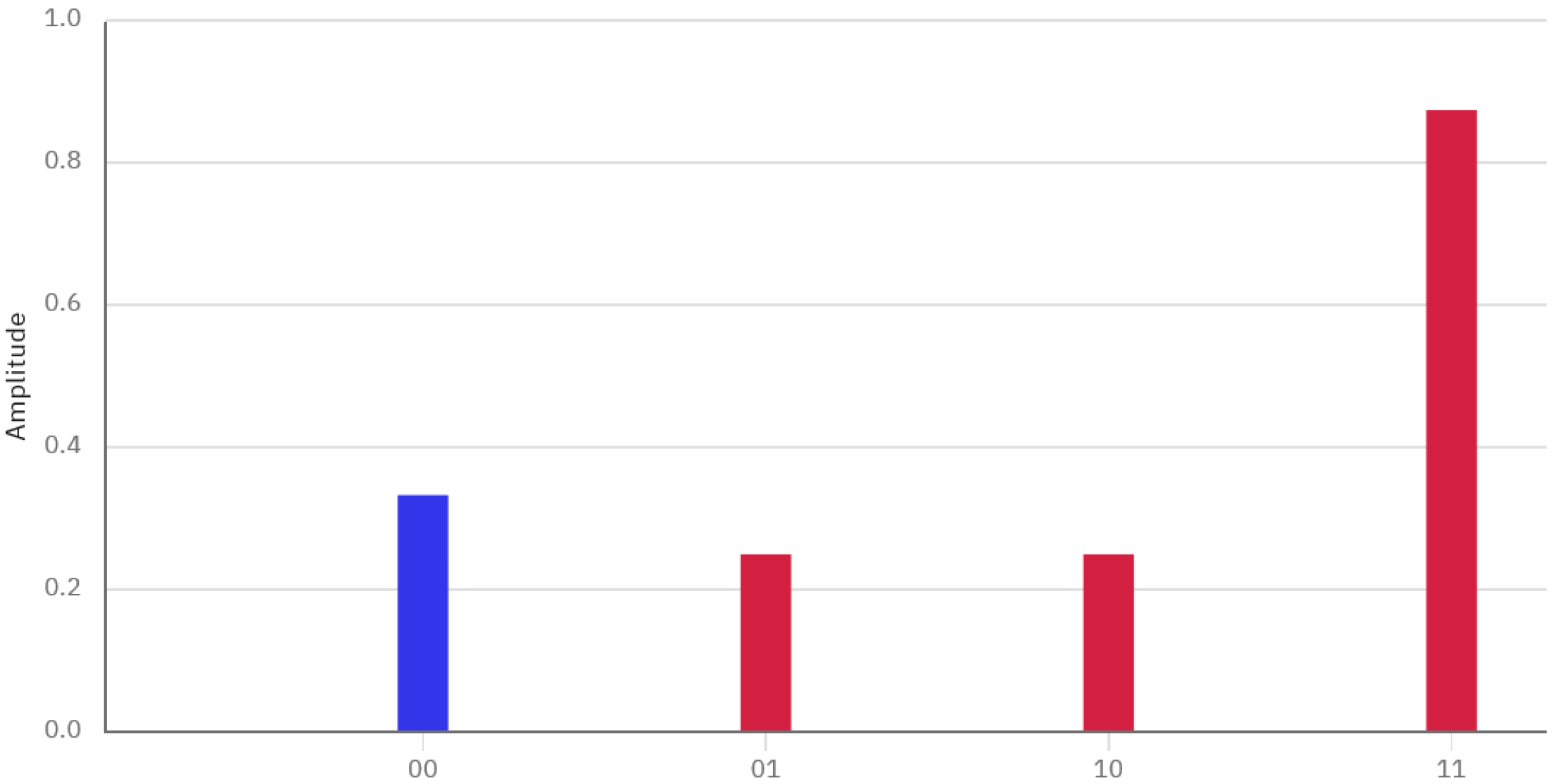
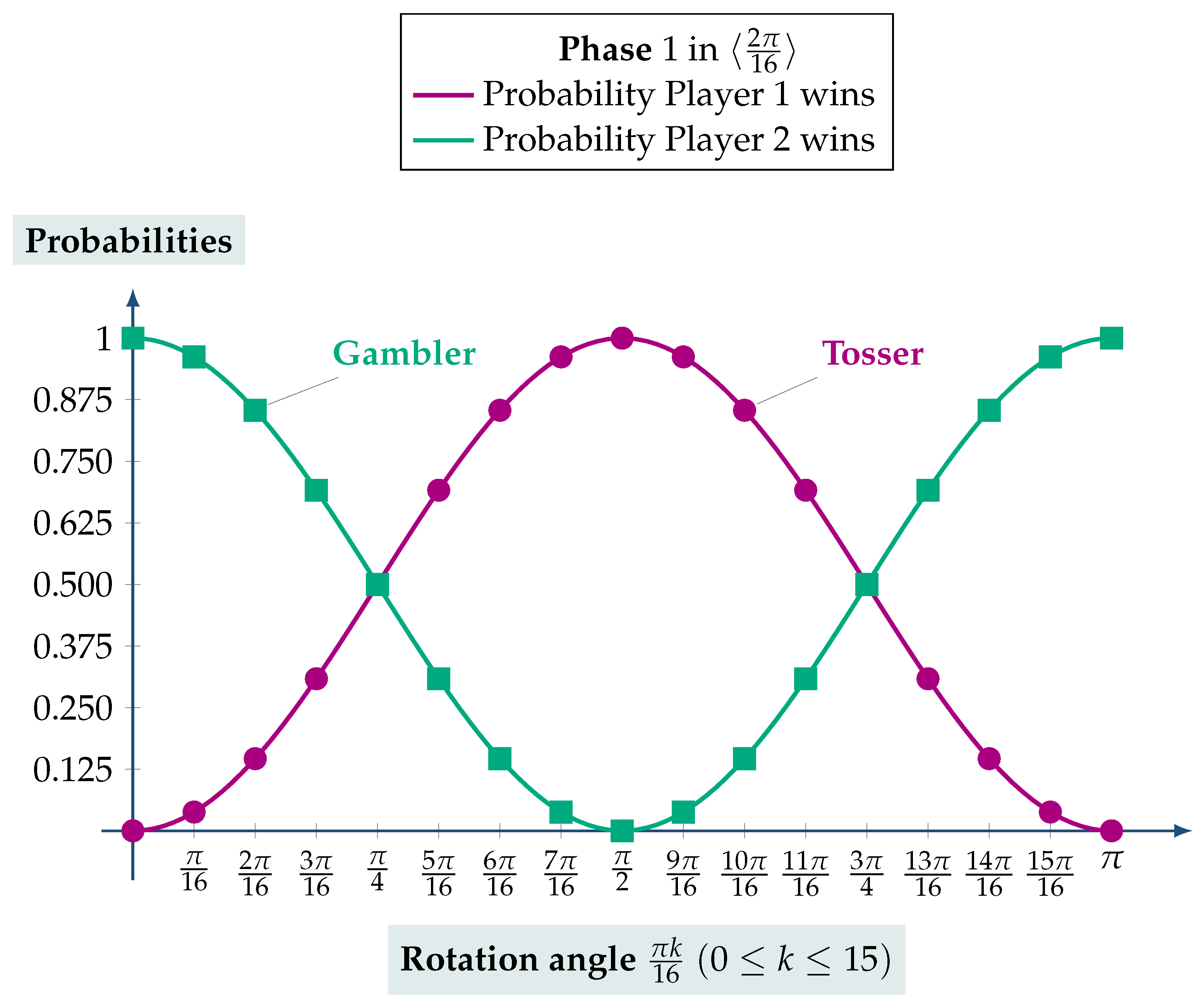
(Playing in the group $\langle \frac{2\pi }{16}\rangle$). This example examines how the QTG evolves up to Phase 1 (see Figure 11), when the game is played in the cyclic rotation group $\langle \frac{2\pi }{16}\rangle$. Practically, this implies that both players may choose for their action one the 16 rotations of this group.

The general form of the action of Player 1 is given by (16) and the state of the two coins by (17). If the game were to end at this point in time, measuring the two coins would find the system in state $|0\rangle |0\rangle$ with probability ${sin}^2\frac{\pi k}{n}$, and in state $|1\rangle |1\rangle$ with probability ${cos}^2\frac{\pi k}{n}$. Hence, the probability that the tosser would win ranges from 0, in case the tosser uses the identity element of the group, namely the 0 radians rotation, to 1, in case he uses the $\frac{\pi }{2}$ radians rotation. For every possible choice of rotation from the $\langle \frac{2\pi }{16}\rangle$ group, the corresponding probability for player 1 is given by the red line of Figure 12. Symmetrically, for every possible choice of rotation from $\langle \frac{2\pi }{16}\rangle$, the corresponding probability for player 2 is given by the green line of Figure 12. The specific numerical values of the players’ probabilities are contained in

Table 3. This table gives the probabilities for each player at the end of Phase 1 when QTG is played in $\langle \frac{2\pi }{16}\rangle$.

Probabilities at the End of Phase 1 in $\langle \frac{2\mathit{\pi }}{16}\rangle$
$k$	0	$\mathbf{1},\mathbf{15}$	$\mathbf{2},\mathbf{14}$	$\mathbf{3},\mathbf{13}$	$\mathbf{4},\mathbf{12}$	$\mathbf{5},\mathbf{11}$	$\mathbf{6},\mathbf{10}$	$\mathbf{7},\mathbf{9}$	8
Tosser	0	$0.038$	$0.146$	$0.309$	$0.5$	$0.691$	$0.854$	$0.962$	1
Gambler	1	$0.962$	$0.854$	$0.691$	$0.5$	$0.309$	$0.146$	$0.038$	0

.       ◃

Continuing with our analysis, let us now proceed to Phase 2 (see Figure 11). During Phase 2, player 2, the gambler, acts by changing the measurement basis. This action is expressed by the tensor product $R_y\left(\frac{2\pi l}{n}\right)\otimes R_y\left(\frac{2\pi l}{n}\right)$ of Equation (10), which is given below in explicit form.

$$\begin{array}{cc}\hfill R_y\left(\frac{2\pi l}{n}\right)\otimes R_y\left(\frac{2\pi l}{n}\right)& \stackrel{\left(12\right)}{=}\left[\begin{array}{cc}\hfill cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}& \hfill cos\frac{\pi l}{n}\end{array}\right]\otimes \left[\begin{array}{cc}\hfill cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}& \hfill cos\frac{\pi l}{n}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}\hfill cos\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \phantom{-}sin\frac{\pi l}{n}sin\frac{\pi l}{n}\\ \hfill cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}sin\frac{\pi l}{n}& -sin\frac{\pi l}{n}cos\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}& -cos\frac{\pi l}{n}sin\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}\end{array}\right].\hfill \end{array}$$

(18)

Therefore, as a result of the gambler’s action, the system of the two coins at the end of Phase 2 will be in the following $|{\psi }_2\rangle$ state.

$$\begin{array}{cc}\hfill |{\psi }_2\rangle & \stackrel{\left(17\right),\left(18\right)}{=}\left[\begin{array}{cccc}\hfill cos\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \phantom{-}sin\frac{\pi l}{n}sin\frac{\pi l}{n}\\ \hfill cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}sin\frac{\pi l}{n}& -sin\frac{\pi l}{n}cos\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill -sin\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}& -cos\frac{\pi l}{n}sin\frac{\pi l}{n}\\ \hfill sin\frac{\pi l}{n}sin\frac{\pi l}{n}& \hfill \phantom{-}sin\frac{\pi l}{n}cos\frac{\pi l}{n}& \hfill \phantom{-}cos\frac{\pi l}{n}sin\frac{\pi l}{n}& \phantom{-}cos\frac{\pi l}{n}cos\frac{\pi l}{n}\end{array}\right]\left[\begin{array}{c}-sin\frac{\pi k}{n}\\ 0\\ 0\\ cos\frac{\pi k}{n}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}\hfill -sin\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}+cos\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}\hfill \\ \hfill -sin\frac{\pi k}{n}cos\frac{\pi l}{n}sin\frac{\pi l}{n}-cos\frac{\pi k}{n}cos\frac{\pi l}{n}sin\frac{\pi l}{n}\hfill \\ \hfill -sin\frac{\pi k}{n}cos\frac{\pi l}{n}sin\frac{\pi l}{n}-cos\frac{\pi k}{n}cos\frac{\pi l}{n}sin\frac{\pi l}{n}\hfill \\ \hfill -sin\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}+cos\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}\hfill \end{array}\right].\hfill \end{array}$$

(19)

After the completion of Phase 2, the measurement takes place. As Formula (19) implies, the probability $P_T$ of player 1 winning, that is of observing the system in state $|0\rangle |0\rangle$, is given by the next equation

$$\begin{array}{c}\hfill P_T(k,l)={\left(cos\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}\right)}^2.\end{array}$$

(20)

In a symmetric way, the probability $P_G$ of player 2 winning, i.e, finding the system in state $|1\rangle |1\rangle$ is

$$\begin{array}{c}\hfill P_G(k,l)={\left(cos\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}\right)}^2.\end{array}$$

(21)

Another important remark is that the probability $P_{\mathrm{draw}}$ that neither player wins, namely that the system ends up in the state $|0\rangle |1\rangle$ or $|1\rangle |0\rangle$, is expressed, after some simplifications, as

$$\begin{array}{c}\hfill P_{\mathrm{draw}}(k,l)=8{sin}^2\left(\pi \left(\frac{k}{n}+\frac{1}{4}\right)\right){sin}^2\left(\frac{\pi l}{n}\right){cos}^2\left(\frac{\pi l}{n}\right),\end{array}$$

(22)

and is, in general, nonzero.

A close examination of Equations (20) and (21) reveals the characteristic property of the QTG. Irrespective of the tosser’s choice of rotation, the subsequent action of the gambler balances the situation and puts both players on a equal footing. For any given k, $0\le k\le n-1$, chosen by the tosser, the gambler picks some orthonomal basis $B_{\frac{2\pi l}{n}}$, $0\le l\le n-1$, which leads to the probabilities $P_T(k,l)$ and $P_G(k,l)$ that express the chances of the former and the latter, respectively, to win the game The crucial observation is that for every basis $B_{\frac{2\pi l}{n}}$, there exists a dual basis $B_{\frac{2\pi l^{*}}{n}}$ that exchanges the aforementioned probabilities, so that $P_T(k,l^{*})=P_G(k,l)$ and $P_G(k,l^{*})=P_T(k,l)$. For instance, say that for some basis $B_{\frac{2\pi l}{n}}$, $P_T(k,l)>P_G(k,l)$, i.e., player 1 is more likely to win than player 2. Then for the dual basis $B_{\frac{2\pi l^{*}}{n}}$, $P_G(k,l^{*})=P_T(k,l)>P_G(k,l)=P_T(k,l^{*})$, which shows that the odds are perfectly reserved and player 2 is now more likely to win than player 1 by exactly the same amount. This fact is formally proved in the next Theorem 1.

Theorem 1.

The characteristic property of the QTG is that for each k, $0\le k\le n-1$, to every orthonomal basis $B_{\frac{2\pi l}{n}}$, $0\le l\le n-1$, corresponds adualbasis $B_{\frac{2\pi l^{*}}{n}}$ such that:

$$\begin{array}{cc}\hfill P_T(k,l^{*})& =P_G(k,l)\hfill \\ \hfill & and\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill P_G(k,l^{*})& =P_T(k,l).\hfill \end{array}$$

(24)

Proof. 

The proof is quite straightforward. First, let us recall some well-known trigonometric identities (see any standard textbook, such as Ref. [51]).

$$\begin{array}{cccc}\hfill cos(\theta \pm \frac{\pi }{2})& =\mp sin\theta \hfill & \hfill sin(\theta \pm \frac{\pi }{2})& =\pm cos\theta \hfill \end{array}$$

(25)

Let us fix a specific k, $0\le k\le n-1$, representing the plane rotation $r^k$ by $\frac{2\pi k}{n}$ radians, which is employed by the tosser during Phase 1. Let us further assume that during Phase 2 the gambler picks the orthonomal basis $B_{\frac{2\pi l}{n}}$ for some l, $0\le l\le n-1$.

Given l, we define its dual, denoted by $l^{*}$, as follows:

$$\begin{array}{c}\hfill l^{*}\equiv \left(l+\frac{n}{2}\right)modn.\end{array}$$

(26)

The above compact definition, can be cast in the more expedient form shown below.

$$\begin{array}{c}{l}^{*}=\left\{\begin{array}{cc}\left[l\right]l+\frac{n}{2}\hfill & \mathrm{if}l+\frac{n}{2}<n\\ l-\frac{n}{2}\hfill & \mathrm{if}l+\frac{n}{2}\ge n\end{array}\right.,0\le l\le n-1.\hfill \end{array}$$

(27)

We now proceed with the proof by distinguishing the following cases.

• $l+\frac{n}{2}<n$. In this case, according to (27), $l^{*}=l+\frac{n}{2}$. Therefore,

  $$\begin{array}{cc}\hfill P_T(k,l^{*})& \stackrel{\left(20\right)}{=}{\left(cos\frac{\pi k}{n}{sin}^2\frac{\pi l^{*}}{n}-sin\frac{\pi k}{n}{cos}^2\frac{\pi l^{*}}{n}\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{sin}^2\left(\frac{2\pi l+\pi n}{2n}\right)-sin\frac{\pi k}{n}{cos}^2\left(\frac{2\pi l+\pi n}{2n}\right)\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{sin}^2\left(\frac{\pi l}{n}+\frac{\pi }{2}\right)-sin\frac{\pi k}{n}{cos}^2\left(\frac{\pi l}{n}+\frac{\pi }{2}\right)\right)}^2\hfill \\ \hfill & \stackrel{\left(25\right)}{=}{\left(cos\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}\right)}^2\hfill \\ \hfill & \stackrel{\left(21\right)}{=}{P}_G(k,l)\hfill \end{array}$$

  (28)

  $$\begin{array}{cc}\hfill & \mathrm{and}\hfill \\ \hfill P_G(k,l^{*})& \stackrel{\left(21\right)}{=}{\left(cos\frac{\pi k}{n}{cos}^2\frac{\pi l^{*}}{n}-sin\frac{\pi k}{n}{sin}^2\frac{\pi l^{*}}{n}\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{cos}^2\left(\frac{2\pi l+\pi n}{2n}\right)-sin\frac{\pi k}{n}{sin}^2\left(\frac{2\pi l+\pi n}{2n}\right)\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{cos}^2\left(\frac{\pi l}{n}+\frac{\pi }{2}\right)-sin\frac{\pi k}{n}{sin}^2\left(\frac{\pi l}{n}+\frac{\pi }{2}\right)\right)}^2\hfill \\ \hfill & \stackrel{\left(25\right)}{=}{\left(cos\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}\right)}^2\hfill \\ \hfill & \stackrel{\left(20\right)}{=}{P}_T(k,l).\hfill \end{array}$$

  (29)
• $l+\frac{n}{2}\ge n$. In this case, according to (27), $l^{*}=l-\frac{n}{2}$. Therefore,

  $$\begin{array}{cc}\hfill P_T(k,l^{*})& \stackrel{\left(21\right)}{=}{\left(cos\frac{\pi k}{n}{sin}^2\frac{\pi l^{*}}{n}-sin\frac{\pi k}{n}{cos}^2\frac{\pi l^{*}}{n}\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{sin}^2\left(\frac{2\pi l-\pi n}{2n}\right)-sin\frac{\pi k}{n}{cos}^2\left(\frac{2\pi l-\pi n}{2n}\right)\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{sin}^2\left(\frac{\pi l}{n}-\frac{\pi }{2}\right)-sin\frac{\pi k}{n}{cos}^2\left(\frac{\pi l}{n}-\frac{\pi }{2}\right)\right)}^2\hfill \\ \hfill & \stackrel{\left(25\right)}{=}{\left(cos\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}\right)}^2\hfill \\ \hfill & \stackrel{\left(21\right)}{=}{P}_G(k,l)\hfill \end{array}$$

  (30)

  $$\begin{array}{cc}\hfill & \mathrm{and}\hfill \\ \hfill P_G(k,l^{*})& \stackrel{\left(21\right)}{=}{\left(cos\frac{\pi k}{n}{cos}^2\frac{\pi l^{*}}{n}-sin\frac{\pi k}{n}{sin}^2\frac{\pi l^{*}}{n}\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{cos}^2\left(\frac{2\pi l-\pi n}{2n}\right)-sin\frac{\pi k}{n}{sin}^2\left(\frac{2\pi l-\pi n}{2n}\right)\right)}^2\hfill \\ \hfill & ={\left(cos\frac{\pi k}{n}{cos}^2\left(\frac{\pi l}{n}-\frac{\pi }{2}\right)-sin\frac{\pi k}{n}{sin}^2\left(\frac{\pi l}{n}-\frac{\pi }{2}\right)\right)}^2\hfill \\ \hfill & \stackrel{\left(25\right)}{=}{\left(cos\frac{\pi k}{n}{sin}^2\frac{\pi l}{n}-sin\frac{\pi k}{n}{cos}^2\frac{\pi l}{n}\right)}^2\hfill \\ \hfill & \stackrel{\left(20\right)}{=}{P}_T(k,l).\hfill \end{array}$$

  (31)

Ergo, for every rotation $r^k$, $0\le k\le n-1$, chosen by the tosser during Phase 1, both players end up with the same probability distribution.     □

Example 2

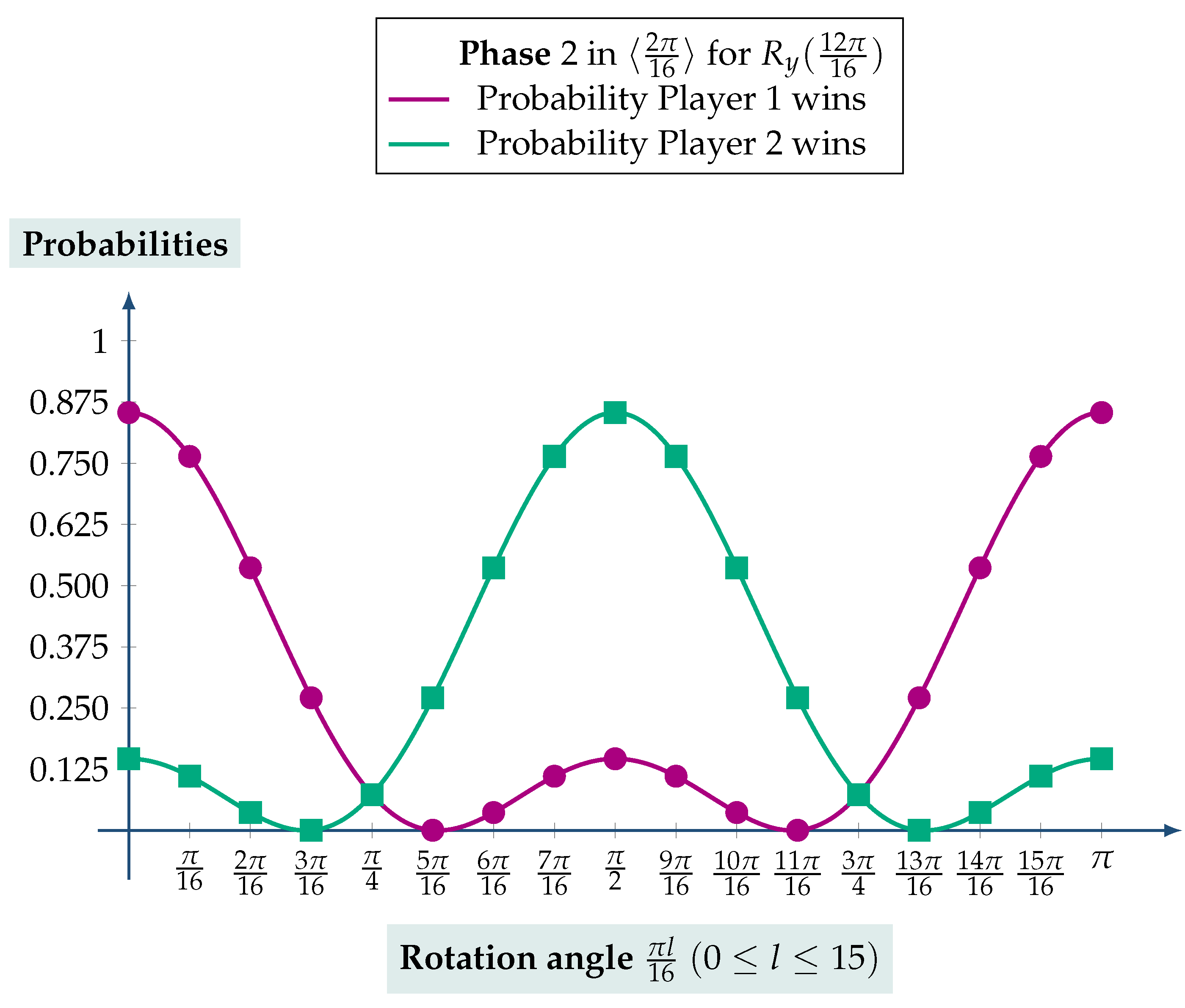
(Playing in the group $\langle \frac{2\pi }{16}\rangle$ continued). This example continues and concludes Example 1 by examining Phase 2 (see Figure 11) of the QTG under the same assumption that the game is played in the cyclic rotation group $\langle \frac{2\pi }{16}\rangle$.

Recall that Figure 12 visualizes the tosser’s and the gambler’s probabilities to win at the end of Phase 1 as a function of the rotation $r^k$, $0\le k\le n-1$, chosen by the tosser, and that the numerical values of the players’ probabilities are contained in Table 3.

Let us consider the scenario in which the tosser chose the rotation $r^6=\frac{12\pi }{16}$ in Phase 1. This choice was implemented via the use of the rotation gate $R_y\left(\frac{12\pi }{16}\right)$, which, in reality, causes a rotation through an angle $\frac{6\pi }{16}$ around the y axis of the Bloch sphere, and gave player 1 probability 0.854 to win at the end of Phase 1, as shown in Table 3. The motivation for such a choice could be that the tosser, being somewhat greedy, wanted a clear advantage over the gambler, while still allowing the latter a nonzero, but very slim, probability to win so as to keep appearances. However, player 2 can still turn the tables and gain the upper hand by picking an appropriate measurement basis. This fact is visualized in Figure 13, which depicts both players’ probabilities as a function of the measurement basis. The exact numerical values for each possible choice of player 2 are given in

Table 4. This table gives the probabilities for each player at the end of Phase 2 when QTG is played in $\langle \frac{2\pi }{16}\rangle$ and player 1 has utilized the rotation gate $R_y\left(\frac{12\pi }{16}\right)$ during Phase 1.

Probabilities at the End of Phase 2 in $\langle \frac{2\mathit{\pi }}{16}\rangle$
$k$	0	$\mathbf{1},\mathbf{15}$	$\mathbf{2},\mathbf{14}$	$\mathbf{3},\mathbf{13}$	$\mathbf{4},\mathbf{12}$	$\mathbf{5},\mathbf{11}$	$\mathbf{6},\mathbf{10}$	$\mathbf{7},\mathbf{9}$	8
Tosser	$0.854$	$0.764$	$0.537$	$0.271$	$0.073$	0	$0.037$	$0.111$	$0.146$
Gambler	$0.146$	$0.111$	$0.037$	0	$0.073$	$0.271$	$0.537$	$0.764$	$0.854$

. With that in mind, it becomes evident that, if player 2 picks $B_{\frac{16\pi }{12}}$ as measurement basis, his probability to win becomes 0.854, equal to the tosser’s probability at the end of Phase 1, which is another verification of Theorem 1.

A final observation is that the tossers choice has affected the range of probabilities of both players. Although both have the same probability distribution as dictated by Theorem 1, the maximum probability for each player at the end of Phase 2 is 0.854, as determined by tosser’s initial choice of $R_y\left(\frac{12\pi }{16}\right)$ during Phase 1.      ◃

The last observation of Example 2, can be cast in the form of the next Corollary 1.

Corollary 1

(Tosser’s choice determines the maximum probability). The tosser’s choice of the rotation gate $R_y\left(\frac{2\pi k}{n}\right)$ during Phase 1, determines the maximum probability at the end of Phase 2 for both players.

7. Discussion and Conclusions

This paper introduces Quantum Tapsilou, a new quantum game inspired by the traditional Greek coin-tossing game known as tapsilou. While the classical version of the game features a straightforward and equal probability distribution, where both players have an equal $\frac{1}{4}$ probability of winning, Quantum Tapsilou introduces a new level of complexity by leveraging principles from quantum mechanics. In Quantum Tapsilou, both players still maintain an equal chance of winning, but these probabilities are now influenced by their prior choices and the utilization of quantum principles. The following two key innovations are at the core of Quantum Tapsilou.

Entanglement via rotation gates instead of relying on the commonly used Hadamard gates for creating entangled states with equal probability amplitudes. Quantum Tapsilou employs rotation gates, specifically $R_y$ rotation gates in order to generate Bell-like states with unequal probability amplitudes, introducing a layer of complexity into the game dynamics. Quantum Tapsilou makes integral use of groups in the sense that both players agree on a specific cyclic rotation group of order n, where n should be a sufficiently large integer to provide players with additional choices and enhance the suspense of the game. This group serves as the foundation of the game and both players select rotations from this group to execute their actions using the corresponding $R_y$ rotation gates. The selection of this group and the specific rotations within it significantly affect the outcome, introducing a strategic element based on group theory.

By incorporating these quantum principles and group theory, Quantum Tapsilou preserves the main aspect of the classical tapsilou game while introducing complexity and variability into the probabilities of winning. Players must carefully consider their choices of rotations within the agreed-upon group and the entangled states generated by the $R_y$ rotation gates to maximize their chances of winning in this intriguing quantum adaptation of a traditional Greek game.

Benefits and Future Applications

A quantum version of Tapsilou provides several advantages over its regular counterpart. These advantages stem from the peculiarities of quantum physics. Quantum games are distinguished by their increased complexity as a result of fundamental principles of superposition and entanglement. This added complexity can make the game more enjoyable and cognitively difficult. Participants in quantum games can create strategies that take advantage of the unique properties of quantum states, such as superposition and entanglement. This allows for more innovative and strategic gameplay, which enhances the overall gaming experience. Quantum games can be used as an educational tool, supporting players in better understanding core quantum concepts including superposition, interference, and quantum measurement. They can also be used to research human decision-making in quantum circumstances and to promote innovation in quantum technologies and algorithms.

These games are useful for testing the capabilities of quantum computers. Researchers can utilize them to conduct experiments, helping to the ongoing development of quantum computing technologies. While the concept of generalized quantum games has immense promise, real implementations are still in their infancy, with many still in the research and development stage. As quantum technologies advance, it is expected that their real-world applications will widen and diversify, delivering unique insights and solutions in a wide range of sectors.

While practical quantum coin tossing implementations are still in the works and may require advanced quantum technologies, the potential applications in cryptography, secure communication, scientific research, education, and decision-making processes are significant and hold great promise as quantum technology advances. Furthermore, several quantum games are meant to demonstrate cryptographic concepts, providing insights into quantum key distribution and secure communication. One of the most promising future applications is quantum cryptography. Quantum coin tossing can be used to generate secure, real random numbers needed for encryption keys and secure communication. This has far-reaching implications for strengthening data security and safeguarding sensitive information in an era where cyber dangers are on the rise. Additionally, these games have the potential to be critical in the evolution of quantum safe multiparty computation. By allowing numerous parties to run computations on their data without exposing the data itself, quantum two-coin tossing supports privacy-preserving data analysis and distributed computing, contributing to breakthroughs in safe and collaborative data processing.

Following the introduction of quantum computers and the potential threat they pose to traditional cryptographic methods, quantum two-coin tossing games can help in the development and testing of quantum-safe cryptographic protocols. In the age of quantum computing, these protocols will ensure the long-term security of digital communication. Quantum two-coin tossing intersects with quantum machine learning, with its implementation into quantum machine learning algorithms potentially improving random number generation. These algorithms are important because they have multiple applications in fields such as optimization, finance, and artificial intelligence.