Countervailing Conflicts of Interest in Delegation Games

Abstract

In this paper, we investigate optimal delegation mechanisms in the presence of countervailing conflicts of interest in the context of principal–agent problems. We introduce two dimensions of conflict of interest—pandering incentives related to the outside option and project biases. We compare three delegation mechanisms: full delegation, veto-based delegation, and communication (no delegation). Contrary to conventional one-dimensional conflict models, our findings reveal a non-monotonic relationship between pandering incentives and bias. These conflicts counterbalance each other, resulting in a principal’s benefit from delegation not strictly decreasing with increased bias. Surprisingly, delegation to a biased agent can be advantageous in certain scenarios. This research sheds light on the complex dynamics of delegation mechanisms when confronted with countervailing conflicts of interest, offering insights into decision-making in principal–agent relationships.

1. Introduction

This paper studies delegation mechanisms, specifically in the context of countervailing conflicts of interest. In a classic principal–agent model, we encounter the familiar scenario of an uninformed principal and an informed agent. As commonly observed in organizational settings, conflicts of interest often hinder the effective aggregation of information. In our model, we introduce two distinct dimensions of conflict of interest: one related to the outside option (pandering incentives) and the other pertaining to project biases. Each of these dimensions, in isolation, disrupts the aggregation of information in decision-making, as noted in studies by Crawford and Sobel (1982, hereafter CS) [1] and Che, Dessein, and Kartik (2013, hereafter CDK) [2]. However, a noteworthy revelation in our study is the counterbalancing effect when both dimensions of conflict of interest are simultaneously at play, a phenomenon elucidated by Chiba and Leong (2015) [3]. We embark on a comparative analysis of three key mechanisms: full delegation, veto-based delegation, and communication (non-delegation). Contrary to prevailing literature, exemplified by Dessein (2002) [4] and CDK [2], we unveil a non-monotonic welfare comparison with respect to bias, holding pandering incentives constant. In this context, delegating decision-making authority to a biased agent can prove advantageous for the principal.

Delegation inherently involves a loss of control, a trade-off that is well-documented. Yet, the inevitable corollary of an uninformed principal retaining decision-making authority is a loss of valuable information. The “delegation principle” underscores the significance of entrusting decision-making power to an informed agent, akin to divisional managers in our case study (Milgrom & Roberts, 1992 [5]; Krishna & Morgan, 2008 [6]). The central question we address in this paper is under what circumstances delegation becomes the principal’s preferred choice. We adopt a framework reminiscent of cheap talk communication models (non-delegation) designed by Chiba and Leong (2015) [3]. In this setup, the principal faces the task of selecting one of two projects or opting for the outside option, whereas the agent possesses noisy information regarding project payoffs. Similar to CS [1], our model acknowledges that the players may disagree about the optimal project (bias). Furthermore, like CDK [2], our model accommodates disagreements over the choice of the outside option, giving rise to pandering incentives. Chiba and Leong (2015) [3] revealed that pandering incentives and bias act as countervailing forces, leading to a non-monotonic relationship between information transmission and the principal’s ex-ante expected payoff, in contrast to the expectations set by CS [1] and CDK [2]. Building upon this insight, our paper delves into the impact of these countervailing conflicts of interest on the principal’s welfare under delegation.

Our findings stand in contrast to prevailing research on delegation, such as Dessein (2002) [4] and CDK [2]. Dessein (2002) [4] extended CS’s spatial model, introducing a scenario where bias exists while pandering incentives do not. In this setting, the principal and agent consistently disagree on the optimal action (bias), rendering it impossible for the principal to fully exploit the agent’s information. CDK [2] explored non-spatial models concerning finite projects and the outside option, giving prominence to pandering incentives while not making bias and noisy information their primary focus. In contrast, our model encompasses both bias and pandering incentives in non-spatial models, incorporating two projects, the outside option, and the agent’s noisy information. This fundamental difference in approach leads to distinct conclusions. Dessein (2002) [4] demonstrated that the principal’s benefit from delegation consistently decreases with bias, with delegation outperforming communication only when bias exceeds a certain threshold. CDK [2], on the other hand, indicated that, as long as pandering incentives allow for informative communication, the principal weakly prefers delegation to communication. Our study, however, unveils the non-monotonic nature of the principal’s preference for delegation relative to bias. Furthermore, even in scenarios where information transmission is possible without delegation, delegation can still be preferred over communication. Additionally, we extend our analysis to compare full delegation and veto-based delegation, a comparison with significant implications for the study of optimal legislative organization, as discussed later in our paper.

This paper’s relevance extends to the broader body of research on optimal delegation, which finds its roots in Holmström’s seminal work in 1977 [7]. Holmström’s [7] framework featured a principal facing a privately informed and biased agent, with monetary transfers unavailable. The principal’s task was to define a set of permissible actions from which the agent could select their preferred action after privately observing the state. Holmström [7] identified general conditions under which the optimal permissible set is defined as an interval. Alonso and Matouschek (2008) [8] delved into the optimal delegation mechanism within the context of quadratic utility functions, considering the presence of bias, and delineated conditions for interval delegation to be optimal. Meanwhile, Goltsman, Hörner, Pavlov, and Squitani (2009) [9] conducted a comparative study encompassing limited delegation (arbitration), delegation to an intermediary (mediation), and non-delegation (negotiation/multi-stage communication). Moreover, researchers such as Amador and Bagwell (2020) [10] and Kartik, Kleiner, and Van Weelden (2021) [11] explored the nexus between delegation and concepts like money burning and veto-bargaining.

This paper explores the application of optimal delegation principles in legislative organization theory. Legislative organization theory investigates situations where legislators seek advice from committees. In the U.S. congressional process, committees play a crucial role in drafting most bills. This process follows specific rules, including open, closed, and modified (intermediate) rules for amending drafts by committees, which correspond to the concepts of no delegation (open rule), veto-based delegation (closed rule), and more nuanced delegation mechanisms.

Previous studies by Gilligan and Krehbiel (1987) [12], Krishna and Morgan (2001) [13], and Martin (1997) [14] have examined scenarios involving closed and open rules within the context of quadratic utility functions, taking into account potential biases. Gilligan and Krehbiel (1987) [12] and Martin (1997) [14] discuss the need to incentivize committee members when the legislature delegates decisions to them. In Krishna and Morgan (2001) [13], they consider two informed committee members and one legislature, highlighting the importance of heterogeneity among committee members.

These studies have shown that the closed rule outperforms the open rule only when bias between the legislature and the committee member(s) is minimal. However, the findings of this paper challenge the conventional wisdom in this context, demonstrating that the optimal choice between full delegation and veto-based delegation depends non-monotonically on bias.

Additionally, our research complements the growing body of empirical studies on legislative delegation. Studies such as Volden (2002) [15] and Gilardi (2005) [16] have delved into the empirical patterns of delegation in various contexts, including the delegation of policy-forming powers and the allocation of regulatory authority in Western Europe. These findings resonate with the implications we present in our paper, suggesting that delegation to an external intermediary can yield substantial benefits for organizations, a trend observed in the work of Brickley, Smith, and Zimmerman (2009) [17].1 Empirical evidence also indicates a positive correlation between the size and complexity of a firm and the extent to which top managers delegate decision rights, as documented in studies by Christie, Joye, and Watts (2003) [18] and Colombo and Delmastro (2004) [19].

The remainder of this paper unfolds as follows: Section 2 reviews the related literature, Section 3 introduces the models for three mechanisms (full delegation, veto-based delegation, and non-delegation or communication), and Section 4 offers insights and conclusions derived from numerical examples and comparisons of these delegation mechanisms in terms of equilibria and welfare. Our proofs can be found in the Appendix A.

2. Model

We present a principal–agent model that explores pandering and bias. We demonstrate that pandering incentives emerge when the principal has limited options and when the initial rankings of projects play a significant role. To illustrate this, we consider a basic scenario where an organization has identified two potential projects, referred to as project 1 and project 2, as discussed in the main text by CDK [2].

In this setting, the organization can either pursue one of the projects, denoted as $P\in \{1,2\}$, or choose not to proceed with any project (the outside option), denoted as $P=⌀$. There are two equally likely states of nature, $\theta \in \left\{1,2\right\}$. A project succeeds only if it aligns with the state of nature, i.e., $P=\theta$; otherwise, it fails. Two actors are involved: a principal who controls the organization’s resources and an agent. The agent privately receives a binary signal, $\sigma \in \left\{1,2\right\}$, with $\sigma$ matching $\theta$ with a probability of $\alpha \in \left(1/2,1\right)$, and not matching $\theta$ otherwise. It is important to note that $\sigma$ is soft information and is not observed by the principal. The signal’s precision $\alpha$ is known to both parties.

Both the principal and the agent are risk-neutral and aim to maximize their payoffs. In the case of project 1 succeeding, both parties receive a benefit of 1. If project 2 succeeds, the principal gains a benefit of $x\in (0,1)$, and the agent gains $t\in \left(0,T\right)$, where T is significantly larger than 1. Their initial preferences for projects coincide when $t<1$, but differ otherwise.

Implementing a project incurs a non-transferable cost for both players. The principal bears a cost of c, while the agent incurs a cost of $\gamma ·c$. The value of $\gamma$ is predetermined and falls within the range $\left[0,\Gamma \right)$, where $\Gamma$ is notably larger than 1. The cost c is uncertain beforehand and is drawn from a uniform distribution with a range of $\left[0,C\right]$, where C is equal to or greater than $\Gamma ·T$.2 Both players observe the value of c before making their decisions.

The principal’s payoff is:

$$\left\{\begin{array}{cc}1-c\hfill & \mathrm{if}P=\theta =1\hfill \\ x-c\hfill & \mathrm{if}P=\theta =2\hfill \\ -c\hfill & \mathrm{if}P\in \left\{1,2\right\}\mathrm{and}P\ne \theta \hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

The agent’s payoff is:

$$\left\{\begin{array}{cc}1-\gamma ·c\hfill & \mathrm{if}P=\theta =1\hfill \\ t-\gamma ·c\hfill & \mathrm{if}P=\theta =2\hfill \\ -\gamma ·c\hfill & \mathrm{if}P\in \left\{1,2\right\}\mathrm{and}P\ne \theta \hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(2)

Both players’ payoff functions, parameters $(x,t,\gamma )$, and the distribution of c are common knowledge.

The aggregation of the agent’s information is of paramount interest to the principal. To investigate the optimal organizational structure, we examine three mechanisms: full delegation ($Fd$), veto-based delegation ($Vd$), and communication (no delegation) ($Nd$).

Under $Fd$, the agent has the authority to choose between projects or the outside option, following this timeline:

• Step 1. Nature selects the state $\theta \in \{1,2\}$.
• Step 2. The agent privately observes a signal $\sigma \in \{1,2\}$.
• Step 3. Both players know the cost $c\in \left[0,C\right]$.
• Step 4. The agent decides whether to pursue a project, $P\in \{1,2\}$, or opt for no project, $P=⌀$.
• Step 5. Payoffs are realized for both players, marking the end of the game.

Under $Vd$, the agent has the authority to choose between projects, but the principal can veto the agent’s choice in favor of the outside option. The timeline changes as follows, with Steps 2 and 4 becoming Steps 2${}^{\prime }$ and 4${}^{\prime }$, respectively:

• Step 2${}^{\prime }$. After observing $\sigma \in \left\{1,2\right\}$, the agent sends a message $m\in \left\{1,2\right\}$ to the principal.3 The principal observes m without noise.
• Step 4${}^{\prime }$. The principal decides whether to pursue the recommended project, $P=m$, or opt for no project, $P=⌀$.

Communication exists between the players without incurring a direct cost to either, but the agent’s message limits the principal’s decision-making.

Contrarily, under $Nd$, the principal chooses between projects or the outside option after receiving the agent’s message. Step 4${}^{\prime }$ under $Vd$ is altered to Step 4″:

• Step 4″. The principal decides whether to pursue a project, $P\in \{1,2\}$, or opt for no project, $P=⌀$.

The agent’s message solely affects the principal’s beliefs, indicating that communication is cost-effective. We will elucidate the results, which are influenced by two dimensions of conflict of interest: one pertaining to projects (bias, measured by $\left|x-t\right|$) and the other to the outside option (pandering incentives, measured by $\gamma$).

We examine perfect Bayesian equilibria.

Let $P^{Fd}\left(c,\sigma \right)$ represent the agent’s choice under $Fd$.

For $d\in${$Vd$, $Nd$}, let $m^d$ denote the agent’s message, let ${\beta }^d\left(\sigma \right)$ denote the probability that the agent sends $m^d=\sigma$, and let $P^d\left(c,m^d\right)$ denote the principal’s strategy.

Define:

$${\mu }^d\left(m^d\right):=Pr\left(\theta =m^d|m^d,{\beta }^d\right),$$

(3)

which is the principal’s posterior belief.

Under $d=Nd$, we assume:

$$Pr\left(\theta =i|m=i,{\beta }^d\right)\ge Pr\left(\theta =i|m=j,{\beta }^d\right)$$

(4)

for $i,j\in \left\{1,2\right\}$ and $i\ne j$. This is equivalent to ${\mu }^d\left(m^d\right)\ge \frac{1}{2}$ for $\forall m^d$.

We assume that ${\beta }^{Nd}\left(1\right)=1$ and ${\beta }^{Nd}\left(2\right)=0$, meaning the agent always sends $m^{Nd}=1$ when there is no information transmission. This is a common assumption in models without delegation, such as CDK models. Under $d=Nd$, messages do not dictate the actions of any players. Therefore, any message, be it $m=1$ or $m=2$, can be used, as long as different messages correspond to different signals. To avoid confusion, we make $m=1$ more likely to be sent than $m=2$ when $\sigma =1$, and vice versa when $\sigma =2$.

For $d\in${$Vd$, $Nd$}, we define five types of equilibria.

Definition 1.

Fix $d\in${$Vd$, $Nd$}.

• In a truthful equilibrium (T), ${\beta }^d\left(1\right)={\beta }^d\left(2\right)=1$.
• In a pandering-toward-1 equilibrium (P1), ${\beta }^d\left(1\right)=1$ and ${\beta }^d\left(2\right)\in \left(0,1\right)$.
• In a pandering-toward-2 equilibrium (P2), ${\beta }^d\left(1\right)\in \left(0,1\right)$ and ${\beta }^d\left(2\right)=1$.
• In a zero-1 equilibrium (Z1), ${\beta }^d\left(1\right)=1$ and ${\beta }^d\left(2\right)=0$.
• In a zero-2 equilibrium (Z2), ${\beta }^d\left(1\right)=0$ and ${\beta }^d\left(2\right)=1$.

Moreover, under Nd, $P^{Nd}\left(c,m^{Nd}\right)\in \left\{m^{Nd},⌀\right\}$ for $\forall m^{Nd}$ in T, P1 or P2; and $P^{Nd}\left(c,m\right)\in \left\{1,⌀\right\}$ for $\forall m^{Nd}$ in Z1.

In T, the agent truthfully reveals his signal (i.e., $m=\sigma$ for all $\sigma$). In P1, the agent panders towards project 1, sending $m=1$ when $\sigma =1$, while using a mix of messages for $\sigma =2$. In P2, the agent panders towards project 2, sending $m=2$ when $\sigma =2$, and using a mix of messages for $\sigma =1$. In Z1, the agent always recommends project 1 (i.e., $m=1$ for all $\sigma$) and does not reveal any information. In Z2, the agent always recommends project 2 (i.e., $m=2$ for all $\sigma$) and does not reveal any information.

We consider T (P1 or P2) as an informative equilibrium. Under Vd or Nd, we focus on an informative equilibrium if it exists.

Under Nd, the principal implements what the agent recommends if the benefit exceeds the cost in T, P1, or P2. The principal implements only project 1 in Z1. In Nd, it is a cheap talk model, so in informative equilibria like T, P1, and P2, the agent’s message strategy ensures that the agent is willing to recommend a project based on their private information, and the principal is willing to implement the recommended project unless the cost exceeds the principal’s expected benefit. If the agent knows the principal will ignore some of their messages, there is no incentive to send the message, and informative communication breaks down. In Z1, the agent always sends $m=1$, meaning no information is revealed to the principal. Consequently, the principal chooses project 1 based on their prior and preferences.

Z2 (where project 1 is never implemented) exists only under Vd. In Z2, the agent always sends $m=2$, meaning no information is conveyed to the principal. However, the principal prefers project 1 to project 2 based on their prior preferences. Under $Nd$, the principal can choose any project, including project 1, so Z2 does not exist. Conversely, under Vd, the principal can only choose project 2 or the outside option, allowing Z2 to exist.

3. Results—Comparison among Three Mechanisms

As demonstrated by Chiba and Leong (2015) [3], the presence of the outside option adds a two-dimensional aspect to conflicts of interest. This duality encompasses conflicts over projects, commonly referred to as “bias”, and conflicts related to the outside option, known as “pandering incentives”. Each dimension of these conflicts individually hampers information transmission, consequently diminishing the principal’s ex-ante expected payoff. It is important to note that pandering incentives become particularly relevant in non-spatial settings featuring multiple projects, where conditional, ex-ante, and interim rankings over these projects, rather than just the distance between a selected project and the optimal one, significantly impact each player’s payoff and, subsequently, their behavior, as illustrated in CDK’s work.

CS [1] examined the influence of bias on cheap talk communications, while Dessein (2002) [4] delved into various delegation mechanisms based on CS’s setup. Consequently, their models exhibit a sense of monotonicity in the following manner: as bias intensifies, both the advantages of communications and the benefits of delegation deteriorate. However, the detrimental impact of bias is restricted to the realm of information transmission under communications, while it continues to escalate under delegation. Consequently, when bias remains below a certain threshold, communication (denoted as “$Nd$”) proves more advantageous than delegation (represented as “$Fd$” and “$Vd$”).

CDK [2], on the other hand, primarily focused on the effects of bias on cheap talk communications ($Nd$) and expanded their analysis to compare delegation mechanisms within a setup where the interim ranking, referred to as the “conditionally better or worse looking project” among discrete projects, holds significance. In this scenario, the agent has incentives to recommend the project that is conditionally better looking, which encapsulates the notion of pandering incentives. When pandering incentives are relatively weak and communication allows for information transmission, the principal mildly prefers delegation over communication.

In contrast, our model introduces a unique dynamic where bias and pandering incentives coexist and, intriguingly, counterbalance each other. This interaction results in non-monotonic behavior. In this context, a larger bias can actually facilitate information transmission, as observed in Chiba and Leong’s (2015) [3] work. With this understanding, our paper embarks on an exploration of how these countervailing conflicts of interest impact the principal’s benefits in the realm of delegation. We illustrate this through two examples.

3.1. Example 1

We begin by considering $\gamma =0$, which implies that only the principal bears the implementation cost. In this scenario, we envision a city government seeking advice from a non-local advisor on whether to build a bridge or a pool. The advisor’s reputation among committee members increases if the chosen project succeeds, leading to higher future client fees. However, the non-local committee member is not affected by the project’s implementation cost, so they have strong incentives to recommend a project with a higher likelihood of success.

The model under $Nd$ aligns with Chiba and Leong (2015) [3]. This simple parametric assumption, $\gamma =0$, allows us to understand the impact of countervailing conflicts of interest on delegation problems.

Proposition 1.

When $\gamma =0$, and we fix α and x, $Fd$ is dominated. Additionally, the principal’s preference between $Vd$ and $Nd$ is not strictly determined by $\left|t-x\right|$.

Proof. 

Refer to the Appendix A. □

Since the agent doesn’t bear any costs, they always opt for a project, regardless of the principal’s cost. Thus, $Fd$ is not an optimal mechanism for the principal.

Next, the welfare comparison between $Vd$ and $Nd$ varies with the bias. The principal is initially biased towards project 1. Therefore, if information sharing fails, the agent cannot induce the selection of project 2 under $Nd$ (this corresponds to $Z1$), while they can achieve this under $Vd$ ($Z2$). In Nd, if the agent’s private information is highly uncertain (small x given $\alpha$), the agent always recommends project 1 ($Z1$) to avoid the outside option as much as possible, leading to communication failure ($Z1$). When the agent has a strong bias toward project 2 (large t given x and $\alpha$), the agent consistently recommends project 2, but the principal ignores the recommendation, resulting in communication failure ($Z1$). In contrast, under $Vd$, the principal can only implement a recommended project or no project, avoiding communication breakdown due to pandering incentives.

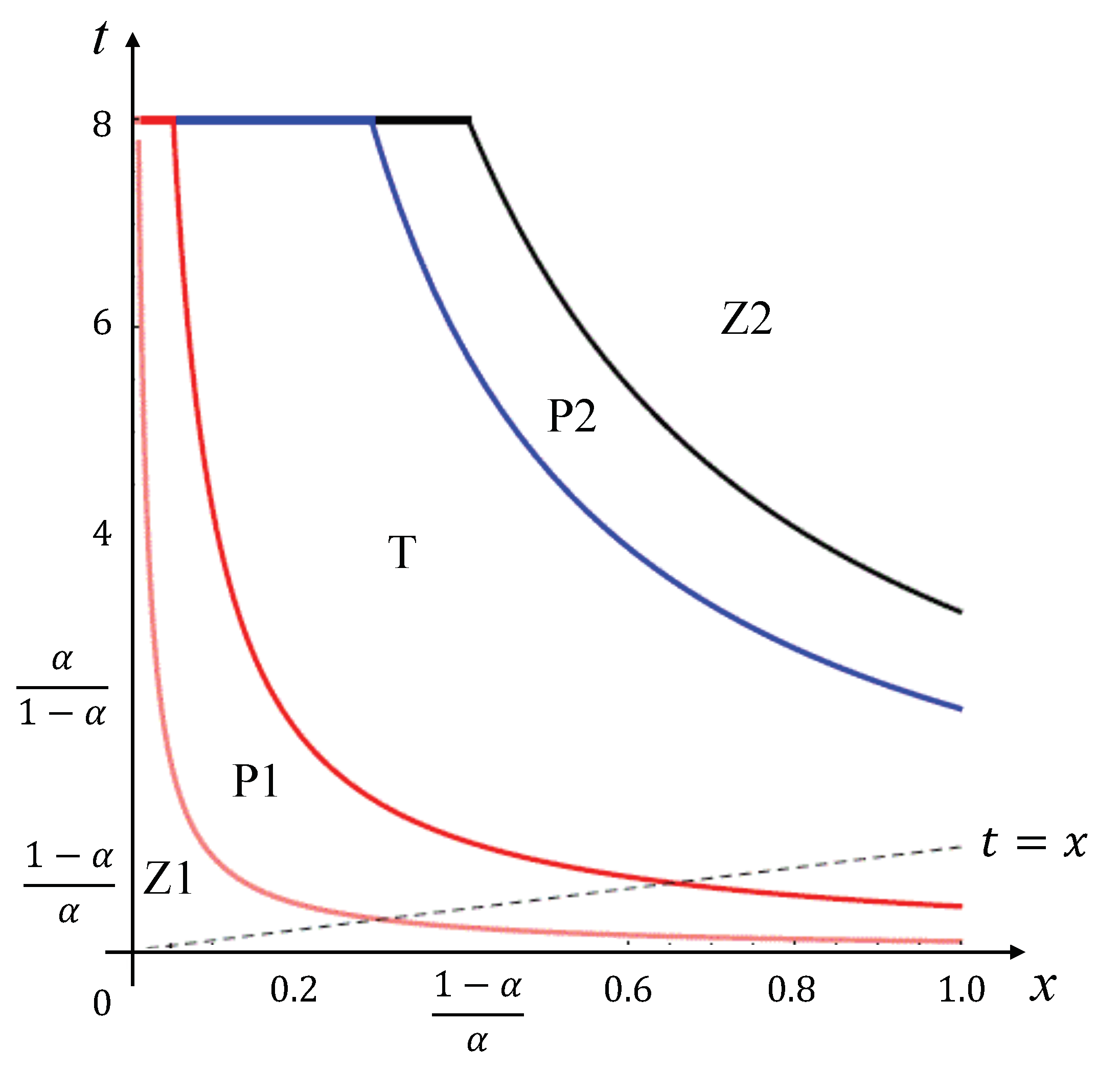
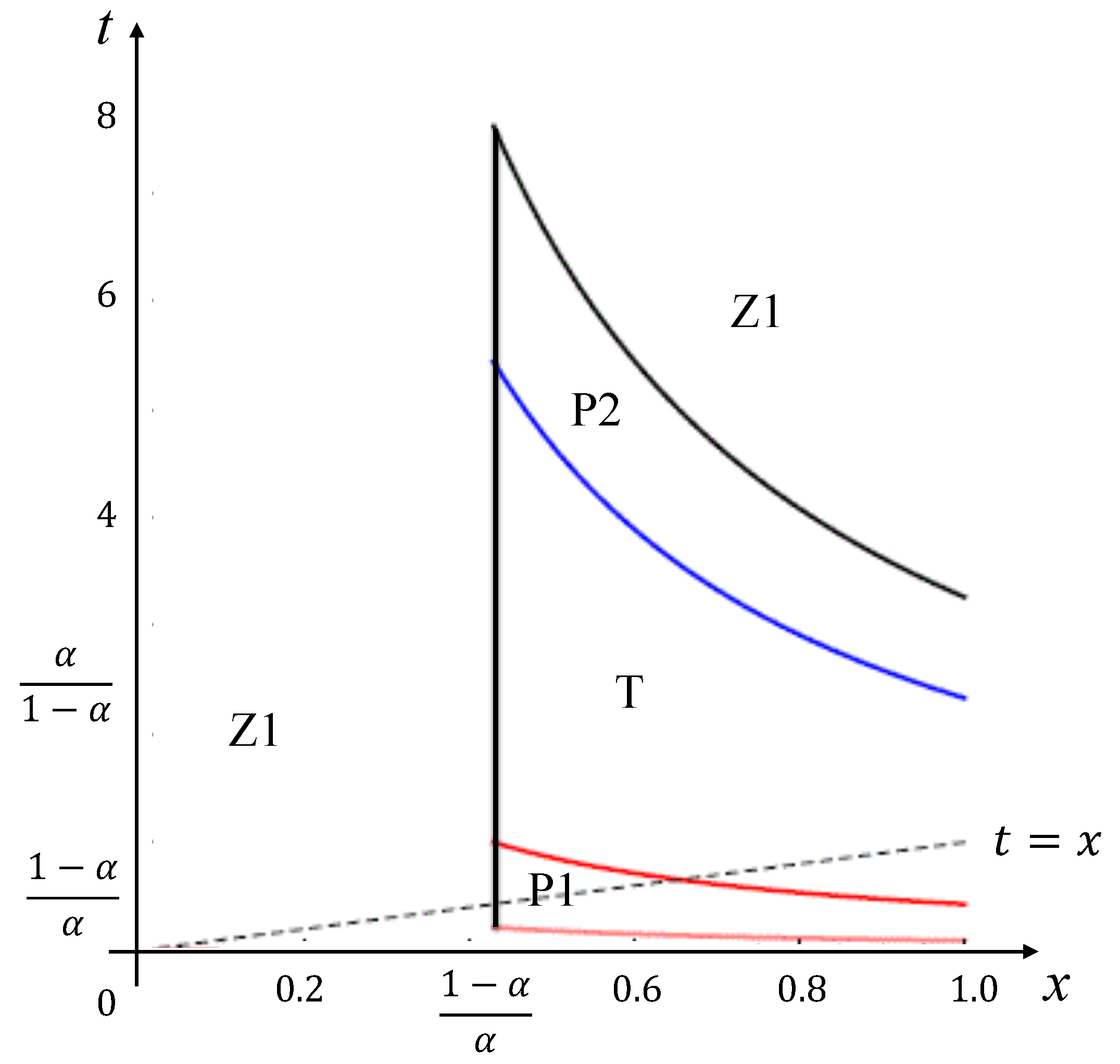
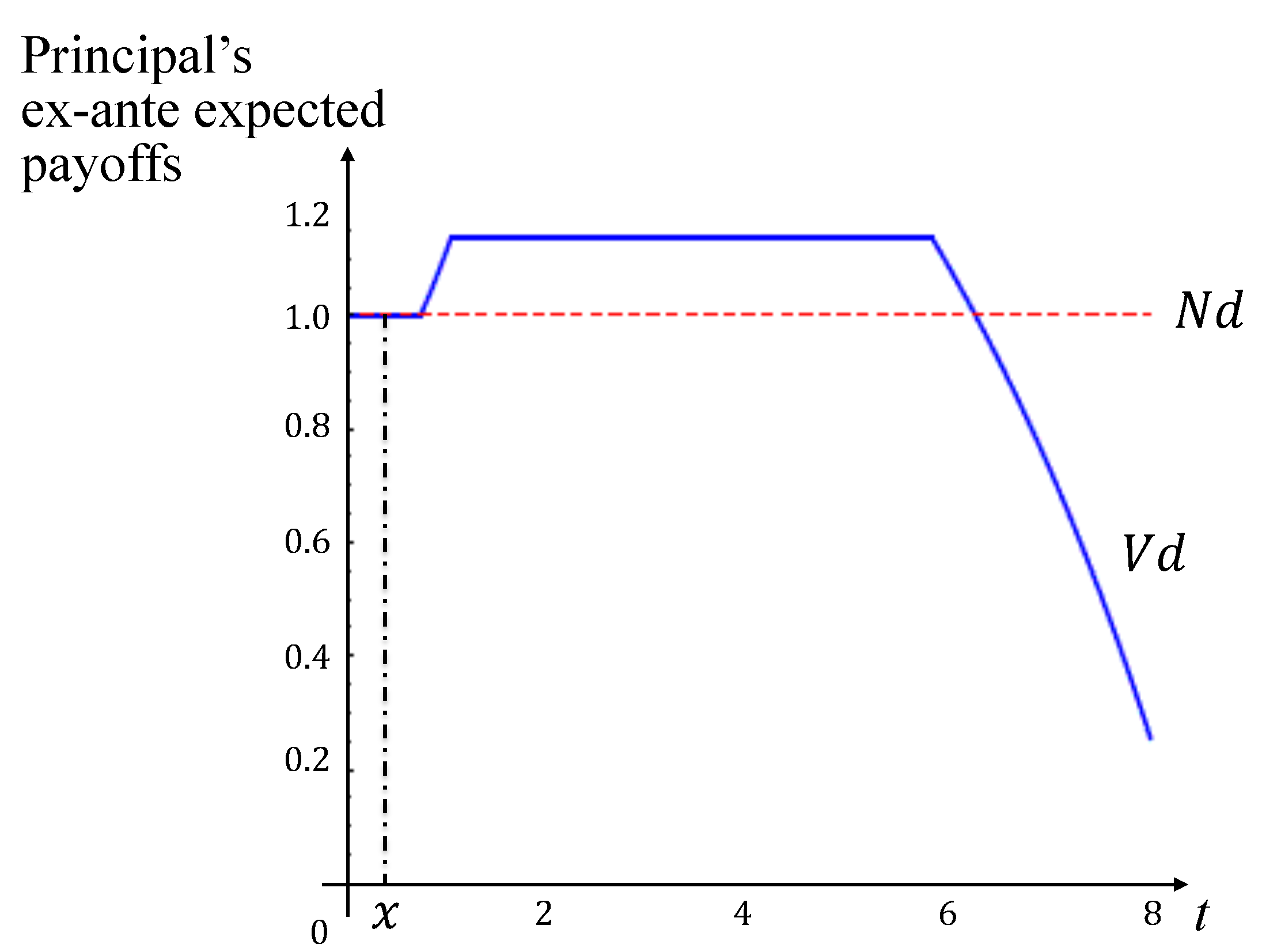
Figure 1 and Figure 2 illustrate the equilibrium outcomes, while Figure 3 charts the principal’s welfare against the agent’s bias.

When $x<\left(1-\alpha \right)/\alpha$, i.e., $\alpha <1/\left(1+x\right)$, the agent’s signal is too noisy for the principal to consider their recommendation in favor of project 1. Consequently, there is no information transmission under $Nd$. In contrast, under $Vd$, the agent’s information can influence the decision-making process. The bias and pandering incentives counteract each other. Therefore, the principal’s welfare is not strictly determined by the bias $\left|x-t\right|$. In this case, $Vd$ outperforms $Nd$ when the bias is moderate, but it lags behind when the bias is not.

If $x>\left(1-\alpha \right)/\alpha$, i.e., $\alpha >1/\left(1+x\right)$, $Nd$ weakly dominates $Vd$ in the following manner. Given a sufficiently large t (where the agent has a strong bias toward project 2), there is no information transmission under $Nd$, and $Z1$ is the equilibrium. The same holds for $Vd$, where $Z2$ is the equilibrium. In such cases, the principal can choose their preferred project (project 1) under $Nd$, whereas project 1 is never chosen under $Vd$. Otherwise (i.e., when the agent’s bias is toward project 1 or is not strong even if they prefer project 2), the principal remains indifferent between the two mechanisms. With a smaller t, information is transmitted under both mechanisms, and the equilibrium is T ($P1$ or $P2$) under both $Vd$ and $Nd$. The final outcome, P, is equivalent under both mechanisms.

Our model shares similarities and differences with Dessein (2002) [4] and CDK [2]. The primary distinction, mainly the presence of countervailing conflicts of interest, leads to differing results from theirs.

Dessein (2002) [4] demonstrated that full delegation dominates (or is dominated by) communication (without delegation) if the conflict of interest over actions, denoted as bias b, is small (large). Dessein [4] examined CS’s model with continuous actions and states, which differs from our model. For example, in the uniform quadratic case, considering no outside options, Dessein [4] showed that full delegation strictly dominates communication when bias is small ($b<1/4$), rather than communication being influential.

On the other hand, CDK [2], like us, examined a model with discrete actions, outside options, and linear payoff functions. However, in their model, the project cost is predetermined and publicly known. They did not consider the project cost but examined varying payoffs for selecting the outside option for different players: a positive payoff for the principal and zero payoff for the agent.

CDK [2] compared different delegation regimes based on comparative statics with respect to the principal’s payoff for the outside option. They claimed that delegation is weakly preferred to communication by the principal when communication is influential (pandering incentives do not prevent communication). In our model, even when communication is not influential, delegation can be strictly preferred to communication by the principal. Moreover, whether communication is influential does not follow a strict monotonic pattern with the bias, and therefore, the principal’s preference for delegation over communication is not strictly tied to the bias.

3.2. Example 2

In this scenario, we set $\gamma =1$, meaning that the agent faces the same level of implementation cost. Let’s consider a practical example where a city government seeks advice from a local committee on whether to build a bridge or a pool. The decision to implement either project impacts tax rates and reflects on the city’s reputation and income. Unlike the previous model with $\gamma =0$, pandering incentives are not as strong here. However, as long as x (the agent’s recommendation) is not equal to t (the true state of nature), the players don’t always see eye to eye on choosing the outside option when the agent’s information is public. Consequently, pandering incentives still play a role in shaping the agent’s message strategy under both delegation mechanisms, $Vd$ and $Nd$.

Proposition 2.

Let’s consider $\gamma =1$. We fix α and x. In this context, $Vd$ proves to be more favorable than $Nd$. Additionally, the principal’s preference ranking between $Fd$ and $Vd$ doesn’t follow a strict monotonic pattern based on the difference $\left|t-x\right|$.

Proof. 

Proof details can be found in the Appendix A. □

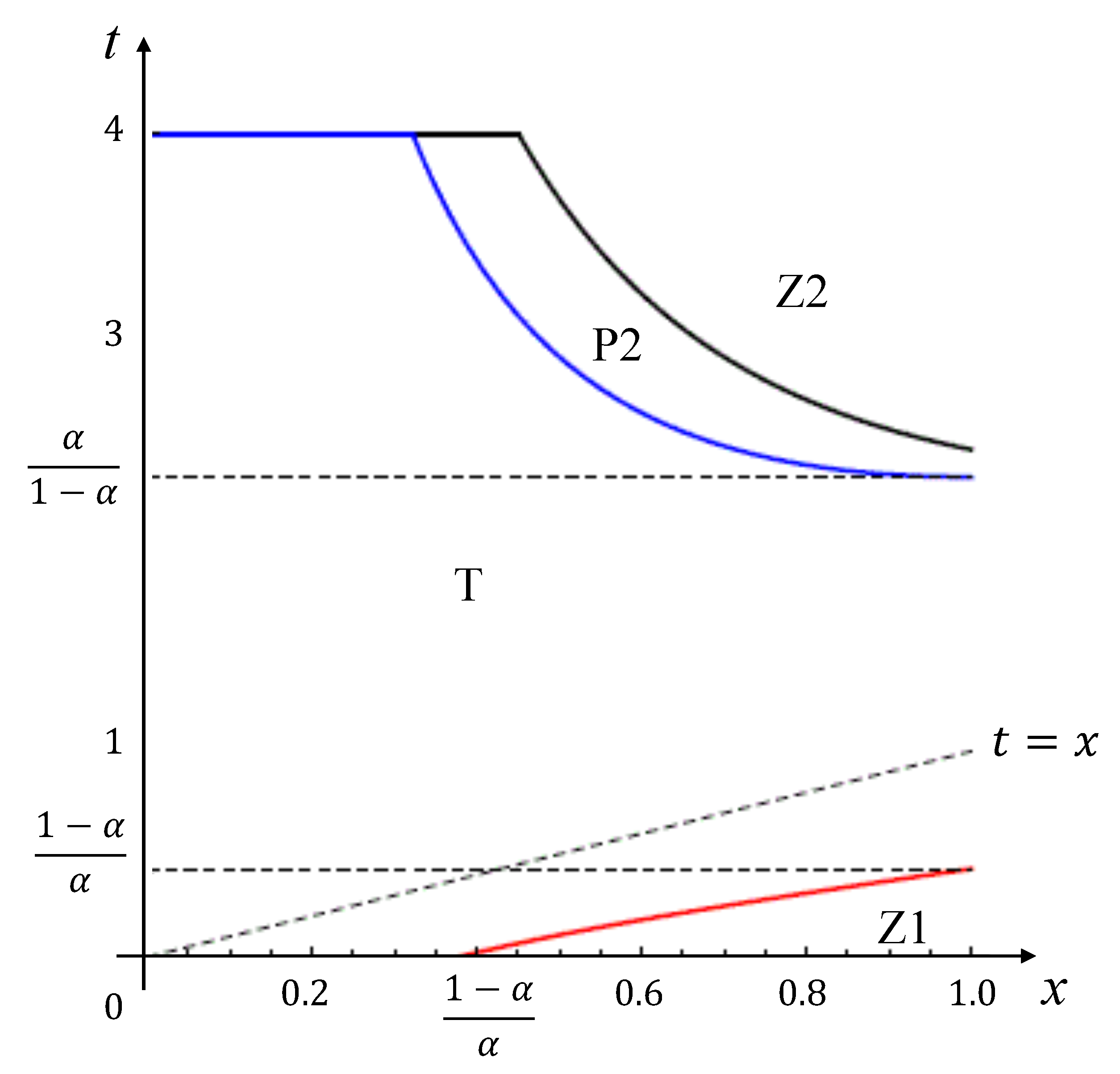
Figure 4 illustrates the equilibrium outcome under $Vd$. On the other hand, under $Fd$, the agent’s signal influences his project choice, represented as P.

$P^{Fd}\left(c,\sigma \right)\in \left\{\sigma ,⌀\right\}$, where it is either $\sigma$ or ⌀ for any $\sigma$, but this only holds if t falls within a specific range $\left[\left(1-\alpha \right)/\alpha ,\alpha /\left(1-\alpha \right)\right]$. If t is below or above this range, the agent’s choice changes accordingly, selecting either 1 or 2 for the project. In all cases, the agent opts for the outside option if the costs outweigh the benefits of other projects.

Figure 5 depicts the principal’s welfare. When t is less than x (implying the agent is also biased towards project 1, and his bias is stronger than the principal’s), $Fd$ doesn’t consistently outperform $Vd$. Specifically, when the bias $\left|t-x\right|$ is significant, $Vd$ takes the lead over $Fd$.

Dessein (2002) [4] demonstrated that, given a reasonable and moderate default action ($E\left(state\right)$=$1/2$), $Fd$ strictly dominates $Vd$ only when the bias is very small ($b<1/4$), allowing for information transmission under $Vd$. This aligns with situations where t closely matches x in our model. In contrast, Marino (2007) [20] established that with an extreme default action, $Vd$ outperforms $Fd$ regardless of the bias level. Mylovanov (2008) [21] proposed that with the optimal selection of the default action, $Vd$ can replicate any optimal outcome for the principal achieved under $Fd$ ($Nd$) for small (large) bias. All of these findings indicate a clear monotonic ranking among mechanisms. The choice of the default action, which corresponds to the determination of each player’s project cost in our model, dictates the dominant mechanism. However, it is important to note that there are many differences between their models and ours. In contrast to our model, theirs incorporates continuum actions, states, and multidimensional conflicts of interest over states. The presence of countervailing conflicts of interest is the key factor driving our non-monotonic result.

4. Future Research

In our future research, we intend to delve into more complex models, such as those involving continuous actions in the uniform quadratic case. We will also explore optimal delegation mechanisms when faced with opposing conflicts of interest, drawing inspiration from the work of Holmström (1977) [7] and Alonso and Matouschek (2008) [8].

Additionally, we plan to broaden our analysis beyond the comparison of delegation, veto-based delegation, and no delegation (communications) in our current setup. We will consider scenarios where a principal often employs an intermediary or engages in continuous exchanges with an agent. This distinction is referred to as Mediation and Negotiation, as discussed in Goltsman, Hörner, Pavlov, and Squitani (2009) [9]. We will investigate the circumstances in which these alternative solutions may outperform full delegation, veto delegation, or one-state communication (no delegation).

Furthermore, our focus will shift towards models involving multiple agents and a principal in organizational settings. We will extend our model to encompass an organization where a principal must decide among multiple projects or no project, with agents sharing project-relevant information and advice. We will address questions regarding the potential advantages of having a mix of different agents as opposed to homogeneous ones and explore the impact of biases between the principal and agents.

Another extension will tackle a problem within an organization involving a head office (principal) and multiple divisions (agents). The organization must make one decision per division, with each division possessing decision-relevant information. We will investigate whether centralizing all decisions at the head office or delegating each decision to each division is preferable, taking into account the presence of opposing conflicts of interest.

Lastly, we aim to explore practical applications of our findings across various domains, such as delegation within a unionized duopoly (Chen, Ko, Tsai, and Lee, 2022 [22]). These future endeavors seek to enhance our understanding of the intricate dynamics surrounding delegation in real-world contexts.

5. Conclusions

This paper explores the concept of optimal delegation within a relatively uncharted, yet realistic scenario. We examine a situation where both bias (disagreement over state-dependent discrete options) and pandering incentives (disagreement over choosing the outside option or not) coexist, influencing the behavior of the principal and agent. Our focus is on three key mechanisms: full delegation, veto-based delegation, and communication (non-delegation). In principal–agent problems, the principal faces a trade-off between losing control associated with delegation and losing valuable information held by an agent associated with no delegation when deciding whether to delegate decision-making authority.

In our setup, the principal must choose between two projects or the outside option, while the agent possesses noisy information about project payoffs. Disagreements between the principal and agent can arise over the optimal project (bias) and the choice of the outside option (pandering incentives).

The interaction between these two dimensions of conflicts of interest creates an intriguing dynamic. They counterbalance each other, leading to a non-monotonic relationship between bias and information transmission in the context of communication (non-delegation). Consequently, our comparative analysis of these three mechanisms reveals a non-monotonic relationship with bias, challenging conventional wisdom by highlighting the potential benefits of delegating decision-making authority to a biased agent.

Our models offer insights that extend to the study of optimal legislative mechanisms, which encompass open, closed, and modified rules. Legislative organization theory examines situations where legislators seek advice from committees. In the U.S. congressional process, committees play a pivotal role in drafting most bills, following specific rules, including open, closed, and modified (intermediate) rules for amending drafts by committees, corresponding to the concepts of no delegation (open rule), veto-based delegation (closed rule), and more nuanced delegation mechanisms. Our findings differ from the existing literature, which predominantly focused on single dimensions of conflicts of interest, and they carry significant implications for the intricate issues faced by legislative organizations.

Our research aligns with empirical studies that observe patterns of delegation in various contexts. For instance, many countries allocate policy-forming powers to regulatory authorities. Another example is the distribution of top executive responsibilities among a CEO and other senior executives in large firms.