Game Theoretic Foundations of the Gately Power Measure for Directed Networks

Abstract

We introduce a new network centrality measure founded on the Gately value for cooperative games with transferable utilities. A directed network is interpreted as representing control or authority relations between players—constituting a hierarchical network. The power distribution embedded within a hierarchical network can be represented through appropriate TU-games. We investigate the properties of these TU-representations and investigate the Gately value of the TU-representation resulting in the Gately power measure. We establish when the Gately measure is a core power gauge, investigate the relationship of the Gately with the $\beta$-measure, and construct an axiomatisation of the Gately measure.

1. Introduction

The concept of network centrality has emerged from sociology, social network analysis, and network science [1,2] into the field of cooperative game theory, giving rise to game theoretic methods to measure the most important and dominant nodes in a hierarchical social network [3]. The underlying method is to construct a cooperative game theoretic representation of characterising features of a network and to apply cooperative game theoretic analysis to create centrality measures for these networks1.

We limit ourselves to directed networks as representations of collections of hierarchical or control relationships between the constituting players in a network. Such hierarchical relationships can be found in employment dynamics between managers and subordinates, the interaction between a professor and her students, rivalry between different sports teams based on past performance between them, or the connections between a government agent and the individuals they oversee. We refer to these relationships as “hierarchical” since this implies that the predecessor node has some level of control or authority over the successor node2. Taking this interpretation as central, we refer to these directed networks as hierarchical.

A hierarchical relationship is between a predecessor and a successor, where the predecessor exercises some form of control or authority over the successor. The most natural representation is that through a TU-game that assigns to every group of players their “total number of successors”, which can be interpreted in various ways. We consider the two standard ways: simply counting the successors of all members of the group, i.e., the number of players that have at least one predecessor that is member of the group, or counting the number of players for which all predecessors are member of that group3. We show that these two TU-representations are dual games. We remark that van den Brink and Borm [6] already characterised the main “strong” successor representation as a convex game [7], implying that its dual “weak” successor representation is a concave game.

A power gauge for a network is now introduced as a vector of weights that are assigned to players in the hierarchical network that represents or measures each player’s authority in that network. A power measure is now introduced as a map that assigns a single power gauge to every hierarchical network. In this paper, we investigate some power measures that assign such gauges founded on game theoretic principles related to the two TU-representations of hierarchical networks considered here. In particular, each simple hierarchical network—in which each player has at most one predecessor—has a natural power gauge in the form of the outdegree of each node in the network, representing the number of successors of a player in that network.

Application of the Shapley value [8] to the successor representations results in the $\beta$-power measure [9]. This is the centre of the set of core power gauges for each network. In the $\beta$-measure, the weight of a player is equally divided among its predecessors. As such, it has a purely individualistic foundation to measuring power.

Applying the Gately value of the successor representations results in a fundamentally different conception of a power measure. Here, the set of dominated nodes is treated as a collective resource that is distributed according to a chosen principle. In the Gately measure, this is the proportional distribution4. This stands in contrast to the individualistic perspective of the $\beta$-measure.

Since, the Gately measure is founded on such different principles, it is not a surprise that the assigned Gately power gauges are not necessarily core power gauges. We identify conditions under which the assigned Gately power gauge is a core power gauge in Theorem 3. In particular, we show that for the class of (weakly) regular hierarchical networks, the Gately power measure assigns a core power gauge for that network.

We are able to devise an axiomatic characterisation of the Gately value as the unique power measure that satisfies three properties. First, it is normalised to the number of nodes that have predecessors, which is satisfied by many other power measures as well. Second, it satisfies “normality”, which imposes that a power measure assigns the full weight of controlling successors with no other predecessors and the power measure of the reduced network with only those nodes that have multiple predecessors. Finally, it satisfies a proportionality property in the sense that the power measure assigned is proportional to how many successors a node has.

Finally, we address the question under which conditions the $\beta$- and Gately power measures are equivalent. We show that for the class of weakly regular hierarchical networks this equivalence holds. This is exactly the class of networks for which the Gately measure assigns a core power gauge. This insight cannot be reversed since there are non-regular networks for which the Gately and $\beta$-measures are equivalent.

• Relationship to the literature

The study of centrality in networks has evolved to be a significant part of network science [1,2]. In economics and the social sciences, there has been a focus on Bonacich centrality in social networks. This centrality measure is founded on the eigenvector of the adjacency matrix that represents the network [10]. In economics, this has been linked to performance indicators of network representations of economic interactions such as production networks [11,12,13]. The nature of these networks is that they are undirected and, therefore, fundamentally different from the hierarchical networks considered here.

Traditionally, the investigation of directed networks focussed on degree centrality—measuring direct dominance relationships [14,15]—and on betweenness centrality, which considers the position of nodes in relation to membership of (critical) pathways in the directed network [16,17,18,19].

Authority and control in networks have only more recently been investigated from different perspectives. Yang-Yu et al. [20] considers an innovative perspective founded on control theory. More prevalent is the study of centrality in hierarchical networks through the $\beta$-measure and its close relatives. van den Brink and Gilles [9] introduced the $\beta$-measure as a natural measure of influence and considered some non-game theoretic characterisations. The $\beta$-measure is closely related to the PageRank measure introduced by Brin and Page [21] and considered throughout the literature on social network centrality measurement.

The $\beta$-measure has been linked to the game theoretic measurement of centrality in directed networks by van den Brink and Gilles [22] and van den Brink and Borm [6]. The $\beta$-measure was identified as the Shapley value of the standard successor representations as TU-representations of domination and control in directed networks. van den Brink et al. [23] develop this further through additional characterisations. Gavilán et al. [5] introduce other, more advanced TU-representations of directed networks and study their Shapley values. They consider a family of centrality measures resulting from this methodology.

Gómez et al. [24], del Pozo et al. [25] and Skibski et al. [26] introduce and explore a game theoretic methodology for measuring network power that is fundamentally different from the methodology used in this paper and the literature reviewed above. These authors consider a well-chosen TU-game on a networked population of players and subsequently compare the allocated payoffs based on the Shapley value in the unrestricted game with the Shapley value of the network-restricted TU-game. The normalisation of the generated differences now exactly measure the network-positional effects on the players, which can be interpreted as a centrality measure.

Finally, with regard to the Gately value as a solution concept for TU-games, this conception was seminally introduced for some specific three-player cost games by Gately [27]. This contribution inspired the further development of the underlying conception of “propensity to disrupt” by Littlechild and Vaidya [28] and Charnes et al. [29], including the definition of several related solution concepts. Littlechild and Vaidya [28] also developed an example of a four-player TU-game in which the Gately value is not a core imputation. More recently, Staudacher and Anwander [30] generalised the scope of the Gately value and identified exact conditions under which this value is well-defined. This has further been developed by Gilles and Mallozzi [31], who showed that the Gately value is always a core imputation for three-player games, devised an axiomatisation for the Gately value for arbitrary TU-games and introduced a generalised Gately value founded on weighted propensities to disrupt.

Our paper is devoted to the theoretical investigation of the concepts and their properties. Nevertheless, concrete applications of this theory go back to Gately’s seminal paper Gately [27]. From these studies and the theoretical properties investigated here, applications to the collective usage of natural resources and collective goods are most natural. Gately seminally developed his conception to study the cost allocation of electricity generation, which was successively studied in Liu and He [32] Shandilya et al. [33].

One of the more natural applications of the network theoretical framework developed here is the study of cost allocation problems related to pollution in river systems and other water provision infrastructure [34]. The literature has mainly focussed on the application of the $\beta$-measure and related Shapley value conceptions for cost allocation in water networks [35,36,37], but it seems appropriate to consider network centrality measures that treat water sources as collective resources rather than singular nodes; this is particular exemplified in the Gately power measure studied here.

• Structure of the paper

Section 2 discusses the foundations of the game theoretic approach that is pursued in this paper. It defines the successor representations and presents their main properties. Furthermore, the standard solution concepts of the core and the Shapley value are applied to these successor representations. Section 3 introduces the Gately measure, which represents a different philosophy of measuring the exercise of control and power in a network. We investigate when the Gately measure assigns a core power gauge to a network, and we devise an axiomatisation of the Gately measure. The paper concludes with a comprehensive comparison of the Gately and $\beta$-measures, identifying exact conditions under which these two measures are equivalent.

2. Game Theoretic Representations of Hierarchical Networks

In our study, we focus on networks with directed links, where each link has specifically the interpretation of being the representation of a hierarchical relationship. In a directed network, the direction of a link indicates that one node is positioned as a predecessor while the other node is considered a successor in that particular relationship. Here, we interpret this explicitly as a control or authority relationship. Therefore, we denote these networks as hierarchical throughout this paper.

In hierarchical networks, predecessors exercise some form of authority over their successors, allowing for the assignment of that control to that particular node. This results in a natural game theoretic representation. We explore these game theoretic representations in this section and investigate the properties of these games.

• Notation: Representing hierarchical networks

Let $N=\{1,\dots ,n\}$ be a finite set of nodes, where $n\in \mathbb{N}$ is the number of nodes considered. Usually, we assume that $n⩾3$. A hierarchical network on N is a map $D:N\to 2^N$ that assigns to every node $i\in N$ a set of successors $D\left(i\right)\subseteq N\setminus \left\{i\right\}$. We explicitly exclude that a node succeeds itself, i.e., $i\notin D\left(i\right)$. The class of all directed networks on node set N is denoted as ${\mathbb{D}}^N=\{D\mid D:N\to 2^N$ with $i\notin D\left(i\right)$ for all $i\in N\}$5.

Inversely, in a directed network $D\in {\mathbb{D}}^N$, for every node $i\in N$, the subset $D^{-1}\left(i\right)=\{j\in N\mid i\in D\left(j\right)\}$ denotes the set of its predecessors in D. Due to the general nature of the networks considered here, we remark that it might be the case that $D\left(i\right)\cap D^{-1}\left(i\right)\ne ⌀$, i.e., some nodes can be successors as well as predecessors of a node.

We introduce the following additional notation to count the number of successors and predecessors of a node in a network $D\in {\mathbb{D}}^N:$

(i)

The map $s_D:N\to \mathbb{N}$ counts the number of successors of a node defined by $s_D\left(i\right)=\#D\left(i\right)$ for $i\in N$;

(ii)

The map $p_D:N\to \mathbb{N}$ counts the number of predecessors of a node defined by $p_D\left(i\right)=\#D^{-1}\left(i\right)$ for $i\in N$;

The previous analysis leads to a natural partitioning of the node set N into different classes based on the number of predecessors of the nodes in a given network $D\in {\mathbb{D}}^N:$

$$\begin{array}{cc}\hfill N_D^o& =\{i\in N\mid D^{-1}\left(i\right)=⌀\}=\{i\in N\mid p_D\left(i\right)=0\}\hfill \\ \hfill N_D& =N\setminus N_D^o=\{i\in N\mid p_D\left(i\right)⩾1\}\hfill \\ \hfill N_D^a& =\{i\in N\mid p_D\left(i\right)=1\}\hfill \\ \hfill N_D^b& =\{i\in N\mid p_D\left(i\right)⩾2\}\hfill \end{array}$$

Note that $N=N_D^o\cup N_D$, $N_D=N_D^a\cup N_D^b$. In particular, $\{N_D^o,N_D^a,N_D^b\}$ forms a partitioning of the node set N. We introduce counters $n_D=\#N_D$, $n_D^a=\#N_D^a$ and $n_D^b=\#N_D^b$, leading to the conclusion that $n_D=n_D^a+n_D^b$.

The constructed partitioning informs the analysis of the game theoretic representation of the hierarchical authority structure imposed by D on the node set N. Our analysis will show that for certain centrality measures, the class of nodes that have multiple predecessors $N_D^b$ plays a critical role in the determination of the assignment of a power index to these predecessors.

The partitioning of the node set N based on the structure imposed by $D\in {\mathbb{D}}^N$ allows for further notation to be introduced for every node $i\in N:$

• $s_D^a\left(i\right)=\#\left[D\left(i\right)\cap N_D^a\right]$ and $s_D^b\left(i\right)=\#\left[D\left(i\right)\cap N_D^b\right]$, resulting in the conclusion that $s_D\left(i\right)=s_D^a\left(i\right)+s_D^b\left(i\right)$.
• From the definitions, above we conclude immediately that

  $$\sum _{i\in N}{s}_D^a\left(i\right)=\#N_D^a$$

  and

  $$\sum _{i\in N}{s}_D^b\left(i\right)=\sum _{j\in N_D^b}{p}_D\left(j\right).$$

• Classes of hierarchical networks

The next definition introduces some normality properties on hierarchical networks that will be used for certain theorems.

Definition 1. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N.

(a) 

The network D is weakly regular if for all nodes $i,j\in N_D^b:p_D\left(i\right)=p_D\left(j\right)$.

The collection of weakly regular hierarchical networks is denoted by ${\mathbb{D}}_w^N\subset {\mathbb{D}}^N$.

(b) 

The network D is regular if for all nodes $i,j\in N_D:p_D\left(i\right)=p_D\left(j\right)$.

The collection of regular hierarchical networks is denoted by ${\mathbb{D}}_r^N\subset {\mathbb{D}}_w^N$.

(c) 

The network D is simple if for every node $i\in N_D:p_D\left(i\right)=1$.

The collection of simple hierarchical networks is denoted by ${\mathbb{D}}_s^N\subset {\mathbb{D}}_r^N$.

In a regular network, each node has either no predecessors or a given fixed number of predecessors. Hence, all nodes with predecessors have exactly the same number of predecessors. In a weakly regular network, each node has either no predecessors, or exactly one predecessor, or a given fixed number $p⩾2$ of predecessors. Clearly, each regular network is weakly regular.

The notion of a simple network further strengthens the requirement of a regular network. It imposes that all nodes either have no predecessors or exactly one predecessor.

Furthermore, van den Brink and Borm [6] introduced the notion of a simple subnetwork of a given network $D\in {\mathbb{D}}^N$ on the node set N. We elaborate here on that definition.

Definition 2. 

Let $D\in {\mathbb{D}}^N$ be a given hierarchical network on N.

A network $T\in {\mathbb{D}}^N$ is a simple subnetwork of D if it satisfies the following two properties:

(i) 

For every node $i\in N:T\left(i\right)\subseteq D\left(i\right)$, and

(ii) 

For every node $j\in N_D:p_T\left(j\right)=1$.

The collection of a simple subnetwork of D is denoted by $\mathcal{S}\left(D\right)$.

The collection of simple subnetworks of a given network can be used to analyse the core of the game theoretic representations of hierarchical games as shown below. It is easy to establish that a hierarchical network D is simple if and only if $\mathcal{S}\left(D\right)=\left\{D\right\}$.

• Measuring power in hierarchical networks

The main objective of our study is to investigate the measurement of power in hierarchical networks. We introduce the notion of a power gauge to express the distribution of power in a given network. In particular, a power gauge is a vector $\delta =({\delta }_1,\dots ,{\delta }_n)$ that assigns a numerical expression ${\delta }_i⩾0$ of the power exercised by a node $i\in N$ in a given network D. Furthermore, the measurement of power using such a gauge is normalised.

Definition 3. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network. A power gauge for D is a vector $\delta =({\delta }_1,\dots ,{\delta }_n)\in {\mathbb{R}}_{+}^N$ such that ${\sum }_{i\in N}{\delta }_i=n_D$.

A power measure on ${\mathbb{D}}^N$ is a function $m:{\mathbb{D}}^N\to {\mathbb{R}}_{+}^N$ such that ${\sum }_{i\in N}{m}_i\left(D\right)=n_D$ for every hierarchical network $D\in {\mathbb{D}}^N$.

This definition introduces the class of power gauges for a particular hierarchical network D as the collection of all normalised power distributions on N. As introduced here, a power measure is now a function that assigns to every possible hierarchical network some power gauge that expresses the power that is exercised in that network. We can also refer to a power measure as a hierarchical centrality measure on the class of hierarchical networks.

The normalisation of a power gauge for a network D to the total number of nodes in $N_D$ is a yardstick that is adopted in the literature on the $\beta$-measure, which we use here as well. This normalisation is in some sense arbitrary, but it allows for a straightforward application of the cooperative game theoretic methodology as advocated here.

2.1. Game Theoretic Representations of Hierarchical Networks

Using the notation introduced above, we are able to device cooperative game theoretic representations of hierarchical networks. We first recall the definition of a TU-game.

Definition 4. 

A cooperative game with transferable utilities—or a “TU-game”—on the node set N is a map $v:2^N\to \mathbb{R}$ such that $v(⌀)=0$.

A TU-game v assigns to every group of nodes $H\subseteq N$ a worth $v\left(H\right)\in \mathbb{R}$. A group of nodes $H\subseteq N$ is also called a coalition of nodes.

A cooperative game with transferable utilities—or “TU-game”—assigns to every non-empty node coalition a certain measurable and distributable worth. In the framework of a TU-game, the fundamental hypothesis is that within each coalition, side payments can be made to allocate the generated worth to the members of the coalition. This makes the notion of a TU-game ideal to investigate and develop power distributions among nodes in a hierarchical network. This is pursued next.

To embody the control or authority represented by a hierarchical network $D\in {\mathbb{D}}^N$ on the node set N as a cooperative game, we introduce some additional notation. For every group of nodes $H\subseteq N$, we denote

$$D\left(H\right)=\{j\in N\mid D^{-1}\left(j\right)\cap H\ne ⌀\}=\bigcup _{i\in H}D\left(i\right)$$

(1)

as the (weak) successors of coalition H in D. A node is a (weak) successor of a node group if at least one of its predecessors is a member of that group.

Similarly, we introduce

$$D^{*}\left(H\right)=\{j\in N\mid ⌀\ne D^{-1}\left(j\right)\subseteq H\}=\{j\in N_D\mid D^{-1}\left(j\right)\subseteq H\}$$

(2)

as the strong successors of coalition H in D. A node is a strong successor of a node group if all predecessors of that node are members of that group. Clearly, strong successors of a node group are completely controlled by the nodes in that particular group and full control can be exercised. This compares to regular or weak successors of a node group over which the nodes in that group only exercise partial control.

The next definition introduces the two main cooperative game theoretic embodiments of this control over other nodes in a network.

Definition 5. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N.

(a) 

The successor representation of D is the TU-game ${\rho }_D:2^N\to \mathbb{N}$ for every coalition $H\subseteq N$ given by ${\rho }_D\left(H\right)=\#D\left(H\right)$, the number of successors of the coalition H in the network D.

(b) 

The partial successor representations of D are given as the two TU-games ${\rho }_D^a,{\rho }_D^b:2^N\to \mathbb{N}$, which for every node coalition $H\subseteq N$ are given by ${\rho }_D^a\left(H\right)=\#\left[D\left(H\right)\cap N_D^a\right]$ and ${\rho }_D^b\left(H\right)=\#\left[D\left(H\right)\cap N_D^b\right]$.

(c) 

The strong successor representation of D is the TU-game ${\sigma }_D:2^N\to \mathbb{N}$ for every coalition $H\subseteq N$ given by ${\sigma }_D\left(H\right)=\#D^{*}\left(H\right)$, the number of strong successors of the coalition H in the network D.

The successor representation ${\rho }_D$ is also known as the “successor game” in the literature, and the strong successor representation ${\sigma }_D$ is known as the “conservative successor game” on D [38]. It is clear that the four TU-games introduced in Definition 5 embody different aspects of the control exercised over nodes in a given hierarchical network. In particular, these TU-games count the number of successors that are under the control of nodes in a selected coalition. We illustrate this with some simple examples.

Example 1. 

Consider the left network D depicted in Figure 1. Network D represents a simple hierarchy with node 2 in the top position. In this network, the two TU-representations are identical since each node has at most one predecessor.

On the other hand, in the right hand network $D^{\prime }$ there is an additional control relationship between the two subordinates, denoted as nodes 4 and 6. This implies that the two TU-representations are different. This is summarised in the next tables:

Coalition H	${\rho }_D\left(H\right)$	${\sigma }_D\left(H\right)$	Coalition H	${\rho }_{D^{\prime }}\left(H\right)$	${\sigma }_{D^{\prime }}\left(H\right)$
$\left\{1\right\}$	0	0	$\left\{4\right\}$	1	0
$\left\{2\right\}$	2	2	$\left\{5\right\}$	2	1
$\left\{3\right\}$	0	0	$\left\{6\right\}$	0	0
$\{1,2\}$	2	2	$\{4,5\}$	2	2
$\{1,3\}$	0	0	$\{4,6\}$	1	0
$\{2,3\}$	2	2	$\{5,6\}$	2	1
$N=\{1,2,3\}$	2	2	$N=\{4,5,6\}$	2	2

The main difference between these two TU-representations is that ρ is just a simple counting function, while σ requires that nodes with multiple predecessors—such as node 6 in network $D^{\prime }$—are only counted if all predecessors are members of the node coalition under consideration.

Figure 1. Two hierarchical networks considered in Example 1.

Figure 1. Two hierarchical networks considered in Example 1.

• Properties of successor representations

The next list collects some simple properties of these four games introduced here.

Proposition 1. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N. Then, the following properties hold regarding the successor representations ${\rho }_D$, ${\rho }_D^a$, ${\rho }_D^b$, and ${\sigma }_D$:

(i) 

For every node, $i\in N:{\rho }_D\left(\left\{i\right\}\right)=s_D\left(i\right)$, and the worth of the whole node set is determined as ${\rho }_D\left(N\right)=n_D=\#N_D$.

(ii) 

For every node, $i\in N:{\sigma }_D\left(\left\{i\right\}\right)=s_D^a\left(i\right)$, and the worth of the whole node set is determined as ${\sigma }_D\left(N\right)=n_D=\#N_D$.

(iii) 

The successor game is the sum of the two partial successor games in the sense that ${\rho }_D\left(H\right)={\rho }_D^a\left(H\right)+{\rho }_D^b\left(H\right)$ for every node coalition $H\in 2^N$.

(iv) 

For every node coalition, $H\subseteq N:{\rho }_D^a\left(H\right)={\sum }_{i\in H}{s}_D^a\left(i\right)$, implying that the partial successor representation ${\rho }_D^a$ is an additive game.

(v) 

For every node coalition, $H\subseteq N:{\rho }_D^b\left(H\right)⩽{\sum }_{i\in H}{s}_D^b\left(i\right)$.

(iv) 

${\sigma }_D={\rho }_D^a+{\widehat{\sigma }}_D$, where for every coalition $H\subseteq N:{\widehat{\sigma }}_D\left(H\right)={\sigma }_D\left(H\right)-{\rho }_D^a\left(H\right)⩽{\rho }_D^b\left(H\right)$.

These properties follow straightforwardly from the definitions; therefore, a proof is omitted.

The next theorem collects some properties of the successor representations that have not been remarked on explicitly in the literature on cooperative game theoretic approaches to representations of hierarchical networks6.

Theorem 1. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N. Then, the following properties hold for the successor representations ${\rho }_D$ and ${\sigma }_D:$

(i) 

The strong successor representation ${\sigma }_D$ is the dual of the successor representation ${\rho }_D$ in the sense that

$${\sigma }_D\left(H\right)={\rho }_D\left(N\right)-{\rho }_D(N\setminus H)for all H\subseteq N.$$

(3)

(ii) 

The strong successor representation ${\sigma }_D$ is decomposable into unanimity games with

$${\sigma }_D=\sum _{j\in N_D}{u}_{D^{-1}\left(j\right)}.$$

(4)

(iii) 

The strong successor representation ${\sigma }_D$ is a convex TU-game [7] in the sense that ${\sigma }_D\left(H\right)+{\sigma }_D\left(K\right)⩽{\sigma }_D(H\cup K)+{\sigma }_D(H\cap K)$ for all $H,K\subseteq N$.

(iv) 

The successor representation ${\rho }_D$ is a concave TU-game in the sense that ${\rho }_D\left(H\right)+{\rho }_D\left(K\right)⩾{\rho }_D(H\cup K)+{\rho }_D(H\cap K)$ for all $H,K\subseteq N$.

Proof. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N, and let the TU-representations ${\rho }_D$ and ${\sigma }_D$ be as defined in Definition 5.

To show assertion (i), let $H\subseteq N$; then, it holds that

$$\begin{array}{cc}\hfill {\rho }_D\left(N\right)-{\rho }_D(N\setminus H)& =n_D-\#D(N\setminus H)=n_D-\#\{j\in N\mid D^{-1}\left(j\right)\cap (N\setminus H)\ne ⌀\}\hfill \\ \hfill & =n_D-\#\{j\in N\mid D^{-1}\left(j\right)\setminus H\ne ⌀\}=\#\{i\in N_D\mid D^{-1}\left(i\right)\setminus H=⌀\}\hfill \\ \hfill & =\#\{i\in N_D\mid D^{-1}\left(i\right)\subseteq H\}={\sigma }_D\left(H\right).\hfill \end{array}$$

This shows that ${\sigma }_D$ is the dual game of ${\rho }_D$.

Assertion (ii) is Lemma 2.2 in van den Brink and Borm [6], and assertion (iii) follows immediately from (ii). Finally, assertion (iv) is implied by the fact that ${\rho }_D$ is the dual game of ${\sigma }_D$—following from assertion (i)—and ${\sigma }_D$ is convex. □

The duality between the successor representation and the strong successor representation implies that some cooperative game theoretic solution concepts result in exactly the same outcomes for both games. In particular, we refer to the core, the Weber set, the Shapley value, and the Gately value of these successor representations as explored below.

2.2. Some Standard Solutions of the Successor Representations

The cooperative game theoretic approach to measuring power or hierarchical centrality is based on the assignment of a power gauge to every individual node in a given hierarchical network. A power measure now refers to a rule or procedure that assigns such a gauge to every node in any hierarchical network. In this section, we set out some well-known concepts for this approach.

In particular, a game theoretic approach allows us to apply basic solution concepts to impose well-accepted properties on power gauges and power measures. The game theoretic notion of the core affords us to impose natural requirements on acceptable measurements of power in hierarchical networks. This is expressed through the following notion.

Definition 6. 

A core power gauge for a given hierarchical network $D\in {\mathbb{D}}^N$ is a power gauge $\delta \in {\mathbb{R}}_{+}^N$ that satisfies the normalisation property ${\sum }_{i\in N}{\delta }_i=n_D$ and for every node coalition $H\subseteq N:{\sum }_{j\in H}{\delta }_j⩾{\sigma }_D\left(H\right)=\#D^{*}\left(H\right)$.

The set of core power gauges for D is denoted by $\mathcal{C}\left(D\right)\subset {\mathbb{R}}_{+}^N$.

The core requirements on a power gauge impose that every group of nodes is collectively assigned at least the number of nodes that it fully controls. This seems a rather natural requirement. The next example provides an illustration of the notion of the core.

Example 2. 

Consider the two hierarchical networks investigated in Example 1. It should be clear that the first network D admits a unique core power gage, namely, one that assigns all power to the top node: $\mathcal{C}\left(D\right)=\left\{\right(0,2,0\left)\right\}$.

On the other hand, in the hierarchical network $D^{\prime }$, power is divided between nodes 4 and 5, taking into account that node 5 should get at least ${\sigma }_{D^{\prime }}\left(\left\{5\right\}\right)=1$. Therefore, the set of core power gauges for $D^{\prime }$ is given by $\mathcal{C}\left(D^{\prime }\right)=\{(t,2-t,0)\mid 0⩽t⩽1\}$.

The following insight investigates the structure of the set of core power gauges for general hierarchical networks.

Proposition 2. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on node set N. Then, the following hold:

(i) 

If D is a simple hierarchical network, then there a unique core power gauge ${\delta }^D\in {\mathbb{R}}_{+}^N$ such that $\mathcal{C}\left(D\right)=\left\{{\delta }^D\right\}$ exists, where ${\delta }_i^D=s_D\left(i\right)$ for every node $i\in N$.

(ii) 

More generally, $\mathcal{C}\left(D\right)$ is equal to the Weber set of ${\sigma }_D$, which is the convex hull of the unique core power gauges of all simple subnetworks of D given by $\mathcal{C}\left(D\right)=\mathrm{Conv}\left\{{\delta }^T\mid T\in \mathcal{S}\left(D\right)\right\}\ne ⌀$.

Proof. 

Let D be a simple hierarchical network. Hence, $p_D\left(i\right)=1$ for all $i\in N_D$. Therefore, for every group of nodes $H\subseteq N$ it holds that ${\sigma }_D\left(H\right)={\rho }_D\left(H\right)={\sum }_{j\in H}{s}_D\left(j\right)$. Therefore, ${\delta }^D=s_D$ as defined above satisfies the core requirement for every node coalition $H\subseteq N$.

Furthermore, suppose that $\delta \in \mathcal{C}\left(D\right)$. Then, from ${\delta }_i⩾s_D\left(i\right)={\delta }_i^D$ for every node $i\in N$ and ${\sum }_{j\in N}{\delta }_j=n_D={\sum }_{j\in N}{\delta }_j^D$ it immediately follows that ${\delta }_i={\delta }_i^D$ for all $i\in N$. This shows that ${\delta }^D$ is the unique core power gauge for the simple hierarchical network D, showing assertion (i).

Assertion (ii) follows immediately from Theorem 4.2 in van den Brink and Borm [6] in combination with assertion (i). □

• The $\beta$-measure

A well-established power measure for hierarchical networks was first introduced by van den Brink and Gilles [9] and further developed in van den Brink and Gilles [22] and van den Brink et al. [23]. This $\beta$-measure is for every node $i\in N$ defined by

$${\beta }_i\left(D\right)=\sum _{j\in D\left(i\right)}\frac{1}{p_D\left(j\right)}.$$

(5)

To illustrate the definition of the $\beta$-measure, we remark that the two simple hierarchical networks considered in Example 1 are determined as $\beta \left(D\right)=(0,2,0)$, which is the unique core power gauge for D, and $\beta \left(D^{\prime }\right)=\left(\frac{1}{2},1\frac{1}{2},0\right)$, which is the centre of $\mathcal{C}\left(D^{\prime }\right)$.

The following proposition collects the main insights from the literature on the $\beta$-measure.

Proposition 3. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network. Then, the following properties hold:

(i) 

The β-measure is a core power gauge: $\beta \left(D\right)\in \mathcal{C}\left(D\right)$.

(ii) 

$\beta \left(D\right)=\phi \left({\rho }_D\right)=\phi \left({\sigma }_D\right)$, where φ is the Shapley value7 on the collection of all cooperative games on N.

3. The Gately Power Measure

Let $v:2^N\to \mathbb{R}$ be a TU-game on the node set N with ${\sum }_{i\in N}v\left(\left\{i\right\}\right)⩽v\left(N\right)⩽{\sum }_{i\in N}{M}_i\left(v\right)$ where $M_i\left(v\right)=v\left(N\right)-v(N-i)$. Then, the Gately value of the game v is given by $g\left(v\right)\in {\mathbb{R}}^N$, which for every node $i\in N$ is defined by

$$g_i\left(v\right)=v\left(\left\{i\right\}\right)+\frac{M_i\left(v\right)-v\left(\left\{i\right\}\right)}{{\sum }_{j\in N}\left(M_j\left(v\right)-v\left(\left\{j\right\}\right)\right)}\left[v\left(N\right)-\sum _{j\in N}v\left(\left\{j\right\}\right)\right]$$

(6)

The Gately value was seminally introduced by Gately [27] and further developed by Littlechild and Vaidya [28], Charnes et al. [29], Staudacher and Anwander [30], and Gilles and Mallozzi [31].

Based on the Gately value for general TU-games, we introduce the Gately power measure on the class of hierarchical networks.

Definition 7. 

The Gately power measure on the class of hierarchical networks ${\mathbb{D}}^N$ on N is the power measure $\xi :{\mathbb{D}}^N\to {\mathbb{R}}^N$ with

$${\xi }_i\left(D\right)=\left\{\begin{array}{cc}{s}_D^a\left(i\right)+\frac{s_D^b\left(i\right)}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}{n}_D^b\hfill & if{N}_D^b\ne ⌀\hfill \\ s_D^a\left(i\right)\hfill & if{N}_D^b=⌀\hfill \end{array}\right.$$

(7)

for every hierarchical network $D\in {\mathbb{D}}^N$ and every node $i\in N$.

To illustrate the definition of the Gately power measure, we again refer to the two simple hierarchical networks considered in Example 1. For both networks, the Gately power gauge is identical to the $\beta$-measure: $\xi \left(D\right)=\beta \left(D\right)=(0,2,0)$ and $\xi \left(D^{\prime }\right)=\beta \left(D^{\prime }\right)=\left(\frac{1}{2},1\frac{1}{2},0\right)$.

We show that both the regular successor representation and the conservative successor representation have identical Gately values, being the Gately power measure.

Theorem 2. 

Let $D\in {\mathbb{D}}^N$ be a directed network on node set N. Then,

$$g\left({\rho }_D\right)=g\left({\sigma }_D\right)=\xi \left(D\right)$$

(8)

Furthermore, the Gately measure ξ is the unique power measure that balances the propensities to disrupt a network given by

$$\frac{s_D^b\left(i\right)}{s_D\left(i\right)-{\xi }_i\left(D\right)}=\frac{s_D^b\left(j\right)}{s_D\left(j\right)-{\xi }_j\left(D\right)}$$

(9)

over all nodes $i,j\in N_D$.

Proof. 

Let $D\in {\mathbb{D}}^N$ be such that $N_D^b\ne ⌀$. Then, its successor representation ${\rho }_D$ is characterised for every $i\in N$ by

$$\begin{array}{cc}\hfill {\rho }_D\left(N\right)& =n_D\hfill \\ \hfill {\rho }_D\left(\left\{i\right\}\right)& =s_D\left(i\right)=\#D\left(i\right)\hfill \\ \hfill {\rho }_D(N-i)& =n_D-\#\left\{j\in N_D^a\mid D^{-1}\left(j\right)=\left\{i\right\}\right\}=n_D-s_D^a\left(i\right)\hfill \end{array}$$

From this, it follows that $M_i\left({\rho }_D\right)={\rho }_D\left(N\right)-{\rho }_D(N-i)=s_D^a\left(i\right)$ for every $i\in N$. Since $N_D^b\ne ⌀$, this implies that ${\rho }_D\left(\left\{i\right\}\right)=s_D\left(i\right)⩾M_i\left({\rho }_D\right)$ for every $i\in N$.

From the previous we further derive that

$$s_D\left(i\right)-M_i\left({\rho }_D\right)=\#\left\{j\in N\mid \left\{i\right\}{D}^{-1}\left(j\right)\right\}=s_D^b\left(i\right)$$

and that

$$\begin{array}{cc}\hfill \sum _{j\in N}{\rho }_D\left(\left\{j\right\}\right)-{\rho }_D\left(N\right)& =\sum _{j\in N}{s}_D\left(j\right)-n_D=\sum _{j\in N}{p}_D\left(j\right)-n_D\hfill \\ \hfill & =\sum _{h\in N_D^b}\left(p_D\left(h\right)-1\right)=\sum _{h\in N_D^b}{p}_D\left(h\right)-n_D^b.\hfill \end{array}$$

These properties imply that ${\rho }_D$ is a regular TU-game as defined in Gilles and Mallozzi [31]. This implies that the Gately value applies to the TU-game ${\rho }_D$.

We now compute the Gately value of the successor representation ${\rho }_D$. We note here that ${\rho }_D$ is a concave cost game, implying that the reverse formulation of (6) needs to be applied. Hence, we derive for every $i\in N$ that

$$\begin{array}{cc}\hfill g_i\left({\rho }_D\right)& ={\rho }_D\left(\left\{i\right\}\right)-\frac{{\rho }_D\left(\left\{i\right\}\right)-M_i\left({\rho }_D\right)}{{\sum }_{j\in N}\left({\rho }_D\left(\left\{i\right\}\right)-M_j\left({\rho }_D\right)\right)}·\left(\sum _{j\in N}{\rho }_D\left(\left\{j\right\}\right)-{\rho }_D\left(N\right)\right)\hfill \\ \hfill & =s_D\left(i\right)-\frac{s_D^b\left(i\right)}{{\sum }_{j\in N}{s}_D^b\left(j\right)}·\left(\sum _{j\in N_D^b}{p}_D\left(j\right)-n_D^b\right)=s_D\left(i\right)-\frac{s_D^b\left(i\right)}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}·\left(\sum _{j\in N_D^b}{p}_D\left(j\right)-n_D^b\right)\hfill \\ \hfill & =s_D\left(i\right)-s_D^b\left(i\right)+\frac{s_D^b\left(i\right)}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}·n_D^b=s_D^a\left(i\right)+\frac{s_D^b\left(i\right)}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}·n_D^b={\xi }_i\left(D\right)\hfill \end{array}$$

Similarly, the conservative successor representation ${\sigma }_D$ for the hierarchical network D is characterised for every $i\in N$ by

$$\begin{array}{cc}\hfill {\sigma }_D\left(N\right)& =n_D\hfill \\ \hfill {\sigma }_D\left(i\right)& =s_D^a\left(i\right)\hfill \\ \hfill {\sigma }_D(N-i)& =n_D-s_D\left(i\right)\hfill \end{array}$$

For the conservative successor representation ${\sigma }_D$, we derive from the above that $M_i\left({\sigma }_D\right)=s_D\left(i\right)$, implying that ${\sigma }_D\left(i\right)⩽M_i\left({\sigma }_D\right)$ for every $i\in N$. Also, ${\sigma }_D\left(i\right)<M_i\left({\sigma }_D\right)$ for some $i\in N$ since $N_D^b\ne ⌀$. Therefore, ${\sigma }_D$ is regular as defined in Gilles and Mallozzi [31]. Hence, the Gately value applies to ${\sigma }_D$.

Since ${\sigma }_D$ is a convex game, the formulation stated in (6) applies. Now, we compute that

$$M_i\left({\sigma }_D\right)-{\sigma }_D\left(i\right)=s_D\left(i\right)-s_D^a\left(i\right)=s_D^b\left(i\right)$$

and

$$\begin{array}{cc}\hfill g_i\left({\sigma }_D\right)& ={\sigma }_D\left(\left\{i\right\}\right)+\frac{M_i\left({\sigma }_D\right)-{\sigma }_D\left(\left\{i\right\}\right)}{{\sum }_{j\in N}\left(M_j\left({\sigma }_D\right)-{\sigma }_D\left(\left\{j\right\}\right)\right)}·\left({\sigma }_D\left(N\right)-\sum _{j\in N}{\sigma }_D\left(\left\{j\right\}\right)\right)\hfill \\ \hfill & =s_D^a\left(i\right)+\frac{s_D^b\left(i\right)}{{\sum }_{j\in N}{s}_D^b\left(j\right)}·n_D^b=s_D^a\left(i\right)+\frac{s_D^b\left(i\right)}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}·n_D^b={\xi }_i\left(D\right)\hfill \end{array}$$

Next, let $D\in {\mathbb{D}}^N$ be such that $N_D^b=⌀$. Then, $p_D\left(j\right)=1$ for all $j\in N_D$. This implies that for every $i\in N:M_i\left({\rho }_D\right)={\rho }_D\left(\left\{i\right\}\right)=s_D\left(i\right)$. Hence, for $i\in N:$

$$g_i\left({\rho }_D\right)={\rho }_D\left(\left\{i\right\}\right)=s_D\left(i\right)=s_D^a\left(i\right)={\xi }_i\left(D\right).$$

Finally, for every $i\in N:M_i\left({\sigma }_D\right)=s_D\left(i\right)=s_D^b\left(i\right)=0$. Hence,

$$g_i\left({\sigma }_D\right)={\sigma }_D\left(\left\{i\right\}\right)=s_D^a\left(i\right)={\xi }_i\left(D\right).$$

Combined with the previous case, this shows the first assertion of the theorem.

Finally, the second assertion of the theorem follows immediately from identifying the propensity to disrupt ([31], Definition 3.2) in the successor representation ${\rho }_D$ for some game theoretic imputation $m\in {\mathbb{R}}^N$ as

$$\frac{M_i\left({\rho }_D\right)-{\rho }_D\left(\left\{i\right\}\right)}{m_i-{\rho }_D\left(\left\{i\right\}\right)}=\frac{s_D^b\left(i\right)-s_D\left(i\right)}{m_i-s_D\left(i\right)}=\frac{s_D^b\left(i\right)}{m_i-s_D\left(i\right)}.$$

Using the definition of a Gately point ([31], Definition 3.2) and noting that ${\xi }_i\left(D\right)=s_D\left(i\right)=0$ for every $i\in N_D^o$, the second assertion of the theorem is confirmed. □

The Gately power measure introduced here is founded on fundamentally different principles than the $\beta$-measure and related power measures. Indeed, the Gately power measure is a member of a family of values that considers the control exercise over the nodes in $N_D^b$ to be a collective resource in any hierarchical network $D\in {\mathbb{D}}^N$. The control is then allocated according to a well-chosen principle. In particular, the Gately measure allocates the control over $N_D^b$ proportionally to the predecessor of the nodes in $N_D^b$. Assuming $N_D^b\ne ⌀$, this proportional allocator is for every node $i\in N$ with $D\left(i\right)\cap N_D^b\ne ⌀$ defined as

$$a_i\left(D\right)=\frac{s_D^b\left(i\right)}{{\sum }_{j\in N}{s}_D^b\left(j\right)}=\frac{s_D^b\left(i\right)}{{\sum }_{h\in N_D^b}{p}_D\left(h\right)}$$

(10)

where the Gately measure is now given by ${\xi }_i\left(D\right)=s_D^a\left(i\right)+a_i\left(D\right)·n_D^b$.

This compares, for example, to the allocation principle based on the egalitarian allocator of the power over the nodes in $N_D^b\ne ⌀$ given by

$$e_i\left(D\right)=\frac{1}{\#\{j\in N\mid D\left(i\right)\cap N_D^b\ne ⌀\}}$$

(11)

and the resulting restricted egalitarian power measure given by ${\epsilon }_i\left(D\right)=s_D^a\left(i\right)+e_i\left(D\right)n_D^b$. We emphasise that the Gately and restricted egalitarian power measures are members of the same family of power measures for hierarchical networks, which have a collective allocative perspective on the control over the nodes in $N_D^b$.

3.1. Properties of the Gately Power Measure

We investigate the properties of the Gately measure from the cooperative game theoretic perspective developed in this paper. We first investigate whether the Gately measure assigns a core power gauge, as is the case for the $\beta$-measure. Second, we consider some characterisations of the Gately measure. In particular, we derive an axiomatisation and investigate some interesting properties of the Gately measure on some special subclasses of hierarchical networks.

• The Gately measure is not necessarily a core power gauge

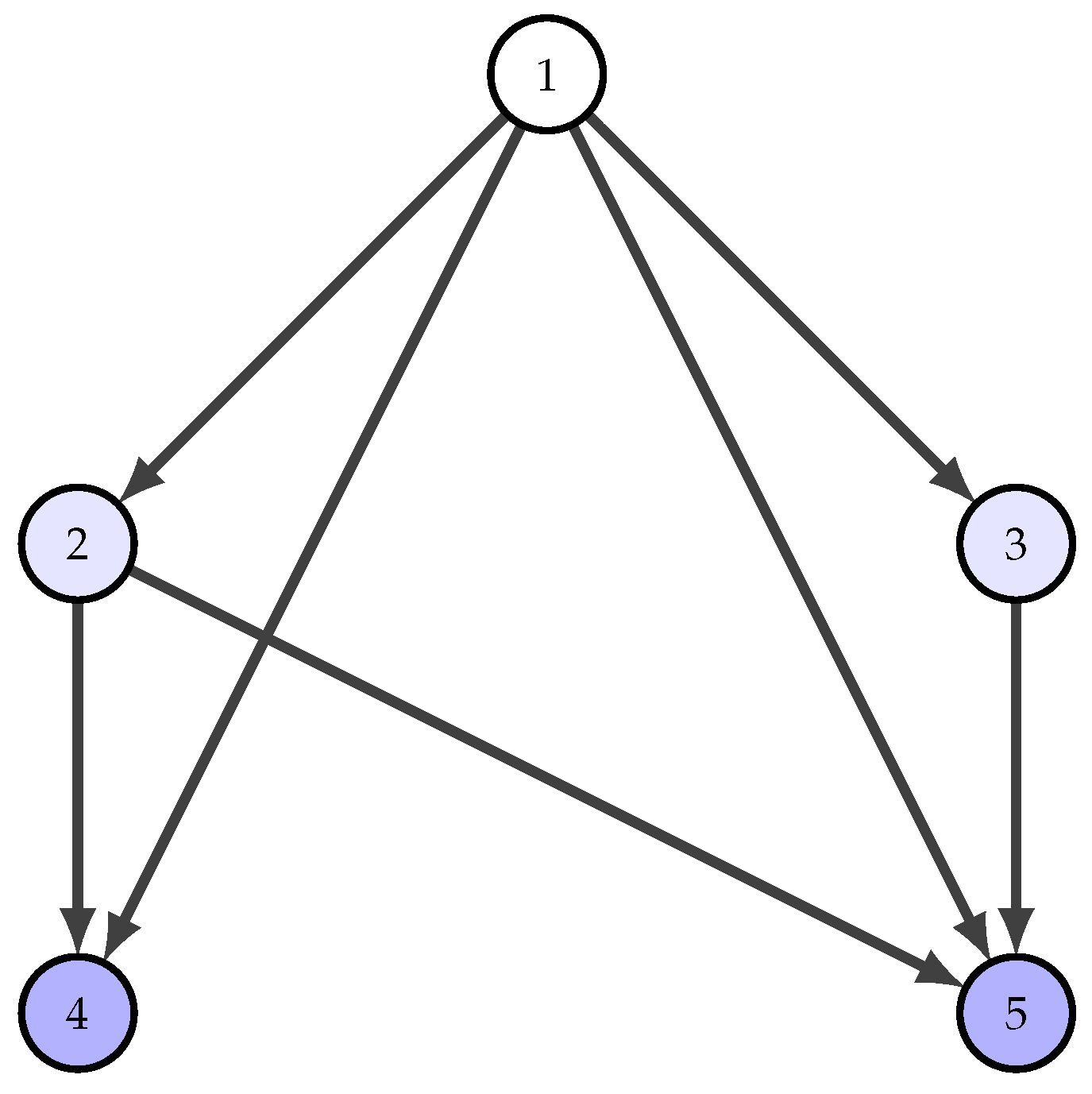
We first establish that contrary to the property that the $\beta$-measure is the geometric centre of the set of core power gauges of a given hierarchical network, its Gately power gauge does not necessarily have to satisfy the core constraints. The next example provides a hierarchical network on a node set consisting of 8 nodes whose Gately measure is not a core power gauge.

Example 3. 

Consider the hierarchical network D depicted in Figure 2 based on a node set $N=\{1,\dots ,8\}$. We note that $N_D=N_D^b=\{6,7,8\}$ and that nodes 1 and 2 fully control node 6, while nodes 3, 4, and 5 fully control nodes 7 and 8.

We compute that $s_D^a\left(i\right)=0$ for all $i\in N$ and that, therefore, any power measure only considers the control arrangements of the nodes in $N_D^b$. In particular,

$$\beta \left(D\right)=\left(\frac{1}{2},\frac{1}{2},\frac{2}{3},\frac{2}{3},\frac{2}{3},0,0,0\right)\in \mathcal{C}\left(D\right)$$

and that

$$\xi \left(D\right)=\left(\frac{3}{8},\frac{3}{8},\frac{3}{4},\frac{3}{4},\frac{3}{4},0,0,0\right)\notin \mathcal{C}\left(D\right).$$

Therefore, ${\xi }_1\left(D\right)+{\xi }_2\left(D\right)=\frac{3}{4}<1={\sigma }_D\left(\{1,2\}\right)$ shows that the Gately measure does not allocate sufficient power to the first two agents. The underlying reason is that the Gately value considers the control of all nodes in $N_D^b$ to be a collective resource that is proportionally distributed according to $s_D^b\left(i\right)$. The relative low values of $s_D^b\left(1\right)=s_D^b\left(2\right)=1$ in comparison with $s_D^b\left(3\right)=s_D^b\left(4\right)=s_D^b\left(5\right)=2$ imply that the assigned share of the first two nodes is less than the total of fully controlled nodes by that node pair.

Figure 2. The hierarchical network considered in Example 3.

Figure 2. The hierarchical network considered in Example 3.

The following theorem establishes under which conditions the Gately measure assigns a core power gauge to a hierarchical network. The class of networks identified in (ii) compares with the classes of networks for which the Gately measure is identical to the $\beta$-measure.

Theorem 3. 

Let $D\in {\mathbb{D}}^N$ be a hierarchical network on N.

(i) 

If $\#\{i\in N\mid D(i)\ne ⌀\}⩽3$, then $\xi \left(D\right)\in \mathcal{C}\left(D\right)$.

(ii) 

If D is weakly regular, i.e., for all $i,j\in N_D^b:p_D\left(i\right)=p_D\left(j\right)$, then $\xi \left(D\right)\in \mathcal{C}\left(D\right)$.

Proof. 

Assertion (i) follows directly from Theorem 4.2 of Gilles and Mallozzi [31]. Here, we note that the strong successor representation ${\sigma }_D$ is essentially a three-player if $\#\{i\in N\mid D(i)\ne ⌀\}=3$ and a two-player game if $\#\{i\in N\mid D(i)\ne ⌀\}=2$. Both cases are covered by Theorem 4.2 of Gilles and Mallozzi, establishing that $\xi \left(D\right)=g\left({\sigma }_D\right)\in \mathcal{C}\left({\sigma }_D\right)=\mathcal{C}\left(D\right)$ as desired.

Let $p⩾2$ such that $p_D\left(j\right)=p$ for all $j\in N_D^b$ as assumed. From this, it follows that for $i\in N:$

$${\xi }_i\left(D\right)=s_D^a\left(i\right)+\frac{n_D^b}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}{s}_D^b\left(i\right)=s_D^a\left(i\right)+\frac{n_D^b}{p·n_D^b}{s}_D^b\left(i\right)=s_D^a\left(i\right)+\frac{1}{p}{s}_D^b\left(i\right)$$

Now, let $H\subseteq N$ be some node coalition. Define

$$K_H=\left\{j\in N_D^b\mid D^{-1}\left(j\right)\subseteq H\right\}\mathrm{and}{k}_H=\#K_H⩽n_D^b.$$

Now, note that

$${\sigma }_d\left(H\right)=\#\left\{j\in N\mid D^{-1}\left(j\right)\subseteq H\right\}=\sum _{i\in H}{s}_D^a\left(i\right)+k_H.$$

Next, we compute

$$\begin{array}{cc}\hfill \sum _{i\in H}{\xi }_i\left(D\right)& =\sum _{i\in H}{s}_D^a\left(i\right)+\frac{1}{p}\sum _{i\in H}{s}_D^b\left(i\right)\hfill \\ \hfill & =\sum _{i\in H}{s}_D^a\left(i\right)+\frac{1}{p}\sum _{i\in H}\left[\#\left\{j\in K_H\mid j\in D\left(i\right)\right\}+\#\left\{j\in N_D^b\setminus K_H\mid j\in D\left(i\right)\right\}\right]\hfill \\ \hfill & ⩾\sum _{i\in H}{s}_D^a\left(i\right)+\frac{1}{p}\sum _{i\in H}\#\left\{j\in K_H\mid j\in D\left(i\right)\right\}\hfill \\ \hfill & =\sum _{i\in H}{s}_D^a\left(i\right)+\frac{1}{p}\sum _{j\in K_H}{p}_D\left(j\right)=\sum _{i\in H}{s}_D^a\left(i\right)+\frac{1}{p}·p{k}_H\hfill \\ \hfill & =\sum _{i\in H}{s}_D^a\left(i\right)+k_H={\sigma }_D\left(H\right).\hfill \end{array}$$

Since H was arbitrary, this establishes that ${\sum }_{i\in H}{\xi }_i\left(D\right)⩾{\sigma }_D\left(H\right)$ for all coalitions $H\subseteq N$ and, therefore, $\xi \left(D\right)\in \mathcal{C}\left({\sigma }_D\right)=\mathcal{C}\left(D\right)$, showing the second assertion of the theorem. □

• An axiomatic characterisation of the Gately power measure

We are able to devise full axiomatisation of the Gately measure on ${\mathbb{D}}^N$ based on three defining properties. In order to state these properties, we define, for every hierarchical network $D\in {\mathbb{D}}^N$ on node set N, its principal restriction as the network $P_D\in {\mathbb{D}}^N$ defined by $P_D\left(i\right)=N_D^b\cap D\left(i\right)$ for every node $i\in N$. Similarly, a hierarchical network $D\in {\mathbb{D}}^N$ is a principal network if $D=P_D$. It is clear that a principal hierarchical network D is characterised by the property that $N_D^a=⌀$, meaning that all nodes with predecessors actually have multiple predecessors.

Theorem 4. 

Let ${\mathbb{D}}^N$ be the class of hierarchical networks on node set N. Then, the Gately power measure $\xi :{\mathbb{D}}^N\to {\mathbb{R}}^N$ is the unique function $m:{\mathbb{D}}^N\to {\mathbb{R}}^N$ that satisfies the following three properties:

(i) 

Normalisation: m is $n_D$-normalised in the sense that ${\sum }_N{m}_i\left(D\right)=n_D$ for all $D\in {\mathbb{D}}^N$;

(ii) 

Normality: For every hierarchical network $D\in {\mathbb{D}}^N$, it holds that

$$m\left(D\right)=s_D^a+m\left(P_D\right)$$

(12)

where $P_D\in {\mathbb{D}}^N$ is the principal restriction of D; and

(iii) 

Restricted proportionality: For every principal network $D\in {\mathbb{D}}^N$ with $D=P_D$, it holds that

$$m\left(D\right)={\lambda }_D{s}_{D}for some {\lambda }_D>0.$$

(13)

Proof. 

We first show that the Gately power measure $\xi$ indeed satisfies these three properties. Normalisation trivially follows from the definition of the Gately measure. Let $D\in {\mathbb{D}}^N$ be an arbitrary hierarchical network on N.

First, if $N_D^b=⌀$, we have that $s_D^b=0\in {\mathbb{R}}^N$ and $\xi \left(D\right)=s_D^a\in {\mathbb{R}}_{+}^N$. Hence, $P_D$ is the empty network with $P_D\left(i\right)=⌀$ for all $i\in N$. Therefore, $s_{P_D}=s_D^b=0$ and $\xi \left(P_D\right)=0=\lambda s_D^b=\lambda s_{P_D}$ for any $\lambda >0$. This implies that $\xi \left(D\right)$ satisfies the normality property as well as restricted proportionality for the case that $N_D^b=⌀$.

Second, in the case that $N_D^b\ne ⌀$, we have that

$$\xi \left(D\right)=s_D^a+\frac{n_D^b}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}{s}_D^b$$

Furthermore, we compute that for every $i\in N:{\xi }_i\left(P_D\right)=\frac{n_D^b}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}{s}_D^b\left(i\right)={\lambda }_D{s}_D^b\left(i\right)$, where ${\lambda }_D=\frac{n_D^b}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}$. This implies that g satisfies restricted proportionality.

Next, let $m:{\mathbb{D}}^N\to {\mathbb{R}}^N$ be a power measure that satisfies the three given properties.

First, consider a network $D\in {\mathbb{D}}^N$ with $N_D^b=⌀$. Hence, $s_D^b=0$, implying with (iii) that $m\left(P_D\right)={\lambda }_D{s}_D^b=0$. Therefore, with (ii), it follows that $m\left(D\right)=s_D^a=\xi \left(D\right)$.

Next, consider $D\in {\mathbb{D}}^N$ with $N_D^b\ne ⌀$. Then, noting that $s_{P_D}=s_D^b$, from (iii) it follows that $m\left(P_D\right)={\lambda }_D{s}_D^b>0$8, and with (ii) this implies that

$$m\left(D\right)=s_D^a+m\left(P_D\right)=s_D^a+{\lambda }_D{s}_D^b>0.$$

Using the normalisation of m stated as property (i), we conclude that ${\lambda }_D=\frac{n_D^b}{{\sum }_{j\in N_D^b}{p}_D\left(j\right)}$ and, therefore, $m\left(D\right)=\xi \left(D\right)$.

Uniqueness of $\xi$ as a power measure that satisfies the three listed properties is immediate and stated here without proof. □

The three properties stated in Theorem 4 have a natural and direct interpretation. In particular, the normality property imposes that the power measure always assigns its uniquely subordinated nodes, which are assigned to a given node, and that the main task of a power measure is to assign a power gauge for the principal restriction of any hierarchical network. This seems to be a rather natural hypothesis, and it is satisfied by other power measures such as the $\beta$-measure.

Restricted proportionality imposes that in a principal network the assigned power gauge is proportional to the number of other nodes that are controlled by that node. Again, this seems a plausible hypothesis, even though it is violated by the $\beta$-measure.

In fact, the three properties are non-redundant as the following simple examples show:

• As indicated above, with regard to the axiomatisation devised in Theorem 4, the $\beta$-measure satisfies the normalisation property (i) as well as the normality property (ii), but not the restricted proportionality property (iii).
  The restricted egalitarian power measure $\epsilon$ is an example of a power measure on ${\mathbb{D}}^N$ that satisfies (i) as well as (ii), but not the restricted proportionality property (iii). We remark that the restricted egalitarian power measure is in the same family of power measures as the Gately measure.
• Consider the proportional power measure $\pi$ on ${\mathbb{D}}^N$ with for every $D\in {\mathbb{D}}^N:$

  $$\pi \left(D\right)=\frac{n_D}{{\sum }_{i\in N}{s}_D\left(i\right)}{s}_D.$$
  Then, this proportional power measure satisfies the normalisation property (i) as well as the restricted proportionality property (iii) but not the normality property (ii) stated in Theorem 4.
• Finally, consider the direct power measure $\alpha$ on ${\mathbb{D}}^N$ with for every $D\in {\mathbb{D}}^N:$

  $$\alpha \left(D\right)=s_D\in {\mathbb{R}}_{+}^N.$$
  This direct power measure $\alpha$ satisfies the restricted proportionality property (iii) as well as the normality property (ii) stated in Theorem 4 but not the stated normalisation property (i).

3.2. A Comparison between the $\beta$-Measure and the Gately Measure

On the class of weakly regular hierarchical networks, the Gately value satisfies the strong property that coincides with the $\beta$-measure. This is explored in the next theorem.

Theorem 5. 

Let $D\in {\mathbb{D}}_w^N$ be a weakly regular hierarchical network on N. Then, the Gately measure coincides with the β-measure, i.e., $\xi \left(D\right)=\beta \left(D\right)$.

Proof. 

To show the assertion, denote by $p=p_D\left(i\right)⩾2$ the common number of predecessors for $i\in N_D^b$. Then, it holds that

$$\sum _{j\in N}{s}_D^b\left(j\right)=\sum _{i\in N_D^b}{p}_D\left(i\right)=p·n_D^b.$$

This implies that

$$\xi \left(D\right)=s_D^a+\frac{n_D^b}{p·n_D^b}{s}_D^b=s_D^a+\frac{1}{p}{s}_D^b=\beta \left(D\right),$$

since for every $i\in N:{\beta }_i\left(D\right)={\sum }_{j\in D\left(i\right)}\frac{1}{p_D\left(j\right)}=s_D^a\left(i\right)+s_D^b\left(i\right)·\frac{1}{p}$. □

Theorems 3 and 5 allow us to delineate networks with non-empty sets of core power gauges that contain either the Gately measure, the $\beta$-measure, or both, as well as determine when both of these measures coincide. This is explored in the next example.

Example 4. 

Consider the network D depicted in Figure 3 on the node set $N=\{1,\dots ,5\}$. Note that this network satisfies the conditions of Theorem 3(i) but not of Theorem 5. Hence, $\xi \left(D\right)\in \mathcal{C}\left(D\right)\ne ⌀$, but $\xi \left(D\right)\ne \beta \left(D\right)\in \mathcal{C}\left(D\right)$.

We compute that the set of core power gauges for this network is given by9

$$\mathcal{C}\left(D\right)=\mathrm{Conv}\left\{(2,1,1,0,0),(3,0,1,0,0),(3,1,0,0,0),(2,2,0,0,0),(4,0,0,0,0)\right\}$$

Next, we determine that the β-measure is in the (weighted) centre of $\mathcal{C}\left(D\right)$ with

$$\beta \left(D\right)=\left(2\frac{5}{6},\frac{5}{6},\frac{1}{3},0,0\right)\in \mathcal{C}\left(D\right)$$

and that the Gately measure is computed as

$$\xi \left(D\right)=\left(2\frac{4}{5},\frac{4}{5},\frac{2}{5},0,0\right)\in \mathcal{C}\left(D\right).$$

Clearly, we have established that in this case $\xi \left(D\right)\ne \beta \left(D\right)$ even though the network D satisfies the condition of Theorem 3(i), implying that the Gately measure is a core power gauge.

Figure 3. Network for Example 4.

Figure 3. Network for Example 4.

A question remaining is whether the assertion of Theorem 5 can be reversed, i.e., if $\xi \left(D\right)=\beta \left(D\right)$ then D has to be weakly regular. The answer to that is negative, as the following example shows.

Example 5. 

Consider the node set $N=\{1,\dots ,8\}$ and the network D depicted in Figure 4. As the colour code indicates, there are four groups of nodes in this network. Nodes 1 and 2 together dominate node 5, while nodes 3 and 4 together dominate nodes 6, 7 and 8.

Clearly, this network is not weakly regular. On the other hand, we claim that $\xi \left(D\right)=\beta \left(D\right)$. Now, we compute that $N_D^a=⌀$, $N_D^b=\{5,6,7,8\}$ and $n_D^b=4$. Furthermore, ${\sum }_{i\in N_D^b}{p}_D\left(i\right)=2+3·2=8$. This implies now that for every $i\in N:$

$${\xi }_i\left(D\right)=\frac{n_D^b}{{\sum }_{i\in N_D^b}{p}_D\left(i\right)}{s}_D^b\left(i\right)=\frac{4}{8}{s}_D^b\left(i\right)=\frac{1}{2}{s}_D^b\left(i\right)$$

resulting in $\xi \left(D\right)=\left(\frac{1}{2},\frac{1}{2},1\frac{1}{2},1\frac{1}{2},0,0,0\right)$ and that this coincides with $\beta \left(D\right)$.

Figure 4. Network for Example 5.

Figure 4. Network for Example 5.

4. Concluding Remarks

In this paper, we have investigated a new network centrality measure founded on the Gately value for cooperative games with transferable utilities. We considered directed networks to be represent control or authority relations between decision makers. The Gately power measure is now introduced as the Gately value of the two main TU-representations of a hierarchical network. We mainly investigated the relationship between this new measure and the other measure founded on game theoretic principles for this class of hierarchical networks.

Directed networks are also studied in evolutionary graph theory [40]: in this case, individuals occupy vertices of a weighted directed graph, and the weight $w_{ij}$ of an edge from vertex i to vertex j denotes the probability of i replacing j. The weight corresponds to the biological notion of fitness where fitter types propagate more readily. It seems fruitful to investigate the hierarchical networks studied in this paper when considering the probability of changing predecessors and successors in line with evolutionary graph theory. This remains outside the scope of the present work and is relegated to future research in this exciting field of innovative research.