1. Introduction
Let V, A be sets representing, respectively, a collection of decision makers (whom we refer to as individuals, voters, agents and so on) and a set of possible alternatives. Exactly one of the alternatives must be implemented as the choice of the collectivity V. Since alternatives do not have identical value for the agents, the problem arises of deducing from the aggregation of the agents’ preferences the social choice to implement.
Let be the set of all preferences on the set A. The underlying mathematical model of collective choice is a function which is named social choice function.
So, asking every agent to report his preference for the alternative to choose, a profile of preferences forms, and the function selects the alternative to realize.
The main issue in this framework of Social Choice Theory is to determine which social choice functions guarantee that no agent has an incentive to deviate from declaring his true preference about the elements of A. Indeed, if the society V adopts an “arbitrary” aggregation rule, it is possible that some agent is induced to false reporting his preference with the purpose of implementing some alternative he considers better, but not an alternative that would be socially desirable. In other words, a social choice function not carefully fixed can be manipulated. Social desirability here has a basic, elementary, interpretation: the political decision of the society is about the rule to adopt; once is fixed, it is desirable that the implemented alternative mirrors the profile of the true preferences of the individuals.
The non-manipulability property we would like a social choice function to enjoy is named strategy-proofness and corresponds to the fact that we look for social choice functions such that every profile P is an equilibrium in the Nash sense. Namely:
for every voter , for every profile , and every preference , letting Q be the profile identical to P except for the voter i, where , one has that the alternative is at least as good as according to .
For many relevant applications, the case of a binary set
of alternatives plays an important role. Think of a community that has to approve or reject a new proposal, or think of ballots between two candidates. This paper deals with such a binary framework. Then, it is worthwhile to observe that if we restrict our attention to social choice functions defined on the smaller domain
where
consists of strict preferences, then the strategy-proof social choice functions can be identified with the
monotone boolean functions. Consequently, it is known that there are
-many strategy-proof social choice functions that can be adopted for determining a binary collective choice in case the voters are not allowed to report an indifference between alternatives (see [
1,
2]). The symbol
stands for the Dedekind number, i.e., the number that counts the monotone boolean functions of
n variables.
The situation is significantly different when we consider strategy-proof social choice functions on
having range of cardinality three or more. In this case, the celebrated Gibbard–Satterthwaite theorem [
3,
4] gives that there are only
-many strategy-proof social choice functions without indifference.
Our article is about a more complex, though still binary, scenario. We assume that each voter not only has the possibility to say that he strictly prefers one of the two alternatives to the other, but he can also declare to be indifferent between them. This possibility results in a larger number of strategy-proof social choice functions. Translating the problem in mathematical terms to allow for indifference between alternatives corresponds to a step from considering the monotone functions from to , to the monotone functions from to .
When the voters can declare indifference among the alternatives, a further notion of strategy-proofness naturally arises: strong group strategy-proofness. This notion is widely studied in [
5], where the authors determine the functional form of social choice functions that are strong group strategy-proof and have range of cardinality two, although the set
A may contain more than two alternatives. The same question was already addressed, for the case where
A has exactly two elements, in the paper [
6]. In both cases, when strong group strategy-proofness is imposed to social choice functions, only very few of them remain, and anonymity emerges if there are three or more agents (see [
5,
6] for details).
The sensitivity of the number of strategy-proof binary social choice functions to the introduction of further axioms is quite strong. The previous is not the only possible example. The addition of a few further, still simple, axioms can reduce this number drastically. In [
7], the Positive Welfare Association (PWA) property is proposed for introducing solidarity in the model under consideration. This axiom, when joined with strategy-proofness, dramatically reduces the number of functions: only the two status quo rules and the two constant functions remain.
We believe that counting the binary strategy-proof social choice functions when indifference is admitted is of interest for the following two reasons. One reason is that we contribute to substantiate the sentence “indifference may help in obtaining positive results” (see [
8], p. 148). Naturally, we are thinking about the existence of more strategy-proofs social choice functions as a positive, and we see how the transition from strict to weak preferences moves up the number of the binary strategy-proof social choice functions.
Another reason deals with the combinatorics involved in the model. Whereas in the case of strict preferences, it is known that one obtains the famous Dedekind numbers sequence, there are no sequences in The On-Line Encyclopedia of Integer Sequences ([
9], accessed on September and November 2021) that can be referred to for characterizing the number of the binary strategy-proof social choice functions when indifference is admitted.
The content of the paper is the following. After the description in
Section 2 of the model, in
Section 3, we present a procedure to obtain the set
of all strategy-proof social choice functions in the case of
voters from the analogous set
of the functions in case the number of voters is
n. The procedure is illustrated for the cases
. In
Section 4, we use the characterization of strategy-proofness based on the notion of ”covering”, a relation between elements of partially ordered sets, to determine
, following a different approach that allows an intuitive geometrical visualization of social choice functions. Finally, in
Section 5, we comment on the number
of the binary strategy-proof social choice functions. In particular, we shall argue that its computation, analogously to that of the Dedekind numbers, is not an elementary task. We provide the values
, and
, whereas, due to the computational complexity involved, we do not compute the expression in decimal form of the numbers
for
.
2. The Model, Notations, Definitions
The set A is the set of alternatives and the set V is the set of voters, or, we say, it is the society. Both sets are assumed to be finite.
Different agents may have different opinions about the alternatives, but the society is called to select exactly one alternative to be realized. The problem is then the aggregation of different points of view in a unique outcome. The taste of the voters is modeled by means of complete, transitive binary relations on the set A. We call them weak preferences or just preferences for the sake of brevity. The set of all preferences on A is denoted by or simply by . Preferences that are also antisymmetric are named strict preferences. They form the subset of .
Suppose , and a, b are two alternatives. The expression “a is preferred to b” and the expression “a is at least as good as b” are used both as equivalent to . The expression “a is strictly preferred to b” and the expression “a is better than b” are used both as equivalent to , and . The case that both and belong to W is referred to as a and b are indifferent.
When each voter expresses his own preference, the state of the society is known. We also say that a profile is formed. State and profile are used synonymously. Formally, a profile is an element P of the set . We sometimes use the notations:
- -
, where is the weak preference of the voter i in the state P;
- -
; where is the restriction of P to the complement of the singleton .
In the theory of collective choice, the society is called to aggregate preferences, in other words to select the unique alternative to be realized on the basis of each profile. Hence, a rule to aggregate preferences has to be chosen and applied. The rule is, in fact, a function associating an alternative to each profile. We introduce the definition formally and fix the main property it has to obey.
Definition 1. Asocial choice functionis a function from the set of all states of the society to the set A of alternatives.
Once a social choice function is fixed, the alternative selected on the basis of a certain profile may change if a voter changes his preference, since this corresponds to a change of the profile. This could suggest to some voter to lie (i.e., to declare a false preference) if he can obtain, on the basis of the new profile, the selection of a different alternative that he considers better. Clearly, it is socially desirable to avoid such a possibility. Therefore, big efforts are deserved to the identification of mechanisms that prevent this occurrence. Social choice functions that cannot be manipulated in the described sense (which means that do not give any voter incentive to lie in any profile) are called strategy-proof. The formal definition follows.
Definition 2. A social choice function ϕ is said to bestrategy-proof(SP, for brevity) if for each voter i, for each profile P and for each profile identical to P in all the components different from i, the alternative is at least as good as the alternative according to the preference .
The previous definition is manifestly inspired to the Nash equilibrium notion. It implies that even if a voter is called to declare his preference knowing all the others’ preferences, he has no incentive to declare any preference different from his own (the true one). The change would not result in the realization of an alternative he considers better.
Stricto sensu, Definition 2 does not cover the case that the domain of social choice function is a subset, call it , of . However, if we consider social choice functions defined on arbitrary subsets of , the strategy-proofness is defined exactly as in Definition 2 integrated with the explicit requirement that the profiles P and Q belong to .
We concentrate our attention to the so-called
binary case, which means that there are exactly two alternatives
The case of two alternatives, interesting per se from the point of view of applications, offers a set of strategy-proof functions rich enough to make its investigation interesting.
Obviously, in the binary case, there are three preferences ():
- -
Alternative a is better than alternative b;
- -
Alternative b is better than alternative a;
- -
Alternatives a and b are indifferent to each other,
that we denote, respectively, by
a,
b and ∼. Hence, from now on, it is
The strategy-proofness of a social choice function can be described in terms of “monotonicity” of the function itself. Although the relation between strategy-proofness and (various) notions of monotonicity is often discussed in the literature, we explain it in detail both for the sake of completeness and to have the exact terms which we refer to.
Let us first order the sets
A and
by setting
between the alternatives and
among the preferences. Then, we order the set
of profiles componentwise: for profiles
P and
Q, we set
The relation ≤ on the set of the profiles is a partial order (i.e., reflexive, transitive, and antisymmetric) which is not complete. In fact, two profiles
P and
Q are not comparable (
and
) when for two different agents
i and
j it is
and
.
Definition 3. A social choice function ϕ is said to bemonotoneif Our aim is to present a result connecting monotonicity to strategy proofness. With the help of two concepts from the theory of partially ordered sets (posets, for short), we clarify that:
- -
To check the strategy-proofness (equivalently monotonicity) of a function, it is sufficient to refer to pairs of profiles “close” to each other, in the sense that there are no other profiles between them (this is the notion of covering);
- -
The equivalence between monotonicity and strategy-proofness does not need the universal domain assumption. Indeed, the equivalence holds true over domains without “gaps”(this is the notion of convexity).
Definition 4. Let s and t be two elements of a partially ordered set . We say that scoverst, and we write , if and there is no element u in S such that .
Definition 5. We say that a subset of a partially ordered set S isconvexif Of course, in , the preference b covers ∼ and the preference ∼ covers a.
It is not difficult to describe explicitly the meaning of covering among profiles in a convex subset of : if , the two profiles only differ for the preference of a single agent, say i, who is indifferent between the two alternatives in one of the two profiles. More precisely, either and , or and . Formally
Proposition 1. Let be a convex subset of . Suppose . Then, P covers Q if and only if there exists such that , and .
Observe that since the set of profiles is finite, when
, there is always between them a chain of profiles
,
, …,
each covering the previous:
This reveals the central role of indifference: moving from one strict preference to another, we
pass through indifference. The same is true moving from a profile to a bigger one.
We are now ready to relate the strategy-proofness of a function with its monotonicity:
Theorem 1. Let be a function whose domain is a convex subset of . Then, the following are equivalent:
- (i)
ϕ is SP;
- (ii)
if then ;
- (iii)
ϕ is monotone.
Proof. (i) ⇒ (ii): Assume that on a profile P that covers profile Q, and, by contradiction, that . Looking at Proposition 1, there is a unique voter i such that differs from .
If , agent i may manipulate (violate SP) declaring in the state P. If , he may do it declaring in the state Q. A contradiction in both cases.
(ii) ⇒ (iii): If
, choose profiles
,
, …,
such that
For each profile it is ; hence, all profiles are elements of the convex set .
From the relation , it follows that for all k, in particular , as wanted.
(iii) ⇒ (i) Assume by contradiction that is not SP. Then, there exists a voter i and two profiles P and Q in only differing in the component i, such that according to the preference the alternative is better than the alternative . Without loss of generality, assume , and b better that a according to , which means that . Given the hypothesis, the two relations and imply that , which is a contradiction. The result is the same assuming , and . □
The previous characterization is crucial in all that follows: both the recursive procedure described in the next section and the graph representation of
Section 4 are based on it.
Remark 1. In the paper [
10], the authors obtain a characterization of strategy-proofness of social choice functions through a notion of monotonicity. It is based on a relation among profiles denoted by
. It is sufficient to observe that
to derive the correspondence between ([
10], Theorem 2.5) and the relations (i) ⇔ (iii) in our Theorem 1.
The characterization of SP obtained in [
11] is based on a binary relation ⊐ called dominance among profiles:
We rewrite the previous relations using our notations:
In ([
11], Theorem 2.12), the authors prove that SP is equivalent to the following implication, called
compatibility with dominance. It is a sort of monotonicity:
Let us make a comparison between their result and our Theorem 1. From the relation
it follows that (*) implies (ii) of Theorem 1. On the other side, from the relations
it follows that (iii) implies (*). Hence, the two mentioned results can be derived from each other. It is worth observing that compatibility with dominance reveals to be equivalent to the simultaneous validity of the two properties (introduced by Barberà et al. in [
5]) of a social choice function of being
essentially -based and
essentially -monotonic.
3. A Recursive Construction of
Recall that denotes the set of all SP binary social choice functions with reference to a set V of n voters. In this section, we describe a recursive procedure to obtain from . Without loss of generality, we name the individuals as in a society of cardinality n and consider the further agent to form the larger society.
Since the restrictions of SP social choice functions remain SP, there is a natural way to obtain from
in
three elements of the set
. It is sufficient to consider the restrictions of
to the sets of profiles having the last component fixed. Precisely, we set:
Hence, the map, injective by definitions,
embeds
into
.
On the converse, an element of belongs to the range of T if and only if its three components are connected as shown in the next theorem.
Theorem 2. Let . The function ϕ defined on as belongs to if and only if the following two implications hold true:Moreover, . Proof. Let be defined as described above and assume that both implications (1) and (2) hold true. To verify the strategy-proofness of , we use characterization (ii) of Theorem 1. Assume that for profiles and , it is and P covers Q.
If , then for an element ℓ in the set , it is and . Moreover, the profile covers . Being ℓ SP, Theorem 1 ensures that from , it follows that , as wanted. If , using Proposition 1, we have that and either
, or
.
In the first case, it is and . Then, the relation follows from (2). In the second case, it is and , and the same relation follows from (1).
Conversely, let be SP. To prove that implication (1) holds, assume that . This means that . Since profile covers , and since is SP, it is also , which means , as wanted. An analogous reasoning proves implication (2). □
The two displayed implications allow to obtain all the elements of from the elements of . Let us see how.
Let
. Define the sets
and
as follows
Then, for every
, after Theorem 2, the function
belongs to
. Hence, finally, we can write
From the operational point of view, formula can be used as the justification of the following algorithm.
- 0
Preliminarly, the elements of (i.e., all the SP binary social choice functions defined on ) and all the profiles are enumerated. This allows to display the elements of in a matrix whose entry stands for the value of the function (numbered) u in the profile (numbered) v.
Next, for every row h of , we proceed by analyzing each component.
- 1
For every element in the selected row, we highlight the elements of the column j that differ from . This identifies the set of rows
- 2
The highlighting is realized in a way that distinguishes the case from the case . To fix the ideas, we can realize this by coloring red if it is a, and blue if it is b.
- 3
The set (respectively, ) consists of all functions occupying rows not cointaining any blue (respectively, red) component.
Example. We show how the above steps work in the cases , i.e., with reference to formula in the cases .
Case .
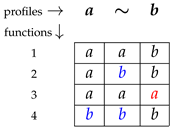
It is straightforward to recognize that . In fact, apart from the two constant functions (that are obviously SP), a (non-constant) SP function necessarily assumes value a on the profile and value b on the profile . The value on the remaining profile ∼ can be any of the two. We list below these four functions obtaining the () matrix with entries a and b. The idea is to number the functions arbitrarily from 1 to 4 to order the profiles arbitrarily (we do it here from the smallest to the biggest) and set as the value of function (numbered) u on the profile (numbered) v.
Applying the described procedure to function 1 (row 1): The first two elements in row 1 are
a; hence, we color blue each element
b that appears in column 1 or in column 2. The third element of row 1 is
b; hence, we color red each element
a in the third column. This is shown next.
![Games 13 00078 i001 Games 13 00078 i001]()
Then, the set
consists of all the rows without blue components, and the set
consists of all the rows without red components:
The (
) functions
of
having as
the function in the first row of
are (for brevity, we list profiles avoiding commas between preferences):
![Games 13 00078 i002 Games 13 00078 i002]()
Repeating the procedure for the remaining rows, we obtain:
We end up with the case where
by listing all the (20) elements of
, organized in the matrix
below.
![Games 13 00078 i003 Games 13 00078 i003]()
Case .
Starting from the latter matrix, we can proceed to obtain
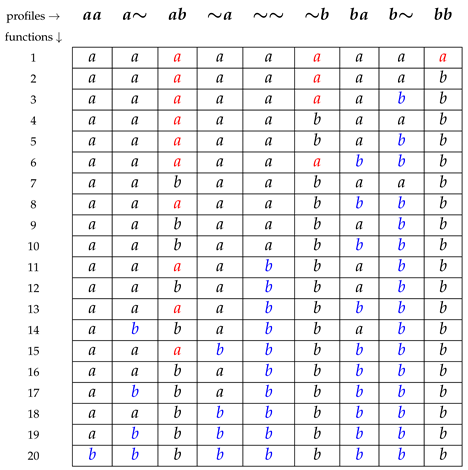
. As in the previous case, we shall present only the analysis for a single row. Fix, as an example, the row number 7. Applying the described procedure, we obtain:
![Games 13 00078 i004 Games 13 00078 i004]()
from which we have:
We have then determined all the functions
of
having as restriction
the element of
corresponding to row 7. There are exactly (
) 40 such functions.
Repeating the procedure for all the rows of the matrix, we obtain the whole .
4. Graphic Representation of 3-Voters SP Social Choice Functions
An expressive way, as it is visualized, to describe binary SP social choice functions by means of diagrams, can be adopted in case of three voters. We devote the present section to this. We present a simple way to translate into a graph the characterization (ii) of strategy-proofness contained in Theorem 1. This is possible since at the same time, we point out the symmetry of the (componentwise) partially ordered set , and the pivotal role played by the state, denoted as , of unanimous indifference, i.e., the state where all voters are indifferent between a and b. A similar, , , notation is used for the other two unanimity states of the society. We also adopt the terminology defined next.
Definition 6. A subset C of a poset is said to besuper order-closedif it contains the majorants of its elements. Formally: C is super order-closed if Analogously, we say that C issub order-closedif Lemma 1. Let be a binary function. Take two sets and such that is sub order-closed and is super order-closed in the poset . Then, ϕ is SP if (and only if) its restriction to is SP.
Proof. Assume the restriction of to the set is SP. If for two profiles and belonging to one has that is better than according to , then either
(hence ), or
(hence ).
In both cases, we obtain a contradiction. Let us consider the first case, the second case being analogous.
Moreover, since , the two order-closedness entail and . This means that both profiles P and Q are in , violating the strategy-proofness of the restriction of . □
With the aim of describing the SP functions
,
we assume:Remark 2. There is no loss of generality in the above assumption. Indeed, first, observe that given the strategy-proofness, each of the two relations , implies that the social choice function is constant. With the purpose of describing the non-constant , we can then assume , and . Moreover, considering the symmetric role played by the two alternatives, limiting to the SP social choice functions assuming value a on the profile of unanimous indifference suffices. Obviously, exchanging a with b everywhere in what follows will give the SP social choice functions assuming value b on the profile of unanimous indifference.
A further simplification is possible in the representation of the non-constant ’s satisfying .
Observe that the relation implies that for each profile , which means for each profile in not containing any b. In other words, under assumption , the function takes value a on the set . We can therefore restrict our attention to the remaining profiles: those in having at least one component equal to b.
Let us set
and notice the following straightforward consequence of Lemma 1.
Proposition 2. For a binary social choice function ϕ, the following conditions are equivalent:
- (i)
ϕ is SP and hold true.
- (ii)
ϕ takes value a on , , and its restriction to is SP.
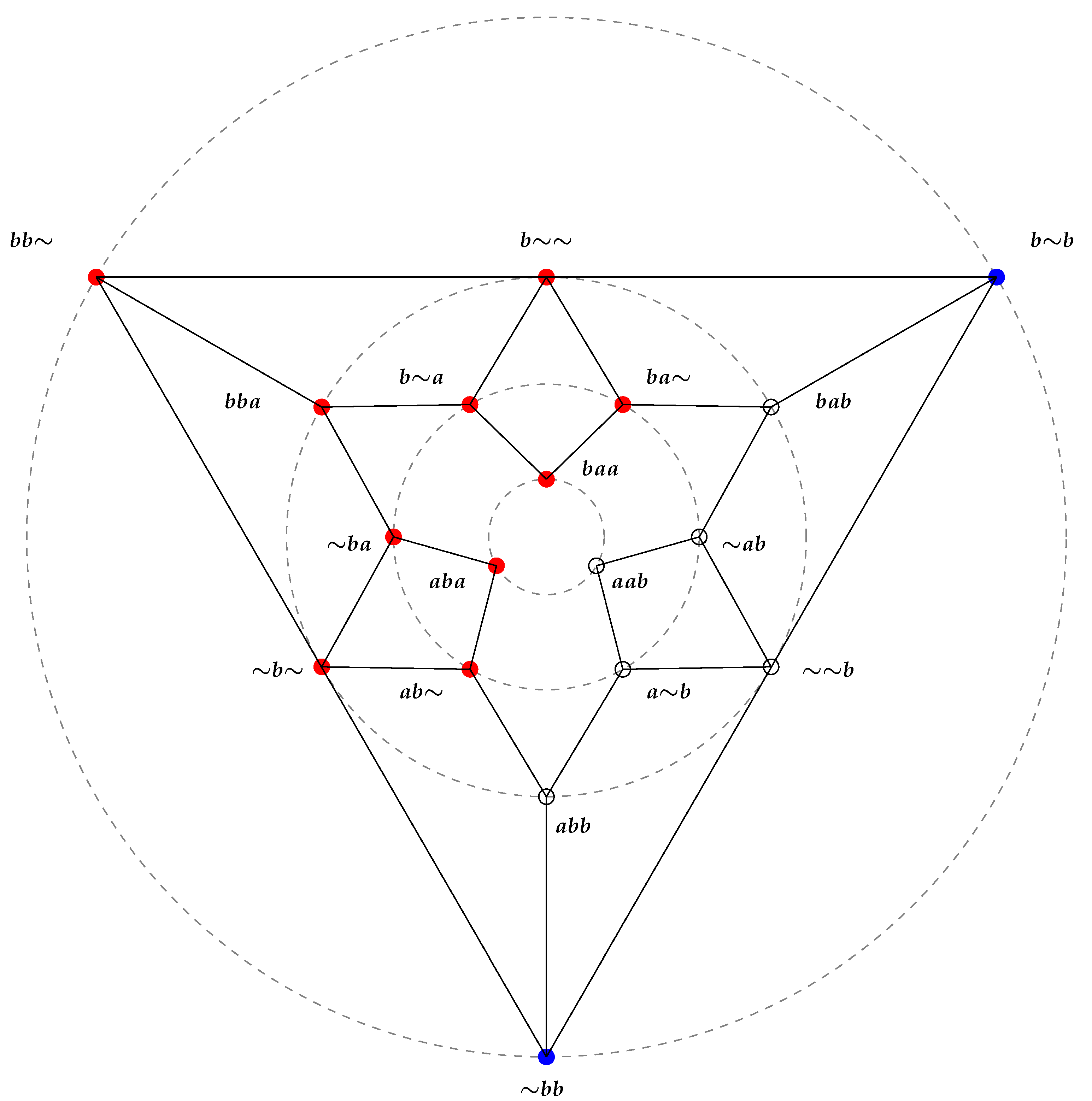
So, after Proposition 2, the study of reduces to that of the strategy-proof functions on the smaller domain . It is a poset under the componentwise ordering adopted in and we can represent it as a directed graph. For , the diagram of the graph is rather complex, so we exemplify the possibility in the case of three agents.
Example. The diagram of for .
For a given profile P, let denote the set of all profiles in covered by P.
The way to obtain the elements of
easily follows from Proposition 1: we have to select one component (which means preference) of the given profile different from
a and replace it by the preference it covers (∼ if it is
b,
a if it is ∼). The resulting profile belongs to
only if it is an element of
, which means only if at least one of its components is
b. We indicate below the sets
for all the elements
P in
:
The edges of as a graph are the pairs of profiles joined when one covers the other. To provide an intuitive view of , we conveniently draw four concentric circles numbered from 1 to 4 according to increasing rays (1 is the smallest, 4 is the biggest), and set the vertices (i.e., the eighteen profiles of ) on the circles according to the following rule:
Profiles in that are not covered by any other profile in are on circle 4;
Profiles in covered by some profile on circle 4 are on circle 3;
Profiles in covered by some profile on circle 3 are on circle 2;
Profiles in covered by some profile on circle 2 are on circle 1.
Consequently, the edges in the following diagrams are directed from outside to inside coherently with the covering relation.
Again, for brevity, we avoid commas among preferences when displaying profiles in the figures.
![Games 13 00078 i005 Games 13 00078 i005]()
Visual examples of SP social choice functions for |V| = 3.
A social choice function associates one of the two alternatives to each of the eighteen vertices of the graph
. We again use colors: we color red the profiles having image
a and we color blue the profiles having image
b. Of course, not all the (
) functions that we obtain coloring the vertices are SP. Since
is a convex subset of
, according to (ii) of Theorem 1, we have to fulfill the condition
This happens if (and only if) the two endpoints of an edge can be differently colored only when red is on the smaller circle. In other words, to recognize whether or not a coloring of the vertices of the graph
is an SP function, it is sufficient (and necessary) to check that all the segments with different colors on the endpoints have the two colors in the “right” order. A few examples follow.
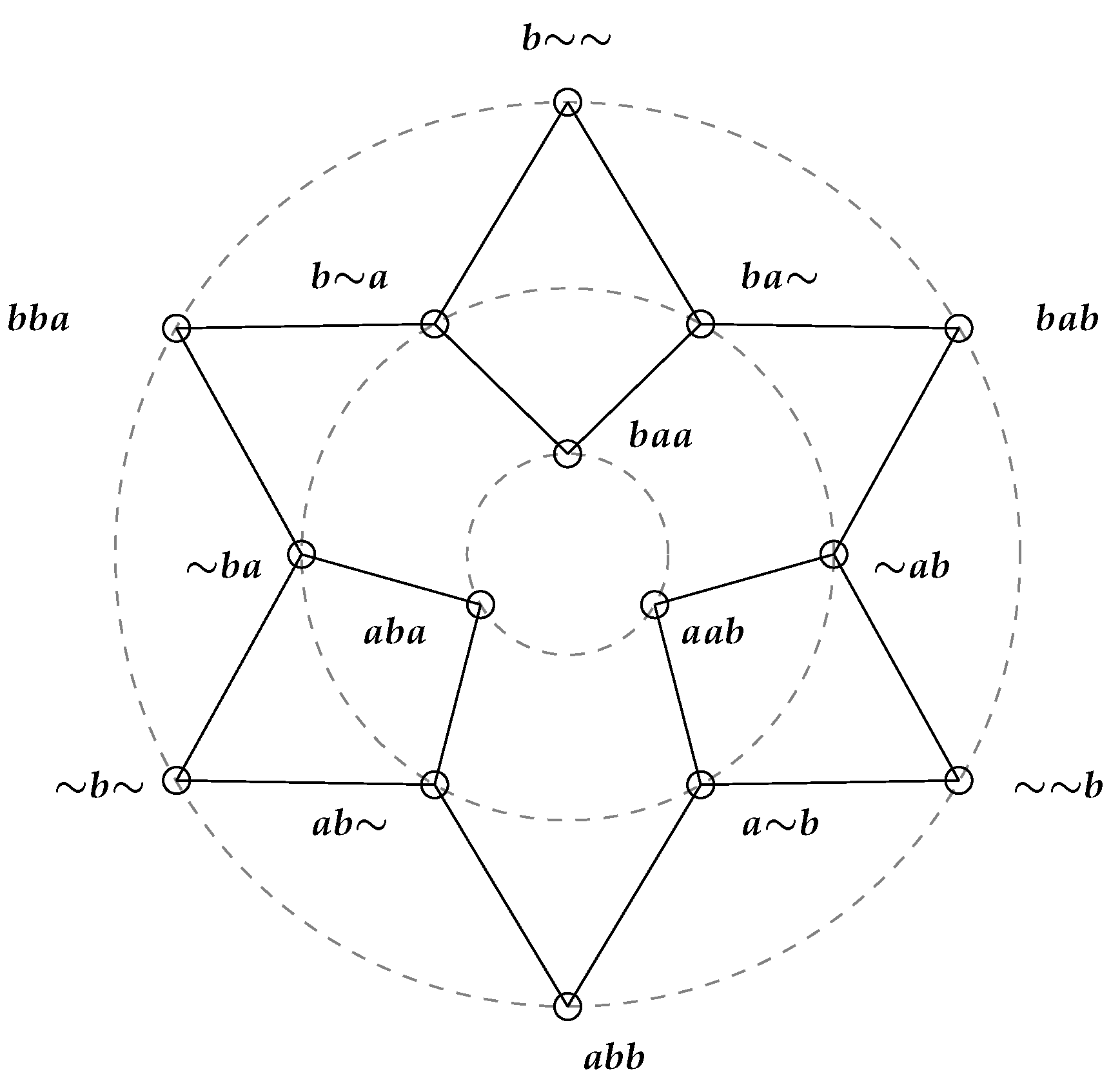
Example 1. Only one SP function having all red vertices on the largest circle (respectively, all blue vertices on the smallest) exists: it is the one with also all the remaining vertices colored red (respectively, blue).
Example 2. If two of the three vertices on the largest circle are red and the third one is blue, necessarily all but one of the remaining vertices will be red. The value on what is left can be assigned either red or blue in any case preserving strategy-proofness. So, this example really deals with six different SP functions. Consider, to fix ideas, the case
, in the next
Figure 1. The value
a has to be assigned to all profiles except
for which the value of
cannot be fixed. We can color it red (
) or blue (
).
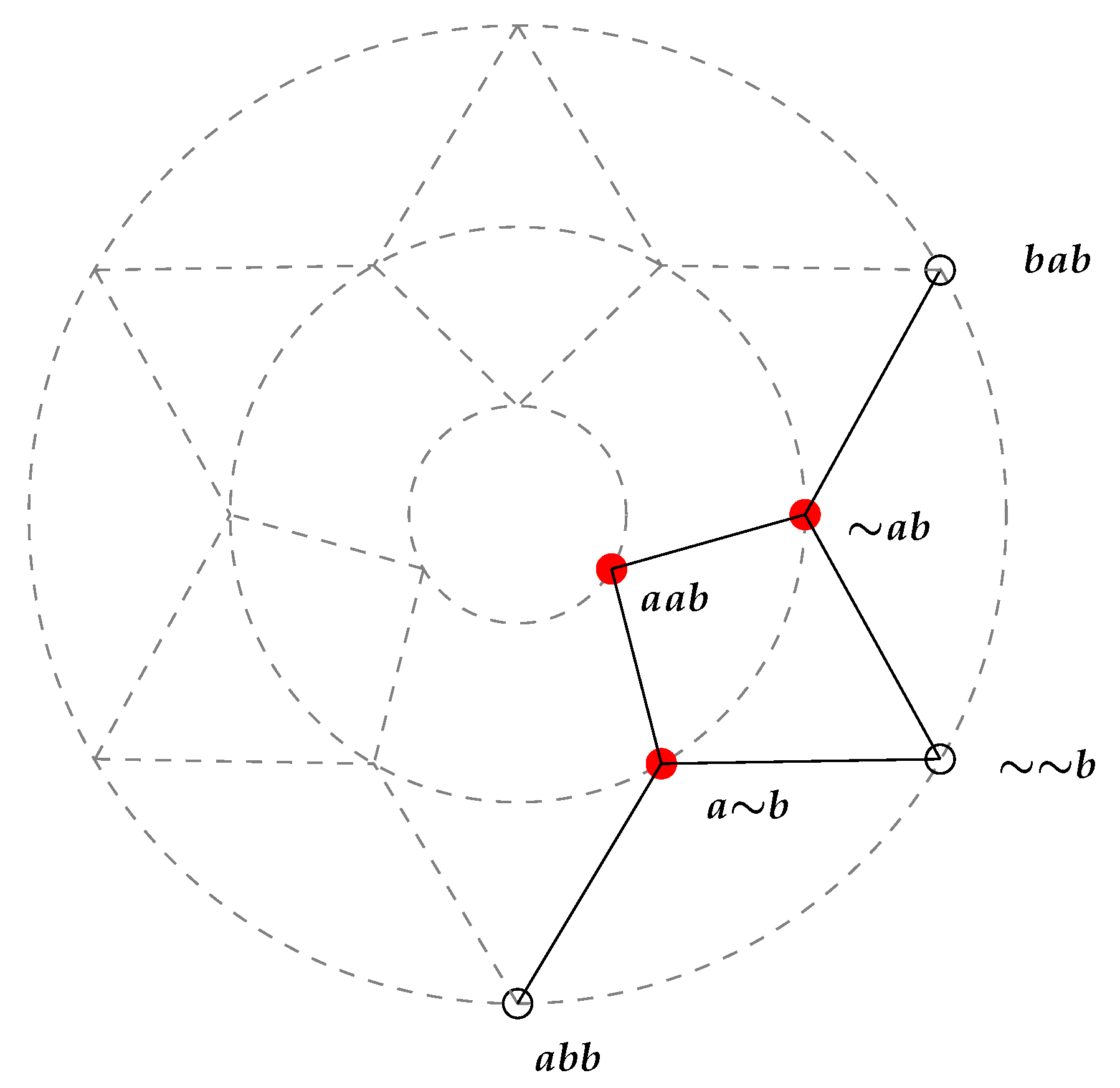
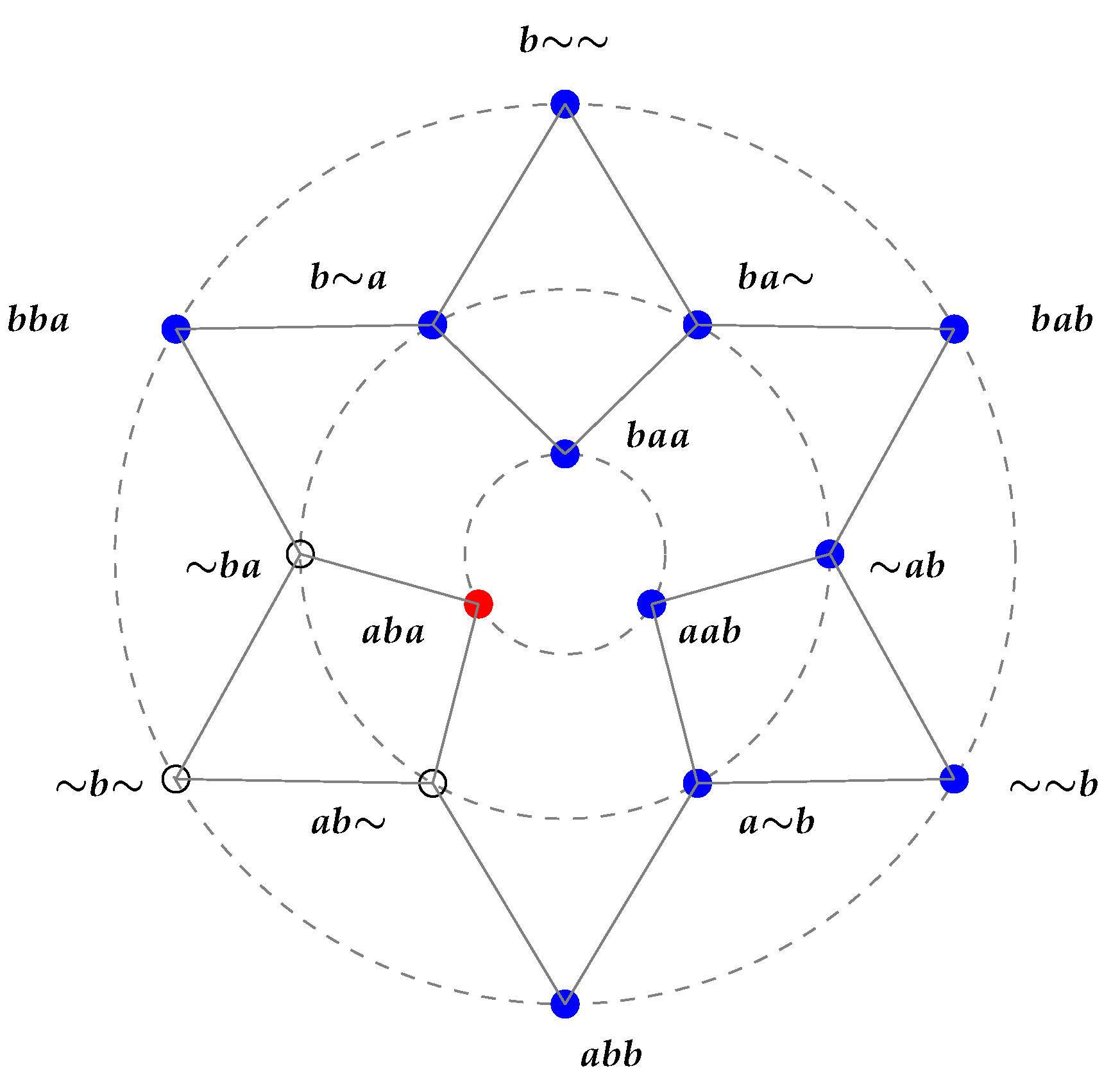
Example 3. If there is exactly one red vertex on circle 4 (in the next
Figure 2 we assume, to fix ideas, that
and
), then six of the remaining profiles remain uncolored, i.e., the value of
is not assigned. However, those blank vertices cannot be colored arbitrarily in order to represent an SP function.
Lemma 1 allows one to obtain all SP functions consistent with the values already assigned in
Figure 2 (in its turn consistent with Assumption 4) by isolating the subgraph
of
Figure 3 and considering all SP functions having
as the domain.
Applying Theorem 1, it can be verified that there are 42 such functions. Some of the possible functions are plotted below (
Figure 4 and
Figure 5), where for the blank vertices (in these cases!), any blue/red color can be assigned.
Example 4. The case of three blue vertices on the largest circle is possible. Again, Lemma 1 can be suitably applied, and one can limit to analyze the SP assignments on the subgraph
in
Figure 6 (i.e., we can avoid plotting the largest circle).
We conclude with a final example.
Example 5. Let us fix the ideas with the case that the value of
is
b on exactly two vertices of the smallest circle (only
). The values of
remain not fixed on three uncolored profiles (see
Figure 7). Differently from the last two cases (of
Figure 4 and
Figure 5), this time, clearly, not all the (
) possibilities are allowed. Only five (obvious) assignments give rise to an SP function (Theorem 1).
5. On the Number of Binary SP Social Choice Functions with Indifference
In our setting, that permits indifference, the number of binary SP social choice functions has been denoted by
. This number can be described in different ways. We present three of them. Note that the first two evoke one of the known characterizations of the Dedekind numbers ([
9], Sequence A000372, accessed on September and November 2021).
Recall that a subset of a partially ordered set is said to be an antichain if it consists of pairwise incomparable distinct elements. Let V be a set with n elements. The number can be defined as the cardinality of the set of all antichains of the partially ordered set (componentwise order). Since the elements of can be easily interpreted as the indicator functions of the subsets of V, we can equivalently refer to as the number of the antichains of the power set of V ordered by set inclusion.
Our first way of describing is the following.
Proposition 3. is the cardinality of the set of all antichains of the partially ordered set or, equivalently, of .
Proof. Let us first observe that the set is obviously order isomorphic to . In addition, note that any -valued function defined on this set can be described by the inverse image of the element b. Theorem 1 says that such a function is SP exactly when is super order-closed. This implies that the number is the number of the super order-closed parts of . At this point, it is sufficient to recall that for finite posets, the super order-closed subsets can be identified with the antichains of the poset. □
A second characterization of the number
is related to the poset of
veto pairs introduced in [
10]. This is the following set
(whose elements are the veto pairs) endowed with the partial order corresponding to the componentwise set inclusion. We have that:
Proposition 4. is the cardinality of the set of all antichains of the partially ordered set .
Proof. It is sufficient to apply ([
10], Theorem 3.3). □
Proposition 4 also gives meaning to , as it happens for . Of course, both numbers have value 2.
Remark 3. The super order-closed subsets of the power set of
V (ordered by inclusion) are referred to as
simple games (respectively,
committees) in the Game (respectively, Social Choice) Theory literature. In other words, ([
1], Theorem 2) characterizes the binary SP social choice functions, in case of strict preferences, as simple games. Since in finite posets, antichains and super order-closed subsets are identifiable, the above-mentioned ([
10], Theorem 3.3) (as it can be verified) extends this simple games characterization to the case of weak preferences, via a parallel extension of the notion of simple games to that of super order-closed subsets of the poset of veto pairs.
One more equivalent characterization of
can derive from [
12] where the authors aim to emphasize the role of the groups of agents having no power to determine the values of a given SP social choice function. This is the motivation to introduce some families of functions, named “powerless revealing”, that are proved to be all and only the SP social choice functions ([
12], Theorem 4). Moreover, they are also proved to be in a one-to-one correspondence with the class of “ineffective” families on the society. For the reader’s convenience, we give the definition:
A map that associates to each subset M of V a part of its power set is said to be an ineffective family on V if
- (i)
, and
- (ii)
.
Proposition 5. is the number of ineffective families on a set V of n elements.
Concerning the values of
, since the sets
are pairwise disjoint, a consequence of the formula
in
Section 3 is that we can express the cardinality of
as follows:
In particular, we have
and
Remark 4. We have to observe that the procedure furnishes the cardinality of on the basis not only of the cardinality of but on the whole set of functions. This suggests that the cardinality of may not suffice to determine even the number of functions belonging to .
As for the sequence of Dedekind numbers, also the sequence
grows quite rapidly and presents similar computational difficulties. We recall that there is an explicit formula for
, due to Kisielewicz [
13]. However, its complexity makes it difficult to be used for any practical purposes. An expression in decimal form for
has not been computed. Analogously, finding the numbers
is not an elementary task.
The next table compares, on the second row, the number of SP binary social choice functions when n (up to eight) voters are not allowed to declare indifference, and on the third row, the number of SP binary social choice functions when declaring indifference is allowed.
| |V| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ded(|V|) | 3 | 6 | 20 | 168 | 7581 | 7828354 | 2414682040998 | 56130437228687557907788 |
| |Φ|V|| | 4 | 20 | 980 | 17792748 | - | - | - | - |
The values
and
have been obtained by means of the Python implementation of the procedure presented in
Section 3. In an informal communication, Giovanni Cutolo (Università Federico II di Napoli) informed us that they can be also obtained by elaborating on the results presented in [
14] (in particular Corollary 3.2 and Theorem 3.3). We are grateful to him for having pointed out this to us. Because of the computational complexity, we have not computed the decimal form expression of the numbers
for
.
Two concluding comments are now in order. First, the Gibbard–Satterthwaite theorem is often seen by social choice theorists as a “negative” result in the sense that the small number of SP social choice functions with range of cardinality at least three makes non-dictatorship incompatible with strategy-proofness. So, one possible hint from the Barberà [
8] general suggestion that introducing indifference may help in obtaining “positive” results is that proposing to voters the option of indifference increases the number of social choice functions with desirable properties. We notice that the possible comparisons between the numbers
and
give an idea of up to what magnitude one can confirm this. With as few as three or four voters, the binary SP social choice functions with indifference are, respectively, 49 or
times those without indifference. There exists a more precise result in this direction if one limits to considering SP functions which are also invariant under permutations of voters: in [
10], it is shown that stepping from strict to weak preferences, the number of anonymous, strategy-proof, binary social choice functions depend exponentially on the number of voters, rather than linearly.
A second comment concerns the distinction between our paper and Campbell et al. [
15]. While the latter is focused on discrediting the belief that the SP functions are few, we have focused on binary social choice functions with indifference, for which we provided formula
to compute
. We in fact computed
and
here.
 Repeating the procedure for the remaining rows, we obtain:
Repeating the procedure for the remaining rows, we obtain: 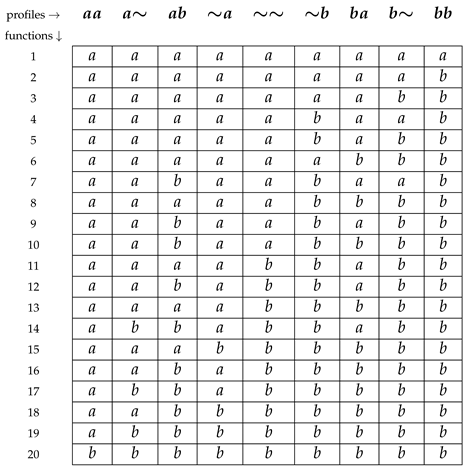
 from which we have:
from which we have: