Abstract
The strategy method is often used in public goods games to measure an individual’s willingness to cooperate depending on the level of cooperation by their groupmates (conditional cooperation). However, while the strategy method is informative, it risks conflating confusion with a desire for fair outcomes, and its presentation may risk inducing elevated levels of conditional cooperation. This problem was highlighted by two previous studies which found that the strategy method could also detect equivalent levels of cooperation even among those grouped with computerized groupmates, indicative of confusion or irrational responses. However, these studies did not use large samples (n = 40 or 72) and only made participants complete the strategy method one time, with computerized groupmates, preventing within-participant comparisons. Here, in contrast, 845 participants completed the strategy method two times, once with human and once with computerized groupmates. Our research aims were twofold: (1) to check the robustness of previous results with a large sample under various presentation conditions; and (2) to use a within-participant design to categorize participants according to how they behaved across the two scenarios. Ideally, a clean and reliable measure of conditional cooperation would find participants conditionally cooperating with humans and not cooperating with computers. Worryingly, only 7% of participants met this criterion. Overall, 83% of participants cooperated with the computers, and the mean contributions towards computers were 89% as large as those towards humans. These results, robust to the various presentation and order effects, pose serious concerns for the measurement of social preferences and question the idea that human cooperation is motivated by a concern for equal outcomes.
1. Introduction
Understanding what motivates human social behaviours is crucial for efforts to tackle many pressing global problems, such as limiting anthropogenic climate change, mitigating pandemics and managing limited resources [1,2,3,4,5]. While evolutionary biology primarily asks how costly social behaviours could evolve, the social sciences often ask which factors govern and motivate social behaviours [6,7,8,9,10,11]. More recently, economic experiments have offered a valuable method for measuring how individuals behave under controlled conditions in response to real, financial, incentives [12,13,14,15,16].
For example, the strategy method of Fischbacher et al. [17] is routinely used in studies of cooperation, social norms and social preferences [18,19]. The method was designed to control for participants’ beliefs about their groupmates’ likely levels of cooperation, which was hypothesized to be a motivating factor in human cooperation. The method forces individuals to specify, in advance, how much they will have to contribute to a public good depending upon how much their groupmates contribute. Widely replicated results across several continents show that many individuals, circa 60%, behave as if motivated by a concern for fairness (or following a ‘fairness norm’ [15,20]), and positively condition their contributions upon the average level of their groupmates’ contributions (conditional cooperation) [19,21,22]. Comparisons with behaviour in the usual ‘direct’ or ‘voluntary’ method have shown that behaviour in the strategy method often correlates reassuringly with behaviour in the direct form [23,24,25], although see [20]. Therefore, these results have been interpreted as evidence that many individuals willingly sacrifice to benefit the group and to equalize outcomes (inequity aversion [26]), even in one-off encounters with strangers. This interpretation forms a keystone in the idea that human cooperation is biologically unique [14,15,27,28,29].
However, while the strategy method cleverly controls for participants’ beliefs about their groupmates [18] and helps to identify the prevalence of various social norms [20], it does not control for other factors such as confusion. Furthermore, the design’s appearance and language prompts participants to condition their contributions, which may unduly influence confused or uncertain participants, or detect knowledge of social norms as opposed to adherence to social norms [20,30]. Consequently, the strategy method risks conflating confusion and/or compliance with suggestive instructions (a form of experimenter demand, [31]) and social preferences. This is a potential problem because the prosocial interpretation requires that participants fully understand the consequences of their decisions and that their costly decisions are motivated by the social consequences (or at least have evolved to serve these social consequences [14,32,33,34,35]). The prosocial interpretation therefore implicitly assumes that such behaviours will not occur if there are no social consequences [36,37].
This potential problem of confounding confusion and social preferences was tested and confirmed in subsequent studies that used games with computerized groupmates as a control treatment [38,39]. Contributions towards computers cannot rationally be motivated by prosocial concerns, such as inequity-aversion, or even by a desire to feel good (‘warm glow’, ‘positive self-image’, or ‘altruism’) [26,40]. Therefore, designs with computerized groupmates maintain the suggestive instructions and the risk of measuring confusion while eliminating social concerns (‘asocial control’) [38,39,41,42,43]. Consequently, if individuals conditionally cooperate with computers that cannot possibly benefit, their behaviour cannot be explained or rationalized as a social preference. This is because such behaviour would violate the conjoint assumptions of the axiom of revealed preferences, specifically, that participants perfectly understand the game and maximize their income in line with their social preferences, i.e., are rational [37]. However, if individuals have erroneous beliefs about the payoff structure of the game, they may think it sensible to condition their contributions upon their computerized groupmates, especially when primed to do so by the experiment [38,39].
These two studies found that the frequencies of ‘social types’, meaning conditional cooperators, non-cooperators, and others, were statistically equivalent in games with computerized groupmates as in prior studies with human groupmates [38,39]. As there can be no rational social preferences towards computers, these results suggest that conditional cooperation is driven by confusion among self-interested participants rather than concerns for fairness. However, these two studies relied on not-large sample sizes of 40 and 72, and were forced to compare their frequencies with prior published studies using different samples rather than within their own participants; this meant they could not test how individuals shifted their strategy-method behaviour in response to either human or computerized groupmates [38,39].
Here we addressed these potential limitations by replicating and expanding upon prior strategy method experiments with computers [38,39]. The participants completed the strategy method two times: once with human groupmates and once with computerized groupmates. We replicated the instructions and comprehension questions of Fischbacher and Gachter [18], with necessary changes for the games with computerized groupmates (a full copy of the instructions are in the Supplementary Methods Section). The participants were told that each of the three computerized groupmates would make a random contribution from 0 to 20 monetary units (MU) and that only their earnings would be affected. The two games were both one-shot encounters and equally incentivized (participants were paid for both). By making participants complete two strategy methods, we made the distinction between human and computerized groupmates more salient than in previous studies that made participants only complete the strategy method one time [38,39]. This could potentially lead to a greater difference in responses between the two setups, for example there may be a greater prosocial shift when playing with humans if behaviour is driven by instinctive prosocial responses to humans [44,45]. As the strategy method controls for beliefs about the likely decisions of groupmates, any differences cannot be attributed to any rational beliefs about groupmates.
We also tested how the role of default contributions could affect the prevalence of conditional cooperation depending on groupmates [46,47]. In most cases, we presented participants with ‘empty’ boxes to input their contributions, as is typically done, but we also presented some participants with either all 0 MU, or all 20 MU (100%) contributions. As there was no financial cost to change the ‘default’ entries, participants should still express their social preferences in the same way, unless they are affected by the suggestive presentation. Although, we note that participants could also save on effort costs by declining to modify the defaults, meaning that if they modified the zero percent defaults, they paid both a financial cost and an effort cost to help their groupmates.
Our advance is three-fold: (1) we allow for within-participant comparisons by making all participants play the strategy method twice, once with human and once with computerized groupmates (note references [39,43] also had within-participant comparisons, but not for the strategy method); (2) we test the robustness of our results by varying a range of presentation factors, such as treatment order (either sequential or simultaneous), and the use of default contributions (either 0% or 100%) [46,47]; and (3) our sample size of 845 participants drastically expands upon those of the previous studies that found high frequencies of conditional cooperators with computers in samples of 40 and 72 [38,39].
2. Results
2.1. Conditional Cooperation with Computers
Overall, behaviours towards computerized groupmates were strikingly similar to those when the participants were grouped with humans (Figure 1). The mean contributions towards computers were 89% as large as those towards humans. Specifically, the mean average contribution across all scenarios in the strategy method towards humans was 34% (6.8 MU, ±95% bootstrapped confidence intervals [6.71, 6.90]) and towards computers was 30% (6.0 MU, ±95% bootstrapped confidence intervals [5.95, 6.14]) (paired Wilcoxon signed-rank test: V = 110110, p < 0.001, Figure 2). The mean Pearson correlation between the participants’ responses and their groupmates’ mean contribution was 0.68 when playing with humans and 0.60 when playing with computers (paired Wilcoxon signed-rank test: V = 106216, p < 0.001, Figure 1). Among those who cooperated with humans (n = 761), 24% responded identically for all 21 scenarios (0–20 MU) in the strategy method with the computers (n = 184/761).
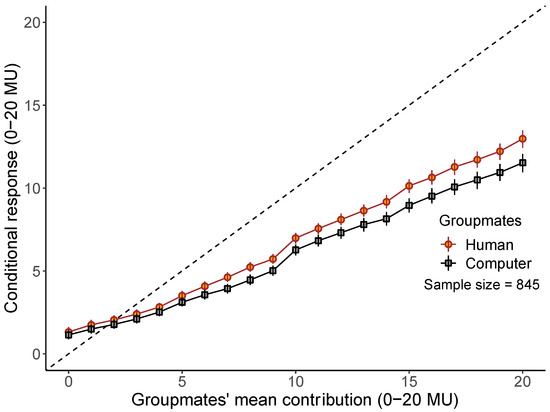
Figure 1.
Conditional cooperation with computers. Mean conditional contributions and 95% bootstrapped confidence interval for each average contribution level of either human (orange circles) or computerized (grey squares) groupmates (dashed diagonal = perfect matching).
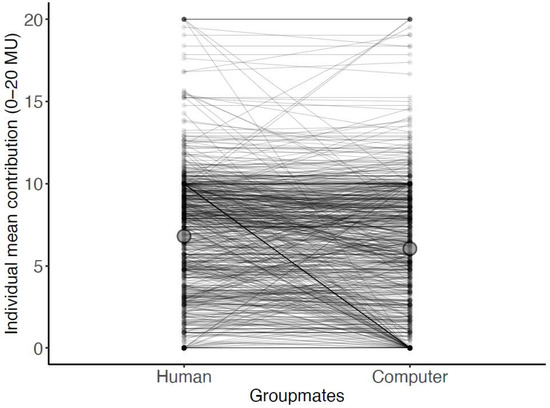
Figure 2.
Individual behaviour. Every individual’s mean contribution with either humans or computers (n = 845). Lines connect individual responses. Larger transparent circle shows the overall mean for each case.
The distribution of behavioural types was largely similar when playing with either humans or computers (Table 1, χ2= 42.6, df = 2, p < 0.0001). We classified free riders and conditional cooperators according to the definitions of Thoni and Volk [19], and we classified the remaining responses as ‘other’. While 76% of the participants expressed conditional cooperation with the human groupmates (n = 638/845), consistent with concerns for fairness (inequity-aversion), 69% also expressed conditional cooperation with computerized groupmates (n = 580/845), consistent with confusion or irrationality (Table 1). For comparison, a recent review found the mean frequency of conditional cooperators to be 62% [19]. The percentages of all participants that were ‘perfect’ conditional cooperators, who always exactly matched the group mean contribution, were 10% with the humans (n = 87/845) and 8% with the computers (n = 71/845). The frequency of free riding (contributing zero in all cases) was 10% with humans (n = 84/845) and 17% with computers (n = 140/845). This means that 83% of the participants (n = 705/845) contributed something towards the computers and failed to maximize their income even when there were no social concerns.

Table 1.
Summary statistics.
2.2. Treatment Order and Framing
Regardless of whether participants were first grouped with humans or computers, or faced both scenarios simultaneously, most participants still conditionally cooperated with the computers (62–73%, Table 1; Supplementary Figure S1). Even when presented with default entries of 0 MU, only 30% remained free riders (n = 19/64), meaning 70% of the participants still made the effort to change the defaults and paid to cooperate with the computers in some way, with 58% doing so conditionally (n = 37/64). Strikingly, of the 64 participants provided with default contributions of 100%, only one became a free rider with the computers, and none did with the humans, while 81% were conditional cooperators with the computers (84% with the humans) (Table 1; Supplementary Figure S2). While defaults clearly can affect behaviour, either through affecting beliefs about the game’s payoffs, or through the effort cost to override them outweighing the financial costs of not changing, they do not prevent the majority of participants conditionally cooperating with the computers.
2.3. Homo Irrationalis
An advantage of our within-subject design was that we could classify individuals according to how they behaved overall with both humans and computers. Homo economicus would maximize their income by contributing only zero towards both human and computerized groupmates. Rational conditional cooperators, motivated by a concern for fairness, should cooperate conditionally with the humans but free ride with the computers (‘true conditional cooperation’). In contrast, if conditional cooperation is driven by confusion or the suggestive instructions, then the confused or irrational individuals will cooperate conditionally with both the humans and computers (‘Homo irrationalis’) [48].
Our results challenge the notion that humans are mostly conditional cooperators motivated by concerns for fairness (Table 2). Instead, we found that 65% of participants classified as Homo irrationalis (n = 550/845), 9% as Homo economicus (n = 73/845), and only 7% as true conditional cooperators (n = 61/845).

Table 2.
Homo irrationalis. Behavioral types according to classification when grouped with Humans and when grouped with Computers.
3. Discussion
Our large-scale replication with 845 participants confirmed that conditional cooperation with computers is common in the strategy method version of public goods games, meaning this finding can no longer be attributed to the sampling error in smaller studies [38,39]. The question now for the field of social preferences is not, do people conditionally cooperate with computers in public goods games, but why [43]? Participants’ confusion about the public goods games’ payoffs would seem a likely explanation, at least in part. It has been shown previously that many participants mis-identify the linear public goods game as an interdependent game, i.e., a stag-hunt game or threshold public goods game, which it is not [38,39,49]. This means participants erroneously think the best response, or optimal strategy to maximize income, is to take into account the contributions of their groupmates, i.e., to conditionally cooperate [39]. This can explain why participants still contribute, conditionally, with computers, and why contributions decline in repeated games that allow for payoff-based learning [50,51,52,53]. Notably, estimates of confusion and estimates for the frequency of conditional cooperators are often similar, at circa 50% [38,39,41,42,50,54,55].
Confusion may also help explain why contributions have been found to differ under identical payoff structures depending on how the public good game is presented/described or ‘framed’ [30,56,57,58,59,60]. If participants are confused or unsure, then different frames could lead to different beliefs about the game’s payoffs. If behaviour is driven by a misunderstanding of the game, then we cannot be sure what game participants think they are responding to, especially as confusion may also interact with differences in personality [43,61]. Future work could aim to identify confusing elements in the instructions by systematically testing variations in how the decision situation is described [62].
Alternatively, it may be that human nature is so hard-wired to cooperate by natural selection and/or life experience (‘internalised’ social norms [35,63,64]) that we still cooperate in unnatural situations in which there is no benefit, such as with computers. For example, one study found that participants who agreed more with the statement that they acted with computers “as if they were playing with humans” cooperated more with computers [43]. While this is consistent with an altruistic instinct overspilling into games with computers, it is also consistent with confused conditional cooperators basing their decisions on their groupmates (be they humans or computers). It is also worth pointing out that our participants were not playing with life-like robots or images that could stimulate psychological responses, or even communicating with computers. They were simply reading dry technical instructions, as they were when dealing with humans. Regardless of how the participants viewed computers, if this hypothesis of ‘hard-wired’ cooperation is true, then it means we still cannot rely upon economic experiments with humans to accurately capture social preferences. This is because such cooperative instincts, or ‘internalised social norms’, could also misfire in unnatural laboratory experiments, such as those creating one-shot encounters with strangers. If behaviour is driven by instinctive or automatic learnt responses, then we cannot be sure what is driving laboratory behaviour, especially in the short term.
Likewise, it could be argued that participants did not believe that they were playing with computers, and believed they were playing with, and thus helping, real people, despite the ‘no deception’ policy of the laboratory (which they were informed of). However, this argument too goes both ways, and could just as easily be applied, perhaps more justifiably so, to situations in which people are told they are playing with humans while instead they may believe they are secretly playing with computers. If behaviours are driven by a mistrust of the laboratory’s instructions, then we cannot be sure what is driving laboratory behaviour.
In summary, we are not denying the strategy method is a useful tool, nor are we ruling out social preferences, and nor are we claiming confusion explains all behaviour in public goods games (nor even behaviour in other economic games). We are saying, however, that any interpretation of the data needs to be consistent with the totality of the evidence across all relevant experiments [65]. One cannot selectively choose when to interpret behaviour as a rational response to a specific situation, i.e., in games with humans, and when to assume it is just a misfiring heuristic, i.e., in games with computers. Great claims have been made about the nature and evolution of human cooperation, largely on the basis of costly decisions taken in one-shot economic games, such as the strategy method [14,15,35,63,66]. However, what if the experiments with computers had been done first? Based on the data in this study, would the results with humans really be so surprising, when contributions towards computers are 89% as large as those with humans and only 7% of the participants conditionally cooperate with humans but do not cooperate with the computers?
In conclusion, our results: (1) show the importance and benefit of control treatments when measuring social behaviours; and (2) caution against characterizing participants’ behaviours purely on the basis of how their costly laboratory decisions affect others [13]. We found that most participants behaved as if either confused or irrational, by cooperating with computers, which is not consistent with any utility function, violating the axiom of revealed preferences [36]. Our results suggest that previous studies may have over-estimated levels of conditional cooperation motivated by concerns for fairness and suggest that public goods experiments often measure levels of confusion and learning rather than accurately document social preferences [38,39,41,42,43,49,50,51,52,53,54,55,67].
4. Materials and Methods
We ran three studies at the University of Lausanne (UNIL), Switzerland, HEC-LABEX facility, which forbids deception. In total, we used 845 participants, and according to the self-reports, we had an approximately equal gender ratio (Female = 430; Male = 403; Other = 2; Declined to respond = 10) and most were aged under 26 years (Less than 20 = 263; 20–25 = 527; 26–30 = 43; 30–35 = 6; Over 35 = 4; Declined to respond = 2). All subjects gave their informed written consent for inclusion before they participated in the study. The studies were conducted in accordance with the Declaration of Helsinki, and the protocols were approved by the Ethics Committee of HEC-LABEX.
We replicated the instructions and comprehension questions of Fischbacher and Gachter [18] (Supplementary Methods). The public goods game always involved groups of four, with a marginal per capita return of 0.4 and an endowment of 20 monetary units (MU) (1 MU = 0.04 or 0.05 CHF). Each computerized groupmate contributed randomly from a uniform distribution (0–20 MU). Participants were told, “The decisions of the computer will be taken in a random and independent way (each virtual player will therefore make its own decision at random).” The income-maximizing contribution was to contribute 0 MU regardless of what one’s groupmates contributed. For the game with computers, participants had to click a button to proceed from the instructions with the words, “I understand that I am in a group with the computer only.”
4.1. Study 1
Study 1 involved 420 participants across 20 sessions of 20–24 participants each, but a presentation error means we exclude all 64 participants from the first three sessions (n = 356 valid). We presented the two strategy methods sequentially, with either humans or computers first. Participants did not know that there would be a second task, and they received limited feedback from the first task to prevent learning.
In each case, we randomized whether participants saw the contributions increasing/decreasing vertically from 0 to 20 MU. The presentation error in the first three sessions was that we failed to show the decreasing contributions correctly.
4.2. Study 2
Study 2 involved 240 participants across 20 sessions of 12 participants each. Three participants were excluded because they had to be discretely replaced by an experimenter. Our design presented the two versions of the strategy method simultaneously and we controlled for potential positional/order effects by randomizing whether humans or computers were on the left side of the screen.
4.3. Study 3
Study 3 involved 252 participants across 16 sessions of 12–16 participants with no exclusions. The design replicated study 2, except that we showed some participants default contributions of either 0 MU (n = 64) or 20 MU (n = 64). Participants could freely overwrite the defaults if they were willing to make the effort [46,47].
4.4. Analyses
We classified free riders and conditional cooperators according to the definitions of Thoni and Volk [19], and we classified all other responses as ‘other’. Free riders always contributed 0 MU. Conditional cooperators had a positive Pearson correlation greater than 0.5 between their responses and the contributions of their groupmates, plus a contribution when their groupmates contributed fully that was higher than their mean conditional response.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/g13060069/s1, Figure S1: Order effects; Figure S2: Default effects; Supplementary Methods: Instructions.
Author Contributions
Conceptualization, M.N.B.-C.; Data curation, M.N.B.-C.; Formal analysis, M.N.B.-C.; Funding acquisition, M.N.B.-C.; Investigation, M.N.B.-C., V.D. and C.G.; Methodology, M.N.B.-C.; Project administration, M.N.B.-C., V.D. and C.G.; Software, M.N.B.-C.; Supervision, M.N.B.-C.; Validation, M.N.B.-C.; Visualization, M.N.B.-C., V.D. and C.G.; Writing—original draft, M.N.B.-C.; Writing—review & editing, M.N.B.-C., V.D. and C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of HEC-Lausanne (protocol code PIN approved on 1 October 2019 (Study 1); protocol code CURL approved on 1 October 2019 (Study 2); protocol code CURL 2 approved on 23 September 2020 (Study 3).
Informed Consent Statement
Informed written consent was obtained from all subjects involved in the study prior to data collection.
Data Availability Statement
Data and analysis script freely available from the Open Science Framework: osf.io/jhqk2.
Acknowledgments
HEC Research Fund (partial funding) and Laurent Lehmann, University of Lausanne (partial funding).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rustagi, D.; Engel, S.; Kosfeld, M. Conditional Cooperation and Costly Monitoring Explain Success in Forest Commons Management. Science 2010, 330, 961–965. [Google Scholar] [CrossRef] [PubMed]
- Milinski, M.; Sommerfeld, R.D.; Krambeck, H.-J.; Reed, F.A.; Marotzke, J. The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 2291–2294. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; May, R.M.; West, S.A. Combined inequality in wealth and risk leads to disaster in the climate change game. Clim. Change 2013, 120, 815–830. [Google Scholar] [CrossRef]
- Bavel, J.J.V.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Crockett, M.J.; Crum, A.J.; Douglas, K.M.; Druckman, J.N.; et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 2020, 4, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Ijzerman, H.; Lewis, N.A.; Przybylski, A.K.; Weinstein, N.; DeBruine, L.; Ritchie, S.J.; Vazire, S.; Forscher, P.; Morey, R.D.; Ivory, J.D.; et al. Use caution when applying behavioural science to policy. Nat. Hum. Behav. 2020, 4, 1092–1094. [Google Scholar] [CrossRef] [PubMed]
- Olson, M. The logic of collective action: Public goods and the theory of groups. In Harvard Series in Economic Studies; Harvard Univ. Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Ostrom, E.; Burger, J.; Field, C.B.; Norgaard, R.B.; Policansky, D. Revisiting the Commons: Local Lessons, Global Challenges. Science 1999, 284, 278–282. [Google Scholar] [CrossRef]
- Camerer, C.F.; Fehr, E. When Does “Economic Man” Dominate Social Behavior? Science 2006, 311, 47–52. [Google Scholar] [CrossRef]
- Kurzban, R.; Burton-Chellew, M.N.; West, S.A. The Evolution of Altruism in Humans. Annu. Rev. Psychol. 2015, 66, 575–599. [Google Scholar] [CrossRef]
- Simpson, B.; Willer, R. Beyond Altruism: Sociological Foundations of Cooperation and Prosocial Behavior. Annu. Rev. Sociol. 2015, 41, 43–63. [Google Scholar] [CrossRef]
- Vincent, B.; Rense, C.; Chris, S. (Eds.) Advances in the Sociology of Trust and Cooperation: Theory, Experiments, and Field Studie; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020. [Google Scholar]
- Camerer, C. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton, N.J., Ed.; Princeton University Press. xv: Woodstock, GA, USA, 2003; 550p. [Google Scholar]
- Weber, R.A.; Camerer, C.F. “Behavioral experiments” in economics. Exp. Econ. 2006, 9, 187–192. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U. The nature of human altruism. Nature 2003, 425, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Schurtenberger, I. Normative foundations of human cooperation. Nat. Hum. Behav. 2018, 2, 458–468. [Google Scholar] [CrossRef] [PubMed]
- Thielmann, I.; Böhm, R.; Ott, M.; Hilbig, B.E. Economic Games: An Introduction and Guide for Research. Collabra Psychol. 2021, 7, 19004. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gachter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gachter, S. Social Preferences, Beliefs, and the Dynamics of Free Riding in Public Goods Experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Thoni, C.; Volk, S. Conditional cooperation: Review and refinement. Econ. Lett. 2018, 171, 37–40. [Google Scholar] [CrossRef]
- Rauhut, H.; Winter, F. A sociological perspective on measuring social norms by means of strategy method experiments. Soc. Sci. Res. 2010, 39, 1181–1194. [Google Scholar] [CrossRef]
- Herrmann, B.; Thoni, C. Measuring conditional cooperation: A replication study in Russia. Exp. Econ. 2009, 12, 87–92. [Google Scholar] [CrossRef]
- Kocher, M.; Cherry, T.; Kroll, S.; Netzer, R.J.; Sutter, M. Conditional cooperation on three continents. Econ. Lett. 2008, 101, 175–178. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Quercia, S. The behavioral validity of the strategy method in public good experiments. J. Econ. Psychol. 2012, 33, 897–913. [Google Scholar] [CrossRef]
- Minozzi, W.; Woon, J. Direct response and the strategy method in an experimental cheap talk game. J. Behav. Exp. Econ. 2020, 85, 101498. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental comparisons. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Camerer, C.F. Experimental, cultural, and neural evidence of deliberate prosociality. Trends Cogn. Sci. 2013, 17, 106–108. [Google Scholar] [CrossRef]
- West, S.A.; el Mouden, C.; Gardner, A. Sixteen common misconceptions about the evolution of cooperation in humans. Evol. Hum. Behav. 2011, 32, 231–296. [Google Scholar] [CrossRef]
- West, S.A.; Cooper, G.A.; Ghoul, M.B.; Griffin, A.S. Ten recent insights for our understanding of cooperation. Nat. Ecol. Evol. 2021, 5, 419–430. [Google Scholar] [CrossRef]
- Columbus, S.; Böhm, R. Norm shifts under the strategy method. Judgm. Decis. Mak. 2021, 16, 1267–1289. [Google Scholar]
- Zizzo, D.J. Experimenter demand effects in economic experiments. Exp. Econ. 2010, 13, 75–98. [Google Scholar] [CrossRef]
- Fehr, E.; Gachter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U.; Gachter, S. Strong reciprocity, human cooperation, and the enforcement of social norms. Hum. Nat. Interdiscip. Biosoc. Perspect. 2002, 13, 1–25. [Google Scholar] [CrossRef]
- Henrich, J. Cultural group selection, coevolutionary processes and large-scale cooperation. J. Econ. Behav. Organ. 2004, 53, 3–35. [Google Scholar] [CrossRef]
- Henrich, J.; Muthukrishna, M. The Origins and Psychology of Human Cooperation. Annu. Rev. Psychol. 2021, 72, 207–240. [Google Scholar] [CrossRef] [PubMed]
- Andreoni, J.; Miller, J. Giving according to garp: An experimental test of the consistency of preferences for altruism. Econometrica 2002, 70, 737–753. [Google Scholar] [CrossRef]
- Sobel, J. Interdependent preferences and reciprocity. J. Econ. Lit. 2005, 43, 392–436. [Google Scholar] [CrossRef]
- Ferraro, P.J.; Vossler, C.A. The Source and Significance of Confusion in Public Goods Experiments. B.E. J. Econ. Anal. Policy 2010, 10. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; El Mouden, C.; West, S.A. Conditional cooperation and confusion in public-goods experiments. Proc. Natl. Acad. Sci. USA 2016, 113, 1291–1296. [Google Scholar] [CrossRef]
- Andreoni, J. Warm-Glow Versus Cold-Prickle-the Effects of Positive and Negative Framing on Cooperation in Experiments. Q. J. Econ. 1995, 110, 1–21. [Google Scholar] [CrossRef]
- Houser, D.; Kurzban, R. Revisiting kindness and confusion in public goods experiments. Am. Econ. Rev. 2002, 92, 1062–1069. [Google Scholar] [CrossRef]
- Shapiro, D.A. The role of utility interdependence in public good experiments. Int. J. Game Theory 2009, 38, 81–106. [Google Scholar] [CrossRef]
- Nielsen, Y.A.; Thielmann, I.; Zettler, I.; Pfattheicher, S. Sharing Money With Humans Versus Computers: On the Role of Honesty-Humility and (Non-)Social Preferences. Soc. Psychol. Personal. Sci. 2021, 13, 1058–1068. [Google Scholar] [CrossRef]
- Rand, D.; Peysakhovich, A.; Kraft-Todd, G.T.; Newman, G.E.; Wurzbacher, O.; Nowak, M.A.; Greene, J.D. Social heuristics shape intuitive cooperation. Nat. Commun. 2014, 5, 3677. [Google Scholar] [CrossRef] [PubMed]
- Peysakhovich, A.; Nowak, M.A.; Rand, D.G. Humans display a ‘cooperative phenotype’ that is domain general and temporally stable. Nat. Commun. 2014, 5, 4939. [Google Scholar] [CrossRef] [PubMed]
- Cappelletti, D.; Mittone, L.; Ploner, M. Are default contributions sticky? An experimental analysis of defaults in public goods provision. J. Econ. Behav. Organ. 2014, 108, 331–342. [Google Scholar] [CrossRef]
- Fosgaard, T.R.; Piovesan, M. Nudge for (the Public) Good: How Defaults Can Affect Cooperation. PLoS ONE 2016, 10, e0145488. [Google Scholar] [CrossRef] [PubMed]
- Stoll, C.; Mehling, M.A. Climate change and carbon pricing: Overcoming three dimensions of failure. Energy Res. Soc. Sci. 2021, 77, 102062. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; Guérin, C. Self-interested learning is more important than fair-minded conditional cooperation in public-goods games. Evol. Hum. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; West, S.A. Prosocial preferences do not explain human cooperation in public-goods games. Proc. Natl. Acad. Sci. USA 2013, 110, 216–221. [Google Scholar] [CrossRef] [PubMed]
- Burton-Chellew, M.N.; Nax, H.H.; West, S.A. Payoff-based learning explains the decline in cooperation in public goods games. Proc. R. Soc. B-Biol. Sci. 2015, 282, 20142678. [Google Scholar] [CrossRef]
- Nax, H.H.; Burton-Chellew, M.N.; West, S.A.; Young, H.P. Learning in a black box. J. Econ. Behav. Organ. 2016, 127, 1–15. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; West, S.A. Payoff-based learning best explains the rate of decline in cooperation across 237 public-goods games. Nat. Hum. Behav. 2021, 5, 1330–1338. [Google Scholar] [CrossRef]
- Andreoni, J. Cooperation in public-goods experiments-kindness or confusion. Am. Econ. Rev. 1995, 85, 891–904. [Google Scholar]
- Kümmerli, R.; Burton-Chellew, M.N.; Ross-Gillespie, A.; West, S.A. Resistance to extreme strategies, rather than prosocial preferences, can explain human cooperation in public goods games. Proc. Natl. Acad. Sci. USA 2010, 107, 10125–10130. [Google Scholar] [CrossRef] [PubMed]
- Dufwenberg, M.; Gächter, S.; Hennig-Schmidt, H. The framing of games and the psychology of play. Games Econ. Behav. 2011, 73, 459–478. [Google Scholar] [CrossRef]
- Lévy-Garboua, L.; Maafi, H.; Masclet, D.; Terracol, A. Risk aversion and framing effects. Exp. Econ. 2012, 15, 128–144. [Google Scholar] [CrossRef]
- Cartwright, E. A comment on framing effects in linear public good games. J. Econ. Sci. Assoc. 2016, 2, 73–84. [Google Scholar] [CrossRef]
- Fosgaard, T.R.; Hansen, L.G.; Wengström, E. Framing and Misperception in Public Good Experiments. Scand. J. Econ. 2017, 119, 435–456. [Google Scholar] [CrossRef]
- Dariel, A. Conditional Cooperation and Framing Effects. Games 2018, 9, 37. [Google Scholar] [CrossRef]
- Thielmann, I.; Spadaro, G.; Balliet, D. Personality and prosocial behavior: A theoretical framework and meta-analysis. Psychol. Bull. 2020, 146, 30–90. [Google Scholar] [CrossRef]
- Bigoni, M.; Dragone, D. Effective and efficient experimental instructions. Econ. Lett. 2012, 117, 460–463. [Google Scholar] [CrossRef]
- Henrich, J.; Boyd, R.; Bowles, S.; Camerer, C.; Fehr, E.; Gintis, H.; McElreath, R.; Alvard, M.; Barr, A.; Ensminger, J.; et al. “Economic man” in cross-cultural perspective: Behavioral experiments in 15 small-scale societies. Behav. Brain Sci. 2005, 28, 795–815; discussion 815–855. [Google Scholar] [CrossRef]
- Gavrilets, S.; Richerson, P.J. Collective action and the evolution of social norm internalization. Proc. Natl. Acad. Sci. 2017, 114, 6068–6073. [Google Scholar] [CrossRef]
- Smith, V.L. Theory and experiment: What are the questions? J. Econ. Behav. Organ. 2010, 73, 3–15. [Google Scholar] [CrossRef]
- Fehr, E.; Henrich, J. Is strong reciprocity a maladaptation? On the evolutionary foundations of human altruism. In Genetic and Cultural Evolution of Cooperation; Hammerstein, P., Ed.; MIT Press: Cambridge, MA, USA, 2003; pp. 55–82. [Google Scholar]
- Andreozzi, L.; Ploner, M.; Saral, A.S. The stability of conditional cooperation: Beliefs alone cannot explain the decline of cooperation in social dilemmas. Sci. Rep. 2020, 10, 13610. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).