Abstract
We consider a clearing problem in peer-to-peer energy markets, where prosumers can trade energy among each other and with the main grid to meet their energy demands. By using a game-theoretic formulation and exploiting operator-theoretic methods for generalized Nash equilibrium seeking, we propose two variants of the state-of-the-art distributed market clearing mechanism with improved convergence speeds. Furthermore, we design a third variant that allows for equilibrium selection, i.e., computing a specific market solution based on a convex preference function of the network operator, e.g., a congestion cost. We provide convergence guarantees and numerically show the advantages of our proposed algorithms in terms of convergence speed up and obtaining reduced grid congestion.
1. Introduction
Peer-to-peer (P2P) energy trading is a concept that has recently gained tremendous interest due to continuously increasing development and installation of distributed generation units, especially renewable sources [1]. In this context, prosumers, i.e., consumers that have a power generation capability, can directly buy or sell energy from each other [2]; thus, they can actively participate in balancing the energy demand and supply of a local electrical grid. Early studies, such as [1], show potential benefits of incorporating P2P trading in the energy management of smart grid and electricity markets. Beside economical advantages, P2P trading can help decreasing peak demand, reducing reserve requirements, and curtailing network loss [3]. For an overview on enabling technologies and recent developments of P2P energy trading, we refer to [2,4].
As each prosumer has its individual (economical) objective, one can use game theory to study decision making in P2P energy markets [5]. For instance, the authors of [6,7] formulate a demand-side management problem of a network that allows P2P trading as a noncooperative game, where each active component aims at minimizing its energy cost while the price depends on the net load of the network (an aggregative game). The solution concept considered in these papers is a Nash equilibrium (NE), i.e., a point where no player has incentive to unilaterally change its decision. Similarly, ref. [8] proposes the economic dispatch problem in a P2P market as that of NE seeking. All these works provide different algorithmic solutions that rely on standard assumptions of continuous NE problems, i.e., convexity and compactness of local feasible sets as well as (strong) monotonicity of the pseudo-gradient game mapping.
Recently, refs. [9,10,11] formulate the market clearing problem in prosumer networks as a generalized Nash equilibrium problem (GNEP), where there are not only coupled cost functions but also coupling constraints among the players, and propose distributed methods to compute a solution. In [9], a multilateral trading among prosumers is considered, whereas [10,11] consider multi-bilateral ones. Furthermore, ref. [11] takes into account the interaction between prosumers and a distribution network operator (DNO), responsible for maintaining the reliability of the electrical network. In addition, by incorporating physical constraints in the formulation, a solution to this market problem is safe and thus acceptable for the DNO.
The above developments are closely connected with that of GNE seeking methods based on monotone operator theory [12]. Distributed equilibrium seeking algorithms are typically designed by exploiting operator splitting, preconditioning, and consensus techniques, see e.g., [13,14]. Specifically for monotone aggregative games, efficient semi-decentralized and distributed algorithms are presented in [15,16]. Furthermore, equilibrium selection methods for games with multiple equilibria have also recently been proposed in [17]. The reader is referred to [12] for an extensive review.
In the context of P2P markets, refs. [10,11] propose a market clearing mechanism based on the preconditioned proximal point (PPP) method [15], which essentially computes a GNE. The algorithm is scalable and has a distributed structure, where prosumers must exchange information with their trading partners and the DNO. Despite the effectiveness of this algorithm, as our main contribution, we enhance its capabilities in two ways, namely, we improve the convergence speed and add the option of selecting a preferred (e.g., optimal) equilibrium.
To improve the convergence rate of ([11], Algorithm 1), we implement the inertial and over-relaxed PPP methods ([15], Sect. IV) and tailor them to fit with the P2P game setting. These two variants retain the convergence guarantee of ([11], Algorithm 1) and use momentum-like steps to accelerate convergence. These extra steps have insignificant computational efforts and do not need additional communication rounds but require auxiliary variables of the size equal with that of the original decision variables. We perform a numerical study to validate the performance of our algorithms.
On the other hand, as multiple equilibrium solutions may exist in this market clearing game, we allow the DNO to provide a preference on the solutions to the game. To this end, we formulate an equilibrium selection problem where the DNO can set a convex preference function that is minimized over the set of (variational) GNE of the game. Then, we modify further the over-relaxed PPP method to obtain an equilibrium selection algorithm. The adjustment is based on the hybrid steepest descent method (HSDM) for fixed-point selection in generalized games [17,18]. We prove convergence under the original assumptions and showcase the efficacy of our equilibrium selection algorithm via numerical simulations where the DNO aims at minimizing some line congestion levels.
The rest of the paper is structured as follows. In Section 2, we provide the GNEP formulation of P2P markets. Then, Section 3 explains the PPP-based market clearing algorithms that have faster convergence rates than the state-of-the-art. Afterward, Section 4 discusses the proposed equilibrium selection algorithm and its advantages. Finally, Section 5 concludes the paper.
1.1. Notation
We denote by () and the set of (non-negative) real numbers and that of natural numbers, respectively. Furthermore, () denotes a matrix/vector with all elements equal to 0 (1). The Kronecker product between the matrices A and B is denoted by . For a matrix , its transpose is . For symmetric , () stands for positive definite (semidefinite) matrix. For any , with square symmetric matrix . The operator stacks its arguments into a column vector, whereas creates a (block) diagonal matrix with its arguments as the (block) diagonal elements. For an operator , and denote the sets of fixed points and zeros, respectively.
1.2. Operator Theory
Let be a nonempty subset of . A single-valued operator is (i) nonexpansive if, for all , ; (ii) attracting nonexpansive if is nonexpansive with and , for all and all ; and (iii) -averaged nonexpansive, for , if there exists a nonexpansive operator such that .
2. Peer-to-Peer Energy Markets as a Generalized Nash Equilibrium Problem
We consider the game-theoretic P2P spot market formulation in ([11], Sect. II), where N prosumers, connected in a distribution network, can trade energy directly with each other. In a spot market, e.g., a day-ahead or an intra-day market, each prosumer aims at economically optimizing its decision variables, i.e., how it wants to meet its energy demands, over a certain time horizon, . Let us denote the set of prosumers by and represent their trading network by an undirected graph denoted by , where denotes the set of links. The link implies that prosumers i and j can exchange energy. Therefore, we denote the set of trading partners of prosumer i by . Trading between two prosumers may occur if one of them has an excess of generated power and its trading partner is willing to buy this power. Furthermore, we suppose that (some) prosumers have local dispatchable components, which can be a distributed generator and/or a battery. Additionally, these prosumers can also buy energy from the main grid at a certain price, which varies depending on the total energy consumption of the network.
Now, let us denote the decision vector of prosumer by where , , and , for all , denote the dispatched powers from local dispatchable components, the power traded with the main grid, and the power exchanged with its trading partners in , respectively. Note that indicates the number of dispatchable components. Furthermore, we denote by the collection of the decision variables of all prosumers except prosumer i. Each prosumer considers the following cost function:
where and are the cost parameters of dispatchable powers [19,20]. The trading cost is defined by [21,22]
with and being the trading price and tariff, respectively, whereas the cost of buying energy from the main grid, , is defined by [20]
where , for all , are the price parameters and denotes the aggregate power on the grid, i.e.,
We note that defines the energy price, which is set by the main grid and is assumed to be proportional with the total consumption. Therefore, most components of depend only on the local variable (denoted by ), except for , which couples the decision variables of all prosumers.
Due to the components’ operational limits, storage dynamics, trading limits, and the power balance of each prosumer, i.e.,
where denotes the power demand of prosumer i, we let be constrained by a local constraint set, denoted by . We note that, based on (2), the power demand of each prosumer can be satisfied (partially) by direct P2P trading. Furthermore, there exist coupling constraints among the prosumers, as follows:
where the equalities in (3) are the reciprocity constraints for all trading partners whereas () defines the bounds on the aggregate power traded with the main grid with and being the lower and upper bounds.
Naturally, when we model this P2P market as a game, prosumers become the players. However, here, we also consider a distribution network operator (DNO) as an additional player (player ), whose objective is simply ensuring a safe operation of the physical network, i.e., the satisfaction of all physical constraints, which include (linearly approximated) power flows, bounds on the voltage angles and magnitudes of the busses, and quadratic constraints on the real and reactive powers. By representing the physical network as another undirected graph denoted by , where and denote the set of busses and that of power lines, respectively, we compactly write the physical variables (the decision variables of the DNO) as
where and denote the voltage angle and magnitude of bus y, denotes the injected power from the main grid, while and denote the active and reactive powers that flow between busses y and z. The set is defined by the aforementioned physical constraints. Additionally, there also exist coupling constraints between the prosumers and the DNO, as follows:
where (6) represents the power balance at all busses, with denoting the set of prosumers connected to bus y and denoting the power injection by prosumer i, i.e.,
whereas (7) guarantees the aggregate power traded with the main grid is equal to the total injected power by the main grid to the busses in the physical network. Thus, by considering the set of all players and denoting , the coupling constraints in this game can be compactly represented by the following affine set:
Now, we can write the generalized Nash equilibrium problem (GNEP) in P2P energy markets as follows:
where , for all , is defined in (1) while , as the DNO is indifferent to the market outcome, and is as defined in (9). A set of strategy is a GNE if it simultaneously satisfies (10), i.e., no player can decrease its cost by unilaterally deviating its strategy ([23], Sect. 2). In this work, we focus on finding a variational GNE—that is, a GNE where all players share equal marginal loss in satisfying the coupling constraints. Finally, we impose the following assumption on the GNEP in (10).
Assumption 1.
For each , the local feasible set is compact and affine whereas is compact and convex. The global feasible set is nonempty and satisfies Slater’s constraint qualification ([24], Eq. (27.50)).
Remark 1.
A detailed formulation of , for each , satisfying its assumption, is provided in ([11], Sect. II). The second part of Assumption 1 is intended to ensure the existence of equilibria.
3. Market Clearing Mechanism with Improved Convergence Speed
In this section, we revisit a distributed market clearing algorithm presented in [11]. The algorithm is based on the preconditioned proximal point (PPP) equilibrium seeking method for generalized aggregative potential games. The PPP method is obtained by evaluating the Karush–Kuhn–Tucker (KKT) optimality conditions of a variational GNE, and thus, suitably designing fixed-point iterations based on the resolvent ([24], Chapter 23) of the KKT operator with a preconditioning technique (see [15] for technical details).
As highlighted in ([15], Sect. IV-B), two variants of the PPP method that can boost the convergence rate are available. These variants use momentum-like steps, i.e., using a linear combination of two consecutive iterations for updates, similar to the heavy ball [25] or Nesterov’s acceleration method [26] for unconstrained convex optimization (c.f. [27], Equations (3) and (4)). We numerically test these two variants, namely, the inertial and over-relaxed PPP methods, tailored for our P2P energy market model, and evaluate whether we can indeed obtain such an improvement.
3.1. Market Clearing Algorithms Based on the Preconditioned Proximal Point Method
Let us start by presenting the PPP-based market clearing mechanism and its variants. To this end, we first introduce the dual variables for all and , ; , for all ; and associated with the coupling constraints in (3), (4), (6), and (7), respectively. We compactly denote these dual variables by . We also need to introduce auxiliary variables associated with all the primal and dual variables, denoted by the accent , i.e., for each , is associated with , and is associated with . The PPP-based market clearing mechanism and its variants are then summarized in Algorithm 1 and its subroutines in Algorithms 2 and 3, where we consider Assumption 2.
| Algorithm 1 PPP-based Market Clearing Mechanism |
 |
| Algorithm 2 Central update of DNO |
Step sizes: set , , , and , for all busses .
|
| Algorithm 3 Local update of prosumer |
Step sizes: For each , set , , for all .
|
Assumption 2.
- a.
- (Inertial PPP variant),,, , for all, and;
- b.
- (Over-relaxed PPP variant),,,, for all, and.
Remark 2.
The standard PPP-based mechanism ([11], Algorithm 1) is obtained by setting for the inertial variant (Assumption 2a) or for the over-relaxed variant (Assumption 2b). In this setup, all the auxiliary variables are essentially redundant copies of the primal and dual variables.
Remark 3.
The derivations of the inertial and over-relaxed algorithms are analogous to those of ([15], Algs. 6 and 6B), with the addition that we must appropriately design the preconditioning matrix to exploit the structure of the coupling constraints.
Proposition 1.
Let Assumptions 1 and either 2a or 2b hold. Then, the sequence generated by Algorithm 1 converges to a variational GNE of the game in (10).
Proof.
The proof is analogous to that of ([11], Prop. 1). When Assumption 2a holds, we can apply ([15], Thm. 2) whereas when Assumption 2b holds, convergence follows immediately from ([24], Prop. 5.16). □
3.2. Rate Improvement Evaluation
We evaluate the convergence rate of the inertial and over-relaxed variants via numerical simulations. To this end, we use the modified IEEE 37-bus and IEEE 123-bus distribution networks with realistic demand profiles ([11], Sect. IV). The former is radial while the latter is larger and has a weakly meshed structure. We perform all simulations in Matlab with OSQP solver for the primal update step of prosumers. For all variants, we use the same step sizes of the DNO and prosumers (satisfying the requirements in Algorithms 2 and 3) while we set for the inertial variant and for the over-relaxed variant, satisfying Assumption 2. For each network, we run Monte Carlo simulations by varying the number of prosumers N and generating 30 random instances for each N. Figure 1 shows the plots of the number of iterations needed to satisfy the stopping criterion. We can observe from Figure 1 that the inertial PPP variant converges the fastest while the over-relaxed variant also converges faster than the standard PPP. On average, the rate improvements by implementing the inertial and over-relaxed variants are and , respectively. We note that, at each iteration, these variants require extra computations whose effect to the computational time is almost negligible.
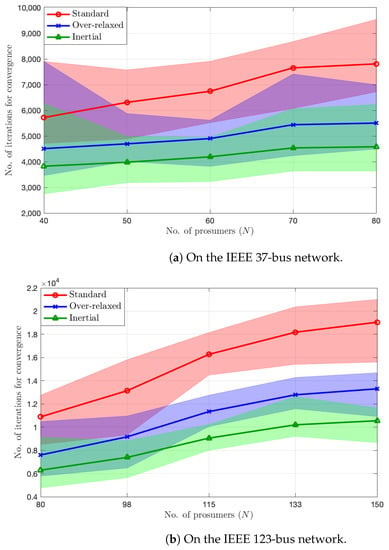
Figure 1.
Convergence rate performances of the standard, over-relaxed, and inertial PPP algorithms. Each point in the solid lines represents the average over 30 random instances (shaded areas).
4. Equilibrium Selection as Preferred by the Network Operator
The GNEP of P2P energy markets might have infinitely many solutions as its pseudodifferential game mapping is merely monotone ([11], Appendix A). Furthermore, the equilibrium seeking algorithms discussed in Section 3 can only find an arbitrary variational GNE (Proposition 1). Meanwhile, the DNO might have some preferences on the game equilibrium. For instance, in order to maintain the longevity of the physical network, the DNO prefers a GNE that minimizes power flows. At the same time, the DNO does not want to interfere the game by introducing a non-zero objective or cost function, which corresponds to its preference, in the game. We note that modifying the definition of in (10) changes the definition of the game in the P2P market and, in turn, may change the set of GNEs. In this section, we pose the problem of selecting an equilibrium of the P2P market in (10) that meets the preference of the DNO as an optimal GNE selection problem. Then, we provide a modification of the equilibrium seeking algorithms in Section 3 into that of equilibrium selection.
4.1. Formulation of Optimal Equilibrium Selection Problem
We can formulate the equilibrium selection problem as an optimization problem of a preference function over the set of variational GNEs. Let us denote the preference function of the DNO that will be minimized by the real-valued function . For instance, to have minimum power flows (in some lines), as discussed earlier, can be defined by the following congestion cost:
where is the set of important power lines chosen by the DNO. By using to denote the set of variational GNEs of the game in (10), we want to solve the following optimization problem:
Assumption 3.
The preference function φ in (14) is convex and continuously differentiable.
4.2. Optimal Equilibrium Selection Algorithm
We are now ready to show a modification of the market clearing mechanism in Section 3 that can solve Problem (14). Specifically, let us consider the over-relaxed variant of Algorithm 1, i.e., when Assumption 2b holds. While we keep using Algorithm 3 for the local update subroutine of each prosumer, we modify the DNO subroutine in Algorithm 2 by substituting the primal variable update in (12) with
where is computed from (11), (as in Assumption 2b), and the step size follows Assumption 4. We note that for any and , satisfies this assumption.
Assumption 4.
For the step size in (16), it holds that , , and .
The crucial change for equilibrium selection is the addition of a descent step using the gradient of the selection function and a vanishing step size to update , intuitively similar to the gradient descent method for unconstrained convex optimization. This alteration is obtained by implementing the approach recently introduced in [17,18], which combines fixed-point selection and operator splitting theories. Specifically, we recast the optimization problem in (14) into that of fixed point selection. Then, we can show that our algorithm is an instance of the HSDM [28] with the over-relaxed PPP operator, and in turn, we can provide a convergence guarantee toward a solution to Problem (14), as formally stated next.
Proposition 2.
Let Assumptions 1, 2b, 3, and 4 hold. Let the sequence be generated by Algorithm 1, where at each iteration, step A—the central update of DNO—follows Algorithm 2, with (12) being replaced by (15) and (16), and step B—the local update of each prosumer —follows Algorithm 3. Then, converges to the set of solutions of Problem (14).
Proof.
See Appendix A. □
4.3. Equilibria That Minimize Line Congestion
Let us now show a numerical simulation study where we evaluate the proposed equilibrium selection algorithm. We consider that the DNO prefers an equilibrium that minimizes the real and reactive power flows throughout the whole network; thus, we consider the selection function as defined in (13) with . Note that we set and randomly generate two test instances from the 37-bus and the 123-bus networks, similarly to those in Section 3.2. We compare the standard PPP algorithm and its counterpart for equilibrium selection discussed in Section 4.2. Additionally, we also run a simulation with the standard PPP algorithm for a modified problem, i.e., the cost function of the DNO in the game defined in (10) is the congestion cost function (). Although the latter case is not realistic as typically the DNO cannot participate in the market, here we consider it as an ideal benchmark. Figure 2 and Table 1 illustrate the simulation results. We can observe that our equilibrium selection algorithm computes a solution with a lower total congestion than the standard PPP method, as expected. Remarkably, this solution has only at most higher congestion than that of the case when is directly imposed as the cost function of the DNO in the game in (10). Thus, without modifying the game and by implementing an equilibrium selection mechanism, the DNO can still reduce line congestions significantly well.
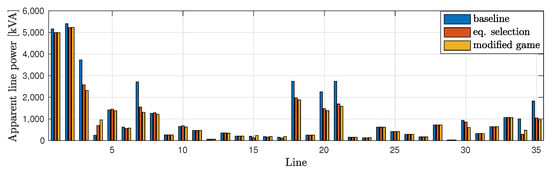
Figure 2.
Apparent power at each line of the IEEE 37-bus network in the simulated scenarios.

Table 1.
Normalized congestion costs in the simulated scenarios.
5. Conclusions
The convergence speed of the PPP-based distributed market clearing mechanism for P2P markets can be remarkably improved via two different types of momentum-like steps, resulting in the inertial and over-relaxed variants. Furthermore, a simple modification based on an equilibrium selection method allows the network operator to impose a preference on the market clearing solutions. These two key results have been validated via numerical studies. Future works include model refinement, e.g., where market aggregators also participate in the game and relaxation of the assumptions on the price functions.
Author Contributions
Conceptualization, W.A. and S.G.; Formal analysis, W.A. and S.G.; Funding acquisition, S.G.; Methodology, W.A. and S.G.; Project administration, S.G.; Software, W.A.; Supervision, S.G.; Validation, W.A.; Visualization, W.A.; Writing—original draft, W.A.; Writing—review and editing, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the ERC under research project COSMOS (802348).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation datasets and codes can be found here: https://github.com/ananduta/P2P_eq_seeking_selection (accessed on 9 August 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DNO | Distribution network operator |
| HSDM | Hybrid steepest descent |
| GNE | Generalized Nash equilibrium |
| GNEP | Generalized Nash equilibrium problem |
| IEEE | Institute of Electrical and Electronics Engineers |
| KKT | Karush–Kuhn–Tucker |
| PPP | Preconditioned proximal point |
| VI | Variational inequality |
Appendix A. Proof of Proposition 2
To establish the proof of Proposition 2, let us first rewrite the game in (10) as follows:
where the equality constraint in (A1) compactly represents (3), (6), and (7) while the inequality constraint in (A1) represents (4) with appropriate vectors , and matrices , . We note that and .
Next, for each , let be the matrix that selects from , i.e., , and let us define . The pseudodifferential mapping of the game is defined by
where is a symmetric matrix whose block component is defined by
As shown in the proof of ([11], Prop. 1), the pseudo-differential mapping in (A2) is maximallly monotone ([24], Def. 20.20).
Furthermore, supposing that Assumption 2b holds, we can show that the set of Algorithms 1, 2, with (15) and (16) replacing (12), and Algorithm 3 is an instance of the HSDM [28] with the over-relaxed PPP operator, denoted by , i.e., the algorithm can be compactly written as
where , and
By the choice of the step sizes given in Algorithms 2 and 3, is positive definite. We note that the standard PPP operator is given by where and are obtained from the KKT optimality conditions of a variational GNE of the game in (10). In this regard, for any primal–dual pair satisfying , the primal variable is a variational GNE of the game in (10).
Moreover, is the Krasnosel’skii–Mann operator associated with . By Assumption 1 and the maximal monotonicity of the pseudo-differential game mapping, is -averaged with respect to the -induced norm [15]. Thus, is also averaged, given that (in fact, for any ). We can now invoke ([29], Theorem 3) to state that the HSDM iterations in (A3) with step size satisfying Assumption 4 converge toward the solution set of the variational inequality (VI) problem:
where . Specifically, due to Assumption 3, is monotone. Moreover, since is averaged, it is attracting nonexpansive ([28], Sec. 2.A). In addition, is bounded due to Assumption 1 and by following ([23], Prop. 12.11) and ([30], Prop. 3.3). Finally, by noting that , the VI in (A4) is equivalent to Problem (14). Thus, the proof is complete.
References
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef]
- Soto, E.A.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Peer-to-peer energy trading: A review of the literature. Appl. Energy 2021, 283, 116268. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D.; Poor, H.V. Peer-to-peer trading in electricity networks: An overview. IEEE Trans. Smart Grid 2020, 11, 3185–3200. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Saha, T.K.; Morstyn, T.; Chapman, A.C.; Alam, M.J.E.; Hanif, S.; Poor, H.V. Peer-to-peer energy systems for connected communities: A review of recent advances and emerging challenges. Appl. Energy 2021, 282, 116131. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.; Poor, H.V.; Wood, K.L. Transforming energy networks via peer-to-peer energy trading: The potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef]
- Noor, S.; Yang, W.; Guo, M.; van Dam, K.H.; Wang, X. Energy demand side management within micro-grid networks enhanced by blockchain. Appl. Energy 2018, 228, 1385–1398. [Google Scholar] [CrossRef]
- Yang, X.; Wang, G.; He, H.; Lu, J.; Zhang, Y. Automated demand response framework in ELNs: Decentralized scheduling and smart contract. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 58–72. [Google Scholar] [CrossRef]
- Bhatti, B.A.; Broadwater, R. Energy trading in the distribution system using a non-model based game theoretic approach. Appl. Energy 2019, 253, 113532. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, F.; Ma, Z.; Chen, Y.; Jia, M.; Wei, W.; Wu, Q. Distributed generalized Nash equilibrium seeking for energy sharing games in prosumers. IEEE Trans. Power Syst. 2021, 36, 3973–3986. [Google Scholar] [CrossRef]
- Belgioioso, G.; Ananduta, W.; Grammatico, S.; Ocampo-Martinez, C. Energy management and peer-to-peer trading in future smart grids: A distributed game-theoretic approach. In Proceedings of the 2020 European Control Conference (ECC), Saint Petersburg, Russia, 12–15 May 2020; pp. 1324–1329. [Google Scholar]
- Belgioioso, G.; Ananduta, W.; Grammatico, S.; Ocampo-Martinez, C. Operationally-safe peer-to-peer energy trading in distribution grids: A game-theoretic market-clearing mechanism. IEEE Trans. Smart Grid 2022. [Google Scholar] [CrossRef]
- Belgioioso, G.; Yi, P.; Grammatico, S.; Pavel, L. Distributed generalized Nash equilibrium seeking: An operator-theoretic perspective. IEEE Control Syst. Mag. 2022, 42, 87–102. [Google Scholar] [CrossRef]
- Yi, P.; Pavel, L. An operator splitting approach for distributed generalized Nash equilibria computation. Automatica 2019, 102, 111–121. [Google Scholar] [CrossRef]
- Bianchi, M.; Belgioioso, G.; Grammatico, S. Fast generalized Nash equilibrium seeking under partial-decision information. Automatica 2022, 136, 110080. [Google Scholar] [CrossRef]
- Belgioioso, G.; Grammatico, S. Semi-decentralized generalized Nash equilibrium seeking in monotone aggregative games. IEEE Trans. Autom. Control. 2021. [Google Scholar] [CrossRef]
- Gadjov, D.; Pavel, L. Single-timescale distributed GNE seeking for aggregative games over networks via forward–backward operator splitting. IEEE Trans. Autom. Control 2021, 66, 3259–3266. [Google Scholar] [CrossRef]
- Benenati, E.; Ananduta, W.; Grammatico, S. Optimal selection and tracking of generalized Nash equilibria in monotone games. arXiv 2022, arXiv:2203.07765. [Google Scholar]
- Benenati, E.; Ananduta, W.; Grammatico, S. On the optimal selection of generalized Nash equilibria in linearly-coupled aggregative games. In Proceedings of the 61st Conference on Decision and Control, Cancún, Mexico, 6–9 December 2022. to appear. [Google Scholar]
- Sorin, E.; Bobo, L.; Pinson, P. Consensus-based approach to peer-to-peer electricity markets With product differentiation. IEEE Trans. Power Syst. 2019, 34, 994–1004. [Google Scholar] [CrossRef]
- Atzeni, I.; Ordóñez, L.G.; Scutari, G.; Palomar, D.P.; Fonollosa, J.R. Demand-side management via distributed energy generation and storage optimization. IEEE Trans. Smart Grid 2013, 4, 866–876. [Google Scholar] [CrossRef]
- Le Cadre, H.; Jacquot, P.; Wan, C.; Alasseur, C. Peer-to-peer electricity market analysis: From variational to generalized Nash equilibrium. Eur. J. Oper. Res. 2020, 282, 753–771. [Google Scholar] [CrossRef]
- Baroche, T.; Moret, F.; Pinson, P. Prosumer markets: A unified formulation. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Facchinei, F.; Pang, J.S. 12 Nash equilibria: The variational approach. In Convex Optimization in Signal Processing and Communications; Palomar, D.P., Eldar, Y.C., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 443–491. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 87. [Google Scholar]
- Ghadimi, E.; Feyzmahdavian, H.R.; Johansson, M. Global convergence of the heavy-ball method for convex optimization. In Proceedings of the 2015 European control conference (ECC), Linz, Austria, 15–17 July 2015; pp. 310–315. [Google Scholar]
- Yamada, I.; Ogura, N. Hybrid steepest descent method for variational inequality problem over the fixed point set of certain quasi-nonexpansive mappings. Numer. Funct. Anal. Optim. 2005, 25, 619–655. [Google Scholar] [CrossRef]
- Ogura, N.; Yamada, I. Nonstrictly convex minimization over the bounded fixed point set of a nonexpansive mapping. Numer. Funct. Anal. Optim. 2003, 24, 129–135. [Google Scholar] [CrossRef]
- Auslender, A.; Teboulle, M. Lagrangian duality and related multiplier methods for variational inequality problems. SIAM J. Optim. 2000, 10, 1097–1115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).