Abstract
We investigate whether tournament prizes that depend on joint output (“variable prize tournaments”) can alleviate the sabotage problem which is otherwise inherent in tournament structures. In a game-theoretical model with three contestants, we compare fixed-prize tournaments with tournaments where prizes depend on contestants’ joint output. Our analysis suggests that the incentives to sabotage in a fixed-prize tournament may be counteracted in a variable-prize tournament such that contestants no longer sabotage, but help one another. We empirically test the implications of our model with the help of a classroom experiment where we compare participants’ choices in a fixed-prize treatment () with those of a variable-prize treatment () in a between-subjects design. Given our parametrization, we expect efforts to be identical in both treatments, and we expect sabotage in the treatment and no sabotage in the treatment. In accordance with the model, we find that participants in the fixed-prize tournament sabotage one another, whereas participants in the variable-prize tournament help one another. At the same time, participants’ effort levels do not vary between the two treatments.
1. Introduction
Tournament incentives where rewards depend on relative rather than absolute performance have become an increasingly important component in organizational compensation: for example, mutual funds managers compete for the highest year-end bonus (Kempf and Ruenzi [1]) and sales directors strive to obtain one of the few available spots in a luxurious incentive trip (Backes-Gellner and Pull [2]). Tournaments are “pervasive” in today’s organizational practice (Casas-Arce and Martinez-Jerez [3]).
However, besides its many advantages (e.g., economizing on measurement costs or filtering common risks), tournament incentives also have severe downsides: tournaments do not only provide incentives for contestants to invest in productive activities to enhance their own performance, but also to invest in destructive activities in an attempt to reduce their competitors’ performance and thus enhance their own chances to win the tournament and be awarded the (fixed) tournament prize.
To date, several measures have been suggested on how to alleviate the sabotage problem in tournaments. One obvious solution is to offer smaller tournament prizes to thus lower contestants’ incentives to invest in destructive activities. However, on the downside, lowering tournament prizes will also reduce contestants’ incentives to invest in productive activities. Further, increasing the costs of sabotage for the contestants, e.g., via an extensive monitoring and sanctioning policy, might help reduce sabotage. Similarly, reducing the effectiveness of sabotage via, e.g., increasing the physical distance between contestants, might also reduce contestants’ incentives to sabotage one another. Likewise, additionally installing team-based incentives might reduce contestants’ incentives to sabotage one another because sabotaging team members will result in a lower expected team bonus (see Danilov et al. [4]).
In our paper, we analyze whether a tournament where prizes are not fixed in advance but rather vary with the joint output produced by all contestants (Güth et al. [5]) alleviates the sabotage problem in tournaments or even induces help. Our study relates to the one by Danilov et al. [4] which analyzes the effects of combining tournament incentives with an additional team incentive. While in the compensation function studied by Danilov et al. [4] one compensation component (i.e., a team incentive) aims at reducing the adverse effects of another (i.e., a fixed-prize tournament incentive), we analyze a setting where the tournament incentive itself is designed in a way to reduce sabotage or to even induce help. That is, we are concerned with a tournament-inherent solution to the sabotage problem.
Besides their potential to contribute to a solution of the sabotage problem, variable-prize tournaments also render a more realistic view on tournament incentives in the organizational practice: Consider, for example, a promotion tournament where three department heads compete for the vacant position of the vice president and where the head of the most profitable department will be promoted to this position. Each department head then has an incentive to increase the profitability of her department and decrease the profitability of the others. However, what in practice will work against this latter effect is that the position of the vice president will be less attractive (in terms of reputation and ultimately also pay) when the company’s overall profitability is low. That is, in this real-life example, the prize for winning the promotion tournament is not fixed, but it will in fact be lower when there is sabotage among the department heads. Hence, in the real world, tournament prizes are often not fixed but variable—which is, however, overlooked in the vast majority of the tournament literature.
Rather, and starting with the seminal work by Lazear and Rosen [6], the tournament literature is concerned with fixed-prize tournaments, in which often not only the sum of the prizes is set in advance, but also each and every prize level. One exception is the so-called J-type (Kräkel [7]; Schöttner [8]) or proportional-prize tournament (Bevia and Corchón [9]; Cason et al. [10]). In these types of tournaments, the prize sum is fixed in advance, but the distribution of the prize money among the different winning positions is variable. As the distribution of the prize money, however, depends on how far one contestant outperforms the other, neither J-tournaments nor proportional-prize tournaments are apt to reduce the sabotage problem.
The class of tournaments that we are studying, i.e., variable-prize tournaments where not only the different prize levels, but also the prize sum, is not fixed in advance, has been introduced to the literature by Güth et al. [5]. While Güth et al. [5] have found that variable-prize tournaments outperform fixed-prize tournaments and piece rates, they have neglected the sabotage problem—which we will focus on in this paper.
Besides contributing to the literature on variable-prize tournaments, our paper also contributes to the literature on sabotage in tournaments. Lazear [11] has theoretically shown that the optimal prize spread in a tournament is smaller when contestants can sabotage one another. In the first published laboratory experiment on sabotage in tournaments, Harbring and Irlenbusch [12] have found that an increase in the prize spread in a (fixed-prize) tournament leads to both higher effort levels and more sabotage (for similar results see Harbring and Irlenbusch [13]). As the latter effect dominates the former, a profit-maximizing principal would rather not provide (fixed-prize) tournament incentives. Installing a variable-prize tournament instead might alleviate the sabotage problem without abolishing the positive incentive effects.
By analyzing the effects of variable-prize tournaments on sabotage, we do not only enhance our theoretical and empirical knowledge on how to mitigate the sabotage problem associated with tournaments and derive important practical implications on how to design a tournament incentive in a way that it does not necessarily lead to sabotage, but also investigate how these incentives might even induce help.
The remainder of this paper is organized as follows: In Section 2, we provide a game-theoretical model which compares the productive and destructive incentives of a fixed-prize tournament with a tournament with output-dependent, variable prizes. Section 3 describes the experimental design and procedure. Section 4 provides an analysis of our experimental data. Section 5 concludes the paper.
2. The Game-Theoretical Model
We consider a group of risk-neutral agents who act simultaneously. Each agent chooses an effort level from the interval that positively affects her own output level . In addition, each agent chooses an activity level from the interval that equally affects the output levels of the other two agents in her group. If , agent increases the output levels of the other two agents (“help”); if , agent reduces them (“sabotage”).
The output of agent was determined by , where are identically and independently distributed random variables with mean zero. To keep the model tractable, we assumed the uniform distribution on the support such that the density is constant.
The costs of choosing effort and activity level are assumed to be convex and specified as and where .
Agent compensation is determined by a rank order tournament: The agent with the highest output received the prize , the agent with the second-highest output receives the prize with , and the agent with the lowest output receives the standardized prize . The probability , , , ) of an agent to receive the prize Wk, is a function of her own effort and activity level as well as of the other agents’ effort and activity level .
The expected payoff function of agent is given by:
In what follows, we derive the symmetric Nash equilibrium prediction as a benchmark assuming that agents maximize their own expected monetary payoff. We distinguish two cases: (1) a scenario where prizes and are fixed and (2) a scenario where prizes and are variable and depend on the joint output of the three agents.
2.1. Case (1): Fixed-Prize Tournament
If the prizes and are fixed, the first-order conditions of agent can be derived as:
and:
where we use the fact that in equilibrium, and (see the mathematical Appendix A).
This leads to the solution:
Hence, in a fixed-prize tournament, inducing positive effort levels always comes at the cost of inducing sabotage: to induce a positive effort level (), the tournament prize has to be positive (), but this positive tournament prize then also leads contestants to sabotage one another ().
2.2. Case (2): Variable-Prize Tournament Where Prizes Depend on Joint Output
As a simple example of a variable-prize tournament with output-dependent prizes and , we assume that and with , whereas , as before. The expected payoff function of agent is:
In the unique symmetric equilibrium, the first-order conditions of all three agents read:
and:
where , , , and (see the mathematical Appendix A).
The first-order conditions constitute a linear two-equation system which can be solved as:
while the equilibrium effort level in a variable-prize tournament is positive (), the sign of the equilibrium activity level depends on the degree of uncertainty, as measured by :
That is, while a variable-prize tournament also induces positive effort levels (), it does not necessarily lead to sabotage but might as well induce help (). Hence, unlike in the fixed-prize tournament, inducing a positive effort level does not necessarily come at the cost of inducing sabotage.
3. Experimental Design and Procedure
We employ this theoretical model to study sabotage and help in a fixed-prize as compared to a variable-prize tournament. To this aim, we undertook a classroom experiment and randomly assigned participants to one of two treatments: one treatment with a fixed-prize tournament () and the other one with a variable-prize tournament () in a between-subjects design.
For the experiment, we used the following parametrization of the variables: , , , and . For the treatment, we set and , and for the treatment, we set and . The benchmark Nash-equilibrium solution for the treatment is and , and the benchmark Nash-equilibrium solution for the treatment is and . That is, given our parametrization, we expect efforts to be identical in both treatments, and we expect sabotage in the treatment and no sabotage in the treatment.
At the beginning of the experiment, each participant was granted an initial endowment of 10 experimental currency units (ECU) (exchange rate: 2 ECU = 1 EUR) to her account and was informed that she would be randomly matched with two other participants of the experiment to form a group of three. Only one round was played. In this single round, participants made the following decisions: First, each participant decided on her level of effort from the interval . To reduce the variance in effort choice, only integer values could be chosen. Second, participants were explicitly asked whether they want to (a) sabotage the other participants in their group, (b) help the other participants in their group, or (c) neither sabotage nor help the other participants in their group. In case they had chosen to sabotage their group members, participants were subsequently asked to which extent they would like to sabotage the other participants in their group; in case they had chosen to help their group members, they were subsequently asked to which extent they would like to help the other participants in their group. Again, only integer values could be chosen. Exerting sabotage or help was as costly as exerting effort. When deciding on effort and the level of sabotage/help, participants did not know the choices of the other participants in their group and they also did not know the value of the random components which were chosen from the interval , separately for each group member.
To determine the winners of the first and second prize in both treatments, the output levels of the three participants within one group were compared. The group member with the highest output level received , the one with the second-highest output level received and the one with the lowest output level received . In case two or even three of the members of one group achieved identical output levels, prize allocation was random among those. If the joint group output in treatment was negative, all group members received a prize of zero ().
The experiment was conducted as a classroom experiment at Baden-Wuerttemberg Cooperative State University Loerrach. Lecture participants were randomly allocated to treatment or treatment and subsequently randomly assigned to groups of three. In total, we ran eight sessions with altogether 123 participants, each of which took part in only one session. A total of 57 participants took part in treatment , and 66 participants took part in treatment . In total, the experiment lasted about one hour, and participants were paid on average EUR 13.99.
Each session consisted of four phases altogether: In phase 1, participants were asked to read the written instructions (see Appendix C) carefully and to raise questions.
Phase 2 was devoted to making sure that participants correctly understood the experiment and the effects of their decisions. To that aim, participants were equipped with a programmed Excel sheet where they could enter fictitious values for effort, sabotage/help, and the random component, both for themselves and for the other two members of their group. The Excel sheet then displayed the resulting output levels of all individual group members, the joint output level, the prize levels, and who would be subsequently awarded which prize. Further, for each group member, the effort costs, the costs of sabotage/help, and the resulting total payouts in ECU were given. Participants had the option to change their entries as often as they wanted and to view the resulting effects before the actual experiment was conducted in phase 3.
Following the experiment, participants filled out a post-experimental questionnaire in phase 4. Here, we first elicited participants’ degree of risk aversion via an incentivized Holt–Laury test, conducted three mini-dictator games (Ayaita and Pull [14]) to measure the extent to which participants are characterized by positional preferences, and measured participants’ degree of nastiness with the help of a joy-of-destruction game (Abbink and Sadrieh [15]). Lastly, we collected information on participants’ gender and included a short form of the BIG5 inventory personality test (Rammstedt et al. [16]) to measure participants’ degrees of extraversion, agreeableness, conscientiousness, neuroticism, and openness.
4. Empirical Results
4.1. Variables and Descriptives
Table 1 provides an overview of our variables and how we measured them: Effort refers to participants’ effort choice. Help refers to participants’ choice of activity level, where a positive value () indicates that the respective participant chose to help her two group members by increasing their output levels, and a negative value indicates that the respective participant chose to sabotage her two group members by reducing their output levels. When , the respective participant chose neither to sabotage nor help her two group members.

Table 1.
Descriptive statistics.
Further, Table 1 also displays the means, standard deviations, and minimum and maximum values of all of our variables for the full sample (i.e., combining the two treatments), and for the two treatments ( and ) separately. Across the two treatments, participants chose an average effort level and an average activity level . That is, participants on average decided to help their group members ().
In the fixed-prize treatment , participants, on average, chose an effort level and an activity level . In the variable-prize treatment , participants, on average, chose and . Hence, average effort levels in the two treatments were quite similar and they were over and above the benchmark equilibrium solution of . (In experimental settings, participants often deviate from the game-theoretical predictions. They might do so for many reasons, and we can only speculate about their motives in our specific setting. For instance, participants might have been overconfident and have overestimated the effects of their effort choice on their probability to win the tournament.) Concerning helping behavior, participants in the fixed-prize treatment , on average, chose to sabotage their group members as predicted (even though to a considerably smaller degree with as compared to ), whereas participants in the variable-prize treatment , on average, chose not to sabotage, but rather to help their group members. (Again, participants thus deviated from the game-theoretical prediction. Choosing to help rather than sabotage their contestants might indicate prosocial preferences. Further, it might also be an outcome of our explicit framing (“sabotage” vs. “help”). Importantly, however, the framing was the same in both treatments, thus ruling out that it has confounded our central result.) While the benchmark equilibrium solution would have predicted participants in the variable-prize treatment neither to help nor sabotage their group members (), participants chose, on average, to help their group members ().
Table 2 displays the Pearson correlation matrix of our variables, including our treatment variable indicating the variable-prize treatment. Only help is significantly correlated with the treatment variable (); all other variables are not significantly related to the treatment. Further, participants’ helping behavior is unrelated to their effort choice.

Table 2.
Correlations.
The pairwise correlations among all explanatory variables are a first check for multicollinearity. As a rule of thumb, an indication of potential multicollinearity are values of 0.7 or higher. In our sample, there are no values higher than 0.45. We additionally examined the variance inflation factors (VIF) for all of our estimation models. As all VIF values were below 1.57, we did not expect our findings to be distorted by multicollinearity (O’Brien [17]).
4.2. Effort
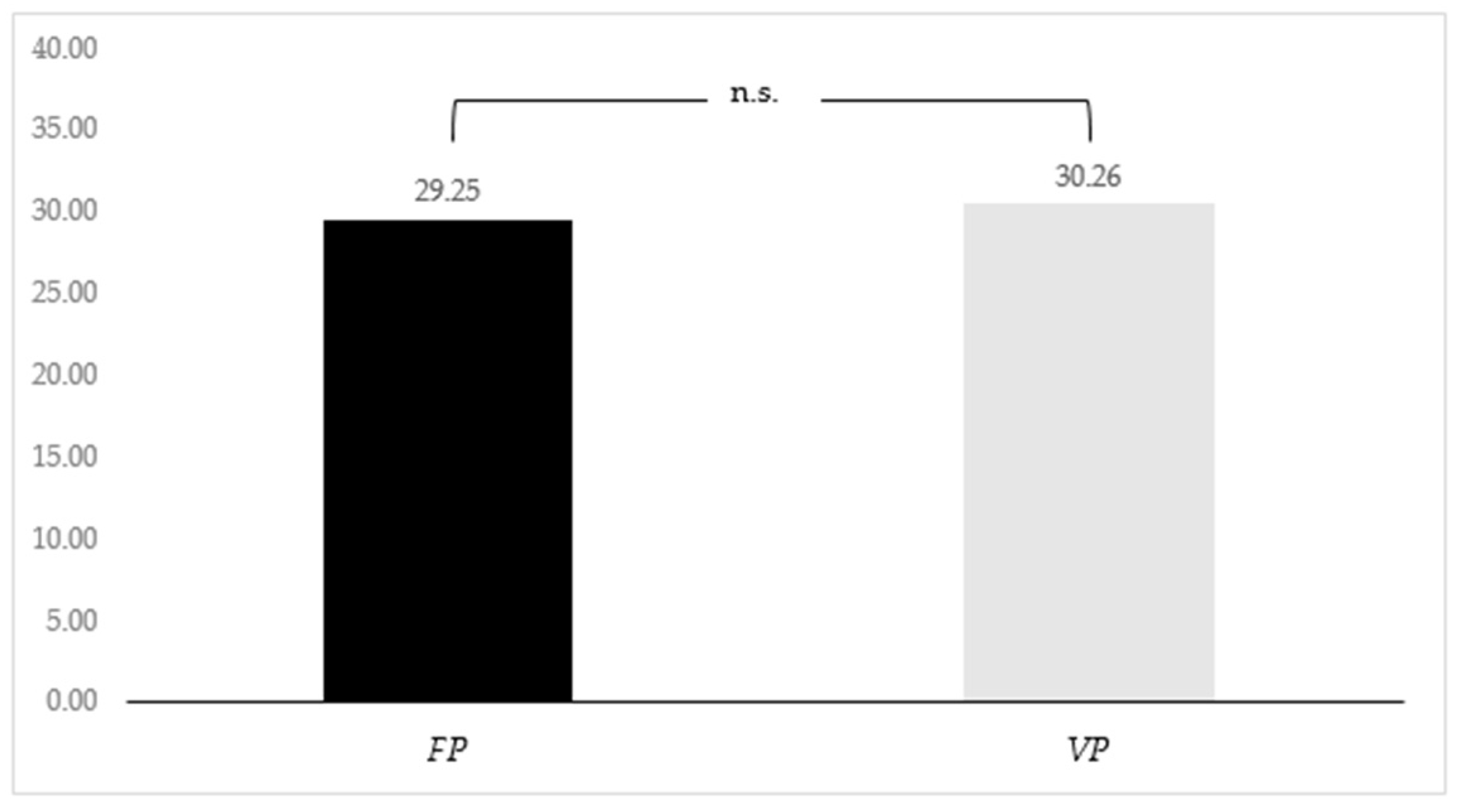
Figure 1 compares the means of the effort choices in the two treatments: the fixed-prize treatment on the left and the variable-prize treatment on the right. We use a t-test to determine whether the two means are different from one another. The average effort level in is slightly higher than the one in (. However, the difference between the two effort levels is statistically non-significant. When regressing participants’ effort choices on the treatment variable ( vs. ), we likewise do not find any treatment effect—irrespective of whether or not we included controls from the main experiment and the post-experimental questionnaire as regressors (see Table A1 in Appendix B).
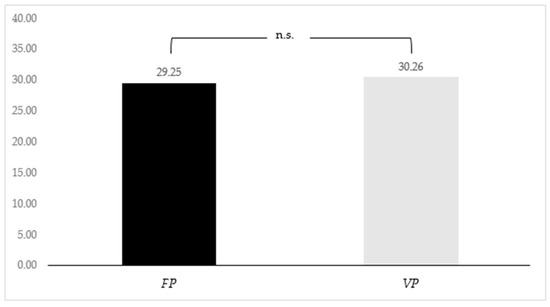
Figure 1.
Average effort choices in vs. .
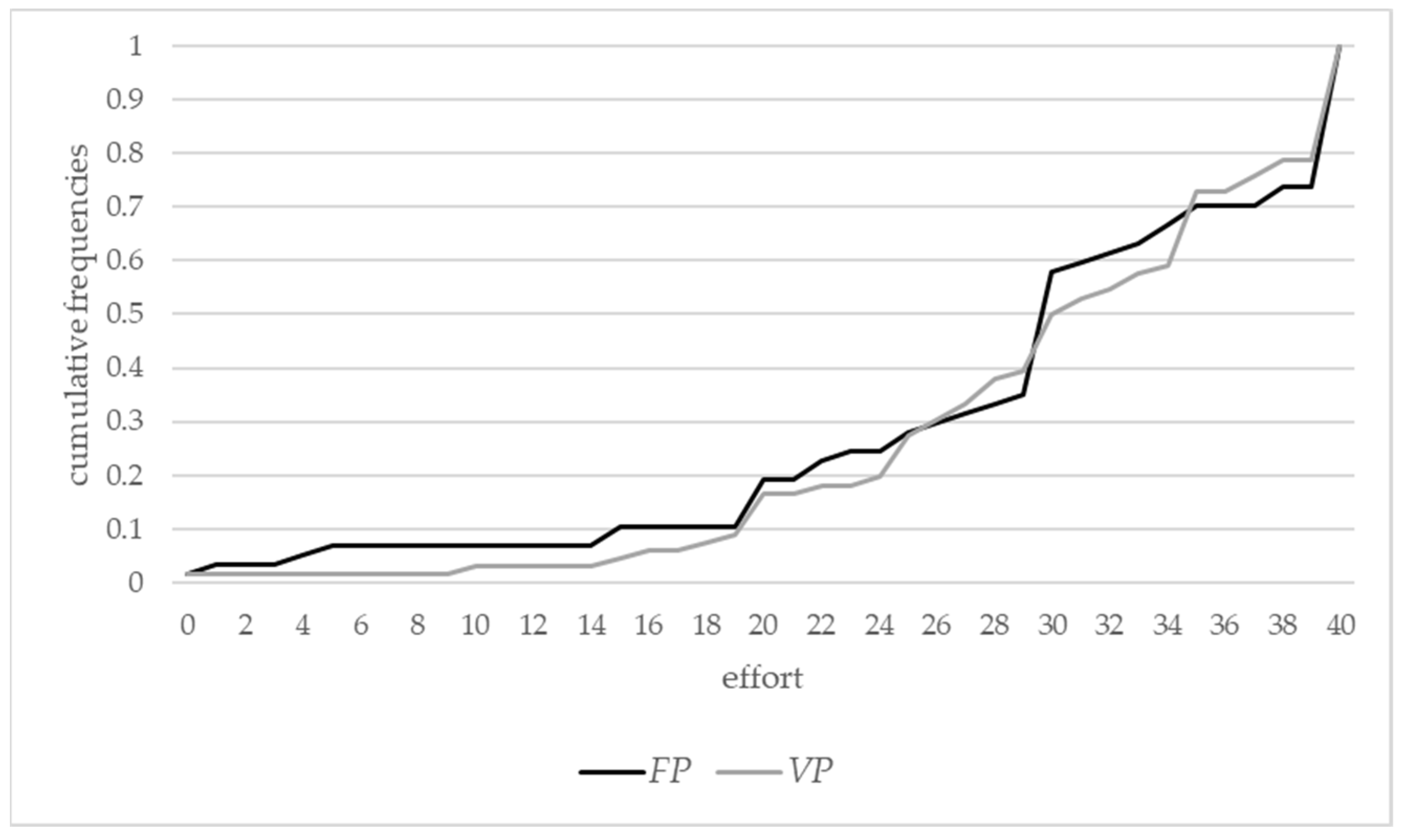
Figure 2 displays the distribution functions of the effort choices in the two treatments. While there are some differences to be observed (e.g., in the fixed-prize treatment , a considerably larger fraction of participants chose an effort level of 15 or lower than in the variable-prize treatment ), the two distribution functions are rather similar.
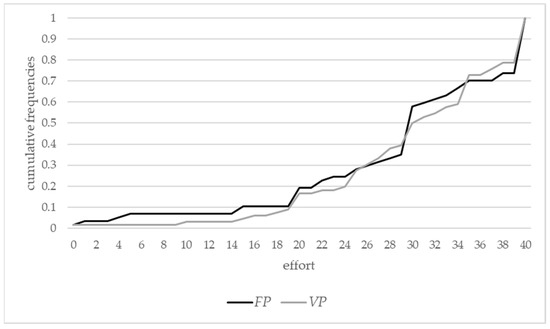
Figure 2.
Distribution functions of effort choices in vs. .
4.3. Help
Next, we compare participants’ helping behavior in the two treatments. We start by comparing the means of the chosen activity level using a t-test. Next, we focus on the extensive margin, and regard participants’ decisions to either help (), sabotage (), or neither help nor sabotage (), and compare their choices across the two treatments, applying a binomial test. Our analysis is followed by comparing the full distribution of choices of activity level in both treatments using a Mann–Whitney U-Test. Lastly, we provide the results of an OLS regression where we regress participants’ choice of activity level on the treatment variable and a set of controls.
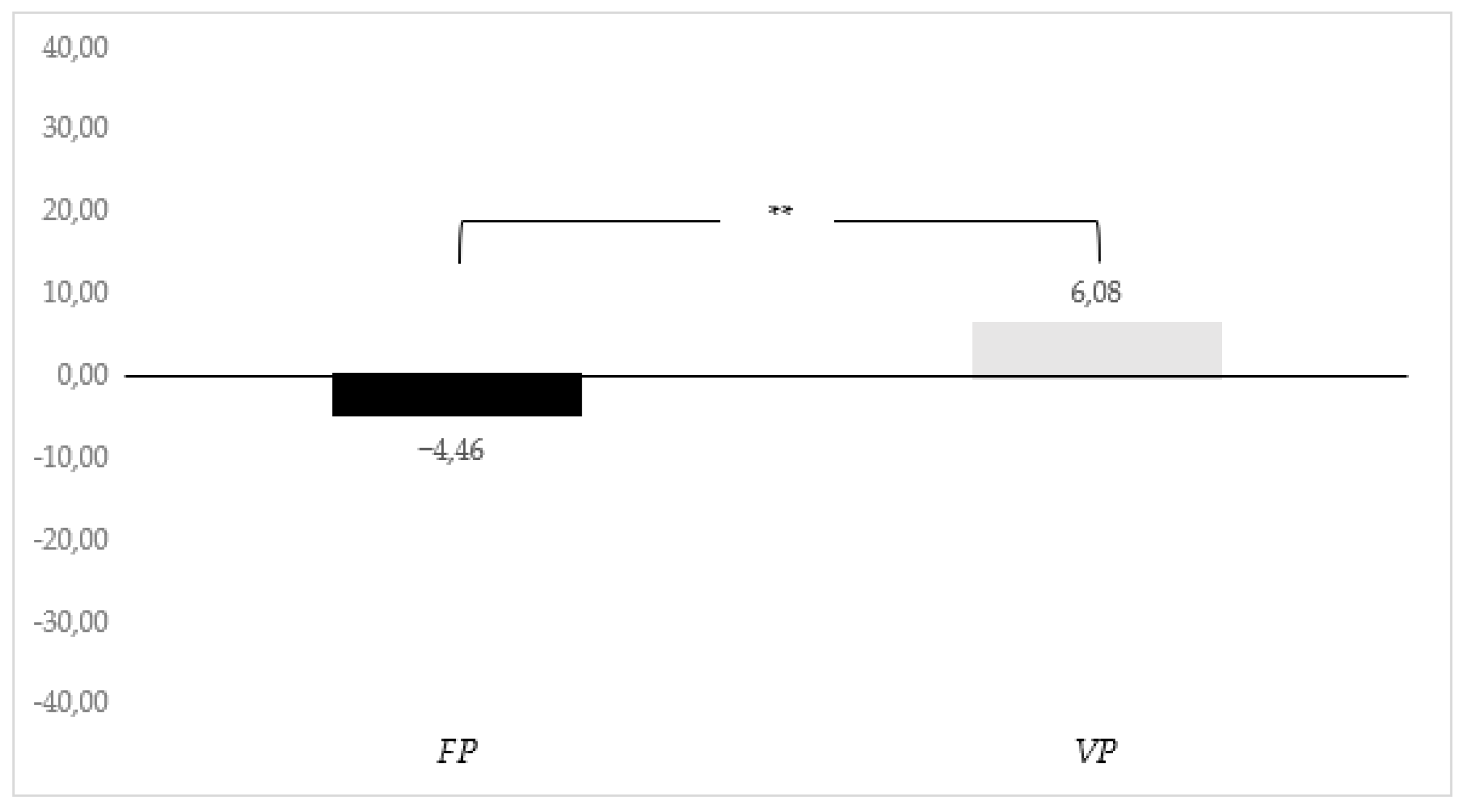
Figure 3 displays participants’ choice of activity level, where a mean activity level indicates that participants on average chose to help their group members, and a mean activity level indicates that participants on average chose to sabotage their group members. On average, participants in the fixed-prize tournament , in fact, chose to sabotage their group members (), while participants in the variable-prize treatment chose to help their group members . The difference is statistically highly significant at the 1% level.
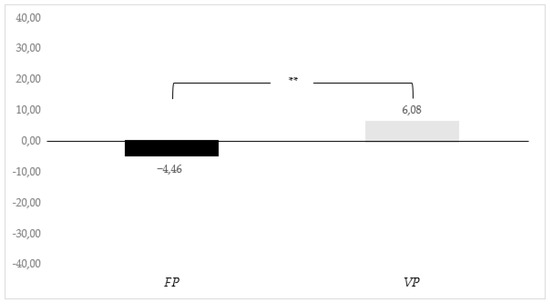
Figure 3.
Average help in vs. .
The differences in help between the two treatments are also highlighted in Table 3, which displays the absolute numbers and shares of participants who chose to help their group members (), sabotage their group members (), or neither help nor sabotage their group members (), separately for the two treatments. The differences between the two treatments are striking: While percent of participants in the fixed-prize treatment chose not to help their group members, less than percent of participants in the variable-prize treatment chose not to help them. Rather, the majority of participants ( percent) in the variable-prize treatment chose to help their group members and increased their output levels–even though this reduced their chances to win the tournament.

Table 3.
The decision to help or sabotage in vs. .
A binominal test reveals the differences between the two treatments to be statistically highly significant—irrespective of whether (a) we did not include the decisions of participants who chose to neither help nor sabotage (Panel A, Table 4), (b) included them as “help” (thus highlighting that the corresponding participants did not choose to sabotage their group members, Panel B, Table 4), or (c) included them as “sabotage” (highlighting that the corresponding participants did not choose to help their group members, Panel C, Table 4).

Table 4.
Binomial tests.
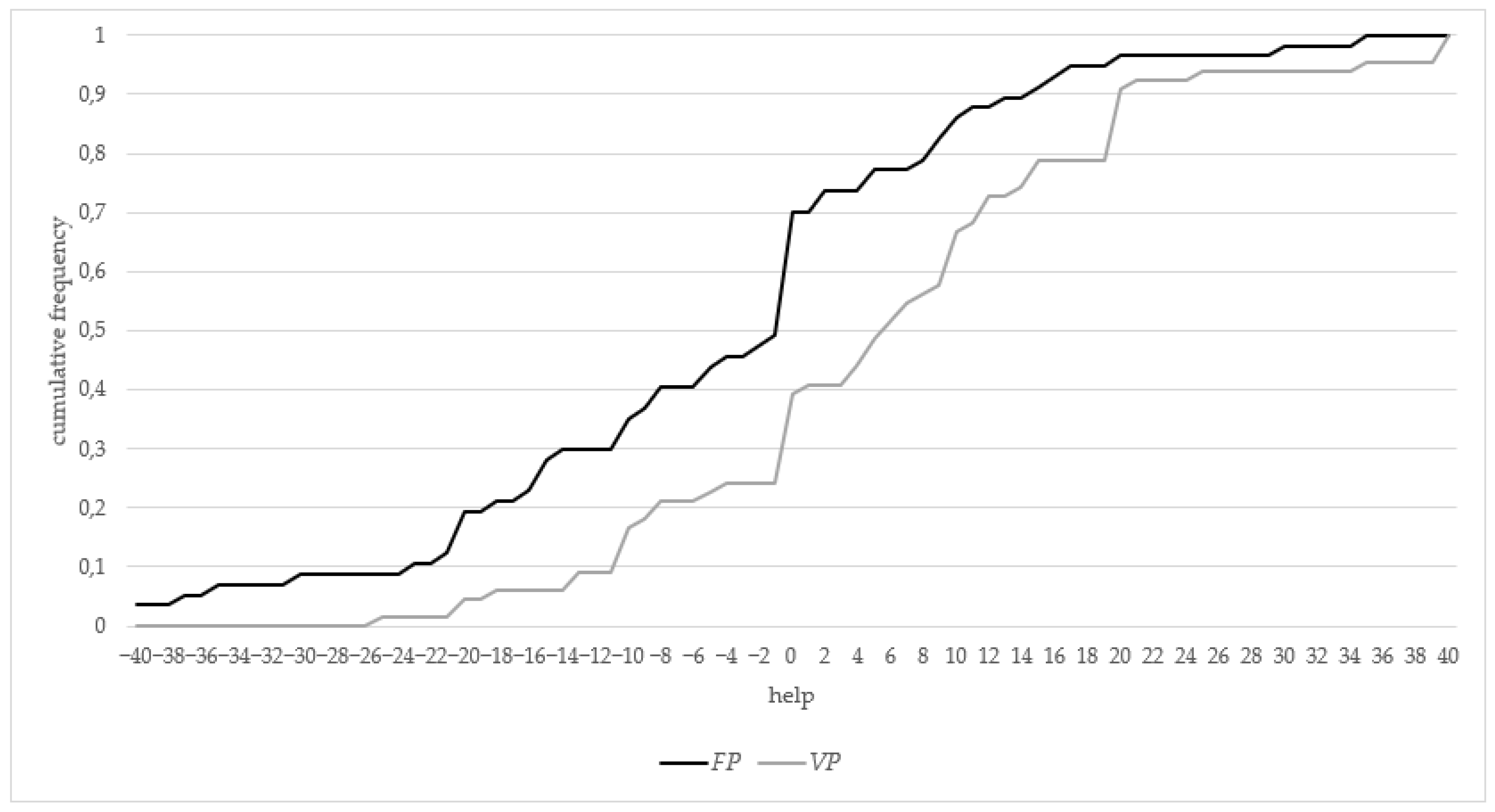
Figure 4 displays the distribution functions of participants’ helping (or sabotaging) behavior in the fixed-prize treatment and the variable-prize treatment . The differences between the two treatments are striking, with the distribution function in the fixed-prize treatment always lying over and above the distribution function for the variable-prize treatment —except for , the maximum level of help. That is, for each and every level of help below the maximum, the cumulative share of participants that offered the said or lower level of help is higher in than it is in . An additionally performed Mann—Whitney U-test also reveals that the two distributions are statistically significantly different from one another (see Table 5 for the details).
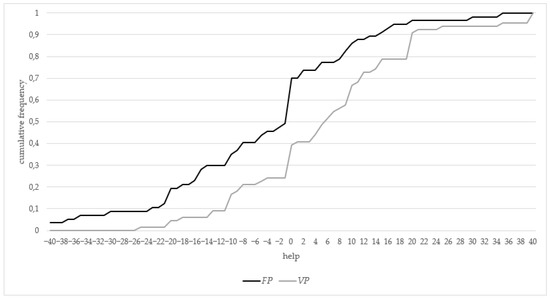
Figure 4.
Distribution functions of helping behavior in FP vs. VP.

Table 5.
Mann—Whitney U-Test.
Table 6 reports the results of several OLS regressions, where we regressed help on the treatment variable for the variable-prize tournament () and subsequently added participants’ effort choice and the controls from the post-experimental questionnaire. In all of our models, the coefficient for is positive and statistically significantly different from zero at the 1% level. That is, participants in the variable-prize treatment () chose a significantly higher level of help than participants in the fixed-prize treatment (). When adding further explanatory variables, the coefficient for the variable-prize treatment even increases in size. In our preferred model, in which we control for a whole set of variables (Model 3), approximately 14 percent of the variance in help are explained, hinting at a reasonable model fit.

Table 6.
OLS regressions for help.
To account for the fact that participants in our experiment first decided on whether they wanted to help or sabotage their group members and only subsequently decided to which extent they wanted to do so, we also ran Hurdle regressions (see Table A2 in Appendix B). We find the variable-prize tournament to be positively linked to choosing help and negatively linked to both choosing sabotage and to the extent of sabotage once the decision to sabotage had been taken. Once the participants decided to help their group members, the variable-prize tournament is, however, no longer linked to the extent to which participants chose to help their group members. As the Hurdle regression for the lower limit, i.e., the hurdle to help, is non-significant, we only display the respective results in the Table A2, Appendix B.
4.4. Utility Levels
Lastly, we compare participants’ (i.e., agents’) utility levels in the two treatments (Table 7). On average, participants made ECU 16.24 in the fixed-prize treatment and ECU 18.57 in the variable-prize treatment (prize money minus the costs of effort and help/sabotage). Hence, agents on average gain from the variable-prize treatment . Table 7 also adds the perspective of the (fictitious) principals. In the variable-prize treatment , the principal receives a considerably higher output per agent (39.18 output units in vs. 25.72 outputs units in ), but her payments per agent are also higher (ECU 23.84 in vs. ECU 21.6 in ). As long as 13.46 additional units of output per agent are worth more than the additional costs of ECU 2.24 per agent, the principals also gain from a variable-prize as opposed to a fixed-prize tournament.

Table 7.
Mean utilities by treatment.
5. Summary and Conclusions
We investigated whether variable tournament prizes that depend on agents’ joint output alleviate the sabotage problem inherent to (fixed-prize) tournament incentives. In a tournament model with three contestants, we compared the effects of a fixed- and a variable-prize tournament with respect to the induced effort levels and with respect to participants’ helping or sabotaging behavior, respectively. Our theoretical analysis suggests that, whenever there are positive incentive effects in a fixed-prize tournament, there are also incentives for the contestants to sabotage one another. To the contrary, in a variable-prize tournament where prizes depend on agents’ joint output, positive incentive effects might go hand in hand with an incentive to help one’s competitors.
We empirically tested the implications of our model with the help of a classroom experiment where we compared participants’ choices in a fixed-prize treatment () with those of a variable-prize treatment () in a between-subjects design. Given our parametrization, we expected efforts to be identical in both treatments, and we expected sabotage in the treatment and no sabotage in the treatment. In accordance with the model, we found that participants in the fixed-prize tournament sabotaged one another, whereas participants in the variable-prize tournament did not sabotage, but helped one another. At the same time, participants’ effort levels did not vary between the two tournaments. Even though the prize money awarded in the variable-prize tournament was (slightly) higher than the one awarded in the fixed-prize tournament, not only the agents, but also the principals would likely gain from variable- as opposed to fixed-prize tournaments. Introducing variable tournament prizes is hence apt to create a win-win situation.
Author Contributions
Conceptualization, T.G. and K.P.; methodology, T.G., K.P. and M.S.; software, T.G.; validation, T.G.; formal analysis, M.S.; investigation, T.G. and K.P.; resources, T.G., K.P., M.S.; data curation, T.G.; writing—original draft, K.P. and M.S.; writing—review and editing, T.G., K.P. and M.S.; visualization, T.G.; supervision, K.P.; project administration, K.P; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support by the Open Access Publishing Fund of the University of Tübingen.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the German Association for Experimental Economic Research e.V. (code no. dFC1UWjc, from 25 April 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Methods and protocols are described in detail to allow others to replicate and build on the published results. All materials, data, computer code, and protocols are available from the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Mathematical Appendix
An agent who exerts effort and activity , while the other two agents exert the equilibrium effort and the equilibrium , wins the tournament with probability:1
The derivatives of the probabilities with respect to effort and activity read:
In the symmetric equilibrium (, ), these derivatives simplify to:
and depend proportionally on the density of the uniform distribution.
The probability for the second rank is:
The derivatives of the probability with respect to effort and activity read:
In the symmetric equilibrium (, ), these derivatives simplify to:
Appendix B. Supplementary Results

Table A1.
OLS regressions for effort.
Table A1.
OLS regressions for effort.
| DV: Effort | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| VP | 1.012 | 2.101 | 2.047 |
| (1.716) | (1.692) | (1.775) | |
| Help | −0.103 + | −0.090 | |
| (0.058) | (0.643) | ||
| Positional Prefences | −0.432 | ||
| (0.960) | |||
| Risk Aversion | 0.127 | ||
| (0.460) | |||
| Nastiness | 0.096 | ||
| (0.537) | |||
| Female | −1.502 | ||
| (ref. category: male) | (2.086) | ||
| Diverse | 1.743 | ||
| (ref. category: male) | (3.983) | ||
| Extraversion | 1.479 | ||
| (1.133) | |||
| Agreeableness | 0.097 | ||
| (0.981) | |||
| Conscientiousness | −0.393 | ||
| (1.121) | |||
| Neuroticism | 0.645 | ||
| (1.080) | |||
| Openness | 0.871 | ||
| (0.978) | |||
| Constant | 29.246 ** | 28.785 ** | 20.791 ** |
| (1.363) | (1.372) | (7.364) | |
| Observations | 123 | 123 | 123 |
| R-squared | 0.003 | 0.031 | 0.068 |
Notes: Robust standard errors in parentheses. ** p < 0.01. * p < 0.05. + p < 0.10.

Table A2.
Hurdle regression.
Table A2.
Hurdle regression.
| DV: Help/Sabotage | Lower Limit = 0 | Upper Limit = 0 |
|---|---|---|
| 5.994 | 5.934 + | |
| (4.607) | (3.280) | |
| Effort | 0.686 | −0.742 ** |
| (0.283) | (0.174) | |
| Positional Prefences | −1.272 | 2.968 * |
| (1.684) | (1.429) | |
| Risk Aversion | 0.180 | 0.819 |
| (0.955) | (0.631) | |
| Nastiness | −1.032 | −0.790 + |
| (0.773) | (0.466) | |
| Female | −5.350 | 6.223 + |
| (ref. category: male) | (4.402) | (3.492) |
| Diverse | omitted | −5.511 |
| (ref. category: male) | (7.186) | |
| Extraversion | −2.308 | 0.074 |
| (2.155) | (1.683) | |
| Agreeableness | 0.383 | −1.744 |
| (2.481) | (1.831) | |
| Conscientiousness | 3.097 | −3.353 |
| (2.715) | (2.237) | |
| Neuroticism | −5.958 ** | −4.192 * |
| (2.187) | (1.713) | |
| Openness | −0.138 | 0.111 |
| (2.413) | (1.332) | |
| Constant | 25.120 | 26.321 + |
| (17.764) | (15.072) | |
| Selection | ||
| 1.027 ** | 0.877 ** | |
| (0.259) | (0.258) | |
| Effort | −0.0089 | −0.021 |
| (0.133) | (0.130) | |
| Positional Prefences | −0.124 | 0.027 |
| (0.141) | (0.140) | |
| Risk Aversion | 0.017 | 0.029 |
| (0.067) | (0.071) | |
| Nastiness | −0.153 * | −0.150 * |
| (0.067) | (0.062) | |
| Female | −0.524 | 0.105 |
| (ref. category: male) | (0.322) | (0.309) |
| Diverse | −5.376 ** | −0.518 |
| (ref. category: male) | (0.487) | 0.854 |
| Extraversion | 0.253 | 0.109 |
| (0.165) | (0.162) | |
| Agreeableness | 0.308 + | 0.151 |
| (0.172) | (0.174) | |
| Conscientiousness | −0.029 | 0.117 |
| (0.164) | (0.170) | |
| Neuroticism | 0.206 | 0.105 |
| (0.158) | (0.149) | |
| Openness | −0.177 | 0.487 |
| (0.122) | (0.126) | |
| Constant | −1.612 | −1.251 |
| (1.172) | (1.163) | |
| Observations | 123 | 123 |
| Prob > Chi² | 0.235 | 0.000 |
| Pseudo R-squared | 0.083 | 0.118 |
Notes: Robust standard errors in parentheses. ** p < 0.01. * p < 0.05. + p < 0.10.
Appendix C. Experimental Instructions
Welcome to our economic decision experiment! The data from the experiment will be treated completely confidentially and will only be evaluated in anonymous form. Therefore, please do not write your name or matriculation number on the survey forms. Participation in this experiment is voluntary. You can terminate your participation at any time without giving reasons and you will not suffer any disadvantages. All your decisions are anonymous, i.e. none of the other participants will know the identity of the person who made a certain decision. The payout is also anonymous, i.e. none of the other participants learns how much the payout of another participant is. Furthermore, no participant is told which other participants (s)he has been matched to. The participants of the experiment come from different study programs. The experiment consists of several sub-experiments. Please work on them one after the other and do not scroll back after you have completed a sub-experiment. Before working on a sub-experiment, please read the instructions for the sub-experiment very carefully. If there is anything you do not understand, please report it visibly. We will then come to you to answer your questions. Our experiment is about real money. Although the payouts in our experiment refer to a fictitious currency (“ECU” = Experimental Currency Unit), all payouts from the sub-experiments are added up at the end of the experiment and are converted into EUR. The exchange rate 1 ECU : 1 EUR is 2 : 1, which means that for two ECU you will receive one EUR at the end of the experiment. You will receive your payout from the experiment at the end of the lecture series. Please keep the sheet on which you determine your personal code word. After revealing your code word, you will receive your payout. The payment will be made in closed envelopes. Please note that only those participants who have taken part in all parts of the experiment and have completed the questionnaire will take part in the payout. It is of utmost importance that you complete all survey forms independently of the other participants and do not communicate with other participants during the experiment.
We thank you very much for your participation in our experiment!
Code word
Now please enter your code word first so that you can receive your payout from the experiment at the end of the lecture series. To generate the code word, please refer to the separate document ("Code word"). If you generate your code word according to the rule described there, you can reconstruct it at any time - even if you should have misplaced the separate document for generating the code word.
IMPORTANT: WITHOUT THIS CODEWORD NO PAYOUT IS POSSIBLE!
Your code word (eight characters, written on one line):
__ __ __ __ __ __ __ __
Part 1 of the experiment
In this first part of the experiment, you are in the role of an employee. After collecting the survey forms, you will be randomly assigned to two other participants who, together with you, will form a group consisting of a total of three employees. You will not be told the identity of the other two group members at any time. Likewise, the other two group members will not receive any information about your identity. For this sub-experiment, you will receive an initial allocation of 10 ECU.
Decisions
- (1)
- Work effort
Each of the three employees in a group chooses his/her work effort from the range {0,...,40}. Note that you can only choose integer values.
- (2)
- Sabotage/help
Then each of the three employees decides whether (s)he will sabotage or help the other two employees in his/her group, or whether (s)he will neither sabotage nor help the other employees in his/her group. In case of a decision for sabotage or help, each of the three employees chooses the amount of sabotage/help from the range {1,...,40}. Again, only integer values can be chosen. If you choose sabotage, the work result of the other two employees in your group will be reduced by the amount you have chosen. If you choose to help, the work result of the other two employees in your group will increase by the amount you have chosen. It is not possible to help only one employee in your group and sabotage the other. Also, the amount of sabotage/help you choose is identical for the two employees in your group. If you decide not to sabotage or help the other two employees in your group, the work result of the other two employees in your group will not change. Both the work effort you choose and the sabotage / assistance you choose will incur individual costs for you. The higher the work effort you choose and the higher the sabotage/help you choose, the higher the associated costs for you. An overview of the exact amount of the costs can be found in Table A3.
Work result
The work result of an employee in a group consists of his/her own, self-selected work effort, any help or sabotage by the other two employees in the group and a random number Z drawn individually for each employee. The random number Z is an integer and, after we have collected the survey questionnaires and randomly assigned your questionnaire to two other questionnaires, is drawn from a uniform distribution from −45 to +45, i.e., any integer number between −45 and +45 (including the two marginal values) is equally likely. The random number Z is determined independently for each employee in each group. The work result of an employee in a group increases with his/her own work effort. The work result also increases when (s)he is helped by other employees in the group. The work result decreases when (s)he is sabotaged by other employees in the group.
The work result of an employee is calculated as follows:
Work result = own, self-selected work effort + possible help by other employees of the group − possible sabotage by other employees of the group + random number Z.
There are several possibilities, e.g.,:
- -
- The other two employees in the group sabotage:
work result = own work effort − sabotage by one of the two employees − sabotage by the other of the two employees + random number Z
- -
- One of the other two employees in the group sabotages, one helps:
work result = own work effort − sabotage by the sabotaging employee + help by the helping employee + random number Z
- -
- The other two employees in the group help:
work result = own work effort + help from one of the two employees + help from the other of the two employees + random number Z
- -
- If none of the other employees in your group choose sabotage or help, your work result will only be affected by the effort you choose and the random number Z.
Payout
In order to determine the amount of the payout from part 1 of the experiment, the work results of the three employees of a group are compared with each other. Depending on how one's own work result compares to the other work results of the group, the following bonuses are awarded: The employee with the highest work result in the group will receive a bonus of 54 ECU. The employee with the second highest work result in the group will receive a bonus of 10.80 ECU. The employee with the third highest (i.e., lowest) work result in the group receives 0 ECU. Note that if two or even three employees in a group have an identical work result, it is randomly determined who gets the higher payout. In order to determine a participant’s payout from the first sub-experiment, the costs of the chosen own work effort as well as the costs of any chosen sabotage or help are subtracted from the awarded bonuses and the initial allocation. Specifically, your own payoff from the first sub-experiment (in ECU) is as follows:
Your payout = Initial allocation + your bonus from comparing your group’s work results-costs of the work effort you chose − costs of the sabotage/help you chose.
Please note that your payout from this first partial experiment could be negative (depending on the choices made by you and the other participants and the random numbers drawn), but that the total amount you will receive from participating in our experiment will not fall below 0 ECU. In order to give you a feeling for the effects of the decisions made by you and other participants and the random numbers, we have prepared an Excel sheet for you to non-bindingly play with various alternatives before conducting the actual experiment. You can find it under the link on the screen.

Table A3.
Overview of costs (in ECU) for own work effort and sabotage/help.
Table A3.
Overview of costs (in ECU) for own work effort and sabotage/help.
| Own Effort/Sabotage/Help | Costs (in ECU) | Own Effort/ Sabotage/Help | Costs (in ECU) |
|---|---|---|---|
| 0 | 0.00 | 21 | 5.51 |
| 1 | 0.01 | 22 | 6.05 |
| 2 | 0.05 | 23 | 6.61 |
| 3 | 0.11 | 24 | 7.20 |
| 4 | 0.20 | 25 | 7.81 |
| 5 | 0.31 | 26 | 8.45 |
| 6 | 0.45 | 27 | 9.11 |
| 7 | 0.61 | 28 | 9.80 |
| 8 | 0.80 | 29 | 10.51 |
| 9 | 1.01 | 30 | 11.25 |
| 10 | 1.25 | 31 | 12.01 |
| 11 | 1.51 | 32 | 12.80 |
| 12 | 1.80 | 33 | 13.61 |
| 13 | 2.11 | 34 | 14.45 |
| 14 | 2.45 | 35 | 15.31 |
| 15 | 2.81 | 36 | 16.20 |
| 16 | 3.20 | 37 | 17.11 |
| 17 | 3.61 | 38 | 18.05 |
| 18 | 4.05 | 39 | 19.01 |
| 19 | 4.51 | 40 | 20.00 |
| 20 | 5.00 |
In the following, we now ask for your decisions. Please do not omit any decision. Otherwise, you are unfortunately not able to participate in the payout.
Please select your work effort first. Please note that your work effort must be at least "0" and at most "40" and may only have integer values in between:
______________________________
Please now choose whether you want to help or sabotage the other two employees in your group or whether you want to neither help nor sabotage them. Please note that you may only tick one of the three options.
- □
- Help
- □
- Sabotage
- □
- Neither help nor sabotage
If you have selected “Neither help nor sabotage”: Please skip the following question about the extent of your help or sabotage.
If you have selected “Help” or “Sabotage”: Please select the extent of your help or sabotage in the next step. Please note that the extent of your help or sabotage must be at least “1” and max. “40” and may only have integer values in between.
______________________________
The first part of the experiment is completed.
Part 2 of the experiment
In this second sub-experiment, you have to take ten decisions. You are not playing with any other participant in this sub-experiment, so your decision only affects your own payoff. Each of your decisions is a choice between two alternatives. In each of the two alternatives, you can win a certain amount of money with probability p or another amount of money with the opposite probability 1-p. The two alternatives differ only in the amount of money, not in the probabilities. After collecting the survey forms, we first randomly draw which of the ten decisions will be relevant for the payoff of the participants. The alternative chosen by you in the decision in question then becomes relevant for your personal payout. To determine which specific amount of money you will receive from the alternative you have chosen a further lottery will be carried out based on the probabilities and amounts specified in the alternative you have chosen.
Please make the following choices now. Make sure that you choose exactly one option for each decision (no multiple choice). Please do not omit any decision. Otherwise, you are unfortunately not able to participate in the payout.
Decision 1:
□ with 10% probability ECU 4.00 or with 90% probability ECU 3.20 or:
□ with 10% probability ECU 7.70 or with 90% probability ECU 0.20
Decision 2:
□ with 20% probability ECU 4.00 or with 80% probability ECU 3.20 or:
□ with 20% probability ECU 7.70 or with 80% probability ECU 0.20
Decision 3:
□ with 30% probability ECU 4.00 or with 70% probability ECU 3.20 or:
□ with 30% probability ECU 7.70 or with 70% probability ECU 0.20
Decision 4:
□ with 40% probability ECU 4.00 or with 60% probability ECU 3.20 or:
□ with 40% probability ECU 7.70 or with 60% probability ECU 0.20
Decision 5:
□ with 50% probability ECU 4.00 or with 50% probability ECU 3.20 or:
□ with 50% probability ECU 7.70 or with 50% probability ECU 0.20
Decision 6:
□ with 60% probability ECU 4.00 or with 40% probability ECU 3.20 or:
□ with 60% probability ECU 7.70 or with 40% probability ECU 0.20
Decision 7:
□ with 70% probability ECU 4.00 or with 30% probability ECU 3.20 or:
□ with 70% probability ECU 7.70 or with 30% probability ECU 0.20
Decision 8:
□ with 80% probability ECU 4.00 or with 20% probability ECU 3.20 or:
□ with 80% probability ECU 7.70 or with 20% probability ECU 0.20
Decision 9:
□ with 90% probability ECU 4.00 or with 10% probability ECU 3.20 or:
□ with 90% probability ECU 7.70 or with 10% probability ECU 0.20
Decision 10:
□ with 100% probability ECU 4.00 or with 0% probability ECU 3.20 or:
□ with 100% probability ECU 7.70 or with 0% probability ECU 0.20
The second part of the experiment is completed.
Part 3 of the experiment
In this third part of the experiment, you take three decisions. In this part of the experiment, you again play together with other participants. Specifically, after all the data collection sheets have been collected, you will be randomly assigned to another participant for this part of the experiment. The assignment will be made anew, i.e. it is very unlikely that you will be assigned to the same experiment participant as in other sub-experiments. For each of the three decisions, you have a choice between two payout structures. A payout structure determines how much money will be paid to you and how much will be paid to the other experiment participant who is randomly assigned to you.
Example:
Decision: Choose the payout structure you prefer:
You receive 2 ECU, the other experiment participant receives 0 ECU. Or:
You receive 1 ECU, the other experiment participant receives 1 ECU.
This means that by deciding between the two payout structures, you decide whether you receive 2 ECU and the experiment participant assigned to you receives 0 ECU (first option) or whether each of you receive 1 ECU instead (second option). After each participant in the experiment has been randomly assigned to another participant after the collection of the survey forms, one of the six decisions made by the two participants in total is randomly drawn for each pair of participants, and the payouts are made on this basis. This means that if you had chosen the first payout structure in the above example, and this decision had been randomly drawn later, you would receive 2 ECU and the participant assigned to you would receive 0 ECU.
Please now take the following decisions. Make sure that you choose exactly one option for each decision (no multiple choice). Please do not skip any decision. Otherwise you are unfortunately not able to participate in the payout.
1st Decision: Choose your preferred payout structure:
□ You will receive 8 ECU, the other experiment participant will receive 8 ECU. Or:
□ You will receive 8 ECU, the other participant in the experiment will receive 4 ECU.
2nd Decision: Choose your preferred payout structure:
□ You will receive 4 ECU, the other experiment participant will receive 8 ECU. Or:
□ You will receive 4 ECU, the other experiment participant will receive 4 ECU.
3rd Decision: Choose your preferred payout structure:
□ You will receive 6 ECU, the other participant in the experiment will receive 8 ECU. Or:
□ You will receive 6 ECU, the other participant in the experiment will receive 4 ECU.
The third part of the experiment is hereby completed.
Part 4 of the experiment
In this fourth part of the experiment, you will again be assigned to a different participant after collecting the questionnaires. The assignment will be made anew, i.e. it is very unlikely that you will be assigned to the same participant as in other sub-experiments.
In this fourth part of the experiment you now have the possibility to reduce the payout of the randomly assigned participant by a maximum of 8 ECU (in steps of 1.00 ECU). The participant randomly assigned to you will also decide on the extent to which your payout will be reduced.
Please tick the extent to which you wish to reduce the payout of the other participant assigned to you:
Be sure to select only one amount (no multiple choice).
□ ECU 0.00
□ ECU 1.00
□ ECU 2.00
□ ECU 3.00
□ ECU 4.00
□ ECU 5.00
□ ECU 6.00
□ ECU 7.00
□ ECU 8.00
The fourth part experiment is completed.
Part 5 of the experiment
Finally, we have a few questions for you. These questions are also part of the experiment. Therefore, please do not omit any questions and answer all questions truthfully and to the best of your knowledge.
Which gender do you feel you most closely belong to?
- □
- Male
- □
- Female
- □
- Diverse
How do you rate yourself personally: How willing are you to take risks in general?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| □ | □ | □ | □ | □ | □ | □ |
| 1 = not at all willing to take risks | ||||||
| 7 = very risky | ||||||
Here are different qualities that a person may have. Probably some qualities will apply to you personally fully and others not at all. For still others, you may be undecided. Please answer using the following scale (please answer all questions).
| Does not apply at all | Fully applicable | ||||
| 1 | 2 | 3 | 4 | 5 | |
| I’m more reserved, distant. | □ | □ | □ | □ | □ |
| I trust others easily, believe in the good in people. | □ | □ | □ | □ | □ |
| I’m comfortable, prone to laziness. | □ | □ | □ | □ | □ |
| I’m relaxed, I don’t let stress get to me. | □ | □ | □ | □ | □ |
| I have little artistic interest. | □ | □ | □ | □ | □ |
| I come out of my shell, I’m social. | □ | □ | □ | □ | □ |
| I tend to criticize others. | □ | □ | □ | □ | □ |
| I do tasks thoroughly. | □ | □ | □ | □ | □ |
| I get nervous and insecure easily. | □ | □ | □ | □ | □ |
| I have an active imagination, am imaginative. | □ | □ | □ | □ | □ |
The experiment is completed.
We thank you for your participation!
Note
| 1 | The general marginal probabilities for the different ranks in the tournaments depending on the distribution functions of the error term are presented in Akerlof and Holden [18]. |
References
- Kempf, A.; Ruenzi, S. Tournaments in mutual-fund families. Rev. Finan. Stud. 2008, 21, 1013–1036. [Google Scholar] [CrossRef]
- Backes-Gellner, U.; Pull, K. Tournament compensation systems, employee heterogeneity, and firm performance. Hum. Resour. Manag. 2013, 52, 375–398. [Google Scholar] [CrossRef]
- Casas-Arce, P.; Martinez-Jerez, F.A. Relative performance compensation, contests, and dynamic incentives. Manag. Sci. 2009, 55, 1306–1320. [Google Scholar] [CrossRef]
- Danilov, A.; Harbring, C.; Irlenbusch, B. Helping under a combination of team and tournament incentives. J. Econ. Behav. Org. 2019, 162, 120–135. [Google Scholar] [CrossRef]
- Güth, W.; Levínský, R.; Pull, K.; Weisel, O. Tournaments and piece rates revisited: A theoretical and experimental study of output-dependent prize tournaments. Rev. Econ. Des. 2016, 20, 69–88. [Google Scholar] [CrossRef]
- Lazear, E.P.; Rosen, S. Rank-order tournaments as optimum labor contracts. J. Pol. Econ. 1981, 89, 841–864. [Google Scholar] [CrossRef]
- Kräkel, M. U-type versus J-type Tournaments as Alternative Solutions to the Unverifiability Problem. Labour Econ. 2003, 10, 359–380. [Google Scholar] [CrossRef]
- Schöttner, A. Precision in u-type and j-type tournaments. Schmalenbach Bus. Rev. 2005, 57, 167–192. [Google Scholar] [CrossRef]
- Bevia, C.; Corchón, L.C. Rational sabotage in cooperative production with heterogeneous agents. BE J. Theor. Econ. 2006, 6, 1–27. [Google Scholar] [CrossRef]
- Cason, T.N.; Masters, W.A.; Sheremeta, R.M. Entry into winner-take-all and proportional-prize contests: An experimental study. J. Public Econ. 2010, 94, 604–611. [Google Scholar] [CrossRef]
- Lazear, E.P. Pay equality and industrial politics. J. Pol. Econ. 1989, 97, 561–580. [Google Scholar] [CrossRef]
- Harbring, C.; Irlenbusch, B. Incentives in tournaments with endogenous prize selection. J. Inst. Theor. Econ. 2005, 161, 636–663. [Google Scholar] [CrossRef]
- Harbring, C.; Irlenbusch, B. Sabotage in tournaments: Evidence from a laboratory experiment. Manag. Sci. 2011, 57, 611–627. [Google Scholar] [CrossRef]
- Ayaita, A.; Pull, K. Positional preferences and narcissism: Evidence from ‘money burning’ dictator games. Appl. Econ. Lett. 2022, 29, 267–271. [Google Scholar] [CrossRef]
- Abbink, K.; Sadrieh, A. The pleasure of being nasty. Econ. Lett. 2009, 105, 306–308. [Google Scholar] [CrossRef]
- Rammstedt, B.; Kemper, C.J.; Klein, M.C.; Beierlein, C.; Kovaleva, A. A short scale for assessing the big five dimensions of personality: 10 item big five inventory (BFI-10). Methods Data Anal. 2013, 7, 17. [Google Scholar]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Akerlof, R.J.; Holden, R.T. The nature of tournaments. Econ. Theory 2012, 51, 289–313. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).