What Can Game Theory Tell Us about an AI ‘Theory of Mind’?
Abstract
:1. Introduction
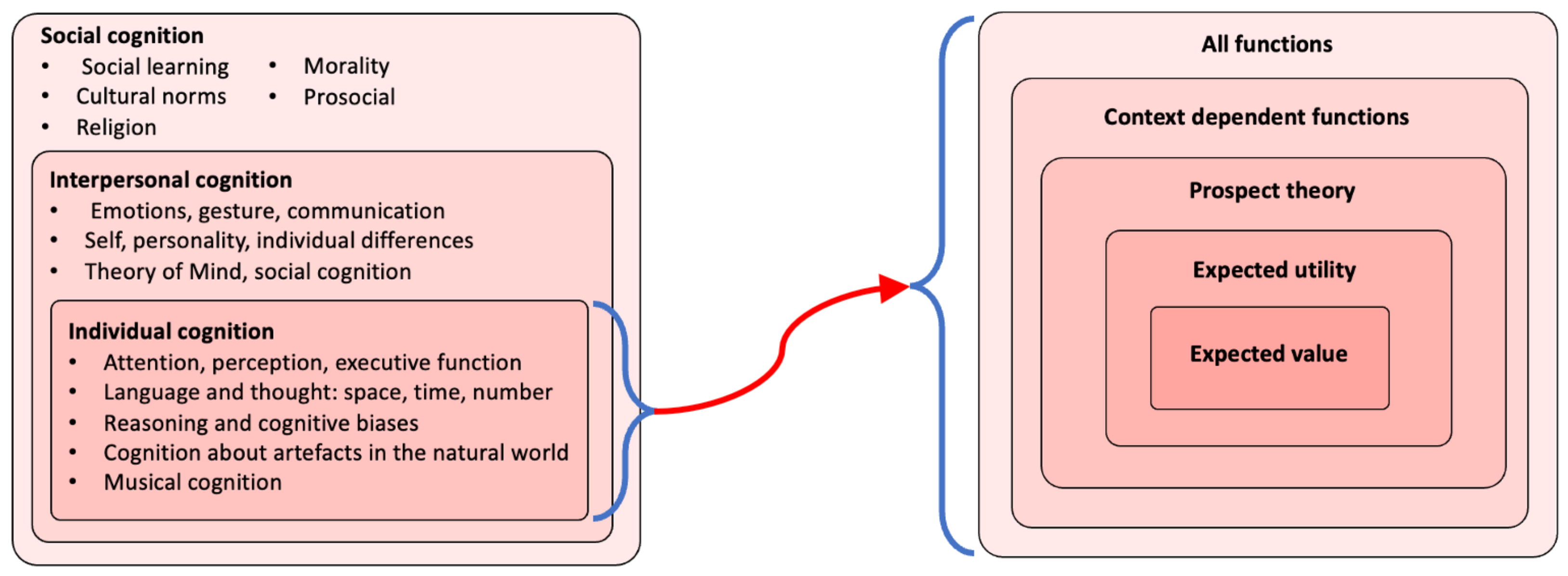
1.1. Individual Cognition
1.2. Social Constraints
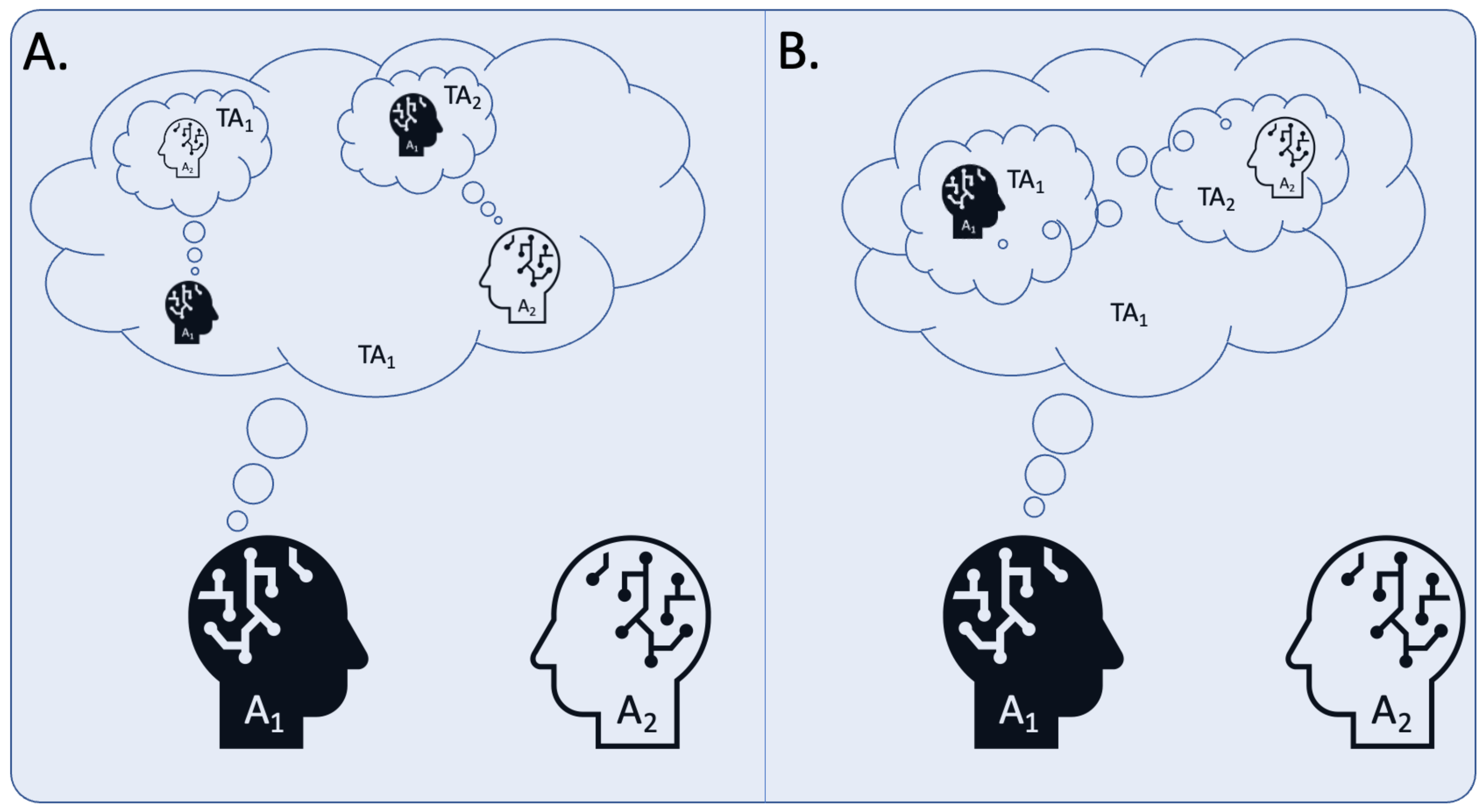
1.3. Theory of Mind and Introspection
2. The ‘Game Theory of Mind’: Neuroscience and Economics in Strategic Interactions
3. The Importance of a Theory of Mind in Human-to-Human Interactions
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Churchill, E.; Maes, P.; Fan, X.; Shneiderman, B.; Shi, Y.; Wang, Q. From human-human collaboration to Human-AI collaboration: Designing AI systems that can work together with people. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; pp. 1–6. [Google Scholar]
- Dellermann, D.; Calma, A.; Lipusch, N.; Weber, T.; Weigel, S.; Ebel, P. The future of human-AI collaboration: A taxonomy of design knowledge for hybrid intelligence systems. arXiv 2021, arXiv:2105.03354. [Google Scholar]
- Bian, L.; Baillargeon, R. When Are Similar Individuals a Group? Early Reasoning About Similarity and In-Group Support. Psychol. Sci. 2022, 33, 752–764. [Google Scholar] [CrossRef] [PubMed]
- Halberstam, Y.; Knight, B. Homophily, group size, and the diffusion of political information in social networks: Evidence from Twitter. J. Public Econ. 2016, 143, 73–88. [Google Scholar] [CrossRef]
- Colleoni, E.; Rozza, A.; Arvidsson, A. Echo chamber or public sphere? Predicting political orientation and measuring political homophily in Twitter using big data. J. Commun. 2014, 64, 317–332. [Google Scholar] [CrossRef]
- Barrett, H.C. Towards a cognitive science of the human: Cross-cultural approaches and their urgency. Trends Cogn. Sci. 2020, 24, 620–638. [Google Scholar] [CrossRef]
- Peterson, J.C.; Bourgin, D.D.; Agrawal, M.; Reichman, D.; Griffiths, T.L. Using large-scale experiments and machine learning to discover theories of human decision-making. Science 2021, 372, 1209–1214. [Google Scholar] [CrossRef]
- Awad, E.; Dsouza, S.; Kim, R.; Schulz, J.; Henrich, J.; Shariff, A.; Bonnefon, J.F.; Rahwan, I. The moral machine experiment. Nature 2018, 563, 59–64. [Google Scholar] [CrossRef]
- Frith, C.; Frith, U. Theory of mind. Curr. Biol. 2005, 15, R644–R645. [Google Scholar] [CrossRef] [Green Version]
- Korkmaz, B. Theory of mind and neurodevelopmental disorders of childhood. Pediatr. Res. 2011, 69, 101–108. [Google Scholar] [CrossRef]
- Hughes, C.; Leekam, S. What are the links between theory of mind and social relations? Review, reflections and new directions for studies of typical and atypical development. Soc. Dev. 2004, 13, 590–619. [Google Scholar] [CrossRef]
- Jack, A.I.; Roepstorff, A. Introspection and cognitive brain mapping: From stimulus–response to script–report. Trends Cogn. Sci. 2002, 6, 333–339. [Google Scholar] [CrossRef]
- Boring, E.G. A history of introspection. Psychol. Bull. 1953, 50, 169. [Google Scholar] [CrossRef] [PubMed]
- Gonzales, C.R.; Fabricius, W.V.; Kupfer, A.S. Introspection plays an early role in children’s explicit theory of mind development. Child Dev. 2018, 89, 1545–1552. [Google Scholar] [CrossRef]
- Newby, G.B. Cognitive space and information space. J. Am. Soc. Inf. Sci. Technol. 2001, 52, 1026–1048. [Google Scholar] [CrossRef]
- Breckler, S.J.; Pratkanis, A.R.; McCann, C.D. The representation of self in multidimensional cognitive space. Br. J. Soc. Psychol. 1991, 30, 97–112. [Google Scholar] [CrossRef]
- Shevlin, H.; Halina, M. Apply rich psychological terms in AI with care. Nat. Mach. Intell. 2019, 1, 165–167. [Google Scholar] [CrossRef]
- Yoshida, W.; Dolan, R.J.; Friston, K.J. Game theory of mind. PLoS Comput. Biol. 2008, 4, e1000254. [Google Scholar] [CrossRef]
- Barraclough, D.J.; Conroy, M.L.; Lee, D. Prefrontal cortex and decision making in a mixed-strategy game. Nat. Neurosci. 2004, 7, 404–410. [Google Scholar] [CrossRef]
- Schultz, W. Neural coding of basic reward terms of animal learning theory, game theory, microeconomics and behavioural ecology. Curr. Opin. Neurobiol. 2004, 14, 139–147. [Google Scholar] [CrossRef]
- Lee, D. Game theory and neural basis of social decision making. Nat. Neurosci. 2008, 11, 404–409. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral game theory and the neural basis of strategic choice. In Neuroeconomics; Elsevier: Amsterdam, The Netherlands, 2009; pp. 193–206. [Google Scholar]
- Harré, M.S. Strategic information processing from behavioural data in iterated games. Entropy 2018, 20, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ong, W.S.; Madlon-Kay, S.; Platt, M.L. Neuronal correlates of strategic cooperation in monkeys. Nat. Neurosci. 2021, 24, 116–128. [Google Scholar] [CrossRef] [PubMed]
- Montague, P.R.; Berns, G.S.; Cohen, J.D.; McClure, S.M.; Pagnoni, G.; Dhamala, M.; Wiest, M.C.; Karpov, I.; King, R.D.; Apple, N.; et al. Hyperscanning: Simultaneous fMRI during linked social interactions. Neuroimage 2002, 16, 1159–1164. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, M.; Camerer, C.F. Self-referential thinking and equilibrium as states of mind in games: fMRI evidence. Games Econ. Behav. 2005, 52, 424–459. [Google Scholar] [CrossRef] [Green Version]
- Fukui, H.; Murai, T.; Shinozaki, J.; Aso, T.; Fukuyama, H.; Hayashi, T.; Hanakawa, T. The neural basis of social tactics: An fMRI study. Neuroimage 2006, 32, 913–920. [Google Scholar] [CrossRef] [Green Version]
- Kuss, K.; Falk, A.; Trautner, P.; Montag, C.; Weber, B.; Fliessbach, K. Neuronal correlates of social decision making are influenced by social value orientation—An fMRI study. Front. Behav. Neurosci. 2015, 9, 40. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.H.; Chen, Y.C.; Kuo, W.J.; Kan, K.; Yang, C.; Yen, N.S. Strategic motives drive proposers to offer fairly in Ultimatum games: An fMRI Study. Sci. Rep. 2017, 7, 527. [Google Scholar] [CrossRef] [Green Version]
- Shaw, D.J.; Czekóová, K.; Staněk, R.; Mareček, R.; Urbánek, T.; Špalek, J.; Kopečková, L.; Řezáč, J.; Brázdil, M. A dual-fMRI investigation of the iterated Ultimatum Game reveals that reciprocal behaviour is associated with neural alignment. Sci. Rep. 2018, 8, 10896. [Google Scholar] [CrossRef] [Green Version]
- Griessinger, T.; Coricelli, G. The neuroeconomics of strategic interaction. Curr. Opin. Behav. Sci. 2015, 3, 73–79. [Google Scholar] [CrossRef]
- Yoshida, W.; Seymour, B.; Friston, K.J.; Dolan, R.J. Neural mechanisms of belief inference during cooperative games. J. Neurosci. 2010, 30, 10744–10751. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A. A model of noisy introspection. Games Econ. Behav. 2004, 46, 365–382. [Google Scholar] [CrossRef] [Green Version]
- McKelvey, R.D.; Palfrey, T.R. Quantal response equilibria for normal form games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Wolpert, D.; Jamison, J.; Newth, D.; Harré, M. Strategic choice of preferences: The persona model. J. Theor. Econ. 2011, 11, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H.; Harré, M.; Olbrich, E.; Bertschinger, N.; Jost, J. Hysteresis effects of changing the parameters of noncooperative games. Phys. Rev. E 2012, 85, 036102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harré, M.S.; Atkinson, S.R.; Hossain, L. Simple nonlinear systems and navigating catastrophes. Eur. Phys. J. B 2013, 86, 289. [Google Scholar] [CrossRef]
- Leonardos, S.; Piliouras, G.; Spendlove, K. Exploration-Exploitation in Multi-Agent Competition: Convergence with Bounded Rationality. Adv. Neural Inf. Process. Syst. 2021, 34, 26318–26331. [Google Scholar]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Regular quantal response equilibrium. Exp. Econ. 2005, 8, 347–367. [Google Scholar] [CrossRef] [Green Version]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Quantal response equilibrium. In Quantal Response Equilibrium; Princeton University Press: Hoboken, NJ, USA, 2016. [Google Scholar]
- Rilling, J.K.; Sanfey, A.G.; Aronson, J.A.; Nystrom, L.E.; Cohen, J.D. The neural correlates of theory of mind within interpersonal interactions. Neuroimage 2004, 22, 1694–1703. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Harré, M. It can be smart to be dumb. 2008; Preprint. [Google Scholar]
- Takagishi, H.; Koizumi, M.; Fujii, T.; Schug, J.; Kameshima, S.; Yamagishi, T. The role of cognitive and emotional perspective taking in economic decision making in the ultimatum game. PLoS ONE 2014, 9, e108462. [Google Scholar] [CrossRef] [Green Version]
- Takagishi, H.; Kameshima, S.; Schug, J.; Koizumi, M.; Yamagishi, T. Theory of mind enhances preference for fairness. J. Exp. Child Psychol. 2010, 105, 130–137. [Google Scholar] [CrossRef] [Green Version]
- Lang, H.; DeAngelo, G.; Bongard, M. Theory of Mind and General Intelligence in Dictator and Ultimatum Games. Games 2018, 9, 16. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, R.I. Neocortex size as a constraint on group size in primates. J. Hum. Evol. 1992, 22, 469–493. [Google Scholar] [CrossRef]
- Dunbar, R.I. The social brain hypothesis. Evol. Anthropol. Issues News Rev. Issues News Rev. 1998, 6, 178–190. [Google Scholar] [CrossRef]
- Dunbar, R.I.; Arnaboldi, V.; Conti, M.; Passarella, A. The structure of online social networks mirrors those in the offline world. Soc. Netw. 2015, 43, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Harré, M.S.; Prokopenko, M. The social brain: Scale-invariant layering of Erdős–Rényi networks in small-scale human societies. J. R. Soc. Interface 2016, 13, 20160044. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, R.I.; Shultz, S. Evolution in the social brain. Science 2007, 317, 1344–1347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powell, J.L.; Lewis, P.A.; Dunbar, R.I.; García-Fiñana, M.; Roberts, N. Orbital prefrontal cortex volume correlates with social cognitive competence. Neuropsychologia 2010, 48, 3554–3562. [Google Scholar] [CrossRef]
- Stiller, J.; Dunbar, R.I. Perspective-taking and memory capacity predict social network size. Soc. Netw. 2007, 29, 93–104. [Google Scholar] [CrossRef]
- Lewis, P.A.; Rezaie, R.; Brown, R.; Roberts, N.; Dunbar, R.I. Ventromedial prefrontal volume predicts understanding of others and social network size. Neuroimage 2011, 57, 1624–1629. [Google Scholar] [CrossRef]
- Harré, M.S. Information theory for agents in artificial intelligence, psychology, and economics. Entropy 2021, 23, 310. [Google Scholar] [CrossRef]
- Ert, E.; Erev, I.; Roth, A.E. A choice prediction competition for social preferences in simple extensive form games: An introduction. Games 2011, 2, 257–276. [Google Scholar] [CrossRef] [Green Version]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Connors, M.H.; Burns, B.D.; Campitelli, G. Expertise in complex decision making: The role of search in chess 70 years after de Groot. Cogn. Sci. 2011, 35, 1567–1579. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ericsson, K.A. Superior Working Memory in Experts. 2018. Available online: https://www.cambridge.org/core/books/abs/cambridge-handbook-of-expertise-and-expert-performance/superior-working-memory-in-experts/8979912B089C15FC7049AC46F940D012 (accessed on 29 April 2022).
- Gobet, F.; Charness, N. Expertise in Chess. 2018. Available online: https://psycnet.apa.org/record/2006-10094-030 (accessed on 29 April 2022).
- Harré, M.; Snyder, A. Intuitive expertise and perceptual templates. Minds Mach. 2012, 22, 167–182. [Google Scholar] [CrossRef]
- Harré, M.; Bossomaier, T.; Snyder, A. The perceptual cues that reshape expert reasoning. Sci. Rep. 2012, 2, 502. [Google Scholar] [CrossRef] [PubMed] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harré, M.S. What Can Game Theory Tell Us about an AI ‘Theory of Mind’? Games 2022, 13, 46. https://doi.org/10.3390/g13030046
Harré MS. What Can Game Theory Tell Us about an AI ‘Theory of Mind’? Games. 2022; 13(3):46. https://doi.org/10.3390/g13030046
Chicago/Turabian StyleHarré, Michael S. 2022. "What Can Game Theory Tell Us about an AI ‘Theory of Mind’?" Games 13, no. 3: 46. https://doi.org/10.3390/g13030046
APA StyleHarré, M. S. (2022). What Can Game Theory Tell Us about an AI ‘Theory of Mind’? Games, 13(3), 46. https://doi.org/10.3390/g13030046





