1. Introduction
The experimental literature on contests often reports significant overspending of subjects compared to the Nash equilibrium—see, [
1,
2,
3,
4], among others, and [
5] for a survey of experimental research on contests. We propose a theoretical rationale for overspending in Tullock contests ([
6]) which is based on the standard level-
k model.
We adopt a standard level-
k model, which works as follows. A player of depth of reasoning
k, or a level-
k player (henceforth, in short, “an
-player”), believes that the other players are
, and thus “best responds” to this belief. In particular,
-players best respond to all other players playing the strategy of
-players,
-players best respond to all other players playing the strategy of
-players, and so on. (Some alternatives of behavior of types
and higher have been proposed. For instance, in [
7,
8] while
-players best respond to uniformly playing
-players,
-players best respond to a mixture of
-players and
-players, and so on. Another alternative is [
9], where
-players best respond to an estimated mixture of players of lower
k, via a one-parameter Poisson distribution. In the present paper, we choose the most simple and common approach that
best responds to all others being
).
-players are nonstrategic in that they form no beliefs over the opponents’ actions and rather play an instinctive reaction to the game. It is common in the literature to assume that
-players uniformly mix over all possible actions ([
7,
8,
9,
10,
11,
12,
13,
14]) and this is backed up by empirical findings. An alternative approach is that
-players choose a salient or intuitive action, also known as a “focal point”. However, as reported by [
13], “the evidence […] generally supports level-
k models in which players anchor beliefs in a uniform random
”.
Furthermore, the literature on auctions often runs parallel to that on contests. Overbidding in auctions has also been documented empirically/experimentally (see, [
15] for an overview) and can in private-value auctions be rationalized by level-
k models ([
12]). We bridge the existing gap between the auction and contest literature by showing that overbidding can also be true in a contest environment due to level-
k reasoning.
In general, there are two main branches of theoretical models that have been proposed to explain overspending. The first branch of models drops the standard specification of the expected utility function of subjects, e.g., assuming an extra non-monetary utility derived either from winning (see [
16] for the case of contests and [
17,
18] for the case of auctions) or from relative payoff (e.g., [
19]), or assuming that subjects assign a distorted value to the probability of winning (e.g., [
20]).
The second branch of models to which this paper belongs suggests that players do not work out all the necessary steps to compute the Nash equilibrium, i.e., subjects are boundedly rational. Two approaches to bounded rationality models are common in the literature. The first is through quantal response equilibrium (QRE) models (see [
21]), where the probability of a certain action is increased with the expected payoff of that action. Applications of QRE models to contests can be found in [
22,
23,
24]. For auctions, overspending based on QRE is shown by [
25]. The second is through level-
k models; for auctions, [
12] show that level-
k models can rationalize overbidding. We provide the missing link that shows that a similar result can be obtained in the realm of contests.
To our knowledge, the only paper applying level-
k models to contests is [
26]. He studied a two-player symmetric Tullock contest and showed that overspending compared to the Nash equilibrium did not occur. This creates a divide between the auction and contest literature where the results are not the same from one literature to the other. We argue that [
26] is a special case and that extending the framework to either more players or allowing for asymmetric players may yield an overspending result in line with the aforementioned parallelism between the literature on auctions and contests. A summary of the link between the contest and auction literature that we contribute to is summarized in
Table 1.
Our main argument relies on the observation that, in a two-player symmetric Tullock contest, the Nash equilibrium is situated at the peak of both players’ best response functions. In such a situation, there is no scope for overspending since the Nash equilibrium is already at the maximum of the players’ best response functions, and hence there is no belief for a best-responding player about the rival’s behavior that would make them exert more effort than their Nash equilibrium one.
In turn, there is no assumption on the behavior of
-players that would make an
player exert strictly more effort than in the Nash equilibrium, even if one were to cherry-pick the actions of the
-players. As noted by [
27] among others, one could always find an arbitrarily cherry-picked behavior of
-players so as to rationalize any individually rational action of
-players, if no further restrictions are imposed. However, in the present paper, we tie our hands by imposing that
-players randomize uniformly over the space of positive efforts with a given upper-bound. Thus, our exercise of rationalizing overspending for any given such upper-bound is non-trivial.
However, we show that it is sufficient to drop one of the main two assumptions in [
26]—namely, symmetry or having two players—to find overspending already for
-players; the intuition relies on the Nash equilibrium no longer being at the peak of the best response function. In particular, we find that overspending occurs in two-player, sufficiently asymmetric contests and in three-player symmetric contests; see, respectively, Propositions 2 and 3. Note that a minimal level of asymmetry is required; otherwise, the Nash equilibrium would be too close to the peak of the best response function.
Hence, despite the level-k model failing to provide a unifying explanation for the phenomenon of overspending in contests, we show that the level-k model can rationalize overspending when departing from the two-player symmetric setting. Therefore, we see our results as a step toward a robust hybrid model of player thinking, including other behavioral models, which could well explain overbidding across different contest settings.
Our theoretical results are also consistent with empirical evidence other than the possibility of overspending. First, the fact that overspending increases with the number of bidders (e.g., [
28]) is consistent with our result that moving from two to three players makes overspending strictly positive for some parameter values. Second, the heterogeneity of contestants’ behavior facing identical contests (e.g., [
4]) is consistent with the fact that the depth of reasoning and the realization of the
’s random behavior may differ across players.
The structure of the paper is as follows. In
Section 2, we introduce the standard model of Tullock contest. In
Section 3, we provide benchmark results for the Nash equilibrium as well as level-
k results in the case of a two-player symmetric contest—thus, paralleling the results of [
26]. In
Section 4, we show that overspending may occur in two-player asymmetric contests, and in
Section 5, in three-player symmetric contests.
Section 6 discusses the results and briefly mentions the level-2 case. Proofs that do not follow directly from the main text are relegated to
Appendix A.
2. Model
Consider a complete information Tullock-contest with
n risk-neutral players indexed by
. Players compete for a prize whose value, without loss of generality, normalizes to 1. Each player
i chooses effort level
and has a probability of winning the prize equal to
, where
and
. If all efforts are 0, the prize is awarded with a fixed probability strictly less than 1 to each player. (This situation is never reached in equilibrium.) The cost of effort is linear, and the marginal cost equals
for player
i. Hence, player
i chooses
to maximize
Throughout the paper, we denote, by
, the Nash equilibrium of such a game, and by
, the effort of
-players in the level-
k version of such a game. In level-
k models, the most frequently observed types are typically
and
, and higher levels are seldom observed. (For estimations of the distribution of subjects’ levels of reasoning see for instance [
11,
29,
30].) Since our ultimate goal is to test whether, at some
k, overspending is rationalizable, and we find that at
, a player already overspends, we only characterize the
and
here, and we briefly discuss the evolution of behavior of higher types in the final discussion.
While, in games with compact action space, the support over which
-players randomly choose their action is unambiguously defined, in contests the strategy space is, potentially, the whole positive real line. Thus, we assume that
-players randomize uniformly over the interval
with
. Note that we take an agnostic view on
, which we allow to be lower, but also greater, than the valuation of the prize. In fact, some experimental evidence shows that subjects may bid more than the prize they might win, e.g., [
2,
4,
31,
32].
can be interpreted as the initial endowment of money that subjects are often given in experiments, and the fact that
-players choose randomly between 0 and their endowment is consistent with the empirical finding that overspending increases with the endowment (see the meta-study by [
28]).
3. Benchmark: Nash Equilibrium and Two-Player Symmetric Contests with Level-k Reasoning
Before presenting our results, we present the main benchmark, the Nash equilibrium with fully rational players, as well as a generalization of the result for two-player symmetric contests with level-
k reasoning in [
26]. These are the two outcomes that we contrast our results with.
Nash equilibrium under full rationality. With two possibly heterogeneous players, the well-known unique Nash equilibrium of the full rationality model for the two players is
where we define
, which is thus the asymmetry between contestants. With
n homogeneous players with cost parameter
,
, the unique Nash equilibrium of the full rationality model is
A full characterization of the equilibrium with
n players and asymmetry is, for instance, in [
33]. Even with just three asymmetric players, there are parameter constellations for which not all contestants exert positive effort, and these endogenous participation issues would confound the results of our paper. In fact, our ultimate goal is to verify the rationalizability of overspending in Tullock contests, and the special cases of three symmetric players and two asymmetric players suffice for this goal.
Two-player symmetric contests with level-k reasoning. We now consider the symmetric two-player contest with level-
k reasoning and prove the impossibility of overspending result. This benchmark thus generalizes the impossibility found in [
26] to any
, where
c is the marginal cost of effort for a player, as he studied the special case of
.
An
-player believes that their rival is
and thus plays uniformly over
. Therefore, the first-order condition (FOC) of
-players of (
1), when they believe that their rival’s effort is uniformly distributed over
, reads
where
denotes the equilibrium strategy of
players in the generalized Bernard model. Note that the left-hand side (LHS) of (
4) is strictly decreasing in
, tends to
∞ as
, and tends to 0 as
. Thus, a unique interior equilibrium
exists and solves (
4).
Since the LHS of (
4) decreases in
, we obtain
where the third line follows by the definition of
in (
3) for the
case.
In [
26] assumes that
, for which the above condition is violated, yielding their result of impossibility of overspending. Routine algebra shows that the LHS of (
5) decreases in
, and its value is 0 when
; thus, (
5) never holds for any
. Hence, we have proven the following generalization of impossibility of overspending in a symmetric two-player contest from [
26].
Proposition 1. Consider a symmetric Tullock contest with . Then, there is no pair such that the level of effort is greater than the effort level at the fully rational Nash equilibrium. That is,
This impossibility result is a direct consequence of the fact that in a two-player symmetric contest the fully rational Nash equilbrium is at the peak of the players’ best response functions. Thus, overspending as opposed to the effort level at the fully rational Nash equilibrium is impossible in such a setting, as already proven by [
26] in the special case of
.
However, this result relies on two important assumptions, namely and . In the next two sections, we show that dropping either of these two assumptions may yield overspending relative to the Nash equilibrium.
4. Overspending in Two-Players Asymmetric Contest
The main point of this section is that introducing asymmetry in players’ costs of effort rationalizes overspending. Without loss of generality, we focus on player 1 and thus consider an -player having marginal cost .
An
-player believes that their rival is
playing uniformly over
. Therefore, it is straightforward to see that
does not enter into the condition of optimal
, and the FOC of
-players writes
As in the benchmark case with symmetric costs (note the similarity between (
6) and (
4)), a unique interior equilibrium
exists and solves (
6).
Since the LHS of (
6) decreases in
, using the definition of
in (2), we obtain
We plot, in
Figure 1, condition (7) in two dimensions, namely
. The shaded area represents combinations
such that the
level of effort is greater than the Nash equilibrium level.
If
, the LHS of (7) tends to
∞, and thus for any finite value of
,
sufficiently large, (7) holds and overspending occurs. Proving the opposite, namely that for any finite value of
,
makes (7) hold, is more subtle, and we prove it in Lemma A1 in the
Appendix A, which also characterizes
(i.e.,
). As
a measures the ratio between
and
(recall that
, by symmetry, we also find a lower bound
below which this is true. Thus, we have proven the following.
Proposition 2. Consider a Tullock contest with . Out of the three parameters , fixing the value of two of these parameters, there exists a value of the remaining parameter such that the level of effort is greater than the Nash equilibrium level, i.e., . If and are the chosen parameters, it also has to be that with and .
Note that a minimum level of asymmetry between players is needed to rationalize overspending because, if instead costs were close enough (the white region of
Figure 1), the Nash equilibrium would be too close to the peak of the best response function, and thus we would not be able to obtain the overspending result. Overspending in the asymmetric level-
k Tullock contest can happen both by a weak or strong player who has sufficiently low or high cost compared to their competitor.
One remark is in order. Within the family of two-players asymmetric contests, we provided a characterization for when an -player overspends as opposed to the Nash equilibrium. It is not clear whether it could be that, if both players are , they both overspend. In other words, fixing for simplicity , is there a pair such that, if both players 1 and 2 were , they both overspend? This question boils down to verifying whether condition (7) and its mirror image, where and (which enters through a) are swapped can simultaneously hold. The answer is positive, and an example is as one can readily verify.
5. Overspending in Three-Players Symmetric Contest
The main point of this section is that introducing a third player in a symmetric contest rationalizes overspending. An
-player believes that their two rivals are
-players mixing uniformly over
. A Tullock contest is an aggregative game, as pioneered by [
34], in that (
1) depends only on
and on the sum of the rival’s efforts
. For this reason,
-players who are up against two rivals behave as if up against one rival whose effort follows a triangular distribution
Z in
—that is, the distribution of the sum of the two uniform random variables both in
, namely:
Therefore, the FOC of the
-players writes
where the first integral accounts for the part of (8) where
and the second integral accounts for the part of (8) where
. Routine algebra relegated to Lemma A2 in the
Appendix A shows that (
9) is equivalent to
As we prove in Lemma A3 in the
Appendix A, the LHS of (
10) decreases in
. Second, as
, the LHS of (
10) approaches
, and as
, it approaches 0. Thus, there exists a unique equilibrium. Such an equilibrium is interior by
.
Since the LHS of (
10) decreases in
,
if and only if the LHS of (
10) with
instead of
is greater than the RHS.
We next show that
, there exists a
such that
, and vice versa,
there is an
such that
. An easy way to do so is to consider
in condition (
10) above since for any
or
c this pins down the value of the other parameter. Note that (
11) satisfies the condition for an interior solution
found above. The intuition behind condition (
11) is that in order to rationalize overspending one has to trade-off
and
c. In fact, high expected effort from
-players (i.e., high
) discourages
-players and thus has to be compensated by low marginal cost of effort
c to guarantee that she still exerts high effort. Similarly, costly effort (i.e., high
c) discourages
-players; however, this is compensated when
-players exert sufficiently low effort (i.e., low
).
As stated above,
, if and only if the LHS of (
10) with
instead of
is greater than the RHS, and thus, under condition (
11) and using the definition of
in (
3) for the special case of
, we obtain that
which holds true. Thus, we have proven the following:
Proposition 3. Consider a symmetric Tullock contest with . Out of the two parameters , fixing the value of one of these parameters, there exists a value of the remaining parameter such that the level of effort is greater than the Nash Equilibrium level, i.e., .
Note that having three players as opposed to two players shifts the Nash equilibrium sufficiently far from the peak of the best response function, and this may yield per se sufficient asymmetry to rationalize overspending. In other words, we do not need further assumptions on sufficient asymmetry, such as or in Proposition 2.
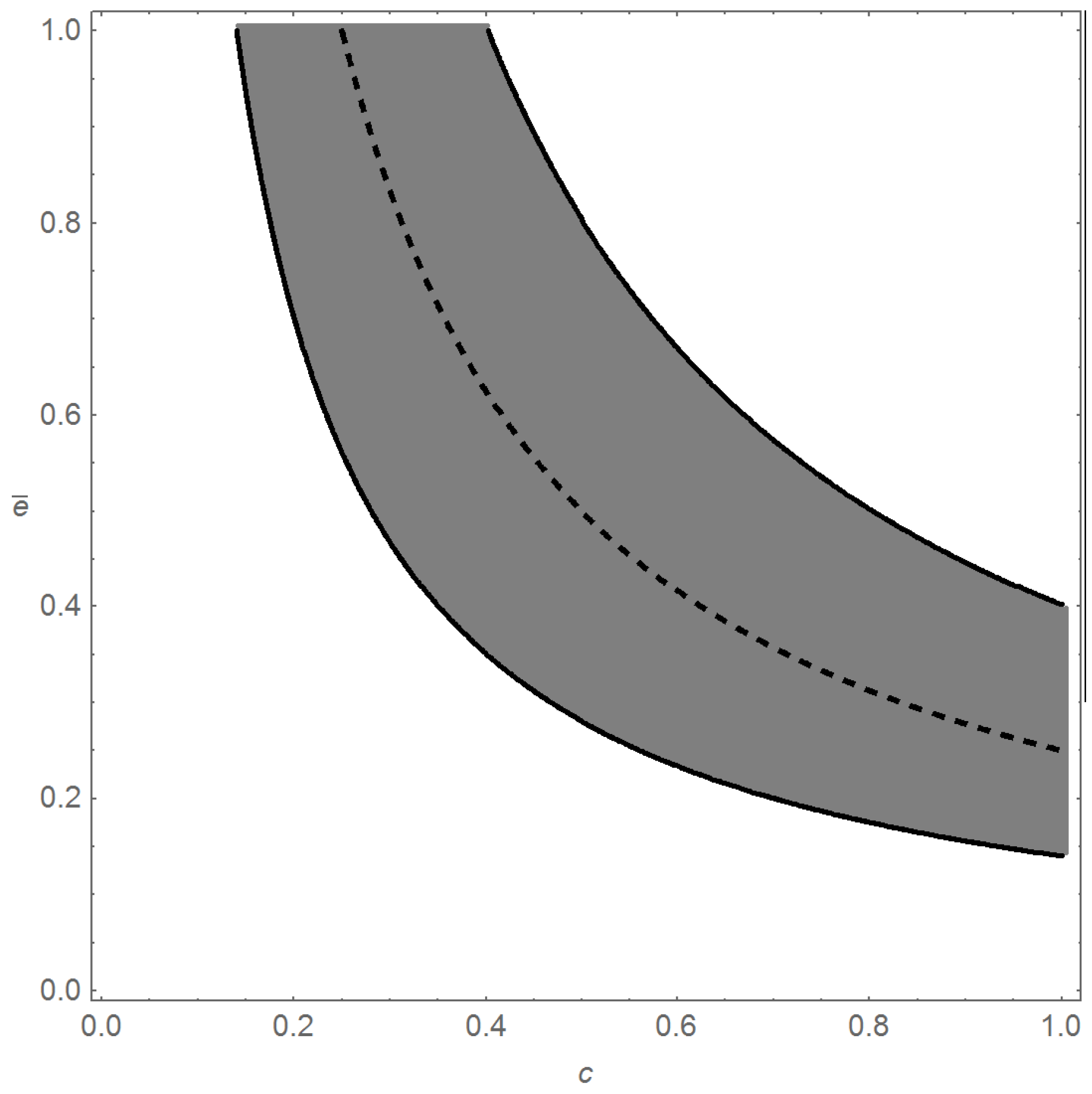
In
Figure 2, we plot in the
-space the region where
. The dashed line is condition (
11), which we used to prove Proposition 3.
6. Discussion and L2
Overbidding in auctions as opposed to the Nash equilibrium has been documented empirically/experimentally and can, in private-value auctions, be rationalized by level-
k models ([
12]). Overspending in contests as opposed to the Nash equilibrium has also been documented empirically/experimentally. We show that level-
k models can rationalize such overspending in Tullock contests. We thus bridge the existing gap between the auction and contest literature, two types of literature that usually work in parallel, by showing that overbidding can also be true in a contest environment due to level-
k reasoning.
The main analysis conducted in the present paper focused on the level of effort since this was found to be sufficient to rationalize overspending. However, one might wonder about the level of effort of -players with . In particular, since we know from empirical evidence that the most frequently observed types are typically and , it is important to focus also on , as we do in the remainder of the paper.
An
player believes that their opponent is an
player, and thus “best responds” to this belief. Such a best response, which maps the effort of the
into the effort of the
, is a strictly concave function with a unique maximum
. More precisely, the best response function of
-players to a certain effort of
-players is
In fact, this characterizes the behavior of any level-k type. Note that reaches its maximum when . Overspending remains possible at in both cases of interest to our analysis, as we explain in what follows, and it may also be possible that both the - and - players overspend.
First, if there are
two asymmetric players, calling 2 the
-player and 1 the
-player, then the condition for overspending of the
-player is
, and the condition for overspending of the
-player is
. Using the definition of
in (12), we can rewrite this last condition as
It is clear that, if we want to rationalize both - and -players’ overspending, the condition for overspending of the -player () is compatible only with the case of the above condition—that is, (13). In other words, it is possible that both - and -players overspend only if the -player is weaker than the -player. Conversely, if instead the -player is stronger than the -player (), then the overspending condition of the -player (14) implies that the -player underspends ().
Second, if there are
three symmetric players, dropping the player-specific subscripts from the notation, we obtain that
and
, and therefore
, and, similarly to the two asymmetric player case,
—an
overspends. It is also interesting to know how
with
evolves if
. Normalizing marginal costs to 1, one can show that
Hence,
implies
, but that the converse is not necessarily true; if
, then we could obtain
or
. For instance, consider the
case. If
, then
. If instead
, then
. Hence, a general analysis of the evolution of
is found not to be characterized by simple rules (such as alternations of overspending and underspending) and, importantly, beyond the scope of the paper, which is to verify the rationalizability of overspending in Tullock contests. Extending the two-symmetric-player setup of [
26] to the cases of three symmetric and two asymmetric
-players proved sufficient for this goal.