1. Introduction
Trust is a ubiquitous experience throughout human life. Trust is required when you ask someone to look over your laptop in a café while you go to the restroom. Trust is required when you talk with your colleague about a bad experience you had with your boss. Trust is required when you describe your health issues to your doctor. Trust has also pivotal consequences on economics and health. For example, trust positively correlates with GDP growth and trust in a doctor correlates with better health outcomes and longer life expectancy [
1,
2,
3]. The social phenomenon of trust has been dissected by different scientific fields. Philosophers have described the conditions under which trust occurs. Psychologists have captured varying dynamics of trusting behaviors. Economists have studied features of trust in game-theoretic terms. Cognitive neuroscientists have unearthed its neural underpinnings. Thanks to all these efforts, we have gone a long way in understanding the psychological, behavioral, and neural mechanisms underlying trusting behaviors and experiences. Previous research has further distinguished different types of trust based on its target and the mechanisms involved, such as institutional trust, group trust, and interpersonal trust [
4,
5,
6].
In the following, I will focus on the psychological and computational mechanisms of interpersonal trust. Interpersonal trust refers to the trust people put in another person and is distinguished from trust in an indistinct group of people (such as football teams) or abstract social entities (such as political parties and institutions). Philosophers conceive of interpersonal trust as an
attitude people have toward those who they think are trustworthy. In particular, the concept of
reliance is central to trust for most philosophers, as trust describes those phenomena of social lives in which someone relies on (expected-to-be trustworthy) others for different purposes [
7]. Importantly, as trusting individuals make themselves dependent on others, trust implies a form of vulnerability to those trusted (such as vulnerability to betrayal). Finally, the characteristics that make the trustee trustworthy vary as a function of the context and the purposes for which individuals trust.
Psychologists have defined interpersonal trust in similar ways. A very widespread, cross-disciplinary, psychological model of trust defines trust as follows: trust refers to the willingness to accept vulnerability based on positive expectations of the other person’s behavior and intentions [
8,
9]. Mayer et al. [
8] also specified that trust implies refraining from exerting social control. Indeed, previous research has shown that the possibility of exerting social control and the active decision of refraining from using it is central to trust [
10,
11], which likely is a behavioral signature of the willingness to accept vulnerability and might in general be related to the positive consequences of strategic ignorance [
12].
In addition, a recent review has discussed two main experimental paradigms that have been implemented across disciplines and have provided us with many insights into the behavioral and neural underpinnings of trusting behaviors [
13]. On the one hand, trust has been studied by investigating people’s tendency to take advice from different sources. For instance, participants might be required to make inferences on some quantities and can use the opinions of others (advisers) to improve their estimations [
14]. These are forms of sequential, interacting paradigms, in which a participant, in the role of adviser, provides pieces of advice that another participant decides to take or discard for solving a monetary task. Here, trust and reciprocity are operationalized by participants’ statistics in advice utilization, and they are in general modulated by manipulations of different social characteristics of the advisers, such as their competence, confidence, and kindness [
15,
16,
17,
18].
On the other hand, trust has been investigated by using another sequential, interacting paradigm, the investment game (IG) [
19,
20]. In the IG (
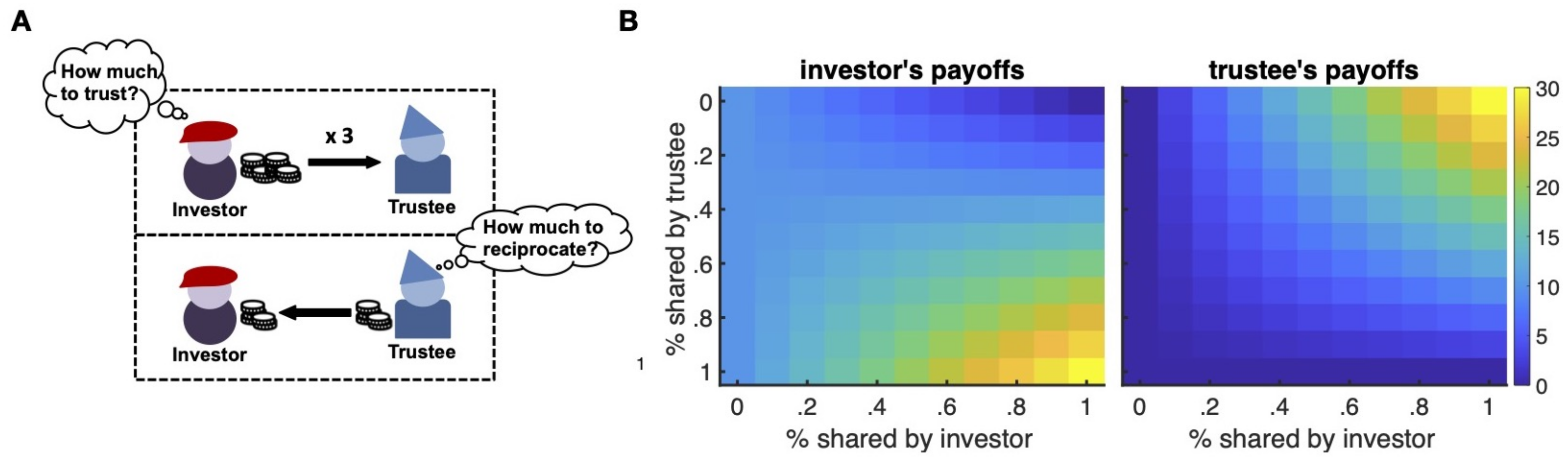
Figure 1A), two players interact as investor and trustee. The investor receives an initial endowment and makes an investment decision about whether to pass any, some, or all of the received endowment to the partner (i.e., the trustee). The amount, if any, invested is multiple by a multiplier that varies across studies, but is typically three and stationary within a study (except in some special cases; see [
21]). After the investor’s decision, the multiple amount is given to the trustee, who can decide to return any portion of what they receive on that trial. The investor’s decision is thought to capture trust, while the trustee’s decision is supposed to capture reciprocity [
20,
22,
23,
24,
25]. At least two general versions of the IG have been used beyond specific modifications of the details of the interacting dynamics or interacting partners. These two IG versions concern the operationalization of trusting behavior and the evolution of the trusting interaction. In particular, trust decisions have been studied either as binary or continuous (on a pre-specified range). In the first case, participants are asked to make an all-or-nothing decision, that is either trust their partner or not [
20,
24,
26,
27,
28,
29,
30,
31]. In the second case, participants are asked to share a proportion with different resolutions [
19,
32,
33,
34]. Further, the interaction can be limited to a single round/trial (one-shot IG) or unfold over multiple rounds/trials (multi-round IG). In the last case, participants might know how many rounds/trials they will interact with each other or not. All these differences have been shown to lead to interestingly varying behavioral and neural dynamics [
35,
36], and recent simulation studies have more formally shown under which conditions trust and trustworthiness in the IG evolve [
37,
38]. In the following, I will focus on the trust dynamics that occur in the IG—mostly within the context of multiple interactions between the investor and the trustee (e.g., multi-round IG). However, some of the things discussed will also apply paradigmatically to the one-shot IG.
Despite many decades of empirical studies on trust in the IG, very little work exists that tries to more formally define the behavior observed in these trusting interactions. This is a general issue in social neuroscience and psychology, where the few computational models that have been implemented and tested have been borrowed from other fields and developed to study other cognitive and learning processes than social mechanisms (such as nonsocial, solo learning processes like in the case of reinforcement learning models) [
39]. This is also the case for trust. There exists computational attempts to model people’s behaviors in the IG. However, the applied models are borrowed from other fields that developed them for other purposes, such as reinforcement learning models and their Bayesian versions [
40,
41] or inequality models [
42,
43] developed for other economic games (e.g., the ultimatum game) [
44]. Here, I attempt a new approach recently suggested as a solution to move the field of social neuroscience and psychology forward [
39]. That is, I aim to generate a computational model of trust in reciprocity inspired by philosophy, social psychology, behavioral economics, and social neuroscience by mapping verbal models to mathematically tractable quantities that will enable psychological assumptions and mechanisms to be clearly quantified and explicitly tested. Thereby, I will leverage the knowledge of years of observations in social psychology and combine it with a mathematical formalism. For this purpose, I will focus on the investor’s dilemma to trust or not to trust their partner in the exemplar interactive environment of the multi-round IG. I will not only show that the proposed model is able to describe some very interesting, paradigmatic behaviors previously observed in the IG, but also make testable predictions about possible behaviors in new versions of the IG that could be used to investigate other trust-relevant social variables.
2. Components of Trust
One essential aspect of trust is the recognition of the other partner’s trustworthiness. Despite a willingness to be vulnerable to those who trust being central for trust to occur, trusting partners do in general trust on the basis of positively-valenced expectations of their interacting partner. These expectations are nurtured by direct and indirect knowledge about the other partner, which justifies beliefs about the partner’s trustworthiness [
45]. Previous research has identified different aspects of a person’s behavior and character that evoke impressions of trustworthiness. An influential work on the determinants of trusting behavior lists three main characteristics of a partner for the formation of trustworthiness impressions: (1) ability; (2) benevolence; and (3) integrity [
8].
The ability dimension is associated with the skills and competencies of a partner that might be helpful to the trusting individual in reaching her/his goals. These skills might be very general and experience-based, like when asking a friend about the work culture in a different work field, or domain- or situation-specific, like when people rely on a doctor for medical issues, but ask a lawyer for legal counseling. The benevolence domain, on the contrary, is related to the intentionality aspect of the interacting partner. In particular, a trusting partner cares about whether the trustee has positive intentions and attitudes toward his/her. This is probably due to the fact that the vulnerable status a trusting partner accepts to be in is a highly risky and dangerous situation that might jeopardize the trusting partner’s social status, reputation, physical integrity, and even personal life. Finally, integrity refers to a moral dimension that describes the degree to which the partner adheres to a set of principles that the trusting partner finds acceptable. This factor is closely associated with the moral character of the trustee and refers to the trustee’s behavioral consistency in his/her congruence to a determined set of values [
13].
At least two of these determinants of trust have previously been successfully studied in the IG. The trustee’s decision of sending back a proportion of the received amount (i.e., reciprocity) is interpreted as a sign of benevolence through which the trustee signals to the investor that he/she has good intentions. This compels trustees to back-transfer money to the investor even when it is not strictly economically advantageous for them [
32]. For instance, decreases in reciprocal behavior, especially after increases in trust levels, disrupt cooperation [
46]. Further, unconditional kindness, but neither positive nor negative reciprocity, has strongly been associated with trusting behaviors [
47]. Similarly, impressions of a partner’s moral and immoral character from previous social interactions have long-lasting effects on individuals’ decisions to trust in subsequent encounters [
48]. Finally, individuals with strong moral characteristics are not only perceived to be more trustworthy but also more likely to be trusted, which is likely due to the fact that they are also believed to be more likely to reciprocate [
49].
Despite a wide array of empirical investigations on the effects of the intentional and moral dimensions on trust in the IG, little is known about how the ability dimension influences people’s trust decisions. One of the difficulties is definitely related to the fact that the IG does not bend itself that easily to investigations of the effects of the trustee’s competence on the investor’s sharing decisions. In the following, I will show how the
vulnerability model formalizes trusting behavior in the IG and captures the effects of the expectations of trustworthiness on trust. In particular, I will show how such expectations are formed based on the impressions of the trustee’s benevolence arising from reciprocal behavior, which signals the trustee’s good intentions and willingness to cooperate. Moreover, I will show how the vulnerability model parameterizes trust attitudes as the theorized, weighting trade-off between the acceptance of vulnerability and positive expectations of the partner’s behavior [
8,
9]. I will then describe a novel experimental setting by employing a modification to the classic IG in order to study the effects of competence on trust. Thereby, I will demonstrate how the vulnerability model can be easily extended to capture the effects of the ability dimension on trust decisions.
3. Formalism
The classic IG is a two-person, sequential task played over a specific horizon
T with a predetermined number of trials (
Figure 1A). If
, the IG is played over a single round (or trial) and is called the one-shot IG. If
, the IG is played over multiple rounds (or trials) and is known as the multi-round IG. Additionally, both versions can be played with a single or different partners. Hence, a one-shot IG can be played sequentially with different trustees, in which case we have a multiple one-shot IG. Similarly, participants as investors can play multiple rounds of the IG with different trustees (i.e., a multiple multi-round IG). The following formalism applies in principle to all these cases with adequate modifications to adapt it to the social environment in which the behavior is studied. In my examples, I will work with a single multi-round IG with
(a very often-used number of trials in experimental research; e.g., [
32]), where an investor interacts with the same trustee over the whole length of the experiment.
Investors receive an initial endowment
and invest a proportion of it (
) in trial
t. The amount, if any, shared by the investor (i.e.,
, which is
) is multiplied by a factor
. This multiplier varies across studies, but is stationary within a study (except in some special cases; see [
21]) and is generally
. After the investor’s decision, the multiple amount is given to the trustee, who can decide to return a proportion
of the endowment
that they receive on that trial. As often done in experimental research, I will imagine that the currency of the endowment is in monetary units (MUs), which can be translated to different currencies with any mapping function. Moreover, I will assume
to be
MUs as the investor’s endowment at the beginning of each new trial, again as often done in experimental research. Since the investor does not know the trustee’s return at the time of choice, the proportion returned by the trustee at this time will be denoted as the random variable
.
Moreover, I will assume a finite discretization of the action space, following empirical research that allows investors and trustees to make only a subset of predefined sharing actions. For instance, binary IGs allow participants to make one of only two possible actions. Some other studies allow participants more actions corresponding to some submultiples of the available amount (a very common version is one with multiples of four from 0 until the total amount of 12). In studies with
, investors are allowed to share any available unit, which is equivalent to letting them share any portion of the received amount (from 0 to the whole amount) in steps of 10%. In such studies, the trustees are endowed with the same action rule, so that they also can share any unit of the received triple amount. However, previous computational work has considered more discrete action spaces for trustees who can have a vaster action space. A convenient practice is to consider similar action spaces for both investors and trustees [
50]. This implies that trustees will be allowed to share only predefined proportions of the available amount. Given the results in previous research highlighting the importance of specific proportions such as 30%, 40%, and 50% in economic games [
51,
52,
53,
54] and the effects of reciprocal behavior in social interactions [
16], I will consider the same proportional action space for both trustees and investors. Hence, if
A is the total number of possible actions for investors and trustees,
represents the range of available actions for the two players from sharing nothing to the complete available endowment in steps of 10%.
Figure 1B provides a snapshot of the dilemma of the investor as a function of the economic interests involved (payoff values). While the investor is incentivized by the payoff structure to share higher amounts and hopes for higher returns by the trustee, the trustee hopes for higher shares, but is incentivized to keep higher portions of the received amounts. How does the investor solve this problem? In particular, as the trustee only loses by returning money to the investor, the economic solution is for the investor not to return any money. However, plenty of empirical studies have shown that both in one-shot and multi-round IGs, people deviate from this optimal solution and do share some amounts. The general explanation of these behavioral patterns is to think of utility as subjective and, hence, modulating different components of the utility computation. For instance, the investor’s payoffs might be reduced by considerations of a possible betrayal, leading to lower trust levels, while the trustee’s payoffs might be reduced by the social disutility of a defection (implying higher back-transfers as a consequence). Further, in multiple interactions, individuals might learn and make inferences about others’ intentions and behavior to reduce the uncertainty associated with their sequential decisions.
3.1. Inequity Aversion Model
A well-known formalization of action utilities for social behaviors in simple two-person interactions is provided by the inequity aversion model proposed by [
44]. Although the inequity aversion model was originally developed to model participants’ fair behavior in the ultimatum game, it has been used in other social experimental paradigms in which it is reasonable to assume fairness concerns, such as the IG [
34,
42,
50]. For this and for completeness reasons, I will here briefly discuss the inequity aversion model and its predictions. Later, I will compare them to the proposed vulnerability model.
The inequity aversion model aims to capture the well-known observation that individuals dislike outcomes that are perceived as inequitable and that they do so more when such inequity is at their disadvantage [
55]. Hence, inequity aversion can be
self-centered when individuals care about their own material payoff relative to that of others and increases with increasing disadvantageous inequity; or
other-centered when individuals care about others’ payoffs relative to their own and increases with increasing advantageous inequity [
13,
44]. Based on this definition, let
be the payoff of person
n at time
t and
be the payoff of person
m at time
t, which both depend on both players’ shares
, and
. The utility of person
n at time
t is then
where
and
are subject-specific parameters (here of person
n) that quantify the degree of disutility derived from advantageous (guilt) and disadvantageous (envy) inequality aversion, respectively. Thus, Equation (
1) describes the utility of an individual
n as the sum of a utility derived by their current payoff
and two potential disutilities—one when person
n ends up having more than his/her partner (i.e., advantageous inequality when
) and one when person
n ends up having less than his/her partner (i.e., disadvantageous inequality when
). When person
n has less than person
m (i.e.,
), person
n is considered to be envious of person
m, while when person
n has more than person
m (i.e.,
), person
n is regarded as feeling guilty of having more than person
m. In both cases, the current material utility
is uniquely reduced by one of these two disutilities and the parameters
and
capture individual differences in people’s sensitivity to these two disutilities. The optimal scenario is represented by the case when the payoff difference between person
n and person
m is zero, which captures people’s universal tendency to fairness [
56,
57]. Moreover, since people have been shown to be more averse to disadvantageous than advantageous inequity [
55], the model parameters have to satisfy the constraint
.
In the context of the IG, if we denote by
the absolute amount back-transferred by the trustee from the received multiple amount (i.e.,
) at time
t,
stands for the investor’s payoff and is equal to
Consequently,
represents the trustee’s payoff and is equal to
which is the amount the trustee keeps from the multiple amounts received after reciprocity.
Finally, results from empirical works suggest that investors make their decisions based on a stochastic policy. If
is the utility of the investor for making investment
and receiving return
at time
t, the probability of
is
where
is the inverse temperature of the softmax function that captures randomness in participants’ decision policy. Specifically, lower
values reflect more diffuse and variable choices.
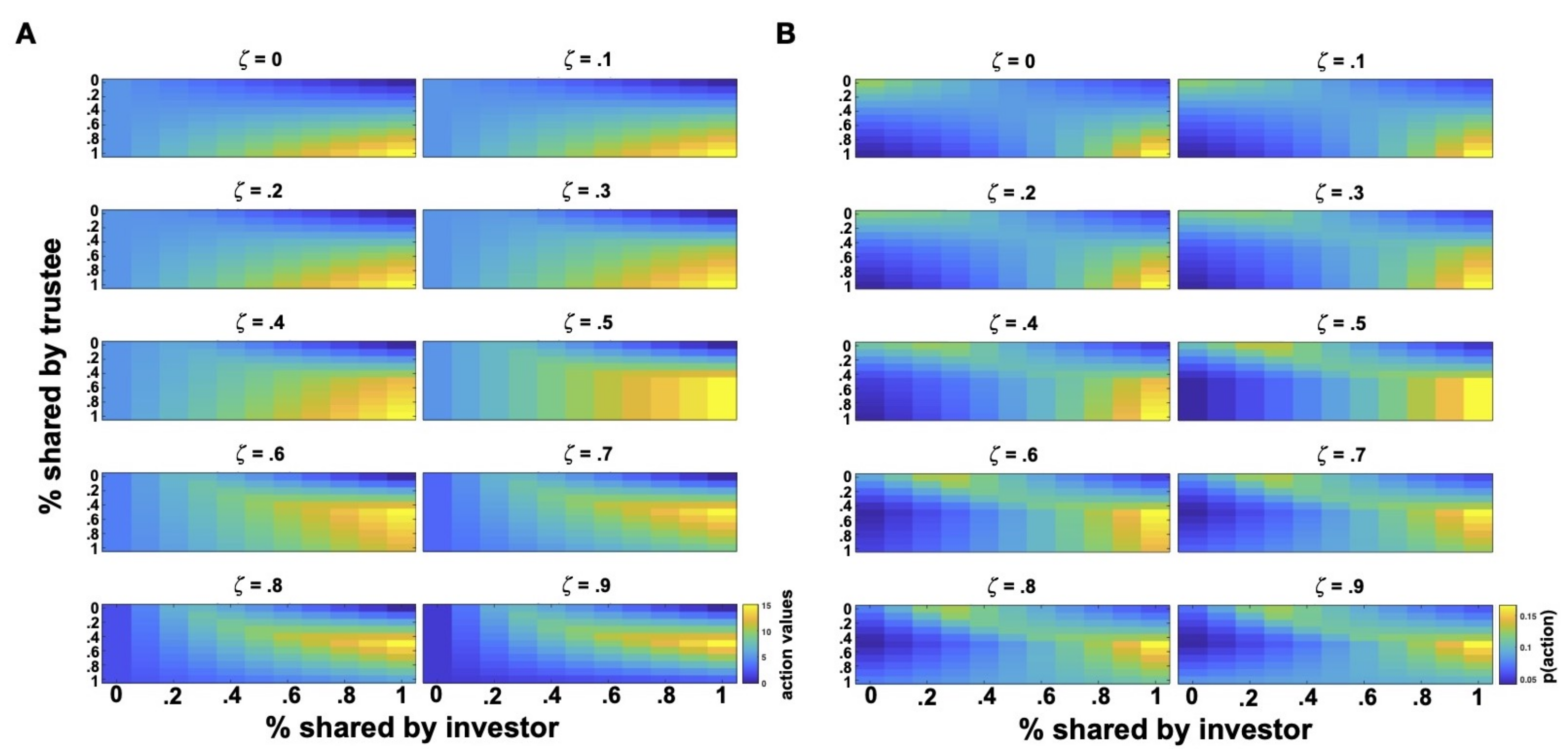
After the definition of a utility function and policy for the investor, we can examine the action values and probabilities across the combinations of
i and
r (investor’s and trustee’s available actions). From
Figure 2, we can easily observe that the model predicts that guilt-free investors (
) prefer a cooperative interaction with high investments and returns that would maximize their payoffs. Similarly, when paired with uncooperative trustees, guilt-free investors prefer sharing nothing. However, when investors are more and more averse to advantageous inequality (higher
values), the model predicts that they should prefer action combinations that yield the most equitable outcomes, which would reflect their increasing fairness concerns. Hence, for interactions with uncooperative trustees, investor’s policy shifts toward higher share proportions (e.g., 20–30%), which should even up the initial disparity caused by the endowment
provided to the investors at the start of the trial
t (as the trustee does not receive any initial endowment, so
). This pattern of policy shift reaches the extremes for very high
values, where we see that investors prefer cooperative trustees that share around half of what they received, with advantageous payoffs increasingly disliked.
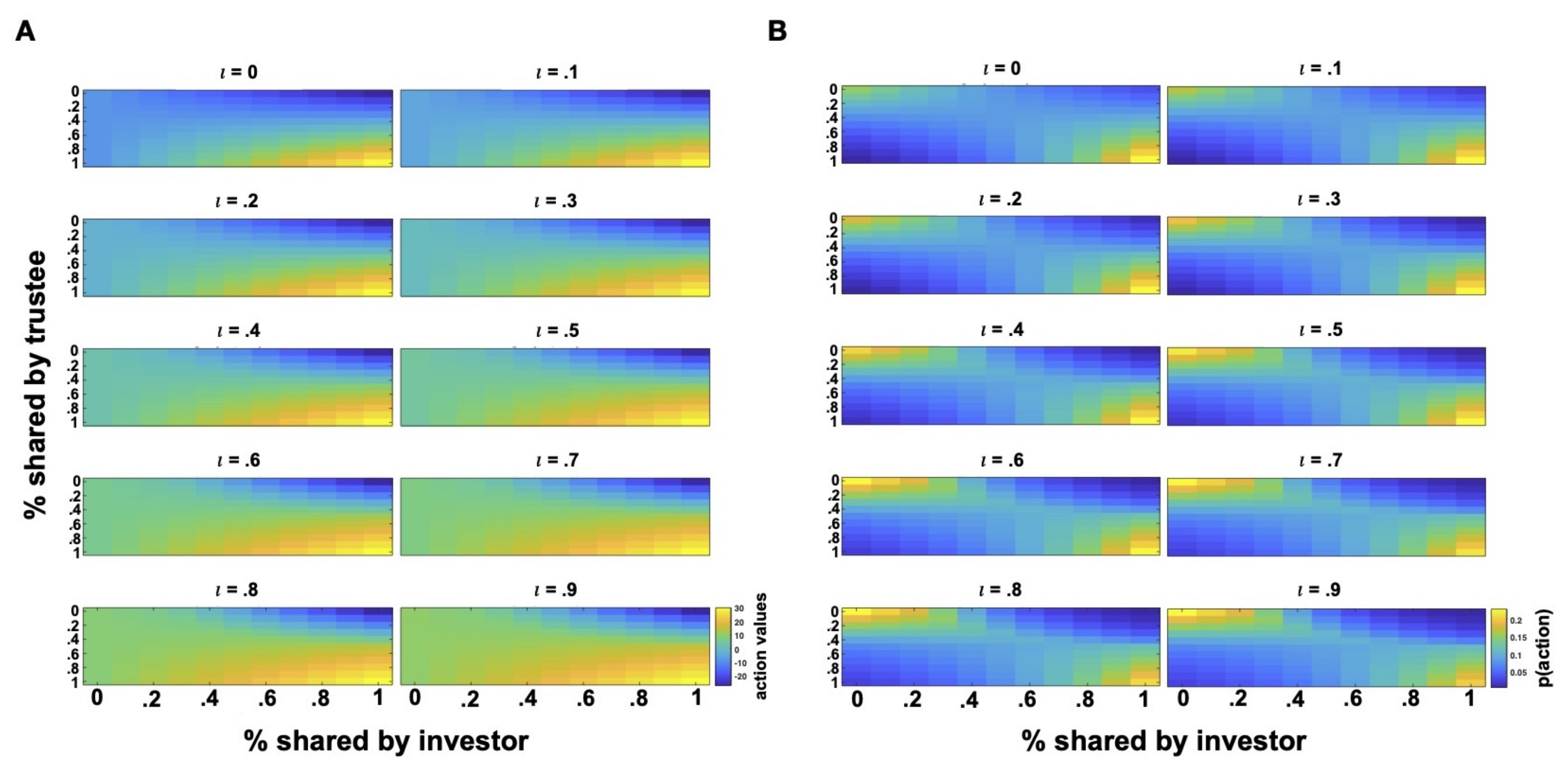
Variations in
values generate a very similar policy space with some subtle differences (
Figure 3). For low
levels, action policies are similar to those generated by low
values with the difference that aversion to disadvantageous inequality more strongly favors lower or no investments with uncooperative trustees (higher action probabilities). For higher
values, the policy does not change much, but sharpens over the two self-interested extremes with action combinations that maximize the investor’s payoffs. That is, higher investments for high returns in cooperative interactions and increasingly lower investments for small returns in uncooperative interactions are enforced by high
values (almost a tit-for-tat or copying strategy). This implies that higher
values yield policies most divergent from those generated by
values, which, on the contrary, shift the policy toward a slightly different action space.
Given that
, the action policy of the inequity aversion model persists on self-interested, payoff-maximizing strategies with very little explorations of other policy regions. This makes it hard to see how inequity-averse investors differ from pure money-maximizers. This is in accord with a previous criticism of the inequity aversion model (see for instance [
58]). Indeed, previous work has used a reduced version of the model that only takes into account advantageous inequity [
50]. However, also in this reduced version, only a small subset of
parameters have been found to generate distinguishable behavioral predictions [
50]. Interestingly, these parameters fall within the same region of the parameter space from which [
44] drew their own parameter values in their original paper.
Moreover, even though fairness concerns are reasonable in the context of the IG, the inequity aversion model is in its essence an outcome-based model that might be more suitable in contexts where a person’s decision outcomes are more salient. On the contrary, in the IG (especially in versions with non-binary action spaces), the actions of the interacting partner become salient. This explains, for example, why even for low investments, trustees still share back some money and, in particular, try to send back at least as much as shared by the investor (which amounts to approximately 30% of their available endowment for ), even though this has the effect of increasing the payoff difference at their disadvantage. Different reasons can be provided to explain such a behavior. For instance, they might be acting so to remunerate the investor for their trust and/or to signal willingness to cooperate (especially in multi-round settings). Indeed, when investors do not see such willingness from the trustee (even if this means he/she needs to put himself/herself in a disadvantageous situation), he/she refrains from trusting any longer. This is probably because the investor is not focusing on minimizing the payoff difference between himself/herself and the trustee, but rather intends to try the trustee for informative inferences on how his/her partner would behave in the future. Among other possible reasons, it is clear that an outcome-based model falls short of adequate explanations for the behavioral patterns observed in the IG.
3.2. Vulnerability Model
The vulnerability model more closely captures the theorized psychological and computational components involved in a decision to trust, both in general and specifically in the IG. In the context of a single exchange in the IG, vulnerability is associated with the investment
, since the investor stands to lose this. Such a possibility is however contingent on what the trustee actually returns. However, when the investor makes his/her decision, he/she only knows
, but does not know what the trustee is going to return. Here, expectations of the trustee’s return function as a proxy for the trustee’s future behavior. Hence, the investor needs to trade-off the possibility of losing the investment against his/her expectations of back-transfers (i.e., the trustee’s future reciprocal behavior). Psychologically speaking, the investment
is likely framed as a potential “loss” with an immediate negative utility for the investor. On the contrary, the expectation of the trustee’s reciprocity
is likely framed as a potential positive “gain”, as it represents what the investor could receive from the trustee (i.e., the return
). The investor thus ponders which proportion of the multiple received endowment (i.e.,
) the trustee will choose to return. This computation enters into the investor’s estimation of his/her utility
at time
t. At the time of the investment, the investor does not know the proportion preferred by the trustee and has to consider the distribution over all possible proportional returns
, where
includes the history of exchanges (investor’s and trustee’s actions) up to time
t. As proportions naturally range between 0 and 1 so that
, I’ will assume that the probability over
has the form of a beta distribution. Hence, the investor’s utility of choosing a particular proportion
i at time
t is
is the beta distribution over all possible proportional returns
and represents the probability of the trustee’s return at time
t based on the observed history of returns until time
t (
). This beta distribution is described by two parameters
and
as follows:
with
r being the trustee’s proportional returns. In multi-round settings, expectations of returns are updated via Bayesian updating on every trial after observing a new proportional return. Hence, the investor’s posterior probability over
r at the next time step
becomes
, where
and
.
N determines the update rate for new observations and is assumed to be
with the special case of
when no updating of the partner’s behavior takes place.
Apart from being likely closer to the psychological definition of trust, this additive temporal decomposition is also computationally more convenient than a formalization that works with payoffs (like in the inequity aversion model), since it allows considering a variety of psychological factors such as loss aversion [
59,
60] or savoring and dread [
61,
62,
63] associated with the duration of vulnerability, which have been previously found to affect the computational processes underlying decisions in different decision-making settings.
Now, let us follow the philosophical and psychological traditions that formalize trust as a general
attitude to make oneself vulnerable to others [
9,
64] and operationalize this attitude as a stationary weighting preference (note, however, that trust attitudes might also change over time). In the context of our formalism, this translates into a competing weighting between the negative consequences of an act of trust (i.e., the loss of the investment generated by the investor’s action
) and the expectations of the partner’s trustworthiness (utility generated by the proportional return chosen by the trustee, i.e.,
). This implies that, beyond all the reasons a trustee might provide to the investor to favor future expectations of returns over the avoidance of vulnerability, investors further differ in their weighting preferences of these two components. For example, facing the same amount of evidence about a partner’s trustworthiness, some individuals might be ready to trust the partner, while others might still remain reluctant and prefer distrusting. Hence, the investor’s utility for a decision to trust is envisioned as a competition between a preference for loss aversion and a preference for trustworthiness expectations as follows:
where
is an individual-specific free parameter that weights the positive expectations of trustworthiness against the negative utility of vulnerability, and hence represents a propensity to trust. This parameter
takes values between 0 and 1
, and in the current implementation, I assume it to be fixed for each investor over the short time period of a game (to implement a stationary weighting preference for the investor). In this respect,
can be thought of as a stable personality trait of the investor, similar to trust conceptualizations in psychology [
65,
66]. However, extensions to include a variable parameter are feasible and can capture other differences in trusting behavior observed in empirical work such as those depending on the social context (e.g., in-group vs. out-group), changing statistics of the environment (e.g., volatile vs. stable environment), or a person’s age [
4,
5,
40,
43].
Like for the inequity aversion model, investors are assumed to make their decisions based on a stochastic policy as in Equation (
2), which can capture idiosyncrasies in the decision-making behaviors of human agents.
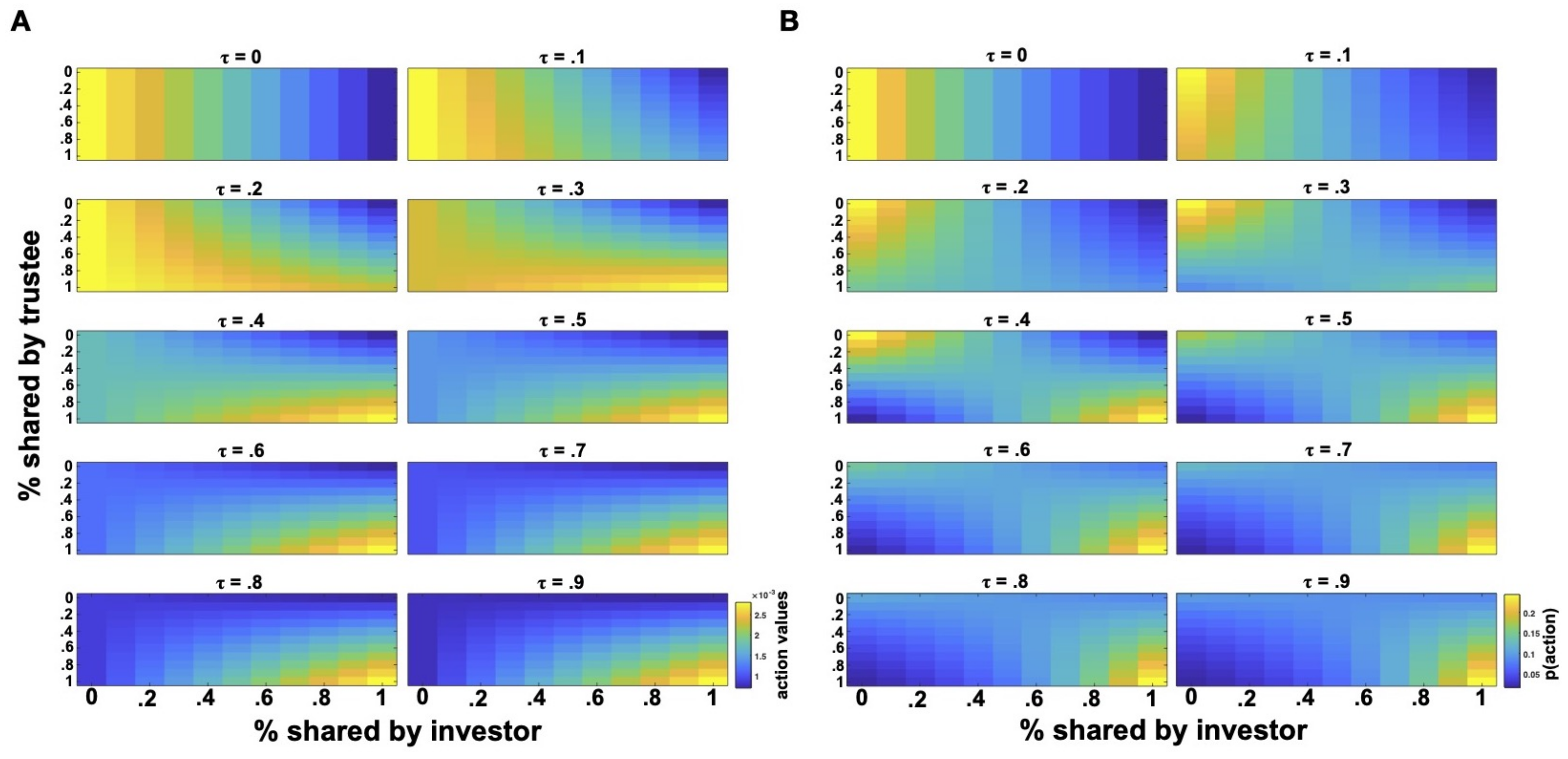
Figure 4 showcases the action values and probabilities generated by the vulnerability model for different propensities to trust (i.e.,
parameter). For very low
parameters, the investor’s policy is centered on low proportions of sharing and barely changes as a function of the trustee’s actions. For the extreme case of
, investors do not put any weight on their expectations of the partner’s trustworthiness and the model makes predictions as if those expectations were 0 (as if the investor knew the trustee will not share anything). For this and similar cases of very low
parameters (e.g.,
), investors give little weight on the potential benefits derived from the partner’s behavior and focus on the immediate loss implied by the investment, leading to very similar action probabilities over the trustee’s action space and showing very distrustful behavior, as sharing nothing or very low proportions turns out to be the preferred strategy. Consequently, we can think of these low
values as generating behavioral solutions similar to those predicted by economic theories, as distrustful investors with these
values will not make themselves vulnerable to the trustee and prefer keeping the received endowment
.
On the contrary, for increasingly higher
values, we see a shift of the policy toward higher sharing proportions, leading to higher trust levels and more cooperative behaviors. In particular, higher
values shift the investor’s preferences toward a more cooperative action space with investors preferring higher investments when interacting with cooperative trustees or no investments if their trustee is uncooperative (e.g., for
or
in
Figure 4). Comparing the action probabilities of the inequity aversion model with those generated by the vulnerability model, we observe that action policies for
are very similar to those of envious investors in
Figure 3, while action policies for
are similar to those of mildly guilty or guilt-free investors in
Figure 2.
These descriptive observations indicate that the vulnerability model is able not only to explore different regions of action policies, but also to cover parts of the action policy space generated by the inequity aversion model. Hence, investors with a weak trust attitude generate behaviors that, in the context of the inequity aversion model, can be interpreted as signaling “envy”, while investors with a strong trust attitude will manifest behaviors that, according to the inequity aversion model, will be more likely categorized as signaling “guilt”. Moreover, when
, the investor maximizes his/her expected payoff by maximizing the expected utility function as given by Equation (
7). This is a special case, as the same does not occur for other values of
. In other words, the corresponding level of trust can be interpreted as being economically rational given the information an investor has. The interesting aspect of the vulnerability model is that it can further capture forms of gullibility, for instance in the case of
, where the investor continues to transfer high shares even in the face of low proportional returns, making his/her subject to exploitation by the trustee.
Hence, the vulnerability model is able to cover a wide range of trusting behaviors, from suspicion (low values) through rational and trustful behaviors ( values in the middle range) to unreasonably inflated/exaggerated trust or gullibility (high values). Further, as the vulnerability model describes the investor’s utility function as incorporating expectations of the partner, it entails a learning mechanism that naturally allows the investor to adapt the realized trusting behavior to the observed behavior of the trustee. The updating of such expectations over time instantiates a learning mechanism, which can be implemented in different ways. In this paper, I will consider an unsophisticated learning mechanism based on the history of observations of returns that updates the beta distribution representing the investor’s expectations of the trustee’s trustworthiness. However, more sophisticated learning mechanisms can be used where the probability distribution over the trustee’s behavior does not only depend on the history of observations, but also on a generative model of the partner’s behavior for planning (see the Discussion).
5. Discussion
In this paper, inspired by philosophy, social psychology, behavioral economics, and social neuroscience, I provided a formalization of psychological and philosophical verbal models of trust as the attitude to rely on expectations of a social partner despite the vulnerability to the trusted partner that the act of trust implies. I have shown behavioral predictions of the model as a function of the investor’s loss aversion and expectations. I have further shown how according to the model, an individual reacts to different interacting dynamics such as attempts to breach and repair trust from the trustee. Finally, I have demonstrated how the model can be extended to incorporate other sources of uncertainty relevant to a decision to trust in a novel environment in which expectations of the trustee’s competence need to be incorporated into the utility function before a trust decision is made.
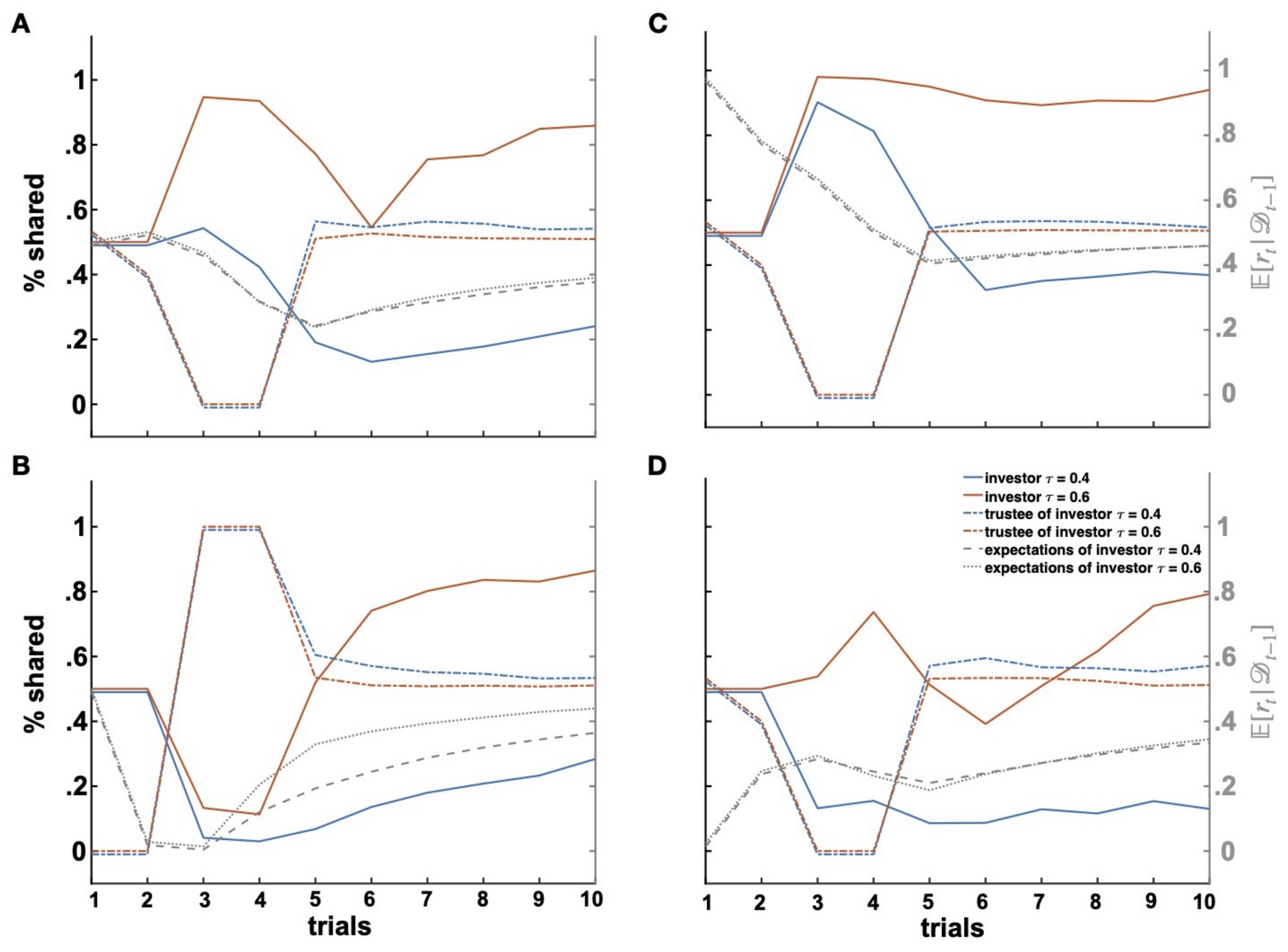
The considered model makes predictions consistent with previous behavioral results and provides a mechanistic understanding of previous observations in empirical work. For instance, the model predicts a gradual decrease of investment after breaches of trust, which is proportional to the change rate of the investor’s expectations of the trustee’s reciprocity. Such a gradual decrease has been interpreted as the investor’s willingness to, on the one hand, keep open the possibility of future cooperation after an adequate trust repair and, on the other, signal disapproval or irritation [
24,
32,
50].
Further, model simulations have shown how implausibly high expectations impair behavioral adaptation to learning. In particular, trustful investors with highly positive expectations were more likely to be exploited by an uncooperative trustee despite the fact that they did learn about the trustee’s exploitation. These behavioral patterns have been observed in different clinical populations such as in individuals with generalized anxiety disorder and individuals with attention deficit hyperactivity disorder (ADHD) [
40,
77,
78]. Importantly, a computational modeling of behaviors in these populations has previously suggested a “learning impairment” with lower rates of learning [
40]. However, this previous model did not incorporate individuals’ expectations of a partner’s behavior, and it is still an open question whether those participants had an actually worse learning performance or whether their behavioral responses were biased by their unrealistic expectations despite accurate learning. Fitting a model that does not account for expectations to the behavioral patterns generated by the vulnerability model in
Figure 5C might most likely suggest an impairment in learning about the trustee’s behavior. However, as the changes in the investor’s expectations show, an individual with unrealistically positive expectations might still be able to correctly learn about a partner’s behavior without him/her being actually reflected in the observed behavior.
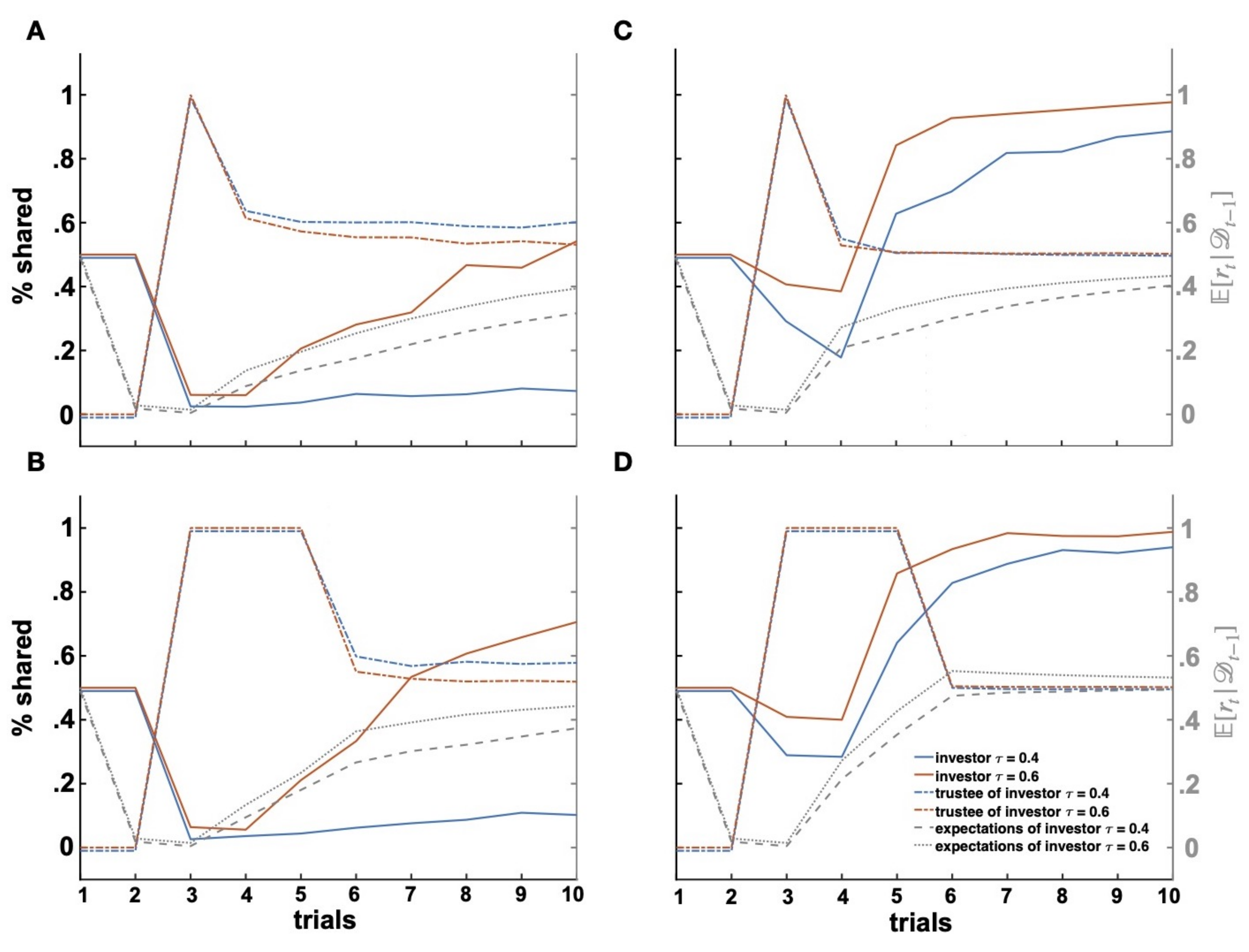
Similarly,
Figure 5D shows how highly negative expectations disrupt the ability to establish or recover a trusting interaction. Previous work has suggested that highly negative expectations in some clinical populations might impede healthy social interactions [
79]. For instance, individuals with borderline personality disorders playing as trustee do not seem to be able to appropriately increase their returns as a response to investment increases, leading to a catastrophic cascade of the social interaction, which is consistent with evidence on impaired interpersonal functioning in borderline personality disorder [
34,
80,
81]. Similarly, individuals with psychosis playing as investor manifest lower baseline trust (especially at the beginning of the interaction) and are less likely to increase investment after trust-honoring reciprocity than healthy individuals, suggesting a reduced sensitivity to social feedback that has been interpreted as reflecting their impairment in sensitivity to interpersonal cues [
82,
83]. Based on these findings, it has been suggested that individuals with borderline personality disorder and psychosis do not accurately learn or respond inadequately to cooperation signals by their social partners [
46,
84,
85,
86,
87,
88]. However, the impact of negative expectations in these populations has not been investigated yet, and in line with a negativity bias in social cue evaluations in individuals with these clinical disorders [
89,
90], we have seen in this paper that highly negative expectations might indeed explain part of the behavioral patterns observed in previous research.
Importantly, even though the following model was inspired by psychological and philosophical conceptualizations of trust, it is consistent with other formalizations in other fields such as finance. For instance, [
91] formalized distrust as a multiplier of a negative disutility that reflects investment uncertainty and reduces expectation of positive investment returns. This formalization is formally equivalent to the one in the present work, but bears some important differences in interpretation. In particular, while [
91] formalized trust only as an anxiety-reduction mechanism associated with the uncertainty over investment-related costs, the following work thinks of trust as both a multiplicative boost to the net expected return and a complementary multiplicative reduction of the possible costs incurred by investors when trusting. The current work’s formalization is more consistent with empirical findings and psychological theories supporting the idea that both one’s sensitivity to potential losses and positive expectations of potential gains should be taken into account in a model of trust [
92].
Further, in the current work, I have shown cases of what we could call “the self-fulfilling prophecy of a lack of trust”. In particular, as forming accurate expectations about the trustee’s behavior is possible only if the investor gives him/her a chance to reciprocate, a lack of trust implies poorer behavioral information about the actual reciprocity of the trustee and, hence, less accurate expectations of the partner. This occurs both when the investor decides to share nothing (with no information whatsoever received from the partner) and when the investor decides to share small amounts (allowing less variability in the possible amounts to share back and, hence, contributing to noisier behavioral information about the partner). This creates a spiral of self-fulfilling prophecies for which the distrustful investor who does not trust much in the first place receives negative reciprocating feedback from the trustee, thereby being confirmed in his/her negative expectations of the partner. In turn, such a confirmation of his/her negative expectations makes distrustful investors behave even more distrustfully in subsequent interactions. As stated above, such dynamics are very close to a variety of real-life interactions, suggesting that the paradigmatic examples considered here might be generalizable. However, not all interactions (in real life and experimental settings) have to abide by this self-fulfilling prophecy of a lack of trust. For instance, when interactions are not asymmetric and participants receive feedback about their partner’s behavior at every time step, such as in many economic games, such as the Prisoner’s Dilemma, this trap of self-fulfilling prophecy can be avoided.
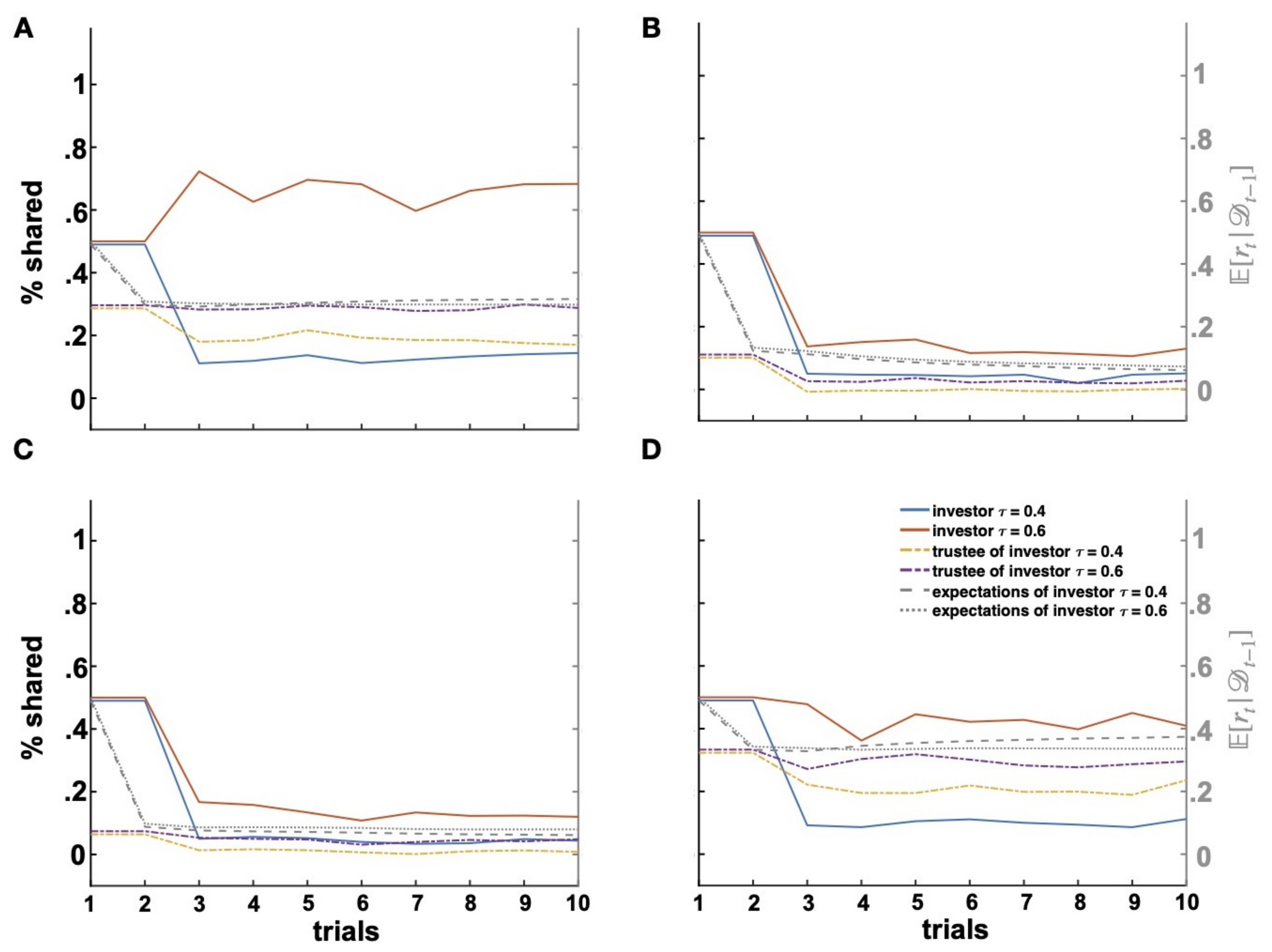
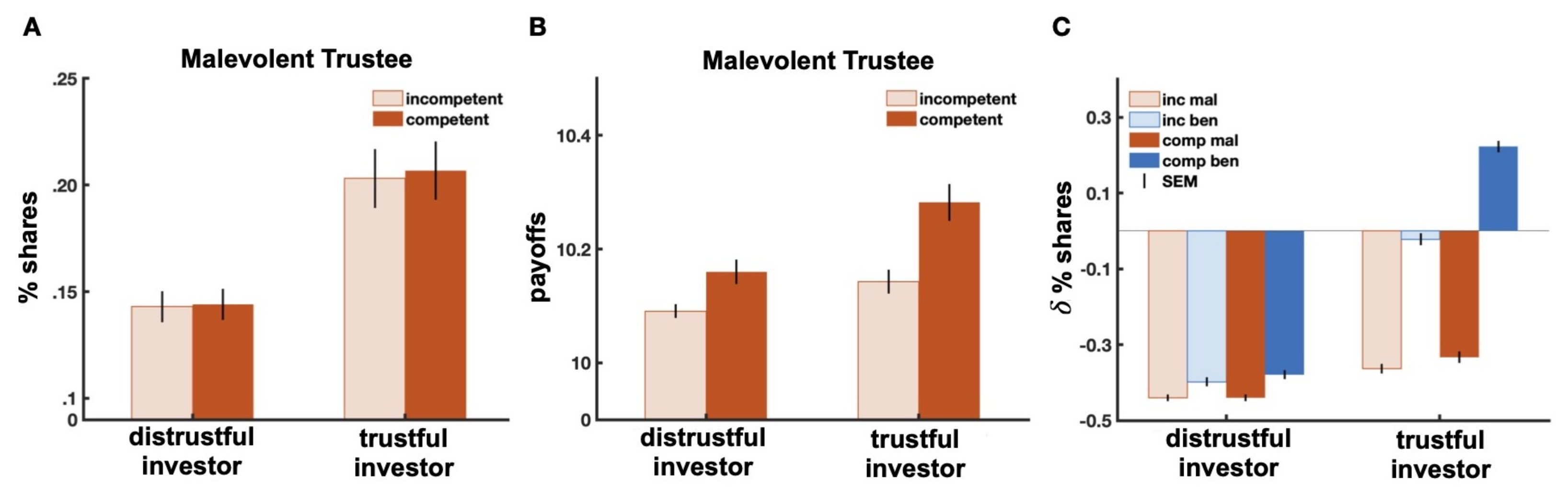
In addition, in the current work, inferences on two different psychological traits of another person and their impact on trust decisions during social interactions have been for the first time explored. Importantly, in the current implementation, the investor was supposed to receive information directly related to both character traits of his/her partner, that is his/her competence and benevolence. This greatly simplifies the inference problem. For instance, knowing how well the trustee does in the performance task likely protects against the breakdown of trust, since it is easier to forgive a mistake than malevolence. However, in many real-life situations, there exists partial observability over psychological features of an interacting partner. For example, when a particular behavior cannot so easily be traced back to one of these psychological traits, some further strategic thinking and planning are necessary to figure out the “true nature” of the interaction and avoid exploitation. Such a partial observability is likely to trigger interesting dynamics worth exploring in future work, for example in games in which the investor does not know the realized multiplier [
21,
93,
94].
Moreover, the vulnerability model is also able to describe economic predictions of rational behavior. In the one-shot IG, a rational, economic agent playing as investor would assume that the trustee does not have any incentives to reciprocate and should hence not trust. According to the vulnerability model, this is equivalent to saying that the positive contribution of the expectations of returns
in Equation (
3) is marginal or non-existent. This implies that the utility function is overly affected by the disutility of sharing
, making the model predict that the investor should not share anything (which would yield the highest utility for the investor). In this case, the model predictions are consistent with a rational agent. The same applies in repeated games. The model currently only mimics open-end interactions (e.g., when participants do not how many rounds they are going to play together), but does not account for the temporal effects of a social exchange. Such temporal effects have been proposed to be accounted for when individuals know how long the interaction with the partner is going to last and are supposed to explain end-game effects [
52]. For instance, the expectations of returns
might be contingent on a utility function of the trustee that takes into account a future investment. In the last round, when this future investment is not possible, the utility of the trustee will be mainly affected by the loss implied by reciprocation, which predicts that the trustee should not share anything. Now, if the expectations of returns
depend on the trustee’s utility function, when the trustee’s utility predicts a defection, the investor should think that reciprocity is less likely (i.e., should have more negative expectations of the trustee’s returns). Hence, the vulnerability model predicts that the investor decreases his/her shares or stops sharing altogether. As the current work does not propose a model of reciprocity (with a utility function for the trustee), future research is needed to address these scenarios.
Another interesting avenue for future research is to investigate how different trust attitudes (for example, the prevalence of different
parameters) might emerge and evolve in populations with different network structures. For instance, previous work has investigated how trust and trustworthiness evolve in different networks by using a binary version of the IG where players have a binary decision to make (trust vs. distrust for the investor and reciprocate vs. betray for the trustee) [
38]. The authors found that trust and trustworthiness evolve only under specific network structures and only for a subset of investment and back-transfer combinations, suggesting how fragile the establishment of prosocial behaviors such as trust and reciprocity is. These results echo empirical evidence showing that a single norm-violating agent reduces compliance with a social norm by a way larger extent than the extent to which a single norm-compliant agent is able to increase it [
95]. However, the work by Kumar et al. [
38] focused only on the prevalence of different behavioral strategies and not on the evolution and diffusion of different social preferences and attitudes. One interesting research question concerns investigations on how robust individual, social preferences, and attitudes are across different populations and under which conditions they thrive and die out.
Despite these advances, the considered model makes a set of simplifying assumptions. First, I assumed that participants are computing their current utility
only with respect to the current endowment
available to them at time
t. However, in repeated interactions, it is conceivable that participants actually keep a cumulative sum of the total gains they have been gathering that modulates the contribution of the negative utility associated with the investment
. This might have the effect of making participants increasingly less loss averse or more loss averse as time passes. Participants might do this especially when they know the horizon length of the game and such a length is short enough or when the total earned sum is shown to them as a feedback at the end of every trial (e.g., in experiments in which participants have information about their earning balance). In multi-round games with the same trustee, it is of course difficult to disentangle these effects from the learning about the trustee’s cooperativeness, as a good balance in such IG versions highly correlates with cooperative trustees that have shared fairly in previous trials (or vice versa). Of course, such effects could be explained by other factors as well, such as acquired familiarity with the game or generalization of previous positive and negative interactions. In particular, it has been shown that experienced and inexperienced individuals implement different investment strategies and even the same individual changes his/her behavior as a function of experience with the game [
52,
54,
58,
96].
Importantly, these effects can also hinge on prospective calculations about the amount of money individuals are likely to earn. For instance, not only participants have been seen to decrease their investments in the last trials of a finite IG with a known number of trials [
34,
52], they have also been seen to share significantly less when they are told that their monetary compensation will only consist of the amount of money they have earned in a small subset of trials (e.g., one or slightly more) randomly drawn at the end of the experiment [
35]. If cumulative earnings reduce the contribution of the negative utility associated with investment
, participants might indeed be more likely to share higher proportions of monetary amounts when they know that the sum of what they earn in each single trial of the experiment is what counts for their final payoffs. As a side note, these two different compensation schemes might frame the experiment either as a reward-poor environment or as a reward-rich environment, thereby creating different preferences that shift participants’ investment behaviors [
97].
Further, in the presented simulations, I showed how the vulnerability model behaves based on different investor’s parameters and on learning about the average behavior of different trustees who implemented fixed behavioral strategies. However, more complicated frameworks might be used to capture more sophisticated cognitive processes during such trusting interactions. For instance, in the current work, the investor’s expectations is based on a non-sophisticated model according to which the investor only maintains a running average of the trustee’s behavior. This is likely the most common strategy employed by investors in the impoverished classic IG. For instance, [
34] reported that at least 50% of their participants playing as investor behaved this way. However, investors might be sensitive to other statistics of the partner’s behavior or employ different inference processes to support their decisions. For example, as the game is repeated more and more often, the beta distribution, which represents the investor’s expectations of the partner’s behavior, becomes more and more concentrated on the average return. This has two consequences: First, highly peaky distributions (e.g., after having seen much evidence) tend to be less sensitive to observations far from the mean. This predicts that investors who know a great deal about their trustee should more strongly dismiss evidence incongruent with their expectations. Such a prediction is consistent with previous work [
40,
41,
98], but in the current implementation, the beta distribution might require an unreasonable amount of observations before a behavioral change can be promoted. Second, investors might also be sensitive not just to the partner’s average behavior, but also to his/her behavioral variability. This behavioral variability of the partner is likely associated with a form of uncertainty of both a psychological (epistemic uncertainty) and mathematical (variance) nature. Previous work has provided some evidence that behavioral variability has a negative impact on people’s trustworthiness impressions of others [
98], indicating that social agents are sensitive to other people’s behavioral consistency when learning about their personality.
Further, some investors might engage in prospective inferences about their partner’s intentions and future behavior, by incorporating beliefs they think they might trigger in their partner by behaving in a particular fashion. These are known as second- (and higher-) order beliefs of and about the interacting partner. For instance, in the current implementation, when trustees exhibit extraordinary levels of reciprocity in one of the considered paradigmatic cases, investors increase their investments without strategic considerations stopping them. However, real participants might think that the trustee wants them to think she/he has started being cooperative to make him/her share more money that the trustee will ultimately keep. Hence, a strategic, far-sighted investor might avoid falling into such a trap by refusing to share altogether. The current myopic model, however, is not able to capture such strategic dynamics. Nonetheless, the utility function of the vulnerability model can be incorporated into more general frameworks that allow such strategic inferences (e.g., into Bayesian inference frameworks such as the partially observable Markov decision processes) [
67].
Finally, the desideratum for every model is its generalizability, that is its ability to extend to other trusting interactions and behaviors. Intuitively, the model is in principle able to capture all interactions that presuppose a weighting trade-off between potential losses and attainable gains made possible by an act of trust. However, different situations are likely to require the modeling of other aspects of a social interaction or other social inferences on a partner’s quality (like in the exemplary case of competence investigated above), which all require extensions and modifications. However, the current model is not only flexible enough to incorporate further expectations and inferences on a partner’s behavior, it also allows capturing a wide range of trust attitudes with a very simple and easily understandable mechanism. Further, beyond explanations of behavior in healthy subjects, the vulnerability model has also proven to generate behavioral patterns akin to behavioral findings previously observed in different clinical populations, suggesting that it has the potential to be employed for predictions relevant for clinical investigations. Hence, the proposed formalization lays the groundwork for new theoretical and empirical investigations for refinements and testing of further behavioral predictions in the multifaceted dynamics of trusting interactions.