Abstract
A formal game-theoretic model of an intertwined supply network, in full and simplified versions, is proposed. Conditions for the sustainable development of an active system are presented in general form and then specified to the class of intertwined supply networks. As an illustration, a concise example of the dynamic Cournot duopoly and a detailed example of the model of Social and Private Interests Coordination Engines (SPICE-model) for a marketing network are considered and analytically investigated and sustainability conditions are established. An important conclusion is that the sustainable development of the active system is possible only under the viability conditions satisfied simultaneously with coordinating the interests of all active agents of the system.
1. Introduction
For the relations between society and nature, sustainable development problems have been the focus of attention of politicians, scientists, and the public for more than forty years. The meaning of this concept is that economic development should ensure social welfare without disturbing the ecological balance: “…development that meets the needs and aspirations of the present without compromising the ability to meet those of the future…” [1] (p. 43). In the 1990s, the concept of “three pillars” became widespread in sustainability theory. According to this concept, it is necessary to simultaneously consider and balance economic, environmental, and social criteria. Therefore, in the mathematical modeling of sustainable development, the state vector should include variables describing the three groups of indicators. On a long or even infinite time horizon, the values of all state variables should belong to a given range, thereby ensuring the sustainable development of the socio-ecological-economic system. This idea was formalized in viability theory [2]. Nowadays, the concept of a circular economy plays a more and more significant role in this area [3,4].
Unfortunately, practice shows that in most countries, the strategies of transition to sustainable development remain nothing more than declarations. As we believe, the problem here is the absence of real agents interested in implementing sustainable development conditions. These conditions cannot be satisfied by themselves and require special control efforts. According to the author’s concept of sustainable management, the sustainable development of an active system can be ensured only if the interests of all active elements (agents) in this system are taken into consideration and coordinated. Thus, research into sustainable development fits the context of motivation theory [5], mechanism design [6,7,8], the theory of active systems [9,10], and the information theory of hierarchical systems [11].
For supply chains, sustainable development issues were analyzed in the position paper by Ivanov and Dolgui [12]. The authors introduced a new generalizing concept of intertwined supply networks (ISNs) as a set of interconnected supply chains; provided a comparative analysis of the concepts of resilience, robustness, stability, and viability; illustrated their approach using the example of an ecological system model, and outlined some lines of further research.
This paper develops and supplements [12] with the author’s concept of sustainable management of active systems [13,14,15,16,17,18]. The contribution of this paper is as follows:
A well-grounded active system interpretation of ISNs is presented, and the role of control in the functioning of various types of ISNs is described.The main objectives of the paper are the following:
- (1)
- to present an active system representation of ISNs, and to describe the functioning of various types of ISNs;
- (2)
- to give a game-theoretic formalization of ISNs with consideration of their structure;
- (3)
- to specify the notions of the system’s sustainability and sustainable management in game-theoretic terms;
- (4)
- to study a dynamic game-theoretic model of Social and Private Interests Coordination Engines (SPICE-model) for ISNs with application to marketing.
The contribution of this paper is as follows:
- a well-grounded active system interpretation of ISNs is presented, and the role of control in the functioning of various types of ISNs is described;
- a game-theoretic formalization of ISNs as active systems is proposed, taking into account their structure. Special cases of the general model are highlighted;
- the notions of the system’s sustainability and sustainable management capability are specified within the deterministic ISN model;
- a dynamic game-theoretic model of Social and Private Interests Coordination Engines (SPICE-model) for ISNs is constructed, and application to marketing is considered. This model is studied for the linear functions of the private interests of influence agents.
As we expect, intertwined supply networks should become an important area of application in the theory of sustainable management of active systems. We launchthis research process in the paper.
In Section 2, a literature review on the topic of the paper is provided. In Section 3, a well-grounded interpretation of an ISN as an active system is presented, and a corresponding game-theoretic model is introduced. In Section 4, the notions of the system’s sustainability and sustainable management capability are given an original interpretation and specified to the deterministic ISN model; also, a concise example of the dynamic Cournot duopoly is considered. In Section 5, as a detailed example, the SPICE-model for ISNs is constructed with application to marketing; also, this model is analytically investigated for the linear functions of private interests of influence agents. In Section 6, concluding remarks are combined, and some lines of further research are discussed.
2. Literature Review
There are numerous publications devoted to the theory of sustainable development and sustainability in its various aspects [1,19,20,21]. The main idea that sustainable development is possible under certain requirements to the state of the socio-ecological-economic system was mathematically formalized in viability theory [2,22,23]. For key economic, environmental, and social indicators, some thresholds are assigned, determining the domain of the system’s viability [24]. An economic trajectory is considered sustainable if, at any time instant, it belongs to a given domain of viability. The viability kernel plays the main mathematical role here. This kernel is the set of all initial states for the trajectories satisfying viability constraints. Martinet [25] suggested defining indicator thresholds by solving an optimization problem. In a series of papers [26,27,28], a connection between the concepts of maximin, viability, and sustainable development capability was established.
A concept for the sustainable management of active systems based on systems analysis, mathematical modeling, and information technology was proposed [13,14,15,16,17,18]. The main idea put forward therein is that the sustainable development of an active system can be achieved (i.e., sustainable development constraints can be satisfied) only if the active agents of this system have an interest in it. More specifically, the weak and strong form of viability conditions in the model of a controlled dynamic system were described; a game-theoretic formalization of hierarchical control methods was suggested, considering sustainable development requirements; several applications-relevant sustainable management problems in various areas were solved.
The problems of considering and coordinating the interests of active agents were studied in the theory of motivation [5], mechanism design [6,7,8], the theory of active systems [9,10], and the information theory of hierarchical systems [11]. The central mathematical apparatus is provided by the theory of dynamic games [29,30,31]. Along with traditional research methods, simulation plays a crucial role here [32].
An important class of models for coordination of interests is the models of the economy of public goods [33]. A modification of these models, the so-called SPICE-models, was suggested and analyzed in static [34,35] and dynamic statements [36,37]. In the SPICE-models, each agent distributes his resource between the production of public good and his private activity. As a result, the agent’s payoff consists of the share of his participation in using public goods and his income from private investments, and it is necessary to choose an optimal allocation of the resource between public and private interests. In addition, the system’s viability requirements can be taken into consideration.
Extensive literature was devoted to control models for different classes of systems with a network structure, including ISNs. For example, note the monographs [38,39] and the reviews [40,41]. Novikov analyzed the relations between game-theoretic and network models [42]. As compared to this paper, the closest approach was described by Sedakov and Zhen [43]. The earlier studies related to this paper can be found in [44,45]. Dynamic SPICE-models on networks, with application to marketing, were considered [46,47]. Viability conditions were taken into account [48]. The main idea was as follows: it suffices to control only the strong subgroups of the influence digraph (opinion leaders), who determine the stable final opinions of all other agents.Tur and Petrosyan [49] analyze strong time-consistent solutions for cooperative differential games with network structure. They introduce a new characteristic function that considers a networked structure. This approach is developed in [50,51].
In the position paper, Ivanov and Dolgui [12] introduced a new generalizing concept of intertwined supply networks (ISNs) as a set of interconnected supply chains; provided a comparative analysis of the concepts of resilience, robustness, stability, and viability; illustrated their approach using the example of an ecological system model, and outlined some lines of further research. Rentizelas et al. [52] consider reverse supply network design for circular economy pathways of wind turbine blades in Europe. Zhao et al. [53] study contract strategy for two competing supply chains selling a substitutable product under demand uncertainty. Kamalahmadi et al. [54] examine the relative impact on supply chain responsiveness of adding flexibility and redundancy. They seek to investigate the effectiveness of flexibility and redundancy in terms of minimizing expected supply chain costs and maximizing expected service delivery when a supply chain is exposed to supplier and environmental disruptions. Their results show that the backup-supplier practice is more effective than the flexible-supplier practice, as measured by cost reduction and service-level improvement. Dolgui et al. [55] analyzed the ripple effect in supply chains compared to the bullwhip effect. The papers [56,57] focused on the impact of epidemics, particularly COVID-19, on global supply chains and their sustainability. Disaster management was also discussed by Dubey et al. [58]. The resilience of supply chains was examined in [59,60,61]. A risk-based systematic approach to supplier selection was presented by Yoon et al. [62]. The spread of risks in supply chains was also studied [63]. The adaptive properties of supply chains were analyzed by Choi et al. [64]. For a large number of firms, the adaptation of supply chains to disruptive influences was modeled within the agent-based framework [65]. An analysis of supply chains in the light of the circular economy concept was given [3,4,66]. Choi et al. [64] presented a comprehensive review of publications on the game-theoretic modeling of production management in a sharing and circular economy, collected in a special issue of the International Journal of Production Research.
We summarize the results of the literature review in Table 1.

Table 1.
Literature review (2019–2022).
3. Intertwined Supply Networks: Control and Formalization
Ivanov and Dolgui [12] introduced the concept of an intertwined supply network (ISN) as a set of interconnected supply chains that jointly provide society and markets with goods and services. Figure 1 shows an ISN versus traditional supply chains and networks.
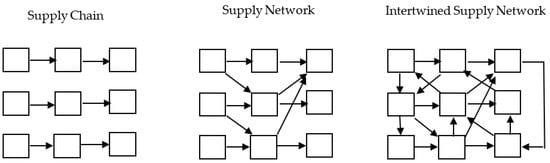
Figure 1.
Linear supply chains, supply networks, and intertwined supply networks [12].
As we believe, an ISN should, first of all, be interpreted as an active system [9,10]. This means that the need to consider and coordinate the interests of active elements (agents) in this system should come to the fore. According to the theory of active systems, active agents have strategic behavior, i.e., make decisions facilitating the realization of their interests. In particular, active agents can deliberately misrepresent information about their characteristics reported to other agents.
Note that, within the systems approach, each element of an ISN is an active system with its internal structure, and the ISN itself is included as an element in some active supersystem of a higher level. For example, a regional ISN consists of enterprises located in a given region of a country and is part of the national ISN. However, this aspect will not be considered below: the subject of study is some separate ISN as an active system.
Within the theory of active systems, we propose the following general model of an ISN:
Here is a finite set of active agents; means the set of all state profiles of active agents; denotes the state of agent i, treated as a function of continuous or discrete time t; is the matrix of links between agents, defined by the interaction coefficients ; gives the set of admissible action profiles of the agents; is an admissible action of agent i at a time instant t; denotes the set of possible type profiles of the agents; indicates the type of agent i; is a probability distribution on the set ; finally, R (the set of real numbers) is the payoff function of agent , and .
A pair determines a weighted digraph specifying the ISN structure. If , then the arc (the arc from the vertex i to vertex j) is absent.
Let be the strategy of agent I, which determines his action depending on his type, and be the profile of all admissible strategies of the agents. Under a given profile , the expected payoff of agent I of type is
where agent I forms his belief about the types of other agents by the Bayes formula with due consideration of the complete probability rule:
Then model (1) is a game with incomplete (asymmetric) information, or a Bayesian game [67], with the ISN structure taken into consideration.
For the sake of simplicity, below we will consider only the deterministic model of a generalized normal-form game with complete information of the form
in which the types of agents are fixed, and the agents use pure strategies. Therefore, the probability distribution on the set of types is not required. In this case, the payoff functions are of the form R, .
For describing the evolution of the agents’ states, it is convenient to adopt the well-known De Groot model of the opinion dynamics in a social group [68]:
where T denotes the game duration (time horizon). Of course, more general (nonlinear) models can be considered, but the state of agent j always changes depending on the actions of those agents I that can influence him, i.e., for which the digraph D contains a corresponding arc .
Note that in the theory of active systems, the aspect of control is crucial for the operation of ISNs. Therefore, it makes sense to consider three special cases of ISNs as follows. Such an approach rests on the models of control on networks [38], in which basic agents and influence agents are often distinguished. Active influence agents impact the basic agents in their interests, formalized by the payoff functions. The basic agents are considered degenerate (passive), without any interests. The state of the basic agents evolves during their interaction and under the purposeful impact of the influence agents.
3.1. Optimal Control in ISNs
The set of agents is , where the number 0 corresponds to a single influence agent, and the other agents are basic. In the linear case, the dynamics equation (Equation (5)) takes the form
where is the degree of impact of the influence agent on basic agent j. If the influence agent has no impact on basic agent j, then . In this case, model (4) reduces to the optimal control problem (here and farther “” denotes the mathematical problem of maximization)
along the trajectories of (6), where: denotes the discount factor; and are the instantaneous payoff function of the influence agent and his terminal payoff, respectively. The horizon T can be finite or infinite; in the latter case, the terminal payoff is absent. The functions can be open-loop or feedback strategies.
3.2. Conflict Control in ISNs
The set of agents is , where the first numbers correspond to the influence agents, and the other numbers to the basic agents. The linear dynamics equation has the form
where is the degree of impact of influence agent l on basic agent j. If influence agent l has no impact on basic agent j, then . Models (4) and (8) represent a differential normal-form game in which the payoff functions of the agents are given by
3.3. Hierarchical Control in ISNs
The set of agents is , where the number 0 corresponds to the upper-level influence agent (called the Principal in the theory of active systems), the next numbers to the other influence agents, and the rest numbers to the basic agents. The Principal coordinates the activity of all influence agents without any direct impact on the basic agents. As before, the dynamics equation has the form (8).The Principal’s interests are described by
and the agents’ interests by (9), and .
Models (8)–(10) are a hierarchical (Stackelberg) differential normal-form game in which the Principal makes the first move.
Of course, more general (nonlinear) models can be considered in all cases. For the continuous-time statement, the sums in the payoff functions are replaced with the integrals and the difference dynamics equations with the differential ones. The diagrams of these structures are shown in Figure 2, with the following abbreviations: optimally controlled intertwined supply networks (OCISNs), conflict controlled intertwined supply networks (CCISNs), and hierarchically controlled intertwined supply networks (HCISNs).
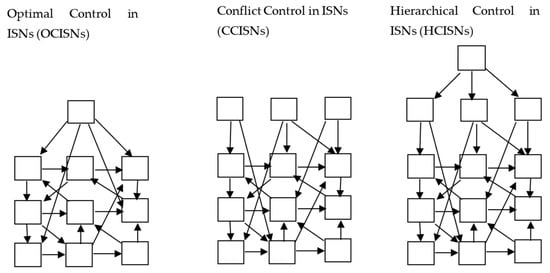
Figure 2.
Optimal, conflict, and hierarchical control in (ISNs).
Let us emphasize that in real ISNs, all agents are active. They are divided into basic agents and influence agents primarily for methodological purposes, for the convenient modeling of control processes. At the same time, in several real situations, the special cases of OCISNs, CCISNs, and HCISNs reflect quite well the subject matter, when the optimal, conflict, or hierarchical control of some ISN plays the primary role, and many of its elements can be considered as relatively passive objects of influence.
4. Notion of Sustainability
4.1. General Case
According to viability theory [2], the viability condition for models (1) or (4), representing the main requirement for sustainable development, can be written as
If at any time instant, the system stays within a given domain , then its development is assumed sustainable. The concept of viability and approaches to its formalization have been discussed in detail in Section 2.
What is much more important, the viability condition, in the form (11) or some other, is necessary but, in principle, insufficient to ensure sustainable development. Active agents, intended to ensure the sustainable development of the system, must be interested in this; otherwise, condition (11) will remain a needless burden for them, and their real actions will not be aimed at fulfilling it.
In the original model (1) or (4), equal agents influence some dynamic object in their interests, simultaneously and independently of each other. At the same time, there are objective requirements (viability conditions) that should be satisfied for the object’s state from the entire active system viewpoint. We write model (4) as a differential normal-form game of players:
Here, is the set of active agents; and represent the instantaneous payoff function and integral payoff functional of agent , respectively; denotes the control of agent at a time instant , and ; is the set of all admissible controls of agent , and ; gives the value of the state variable at a time instant ; specifies an initial state; is a given function determining state variations over time; finally, means the discount factor. In the general case, the state variable and control can be vectors. The infinite time horizon better suits the concept of sustainable development, although problem statements with are also possible. Also, we make the following assumptions. First, the sets are compact in the corresponding vector spaces. Second, the vectorfunction is continuous in and continuously differentiable in the other variables. Third, there exists a constant such that for any , and , where the denotation is the norm of a vector. Fourth, the functions are continuous in all variables. Fifth, the functions satisfying the constraint (13) are piecewise continuous in , smooth in for all , and belong to the classes of admissible feedback strategies.
The viability condition has the form (11). Note that in the original statement, condition (11) is external for the set of agents, i.e., they are not interested in its implementation. Therefore, initially, the model cannot be considered as a differential game (12)–(14) with the additional state-space constraints (11).
The solution of the game (12)–(14) will be understood as the set of Nash equilibria , under the assumption (otherwise, the problem makes no sense). In particular, if are convex and compact whereas are concave in on for all , .
Denote by the set of controls ensuring viability, assuming again that (otherwise, further considerations become pointless). If , then the sustainable management problem (11)–(14) has a solution. The controls ensure viability, and the interests of all agents are also taken into consideration through a Nash equilibrium in their game (the compatibility of interests).
For a detailed treatment of the problem of compatibility of interests, we introduce the social welfare functional
Then, under the condition
the viability requirements (11) are perfectly compatible with social welfare. In the opposite case, i.e., when
the viability requirements are not perfectly compatible with social welfare. Next, if
then the viability requirements are perfectly compatible with the private interests of all agents. In the opposite case, i.e., when
the viability requirements are not compatible with the private interests of some agents. Obviously, (17) → (15), and (16) → (18).
If , then the sustainable management control (11)–(14) in the original statement has no solution.
If , but (16) or at least (18) holds, then the problem is solvable, but the social welfare in general or at least the interests of some agents will suffer if the viability conditions are satisfied. In these cases, there are two possible ways to modify the problem statement; see below.
Collaboration is a method in which all agents agree to ensure the viability condition (11), voluntarily and consciously. In this case only, the sustainable management problem for active systems with independent agents is described by the differential normal-form game with the state-space constraints (11)–(14).
In particular, independent agents can cooperate, form agrand coalition, and jointly maximize the total payoff functional (social welfare) with respect to all control variables. Then, the differential normal-form game (12)–(14) is replaced with the optimal control problem
with the constraints (13) and (14).
We introduce the set of arguments of function J at which the maximum is achieved, i.e., . If , then the sustainable management problem for active systems in the cooperative statement has a solution. Note that in this problem, , i.e., the condition makes viability compatible with social welfare.
In the case of collaboration, all agents (members of the grand coalition) agree to ensure the viability condition (11). For the grand coalition, the optimal control problem with state-space constraints (11), (13), (14), and (19) arises accordingly.
Suppose that the control problem in the original statement has no solution, and collaboration is not applicable in practice. In this case, the Principal should be introduced into the system, with the main goal to ensure viability via hierarchical influence on the sets of admissible controls of the agents (compulsion) or their payoff functionals (impulsion); for details, see [13,14]. This leads to a hierarchical differential game of the form
subject to the additional constraints (11) and (13). Here, and are the Principal’s instantaneous payoff function and integral payoff functional, respectively; represents the vector of impulsion controls; finally, denotes the vector of compulsion controls. Note that in this case, the model turns into a hierarchical differential Stackelberg game with state-space constraints: fulfilling the viability condition (11) is the Principal’s main goal. The set of Nash equilibria in the agents’ game takes the form since the solutions of this game depend on the Principal’s actions. For this model, the same mathematical requirements are imposed as for models (12)–(14).
We introduce the following sets of agent controls:
- , which globally maximizes the payoff functional of the Principal;
- , which ensures the compatibility of the agents’ interests with the Principal’s interests, albeit neglecting viability;
- , which ensures viability with due consideration of the Principal’s interests, albeit neglecting the agents’ interests;
- , which ensures viability with due consideration of the agents’ interests, albeit neglecting the Principal’s interests;
- , which ensures viability with the perfect compatibility of all interests.
If , then the sustainable management problem (11), (14), (20)–(23) has a solution in the hierarchical statement. The non-emptiness of the sets , gives a theoretical possibility to solve the problem. However, this possibility is rather ambiguous in practice since either the agents’ interests or the Principal’s interests are not considered.
The following pairs of classification attributes determine the information structures of the differential games:
- open-loop strategies (Stackelberg games) or feedback strategies (inverse Stackelberg games); see [69];
- compulsion or impulsion ;
- the deterministic or stochastic model.
For assessing the concordance of interests in quantitative terms, a reasonable approach is to use the indices of system compatibility. For the model without the Principal, this index has the form
where and . Thus, characterizes the difference between the global maximum of social welfare and its value in the worst-case Nash equilibrium. Note that for this purpose, the price of anarchy is often used as well [70]
For the model with the Principal, the system compatibility index can be written as
where and .
The index characterizes the compatibility of interests from the Principal’s viewpoint. In both cases, the perfect compatibility of interests occurs under . The condition indicates almost perfect compatibility.
When solving problems (11) and (14), and (20)–(23), it is sometimes convenient to single out the following situations:
- The Principal shows indifference, , being interested only in the viability condition (11). Then, the set becomes needless, and it remains to verify the condition
- The Principal maximizes the social welfare
in this case, the interests of the Principal and agents are co-directed.
Note that the Principal’s capabilities on the compulsion and impulsion of agents incur costs and are therefore limited. Let us introduce the functions , which characterize the administrative and economic costs of the Principal, respectively. It is natural to assume that: and , where denotes the maximum value of the state variable, and is monotonically decreasing on ; , and is monotonically increasing on . Then the Principal’s budget constraints have the following form:
- in the case of compulsion,
- in the case of impulsion,
Here, R is the Principal’s budget.
Well, sustainable development (sustainability: S) is possible under the two conditions satisfied simultaneously, namely, viability (V) and the compatibility of interests (C):
The viability condition always has the form (11). The conditions for the compatibility of interests depend on the structural configuration of the active system ; see the description above. If both conditions on the right-hand side of (30) hold, then the ISN is resistant to internal and external disturbances, including emergencies and threats.
Different statements of the sustainable management problem for active systems are combined in Table 2.

Table 2.
Sustainable management problems for active systems.
4.2. Sustainability of Intertwined Supply Networks
Intertwined supply networks represent active organizational and economic systems. For this class of systems, strategic behavior is critical, which is expressed primarily in the desire of economic agents to maximize their profits. At the same time, the real interests of active agents have a more complex character. First, along with the natural desire to profit as quickly as possible, economic agents should take care of the long-term successful operation of enterprises and organizations. Second, besides the purely economic component, the social responsibility of business, the awareness of environmental problems, and protection against threats of anthropogenic, technogenic, and biological nature are playing an increasing role. Taken together, these factors form the viability conditions for ISNs.
Thus, in model (4), is a structural digraph of an ISN that determines the set of active agents and links between them; represents the set of states of agent i, and denotes the set of his admissible actions; ℝ is the payoff function of agent i, . The viability condition (11) for the state vector can be written as
As a rule, the viability domains are given by inequalities of one of the following types:
Here, and are some thresholds for each indicator.For example, for an industrial enterprise, the viability conditions for emissions of pollutants have the form (32); for profit, the form (33); for wages, the form (34), taking into consideration the total wages fund.
As an illustrative example of ISNs, consider a dynamic Cournot duopoly of the form
where is the output of firm i at step t; denotes the specific costs; finally, is the demand parameter. Then describes the profit of firm i at step t. Assuming that , the state of firm i evolves according to Equation (35). The total discounted profit of firm i on the infinite horizon is given by
where and is the discount factor.
Denote by the output of each firm in cooperation (cartel collusion), supposing that in this case, all firms have the same outputs. Let us choose the viability condition in the integral form
Consider possible ways to ensure this condition in the infinite-horizon repeated game (35), (36). First, assume that all firms have agreed on an output for any step. If at a step t one of the firms has a different output, then starting from the step (t + 1), the agreement becomes invalid, and the output of each firm is equal to the equilibrium value .
In the one-step game (35), the Nash equilibrium is calculated from the system of equations
Note that the response function of player I is
Due to the players’ symmetry, , and the solution of (38) is
For the equal outputs , we obtain
and hence the cooperative solution and the corresponding payoff are
Let player 1 violate the agreement immediately. Then
In view of (39), the value is , and consequently, . Under the above assumptions, the total payoff of player 1 takes the form
Complying with the agreement, player 1 obtains the total payoff
Therefore, the breach of the agreement is non-beneficial under the condition
After some trivial transformations, we arrive at .
Now suppose that when player 1 deviates from the cooperative agreement, player 2 uses the punishment strategy. This strategy can be calculated from the condition , which yields . Being aware of this fact, starting from the step t = 1, player 1 will choose the optimal response , i.e., . In this case, . Then, the total payoff of player 1 takes the form
Hence, the condition of non-beneficial breach of agreement is , or after simple transformations,
Thus, with a sufficiently large value of the discount factor, trigger strategies of various types ensure the viability of this ISN.
In addition, note that in this model,
5. SPICE-Models of Intertwined Supply Networks in Marketing
As a detailed example, we present the model of Social and Private Interests Coordination Engines (SPICE-model) for a marketing network.
There are elements of a marketing network, namely, the coordinating Principal, influence agents (firms), and basic agents (consumers). The Principal has some amount of resources to be distributed among the influence agents, which use these resources to attract consumers to purchase the goods or services. The system’s state dynamics are characterized by the opinions of the basic agents—their planned purchases of goods or services from the firms. The opinions are formed during the interaction of basic agents with each other (taking into consideration their own opinions), under the marketing impact exerted by the influence agents.
The influence agents have a common interest, expressed by the desire to maximize the opinions of the basic agents, and some private interests, associated, e.g., with third-party investments. Therefore, their problem is to distribute the marketing budget optimally, allocated by the Principal, between the implementation of these interests. The Principal’s problem is to maximize the opinions of the basic agents, considering the costs of marketing, and to ensure the viability conditions for the entire system. According to these conditions, the total opinion of the basic agents should belong to a given range on the entire planning horizon.
These considerations lead to the model
Here n denotes the number of the basic agents (the size of the target audience); m is the number of the influence agents (competing firms). If firm i has no impact on agent j, then . In addition, R is the total marketing budget of the Principal; T gives the duration of this game (planning horizon); and are the payoff functionals of the Principal and influence agents, respectively; is the marketing budget of the Principal allocated to agent i at an instant t; reflects the opinion of basic agent j at an instant t; specifies the costs of the marketing impact of influence agent i on basic agent j at an instant t; is the degree of impact of influence agent i on basic agent j; denotes the discount factor; finally, is the coefficient of impact of basic agent i on the opinion increase of agent j, with the additional constraints and , where .
Let us explain the negative coefficient of impact of basic agent i on his opinion increase. The opinion increase of basic agent i is considered with respect to his initial opinion: the former is the initial opinion of basic agent i multiplied by some positive coefficient, minus his opinion at the current instant. In other words, the absolute value is the share in the opinion of basic agent i that he will replace with the opinions of other agents. In particular, if basic agent i absolutes the truth of his opinion (“there are only two opinions: mine and the wrong one!”), this stubborn agent will not change his opinion, which is reflected in his opinion increase by the coefficient , and he will not listen to anyone’s opinion (i.e., for ). If basic agent i annihilates his own opinion (“what will the others say?”), then the rejection of his opinion is expressed by the minimum coefficient of impact on his opinion increase (in this case, ), and (his opinion is entirely replaced with the other opinions).
Solving the problem of firm i, we can replace the n state variables with their sum, denoting by x the single state variable , where . Then , and conditions (41) and (42) take the forms
and
respectively.
Supposing that the Bellman function is linear, under the condition , from the Hamilton–Jacobi–Bellman equation we obtain the relation
where denotes the amount of resources allocated by the influence agent to attract the basic agents. The optimal amount of these resources is given by
In view of (45), the expression (44) can be written in the form
Now we study the Principal’s strategy. The Principal can only increase the value , allocating his resources to the firms. Then the optimal strategy of the Principal is obvious. From the problem statement, it follows that .
The Principal solves the problem
subject to the constraints , , , and , , where , , , and .
Clearly, to optimize his objective function, the Principal should optimally increase the value until reaching the value . Then he should stop allocating the resources to the firms. In this case, the value will remain equal to on the remainder of the planning horizon.
For implementing this strategy, at the instant the Principal should determine the instant when the value will become equal to under the corresponding strategy.
Under the condition , the Hamilton–Jacobi–Bellman equation with the linear Bellman function yields the optimal values . However, the Principal knows that not all resources will be spent on social interests. Hence, the optimal amount of resources that the Principal will allocate to the influence agent is , thereby compelling the agents to spend all their resources on social interests.
Substituting the expression (46) into Equation (43) for the sum of the state variables x, we obtain
Integrating this equation, we find
Thus, is the instant when the right-hand side of the expression (47) will reach the value . Knowing the value , we can reformulate the Principal’s problem as follows:
subject to the constraints , , , , and (47).
Additionally, we establish the following facts: under the condition , the optimal amount of resources is , where , ; under the condition , the Principal is ready to allocate the influence agents the amount
but only if they will spend these resources ultimately on social interests.
If the inequality
holds at least for one influence agent, then the amount of resources for her reduces to the value that she is ready to spend on social interests, i.e., .
The sets of agents for which inequality (49) is satisfied (or not) depend on time. Let K(t) be the set of agents for which condition (49) holds, and L(t) be the set of agents for which inequality (49) does not hold. The following result is easy to show: if at least two of the coefficients pi have different values, the sets K(t) and L(t) are non-empty at those instants when the Principal does not have enough resources. Therefore, taking into consideration the expression (48),
Thus, for those agents who can spend resources on private interests, the supply of resources is reduced, and the remaining resources are allocated proportionally between those agents who spend them on social interests. At the remaining instants , .
There exists a unique instant at which the resources are enough, and . The resources may be not enough only under the condition , and only at the instants . In view of the aforesaid, we write:
To calculate , assume that each influence agent maximizes not his utility, but the Principal’s utility under a given strategy of the latter, i.e., solves the problem
subject to the constraints
If , then the optimal strategy of each firm is obvious: it should not invest in marketing. Moreover, this is impossible because, in this case, the Principal allocates no financial resources to the firms, i.e., .
Let . Unlike the Principal, no influence agent can a priori estimate the instant h when the sum of the state variables will reach the value . However, this estimate turns out needless because the optimal strategies of firms are independent of the length of the planning horizon. Consider the game on the time interval . Using the same considerations as for the optimization of , we obtain the following optimal strategies of the Principal and influence agents:
As a result, . In addition,
where is calculated by Formulas (50) and (51). From (52) we can express the value , the instant when the right-hand side of Equation (52) reaches the value . Then , , , , where is given by Formulas (50) and (51).
By analogy with the previous case, we can demonstrate the existence of a unique instant such that the resources are not enough for .
Accordingly, we write
For the Principal, the system compatibility index (26) takes the form
For social welfare, the system compatibility index (24) differs from its counterpart for the Principal: the private incomes of all agents are added to and . However, since in this case, the agents cannot spend resources on social interests, both indices coincide.
Therefore, in the model under consideration, the viability condition holds if . The total opinion cannot decrease, i.e., the left-hand part of the inequality is satisfied. Upon reaching the upper bound of this state-space constraint, the Principal should stop allocating the resources to the influence agents, and the right part of the inequality will be satisfied accordingly.
The compatibility condition holds partially since the agents have private interests, which are not fully realized due to the Principal. The system compatibility index tends to 1 as the coefficients of private activity vanish. This result was established in [45], where a similar model was studied without considering the private interests of influence agents.
6. Conclusions
Ivanov and Dolgui [12] introduced the concept of intertwined supply networks (ISNs) as a set of interconnected supply chains and considered their sustainability. This paper has developed and supplemented [12] with the author’s theory of sustainable management of active systems. A formal game-theoretic model of an intertwined supply network, in full and simplified versions, has been proposed. Conditions for the sustainable development of an active system have been presented in general form and then specified inthe case of intertwined supply networks. As an illustration, a concise example of the dynamic Cournot duopoly and a detailed example of the model of Social and Private Interests Coordination Engines (SPICE-model) for a marketing network have been considered and analytically investigated, and sustainability conditions have been established. An important conclusion is that the sustainable development of the active system is possible only under the viability conditions satisfied simultaneously with coordinating the interests of all active agents of the system.
The proposed game-theoretic approach permits considerationof strategic aspects of intertwined supply networks. It is very important to emphasize that in the sustainability theory the viability conditions are not explicitly connected with coordinating the interests of all active agents of the system. The viability requirements are just formulated without mentioning a subject or subjects of their implementation. In this case, sustainability remains only a declaration.
Certainly, many important issues stay beyond the consideration in this paper, which is only a first step. It is necessary to specify game-theoretic models for different types of ISNs. Stochastic models seem to be more adequate forreal situations. Games in the form of characteristic functions are useful for the analysis of possible allocations of the cooperative income and stability of business and political agreements.
It seems promising to develop further the theory of sustainable management of active systems as applied to intertwined supply networks. Particularly, we will investigate regional social–ecological–economic systems as intertwined supply networks. It seems prospective to use cognitive maps as a base for mathematical modeling with a game-theoretic description of the control subsystem. Additionally, cooperative games and stochastic game-theoretic models will be studied.
As for practical implications, first of all, the companies will receive an adequate tool for conceptual analysis of intertwined supply networks, for example, in the modernization of logistic chains. Some specific results of the mathematical analysis may be used as immediate practical recommendations, for example, in resource allocation in marketing.
Author Contributions
Conceptualization, review, methodology, and formal analysis and investigation G.O.; investigation, O.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Commission on Environment and Development (WCED). Our Common Future; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Aubin, J.P. Viability Theory; Boston: Birkhäuser, Switzerland, 1991. [Google Scholar]
- Govindan, K.; Hasanagic, M. A Systematic Review on Drivers, Barriers, and Practices Towards Circular Economy: A Supply Chain Perspective. Int. J. Prod. Res. 2018, 56, 278–311. [Google Scholar] [CrossRef]
- Howard, M.; Hopkinson, P.; Miemczyk, J. The Regenerative Supply Chain: A Framework for Developing Circular Economy Indicators. Int. J. Prod. Res. 2018, 57, 7300–7318. [Google Scholar] [CrossRef] [Green Version]
- Laffont, J.-J.; Martimort, D. The Theory of Incentives: The Principal-Agent Model; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Myerson, R. Incentive Compatibility and the Bargaining Problem. Econometrica 1979, 47, 61–73. [Google Scholar] [CrossRef] [Green Version]
- Myerson, R. Optimal Coordination Mechanisms in Generalized Principal-Agent Models. J. Math. Econ. 1982, 10, 67–81. [Google Scholar] [CrossRef]
- Myerson, R. Mechanism Design by an Informed Principal. Econometrica 1983, 51, 1767–1798. [Google Scholar] [CrossRef]
- Burkov, V.N.; Gubko, M.V.; Kondrat’ev, V.V.; Korgin, N.A.; Novikov, D.A. Mechanism Design and Management: Mathematical Methods for Smart Organizations; Novikov, D., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2013. [Google Scholar]
- Novikov, D. Theory of Control in Organizations; Nova Science Publishers: Hauppauge, NY, USA, 2013. [Google Scholar]
- Gorelov, M.A.; Kononenko, F.A. Dynamic Models of Conflicts. III. Hierarchical Games. Autom. Remote Control 2015, 76, 264–277. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. Viability of Intertwined Supply Networks: Extending the Supply Chain Resilience Angles towards Survivability. A Position Paper Motivated by COVID-19 Outbreak. Int. J. Prod. Res. 2020, 58, 2904–2915. [Google Scholar] [CrossRef] [Green Version]
- Ougolnitsky, G. Sustainable Management; Nova Science Publishers: Hauppauge, NY, USA, 2011. [Google Scholar]
- Ougolnitsky, G. Game Theoretic Formalization of the Concept of Sustainable Development in the Hierarchical Control Systems. Ann. Oper. Res. 2014, 220, 69–86. [Google Scholar] [CrossRef]
- Ougolnitsky, G.A. Sustainable Management as a Key to Sustainable Development. In Sustainable Development: Processes, Challenges and Prospects; Reyes, D., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 87–128. [Google Scholar]
- Ougolnitsky, G.A. A System Approach to the Regional Sustainable Management. Adv. Syst. Sci. Appl. 2017, 17, 52–62. [Google Scholar]
- Ugol’nitskii, G.A.; Usov, A.B. Equilibria in Models of Hierarchically Organized Dynamic Systems with Regard to Sustainable Development Conditions. Autom. Remote Control 2014, 75, 1055–1068. [Google Scholar] [CrossRef]
- Kornienko, S.A.; Ougolnitsky, G.A. Dynamic Stackelberg Games with Requirements to the Controlled System as a Model of Sustainable Environmental Management. Adv. Syst. Sci. Appl. 2014, 14, 325–345. [Google Scholar]
- Kates, R.W.; Clark, W.C.; Corell, R.; Hall, J.M.; Jaeger, C.C.; Lowe, I.; Mccarthy, J.J.; Schellnhuber, H.J.; Bolin, B.; Dickson, N.M.; et al. Sustainability Science. Science 2001, 292, 641–642. [Google Scholar] [CrossRef] [PubMed]
- Pinter, L.; Hardi, P.; Martinucci, A.; Hall, J. Bellagio STAMP: Principles for Sustainability Assessment and Measurement. Ecol. Indic. 2012, 17, 20–28. [Google Scholar] [CrossRef]
- Zaccai, E. Over Two Decades in Pursuit of Sustainable Development: Influence, Transformations, Limits. Environ. Dev. 2012, 1, 79–90. [Google Scholar] [CrossRef]
- Bonneuil, N.; Saint-Pierre, P. Population Viability in Three Trophic-Level Food Chains. Appl. Math. Comput. 2005, 169, 1086–1105. [Google Scholar] [CrossRef] [Green Version]
- Bonneuil, N.; Boucekkine, R. Viable Nash Equilibria in the Problem of Common Pollution. Pure Appl. Funct. Anal. 2017, 2, 427–440. [Google Scholar]
- Martinet, V.; Doyen, L. Sustainability of an Economy with an Exhaustible Resource: A Viable Control Approach. Resour. Energy Econ. 2007, 29, 17–39. [Google Scholar] [CrossRef]
- Martinet, V. A Characterization of Sustainability with Indicators. J. Environ. Econ. Manag. 2011, 61, 183–197. [Google Scholar] [CrossRef]
- Cairns, R.D.; Long, N.V. Maximin: A Direct Approach to Sustainability. Environ. Dev. Econ. 2006, 11, 275–300. [Google Scholar] [CrossRef]
- Cairns, R.D.; Martinet, V. An Environmental-Economic Measure of Sustainable Development. Eur. Econ. Rev. 2014, 69, 4–17. [Google Scholar] [CrossRef] [Green Version]
- Doyen, L.; Martinet, V. Maximin, Viability and Sustainability. J. Econ. Dyn. Control 2012, 36, 1414–1430. [Google Scholar] [CrossRef] [Green Version]
- Basar, T.; Olsder, G. Dynamic Noncooperative Game Theory; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Dockner, E.; Jorgensen, S.; Long, N.V.; Sorger, G. Differential Games in Economics and Management Science; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Yeung, D.W.K.; Petrosyan, L. Subgame Consistent Economic Optimization; Birkhauser: Basel, Switzerland, 2012. [Google Scholar]
- Ougolnitsky, G.A.; Usov, A.B. Computer Simulations as a Solution Method for Differential Games. In Computer Simulations: Advances in Research and Applications; Pfeffer, M.D., Bachmaier, E., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2018; pp. 63–106. [Google Scholar]
- Long, N.V. A Survey of Dynamic Games in Economics; World Scientific Publishing Company: Singapore, 2010. [Google Scholar]
- Gorbaneva, O.I.; Ougolnitsky, G.A. System Compatibility, Price of Anarchy and Control Mechanisms in the Models of Concordance of Private and Public Interests. Adv. Syst. Sci. Appl. 2015, 15, 45–59. [Google Scholar]
- Gorbaneva, O.I.; Ougolnitsky, G. Static Models of Coordination of Social and Private Interests in Resource Allocation. Autom. Remote Control 2018, 79, 1319–1341. [Google Scholar] [CrossRef]
- Sukhinov, A.I.; Ougolnitsky, G.A.; Usov, A.B. Methods of Solving the Theoretic Game Models for Coordinating Interests in Regulating the Fishery Industry. Math. Models Comput. Simul. 2020, 12, 176–184. [Google Scholar] [CrossRef]
- Ugol’nitskii, G.A.; Usov, A.B. Dynamic Models for Coordinating Private and Public Interests in Economic Corruption. J. Comput. Syst. Sci. Int. 2020, 59, 39–48. [Google Scholar] [CrossRef]
- Chkhartishvili, A.; Gubanov, D.; Novikov, D. Social Networks: Models of Information Influence, Control, and Confrontation; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Jackson, M. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Proskurnikov, A.; Tempo, R. A Tutorial on Modeling and Analysis of Dynamic Social Networks. Part I. Annu. Rev. Control 2017, 43, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Proskurnikov, A.; Tempo, R. A Tutorial on Modeling and Analysis of Dynamic Social Networks. Part II. Annu. Rev. Control 2018, 45, 166–190. [Google Scholar] [CrossRef] [Green Version]
- Novikov, D.A. Games and Networks. Autom. Remote Control 2014, 75, 1145–1154. [Google Scholar] [CrossRef]
- Sedakov, A.; Zhen, M. Opinion Dynamics Game in a Social Network with Two Influence Nodes. Vestn. SPb Gos. Univ. Ser. Appl. Math. Inform. Sci. Contr. Proc. 2019, 15, 118–125. [Google Scholar] [CrossRef] [Green Version]
- Agieva, M.T.; Korolev, A.V.; Ougolnitsk, G.A. Modeling and Simulation of Impact and Control in Social Networks, The First International EURO Mini-Conference on Modelling and Simulation of Social-Behavioural Phenomena in Creative Societies (MSBC 2019), Vilnius, Lithuania, 18–20 September 2019. In Communications in Computer and Information Science; Agarwal, N., Sakalauskas, L., Weber, G.-W., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1079, pp. 29–40. [Google Scholar]
- Korolev, A.V.; Ougolnitsky, G.A. Optimal Resource Allocation in the Difference and Differential Stackelberg Games on Marketing Networks. J. Dyn. Games 2020, 7, 141–162. [Google Scholar] [CrossRef] [Green Version]
- Agieva, M.; Gorbaneva, O. Dynamic SPICE-model of Resource Allocation in Marketing Networks. In Contributions to Game Theory and Management; Springer: Berlin/Heidelberg, Germany, 2020; Volume 13, pp. 8–23. [Google Scholar]
- Agieva, M.; Gorbaneva, O.; Ougolnitsky, G. Dynamic SPICE-model of Resource Allocation in Marketing Networks with Co-directed Interests. In Proceedings of the 2nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA2020), Lipetsk, Russia, 12–14 November 2020. [Google Scholar]
- Agieva, M.; Korolev, A.V.; Ougolnitsky, G.A. Game Theoretic Models of Sustainable Management in Marketing Networks. In Contributions to Game Theory and Management; Springer: Berlin/Heidelberg, Germany, 2020; Volume 13, pp. 24–56. [Google Scholar]
- Tur, A.; Petrosyan, L. Strong Time-Consistent Solution for Cooperative Differential Games with Network Structure. Mathematics 2021, 9, 755. [Google Scholar] [CrossRef]
- Petrosyan, L.A.; Yeung, D.W.K. Shapley value for differential network games: Theory and application. J. Dyn. Games 2021, 8, 151–166. [Google Scholar] [CrossRef]
- Petrosyan, L.; Bulgakova, M.; Sedakov, A. Time-Consistent Solutions for Two-Stage Network Games with Pairwise Interactions. Mob. Netw. Appl. 2021, 26, 491–500. [Google Scholar] [CrossRef]
- Rentizelas, A.; Trivyza, N.; Oswald, S.; Siegl, S. Reverse supply network design for circular economy pathways of wind turbine blades in Europe. Int. J. Prod. Res. 2022, 60, 1795–1814. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, J.; Ai, X. Contract strategy in the presence of chain to chain competition. Int. J. Prod. Res. 2022, 60, 1913–1931. [Google Scholar] [CrossRef]
- Kamalahmadi, M.; Shekarian, M.; Parast, M.M. The impact of flexibility and redundancy on improving supply chain resilience to disruptions. Int. J. Prod. Res. 2022, 60, 1992–2020. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D.; Sokolov, B. Ripple Effect in the Supply Chain: An Analysis and Recent Literature. Int. J. Prod. Res. 2018, 56, 414–430. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, D. Predicting the Impact of Epidemic Outbreaks on the Global Supply Chains: A Simulation-Based Analysis on the Example of Coronavirus (COVID-19/SARS-CoV-2) Case. Transp. Res. Part E 2020, 136, 101922. [Google Scholar] [CrossRef]
- Ivanov, D.; Das, A. Coronavirus (COVID-19/SARS-CoV-2) and Supply Chain Resilience: A Research Note. Int. J. Integr. Supply Manag. 2020, 13, 90–102. [Google Scholar] [CrossRef]
- Dubey, R.; Gunasekarann, A.; Papadopoulos, T. Disaster Relief Operations: Past, Present and Future. Ann. Oper. Res. 2019, 283, 1–8. [Google Scholar] [CrossRef]
- Fraccascia, L.; Giannoccaro, I.; Albino, V. Rethinking Resilience in Industrial Symbiosis: Conceptualization and Measurements. Ecol. Econ. 2017, 137, 148–162. [Google Scholar] [CrossRef]
- Hosseini, S.; Ivanov, D.; Dolgui, A. Review of Quantitative Methods for Supply Chain Resilience Analysis. Transp. Res. Part. E 2019, 125, 285–307. [Google Scholar] [CrossRef]
- Wang, J.; Dou, R.; Muddada, R.R.; Zhang, W. Management of a Holistic Supply Chain Network for Proactive Resilience: Theory and Case Study. Comput. Ind. Eng. 2018, 125, 668–677. [Google Scholar] [CrossRef]
- Yoon, J.; Talluri, S.; Yildiz, H.; Ho, W. Models for Supplier Selection and Risk Mitigation: A Holistic Approach. Int. J. Prod. Res. 2018, 56, 3636–3661. [Google Scholar] [CrossRef]
- Basole, R.C.; Bellamy, M.A. Supply Network Structure, Visibility, and Risk Diffusion: A Computational Approach. Decis. Sci. 2014, 45, 753–789. [Google Scholar] [CrossRef]
- Choi, T.-M.; Taleizadeh, A.A.; Yue, X. Game Theory Applications in Production Research in the Sharing and Circular Economy Era. Int. J. Prod. Res. 2020, 58, 118–127. [Google Scholar] [CrossRef] [Green Version]
- Zhao, K.; Zuo, Z.; Blackhurst, J.V. Modelling Supply Chain Adaptation for Disruptions: An Empirically Grounded Complex Adaptive Systems Approach. J. Oper. Manag. 2019, 65, 190–212. [Google Scholar] [CrossRef]
- Bressanelli, G.; Perona, M.; Saccani, N. Challenges in Supply Chain Redesign for the Circular Economy: A Literature Review and a Multiple Case Study. Int. J. Prod. Res. 2018, 57, 7395–7422. [Google Scholar] [CrossRef] [Green Version]
- Harsanyi, J.C. Games with Incomplete Information Played by Bayesian Players. Manag. Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- De Groot, M.H. Reaching a Consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Olsder, G.J. Phenomena in Inverse Stackelberg Games. Part 2: Dynamic Problems. J. Optim. Theory Appl. 2009, 143, 601–618. [Google Scholar] [CrossRef] [Green Version]
- Papadimitriou, C.H. Algorithms, Games, and the Internet. In Proceedings of the 33rd Symposium on Theory of Computing, Crete, Greece, 6–8 July 2001; pp. 749–753. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).