Abstract
In this article, we consider technology leaders (which are innovators) and technology followers (which are non-innovators) to provide a new theoretical explanation for the well-cited empirical evidence of an inverted-U relationship between competition and aggregate innovation. We consider a two-stage game with a deterministic Research and Development (R&D) process, where the leaders first determine their R&D investments simultaneously and then all leaders and followers determine their outputs simultaneously. We show that the inverted-U relationship between competition and aggregate innovation occurs if competition is affected by the number of technology followers. However, the presence of more technology leaders decreases individual R&D investments while increasing aggregate R&D investments. If the total number of firms remains the same but the composition of technology leaders and followers changes in favor of leaders (followers), individual R&D investments decrease (increase) but aggregate R&D investments increase (decrease). The relationship between competition and R&D investments can be U-shaped if the intensity of competition is measured by product substitutability. Contrary to the standard expectation, the presence of more firms may reduce welfare.
JEL Classifications:
D43; L13; O33
1. Introduction
Economists have long been interested in understanding the relationship between competition and innovation which, in the words of Shapiro [1], is one of the most important questions in industrial organization. The debate goes back to the pioneering works of Arrow and Schumpeter [2,3], which focused on perfectly competitive markets and monopolies. The more recent literature examines the relationship in the context of imperfect competition and oligopolistic markets.
In this paper, we contribute to this age-old debate by considering technology leaders (which are innovators in our analysis) and technology followers (which are non-innovators in our analysis). As Vives [4] mentioned, “Innovation is claimed to be the engine of growth (see e.g., Aghion & Howitt, Grossman & Helpman and Romer [5,6,7,8,9,10]) and therefore it is crucial to understand its determinants.” While the literature discussed below looked at several determinants of innovation, the extant literature ignored the fact that technology leaders and followers co-exist in reality. We include this dimension to expand this extensive and lively literature.
We consider a Cournot oligopoly with n technology leaders and m technology followers, (See, for example, [11,12,13], to name a few, which consider innovating and non-innovating firms in different contexts.), where innovation is assumed to be deterministic (as in Cellini & Lambertini, Ishida et al, Mukherjee & Ray and Spence [14,15,16,17]), and the firms produce horizontally differentiated products. Firms face demand functions similar to those considered in Cellini & Lambertini, and Sacco & Schmutzler [14,18].
In this framework (One of the demand functions considered in Schumpeter [3] is similar to ours), we show how (i) the number of technology leaders and followers, (ii) the degree of product substitutability, and (iii) the composition of technology leaders and followers affect the equilibrium R&D investments and the resulting social welfare.
By combining volume and composition of competitors alongside product diversity, we are able to provide a richer and more granular view of the relationship between competition and innovation. By keeping the demand function comparable to the that described in the existing literature and allowing for deterministic innovation, we are able to achieve nice contrasts with the existing literature. In this way, our paper complements and expands the current literature by providing new results without negating any of the currently known explanations.
We provide a new theoretical explanation for the well-cited empirical evidence of an inverted-U relationship between competition and aggregate innovation (Aghion et al. [19]). Aghion et al. [19] provides a theoretical explanation for the inverted-U relationship based on stochastic step-by-step innovation. However, to our knowledge, there is no theoretical explanation for the inverted-U relationship between competition and aggregate innovation for non-stochastic innovation or deterministic R&D, which is widely considered in the literature [4,14,15,16,17,20,21,22].
We show that the inverted-U relationship may occur for non-stochastic or deterministic Research and Development (R&D) in the presence of technology leaders and technology followers. This may happen if competition is affected by the number of technology followers. Thus, our paper makes an important contribution to the competition and innovation literature by including a simpler, widely used framework of deterministic innovation.
Our work complements the influential work of Aghion et al. [19] by being able to generate the inverted-U relationship between competition and aggregate innovation even in the presence of deterministic innovation with standard demand functions. This contribution results in a more robust inverted-U relationship between competition and aggregate innovation.
We find that the presence of a larger number of technology leaders decreases individual R&D investments but increases aggregate R&D investments. If the total number of firms remains the same but the composition of technology leaders and followers changes in favor of the leaders (followers), the individual R&D investments decrease (increase) but the aggregate R&D investments increase (decrease). The relationship between competition and R&D investments can be U-shaped if the intensity of competition is measured by product substitutability.
Contrary to the standard expectation that competition and welfare both increase with the number of firms, we show that the presence of a larger number of firms may reduce welfare. In this way, our paper also contributes to the established literature on welfare reducing entry [16,23,24,25].
Welfare reducing entry is a lively and fascinating phenomenon, as the classical theory of competition generally argues that a larger number of competitors would drive the market more towards perfect competition that improves welfare, in contrast to an imperfectly competitive situation. Contrary to that standard insight, welfare reducing entry essentially posits that welfare may suffer adversely with the entry of a firm into the market.
A general feature of the current literature is to consider all firms as innovators or technology leaders. (Bester & Petrakis [11] is an exception. They considered innovating and non-innovating firms while examining the effects of different types of competition, viz., Cournot and Bertrand on R&D investments. Unlike them, we show the effects of the number of firms and product differentiation on R&D investments). This assumption may sound innocuous at the outset, but it may not entirely align with market realities. It is rarely the case that each firm in an industry engages in innovative activities at the same level of intensity as other firms. In other words, markets are mostly dominated by a fraction of firms that engage in innovative activities, while others are content to use generally available technologies to earn profits, so long as it is achievable under certain circumstances. The presence of non-innovating firms alongside innovating firms has been captured in a number of studies in the literature [26,27]. (Whether firms undertake R&D may depend on several factors, such as market orientation, business objectives, competitive advantages, absorptive capacity, and internal knowledge resources).
There are also strong empirical reasons for building our model this way. According to Eurostat in March 2017 (https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Archive:Innovation_statistics&oldid=510766, accessed on 27 November 2021), during 2012–2014 almost half of all enterprises in the European Union (EU) undertook some form of innovation activity. In other words, a significant number of the EU firms did not undertake any innovative activities during 2012–2014. In the pharmaceutical industry, for example, not all firms innovate, as the industry is populated by a significant number of firms that take advantage of generic products after the expiration of patents, while not devoting significant resources to R&D activities to invent new drugs or earn new patents.
There are also vast differences in innovative activities across nations and continents, and those differences often lead to different paths of economic development. Although firms from some developing or newly industrialized countries engage in innovative activities, most of the world’s innovating firms and new technologies are overly concentrated in the developed countries (see the references in Mukherjee & Sinha [28]). For example, the big technology, telecommunication, e-commerce, and entertainment companies such as Apple, Microsoft, Google, Amazon, Cisco, Oracle, Facebook, Instagram, WhatsApp, Twitter, IBM, Intel, HP, Dell, AT&T, and Disney, are all American companies whose products are used by billions of people from all over the world.
With notable exceptions such as Samsung (South Korea), LG (South Korea), Huawei (China), Alibaba (China), Hitachi (Japan), and Panasonic (Japan), very few globally dominant large technology companies come from other countries. The same goes for the automotive sector. Most of the world’s new automotive technologies come from only a handful of countries, such as the USA (GM, Ford, Chrysler, Tesla, etc.), Japan (Toyota, Honda, Nissan, Mitsubishi, etc.), Korea (Kia and Hyundai) and Germany (Mercedes, Volkswagen, BMW, etc.). Hence, the majority of countries are primarily users of such advanced technologies, and not primary innovators. Simply put, the overall global market is inhabited by both technology leaders and technology followers.
Given the non-uniformness of innovative activities across firms, the applicability of the existing literature (reviewed in the next section) examining the relationship between competition and innovation may be limited. This is simply because the strategic interactions in the R&D stage are much lower in industries with a limited number of technology leaders than in industries with many innovators. This strategic interaction is the key driver for our results. By exploiting the difference between industries where the proportion of innovators varies significantly, we provide a new perspective to the literature on competition and innovation. We show how different concentrations of technology leaders and followers, as well as product substitutability, affect innovation and social welfare.
Focusing on both innovating and non-innovating firms, our results provide the following testable hypotheses for future empirical studies: first, given the number of innovators, we would expect more R&D investments in industries with a moderate number of non-innovators, compared to industries with small and large numbers of non-innovators; second, for a given number of non-innovators, we would expect less individual R&D investment but more aggregate R&D investment as the number of innovators increases; third, for a given number of innovators and non-innovators, we would expect more R&D investments for low- and high-product differentiation, compared to moderate product differentiation; finally, when looking at industries with similar total numbers of firms, we would expect less individual R&D investment but more aggregate R&D investment in industries with more innovators.
The remainder of this paper is organized as follows: we review the literature in Section 2; Section 3 describes the main model and shows the results of competition and R&D investments by considering the changes in technology leaders, technology followers, and product substitutability; Section 4 considers the effects of a change in the number of technology leaders, while keeping the total number of firms the same; Section 5 suggests some possible future research; and Section 6 provides some concluding remarks.
2. Literature Review
The debate concerning the relationship between competition and innovation goes back to Arrow and Schumpeter [2,3]. While they considered a perfectly competitive market and a monopoly to show the effects of competition on innovation, more recent literature focused on oligopolistic markets. Given the vast literature on competition and innovation, we will discuss some related papers in the following discussion. While our discussion is topical and pertinent to the specific studies mentioned in this paper, one may look at Shapiro and Gilbert [1,29] for nice overviews of this literature.
In one of the earlier studies, Spence [17] showed that with a deterministic R&D and a constant elasticity demand curve, the relationship between the number of innovating firms and individual R&D investments is inverted-U-shaped. Hence, he did not explain the empirical evidence of an inverted-U relationship between competition and aggregate innovation.
In a patent race model with Cournot competition, Delbono & Denicolò [30] showed that if R&D is non-drastic, a higher competition has an ambiguous effect on R&D investment, but for a drastic R&D, a higher competition increases R&D investment. Using the Lerner index as a measure of competition, Aghion et al. [19] showed that competition and aggregate innovation have an inverted-U relationship. (Earlier empirical papers by Blundell et al, Geroski and Nickell [31,32,33] found a positive relationship between competition and innovation). They used a theoretical model with stochastic step-by-step innovation to explain the inverted-U relationship while measuring competition as the inability to collude. Considering stochastic innovation and mergers to reduce competition, Federico et al. [34,35] showed that increased competition increases drastic product innovation. In contrast, we explain the inverted-U relationship between competition and aggregate innovation for non-stochastic innovation.
Banker et al. [36] showed how competition affects firms’ investments in quality. They found that if competition is increased by making a firm’s demand potential more symmetric, a higher competition decreases (increases) investment in quality by the firm with a high (low) demand potential. Comparing competition with cooperation, they showed that investment in quality is higher under competition unless the synergic benefit from cooperation is large. If competition is created by more firms, investment in quality decreases if the cost of quality improvement is independent of competition intensity. If the competitive intensity creates a synergic benefit and the cost of quality improvement decreases with competitive intensity, the presence of more firms may increase investment in quality.
Applying the real options approach, Childs & Triantis [37] considered investments in multiple projects and showed that competition that alters the drift of the net present value of a project decreases overall investment. (One may look at Trigeorgis [38] for the effects of competitive entry on investment decisions in a real options setting).
Vives [4] considered that firms choose investment-price or investment-output pairs in a two-stage open-loop game, i.e., where the actions in the first stage are not perfectly observable. In this framework, he showed that more firms reduce R&D investments, (The negative relationship between competition and innovation can be found in many other papers, such as [39,40,41,42,43,44,45]), but lower product differentiation increases R&D investment if the total market for varieties does not shrink. He showed that these results are quite general, in that they hold up under different demand structures and with or without entry. (Although Vives [4] considered a very general model, his analysis did not explain the inverted-U relationship. He was trying intuitively to reconcile the inverted-U relationship with his analysis by appealing to the liquidation effect. As he mentioned in footnote 25 of his paper, “We might also try to explain an inverted-U relationship between an average Lerner index and average innovation output (or effort) in an industry with asymmetric firms and composition effects.” However, he did not carry out any analyses with asymmetric firms). Boudreau et al. [46] showed empirically that increased competition decreases (increases) R&D investments in contests for low-uncertainty (high-uncertainty) problems.
In a dynamic model with deterministic R&D and Bertrand competition, Cellini & Lambertini [14] showed that more firms increase R&D investment, but a lower product differentiation either decreases R&D investment or creates a U-shaped relationship. Sacco and Schmutzler [18] showed that there can be a U-shaped relationship between competition and innovation when the higher competition is measured by lower product differentiation. While their laboratory experiments partly confirmed the U-shaped relationship in a reduced one-stage version of the game, the two-stage version showed a negative relationship. (There is some experimental evidence showing that competition, measured in terms of the number of firms, reduces R&D investments Darai et al, Isaac & Reynolds [47,48,49]).
Schumtzler [50] considered a duopoly model to show the effects of product differentiation on R&D investments for different demand specifications. For a demand function similar to the one considered in this paper, he showed that if the firms are symmetric, lower product differentiation creates a U-shaped (negative) relationship with R&D investments under Cournot (Bertrand) competition. However, if a firm has a lower marginal cost initially, lower product differentiation increases its R&D investments. In the working paper version ([51]), he showed that if there are more firms, there is a negative relationship between competition and innovation if the firms are symmetric. However, if the entrant is less efficient than the incumbent, entry may raise the investment of the incumbent.
Ishida et al. [15] showed that an increase in the number of high-cost firms increases the R&D investments of low-cost firms. Mukherjee & Ray [16] extended this analysis to focus on asymmetric R&D capabilities and showed that R&D investments and profits reduce with more firms, irrespective of their R&D capabilities. They also showed that more firms may reduce welfare, irrespective of their R&D capabilities. (There is a literature showing how different types of competition, viz., Bertrand and Cournot competition, affect innovation (see, e.g., [11,49,52,53,54,55,56,57]). However, unlike the present paper, those papers consider the effects of different strategic variables on innovation. In contrast, we consider the effect of the number of firms, while maintaining the same strategic variable).
Spulber [58] showed the effects of competition among producers and competition among inventors on the incentive for innovation. It showed that competition among producers increases the incentive for innovation, while competition among inventors also increases the incentive for innovation when the product market is competitive. Spulber [59] showed that the relationship between competition and innovation may depend on the strength of intellectual property protection. Competitive pressure increases innovation if intellectual property protection is appropriable. However, competitive pressure may reduce innovation if intellectual property protection is not fully appropriable. (Spulber [60] discussed how competition policy may reduce the incentive for innovation by weakening intellectual property protection. Spulber [61] discussed how technology standards, the competitive conduct of firms, and economic performance are jointly determined via markets and cooperative institutions). These papers considered a situation where the inventors were different from the producers. The inventors invented new technologies and sold their technologies to producers. In contrast, we consider vertical integration of innovation and production. (One may also look at Spulber [62] for further discussions on this issue).
There is literature that showed how mergers and overlapping ownership, influencing the intensity of competition, affect innovation. Considering stochastic R&D, Federico et al. [34,35] showed that mergers reduce the R&D investments of merged entities. Denicolò & Polo [63] showed that mergers may increase the R&D investments of merged entities if the probability of failure in innovation is log-concave, which encourages e merged firms not to operate all possible research labs, thus helping to avoid duplication of R&D efforts by merged firms. Using a deterministic R&D process, Motta & Tarantino [64] showed that in the absence of spillovers and synergy, merger reduces R&D investments. Bourreau and Jullien [65] showed that merger may increase investment in innovation by expanding demand due to increased market coverage. Using deterministic R&D, López & Vives [66] showed that an increase in overlapping ownership, which increases collusive behavior, decreases investments in process innovation in the absence of knowledge spillover. Unlike our paper, none of these papers explained the inverted-U relationship between competition and innovation.
Although the papers mentioned above examined the relationship between competition and innovation under different economic scenarios, they could not explain the inverted-U relationship between competition and aggregate innovation for non-stochastic innovation. A common feature of those papers was to consider that all firms are innovators which, as mentioned in the introduction, is not necessarily the case. When we adopt a more realistic set-up with innovators and non-innovators, we can explain the inverted-U relationship between competition and aggregate innovation for non-stochastic innovation. Our analysis with innovators and non-innovators complements and contrasts with the existing literature. (We considered exogenous number of firms, which is often considered in the literature we reviewed. Numerous other papers consider the market structure and innovation, endogenously and jointly. [4,40,41,44,67,68,69] We provide only an overview that is relevant to our investigation).
Our paper also complements the literature on welfare-reducing entry. While this literature showed the implications of cost asymmetry (Klemperer and Lahiri & Ono [24,25]) and government policies (Dinda & Mukherjee [23]), we show the implications of innovation. While Mukherjee & Ray [16] also showed that higher competition may reduce welfare, they considered neither innovating and non-innovating firms, nor the effects of competition on innovation. (There is other literature showing that free entry of firms can be welfare reducing. See Mankiw & Whinston [70] for a pioneering work in this area. However, there is no free entry in our analysis).
The differences between the innovativeness of firms have also attracted considerable academic interest in general management and accounting literature. In a recent study covering 4545 American firms between 1968 and 2018, Machokoto et al. [71] found significant relationship between competition and firms’ innovativeness. The willingness and ability of firms to learn innovative activities over time in Machokoto [71] was entirely consistent with the general feature that not all firms in an industry may be equally innovative, although they may learn in the long term.
Although the differences in innovativeness across firms, industries, and countries are well-documented, the drivers of the same differences are also the subject of intense focus. The culture of innovation has been identified as one of the major drivers for the differences in innovative activities Chandler & Krajcsak and Lam et al. [72,73]. The critical role of diversity has also been studied as a potential driver for the differences in innovativeness as in Hewlett et al. [74].
3. The Model and the Results
Consider an economy with n technology leaders (innovating firms) and m technology followers (non-innovating firms), who compete in the product market like Cournot oligopolists. We assume that the firms produce horizontally differentiated products, and that there is at least one firm in each category, i.e., .
Financial constraints or lack of relevant technical knowledge may prevent some firms from engaging in innovative activities. It is also possible that the technology followers are in geographic regions that are not rich in R&D workforce. In geographic terms, we may also assume that the technology leaders are from developed countries, which are in possession of a rich set of innovative capabilities including financial architecture, legal expertise, political support, and an R&D workforce that is trained in the latest scientific and technical knowledge.
The technology followers may be assumed to be from developing countries or from regions lacking an R&D infrastructure and workforce, in that they have yet to build an appropriate innovation-related infrastructure and educational ecosystem to undertake complex R&D activities. For simplicity, and to keep our model tractable, we will consider the number of firms as a continuous variable.
All firms enjoy the same initial constant marginal cost of production, c. This assumption is made to eliminate the effects of initial cost asymmetry on our results, so that we are able to capture the impact of technology leaders and followers in a more straightforward way. We assume that innovation leads to lower cost of production. The ith technology leader, can invest amount in R&D to reduce its cost of production to . The cost of R&D, is increasing and sufficiently convex to guarantee interior solutions. The R&D cost function suggests that there is diminishing return for R&D expenditures. (This is a standard assumption in the literature. [20] A justification for this assumption is that “the technological possibilities linking R&D inputs and innovative outputs do not display any economies of scale with respect to the size of the firm in which R&D is undertaken” (Dasgupta [75], p. 523)).
We assume that the inverse market demand functions of the ith technology leader and the jth technology follower are, respectively
where , and and represent the ith technology leader’s price and the jth technology follower’s price, respectively, and and denote the ith technology leader’s output and the jth technology follower’s output, respectively. The parameter shows the degree of product substitutability. The goods are perfect substitutes for and they are independent for .
We consider the following game. At stage 1, the technology leaders determine their R&D investments simultaneously, and the outcome of R&D is realized. At stage 2, the firms choose their outputs simultaneously, and the profits are realized. We solve the game through backward induction.
The profit functions of the ith technology leader and the jth technology follower are, respectively:
Given the R&D investments of the technology leaders, the equilibrium outputs can be determined as:
By way of a simple partial statics, we obtain the following:
where is the R&D investment vector of all innovating firms other than . The equations in (5) show that a higher R&D investment of the ith technology leader increases its own output but decreases the outputs of technology followers and other technology leaders by making the ith technology leader firm more cost-efficient.
At stage 1, the ith technology leader determines its R&D investment. The relevant first-order equations are the following:
where, on the right-hand side of the first equation, the first term is equal to zero due to the envelope theorem, and the last term is .
The strategic effect on other technology leaders indicates that the R&D investment of the ith technology leader firm increases its own profit by reducing the rival technology leaders’ outputs. The strategic effect on technology followers indicates that the R&D investment of the ith technology leader increases its profit by reducing the technology followers’ outputs. These effects, taken together, show how the ith technology leader’s R&D investment increases its profit through the strategic effects on the rival firms’ outputs.
The output effect indicates that the R&D investment of the ith technology leader increases its profit by increasing its own output consequent to the declining costs resulting from successful innovative activities.
Hence, these three effects, taken together, show the ith technology leader’s marginal benefit (MB) from R&D investment. However, the cost effect shows how the R&D investment of the ith technology leader reduces its profit due to the cost of R&D investment. Hence, the cost effect shows the ith technology leader’s marginal cost (MC) of R&D investment.
Due to the symmetric first-order conditions for R&D investments, the equilibrium R&D investments, , is provided by the following equation:
MB = MC, or
Hence, the equilibrium outputs are:
3.1. Discussion and Analysis
Changes in the Total Number of Firms
We are now able to show the effects of competition on R&D investments. From Equation (7), we obtain the following:
It follows from Equation (8) that if . However, if then
implying that for a given degree of product differentiation, , and the number of innovators, n, for smaller values of m but for larger values of m. Hence, given that the second-order conditions for profit maximization with respect to R&D investments are satisfied, the relationship between m (the number of followers) and the R&D investment of each technology leader shows an inverted-U relationship if .
From Equation (7), we also obtain the following:
Equation (9) suggests that, given the number of technology followers, if the number of technology leaders increases, it decreases each technology leader’s marginal benefit from innovation. Hence, given that the second-order conditions for profit maximization with respect to R&D investments are satisfied, if the number of innovating firms increases, this reduces the R&D investment of each technology leader.
Table 1 summarizes the strategic effects on other technology leaders and followers, the output effect, and the total effect created by a change in the number of technology leaders and technology followers when the total number of firms, K = m + n, increases.

Table 1.
The impact of the number of firms on individual R&D investment.
As shown in Table 1, the strategic effects of m on other technology leaders and the output of the concerned technology leader are always negative, but the strategic effect on technology followers is ambiguous and depends on . When we combine these three effects, we find a non-monotonic relationship between m and the R&D investment of each technology leader.
The strategic effect of n on other technology leaders is ambiguous, depending on . However, the strategic effects of n on technology followers and the output of the concerned technology leader are negative. When the strategic impact on other technology leaders is negative, it is clear that the total effect is negative. When the strategic effect on other technology leaders is positive, it is always dominated by the latter two negative effects. Thus, an increase in n reduces the equilibrium of the R&D investment of each technology leader.
Assuming that , we obtain the symmetric equilibrium R&D investment of each technology leader as follows:
Figure 1a plots for , and . (We can obtain for these parameter values).
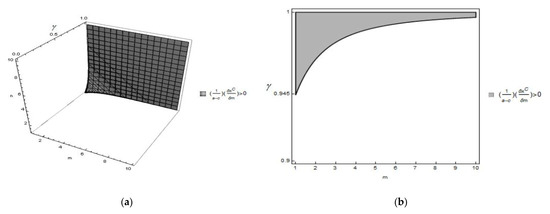
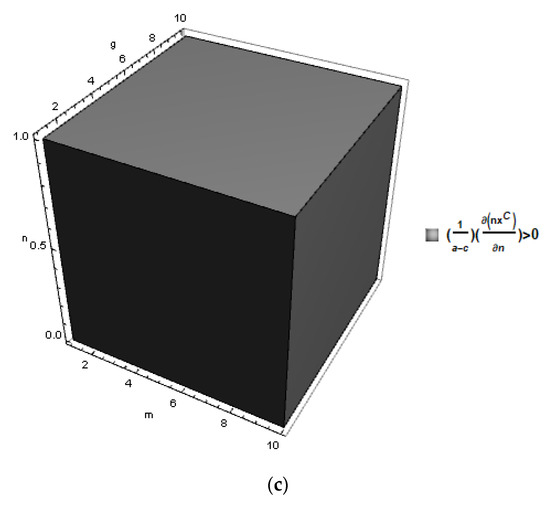
Figure 1.
(a) for , and ; (b) for n = 2, and ; (c) for , and .
The shaded (white) region in Figure 1a shows . Figure 1b magnifies the shaded region of Figure 1a by considering that n = 2 and .
It follows from Figure 1a,b that if the products are not close substitutes (i.e., ), there is a negative relationship between m and the R&D investment of each technology leader. On the other hand, if the products are perfect substitutes (i.e., ), there is a positive relationship between m and the R&D investment of each technology leader, as . However, if the products are close substitutes but not perfect substitutes, the relationship between m and the R&D investment of each technology leader is positive for lower values of m, but negative for higher values of m, thus showing an inverted-U relationship between the number of technology followers and the R&D investment of each technology leader. As the number of technology leaders is independent of the number of technology followers, the number of technology followers and the aggregate R&D investments of the technology leader will also show an inverted-U relationship.
It follows from Equation (9) that the presence of more technology leaders, i.e., a higher n, decreases the R&D investment of each technology leader. Next, we show the effects of n on the aggregate R&D investments of the technology leaders. At the symmetric equilibrium, the aggregate R&D investment is . We get , where . Figure 1c shows a case with , and .
Figure 1c shows that an increase in the number of technology leaders increases the aggregate R&D investments of the technology leaders. If the number of technology leaders increases, there are more innovators investing in R&D, which has a positive direct effect on aggregate R&D investment. However, we have already seen that a new technology leader will reduce the R&D investment of each existing technology leader, which has a negative indirect effect on aggregate R&D investment. We find that the former direct effect dominates the latter indirect effect, and the presence of more technology leaders increases aggregate R&D investments.
The following proposition summarizes the above discussion.
Proposition 1.
(i) Given the number of technology leaders, there can be an inverted-U relationship between the number of technology followers and individual as well as aggregate R&D investments. (ii) Given the number of technology followers, an increase in the number of technology leaders reduces the equilibrium R&D investment of each technology leader but increases the equilibrium aggregate R&D investments of technology leaders.
Proposition 1 (i) shows that there can be an inverted-U relationship between competition and aggregate innovation when we change the number of technology followers.
The intuition for Proposition 1 is as follows: more firms create two opposing effects. On the one hand, more firms reduce the technology leaders’ marginal benefits from innovation, which tends to reduce R&D investments. On the other hand, more firms encourage technology leaders to invest more to improve their competitive positions. While the first effect has a Schumpeterian overtone, the second effect is similar to Arrow’s replacement effect, or the escape competition effect of [19].
If the new firm is a technology leader, we find that the first effect dominates the second effect, and more technology leaders reduce the equilibrium R&D investment of each technology leader by lowering technology leaders’ marginal benefits from innovation. As the new firm is a technology leader, the replacement effect or the escape competition effect is not strong enough to outweigh the first effect. However, the R&D investment of the new technology leader adds to aggregate R&D investment. Hence, even if more technology leaders reduce the individual R&D investments of the technology leaders, it increases the aggregate R&D investments of the technology leaders.
If the new firm is a technology follower, the replacement effect or the escape competition effect is stronger when compared to the situation where the entrant is a technology leader, as it is easier to steal market share from a high-cost technology follower than from a low-cost technology leader. Hence, more technology followers may increase or decrease individual as well as aggregate R&D investments.
3.2. The Effects of a Change in
Figure 2 shows the relationship between and R&D investment for , and .
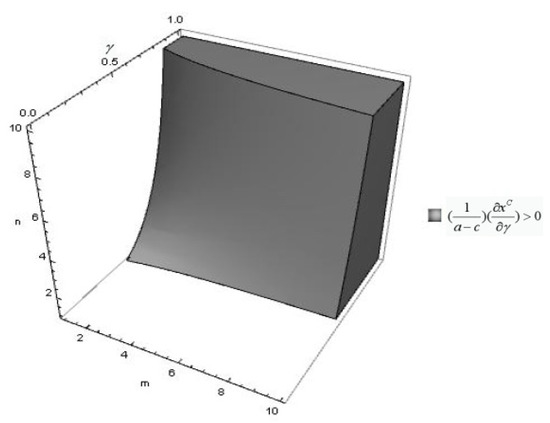
Figure 2.
for , and .
The shaded (white) region in Figure 2 shows . It follows from Figure 2 that the relationship between and the R&D investment of each technology leader is negative (positive) for low (high) , thus, showing a U-shaped relationship. As the number of technology leaders only affects the magnitude but not the sign of this relationship, the relationship between and aggregate R&D investments is also U-shaped.
Cellini & Lambertini, Sacco & Schmutzler and Schmutzler [14,18,50] also found similar results. However, unlike Cellini & Lambertini [14], we consider Cournot competition with innovating and non-innovating firms, and unlike Sacco & Schmutzler and Schmutzler [18,50], we consider oligopoly with innovating and non-innovating firms. Thus, we complement these previous papers.
The above discussion is summarized in the following proposition.
Proposition 2.
For a given n and m, the relationship between competition and individual as well as aggregate R&D investments can be U-shaped if the higher competition is due to higher product substitutability.
3.3. Welfare Implications
It is generally believed that competition increases welfare. We will show in this subsection that increased competition may reduce welfare.
As all technology leaders produce the same outputs and all technology followers produce the same outputs, we obtain equilibrium welfare as follows:
First, consider the effects of a change in the number of technology leaders, n, on welfare. Assume that . We plot in Figure 3 for , and .
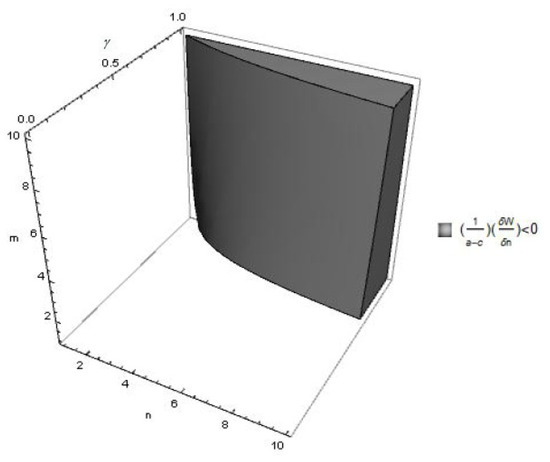
Figure 3.
for , and .
The shaded (white) region in Figure 3 shows . It follows from Figure 3 that a higher n reduces welfare if the products are close substitutes (i.e., is high). The reason for this result is as follows: on the one hand, a higher n tends to increase welfare by increasing competition; on the other hand, it tends to reduce welfare by reducing marginal cost reduction by each technology leader. If the products are close substitutes (i.e., is high), the firms face significant competition from each other, and a higher n creates a significantly adverse effect on marginal cost reduction by the technology leaders, which dominates the welfare-increasing effect of a higher n. In this situation, a higher n reduces welfare. However, if the products are not close substitutes, the intensity of competition is low, and a higher n does not significantly reduce marginal cost reduction by technology leaders. In this situation, the former effect dominates the latter effect to increase welfare following a higher n.
Unlike Klemperer and Lahiri & Ono [24,25], this result shows that entry of a firm may reduce welfare even if the entrant is not cost-inefficient. This result complements Mukherjee & Ray [16] by showing that entry of an innovator may reduce welfare in the presence of innovating and non-innovating firms.
Next, we consider the effects of m on welfare. We know from Klemperer and Lahiri & Ono [24,25] that entry of a firm may reduce welfare if the entrant has sufficiently higher marginal costs than the incumbents. This happens because the entry of a high-cost entrant creates production inefficiency by stealing business from low-cost incumbents. Entry of a technology follower creates a similar situation in the presence of technology leaders, with the exception that it affects the marginal costs of technology leaders by affecting their R&D investments. We show in Figure 4 that the presence of more technology followers may create lower welfare, as in Klemperer and Lahiri & Ono [24,25].
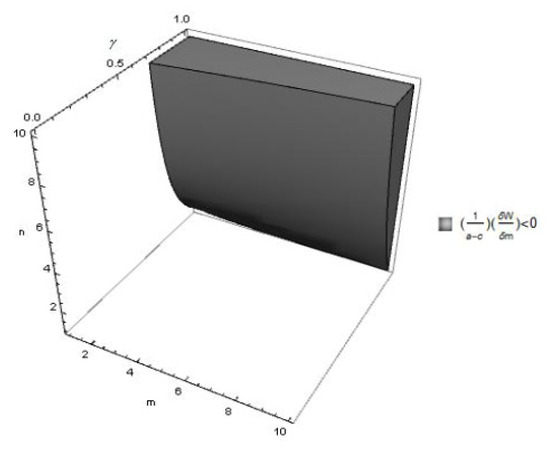
Figure 4.
for , and .
The shaded (white) region in Figure 4 shows . Figure 4 shows that a higher m increases welfare if the products are close substitutes (i.e., is high). If the products are close substitutes (i.e., is high), more technology followers increase R&D investments (which follows from Equation (8)), but, as in Klemperer and Lahiri & Ono [24,25], they create production inefficiency by stealing business from technology leaders. We find that the production inefficiency effect dominates the positive effect on innovation, and a higher m reduces welfare. However, if the products are not close substitutes, the intensity of competition is low, and therefore the adverse production inefficiency effect is weak. Although a higher m reduces R&D investments in this situation (which follows from Equation (8)), the positive effect of higher competition dominates the effect on innovation and the effect due to production inefficiency, and a higher m increases welfare.
Next, we consider the relationship between and welfare in Figure 5 for , and . We have considered a demand function such as that considered in Singh & Vives [76]. It follows from Singh & Vives [76] that a higher reduces welfare for the given marginal costs of the firms. This happens because a higher , while increasing competition, reduces market size. This adverse market size effect dominates the positive effect of competition, and a higher reduces welfare. Singh & Vives [76] did not consider innovation. However, we find that a similar result holds even with innovation.
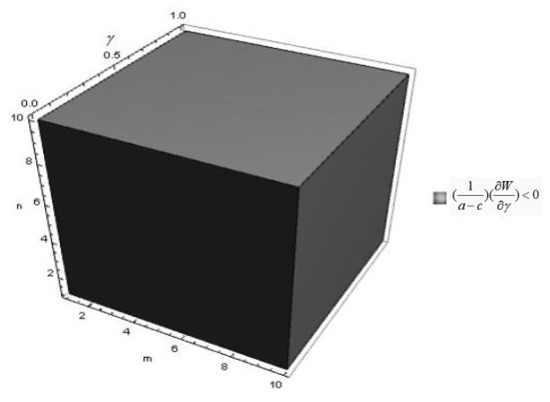
Figure 5.
for , and .
4. Changes in the Composition of Firms
The previous subsection looked at the effects of a change in the number of firms when the total number of firms increases. In this subsection, we want to see the effects of a change in the composition of firms when the total number of firms, K = m + n, remains unchanged, but the ratio of the technology leaders to followers changes in the market. Hence, this situation shows how R&D investment changes when a technology follower becomes a technology leader, or vice versa.
Substituting into Equation (6), we have the following:
Imposing symmetry on Equation (11), we obtain the effect of a change in m on MB for a given K as follows:
Table 2 summarizes the strategic effects on other technology leaders and followers, the output effect, and the total effect created by a change in the number of firms when the total number of firms K = m + n is constant.

Table 2.
The impact of the number of firms on individual R&D investment when K is constant.
Next, we show the impact on aggregate R&D investments. When the total number of firms is constant, the aggregate R&D investments are and . For a given K, although a lower m (i.e., a higher n) reduces individual R&D investment, as shown above, a lower m tends to increase aggregate R&D investments by increasing the number of technology leaders, n. We find that the former effect is dominated by the latter effect, and a lower m increases aggregate R&D investments.
The following proposition summarizes the above discussion.
Proposition 3.
Suppose that K = n + m firms compete like Cournot oligopolists. If the total number of firms, K, is constant, a decrease in m, i.e., an increase in n (an increase in m, i.e., a decrease in n) decreases (increases) the equilibrium individual R&D investment but increases (decreases) the equilibrium aggregate R&D investment.
The reason for the above result is as follows: if the number of technology followers decreases, i.e., the number of technology leaders increases, the intensity of competition faced by the remaining technology leaders increases, as a high-cost technology follower is replaced by a low-cost technology leader. Hence, the R&D investment of each technology leader decreases in this situation due to higher competition. However, the R&D investment of the new technology leader adds to aggregate R&D investment. Hence, more technology leaders increase aggregate R&D investments even if they reduce the individual R&D investments of the technology leader. The opposite occurs if the composition changes in favor of technology followers.
Welfare Implications
As in the previous section, where we considered that a change in n and m also changes the total number of firms, we show in this subsection that welfare may reduce if the total number of firms does not change but the composition of technology leaders and followers changes. We show in Figure 6 that welfare may reduce if there are more technology leaders. We plot in Figure 6 for , and .
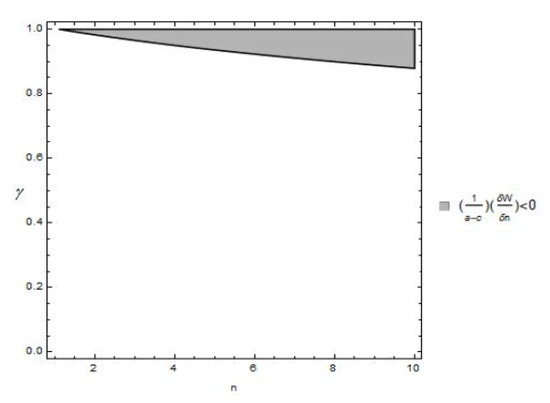
Figure 6.
for , and .
5. Some Possible Future Research
We developed a model with innovating and non-innovating firms to explain the well-cited inverted-U relationship between competition and innovation under a deterministic R&D process. However, we abstracted our analysis from certain aspects that can be considered in future to extend our research.
First, having assumed quantity competition in the product market, a natural extension would be to see how a different type of product-market competition, such as price competition, affects the relationship between competition and innovation in the presence of innovating and non-innovating firms.
Second, it would be interesting to see the implications of innovating and non-innovating firms when the R&D process is stochastic.
Third, we have assumed a given number of innovating and non-innovating firms. It is understandable that as the number of innovating firms increases, it becomes difficult for non-innovating firms to compete in the product market. Hence, an endogenous determination of innovating and non-innovating firms would be another possible extension of our analysis.
Fourth, like the extant literature, we assumed that all the innovators determine their investments non-cooperatively and that all firms determine their product market strategies non-cooperatively. However, it is well known that firms often engage in cooperative R&D activities. Similarly, firms often engage in product-market collaboration. Hence, our analysis can be extended to explore the implications of cooperation in R&D, as well as in product-market behavior.
Fifth, like the extant literature, we ignored the role of input markets, in which final goods producers often bargain with input suppliers for input prices. Hence, another extension of our paper will be the incorporation of strategic input price determination into our analysis.
Sixth, we considered a two-stage game where firms know the R&D outcomes as they pursue product-market strategies. An alternative situation would be to consider a simultaneous determination of R&D investments and product-market strategies.
6. Conclusions
We provide the literature with a new perspective on competition and innovation by considering technology leaders or innovating firms and technology followers or non-innovating firms. Both inhabit a unified market and strategically affect each other. This framework helps to explain the well-cited empirical evidence of an inverted-U relationship between competition and aggregate innovation. This may happen if competition is affected by the number of technology followers.
We also show the implications of the number of technology leaders, product differentiation, and the composition of technology leaders and technology followers for individual and aggregate R&D investments. The presence of more technology leaders decreases individual R&D investments but increases aggregate R&D investments. If the total number of firms remains the same but the composition of technology leaders and followers changes in favor of leaders (followers), individual R&D investments decrease (increase) but aggregate R&D investments increase (decrease). The relationship between competition and R&D investments can be U-shaped if the intensity of competition is measured by product substitutability. We further show that the presence of more firms may reduce welfare, contrasting with the classic view that more competition increases social welfare.
Our results are important for competition policies, particularly because the factors of legal structure, intellectual law enforcement, availability of venture capital, and innovative infrastructure (such as the supply of a STEM-educated labor force, etc.) all play very important roles in determining the fraction of firms that feel comfortable in engaging in or expanding their innovative activities.
Author Contributions
Conceptualization, K.-C.T., A.M. and A.R.; Methodology, K.-C.T., A.M. and A.R.; Software, K.-C.T., A.M. and A.R.; Formal analysis, K.-C.T., A.M. and A.R.; Writing—original draft preparation, K.-C.T., A.M. and A.R.; Writing—review and editing, K.-C.T., A.M. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
No external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shapiro, C. Competition and innovation: Did Arrow hit the bull’s eye? In The Rate and Direction of Inventive Activity Revisited; Lerner, J., Stern, S., Eds.; National Bureau of Economic Research, University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Arrow, K. Economic welfare and the allocation of resources for invention. In The Rate and Direction of Inventive Activity; Nelson, R., Ed.; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Schumpeter, J. Capitalism, Socialism and Democracy; Allan and Unwin: London, UK, 1943. [Google Scholar]
- Vives, X. Innovation and competitive pressure. J. Ind. Econ. 2008, 56, 419–469. [Google Scholar] [CrossRef]
- Aghion, P.; Howitt, P. A model of growth through creative destruction. Econometrica 1992, 60, 323–351. [Google Scholar] [CrossRef]
- Aghion, P.; Howitt, P. Endogenous Growth Theory; MIT Press: Cambridge, MA, USA; London, UK, 1998. [Google Scholar]
- Grossman, G.M.; Helpman, E. Product development and international trade. J. Politi-Econ. 1989, 97, 1261–1283. [Google Scholar] [CrossRef]
- Grossman, G.M.; Helpman, E. Innovation and Growth in the Global Economy; MIT Press: Cambridge, MA, USA; London, UK, 1991. [Google Scholar]
- Grossman, G.M.; Helpman, E. Endogenous innovation in the theory of growth. J. Econ. Perspect. 1994, 8, 23–44. [Google Scholar] [CrossRef]
- Romer, P.M. Endogenous technological change. J. Politi-Econ. 1990, 98, 71–102. [Google Scholar] [CrossRef]
- Bester, H.; Petrakis, E. The incentives for cost reduction in a differentiated industry. Int. J. Ind. Organ. 1993, 11, 519–534. [Google Scholar] [CrossRef]
- Gallini, N.T. Patent policy and costly imitation. Rand J. Econ. 1992, 23, 52–63. [Google Scholar] [CrossRef]
- Mukherjee, A.; Pennings, E. Imitation, patent protection and welfare. Oxf. Econ. Papers 2004, 56, 715–733. [Google Scholar] [CrossRef]
- Cellini, R.; Lambertini, L. R&D incentives under Bertrand competition: A differential game. Jap. Econ. Rev. 2011, 62, 387–400. [Google Scholar]
- Ishida, J.; Matsumura, T.; Matsushima, N. Market competition, R&D and firm profits in asymmetric oligopoly. J. Ind. Econ. 2011, 59, 484–505. [Google Scholar]
- Mukherjee, A.; Ray, A. Entry, profit and welfare under asymmetric R&D cost. Manch. Sch. 2014, 82, 284–295. [Google Scholar]
- Spence, M. Cost reduction, competition and industry performance. Econometrica 1984, 52, 101–122. [Google Scholar] [CrossRef]
- Sacco, D.; Schmutzler, A. Is there a U-shaped relation between competition and investment? Int. J. Ind. Organ. 2011, 29, 65–73. [Google Scholar] [CrossRef]
- Aghion, P.; Bloom, N.; Blundell, R.; Griffith, R.; Howitt, P. Competition and innovation: An inverted-U relationship. Q. J. Econ. 2005, 120, 701–728. [Google Scholar]
- D’Aspremont, C.; Jacquemin, A. Cooperative and noncooperative R&D in duopoly with spillovers. Am. Econ. Rev. 1988, 78, 1133–1137. [Google Scholar]
- Kamien, M.I.; Muller, E.; Zang, I. Research joint ventures and RJV cartels. Am. Econ. Rev. 1992, 82, 1293–1306. [Google Scholar]
- Suzumura, K. Cooperative and noncooperative research in oligopoly with spillovers. Am. Econ. Rev. 1992, 82, 1307–1320. [Google Scholar]
- Dinda, S.; Mukherjee, A. A note on the adverse effect of competition on consumers. J. Pub. Econ. Theory 2014, 16, 157–163. [Google Scholar] [CrossRef][Green Version]
- Klemperer, P. Welfare effects of entry into markets with switching costs. J. Ind. Econ. 1988, XXXVII, 159–165. [Google Scholar] [CrossRef]
- Lahiri, S.; Ono, Y. Helping minor firms reduce welfare. Econ. J. 1988, 98, 1199–1202. [Google Scholar] [CrossRef]
- Cuervo-Cazurra, A.; Annique Un, C. Why some firms never invest in formal R&D. Strat. Manag. J. 2010, 31, 759–779. [Google Scholar]
- Harris, R.; Trainor, M. A matching analysis of why some firms in peripheral regions undertake R&D whereas others do not. Econ. Innov. New Technol. 2011, 20, 367–385. [Google Scholar]
- Mukherjee, A.; Sinha, U.B. Patent protection, southern innovation and welfare in a north-south trade model. Economica 2013, 80, 248–273. [Google Scholar] [CrossRef]
- Gilbert, R.J. Competition and innovation. J. Ind. Organ. Educ. 2006, 1, 1–23. [Google Scholar] [CrossRef]
- Delbono, F.; Denicolò, V. Incentives to innovate in a Cournot oligopoly. Q. J. Econ. 1991, 106, 951–961. [Google Scholar] [CrossRef]
- Blundell, R.; Griffith, R.; Van Reenen, J. Market share, market value and innovation in a panel of British manufacturing firms. Rev. Eco. Stud. 1999, LXVI, 529–554. [Google Scholar] [CrossRef]
- Geroski, P. Market Structure, Corporate Performance and Innovative Activity; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Nickell, S. Competition and corporate performance. J. Politi-Econ. 1996, CIV, 724–746. [Google Scholar] [CrossRef]
- Federico, G.; Langus, G.; Valletti, T. A simple model of mergers and innovation. Econ. Lett. 2017, 157, 136–140. [Google Scholar] [CrossRef]
- Federico, G.; Langus, G.; Valletti, T. Horizontal mergers and product innovation. Int. J. Ind. Organ. 2018, 59, 1–23. [Google Scholar] [CrossRef]
- Banker, R.D.; Khosla, I.; Sinha, K.K. Quality and competition. Manag Sci. 1998, 44, 1179–1192. [Google Scholar] [CrossRef]
- Childs, P.U.; Triantis, A.J. Dynamic R&D investment policies. Manag. Sci. 1999, 45, 1359–1377. [Google Scholar]
- Trigeorgis, L. Real Options: Managerial Flexibility and Strategy in Resource Allocation; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Cabral, M.B. R&D competition when firms choose variance. J. Econ. Manag. Strategy 2003, 12, 139–150. [Google Scholar]
- Dasgupta, P.; Stiglitz, J. Industrial structure and the nature of innovative activity. Econ. J. 1980, 90, 266–293. [Google Scholar] [CrossRef]
- Dasgupta, P.; Stiglitz, J. Uncertainty, industrial structure, and the speed of R&D. Bell J. Econ. 1980, 11, 1–28. [Google Scholar]
- Gilbert, R.J.; Newbery, D.M.G. Preemptive patenting and the persistence of monopoly. Am. Econ. Rev. 1982, 72, 514–526. [Google Scholar]
- Kamien, M.I.; Schwartz, N.L. On the degree of rivalry for maximum innovative activity. Q. J. Econ. 1976, 90, 245–260. [Google Scholar] [CrossRef]
- Sutton, J. Schumpeter lecture: Technology and market structure. Eur. Econ. Rev. 1996, 40, 511–530. [Google Scholar] [CrossRef]
- Tandon, P. Innovation, market structure, and welfare. Am. Econ. Rev. 1984, 74, 394–403. [Google Scholar]
- Boudreau, K.J.; Lacetera, N.; Lakhani, K.R. Incentives and problem uncertainty in innovation contests: An empirical analysis. Manag. Sci. 2011, 57, 843–863. [Google Scholar] [CrossRef]
- Darai, D.; Sacco, D.; Schmutzler, A. Competition and innovation: An experimental investigation. Exp. Econ. 2010, 13, 439–460. [Google Scholar] [CrossRef]
- Isaac, R.M.; Reynolds, S.S. Appropriability and market structure in a stochastic invention model. Q. J. Econ. 1988, 103, 647–671. [Google Scholar] [CrossRef]
- Isaac, R.M.; Reynolds, S.S. Schumpeterian competition in experimental markets. J. Econ. Behav. Organ. 1992, 17, 59–100. [Google Scholar] [CrossRef]
- Schumtzler, A. Competition and investment—A unified approach. Int. J. Ind. Organ. 2013, 31, 477–487. [Google Scholar] [CrossRef]
- Schumtzler, A. The relation between competition and investment—Why is it such a mess? In Working Paper No. 0716; University of Zurich: Zurich, Switzerland, 2010. [Google Scholar]
- Belleflamme, P.; Vergari, C. Incentives to innovative in oligopolies. Manag. Sch. 2011, 79, 6–28. [Google Scholar]
- Bonanno, G.; Haworth, B. Intensity of competition and the choice between product and process innovation. Int. J. Ind. Organ. 1998, 16, 495–510. [Google Scholar] [CrossRef]
- D’Aspremont, C.; Ferreira, R.D.S.; Gérard-Varet, L.-A. Strategic R&D investment, competition toughness and growth. Int. J. Econ. Theory 2010, 6, 273–295. [Google Scholar]
- Delbono, F.; Denicolò, V. R&D investment in a symmetric and homogeneous oligopoly. Int. J. Ind. Organ. 1990, 8, 297–313. [Google Scholar]
- Qiu, L.D. On the dynamic efficiency of Bertrand and Cournot equilibria. J. Econ. Theory 1997, 75, 213–229. [Google Scholar] [CrossRef]
- Symeonidis, G. Comparing Cournot and Bertrand equilibria in a differentiated duopoly with product R&D. Int. J. Ind. Organ. 2003, 21, 39–55. [Google Scholar]
- Spulber, D.F. Competing inventors and the incentive to invent. Ind. Corp. Chang. 2012, 22, 33–72. [Google Scholar] [CrossRef]
- Spulber, D.F. How do competitive pressures affect incentives to innovate when there is a market for inventions? J. Politi-Econ. 2013, 121, 1007–1054. [Google Scholar] [CrossRef]
- Spulber, D.F. Competition policy and the incentive to innovate: The dynamic effects of Microsoft v. Commission. Yale J. Reg. 2008, 25, 247–301. [Google Scholar] [CrossRef][Green Version]
- Spulber, D.F. Innovation economics: The interplay among technology standards, competitive conduct and economic Performance. J. Compet. Law Econ. 2013, 9, 777–825. [Google Scholar] [CrossRef]
- Spulber, D.F. The Innovative Entrepreneur; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Denicolò, V.; Polo, M. Duplicative research, mergers and innovation. Econ. Lett. 2018, 166, 56–59. [Google Scholar] [CrossRef]
- Motta, M.; Tarantino, E. The effect of horizontal mergers, when firms compete in prices and investments. Int. J. Ind. Organ. 2021, 78, 102774. [Google Scholar] [CrossRef]
- Bourreau, M.; Jullien, B. Mergers, investments, and demand expansion. Econ. Lett. 2018, 167, 136–141. [Google Scholar] [CrossRef]
- López, A.; Vives, X. Overlapping ownership, R&D Spillovers, and antitrust policy. J. Politi-Econ. 2019, 127, 2394–2437. [Google Scholar]
- Sutton, J. Technology and Market Structure: Theory and History; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Sutton, J. Sunk Costs and Market Structure: Price Competition, Advertising, and the Evolution on Concentration; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Vives, X. Nash equilibrium with strategic complementarities. J. Math. Econ. 1990, 19, 305–321. [Google Scholar] [CrossRef]
- Mankiw, A.G.; Whinston, M.D. Free entry and social inefficiency. Rand J. Econ. 1986, 17, 48–58. [Google Scholar] [CrossRef]
- Machokoto, M.; Gyimah, D.; Ntim, C.G. Do peer firms influence innovation? Br. Account. Rev. 2021, 53, 100988. [Google Scholar] [CrossRef]
- Chandler, N.; Krajcsák, Z. Intrapreneurial fit and misfit: Enterprising behavior, preferred organizational and open innovation culture. J. Open Innov. Technol. Mark. Complex. 2021, 7, 61. [Google Scholar] [CrossRef]
- Lam, L.; Nguyen, P.; Le, N.; Tran, K. The relation among organizational culture, knowledge management, and innovation capability: Its implication for open innovation. J. Open Innov. Technol. Mark. Complex. 2021, 7, 66. [Google Scholar] [CrossRef]
- Hewlett, S.A.; Marshall, M.; Sherbin, L. How diversity can drive innovation. Harv. Bus. Rev. 2013, 91, 30. [Google Scholar]
- Dasgupta, P. The theory of technological competition. In New Developments in the Analysis of Market Structure; Stiglitz, J., Mathewson, F., Eds.; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Singh, A.; Vives, X. Price and quantity competition in a differentiated duopoly. Rand J. Econ. 1984, 15, 546–554. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).