Abstract
This paper provides a model of the repeated prisoner’s dilemma in which cheap-talk communication is necessary in order to achieve cooperative outcomes in a long-term relationship. The model is one of complete information. I consider a continuous time repeated prisoner’s dilemma game where informative signals about another player’s past actions arrive following a Poisson process; actions have to be held fixed for a certain time. I assume that signals are privately observed by players. I consider an environment where signals are noisy, and the correlation of signals is higher if both players cooperate. We show that, provided that players can change their actions arbitrary frequently, there exists an equilibrium with communication that strictly Pareto-dominates all equilibria without communication.
1. Introduction
In this paper, I identify an environment in which communication is necessary to achieve cooperation. I consider a model of the repeated prisoner’s dilemma game with complete information and private monitoring (a repeated game in which players can only get noisy signals on other players’ past actions, and moreover, the signals are private information of the player). I borrow the specifications of the model from Abreu, Milgrom and Pearce [1] (henceforth AMP)—this is a continuous time model in which actions have to be held fixed for a certain period, and a noisy signal arrives following a stochastic process. I depart from AMP, however, by assuming monitoring is private instead of public. It is assumed that the monitoring structure has the following properties. First, private signals are sufficiently noisy. Second, like Aoyagi [2] and Zheng [3], the degree of their correlation depends on actions, and it is higher when both players cooperate than when one of them defects. Finally, regardless of action pair, the correlation is high enough so that given one player gets a signal, it is more likely that the other player also observes a signal.
The main result of the paper is that there exists an equilibrium with communication that strictly Pareto-dominates all equilibria without communication, provided that the period over which actions are held fixed is sufficiently short. In this model, communication not only facilitates coordination, as in Compte [4] and Kandori and Matsushima [5], but also helps players to find defects. To see this, notice that if the signals disagree across players, that is a sign of a defect. Signals that are too noisy to sustain cooperation if observed individually are informative enough to sustain cooperation when they indicate disagreement. Of course because of private monitoring, players cannot utilize this information. Communication, however, allows players to get information about the other players’ signals.
Thus, this paper provides a channel through which communication facilitates cooperation. Note also that in our model, messages are not verifiable. This result suggests that antitrust authorities may have to be careful even when exchanging unverifiable messages.
Lately, Awaya and Krishna [6,7] and Spector [8] also showed the necessity of communication. In particular, Awaya and Krishna [6] considered Stigler’s [9] secret price cutting model where firms compete in prices and sales are drawn from a log-normal distribution. Awaya and Krishna [7] considered a general game with finite action and signal space. This paper is a precursor to these. AMP specification helps to state the result in a cleaner manner. In particular, unlike Awaya and Krishna [6,7], this paper does not focus on the limiting case where signals are arbitrarily noisy.
A remark is in order. While this paper shows that without communication, cooperation cannot be achieved, this result does not contradict folk theorem (see Sugaya [10]). Folk theorem fixes other parameters, and works on the limit when players become very patient. In this paper, on the other hand, the patience of players is fixed.
More broadly, this paper relates to the recent advances in the dynamic prisoner’s dilemma and social dilemma games that examine when cooperation can be achieved. For example, using the evolutionary approach, Szolnoki and Perc [11] and Danku et al. [12] pointed to importance of knowing others’ strategies to achieve cooperation. In this study, in contrast, communication was used to learn other’s past signals, not strategies.
2. Preliminaries
2.1. Repeated Game
Consider the following prisoner’s dilemma as the stage game with expected payoffs, denoted by G:
The time structure is borrowed from AMP. This prisoner’s dilemma game is played continuously over the time interval . The payoffs in the matrix above are flow rates of payoff. The interest rate is denoted by r, and so if the payoff at time t is , then the net present value of payoffs for the whole game is . Notice r represents patience of players, and the smaller the r is, the more patient the players are.
It is assumed that actions have to be held fixed for a certain time interval denoted by . In other words, players can choose their actions only at periods . In effect, the “discount factor” is interpreted as .
Like AMP, I assume that the signals arrive following a stochastic process which depends on the pair of actions. Unlike AMP, however, I assume that the signal is private. In particular, it follows the following process. Let represent arrival or absence of a signal to player i, where s (resp. o) denotes arrival (resp. absence). Given an action pair , the probability that each player gets a signal within a time interval is given by the following figure:
 where . It is clear that each element is smaller than 1. Later I will present an assumption that guarantees each element of the figure is strictly positive when . The time interval is assumed to be small enough so that the probability that a signal is observed more than once within is negligible. Finally, Figure 1 is stated in terms of expected payoffs. One interpretation is that the game ends with probability r and players get payoffs only after it ends.
where . It is clear that each element is smaller than 1. Later I will present an assumption that guarantees each element of the figure is strictly positive when . The time interval is assumed to be small enough so that the probability that a signal is observed more than once within is negligible. Finally, Figure 1 is stated in terms of expected payoffs. One interpretation is that the game ends with probability r and players get payoffs only after it ends.
 where . It is clear that each element is smaller than 1. Later I will present an assumption that guarantees each element of the figure is strictly positive when . The time interval is assumed to be small enough so that the probability that a signal is observed more than once within is negligible. Finally, Figure 1 is stated in terms of expected payoffs. One interpretation is that the game ends with probability r and players get payoffs only after it ends.
where . It is clear that each element is smaller than 1. Later I will present an assumption that guarantees each element of the figure is strictly positive when . The time interval is assumed to be small enough so that the probability that a signal is observed more than once within is negligible. Finally, Figure 1 is stated in terms of expected payoffs. One interpretation is that the game ends with probability r and players get payoffs only after it ends.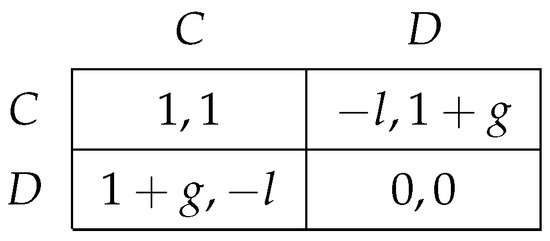
Figure 1.
The payoff matrix.
where g, l > 0.
Notice that the marginal probability that a private signal arrives is given by
In other words, is the arrival rate of a signal to a player. From this, we can interpret as a measure of noisiness of the signal. The private signal is noisier if is smaller. An extreme case is . In this case, the signal is completely noise.
Notice also that
Hence, is an arrival rate of an event in which the arrival of a signal differs among players. If is small, then signals are highly correlated in the sense that if one player gets the signal, then the other players will also get the signal, most likely.
I will assume that (i) private signals are noisy relative to the patience of players, (ii) the degree of their correlation depends on actions and it is higher when both players cooperate than when one of them defects, and (iii) regardless of action pair, the correlation is high enough so that given a player gets a signal, it is more likely that the other player also observes a signal. Formally, first
Assumption 1.
This assumption states the relationship between the noisiness of the private signals and the patience of the players. Roughly, the assumption is easily satisfied when (i) the private signal is noisy and (ii) the players are impatient. Second,
Assumption 2.
This assumption implies that , or the disagreement over arrivals happens more frequently when a player defects than when both players cooperate. To see the implication of this assumption, consider a fictitious case in which signals are public in the sense that both players could commonly observe the pair of signals , instead of their own signal . Then the event constitutes the arrival of bad news in terms of AMP—an event which occurs more frequently when a player defects.
Lemma 1.
Finally, assume
Assumption 3.
For any a,
This assumption means that given if a player gets a signal, it is likely that the other player also observes a signal. To see this, just observe that
Additionally, notice that this assumption guarantees that the first element of the figure takes a strictly positive value when .
Note that similar assumptions—such as that signals based on past actions are highly correlated, and correlation is higher when they cooperate—appear in other contexts. See, for example, Fleckinger [13] and Awaya and Do [14].
I will provide some parametric examples that satisfy all these assumptions.
Example 1.
Let and . Additionally, let for any a and
It is clear that Assumption 1 is satisfied, because right-hand side is 0. Assumption 3 is clearly satisfied as well. To see Assumption 2,
Example 2.
Again let , , and
Now let
To see that these satisfy Assumption 1, notice and
The remaining assumptions follow by the same reason as above.
Now I am ready to define histories and strategies. Let
be the history of actions that player i took at periods , and
be the history of signals that player i has observed by period . Recall that is assumed to be small enough so that the probability so that the signal is observed twice within is negligible.
A pure strategy for player i is a sequence of functions where
and for
where ∅ is the null history (throughout the paper, subscripts indicate players, superscripts indicate periods, and bold letters indicate histories). An implicit assumption here is that a player can condition his action on a signal he observes in a certain instance. This assumption is innocuous because this event happens with probability zero.
2.2. Repeated Game with Communication
Next consider an infinite horizon repeated game version of the stage game in which players can communicate. They can send messages in a finite set and let . Communication entails no cost so that it is “cheap talk”. All messages are observed publicly and without any error.
Assume players send messages only when they decide their actions, that is, at . The communication is done by an instance without taking any physical time, and when players decide their actions they can take the message sent at that moment into account.
Formally, let
be the history of messages that player i send at periods , and let
A pure strategy in this game is a pair of where is a sequence of message strategies and is a sequence of action strategies. Then
and for
Again it is assumed that a player can condition a message sent, or an action taken, on a signal observed at the instance.
3. The Result
The main result of the paper is that communication is necessary to achieve cooperation.
Theorem 1.
There exists an equilibrium with communication that strictly Pareto-dominates all equilibria without communication, provided that players can change their actions in an arbitrarily small instant.
The theorem is established by showing the following two propositions whose proofs appear in the next section. The first proposition states the negative result that the trivial equilibrium is the only equilibrium if communication is impossible.
Proposition 1.
Suppose communication is impossible. Then there exists a such that for any repetition of mutual defection is the only equilibrium.
This proposition is a consequence of an assumption that signal is too noisy. I provide for the examples discussed before.
Example 3
(Continuation of Example 1). Take parameter values provided in Example 1. Then the trivial equilibrium is the only equilibrium for any Δ. In other words, can be any value.
The reason here is clear. As , the signal generated by playing C is exactly the same as playing D. In other words, there is no way to detect defection, even statistically. Hence, it is rational to play the stage-game dominant strategy, D.
Example 4
(Continuation of Example 2). Take parameter value provided in Example 2 and let . Then it is shown that the trivial equilibrium is the only equilibrium. The argument is found in the next section.
The second proposition states the positive result that a better outcome (than the trivial equilibrium) can be achieved in the equilibrium if communication is possible.
Proposition 2.
Suppose communication is possible. Let be the supremum of the symmetric equilibrium payoff when players can change their actions at time interval Δ. Then
The rough idea of the proof is as follows. As is already mentioned, the disagreement of the signal constitutes bad news. Now consider a fictitious public monitoring game in which each players could observe signals of both players. Then, Proposition 5 of AMP applies here, and it is shown there exists a non-trivial equilibrium in the limit as . Now the remaining task is to show truth telling. It is shown that given an arrival (resp. absence) of a signal to a player, it is more likely that an arrives (resp. absence) of the signal happens to the other player regardless of action pair. This means that truth telling minimizes the probability of an arrival of bad news, which is disagreement over the arrival times of signals.
Example 5
(Continuation of Examples 1 and 2). Given parameter values provided Examples 1 and 2,
4. Proofs
4.1. Without Communication
We first establish that without communication, players cannot cooperate. The intuition is that because signals only contain noisy information about past behavior of the opponent (Assumption 1), deviations are hardly detected and so will be left unpunished.
By way of contradiction, suppose there is an equilibrium in which at least one player—say player i—cooperates at some histories. Without loss of generality, suppose player i cooperates in period following after a history . For this to be rational, player i’s future payoff must non trivially depend on whether gets a signal or not during .
Now let be the continuation payoff of player i when player gets a private signal in and be the continuation payoff of player i when player does not. Of course, these expected continuation payoffs depend on history . As and are continuation payoffs, they are bounded, and in particular,
Take an action pair . Then the lifetime payoff of player i given a is given by
where is the stage-game payoff given an action pair. Let the value be denoted by . Notice for given player ’s strategy , the lifetime payoff when he takes an action is given by
where the expectation is taking over player ’ action , following his strategy .
In the following, I show that for any ,
that is, in contrast to the assumption, it is not rational to play C.
To see this, first define
Then,
and hence,
This value takes a strictly positive value by the following reason. First observe that for any ,
Second,
By combining these inequalities, I have
The right-hand side is strictly positive by Assumption 1. Now the claim follows because is bounded away from 0 for any .
Now consider the following example again.
Example 6
(Continuation of Examples 2 and 4). First notice that
where the last inequality follows from the facts that
and
Now because , . Also,
Thus,
4.2. With Communication
Next we establish that players can cooperate if communication is available. Here, communication plays a role to “aggregate” signals. Correlation across signals are higher when they cooperate (Assumption 2). Thus, by aggregating signals and checking correlation, players can learn more about their past behavior. Thus, with communication, deviations are easily detected and punished.
The outline of the proof is as follows. First, consider the fictitious case where each player can observe the signals of both players . Recall that Assumption 2 implies that disagreement in signals is bad news that occurs more likely when a player plays D. This fictitious game is one of the public monitoring games that AMP considered with the interpretation that is bad news, and they established that some degree of cooperation can be achieved. This part is stated in Lemma 2.
Note also that this game is equivalent to the original game with communication: each player follows truth telling—that is, sends a message that says the player observes a signal if and only if he actually does—with disagreement being bad news.
Then the statement is established by showing that players have incentives to report truthfully. This is established in Lemma 3.
4.2.1. Fictitious “Public Monitoring” Game
Consider again a fictitious public monitoring game in which each player can observe the signals of both players . Let be the supremum of the symmetric perfect public equilibrium payoff of this fictitious game (following AMP, I use “symmetric” in the sense that the equilibrium specifies symmetric actions after all histories). Now Assumption 2 implies that the first case of Proposition 5 of AMP applies here (with the interpretation that is bad news), and hence the following lemma is an immediate corollary of the proposition.
Lemma 2.
4.2.2. Truth Telling
I complete the proof by showing that players have an incentive to report truthfully. As a disagreement over arrivals of signals constitutes bad news, each player tries to minimize the probability of disagreement when he sends a message. Now I will establish that truth telling minimizes the probability of the disagreement given that the other player also tells the truth, regardless of action pair.
To show this, it is sufficient to see that given the arrival (resp. absence) of a signal to a player, it is more likely that one will arrive (resp. absence) to the other player also, or
Lemma 3.
For any , and ,
Proof.
First consider the case where . In this case,
and hence
Next I show the case where . To see this, first observe that
By using l’Hôpital’s rule, I get
Now Assumption 3 implies the inequality. □
This completes the proof with communication.
Funding
The research was supported by a grant from the National Science Foundation (SES-1626783).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I am most grateful to Vijay Krishna for his guidance and encouragement. I also thank Kalyan Chatterjee, Ed Green, Tadashi Sekiguchi, Satoru Takahashi, Neil Wallace, Yuichi Yamamoto and participants of the 24th International Game Theory Conference at Stony Brook and the 2013 Asian Meeting of the Econometric Society at National University Singapore for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abreu, D.; Milgrom, P.; Pearce, D. Information and timing in repeated partnerships. Econometrica 1991, 59, 1713–1733. [Google Scholar] [CrossRef]
- Aoyagi, M. Collusion in dynamic Bertrand oligopoly with correlated private signals and communication. J. Econom. Theory 2002, 102, 229–248. [Google Scholar] [CrossRef][Green Version]
- Zheng, B. Approximate efficiency in repeated games with correlated private signals. Games Econom. Beh. 2008, 63, 406–416. [Google Scholar] [CrossRef]
- Compte, O. Communication in repeated games with imperfect private monitoring. Econometrica 1998, 66, 597–626. [Google Scholar] [CrossRef]
- Kandori, M.; Matsushima, H. Private observation, communication and collusion. Econometrica 1998, 66, 627–652. [Google Scholar] [CrossRef]
- Awaya, Y.; Krishna, V. On communication and collusion. Am. Econom. Rev. 2016, 106, 285–315. [Google Scholar] [CrossRef]
- Awaya, Y.; Krishna, V. Communication and cooperation in repeated games. Theor. Econom. 2019, 14, 513–553. [Google Scholar] [CrossRef]
- Spector, D. Cheap talk, monitoring and collusion. Mimeo 2017. [Google Scholar]
- Stigler, G.J. A theory of oligopoly. J. Polit. Econom. 1964, 72, 44–61. [Google Scholar] [CrossRef]
- Sugaya, T. Folk Theorem in Repeated Games with Private Monitoring. Mimeo 2021. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Reentrant phase transitions and defensive alliances in social dilemmas with informed strategies. EPL Europhys.Lett. 2015, 110, 38003. [Google Scholar] [CrossRef]
- Danku, Z.; Perc, M.; Szolnoki, A. Knowing the past improves cooperation in the future. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Fleckinger, P. Correlation and relative performance evaluation. J. Econom. Theory 2012, 147, 93–117. [Google Scholar] [CrossRef]
- Awaya, Y.; Do, J. Incentives under equal-pay constraint and subjective peer evaluation. Mimeo 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).