The Number of Parties and Decision-Making in Legislatures

Abstract

This paper proposes a model of a legislature, formed by several parties, which has to vote for or against a certain bill in the presence of a lobbyist interested in a certain vote outcome. We show that the ease with which the lobbyist can manipulate a legislature decision increases with the number of elected parties, and, consequently, decreases with an electoral threshold. On the other hand, a lower electoral threshold increases the representativeness of a legislature. We combine these two effects in a notion of fairness. We show the existence of an electoral threshold that optimizes the fairness of a political system, which is close to 1–5%. Namely, the optimal threshold (in our sense) is close to thresholds that exist in most parliamentary democracies.

1. Introduction

Some decisions only affect a decision-maker and his utility. However, others may affect more people and, therefore, their utilities too. In such a case, it would be fair for such decisions to be the product of a collective will. But what if a decision affects every citizen in a city or even in a whole country? It would be fair to ask everyone’s opinion, although this feat is probably not feasible. Buchanan and Tullock [1] in their classic text point out that as more actors participate in collective decision making, it is more difficult to reach an agreement. When there are many people who have to decide, the decision-making process takes more time, hence, it would seem to be more convenient to narrow the group of decision-makers. In modern democratic societies, the solution (the best existing, but not absolute best) is to elect representatives, to whom the power to decide is delegated. The most typical example is a parliament, formed by representatives elected by citizens: parliament is charged with the power of making decisions that affect the whole country.

A large number of different electoral rules and their variations inform most political systems. Arguably, the most desirable feature of a voting procedure is that voters reveal their opinions sincerely, namely, vote according to their preferences. The sincerity of the voters is important when these voters are the citizens electing representatives, but it is even more important when these voters are the elected representatives, who are in charge of deciding the future of the whole country.

Every citizen of a democratic country supports a certain candidate or a party in order to delegate to them his decision power. The voter puts his trust in the representative, based on electoral campaign statements. It is then not surprising that the voter wants to be sure that politicians are honest, and act as they promised during their electoral campaign. However, it is easier to influence the decision of a smaller group of elected representatives, for instance, by bribing some of them, than the decision of a whole group of citizens. The difficulties of manipulating larger groups are commonly explained by higher transaction costs or incomplete information about preferences of voters. In this research we refer to another aspect, which is lobbyist activity. Consequently, if we solve the problem of difficult decision-making in a large group by reducing the number of decision-makers, we might create a problem of manipulability, since it is easier to manipulate a smaller group than a large group. Thus, if it is found to be easy to strategically influence voting outcomes, one cannot be confident about the reliability and legitimacy of political decisions.

The manipulation of the decisions of a legislature once it is elected is widely studied in lobbying literature; see, for instance, ref [2].

It should be mentioned that [1] consider vote trading to be a process that is not necessarily negative. For example, agreement among parties about mutual support (logrolling) may help to protect minority rights. Yet, this is true only if members of a legislature honestly represent the interests of their constituency. If a legislature is manipulable, this is hardly guaranteed.

However, the question of the sincerity and manipulability of a particular party is not relevant for its supporters if this party does not secure any seats in the legislature due to the applied electoral threshold, which deters parties that do not get enough support to enter the legislature. Not only do votes affect the share of party representation but also the voting rule, and the electoral threshold, as an important part of this rule, partly determines electoral success. The 2015 Catalan (i.e., Catalonia, Spain) general election offers an outstanding example of how an electoral threshold can create a misrepresentation in a legislature. Each of 11 parties which participated in the elections were requested to declare their opinion on the matter of Catalonia’s independence. In the election, 48.05% of voters voted for ‘yes’ parties and 50.82% voted for ‘no’ parties. Yet, since one ‘no’ party and the indifferent parties did not pass the electoral threshold of 3%, it appears that 72 MPs (53.33%) belong to ‘yes’ parties, while 63 MPs (46.66%) belong to ‘no’ parties. Therefore, the electoral threshold caused a difference between the opinions of voters and representatives. It should be mentioned that the electoral threshold in Catalonia is calculated at a district level and may lead to overrepresentation of rural areas, where independence supporters are more popular. Yet the ability of the electoral threshold to lead to misrepresentation of voters is common to all electoral systems where it is applied. At the same time, the voters cannot be sure that the parties will vote for or against independence as they promised. Their votes can change due to modification of their initial positions or because of (il)legal pressure from outside parliament.

This situation inspired us to propose a model of a legislature, formed by several parties, which have to vote for or against a certain bill. The decision is made by simple majority. We study the effect of the electoral threshold on the ease of a lobbyist influencing a voting outcome, through its impact on the number of parties in the legislature. We conclude that it is easier for a lobbyist to influence a legislature comprising more parties. The intuition is that if the number of parties increases, the probability of a lobbyist finding parties that will agree to change their position also increases.

To be more realistic, we assume that the parties differ not only in the number of seats in parliament, but also in their political views. Assuming that the “Yes” answer favors the left wing, a strongly right wing party is less likely to be bribed for a “Yes” decision, or the price to be paid for its vote will be much higher than for a central party or a right wing party with more moderate views. We define an expected bribe required to change an outcome of a vote in the parliament as a measure of ease of manipulation of parliament’s decision. We claim that it is easier to manipulate decisions as the number of parties in a legislature increases.

Next, to model the possible composition of the parliament given the popular views of the citizens, we extend the model by introducing citizens who supported the parties. In this case, the composition of the parliament depends not only on the views of the citizens but also on the electoral threshold. We do not model a strategy of citizens here, assuming that their preferences coincide with the position of the party they support. We assume the number of supporters of each party to be randomly picked. We assume that the lobbyist tries to manipulate the legislature decision by offering payment to parties for a change in vote favorable to the lobbyist. The maximal total amount of payment that the lobbyist agrees to make depends on the intensity of the lobbyist’s support of the bill, support which is randomly determined.

Hence, the lobbyist is required to solve an optimization problem: obtaining a simple majority of votes, while minimizing total payment to the parties. If this total amount of payment required by parties is below the maximal total amount that the lobbyist agrees to pay, then the desired decision is obtained. Otherwise, parties vote according to the stances of their supporters. We calculate the probability of the final decision by the legislature coinciding with the popular will (we call this probability the fairness of the political system). The fairness of the political system negatively depends on the effects of both misrepresentation (which increases with an electoral threshold) and ease of manipulation (which decreases with an electoral threshold).

We analyze how the fairness of the political system depends on the electoral threshold. Our simulations show that, for thresholds that exist in most parliamentary democracies with a proportional representation system (1–5%), the ‘fairness’ in our sense is close to optimal. As for thresholds higher than 5%, ‘fairness’ decreases with the threshold. To the best of our knowledge, this is the first justification by a mathematical model of electoral thresholds of 1–5% that exist in most parliamentary democracies.

It is not clear how vulnerability of a political system for manipulation can be tested empirically. However, it can be tested by laboratory experiments, as done by [3,4] and many others. The level of misrepresentation is easier to test. In a sample of 787 election results in 37 countries from 1900 to 2020 (taken from http://www.parlgov.org/ accessed on: 8 October, 2021), the correlation between the number of parties and the share of wasted votes is −0.055. The wasted votes are votes given to parties that did not pass the electoral threshold. The negative correlation shows that a large number of parties is associated with misrepresentation. We use the number of parties as a measure instead of the electoral threshold since the latter is defined differently in different countries. In many countries it is defined on a local level.

To the best of our knowledge, we introduce a novel notion of fairness. It differs from the well-known referendum paradox [5], since we combine ease of manipulation with misrepresentation. We consider a vulnerability to manipulation by an outside lobbyist, and not to strategic voting of voters (see [6]).

Different characteristics of electoral systems are studied in the literature. For instance, ref [7] analyzes allocation of weights to representatives, which maximizes voter utility. See [8] for a survey of notions of fair representation of voters.

Generally, manipulation of voting procedures is studied by scholars from different points of view. Researchers in the field of social choice analyze different electoral systems and their ease of manipulation; see, for instance [9,10,11,12]. The question of what happens if competing parties are allowed to buy votes is also studied by [13]. In [14] there is competition between two lobbyists. Scholars from the field of computational social choice have investigated the computational complexity of influencing elections through bribery; see, for instance, ref [15,16].

For probabilistic voting methodology, see [17].

A basic theoretical model was suggested by [2]. In this model, an outside lobbyist bribes voters. An optimal policy for the lobbyist is examined. Ref. [18] compares equilibrium prices paid by a lobbyist in a cooperative game theory solution. As for empirical studies, Ref. [19] shows that the level of corruption depends on a combination of the electoral system and number of parties. However, their approach is completely different from ours. They conjecture that with a higher number of parties, more actors monitor government activity, which may impede corruption. In our paper we do not consider monitoring. Also [20] recently provided evidence from Brazil, where larger municipalities tend to be more corrupted, but this phenomena is attenuated by better representation of opposition.

We focus on the electoral threshold, but other parameters of a legislature are also important. In particular, the majority quota required has a significant role in modelling of decision-making. For instance, Refs. [21,22,23,24,25,26] preferred a majority quota (in this paper we assume simple majority). Ref. [27] studies loss aversion and attitude to political decisions.

2. Model and Results

2.1. Number of Parties

Let n be the number of parties in a legislature. Let $D_i\in [-1,1]$, $i=1,\dots ,n$ be the ideological position of party i on the bill suggested to be voted for/against. A nonpositive $D_i$ means that the party i supports the bill but votes against it for payment $|D_i|$ or more. A positive $D_i$ means that the party i opposes the bill, but votes for it for payment $D_i$ or more. Assume that positions of parties are random. For each $i\in \{1,\dots ,n\}$

$$D_i=2X_i-1$$

(1)

where $X_i\in [0,1]$ are independent, $X_i\sim Beta(\alpha ,\alpha )$, $\alpha$ is a given parameter. Beta distribution is convenient to model a random variable with support from 0 to 1. Moreover, some widely used distributions are special cases of Beta distribution. For instance, $Beta(1,1)$ is the uniform distribution on $[0,1]$. As $\alpha \to \infty$, the distribution $Beta(\alpha ,\alpha )$ converges to $X_i=\frac{1}{2}$ with probability 1. Namely, as $\alpha$ increases, $D_i$s are closer to 0 with increasing probability, which means a less ideologically polarized political system. See [28] for measurement of ideological polarization in OECD countries.

After D is drawn, it is common knowledge.

We assume that each party has strong party discipline, hence all members of the party cast the same vote. The number of seats in the legislature controlled by each party is its voting weight $w_i\ge 0$, which is assumed to be random and independent. A simple majority of votes is required to accept the bill.

Let L denote the lobbyist. Without loss of generality, we assume that the lobbyist is interested in the bill passing. If the lobbyist is for or against the bill with equal probability, the results are the same. The lobbyist offers each party a nonnegative payment $P_i\in [0,1]$ for voting for the bill, and every party accepts the offer if

$$P_i-D_i\ge 0$$

L minimizes the total amount of payment to parties, subject to the total weight of parties which support the bill being a simple majority of the total weight of parties in the legislature. Namely, the lobbyist solves

$$T\left(n\right)=min\left\{\sum _{i=1}^n{P}_i\right\}s.t.\sum _{P_i-D_i\ge 0}{w}_i>\frac{{\sum }_{j=1}^n{w}_j}{2}$$

(2)

$T\left(n\right)$ is calculated for a realization of $(w_1,w_2,\dots ,w_n)$ and $(D_1,D_2,\dots ,D_n)$. The two vectors—weights and ideological positions—are assumed to be independent of each other. The expected $T\left(n\right)$ will be denoted as $E\left(T\right(n\left)\right)$, which characterizes the ease of manipulation of the decision of the legislature. A low $E\left(T\right(n\left)\right)$ means high ease of manipulation.

2.1.1. Analytical Result

We consider a special case where $\alpha =1$, namely, $X_i\sim U[0,1]$ and, therefore, $D_i\sim U[-1,1]$. In addition, assume uniform distribution of party weights on a simplex. Then, it is easier to manipulate if there are three parties rather than if there are two:

Proposition 1.

Let $W>0$. Let $\alpha =1$ and $(w_1,\dots ,w_n)$ be uniformly distributed on

$$\left\{(w_1,\dots ,w_n)\right|\sum _{i=1}^n{w}_i=W\}.$$

Then $E\left(T\right(2\left)\right)>E\left(T\right(3\left)\right)$.

See proof in the Appendix A.

2.1.2. Numerical Result

We show numerically that the result of Section 2.1.1 holds for general n. Assume the Poisson distribution of weights, $w_i\sim Poiss\left(\lambda \right)$ for each $i\in \{1,\dots ,n\}$, $\lambda$ is a given parameter (for example, Myerson [29] models a number of supporters of some political opinion as the Poisson variable). All $w_i$s are i.i.d. Note that we assume that the total number of seats in the legislature is not fixed (the German Bundestag is an example of such a legislature). 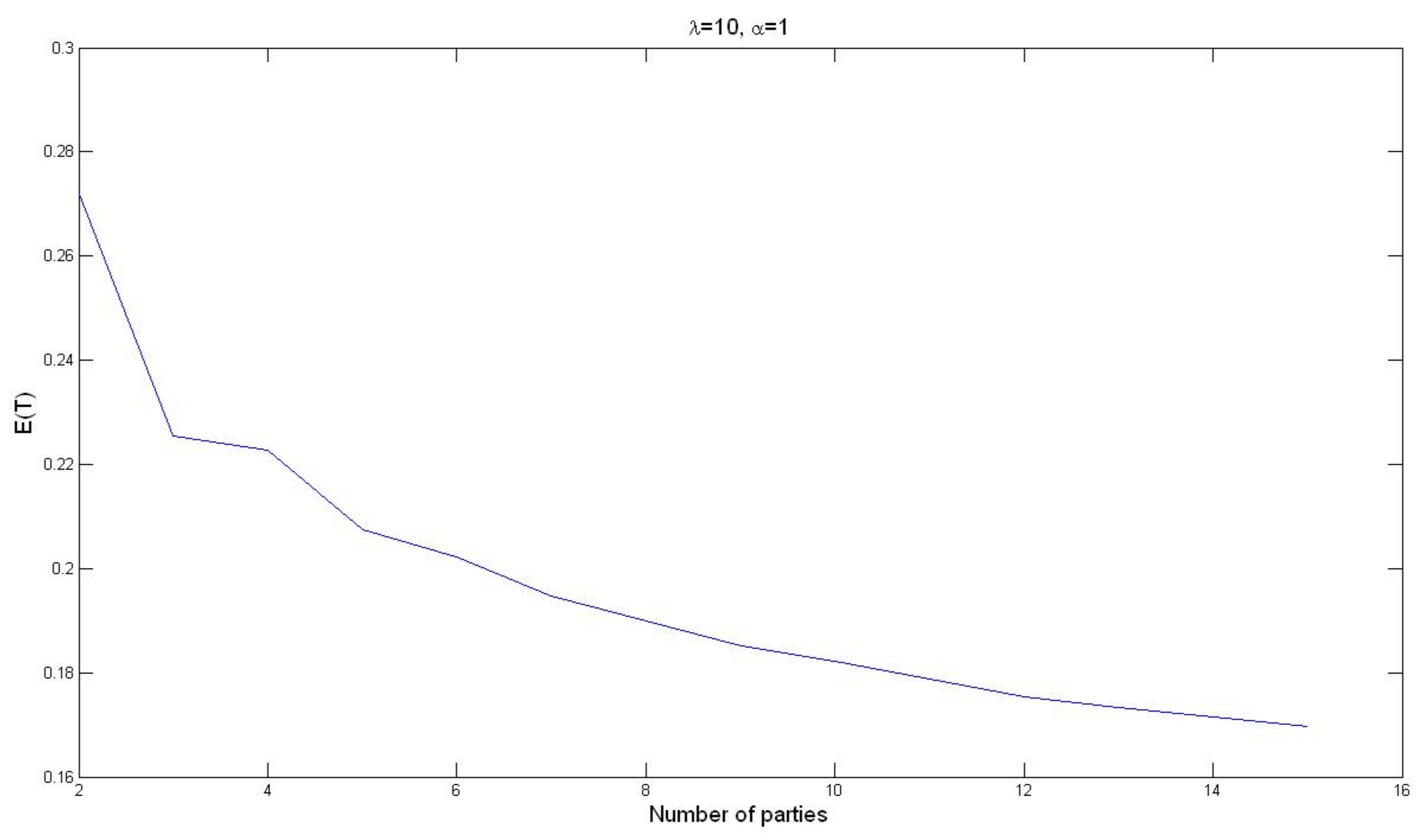Figure 1 presents the results of a Monte Carlo simulation for $E_T\left(n\right)$ depending on n (the number of trials is 1,000,000, $\alpha =1$ and $\lambda =10$). It shows that the ease of manipulation increases with the number of parties, namely, the expected total payment required decreases.

2.2. Given Electoral Threshold

As we have shown previously, a large number of parties is easier to manipulate. One of the institutional tools to reduce number of parties is electoral threshold. However, electoral threshold may lead to misrepresentation of voters, because some parties do not pass the threshold, as defined below. In this section, we analyze the optimal electoral threshold.

Let a random number of parties compete in elections for a given number of seats in a legislature: $n^{\prime }\sim Poiss\left({\lambda }_p\right)$, ${\lambda }_p$ is a given parameter. Even before the elections, all the candidate parties have their political standings for or against the bill to be voted for after elections: $D_i^{\prime }\in [-1,1]$, $i=1,\dots ,n^{\prime }$. $D_i^{\prime }$ is randomly picked as in (1). All $D_i^{\prime }$ are independent.

For $i=\{1,\dots ,n^{\prime }\}$, let $v_i\sim Poiss\left({\lambda }^{\ast }\right)$ be the number of popular votes received by party i, where ${\lambda }^{\ast }$ is a given parameter. Assuming that each party position coincides with its voters’ position, we define popular preference $\mathsf{\Pi }\in \{A,R,I\}$ with regard to the bill as “Accept”, “Reject”, or “Indifferent”:

$$\mathsf{\Pi }=\left\{\begin{array}{cc}A,\hfill & \sum _{D_i^{\prime }\le 0}{v}_i>\sum _{D_i^{\prime }>0}{v}_i\hfill \\ R,\hfill & \sum _{D_i^{\prime }\le 0}{v}_i<\sum _{D_i^{\prime }>0}{v}_i\hfill \\ I,\hfill & \sum _{D_i^{\prime }\le 0}{v}_i=\sum _{D_i^{\prime }>0}{v}_i\hfill \end{array}\right.$$

A widely-used institutional rule which is implemented in general elections is the electoral threshold. Parties that obtain a share of the popular vote lower than the predefined threshold do not receive any representation in the legislature. Let the electoral threshold $t\in [0,1]$ be given. Party i passes the threshold t iff $v_i>t{\sum }_{j=1}^{n^{\prime }}{v}_j$. Therefore,

$$n=\left\{i\in n^{\prime }{v}_i>t\sum _{j=1}^{n^{\prime }}{v}_j\right\}$$

A mapping $\pi :\{1,\dots ,n\}\to \{1,\dots ,n^{\prime }\}$ is interpreted as follows: if party $i\in \{1,\dots ,n^{\prime }\}$ passed the threshold t, its index among other parties which passed the threshold is ${\pi }^{-1}\left(i\right)$.

Seats are allocated to n parties proportionally to their popular vote share, where surplus votes are allocated according to the widely-used d’Hondt method (see [30]). Results for seats allocated using the Largest Remainder method are similar. Given $v_{\pi \left(1\right)},\dots ,v_{\pi \left(n\right)}$, let $w_1,\dots ,w_n$ be the number of seats, or non-negative weights, allocated to n parties. It should be emphasized that, since number of seats is an integer, the minimal feasible weight of party is equivalent to one seat. Thus, there is always a positive threshold, even if formally it may be defined as zero.

$D_i$ is an initial position of party i, which passed the threshold, on the bill. Similarly to Section 2.1, $|D_i|$ means the minimal demand for payment to party i to vote against its own preference, that is, against the bill if $D_i<0$ and in favor of the bill if $D_i>0$. Note, that $D_i\le 0$ means that party i supports the bill if there is no payment.

As in Section 2.1, $P_i\in [0,1]$ is the lobbyist’s payment offer to party i, $i\in \{1,\cdots ,n\}$, which accepts it iff

$$P_i-D_i\ge 0$$

All parameters, after being drawn, are common knowledge.

The lobbyist L’s standing $D_L$ about the bill is randomly chosen as in (1). Negative $D_L$ means that L supports the bill, positive means that s/he opposes it and $D_L=0$ means indifference. L agrees to pay parties for changing their standing about the bill an amount lower than $|D_L|$. If this sum is not sufficient to assure the majority in the legislature desired by the lobbyist, s/he prefers to not make any payment. Let

$$D_i=\left\{\begin{array}{cc}{D}_{\pi \left(i\right)}^{\prime }\hfill & ,D_L\le 0\hfill \\ -D_{\pi \left(i\right)}^{\prime }\hfill & ,D_L>0\hfill \end{array}\right.$$

$i=1,\dots ,n$.

L offers non-negative payments $P_1,\dots ,P_n$ to parties, such that the total payment $T\left(n\right)$ minimizes (2). If $T\left(n\right)<|D_L|$, the legislature adopts the decision ${\mathsf{\Pi }}_l\left(t\right)$ about the bill as desired by the lobbyist, namely,

$${\mathsf{\Pi }}_l\left(t\right)=\left\{\begin{array}{cc}A,\hfill & D_L<0\hfill \\ R,\hfill & D_L>0\hfill \\ I,\hfill & D_L=0\hfill \end{array}\right.$$

In the case $T\left(n\right)\ge |D_L|$, the lobbyist does not make any payment and parties in the legislature vote according to their initial standings. Namely, for $T\left(n\right)\ge |D_L|$

$${\mathsf{\Pi }}_l\left(t\right)=\left\{\begin{array}{cc}A,\hfill & \sum _{D_i<0}{w}_i>\sum _{D_i>0}{w}_i\hfill \\ R,\hfill & \sum _{D_i<0}{w}_i<\sum _{D_i>0}{w}_i\hfill \\ I,\hfill & \sum _{D_i<0}{w}_i=\sum _{D_i>0}{w}_i\hfill \end{array}\right.$$

We define the fairness of the threshold t as the probability that $\mathsf{\Pi }={\mathsf{\Pi }}_l\left(t\right)$. To summarize, ${\mathsf{\Pi }}_l\left(t\right)=\mathsf{\Pi }$ if one of following takes place: the lobbyist agrees with the majority in the legislature, which coincides with majority of the electorate, or the majority in the legislature coincides with the majority of voters, but is different from the lobbyist’s opinion. However, the lobbyist is not interested in investing enough to bribe the parties. There is also a possibility that the lobbyist and the majority of voters agree, but seat allocation in the legislature provides a majority with the opposite opinion. In this case, the lobbyist can still bribe some of the parties and “fix” misrepresentation of voters.

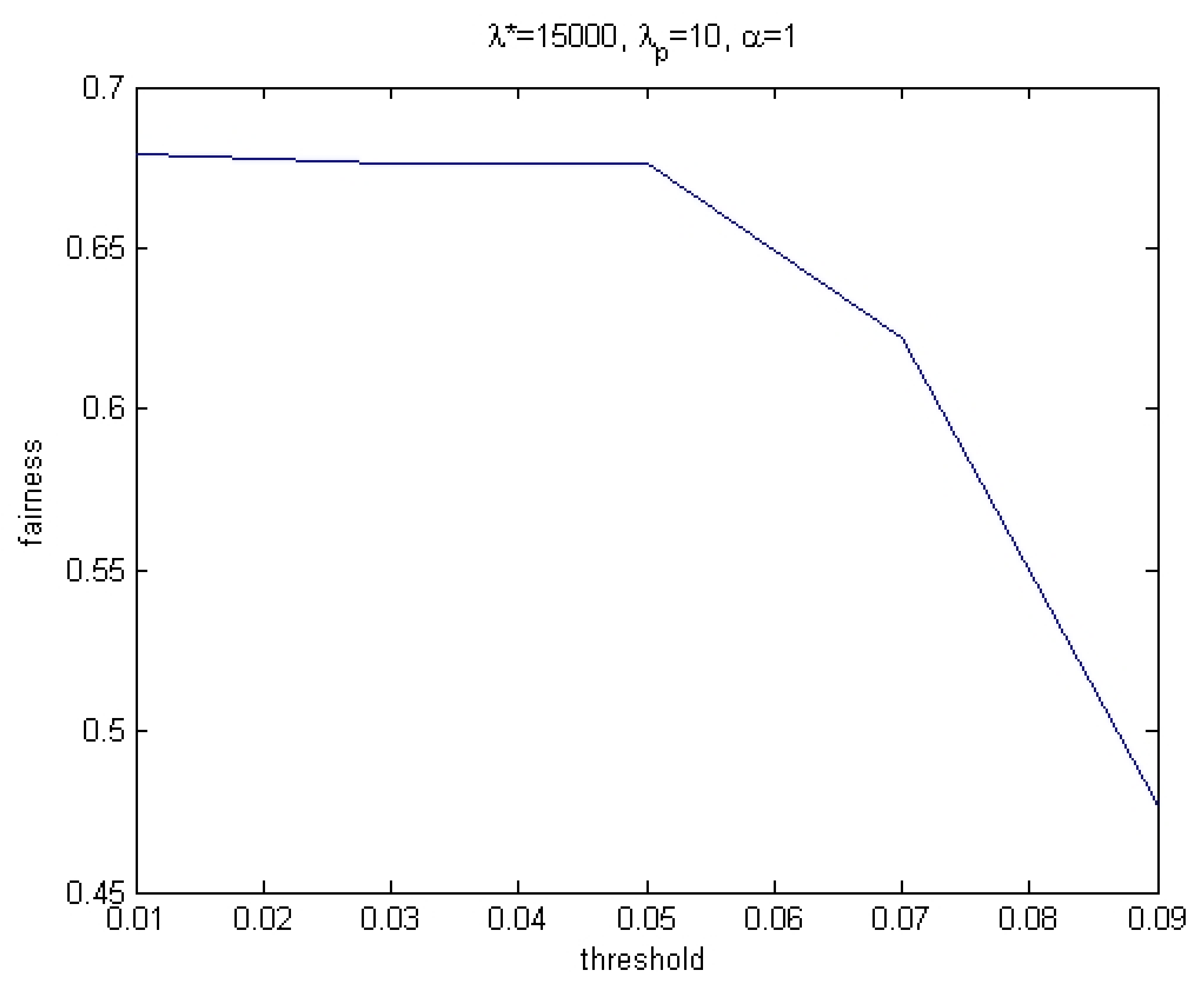
Figure 2 presents results for 100 seats, 100,000 trials, $\alpha =1$. We show thresholds below 10%, because, to the best of our knowledge, the highest existing threshold is 10% in Turkey.

It follows from Figure 2, that for thresholds below 5%, fairness does not suffer. As for thresholds higher than 5%, the ‘fairness’ decreases with the threshold.

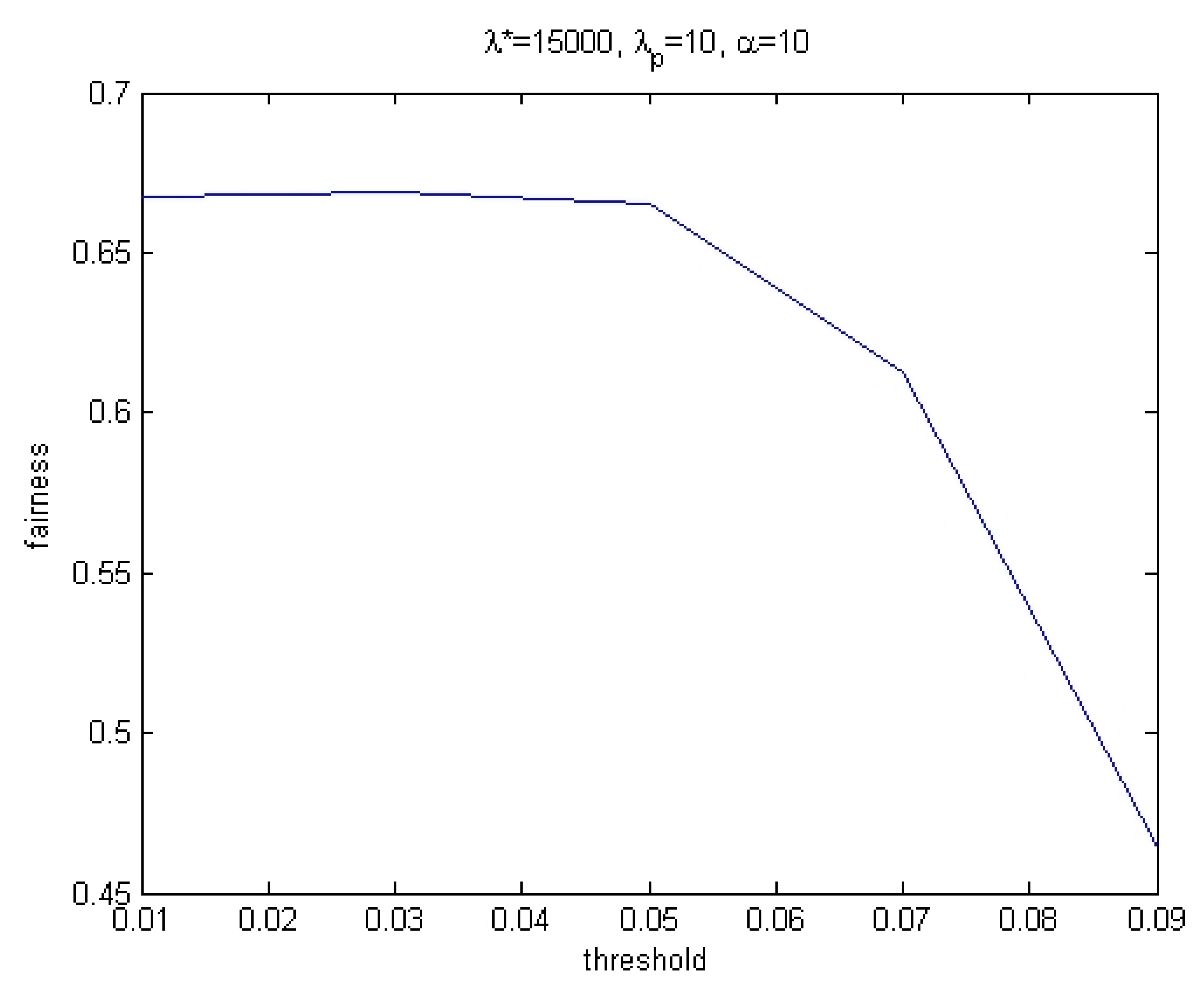
Remark 1.

Results for different values of α are similar for models in Section 2.1 and Section 2.2. These models should not be sensitive to changes in the number of seats, in ${\lambda }_p$ and ${\lambda }^{\ast }$, since results depend on the fraction of seats/popular votes of each party out of a total number of seats/popular votes.

Note that as $\alpha$ increases to infinity, the probability that most $D_i$s are close to zero increases (recall, $\alpha$ is the parameter of the Beta distribution which is used to draw D). Namely, higher $\alpha$ means less polarized political system. By that, we mean a system where most parties are close to the ideological center (in our model, $D_i$ is close to zero). However, increasing $\alpha$ does not change our results. As an illustration, see Figure 3 for 100 seats, 100,000 trials, $\alpha =10$.

The fact that political polarization does not affect results seems surprising at first glance. If many $D_i$ values are close to 0, it should be possible for the lobbyist to bribe some parties with high probability. However, the lobbyist himself is drawn from the same distribution and his willingness to pay is also lower.

3. Final Remarks

The number of parties that enter into the legislature is conditioned by the electoral threshold. With a higher threshold, fewer parties succeed in obtaining seats in the legislature. As we show, the ease of manipulating the legislature decision increases with the number of parties. One may derive that an extremely high threshold, such that only two parties will pass over it, is optimal. However, in many democracies this is not the case. In parliaments elected according to the proportional representation system, the electoral threshold is, with few exceptions, between $1\%$ to $5\%$, and the number of parties is normally between 3 and 10. Obviously, the main reason that many democracies do not impose a severe constraint on the number of parties is their desire to avoid an extreme misrepresentation of voters. In this sense, a lower threshold improves the representativeness of the legislature. On the other hand, as we argue in this paper, a lower threshold makes it easier to manipulate the legislature decision. We find that for thresholds that exist in most parliamentary democracies with a proportional representation system (1–5%), the ‘fairness’ in our sense is close to optimal. As for thresholds higher than 5%, the ‘fairness’ decreases with the threshold.

Our model does not predict how the number of seats held by a party affects the lobbyist’s willingness to bribe that party. It is not clear whether the lobbyist prefers bribing a party that holds a high number of seats rather than bribing multiple parties, each holding a lower number of seats.

In some real-world examples, a supermajority is required to accept bills. For example, in Italy two-thirds of votes are required for approval of constitutional reform. Our analysis becomes more complicated in the case of a supermajority. The stance of the lobbyist does not change the result in Section 2.1. This symmetry may not hold if a supermajority is required. For example, if 66% of votes are needed for the “yes” decision, and the lobbyist supports “yes”, the task of bribing parties is more difficult than if he supports “no”, since only 34% of votes are required for a “no” decision.