Abstract
Classical evolutionary game theory allows one to analyze the population dynamics of interacting individuals playing different strategies (broadly defined) in a population. To expand the scope of this framework to allow us to examine the evolution of these individuals’ strategies over time, we present the idea of a fitness-generating (G) function. Under this model, we can simultaneously consider population (ecological) and strategy (evolutionary) dynamics. In this paper, we briefly outline the differences between game theory and classical evolutionary game theory. We then introduce the G function framework, deriving the model from fundamental biological principles. We introduce the concept of a G-function species, explain the process of modeling with G functions, and define the conditions for evolutionary stable strategies (ESS). We conclude by presenting expository examples of G function model construction and simulations in the context of predator–prey dynamics and the evolution of drug resistance in cancer.
MSC:
91A16; 91A22; 91A80; 92B05; 92D25; 92D15; 92D40
1. Introduction
Evolutionary game theory, a mathematical framework conceived by John Maynard Smith and George Robert Price in their seminal paper on the logic of animal conflict [1], is an extension of game theory to evolving populations in biology that helps us understand the effects of selective pressures on the population dynamics of interacting agents in a population. These individuals may have different strategies (phenotypes) that affect their interactions with one another. The strategies could be anything from behavioral traits such as aggression to body size or cell transporter expression. Classical evolutionary game theory (EGT) allows us to mathematically examine the population dynamics of these strategies over time; however, it is difficult to incorporate the evolution of strategies into these dynamics. EGT traditionally assumes phenotypes to be fixed, a justifiable assumption for many problems such as the classical hawk-dove game in which the evolution of strategies which impact agent interaction is relatively constrained. However, there are other problems such as the evolution of foraging behavior in response to deforestation or predator–prey coevolution in which the evolution of strategies is a critical part of the underlying species’ ecological dynamics.
Although several methods have been developed to address this problem such as the individual fitness function approach [2] and the canonical equation of adaptive dynamics [3,4,5], for simplicity, we will only consider the G function approach here. This approach effectively serves as a unified framework for EGT and natural selection. Here, we review the basic tenets of classical evolutionary game theory and provide an overview of the G function approach, building up from the “G function species concept” to constructing the basic theory to simulating real-world examples. Both biologists and game theorists stand to gain from this paper. Biologists will learn simple, concrete ways to model evolution by natural selection in their field of interest, from the cellular to the ecosystem level. Game theorists will learn about the technicalities of the G function approach and its potential to expand the scope of evolutionary game theory. Both audiences will be able to appreciate the ever-expanding scope of EGT, starting with pairwise within-species games all the way to between-species interactions, speciation, niche coevolution, and even micro- and macro-evolution. Interested readers can refer to [6] for a more detailed treatment of G functions with several applicable biological examples, more rigorous development of solution concepts [7], and more thorough comparisons with other modern evolutionary game theoretic approaches such as adaptive dynamics [8] and the individual fitness function approach [2].
In this paper, we first compare classical game theory and EGT. We then introduce the G function framework and show how it can consider both population (ecological) and strategy (evolutionary) dynamics simultaneously. We construct the G function framework from the basic tenets of evolution by natural selection and introduce the idea of the G species concept. Next, we construct general equations for population and strategy dynamics and discuss basic solution concepts, leading to the ESS maximum principle. We then provide a recipe for constructing G functions and illustrate this process through constructing eco-evolutionary models of predator–prey dynamics and the evolution of drug resistance. By the end of this paper, readers should understand the key ideas in the development of evolutionary game theory and the potential for constructing and using G functions to simultaneously model ecological and evolutionary dynamics. Readers should also be able to construct and analyze their own G function models for biological problems of interest with an understanding of fundamental equilibrium and solution concepts.
2. Evolutionary Game Theory: Darwinian Dynamics and G Functions
Before discussing modeling and analysis of EGT, it is worth noting the key similarities and differences between EGT and classical game theory. Game theory has come a long way since its inception in the 1940s by John von Neumann and Oskar Morgenstern. It now encompasses a great variety of context including dynamic, differential, combinatorial, multistage, stochastic, and quantum games. Here, we focus on how EGT arose from classical game theory. Game theory was originally developed to provide a framework for determining players’ optimal strategies when an individual’s success depends on their choice of strategy and that of the other players [9]. This is most apparent in zero-sum games in which one player’s winnings necessarily become another player’s losses. However, albeit in a less extreme sense, this conflict is also present in non-zero sum games since what maximizes payoffs for one player does not necessarily do so for another. In classical game theory, players choose their strategies and it is assumed that players act rationally, in their own self-interest [10,11,12,13]. The central question classical game theorists aim to answer is: “Given a situation, what should a rational player do?” I.e., which strategy (or what frequencies of mixed strategies) will confer the player with the highest payoff, assuming that the competitors are rational players as well? In this formulation, both ecological and evolutionary dynamics are absent. To incorporate these dynamics, EGT built upon the framework of classical game theory by replacing the assumptions of rationality and self-interest with population dynamics and stability associated with Darwinian fitness. Strategies are endowed and persist teleonomically, in the trial-and-error fashion characteristic of natural selection. Namely, instead of players choosing their strategies, they “inherit” them from their parents. Players with higher fitnesses reproduce at higher rates, leaving behind progeny similar to them (like begets like). This iterative process leads to the quality of apparent purposefulness and goal-directed change that is ubiquitous in biology, from the neck of the giraffe to the eye of the human. The central question that evolutionary game theorists ask is: “Given a population with interacting phenotypes, how will their population dynamics change over time?” Usually, the population equilibria and corresponding stability are of utmost interest, though depending on the problem and the time scales involved, sometimes we are interested in the initial population dynamics. The key differences between classical game theory and EGT are summarized in Figure 1.
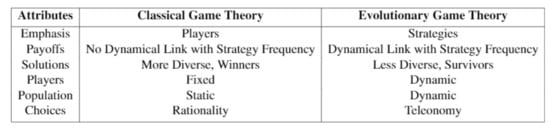
Figure 1.
Differences Between Classical Game Theory and Evolutionary Game Theory.
2.1. Introduction to G Functions
There are many problems in evolutionary biology in which ecological and evolutionary dynamics are tightly coupled. Consider, for example, the evolution of drug resistance in cancer cell lines [14], evolutionary responses to fish harvesting [15,16], changes in mating/foraging behaviors in response to resource availability and predation [17,18,19], or changes in life history traits as a result of climate change [20,21,22]. In these cases, the evolutionary trajectories of the species play a key role in the persistence of the population. To simultaneously model the population and strategy dynamics of populations, we use the G function approach. Under this simple differential equation-based framework, we are able to couple the population and strategy dynamics into what we call Darwinian dynamics.
We will begin by constructing the G function framework for the most basic case: Scalar valued traits with a single G function. Then, we will show how the same principles apply to more complicated scenarios such as multiple G functions (predator–prey example) and vector-value strategies (combination therapy in cancer example). To do this, we begin from fundamental principles, with the key tenets of natural selection. Darwin’s theory of evolution by natural selection requires three ingredients. First, there must be heritable variation: Like begets like but with “mistakes”. Second, there must be a struggle for existence [23,24]. Namely, populations have the capacity to grow exponentially under ideal conditions. Yet, limits to growth ensure that no population can grow exponentially forever [25]. Third, heritable variation influences the struggle: Some heritable phenotypes (strategies) beat other phenotypes in the struggle.
These principles form the basis for the G function framework. Heritable variation is represented by each individual (i) having a heritable strategy, , which is confined to be an element of the species’ strategy set, U. This strategy set captures the set of evolutionarily feasible strategies for the trait under consideration and may be either discrete or continuous. For example, U may describe a continuous range of body sizes in reptiles or, as in the hawk-dove case, may represent discrete behavioral strategies. In this paper, we will solely discuss continuous traits, but adaptations to our models can provide analogous results for discrete traits [6,26]. Apart from the G function literature, discrete traits have been thoroughly studied in EGT [27,28,29,30] and is an active area of investigation, in both theoretical [31] and applied settings [32,33]. The struggle for existence is given by the fitness generating function, in which the individual per capita growth rate depends on strategies and population densities of all members in the population, ( and , respectively). The idea of heritable variation impacting the struggle is captured through the dependence of individual per capita rate on the individual’s strategy, . The major components of the G function framework discussed thus far are summarized in Table 1.

Table 1.
Core Components of the G Function Framework.
Before building equations for the population and strategy dynamics, let us briefly discuss properties of the fitness generating function, G. The G function describes the per capita growth rate of individuals of an evolutionarily identical group, removing the need to define different functions for evolutionarily identical individuals that use different strategies. Evolutionarily identical individuals are individuals with the same strategy set and expected payoffs from playing the same strategies. More formally, we can define species under the G species concept as those which share the same strategy set and consequences of possessing a given strategy in an environment (i.e., the same G function). This definition is intentionally flexible since, depending on the problem of interest, the species definition may be more or less strict. For example, if one is interested in broad niche partitioning and habitat selection phenomena on the Galapagos islands, it might make sense to create three groups with three different G functions: Birds, mammals, and reptiles. However, if one is interested in foraging questions within birds on the island, it would be essential to distinguish finches, penguins, hawks, and boobies from one another. Individuals that have identical G functions but have different strategies are not classified as different species, but rather different morphs of the same species.
It is important to note that there are two factors that influence the G function: The bauplan and the environment in which the game is played out. The bauplan, originally used by Carl Linnaeus to place organisms on the tree of life, is a set of design rules that describe features common to all members of a defined group of species [34,35]. It can be thought of as a “blueprint” for a group of animals: Common, shared characters and constraints such as symmetry, segmentation, and limb disposition upon which each individual animal can build. To be more precise, the bauplan outlines the strategy set and the ways in which interactions with the environment affect the fitness of agents in the population [35,36,37]. The G function emerges when this bauplan is combined with the environment such that changes in the environment, while not affecting the bauplan, modifies the G function. Thus, one would need to use multiple G functions if one is dealing with species with different bauplans (even if in the same environment) or in different environments (even if with the same bauplan). Now, we are ready to lay down the population and strategy dynamics.
2.2. Population and Strategy Dynamics
The population and strategy dynamics form the core of the G function framework and are based on two simple differential equations. While we will construct our model on the assumption of continuous time, analogous methods can be applied to construct difference equation models based on discrete time. Such discrete models can be particularly valuable when working with experimental measurements which are taken annually, for example. Since G was described above as a fitness generating function, giving us the per capita growth rate, we can capture the population dynamics by multiplying it by the current population of the species:
Now, let us construct the equation for strategy dynamics to determine how the population’s trait value will evolve over time. Intuitively, this depends on the local gradient of the G function: How the fitness generating function changes due to perturbations in the trait value and the rate at which species are able to scale this fitness gradient, i.e., the rate of evolution, or evolvability. This can be formalized in the following equation:
In this equation, is a measure of heritability and additive genetic variance, in accordance with Fisher’s fundamental theorem of natural selection. It captures the rate of evolutionary change in the species’ trait value and can be influenced by many factors such as mutation rate, population size and structure, and the mechanisms of genetic inheritance. The term represents the local gradient of the fitness generating function.
Inspired by Wright’s fitness landscape [38], we can visualize strategy dynamics on an adaptive landscape as seen in Figure 2. To do this, given the other individuals’ strategies (u) and population densities (x), we can plot the per capita growth rate as a function of the focal individual’s strategy (v). Unlike Wright’s fitness landscape, the adaptive landscape changes over time, with changes in densities and strategies of organisms in the population continually molding its shape.
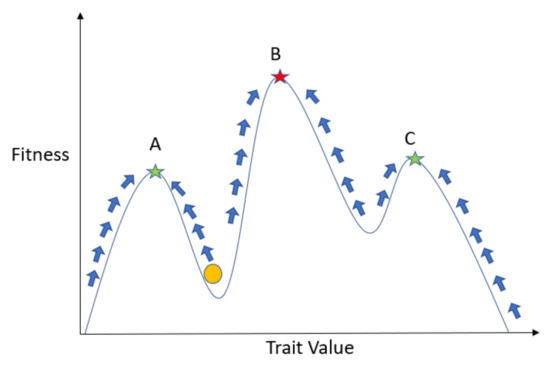
Figure 2.
Example snapshot of adaptive landscape. This figure depicts a temporal snapshot of a possible adaptive landscape. The x-axis represents the trait value under consideration and the y-axis represents the fitness of the individual. The adaptive landscape then depicts the fitness conferred to an individual adopting a given trait value at a given time. In reality, adaptive landscapes are highly dynamic, changing in response to species’ population sizes and strategy frequencies.
It is worth briefly noting the importance of including the strategy of the focal individual in the fitness generating function. Its absence, as is the case in other EGT formulations [39], leads to frequency independence among agents with the same strategy. When placed in a frequency-dependent setting, this framework leads to group selection, in which a group of agents try to maximize the fitness of the entire group [40,41,42]. It is only by including v that we are able to model individual selection, in which each agent is attempting to maximize its own growth rate.
In this adaptive landscape, assume the yellow circle represents the current location of the species’ trait. To maximize its fitness, the species will scale the landscape to reach a peak, as can be seen in the figure by the trajectories delineated by the blue arrows. For simplicity, a static image of an adaptive landscape is shown–in reality, the adaptive landscape is constantly changing. The change in strategy at each time step is then determined by two factors: The slope of the landscape itself () and the “step size” (). As alluded to before, evolution acts as a greedy algorithm, making locally optimal choices at each step. Therefore, species can often get trapped in local peaks (depicted in Figure 2 by the green stars) and never reach the global peak (depicted by the red star). For example, if the species started closer to the “A peak”, it would ascend that hill and reach a local peak at A. Intuitively, the only way for the species to get out of this local peak is for the adaptive landscape to change in a way such that “A” is no longer a peak or for the step size (evolvability) to be so large that the species can “step over” the valley in the landscape.
Together, population and strategy dynamics constitute Darwinian dynamics, which allow us to examine both the ecological and evolutionary trajectories of the population. It is worth noting that inherent in our model construction is the assumption of repeatable and reversible evolution within a G function, a highly contentious topic which has been treated extensively in the scientific literature [43,44,45,46,47,48]. Now that we have an understanding of Darwinian dynamics, we can outline basic solution concepts. In evolutionary game theory, the central equilibrium concept is the evolutionary stable strategy (ESS). The ESS is traditionally defined as an equilibrium which is uninvadable: When common in the population, agents adopting this strategy must have a higher fitness than any possible rare mutant in that particular environment [1]. Here, we build upon this definition by additionally enforcing the need for convergence stability [49], a concept inspired by Eshel’s idea of a continuously stable strategy [50,51,52]. This requirement means that natural selection favors strategies which are robust to perturbations in and , ensuring that the equilibrium is a likely result of natural selection [6,53]. In other words, like an evolutionary attractor, a strategy is convergent stable if strategies successively closer to it can invade a population using any nearby strategy [54].
This idea of convergence stability stimulated research into evolutionary invasion analysis, often called adaptive dynamics [55]. This modeling framework, closely related to the G function approach, aims to understand the long-term consequences of the introduction of small phenotypic mutations in the trait under consideration. That is, it aims to identify conditions under which mutants become extinct, coexist, or invade the population. To do this, invasion fitness functions, rather than G functions, are used to quantify the mutant’s growth rate upon introduction, in small numbers, into a resident population [56]. It is assumed that the fate of mutants can be gleaned from their initial growth rates upon introduction into the population in small numbers: Positive growth rates lead to persistence in the population and negative growth rates lead to extinction [57]. It takes a mutation-centric view of evolutionary speed (depends on mutation rates and variances in mutation effects), while the G function approach is agnostic of the mechanism by which this evolvability is generated. Furthermore, implicit in the adaptive dynamic interpretation of convergence stability is the assumption of time-scale separation between ecological and evolutionary processes, with the population dynamics effectively equilibrating instantaneously, implying a fixed, unchanging adaptive landscape. While the ecological time scale may often be much faster than the evolutionary time scale, this assumption need not always hold, such as in the rapid evolution of the beak size of Darwin’s finches [58]. Originally derived for mutation-limited evolution in large, monomorphic, asexual populations [3], the scope of adaptive dynamics has greatly increased in recent years [59] and, although it is still quite similar to the G function framework, it is primarily concerned with the transient dynamics that occur upon introduction of mutants into a population, focusing more on evolutionary branching than on ESS composition. As we will see in the predator–prey and combination therapy examples at the end of the paper, one major benefit of the G function framework is that it allows for the natural incorporation of several G functions with many different traits that impact fitness, whereas classical adaptive dynamics approaches are confined to a single trait within a single species.
It is important to recognize that convergence stability and resistance to invasion are independent conditions: One does not imply the other. Resistance to invasion without convergence stability, though unbeatable, may never be reached even if the population is using a nearby strategy [60,61]. Similarly, convergence stability without resistance to invasion can lead to convergent stable minima: Valleys on the adaptive landscape which can be invaded by species whose strategies lie on the peaks. Intuitively, though the strategy still scales up the adaptive landscape, the valley evolves toward the strategy, eventually trapping it in a minimum. This then gives rise to evolutionary branching and adaptive speciation [59]. There are other, more sophisticated strategy and solution concepts such as mutual invasibility, which refers to pairs of strategies close to the ESS which can invade one another when the other is rare, and the neighborhood invader strategy, a strategy which can invade any population with a nearby strategy. Though these concepts are highly relevant to understanding eco-evolutionary dynamics across all scales of biological organization, for simplicity, we omit further discussion of them here and instead refer the reader to [7,54,59,62] for more information.
First, let us formalize the condition of resistance to invasion in what is called the ESS maximum principle: A necessary but not sufficient condition for an ESS. Darwinian dynamics are composed of both strategy and population dynamics. Thus, at an eco-evolutionary equilibrium, we require both the population and the strategy of the species to be at equilibrium:
Furthermore, we must ensure that the equilibrium occurs at a peak, not a valley, on the adaptive landscape. We can do this by enforcing the following condition:
This way, we have ensured resistance to invasion in our equilibria. We call any solution found using this maximum principle an ESS candidate. Note that, implicit in this definition is the possibility of more than one ESS candidate. That is, it is possible for the ESS to contain more than one strategy if there is more than one peak in the adaptive landscape at the eco-evolutionary equilibrium. To ensure that an ESS candidate is indeed a true ESS, we must check that convergence stability holds. Intuitively, this requires Darwinian dynamics to return the system back to its equilibrium value in response to perturbations in the population density and strategy. While much formal mathematical analysis has gone into the concept of convergence stability, this discussion will be omitted here. One easy way to check for convergence stability is to see whether the ESS candidate can be reached by simulating Darwinian dynamics. Note that this does not technically prove the solution is an ESS since one must check all points in the neighborhood of , but it is a good indicator that the solution is convergent stable.
2.3. G Function Modeling Recipe
Now, let us turn to the problem of constructing G functions. To do this, we first focus on creating a model of the underlying ecological dynamics of the system. Depending on the problem, this can include life history considerations [63], resource availability [64], effects of competition [65], predation [66,67], etc. Then, we must decide how many groups of evolutionarily identical individuals are involved (and thus, how many G functions are needed). For example, a model of density-dependent population growth of moose on Isle Royale may need only a single G function. However, if we want to model trophic interactions, say between the wolves and moose on the island, we will need two G functions: One for the prey and one for the predators. Next, we must choose the key strategies associated with the species dynamics and their respective strategy sets (remember: This can be discrete and/or continuous). While we have mainly focused on single scalar strategies here, it is possible to consider several strategies simultaneously. Defining the strategy set may be a tricky matter, requiring careful consideration of the genetic and physical constraints on the trait of interest. Once the strategies and strategy sets have been defined, we can construct our G functions. To do this, we must consider how the focal individual’s strategy, v, and the strategies of other organisms in the population, u, affect the values of key parameters in the model. Once we are able to represent these parameters as functions of v, u, and x, we have our G function. This model can then be simulated using the Darwinian dynamics developed in the previous section to observe the ecological and evolutionary dynamics of the species.
3. Example: Predator–Prey (Multiple G Functions)
To provide an example of the construction and analysis of G function models, we turn to one of the most well studied phenomena in ecology: Predator–prey dynamics. We first nail down the ecological portion of our model. Assuming all prey and all predators are evolutionarily identical, we will have one G function for the predators and one G function for the prey. Though the eco-evolutionary dynamics between predator and prey are complex and multifaceted, for simplicity, we use a logistic Lotka-Volterra style model as our ecological base:
where x is the prey population, y is the predator population, are the intrinsic growth rates of the prey and predator respectively, a is the competitive impact of the prey, K is the prey’s carrying capacity, b is the probability for the predator to capture the prey in a given time frame, and c is the conversion efficiency from prey to predator (i.e., how many prey must a predator consume to reproduce).
Now, let us think about the evolutionary component of our model, namely, what are the key strategies that we will allow to evolve? Since we are interested in the interactions between predator and prey, we define our key strategies as “pursuit” () and “evasion” () terms for the predator and prey, respectively. Intentionally kept general, these terms could represent the evolution of behavioral tendencies, like the movement patterns of snakes in response to aerial predators, or a more physiological change, like the newt’s production of tetrodotoxin in response to snake predation. Since we are dealing with both prey and predator species, to avoid confusion, we let v represent the focal prey’s strategy and let w be the focal predator’s strategy. Now, we consider which parameters in the model will vary based on v, w, u, , x, and y. Here, we choose to allow the carrying capacity (K), the competition coefficient (a), and the predation term (b) to vary based on the strategies of the predator and prey. Namely, we assume that a strategy of maximizes a prey’s carrying capacity. Deviations from this, for example as a result of evolving to predatory pressures, decrease the carrying capacity in a Gaussian fashion:
Here, denotes the absolute carrying capacity and modulates the breadth of the Gaussian distribution; in other words, how sensitive the carrying capacity is to changes in v. For the intraspecific competition function we use:
This form assumes that like competes most with like for resources and space. Thus, two prey species will compete more if their trait values are similar rather than dissimilar. The competition function has the property that when a focal individual’s trait equals that of its competitor, , then the competition coefficient is unity: . The term represents the breadth of the competition function, providing a marker for how much species can avoid competition by having divergent trait values and thus occupying different niches. For the predation function, from the prey’s point of view, we have:
From the predator’s point of view, we have:
In these equations, divergence of the prey’s strategy from the predator’s strategy reduces the severity of predation. The term is provided to indicate the maximum probability of a predator capturing a prey in a given time interval. The term is the breadth of the predation function, telling us to what extent prey can avoid predation by having a different trait value than predators. We can now consolidate these equations into a fully constructed G function model for an arbitrary number of prey and predator species. Keep in mind again that the G function captures the per capita growth rate of the populations.
Now that we have our model, let us run some basic simulations to probe the eco-evolutionary dynamics of the predator and prey. To do so, we use the parameter values indicated in Table 2.

Table 2.
Parameter values used in predator–prey simulations.
First, as our control simulation, we start the prey at and and the predators at and and simulate the model for 1000 time steps in Figure 3.
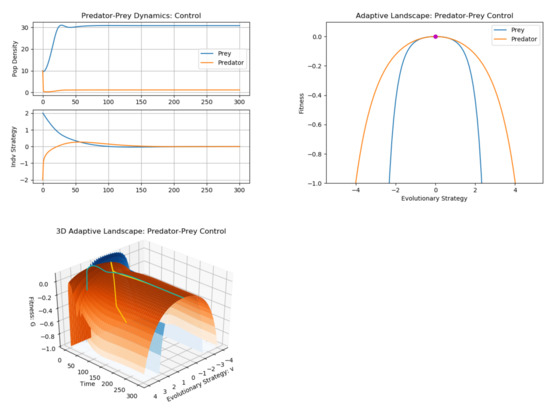
Figure 3.
Predator–prey control simulations. The first panel depicts the population and strategy dynamics of predator (orange/gold) and prey (blue/cyan). The second panel is a snapshot of the adaptive landscape at the eco-evolutionary equilibrium. The third panel is a 3D adaptive landscape, showing the changes in the adaptive landscape over time. Note that the adaptive landscape stays relatively constant over time and the ESS for both prey and predator occur when their focal strategies are 0.
As we can see in this figure, both strategy equilibria occurred at 0, the strategy which maximizes the prey’s carrying capacity, with the predator closely tracking the prey’s strategy. From the adaptive landscape, we see that there exists only one peak, at , which both the predator and prey occupy. Furthermore, the adaptive landscape seems relatively static over time, owing to the quick equilibration of population and strategy dynamics. Note that there are two selective pressures at work: Stabilizing selection towards induced by maximizing carrying capacity and divergent selection away from (at equilibrium) induced by predation. Since our ESS stays at , we can infer that the impact of predation is not great enough to push the prey’s strategy away from 0.
So what happens if we increase the effect of predation by increasing maximal capture probability, ? To do this, we re-run the simulation using the same initial conditions, but tripling the maximal capture probability. The results can be seen in Figure 4.
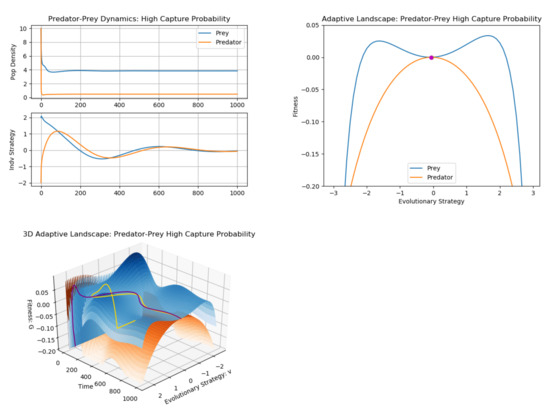
Figure 4.
Predator–prey high maximal capture probability simulations. The first panel shows the population and strategy dynamics of predator (orange/gold) and prey (blue/purple). The second panel shows the adaptive landscape at equilibrium and the third panel is the 3D adaptive landscape. This time, we see a highly dynamic adaptive landscape, paralleling the oscillatory behavior noticed in the strategy dynamics. Though the strategy equilibria for predator and prey still coincide, the equilibrium is an ESS for the predator but is a convergent stable minimum for the prey, indicating the possibility for invasibility and speciation of the prey.
Now, the effect of predation is great enough to cause damped oscillations in the strategy movement of the predator and prey. The prey, to avoid predation, oscillates around the equilibrium at 0 in a damped fashion, tracked by the predator. Remember that these oscillations reflect the underlying dynamically changing nature of the adaptive landscape, with the species attempting to scale continually changing peaks. We can clearly see the emergence and persistence of two peaks in the prey’s adaptive landscape. Furthermore, we see the prey stuck in a valley (local minimum) in the adaptive landscape–a convergent stable minimum. This equilibrium is thus not an ESS since it can be invaded by strategies on the two peaks surrounding it. Biologically, this points to the possibility of speciation to occur, with the prey choosing different strategies on either side of the valley. To further investigate this potential speciation event, we introduce a second prey species into our system. For illustrative purposes, we use the same parameter values for both prey species, but use slightly different initial strategy conditions. Specifically, we let , , , and . We simulate the model for 1000 time steps in Figure 5.
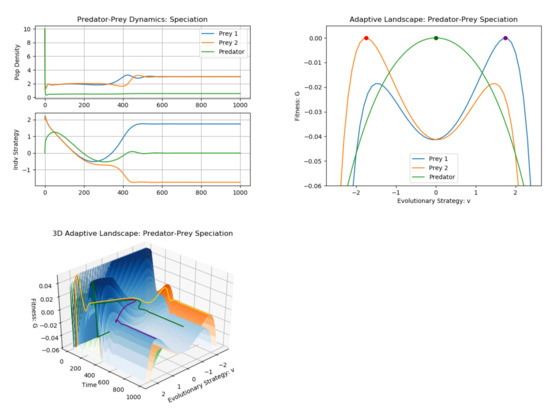
Figure 5.
Predator–prey speciation event simulations. The first panel shows the population and strategy dynamics of predator (green), prey 1 (blue/purple), and prey 2 (orange/gold). The second panel shows the adaptive landscape at equilibrium and the third panel is the 3D adaptive landscape (for visualization purposes, fitness values above 0.05 were truncated). Again, the adaptive landscape greatly changes over time, particularly in the first half of the simulation. Speciation clearly occurs, with the prey occupying strategy peaks on either side of the predator’s (generalist) strategy.
First, let us briefly consider the evolution of the adaptive landscape over time. During the first half of the simulation, the landscape is dynamically changing, with the species chasing moving peaks. The adaptive landscape stabilizes during the second half of the simulation and the predator and prey are able to reach eco-evolutionary equilibria. We can clearly see speciation occurring here, with the prey choosing peaks on opposite sides of the predator strategy. Through disruptive selection, the prey choose strategies on either side of the predator’s strategy, while the predator employs a generalist strategy, allowing itself to capture both species of prey. Furthermore, note the valley (local minimum) in both prey’s adaptive landscapes at the predator’s strategy. Such predator-induced speciation events can often be seen in nature. For example, in response to rat predation, the land snails Iberus g. gualtieranus of in Sierra Elvira have evolved two separate evasion strategies: Narrow shells and high shells. The former allow the snails to enter refuges inaccessible to predator, while the rats avoid the latter due to difficulties in handling large prey [68]. Similar results were seen in the body size of the Neotropical apple snail Pomaceaflagellata in response to avian predators [69]. Again, note that we have presented a highly simplified version of predator–prey dynamics here. The model can be expanded in many ways including, for example, the addition of even more predator and prey species, incorporation of sexual selection, and double binds [67].
4. Example: Combination Therapy in Cancer (Vector-Valued Strategies)
Let’s walk through one more example. This time, we will consider the effects of combination therapy on cancer cells. As before, we start by outlining the ecological dynamics. While cancer is an incredibly complex disease involving intricate interactions among heterogeneous cancer cells, normal cells, and immune cells, we choose to just focus on cancer cell dynamics here. Furthermore, we assume all cancer cells are evolutionarily identical. This means we will just have a single G function in our model. Suppose cancer cells grow in a logistic fashion and are killed in a density-independent manner (i.e., constant per capita death rate) by two different drugs. Then, we can construct our ecological base as follows:
where x is the population of cancer cells, r is the intrinsic growth rate, K is the carrying capacity, and and are the killing rates of the cancer cells by drugs 1 and 2 respectively.
Next, let us consider the evolutionary dynamics. We can imagine that the cancer cells will evolve strategies to develop resistance to both drugs we will administer. Thus, we have what’s called a vector-valued strategy: where and describe the resistance strategies of the cancer cells to drugs 1 and 2 respectively. Correspondingly, we let represent the focal cell’s strategy, with and describing the focal cell’s resistance strategies to drugs 1 and 2. Initially, these strategies will start at 0, but will evolve upwards as drug resistance is gained. Now, we must think about which parameters in our ecological model will vary based on v, u, and x. Naturally, since our strategies capture drug resistance, we allow and to vary as a function of v. Namely, assuming a Michaelis-Menten form, we let:
where m is a measure of dosage and efficacy of the drug, captures initial drug resistance, and b quantifies how much evolving a resistant strategy can help avoid effects of the drug. We now write down our fully constructed G function model:
However, before we dive into some simulations, one question remains: How do our resistance strategies, and , impact each other? In other words, how does gaining resistance to one drug impact the cell’s response to the other drug? Whenever we deal with vector-valued strategies, this is something we must think about carefully. Here, we will consider three cases: (1) Cross-resistance: Becoming resistant to the one drug confers some resistance against the other (2) independence: Gaining resistance to one drug does not change the efficacy of the other drug (3) double bind: The evolution of resistance to one drug makes the cancer cell population more susceptible to the effects of the other drug.
We can mathematically formalize this using a covariance matrix. This matrix neatly organizes the additive genetic variance for each strategy and the covariance between the two strategies, quantifying how changes in one strategy impact the other. The covariance matrix for our case is shown below:
where represents variance and represents covariance. Using this, we can capture the evolution of each strategy as follows:
In other words, we have:
As we can see, the evolution of resistance to one drug depends not only on its own variance and fitness gradient, but also its covariance with the other drug resistance strategy and its fitness gradient. Under this framework, if the two drugs are independent, the covariance terms will vanish. This uncouples the evolution of the two strategies and we are left with our standard evolutionary dynamics. On the other hand, if there is cross-resistance, will be positive: Resistance to one drug automatically confers some resistance to the other. Analogously, double binds are characterized by negative values for : Resistance to one drug reduces the cancer cell’s resistance to the other. Note that inherent in this formulation are the following three assumptions: (1) Resistance strategies are non-independent, (2) the cell’s resistance strategy sets have no upper bound, and (3) there is no cost to resistance. Let us briefly discuss ways in which we might relax each of these assumptions.
Consider the first assumption: Non-independence of strategies. In some cases, though cross-resistance and double-binds between drugs may be observed, the resistance mechanisms cells use for each drug act independently of each other. Then, rather than using the covariance matrix to couple the traits together, we can make the efficacy term, , dependent on where . In other words, the drug’s efficacy depends on the cell’s resistance strategy to the other trait. Depending on whether the drugs are cross-resistant or are used in a double bind, this will be a decreasing or increasing function of , respectively.
Now, let us turn to the second assumption on the lack of strategy bounds. Often, there are biological limits to the resistance strategies cancer cells use: For example, cells can only produce so many drug antiporters to prevent entry of a drug into the cell. To take this into account, we can constrain the cell’s evolutionary set by enforcing the requirement that where represents the limit of the resistance strategy. When this occurs, the cells may find themselves on a slope of their adaptive landscape, but are prevented from evolving further due to this constraint.
Finally, consider the assumption of the absence of a cost of resistance. In many contexts, there is a cost of resistance [70,71]: For example, modification of a metabolic pathway in a cell to avoid effects of a targeted therapy may be less energetically efficient. In order to incorporate the cost of resistance, we can modify the carrying capacity, K, to be a function of , as done in our predator–prey model. This leads to a trade-off between maximizing carrying capacity and maximizing drug resistance, preventing the resistance strategies from growing without bound.
Now, let us investigate the effects of independent, cross-resistant, and double bind therapies. The parameters we use in our simulations can be found in Table 3. In each case, we allow the cancer cells to grow for the first 200 time steps, administer the first drug for the next 400 time steps, and give the second drug for the last 400 time steps. For simplicity, these drugs were endowed with the same properties (i.e., , , and ). The results can be seen in Figure 6.

Table 3.
Parameter values used in combination therapy simulations.
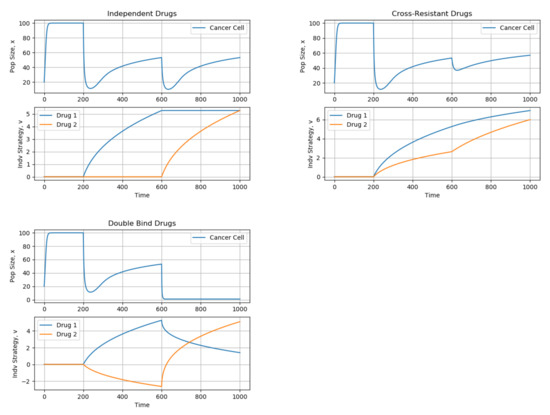
Figure 6.
Effects of Independent, Cross-Resistant, and Double Bind Drugs on Cancer Cell Dynamics.
As expected, during the first 200 time steps when no drug is being administered, both strategies and remain at 0. When the drugs act independently, for the next 400 time steps, only strategy evolves, while remains at 0. Similarly, from time 600 to 1000, only evolves while the resistance to the first drug remains constant. As a result, the impacts of the first and second drug on the cancer cell population are the same. Now, consider what happens in the cross-resistant case. As the cells gain resistance to the first drug, they inherently become resistant (though to a lower extent) to the second drug. Thus, when the second drug is administered, there is not as much of an impact on the population dynamics. Finally, let us look at the double-bind scenario. Here, the resistance strategies of the cancer cells to the two drugs move in opposite directions: From time 200 to 600, though the cells gain resistance to drug 1, they become sensitized to drug 2. Thus, when the second drug is administered at time 600, it is more effective than the first treatment and even drives the cancer cell population to extinction.
These qualitative results are in accordance with what is observed clinically. For example, cross-resistance between androgen receptor signaling inhibitors and taxane chemotherapy has been shown to severely hamper the efficacy of advanced prostate cancer treatment [72]. On the other hand, in a clinical trial for advanced small cell lung cancer, a double bind between a p53 vaccine and chemotherapy led to significantly improved patient outcomes [32,73]. The model presented here is a simplistic one and could be expanded to include competition among different cancer clades and the addition of other cell types such as pro- and anti-tumor immune cells and normal cells. However, our modeling shows that an understanding of how the evolution of resistance to one drug impacts a cancer cell’s susceptibility to another is critical to design evolutionarily-enlightened cancer combination therapies.
5. Discussion
In this expository paper, we briefly compared classical game theory and evolutionary game theory. We then introduced the idea of G functions and showed their potential to simultaneously consider ecological and evolutionary dynamics. We reviewed the two key aspects comprising the Darwinian dynamics of the G function approach: Population and strategy dynamics, deriving them from the fundamental principles of evolution by natural selection. We discussed the idea of the “G species concept”, covered the two aspects of the fitness generating function (the bauplan and environment), and provided a general recipe for constructing G functions. We illustrated this process by building models of predator–prey dynamics and the evolution of drug resistance. Throughout the paper, we focus on the G function framework for continuous traits, but these models can be adapted to encompass discrete traits in bilinear and nonlinear matrix games as well. This requires a frequency formulation of the G function and different definitions for the ESS and ESS maximum principle. For a detailed exposition of G functions for discrete traits, interested readers can refer to work done by Vincent and Cressman [26].
By now, we hope that the readers have understood the basics of the differential equation-based G function framework and can appreciate the ability for it to simultaneously capture both ecological and evolutionary dynamics. We urge the reader to view the G function framework as an elegant, methodical way of organizing our thoughts into simple differential equation models to capture natural selection in evolving populations, rather than as a completely novel modeling approach. As such, much of the mathematical machinery of dynamical system theory is directly translatable to analysis of models of these types. Though the G function approach has traditionally been used to investigate biological questions, it is broadly applicable to any system capable of evolving. Consider the problem of choosing adaptive learning rates in machine learning algorithms [74,75,76], for instance in competitive gradient descent [77]. In this case, a learning rate must be chosen that controls the speed at which agents descend an error manifold, until they reach a minima (similar to scaling an adaptive landscape to reach fitness peaks). Optimal learning schedules for such problems may be devised that are informed by the role of evolvability on the evolutionary dynamics of species in the G function framework. In market analysis, invasion potential of a new firm into an existing market and coexistence analysis of competing firms has been modeled using generalizations of the Lotka-Volterra competition models discussed here. The authors do this in the context of adaptive dynamics [78]. Finally, a topic of interest in psychology and sociology considers how individual behavior influences group dynamics, a problem that is well suited to the G-function framework that explicitly models feedback among the individuals and other agents in the population.
It is worth noting that the G function framework is best suited for scenarios with large population sizes, low mutation rates, and small mutation steps. Many biological problems of interest satisfy these three conditions and using a mean-field, deterministic approach such as G functions allows for simple, interpretable models that often have analytical solutions. However, when these conditions are not met, other approaches must be considered [79]. For example, when working with small populations, stochasticity becomes critical. Agent-based models, in which each agent has a strategy that determines its decisions and interactions with other agents, work well for these problems [80]. This approach works particularly well when communication among agents and spatial components of the game are critical. Another stochastic approach that can be used is the minimal process method [3,81], in which the population is represented by a point cloud in trait space with each point capturing an individual’s trait value. Over time, this cloud drifts stochastically as a result of mutation and selection [82]. When populations are large, however, tracking the evolution of each individual’s strategy over time is not feasible. If mutations occur at a low rate, evolutionary change occurs as a sequence of trait substitutions: Mutants with a positive invasion fitness invade the resident population, replacing the resident trait with their own [83]. Over time, these trait substitutions produce a directed random walk [3,81]. If in addition these mutations steps are small in size, the G function framework introduced here and the canonical equation of adaptive dynamics [3,81] serve as good mean-field approximations to track the evolution of the mean trait in the population over time. However, if mutation rates are high, reaction-diffusion and integro-differential equation models are instead used, depending on whether mutations are local or global respectively [84].
This being said, the G function framework is highly malleable and can incorporate complex life history patterns and population structures, unlimited numbers of species and strategies, environmental engineering by agents in the population, resource availability, and much more. It is clear that evolution manifests itself in the most magnificent forms in the game of life, steering the dynamics of species since the beginning of time, leading to “endless forms most beautiful”. It is essential to our understanding of every biological system, acting upon the smallest microorganisms to the largest ecosystems, on the timescale of seconds to billions of years. As such, providing a clear, concise, and unifying framework for its modeling is essential for developing any possible unified theory of biology.
Author Contributions
A.B. and J.S.B. conceptualized the article; A.B. wrote initial draft and performed all simulations; A.B. and J.S.B. edited and finalized the article. All authors have read and agreed to the published version of the manuscript.
Funding
A.B. is supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1746051. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation. J.S.B. is supported by NIH/NCI “Cancer as a complex adaptive system” U54CA193489, NIH/NCI U54 Supplement “The tumor-host evolutionary arms race”, and NIH/NCI “Eco-evolutionary drivers of clonal dynamics during UV-induced skin carcinogenesis” R01CA258089.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data was used in this study. Codes used to produce all plots in this paper can be found at the following publicly accessible GitHub page: https://github.com/abukkuri/GFuncReviewPaper, accessed on 10 September 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Cohen, Y.; Vincent, T.L.; Brown, J.S. A G-function approach to fitness minima, fitness maxima, evolutionarily stable strategies and adaptive landscapes. Evol. Ecol. Res. 1999, 1, 923–942. [Google Scholar]
- Dieckmann, U.; Law, R. The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 1996, 34, 579–612. [Google Scholar] [CrossRef]
- Metz, J.A.J.; de Kovel, C.G. The canonical equation of adaptive dynamics for Mendelian diploids and haplo-diploids. Interface Focus 2013, 3, 20130025. [Google Scholar] [CrossRef] [Green Version]
- Metz, J.A.J.; Staňková, K.; Johansson, J. The canonical equation of adaptive dynamics for life histories: From fitness-returns to selection gradients and Pontryagin’s maximum principle. J. Math. Biol. 2016, 72, 1125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vincent, T.L.; Brown, J.S. Evolutionary Game Theory, Natural Selection, and Darwinian Dynamics; Cambridge University Press: Cambridge, UK, 2005; pp. 1–382. [Google Scholar] [CrossRef]
- Apaloo, J.; Brown, J.S.; Vincent, T.L. Evolutionary game theory: ESS, convergence stability, and NIS. Evol. Ecol. Res. 2009, 11, 489–515. [Google Scholar]
- Mcgill, B.J.; Brown, J.S. Evolutionary Game Theory and Adaptive Dynamics of Continuous Traits. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 403–435. [Google Scholar] [CrossRef] [Green Version]
- Von Neumann, J. Zur Theorie der Gesellschaftsspiele. Math. Ann. 1928, 100, 295–320. [Google Scholar] [CrossRef]
- Basu, K. On the non-existence of a rationality definition for extensive games. Int. J. Game Theory 1990, 19, 33–44. [Google Scholar] [CrossRef]
- Basu, K. The traveler’s dilemma: Paradoxes of rationality in game theory. Am. Econ. Rev. 1994, 84, 391–395. [Google Scholar] [CrossRef]
- Colman, A.M. Cooperation, psychological game theory, and limitations of rationality in social interaction. Behav. Brain Sci. 2003, 26, 139–153. [Google Scholar] [CrossRef] [Green Version]
- Korobkin, R.B.; Ulen, T.S. Law and Behavioral Science: Removing the Rationality Assumption from Law and Economics. Calif. Law Rev. 2000, 88, 1051. [Google Scholar] [CrossRef]
- Bukkuri, A. Optimal Control Analysis of Combined Chemotherapy-Immunotherapy Treatment Regimens in a PKPD Cancer Evolution Model. Biomath 2020, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Blythe, S.P.; Stokes, T.K. Some Consequences of Size-Selective Harvesting on Fitness and on Yield. Math. Med. Biol. 1990, 7, 41–53. [Google Scholar] [CrossRef]
- Law, R.; Grey, D.R. Evolution of yields from populations with age-specific cropping. Evol. Ecol. 1989, 3, 343–359. [Google Scholar] [CrossRef]
- Bierbach, D.; Schulte, M.; Herrmann, N.; Tobler, M.; Stadler, S.; Jung, C.T.; Kunkel, B.; Riesch, R.; Klaus, S.; Ziege, M.; et al. Predator-induced changes of female mating preferences: Innate and experiential effects. BMC Evol. Biol. 2011, 11, 190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dill, L.M. Male mating strategies under predation risk: Do females call the shots? Behav. Ecol. 1999, 10, 452–461. [Google Scholar] [CrossRef]
- Franklin, A.M.; Squires, Z.E.; Stuart-Fox, D. Does predation risk affect mating behavior? An experimental test in dumpling squid (Euprymna tasmanica). PLoS ONE 2014, 9, e115027. [Google Scholar] [CrossRef]
- Ghazy, N.A.; Gotoh, T.; Suzuki, T. Impact of global warming scenarios on life-history traits of Tetranychus evansi (Acari: Tetranychidae). BMC Ecol. 2019, 19, 48. [Google Scholar] [CrossRef] [Green Version]
- Lancaster, L.T.; Morrison, G.; Fitt, R.N. Life history trade-offs, the intensity of competition, and coexistence in novel and evolving communities under climate change. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160046. [Google Scholar] [CrossRef] [Green Version]
- Williams, J.L.; Jacquemyn, H.; Ochocki, B.M.; Brys, R.; Miller, T.E.X. Life history evolution under climate change and its influence on the population dynamics of a long-lived plant. J. Ecol. 2015, 103, 798–808. [Google Scholar] [CrossRef]
- Gause, G. The Struggle for Existence. Ann. Entomol. Soc. Am. 1935, 28, 59. [Google Scholar] [CrossRef]
- Mallet, J. The struggle for existence: How the notion of carrying capacity, K, obscures the links between demography, Darwinian evolution, and speciation. Evol. Ecol. Res. 2012, 14, 627–665. [Google Scholar]
- Turchin, P. Does population ecology have general laws? Oikos 2001, 94, 17–26. [Google Scholar] [CrossRef] [Green Version]
- Vincent, T.L.; Cressman, R. An ESS Maximum Principle for Matrix Games. Theor. Popul. Biol. 2000, 58, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Broom, M.; Rychtar, J. Game-Theoretical Models in Biology; CRC Press: Boca Raton, FL, USA, 2013; pp. 1–520. [Google Scholar]
- Nowak, M. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006; pp. 1–384. [Google Scholar]
- Sandholm, W. Population Games and Evolutionary Dynamics; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Weibull, J. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1987; pp. 1–265. [Google Scholar]
- Day, T.; Taylor, P.D. Evolutionary dynamics and stability in discrete and continuous games. Evol. Ecol. Res. 2003, 5, 605–613. [Google Scholar]
- Basanta, D.; Gatenby, R.A.; Anderson, A.R. Exploiting evolution to treat drug resistance: Combination therapy and the double bind. Mol. Pharm. 2012, 9, 914–921. [Google Scholar] [CrossRef] [PubMed]
- Wölfl, B.; te Rietmole, H.; Salvioli, M.; Kaznatcheev, A.; Thuijsman, F.; Brown, J.S.; Burgering, B.; Staňková, K. The Contribution of Evolutionary Game Theory to Understanding and Treating Cancer. Dyn. Games Appl. 2021, 1–30. [Google Scholar] [CrossRef]
- Rieppel, O. ’Type’ in morphology and phylogeny. J. Morphol. 2006, 267, 528–535. [Google Scholar] [CrossRef] [PubMed]
- Willmore, K.E. The Body Plan Concept and Its Centrality in Evo-Devo. Evol. Educ. Outreach 2012, 5, 219–230. [Google Scholar] [CrossRef] [Green Version]
- Brown, J.S. Why Darwin would have loved evolutionary game theory. Proc. R. Soc. B Biol. Sci. 2016, 283, 20160847. [Google Scholar] [CrossRef] [Green Version]
- Shubin, N.H. The Implications of “The Bauplan” for Development and Evolution of the Tetrapod Limb. In Developmental Patterning of the Vertebrate Limb; Springer: Boston, MA, USA, 1991; pp. 411–421. [Google Scholar] [CrossRef]
- Wright, S. The Roles of Mutation, Inbreeding, Crossbreeding and Selection in Evolution. In Proceedings of the 6th International Congress of Genetics, Ithaca, NY, USA, 6 December 1932; pp. 356–366. [Google Scholar]
- Roughgarden, J. Resource partitioning among competing species-A coevolutionary approach. Theor. Popul. Biol. 1976, 9, 388–424. [Google Scholar] [CrossRef]
- Abrams, P.A. Alternative Models of Character Displacement and Niche Shift. I. Adaptive Shifts in Resource Use when there is Competition for Nutritionally Nonsubstitutable Resources. Evolution 1987, 41, 651–661. [Google Scholar] [CrossRef]
- Brown, J.; Vincent, T. Coevolution as an Evolutionary Game. Evolution 1987, 41, 66–79. [Google Scholar] [CrossRef] [Green Version]
- Taper, M.L.; Case, T.J. Models of Character Displacement and the Theoretical Robustness of Taxon Cycles. Evolution 1992, 46, 317–333. [Google Scholar] [CrossRef] [Green Version]
- Beatty, J.; Carrera, I. When what had to happen was not bound to happen: History, chance, narrative, evolution. J. Philos. Hist. 2011, 5, 471–495. [Google Scholar] [CrossRef]
- Blount, Z.D.; Lenski, R.E.; Losos, J.B. Contingency and determinism in evolution: Replaying life’s tape. Science 2018, 362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Losos, J.B. Adaptive radiation, ecological opportunity, and evolutionary determinism: American society of naturalists E. O. Wilson award address. Am. Nat. 2010, 175, 623–639. [Google Scholar] [CrossRef]
- Mahler, D.L.; Ingram, T.; Revell, L.J.; Losos, J.B. Exceptional convergence on the macroevolutionary landscape in island lizard radiations. Science 2013, 341, 292–295. [Google Scholar] [CrossRef] [PubMed]
- Morris, S.C. Evolution: Like any other science it is predictable. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 133–145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powell, S.; Price, S.L.; Kronauer, D.J. Trait evolution is reversible, repeatable, and decoupled in the soldier caste of turtle ants. Proc. Natl. Acad. Sci. USA 2020, 117, 6608–6615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christiansen, F.B. On Conditions for Evolutionary Stability for a Continuously Varying Character. Am. Nat. 1991, 138, 37–50. [Google Scholar] [CrossRef]
- Eshel, I. Evolutionary and continuous stability. J. Theor. Biol. 1983, 103, 99–111. [Google Scholar] [CrossRef]
- Eshel, I. On the changing concept of evolutionary population stability as a reflection of a changing point of view in the quantitative theory of evolution. J. Math. Biol. 1996, 34, 485–510. [Google Scholar] [CrossRef]
- Eshel, I.; Motro, U. Kin selection and strong evolutionary stability of mutual help. Theor. Popul. Biol. 1981, 19, 420–433. [Google Scholar] [CrossRef]
- Vincent, T.L.; Brown, J.S. Stability in an evolutionary game. Theor. Popul. Biol. 1984, 26, 408–427. [Google Scholar] [CrossRef]
- Apaloo, J. Revisiting strategic models of evolution: The concept of neighborhood invader strategies. Theor. Popul. Biol. 1997, 52, 71–77. [Google Scholar] [CrossRef]
- Metz, J.; Geritz, S.; Meszena, G.; Jacobs, F.; Heerwaarden, J.V. Adaptive dynamics: A geometrical study of the consequences of nearly faithful reproduction. Stoch. Spat. Struct. Dyn. Syst. 1996, 45, 183–231. [Google Scholar]
- Brännström, A.; Johansson, J.; von Festenberg, N. The Hitchhiker’s guide to adaptive dynamics. Games 2013, 4, 304–328. [Google Scholar] [CrossRef] [Green Version]
- Diekmann, O. A Beginner’s Guide to Adaptive Dynamics. Math. Model. Popul. Dyn. 2004, 63, 47–86. [Google Scholar]
- Grant, P.R.; Grant, B.R. Unpredictable evolution in a 30-year study of Darwin’s finches. Science 2002, 296, 707–711. [Google Scholar] [CrossRef] [Green Version]
- Geritz, S.A.; Kisdi, E.; Meszéna, G.; Metz, J.A. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 1998, 12, 35–57. [Google Scholar] [CrossRef]
- Bomze, I.; Weibull, J. Does Neutral Stability Imply Lyapunov Stability? Games Econ. Behav. 1995, 11, 173–192. [Google Scholar] [CrossRef]
- Hamilton, W.D. Extraordinary sex ratios. Science 1967, 156, 477–488. [Google Scholar] [CrossRef] [PubMed]
- Geritz, S.A.; Metz, J.A.; Kisdi, E.; Meszéna, G. Dynamics of adaptation and evolutionary branching. Phys. Rev. Lett. 1997, 78, 2024–2027. [Google Scholar] [CrossRef] [Green Version]
- Cunningham, J.J.; Gatenby, R.A.; Brown, J.S. Evolutionary Dynamics in Cancer Therapy. Mol. Pharm. 2011, 8, 2094–2100. [Google Scholar] [CrossRef] [PubMed]
- Vincent, T.L.; Vincent, T.L. Using the ESS Maximum Principle to Explore Root-shoot Allocation, Competition and Coexistence. J. Theor. Biol. 1996, 180, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Bukkuri, A.; Gatenby, R.A.; Brown, J.S. GLUT1 Production in Cancer Cells: A Tragedy of the Commons. 2021; submitted. [Google Scholar]
- Brown, J.S.; Vincent, T.L. Organization of Predator–Prey Communities as an Evolutionary Game. Evolution 1992, 46, 1269–1283. [Google Scholar] [CrossRef] [PubMed]
- Bukkuri, A.; Brown, J. Coevolution, Red Queen Dynamics, Zahavi Handicap, and Double Binds: From Ecology to Cancer. 2021; in preparation. [Google Scholar]
- Moreno-Rueda, G. Disruptive selection by predation offsets stabilizing selection on shell morphology in the land snail Iberus g. gualtieranus. Evol. Ecol. 2009, 23, 463–471. [Google Scholar] [CrossRef]
- Reed, W.L.; Janzen, F.J. Natural selection by avian predators on size and colour of a freshwater snail (Pomacea flagellata). Biol. J. Linn. Soc. 1999, 67, 331–342. [Google Scholar] [CrossRef]
- Gatenby, R.; Brown, J. The evolution and ecology of resistance in cancer therapy. Cold Spring Harb. Perspect. Med. 2018, 8, a033415. [Google Scholar] [CrossRef]
- Strobl, M.A.; West, J.; Viossat, Y.; Damaghi, M.; Robertson-Tessi, M.; Brown, J.S.; Gatenby, R.A.; Maini, P.K.; Anderson, A.R. Turnover modulates the need for a cost of resistance in adaptive therapy. Cancer Res. 2021, 81, 1135–1147. [Google Scholar] [CrossRef]
- Buck, S.A.; Koolen, S.L.; Mathijssen, R.H.; de Wit, R.; van Soest, R.J. Cross-resistance and drug sequence in prostate cancer. Drug Resist. Updat. 2021, 56, 100761. [Google Scholar] [CrossRef] [PubMed]
- Antonia, S.J.; Mirza, N.; Fricke, I.; Chiappori, A.; Thompson, P.; Williams, N.; Bepler, G.; Simon, G.; Janssen, W.; Lee, J.H.; et al. Combination of p53 cancer vaccine with chemotherapy in patients with extensive stage small cell lung cancer. Clin. Cancer Res. 2006, 12, 878–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amine, K. Multiobjective Simulated Annealing: Principles and Algorithm Variants. Adv. Oper. Res. 2019, 2019, 8134674. [Google Scholar] [CrossRef]
- Guttenberg, N.; Virgo, N.; Penn, A. On the potential for open-endedness in neural networks. Artif. Life 2019, 25, 145–167. [Google Scholar] [CrossRef] [Green Version]
- Suman, B.; Kumar, P. A Survey of Simulated Annealing as a Tool for Single and Multiobjective Optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Schäfer, F.; Anandkumar, A. Competitive Gradient Descent. Adv. Neural Inf. Process. Syst. 2019, 32, 1–11. [Google Scholar]
- Toro-Zapata, H.D.; Olivar-Tost, G.; Dercole, F. Conditions on the Energy Market Diversification from Adaptive Dynamics. Math. Probl. Eng. 2018, 2018, 9181636. [Google Scholar] [CrossRef]
- Bukkuri, A.; Pienta, K.J.; Amend, S.R.; Hammarlund, E.U.; Brown, J.S. The Contribution of Evolvability to the Eco-Evolutionary Dynamics of Competing Species. 2021; submitted. [Google Scholar]
- Adami, C.; Schossau, J.; Hintze, A. Evolutionary game theory using agent-based methods. Phys. Life Rev. 2016, 19, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, U.; Marrow, P.; Law, R. Evolutionary cycling in predator–prey interactions: Population dynamics and the red queen. J. Theor. Biol. 1995, 176, 91–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dieckmann, U.; Ferrière, R. Adaptive Dynamics and Evolving Biodiversity. In Evolutionary Conservation Biology; Ferrière, R., Dieckmann, U., Couvet, D., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 188–224. [Google Scholar] [CrossRef] [Green Version]
- Metz, J.A.; Nisbet, R.M.; Geritz, S.A. How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 1992, 7, 198–202. [Google Scholar] [CrossRef]
- Cohen, Y.; Galiano, G. Evolutionary Distributions and Competition by Way of Reaction-Diffusion and by Way of Convolution. Bull. Math. Biol. 2013, 75, 2305–2323. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).