Abstract
In hedonic games, coalitions are created as a result of the strategic interaction of independent players. In particular, in additively separable hedonic games, every player has valuations for all other ones, and the utility for belonging to a coalition is given by the sum of the valuations for all other players belonging to it. So far, non-cooperative hedonic games have been considered in the literature only with respect to totally selfish players. Starting from the fundamental class of additively separable hedonic games, we define and study a new model in which, given a social graph, players also care about the happiness of their friends: we call this class of games social context additively separable hedonic games (SCASHGs). We focus on the fundamental stability notion of Nash equilibrium, and study the existence, convergence and performance of stable outcomes (with respect to the classical notions of price of anarchy and price of stability) in SCASHGs. In particular, we show that SCASHGs are potential games, and therefore Nash equilibria always exist and can be reached after a sequence of Nash moves of the players. Finally, we provide tight or asymptotically tight bounds on the price of anarchy and the price of stability of SCASHGs.
1. Introduction
In many economic, social and political situations, individuals carry out activities in groups rather than alone and on their own. In these scenarios, understanding the happiness of each member of the group becomes of crucial importance. As examples, the utility of an individual in a group sharing a resource depends both on the consumption level of the resource and on the identity of the members in the group; similarly, the utility for a party belonging to a political coalition depends both on the party trait and on the identity of its members. Moreover, another important issue is that of investigating the dynamics that regulates coalition formation.
Dréze and Greenberg [1] introduced hedonic games, in which players have preferences over the set of all possible player coalitions. In particular, the utility of a player only depends on the composition of the coalition (or group) she belongs to. Hedonic games constitute a framework for formally studying the stability and the evolution of the process of forming player coalitions. Given that they model natural behavioral dynamics of real-life situations, this class of games has received great interest in the literature: in economic, social and political environments, in fact, individuals perform activities in groups rather than by themselves. Consider, for instance, the following scenarios: a company has to assign its employees to different work teams so that they can profitably collaborate; in a social network, users want to form groups in which they can speak of and share common interests.
Additively separable hedonic games constitute a natural and succinctly representable class of hedonic games. In these games, each player has a value for any other player, and the utility of a coalition to a particular player is simply the sum of the values she assigns to the members of her coalition. Additive separability satisfies a number of desirable axiomatic properties [2] and are the non-transferable utility generalization of graph games studied by Deng and Papadimitriou [3]. While the standard model of additively separable hedonic games assumes that players are totally selfish, in this paper we are interested in analyzing the case in which players take into account also the happiness of their friends, therefore adding to the original model a sort of altruism. Coming back to the above described scenarios, it is likely that, among the corporate employees, several friendship relations exist, not necessarily between people able to profitably collaborate together. Moreover, social network users often include people coming from the same family; even if they are of different ages and therefore are expected to gladly belong to different groups, they are also interested in the happiness of their relatives. We call these games Social Context Additively Separable Hedonic Games (SCASHGs) and we believe that they are able to model in a more accurate way the phenomenon of coalition formation in many realistic scenarios. In fact, in SCASHGs the behavior of every player also depends on the happiness of her friends, as it is in the above described scenarios.
In SCASHGs, valuations are additive and each player i has a valuation for any other player j, but there is a crucial difference with respect to the classical additively separable hedonic games: while in the classical model the utility of a coalition to a particular player is simply given by the sum of the valuations she assigns to the members of her coalition, in SCASHGs there is another additive term that contributes to form the utility of a player, that is equal to the sum of the valuations her friends assign to the members of their own coalitions (this contribution is multiplied by a given parameter ). In particular, for , SCASHGs are equivalent to the classical additively separable hedonic games (i.e., a totally selfish setting is considered), while for a fully altruistic setting can be modeled.
In order to model the friendship relations, a SCASHG is also defined by a graph representing an underlying social network: nodes are players and an edge connecting two players expresses friendship between them. Arguably, as a first step in the study of SCASHGs, it is natural to consider symmetric friendship relations and therefore, in this paper, we focus on undirected graphs.
In Figure 1, for example, we can see that the utility of player 5 is equal to , where is the sum of valuations of the players in her coalition and is the sum of valuations her friends 1, 2 and 3 assign to the members of their own coalitions, multiplied by .

Figure 1.
A social network G, a coalition structure and the non-null valuations .
Our aim is to study the existence and performance of natural stable outcomes for SCASHGs. We will focus on Nash stable outcomes, i.e., outcomes in which no player can improve her utility by unilaterally changing her own coalition. In particular, we evaluate the performance of Nash outcomes for SCASHGs by means of the widely used notions of price of anarchy and price of stability: the former is defined as the ratio between the social optimum value and the social value of the worst stable outcome, while the latter is defined as the ratio between the social optimum value and the social value of the best stable outcome.
1.1. Our Results
First of all, we provide an exact potential function for SCASHGs, thus proving that these games always possess a pure Nash equilibrium and also that the convergence to Nash equilibria is guaranteed. In order to evaluate the performance of SCASHGs, we consider two social welfare functions. The first social function, , is given by the summation, for each player, of the values she assigns to the members of her coalition, while the second social function, denoted by , is the summation of the players’ utilities (taking into account, for any player, also the contribution due to the valuations of her friends multiplied by ). In fact, we evaluate, for both of them, the performance of the Nash outcomes by means of the notions of price of anarchy and price of stability ( and denote the price of anarchy with respect to and , respectively; analogously and denote the price of stability with respect to and , respectively).
In presence of negative valuations, both and (and therefore also and ) can be unbounded. Furthermore, in some cases we are able to provide instances in which the social value of any equilibrium is negative while the optimal solution lead to a positive outcome.
We subsequently turn our attention to the case of non-negative valuations and prove that the price of anarchy is , while the price of stability is 1.
1.2. Related Work
Hedonic games have been broadly studied in the literature. They have been first considered by Dréze and Greenberg [1], who analyze them under a cooperative perspective. Bogomolnaia and Jackson [4] and Banerjee et al. [5] then have defined hedonic games in their present form as a simple but very versatile model of coalition formation. Feldman et al. [6] investigate some interesting subclasses of hedonic games from a non-cooperative point of view, by characterizing Nash equilibria and providing upper and lower bounds on both the price of stability and the price of anarchy. Peters and Elkind [7] consider several classes of hedonic games and identify simple conditions on expressivity that are sufficient for the problem of checking whether a given game admits a stable outcome to be computationally hard.
Additively separable hedonic games have been first considered by Bogomolnaia and Jackson [4] who show that Nash stable outcomes are not guaranteed to exist for games with asymmetric valuations. However, for symmetric valuations, the existence of a Nash stable outcome is guaranteed by potential function argument [4]. Ballester [8] and Sung and Dimitrov [9] show that the problem of checking whether an instance admit a Nash stable outcome is NP-complete and NP-complete in the strong sense, respectively. Olsen [10] proves that the problem of deciding whether a non-trivial Nash stable coalition exists in additively separable hedonic games with non-negative and symmetric preferences is NP-complete. Aziz et al. [11] show that checking the existence of a core stable outcome is NP-hard even for symmetric valuations. Concerning the performance of Nash stable outcomes in additively separable hedonic games with symmetric valuations, it is easy to check that the price of anarchy is unbounded [12] and that the price of stability is 1 since an optimal outcome is always Nash stable (it can be easily proved by using the potential function).
Fractional hedonic games are close to additively separable ones. The difference is that the utility of each player is divided by the size of her coalition. They have been first considered by Aziz et al. [13] (see also [14]), who prove that the core can be empty for asymmetric valuations and that it is not empty for some special cases. Brandl et al. [15] also study the existence of core as well as individual stability in fractional hedonic games. Bilò et al. [16] consider Nash stable outcomes for fractional hedonic games and study their existence and complexity. Kaklamanis et al. [17] also consider Nash stable outcomes and provide some improved results on the price of stability. Carosi et al. [18] consider local core stability in fractional hedonic games with binary symmetric valuations and show that any local core dynamics converges, which implies that a local core stable coalition structure always exists. Finally, Aziz et al. [19] consider the computational complexity of computing welfare maximizing partitions (not necessarily Nash stable) for fractional hedonic games played on undirected graphs.
Modified fractional hedonic games are very similar to fractional hedonic ones. The difference is that the utility of each player is averaged over all the other members of that coalition (i.e., excluding herself). Olsen [20] is the first to consider these games and investigates computational issues about Nash stable outcomes. Monaco et al. [21,22] completely characterize the existence of fundamental stable outcomes and show tight results on their performance. Elkind et al. [23] study the set of Pareto optimal outcomes for modified fractional hedonic games with symmetric valuations.
From a different perspective, strategy proof mechanisms for additively separable hedonic and fractional hedonic games have been proposed in [24,25]. Moreover, Flammini et al. [26] consider the problem of maximizing the social welfare in additively separable and fractional hedonic games in the online setting. Hedonic games are being widely investigated also under different utility definitions: For instance, in [27,28], coalition formation games, in which player utilities are proportional to their harmonic centralities in the respective coalitions, are considered.
In our paper, we deal with selfish players having also a certain degree of altruism. To this respect, our work is related to social context games. These games have been introduced in [29] and are defined by an underlying game in strategic form, and a social context consisting of an undirected graph and an aggregation function. In [29], the authors consider resource selection games as the underlying game and they study the existence of pure strategy Nash equilibrium. Building on this model, Bilò et al. [30] investigate social context games in which the underlying games are linear congestion games and Shapley cost sharing games, while the aggregation functions are min, max and sum. Moreover, Anagnostopoulos et al. [31] study the effects of the altruistic behavior of players showing that the price of anarchy may increase as the players become more altruistic. They show that this increase is modest for congestion games and min-sum scheduling games, whereas it might be drastic for generalized second price auctions. The interests on altruistic players have been also modeled and studied by Hoefer and Skopalik [32]: they focus on the existence and complexity of pure Nash equilibria with altruistic players in atomic congestion games. Chen et al. [33] study the inefficiency of equilibria for several classes of games such as cost-sharing games, utility games and linear congestion games. Salehi-Abari and Boutilier [34] study social choice with empathetic preferences and their local empathetic model is related to the model presented in [35]. Finally, Brânzei and Larson [36] study social distance games. In these games a player’s opinion on her friends (players of distance one) has the highest weight while her opinion on players farther away counts less.
To the best of our knowledge, few papers deal with the notion of altruism in hedonic games. Nguyen et al. [35] define altruistic hedonic games where the satisfaction of players’ friends is taken into account according to three degrees of altruism, from being selfish first, over aggregating opinions of a player and her friends equally, to altruistically letting one’s friends decide first. They study both the axiomatic properties of these games and the computational complexity of problems related to common stability concepts. In [37], Umar and Mesbah model the problem of joint coalition formation and bandwidth allocation in ad hoc radio networks made of selfish/altruistic nodes as a hedonic coalition formation game with non-transferable utility. The authors study the computational complexity and convergence properties of the proposed hedonic algorithm under selfish and altruistic preferences, and present means to guarantee Nash stability.
Finally, it is also worth mentioning some related literature on network formation games, in which interestingly the considered games are shown to be potential games as in our paper: in [38], Badev deals with a setting in which the utility of the players is influenced by the friendship relations and vice-versa, while Kinateder and Merlino [39] study a network creation game in which benefits are shared among neighbors. Mele [40] proposes an empirical model of social network formation, combining strategic and random connections among players. Bourlès et al. [41] provide an interesting analysis of altruism in networks: agents are embedded in a fixed network and care about the well-being of their network neighbors, i.e., they may provide financial support to their poorer friends.
1.3. Paper Organization
The paper is organized as follows. In Section 2 we formally define social context additively separable hedonic games. The technical contributions of the paper are then presented in Section 3, Section 4 and Section 5 which address the existence of Nash outcomes, the results on the price of anarchy and those on the price of stability, respectively. Finally, in Section 6 we list some interesting open problems.
2. Model
For an integer , denote by the set .
We model Social Context Additively Separable Hedonic Games (SCASHGs) by means of a valuation function v, an undirected graph and a given parameter . We denote with the number of nodes of G and with E the set of edges between the nodes, which represent the friendship relation. is the symmetric valuation function. We do not require any dependence between v and H, thus allowing for two friends to have a mutual negative valuation (as it is in the scenario described in the Introduction, in which, among the corporate employees, several friendship relations may exist, not necessarily between people able to profitably collaborate together). Nevertheless, all obtained results also hold for the special notable case in which the valuations between friends have to be positive: all positive results clearly hold also in this specific setting, while all remaining ones (given in Proposition 1, Theorem 2, Theorem 5 and Theorem 6) exploit constructions in which negative valuations exist only between players not connected by an edge in graph G. For the sake of convenience, we adopt the notation and to denote the pair and its valuation , respectively.
Given a symmetric valuation function v, an undirected graph and a value for , the Social Context Additively Separable Hedonic Game induced by G, v and , denoted as , is the game in which each node is associated with a player. We assume that players are numbered from 1 to n and, for every , each player chooses to join a certain coalition among n candidate ones: the strategy of player i is an integer , meaning that player i is selecting candidate coalition .
A strategy profile directly induces an outcome , in which, for any , . In turn, an outcome naturally induces a coalition structure, i.e., a partition of the set of players into coalitions such that, for any , (i.e., empty candidate coalitions are excluded from the partition), and for any with . For the sake of brevity, we denote by also the coalition structure induced by . If , we say that player i is a member of the coalition . We denote by the coalition in of which player i is a member. In an outcome , the utility of player i is defined as
where, for every , .
Each player chooses the coalition she belongs to with the aim of maximizing her utility. We denote by , the new coalition structure obtained from by moving player i from to ; formally, . A player deviates if she changes the coalition she belongs to. Given an outcome , an improving move (or simply a move) for player i is a deviation to any coalition that strictly increases her utility, i.e., . Moreover, player i performs a best-response in coalition structure by choosing a coalition providing her the highest possible utility (notice that a best-response is also a move when there exists a coalition such that . A player is stable if she cannot perform a move. An outcome is (pure) Nash stable (or a Nash equilibrium) if every player is stable. An improving dynamics, or simply a dynamics, is a sequence of improving moves, while a best-response dynamics is a sequence of best-responses. A game has the finite improvement path property if it does not admit an improvement dynamics of infinite length. Clearly, a game possessing the finite improvement path property always admits a Nash stable outcome. We denote with the set of Nash stable outcomes of .
The social welfare of a coalition structure is the summation of the players’ utilities, i.e., .
We define also a second social welfare function which is given by the summation, for each player, of the valuations she assigns to the members of her coalition (without considering her friends’ utilities).
Given a game , an optimum coalition structure (respectively ) is one that maximizes the social welfare (respectively of . The price of anarchy of a social context additively separable hedonic game is defined as the worst-case ratio between the social welfare of a socially optimum outcome and that of a Nash equilibrium. Formally,
and
Analogously, the price of stability of is defined as the best-case ratio between the social welfare of a socially optimum outcome and that of a Nash equilibrium. Formally,
and
3. Nash Stable Outcomes
In this section we consider Nash stable outcomes.
We first show that the social context radically modifies the notion of stability of additively separable hedonic games. To this aim, consider the instance whose graph G and valuations are depicted in Figure 2. On the one hand, the coalition structure is Nash stable when (i.e., without considering social effects): the utility of players are , respectively. Player 1 is earning as much as possible, and therefore has no incentive to deviate; player 2 would obtain a utility of 2 by joining the coalition of player 3, while it would obtain a utility of 0 by going alone; player 3 would obtain a utility of by joining the coalition of players 1 and 2. On the other hand, the same coalition structure is not Nash stable when , i.e., when considering the effect of social context. In fact, in this case the utility of player 2 is again , while she would obtain a utility of by joining the same coalition of player 3. Interestingly, it is also possible to build an instance in which the converse does not hold: Consider the instance exploited in the proof of Theorem 2. Here, the grand coalition is Nash stable and is such that every player is getting a negative utility. If we do not consider social context effects on the player utilities, the grand coalition would not be Nash stable because every player would clearly prefer to form a new coalition alone, so getting utility 0.

Figure 2.
Graph G and valuations .
We now show that a stable outcome is guaranteed to exist and also that the finite improvement path property holds for SCASHGs, because these games admit the potential function.
with , where, for each pair of players , we define if and if .
Thus, we can rewrite the potential function as
In the following theorem, we prove that is an exact potential function for our game.
Theorem 1.
Φ is a potential function for SCASHGs.
Proof.
Given two stable outcomes and where is obtained from after a player i performs a move, we prove that the following holds:
For the left hand side of Equation (1), by applying the definition of , we obtain that:
In the right hand side we obtain that:
Hence, the proof follows. □
4. Price of Anarchy
In this section we evaluate the performance of Nash stable outcomes with respect to the notion of price of anarchy.
We first show that the price of anarchy is unbounded for general valuations. It is already known that the price of anarchy of additively separable hedonic games is unbounded [12]. The following proposition is an easy extension to our setting with social context. The following result holds for both the social welfare functions and .
Proposition 1.
For any , there exists a function v (also admitting negative valuations), such that and are unbounded, where .
Proof.

Let be the players’ valuations as shown in Figure 3, with . As , we can easily note that the values of the two social welfare functions and are equal for every coalition structure.

Figure 3.
Graph G and valuations .
On the one hand, there exists outcome with and therefore and . On the other hand, it can be easily verified that outcome with is a Nash equilibrium. Therefore, and , thus proving the claim for tending to 0. □
For more involved social graphs, we are also able to show a stronger result, holding even for the case of the price of stability (analyzed in Section 5): by Theorem 5, there exists a SCASHG in which every Nash equilibrium is such that is negative, while is positive. We now prove a similar result for the social welfare function .
Theorem 2.
For any , there exists a graph G and a function v (also admitting negative valuations) inducing , such that while for a Nash stable outcome of .
Proof.

Let G be the social graph depicted in Figure 4 and let be the valuations as represented in Figure 4, with such that .

Figure 4.
Graph G and valuations .
On the one hand, coalition structure is such that , and therefore .
On the other hand, a Nash equilibrium is the grand coalition, in which all players are in the same coalition and, as can be easily checked, . Indeed, players and 6 have all the same utility when they are in the grand coalition while, if any of them deviates, the best she can do is forming a new coalition alone, in which she would have utility . Moreover, players 2 and 4 have the same utility and if any of them deviates forming another coalition, her utility would become for . □
The above results can be interpreted as follows: having negative valuations towards some players can preclude the possibility to form a group with other players for which the valuation is positive, when the former and the latter are already together in the same group. It is worth noticing that such a situation also arises in the classical model of additively separable hedonic games (notice that in Proposition 1 the social graph is without edges). This phenomenon shows how, in social and economic scenarios, players having difficulties to collaborate with other ones can decrease the global quality of stable outcomes. Given these negative results, in what follows we focus on the case in which the valuation function does not assume negative values, i.e., for any with .
In order to prove the upper bounds to and , we need some additional notation and definitions. Given any outcome , let be the sum of the valuations of player i toward her friends belonging to , i.e , and, analogously, let be the sum of the valuations of player i toward players belonging to and not being her friends. Finally, we denote by the maximum valuation of player i, i.e. .
The following theorems provide asymptotically matching upper and lower bounds to and .
Theorem 3.
For any , any graph G and any function v not admitting negative valuations, and .
Proof.
Given a Nash stable outcome , for every player it holds that
To prove inequality 2, recall that , where, for every , . By the definitions of and , . Moreover, let : it follows that . Let j be the player such that . If j belongs in to the same coalition of i, inequality 2 trivially holds. Otherwise, notice that if player i changes her strategy by joining the coalition containing player j, inducing in this way a new coalition structure , we obtain , because the contributions of the friends of i not connected to player i in remain unchanged in . Therefore, if player i would increase her utility by changing her strategy: a contradiction to the fact that is Nash stable.
Moreover, it trivially holds that in all coalition structures, including the optimal outcomes and , is at most . Thus, and .
Analogously, for the social welfare function , since and , by recalling the definition of , we obtain that
thus proving the claim. □
We now focus on the lower bound on and .
Theorem 4.
For every even positive integer n and every , there exists a graph G with n vertices and a valuation function v (not admitting negative valuations) such that and .
Proof.
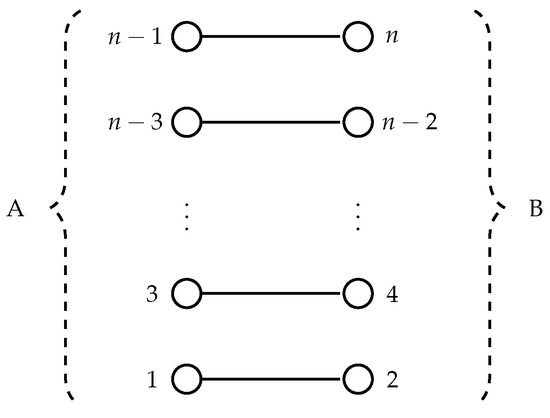
Consider the bipartite graph with n vertices depicted in Figure 5 (note that and ), and let v be the valuation function such that

Figure 5.
The bipartite graph G.
- for every ;
- for all pairs such that and ;
- for all remaining pairs.
On the one hand, as can be easily checked, the grand coalition is such that, for every , . Therefore, the optimal outcome is such that and the optimal outcome is such that .
On the other hand, the coalition structure in which there are non-empty coalitions for is a Nash stable outcome; in fact, for every , and , while a deviation of player i to another non-empty candidate coalition would induce a new coalition structure such that , because for player connected in G to player i it holds . Moreover, a deviation of player i to an empty candidate coalition would induce a new coalition structure such that , again because for player connected in G to player i it holds . A completely symmetric argument holds for every player .
It follows that
Analogously, for the social welfare function , it holds that
□
5. Price of Stability
In this section we present our results on the price of stability. First of all, notice that, if all valuations are non-negative, with respect to both social welfare functions and , the grand coalition is at the same time an optimal solution and a Nash stable outcome, thus implying that .
Therefore, in the following we deal with the case of general valuations, i.e., we allow the valuation function to assume negative values. We first show that, for the social welfare function , there exists a SCASHG in which every Nash equilibrium is such that is negative, while is positive.
Theorem 5.
For any , there exists a graph G and a function v (admitting also negative valuations) inducing , such that while for every Nash stable outcome of .
Proof.

Let us consider the graph G depicted in Figure 6 and the valuation function v whose non-null values are listed in Figure 6, and in which is an arbitrary positive parameter.

Figure 6.
Graph G and valuations .
Now we want to show that in every Nash stable outcome players 1, 2 and 3 belong to the same coalition.
First of all, notice that, for any , for any ; it follows that it is possible to discard players in the following discussion. The outcome in which players 1, 2 and 3 belong to three different coalitions is not Nash stable because, for instance, player 1 would increase her utility from 0 to by joining the coalition of player 2. The outcome in which players 1 and 2 are in a coalition and player 3 in another one is not Nash stable because player 3 would increase her utility from to by joining the coalition of players 1 and 2 (notice that a symmetric argument holds for the outcome in which players 2 and 3 are in a coalition and player 1 in another one). Finally, the outcome in which players 1 and 3 are in a coalition and player 2 in another one is not Nash stable because, for instance, player 1 would increase her utility from to 0 by forming alone a new coalition. It follows that in any Nash equilibrium (recall that by Theorem 1 a Nash equilibrium always exists) players 1, 2 and 3 belong to the same coalition.
It can be easily verified that and . Moreover, since , it follows that for any , .
Therefore,
for n approaching infinity.
In order to complete the proof, it is sufficient to note that there exists a coalition structure (for instance the one in which players 1 and 2 belong to the same coalition and all other players are alone in different coalitions) with positive social welfare. □
Now we focus our attention on the social welfare function and we show that is unbounded for tending to 1.
Theorem 6.
Given any , there exist a value of α, a graph G and a function v (admitting also negative valuations) such that .
Proof.

Let us consider the graph G depicted in Figure 7 and the valuation function v whose non-null values are listed in Figure 7, and in which and .

Figure 7.
Graph G and valuations .
By exploiting the same arguments used in the proof of Theorem 5, it is possible to show that the unique Nash stable outcome is given by the grand coalition.
It can be easily verified that and . Therefore, .
Moreover, there exists coalition structure with social welfare . Thus, it holds that .
Therefore, for any ,
for . Since , it is possible to choose such that and the claim follows. □
6. Open Problems
Starting from the fundamental class of additively separable hedonic games, we have defined and studied a new model in which, given a social graph, players also care about the happiness of their friends. Our work leads to many future research directions.
First of all, it would be interesting to study particular significant classes of graph topologies, in order to obtain a reduced price of anarchy. Moreover, the study of other stability notions such as strong Nash outcomes and core stable outcomes also deserves further investigation.
This is a first study toward the understanding of social effects in hedonic games. Several research directions (or their combinations) can be pursued along this line:
- the problem in which valuations can be different from zero only between players for which edge belongs to the social graph (and not for all pairs of players);
- the setting in which the valuations are not symmetric;
- the problem in which an edge-weighted social graph is considered, with the weights denoting how important is a player for another one;
- different combinations of the classical utilities of the friends, that in this first work have been combined in an additive way;
- the problem defined with player-specific parameters , in which every player has a different degree of altruism.
Finally, it would be interesting to study social context games in the setting of fractional hedonic games in which the utility of a player (according to the current model of additively separable hedonic games) is divided by the number of players in the coalition she belongs to, and modified fractional hedonic games in which the utility of a player is averaged over all other members of that coalition, that is, excluding herself.
Author Contributions
Conceptualization, G.M., L.M. and Y.V.; methodology, G.M. and L.M. and Y.V.; validation, G.M. and L.M. and Y.V.; formal analysis, G.M., L.M. and Y.V.; investigation, G.M., L.M. and Y.V.; writing—original, G.M., L.M. and Y.V.; draft preparation, G.M., L.M. and Y.V.; writing—review and editing, G.M., L.M. and Y.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dréze, J.H.; Greenberg, J. Hedonic coalitions: Optimality and stability. Econometrica 1980, 48, 987–1003. [Google Scholar] [CrossRef]
- Aziz, H.; Brandt, F.; Seedig, H.G. Stable Partitions in Additively Separable Hedonic Games; AAMAS, ACM: New York, NY, USA, 2011; pp. 183–190. [Google Scholar]
- Deng, X.; Papadimitriou, C.H. On the complexity of cooperative solution concepts. Math. Operat. Res. 1994, 19, 257–266. [Google Scholar] [CrossRef]
- Bogomolnaia, A.; Jackson, M.O. The Stability of Hedonic Coalition Structures. Games Econ. Behav. 2002, 38, 201–230. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Konishi, H.; Sönmez, T. Core in a simple coalition formation game. Soc. Choice Welf. 2001, 18, 135–153. [Google Scholar] [CrossRef] [Green Version]
- Feldman, M.; Lewin-Eytan, L.; Naor, J. Hedonic Clustering Games. ACM Trans. Parallel Comput. 2015, 2, 4:1–4:48. [Google Scholar] [CrossRef]
- Peters, D.; Elkind, E. Simple Causes of Complexity in Hedonic Games; AAMAS, ACM: New York, NY, USA, 2015; pp. 617–623. [Google Scholar]
- Ballester, C. NP-completeness in hedonic games. Games Econ. Behav. 2004, 49, 1–30. [Google Scholar] [CrossRef]
- Sung, S.C.; Dimitrov, D. Computational complexity in additive hedonic games. Eur. J. Oper. Res. 2010, 203, 635–639. [Google Scholar] [CrossRef] [Green Version]
- Olsen, M. Nash Stability in Additively Separable Hedonic Games and Community Structures. Theory Comput. Syst. 2009, 45, 917–925. [Google Scholar] [CrossRef]
- Aziz, H.; Brandt, F.; Seedig, H.G. Computing desirable partitions in additively separable hedonic games. Artif. Intell. 2013, 195, 316–334. [Google Scholar] [CrossRef] [Green Version]
- Bilò, V.; Fanelli, A.; Flammini, M.; Monaco, G.; Moscardelli, L. Optimality and Nash Stability in Additively Separable Generalized Group Activity Selection Problems; IJCAI: Macao, China, 2019; pp. 102–108. [Google Scholar]
- Aziz, H.; Brandt, F.; Harrenstein, P. Fractional Hedonic Games; AAMAS, ACM: New York, NY, USA, 2014; pp. 5–12. [Google Scholar]
- Aziz, H.; Brandl, F.; Brandt, F.; Harrenstein, P.; Olsen, M.; Peters, D. Fractional Hedonic Games. ACM Trans. Econ. Comput. 2019, 7, 6:1–6:29. [Google Scholar] [CrossRef]
- Brandl, F.; Brandt, F.; Strobel, M. Fractional Hedonic Games: Individual and Group Stability; AAMAS, ACM: New York, NY, USA, 2015; pp. 1219–1227. [Google Scholar]
- Bilò, V.; Fanelli, A.; Flammini, M.; Monaco, G.; Moscardelli, L. Nash Stable Outcomes in Fractional Hedonic Games: Existence, Efficiency and Computation. J. Artif. Intell. Res. 2018, 62, 315–371. [Google Scholar] [CrossRef] [Green Version]
- Kaklamanis, C.; Kanellopoulos, P.; Papaioannou, K. The Price of Stability of Simple Symmetric Fractional Hedonic Games. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2016; Volume 9928, pp. 220–232. [Google Scholar]
- Carosi, R.; Monaco, G.; Moscardelli, L. Local Core Stability in Simple Symmetric Fractional Hedonic Games; AAMAS, ACM: New York, NY, USA, 2019; pp. 574–582. [Google Scholar]
- Aziz, H.; Gaspers, S.; Gudmundsson, J.; Mestre, J.; Täubig, H. Welfare Maximization in Fractional Hedonic Games; AAAI Press: Palo Alto, CA, USA, 2015; pp. 461–467. [Google Scholar]
- Olsen, M. On Defining and Computing Communities; CATS, 2012; pp. 97–102. [Google Scholar]
- Monaco, G.; Moscardelli, L.; Velaj, Y. On the Performance of Stable Outcomes in Modified Fractional Hedonic Games with Egalitarian Social Welfare; AAMAS, ACM: New York, NY, USA, 2019; pp. 873–881. [Google Scholar]
- Monaco, G.; Moscardelli, L.; Velaj, Y. Stable outcomes in modified fractional hedonic games. Auton. Agents Multi Agent Syst. 2020, 34, 4. [Google Scholar] [CrossRef] [Green Version]
- Elkind, E.; Fanelli, A.; Flammini, M. Price of Pareto Optimality in Hedonic Games; AAAI Press: Palo Alto, CA, USA, 2016; pp. 475–481. [Google Scholar]
- Flammini, M.; Kodric, B.; Monaco, G.; Zhang, Q. Strategyproof Mechanisms for Additively Separable and Fractional Hedonic Games. J. Artif. Intel. Res. 2021, 70, 1253–1279. [Google Scholar]
- Wright, M.; Vorobeychik, Y. Mechanism Design for Team Formation; AAAI Press: Palo Alto, CA, USA, 2015; pp. 1050–1056. [Google Scholar]
- Flammini, M.; Monaco, G.; Moscardelli, L.; Shalom, M.; Zaks, S. Online Coalition Structure Generation in Graph Games; AAMAS, ACM: New York, NY, USA, 2018; pp. 1353–1361. [Google Scholar]
- Balliu, A.; Flammini, M.; Melideo, G.; Olivetti, D. Nash Stability in Social Distance Games; AAAI Press: Palo Alto, CA, USA, 2017; pp. 342–348. [Google Scholar]
- Balliu, A.; Flammini, M.; Olivetti, D. On Pareto Optimality in Social Distance Games; AAAI Press: Palo Alto, CA, USA, 2017; pp. 349–355. [Google Scholar]
- Ashlagi, I.; Krysta, P.; Tennenholtz, M. Social Context Games. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2008; Volume 5385, pp. 675–683. [Google Scholar]
- Bilò, V.; Celi, A.; Flammini, M.; Gallotti, V. Social Context Congestion Games. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2011; Volume 6796, pp. 282–293. [Google Scholar]
- Anagnostopoulos, A.; Becchetti, L.; de Keijzer, B.; Schäfer, G. Inefficiency of Games with Social Context. Theory Comput. Syst. 2015, 57, 782–804. [Google Scholar] [CrossRef] [Green Version]
- Hoefer, M.; Skopalik, A. Altruism in Atomic Congestion Games. ACM Trans. Econ. and Comput. 2013, 1, 21:1–21:21. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; de Keijzer, B.; Kempe, D.; Schäfer, G. The Robust Price of Anarchy of Altruistic Games. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2011; Volume 7090, pp. 383–390. [Google Scholar]
- Salehi-Abari, A.; Boutilier, C. Empathetic Social Choice on Social Networks; AAMAS, ACM: New York, NY, USA, 2014; pp. 693–700. [Google Scholar]
- Nguyen, N.; Rey, A.; Rey, L.; Rothe, J.; Schend, L. Altruistic Hedonic Games; AAMAS, ACM: New York, NY, USA, 2016; pp. 251–259. [Google Scholar]
- Brânzei, S.; Larson, K. Social Distance Games; IFAAMAS, 2011; pp. 1281–1282. [Google Scholar]
- Umar, R.; Mesbah, W. Throughput-efficient coalition formation of selfish/altruistic nodes in ad hoc networks: A hedonic game approach. Telecommun. Syst. 2018, 67, 95–111. [Google Scholar] [CrossRef]
- Badev, A. Nash Equilibria on (Un)Stable Networks. Econometrica 2021, 89, 1179–1206. [Google Scholar] [CrossRef]
- Kinateder, M.; Merlino, L.P. The Evolution of Networks and Local Public Good Provision: A Potential Approach. Games 2021, 12, 55. [Google Scholar] [CrossRef]
- Mele, A. A Structural Model of Dense Network Formation. Econometrica 2017, 85, 825–850. [Google Scholar] [CrossRef] [Green Version]
- Bourlès, R.; Bramoullé, Y.; Perez-Richet, E. Altruism in Networks. Econometrica 2017, 85, 675–689. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).