1. Introduction
Broadly speaking, ransomware is a form of malware in which the victim of a cyber-attack is blackmailed. The term has recently become synonymous with crypto-ransomware wherein the files on a victims device are encrytped and a ransom is demanded for the key to decrypt those files [
1,
2,
3,
4]. While ransomware dates back to the AIDS Trojan in 1989, it has come to prominence over the last five years or so with an explosion in the number of ransomware strands and victims [
5]. Critical to this rapid evolution has been the wider awareness of crypto-graphically sound techniques for encrypting files in a way that does not allow reverse engineering [
6]. Such techniques mean a victim has no way of recovering encrypted files without a back-up or the private key held by the criminals.
Ransomware offers a viable, long term business model for criminals [
7]. In particular, if a victim has no back-up and values the encrypted files then they may decide the ransom is worth paying. Survey evidence suggests that many businesses do indeed pay the ransom [
8]. We also have evidence of large profits for ransomware criminals [
9,
10]. The example of South Korean web-hosting firm Nayana paying a
$1 million ransom in 2017 amply demonstrates how lucrative ransomware can be for criminals. Given that the probability of being prosecuted is low, it is no surprise that we now see hundreds, if not thousands, of ransomware strands in the wild. Each strand may only last a few months before the authorities and security experts ‘catch up’ but new variants continually emerge.
While ransomware offers a long-term business model it is clear that this model relies on an element of trust between victim and criminal. Victims will only pay the ransom if they believe that paying the ransom gives them a good enough chance of getting their files back [
11]. This, in turn, suggests that criminals would benefit from a reputation for honouring ransom payments. CryptoLocker and CryptoWall are two examples of ransomware strands that had a good reputation for returning files [
12,
13]. There are plenty of examples, like WannaCry, with a bad reputation. So, should the criminal return the files, take the money and run, or simply demand more money? Recent evidence suggests that victims who pay the ransom recover their data around 50% of the time [
14].
1 That may be enough to tempt victims to try their luck and pay up. So, have the criminals, consciously or not, hit upon a good strategy?
In this paper we analyze reputation formation in a simplified repeated game. In each period a new victim decides whether or not to pay the ransom and the criminal decides whether or not to return the files. We assume that victims learn from the past experience of other victims. We also allow that it is costly for the criminal to return access to files because of, say, the costs of a ‘customer service’ to guide victims on how to decrypt files. In a baseline case where victims are unresponsive to past experience we show that it is optimal for the criminal to not return files. In the other extreme where victims are highly responsive to past experience the criminal should always return the files. We then explore the middle ground to see where the tipping point lies above which it is optimal for the criminal to return files. We find that if a criminal’s reputation will be based solely on their own actions then in all but the most extreme settings it is optimal for the criminal to return the files. If, however, the criminal’s reputation is affected by what other criminals are doing then it may not be optimal to return the files.
We will discuss the implications of our findings for law enforcement more as we proceed. But we note here that the findings of this paper can help inform on the threat analysis of ransomware strands. If a particular strand has a poor reputation then it would be in the interests of law enforcement to advertise this, in order to undermine the business model of the criminals. Either way we would not expect the strand to last long. By contrast, a strand with a good reputation has a viable long term future, and so is of a higher threat. This may encourage copy-cats (who do not return files). Or it may be that criminals join behind a ‘successful strand’, as with Cerber [
15]. Or that ‘successful strands’ are ‘reborn’ in the game of cat and mouse with law enforcement and security experts, as we saw with Locky [
16]. All this suggests that reputation is a factor that should go into threat analysis, alongside more familiar factors such as the ease with which the strand can be detected by common anti-virus software.
Our work builds upon a number of papers using economics and game theory to analyze ransomware. Hernandez-Castro et al. (2017) show how the optimal ransom demand depends on the distribution of valuations in the population and the information criminals can discern about willingness to pay [
7]. Caulfield et al. (2019) analyze how criminals can learn over time about the distribution of valuations in the population [
17]. Caporusso et al. (2018) set out the basic rationale for using game theory to model the interaction between ransomware criminal and victim [
18]. Laszka et al. (2017) consider the strategic role of back-ups [
19] while Cartwright et al. (2019) look at the role of irrational aggression and deterrence [
20]. We recognize that there is also a related literature looking at the game theory of hostage taking situations, typically framed in a terrorist context [
20,
21,
22,
23].
In none of the papers and models just mentioned is reputation explicitly modelled. Instead the focus is more on criminal and victim interaction in a one-shot context or how criminals can learn over time. The key contribution of our paper is, therefore, to move to a
repeated game setting in which victims can collectively learn from past experience. This moves the focus somewhat away from the criminal onto how victims react to an attack. For instance, how do victims form beliefs and how does that influence their decision to pay the ransom [
24]. We would argue that such questions should critically inform policy and advice on how to intervene in the ransomware business model. In particular, the criminals have already had time to learn from experience about how to make ransomware work and so can be expected to have a more sophisticated, forward looking strategy. To be ahead of the game we need to understand optimal behaviour in this setting.
2. Model
There is a continuum of potential victims. Each victim
i is characterized by the amount she values her files
. The population distribution of valuations is given by function
q, where
, for any
, is the proportion of victims who value their files more than
v. We shall as an example consider the linear distribution
, where
a and
b are parameters.
2 In stage 1 of the game a victim is randomly drawn from the population and her electronic device is attacked by a criminal. The victim knows her valuation
. The only information the criminal has is that
is drawn from distribution
q. He does not, therefore, know
.
In stage 2 of the game the criminal chooses a take-it-or-leave-it ransom demand
r. In stage 3 of the game the victim decides whether or not to pay the ransom. Let
p denote the victim’s choice, where
indicates pay and
indicates not pay. In stage 4 of the game the criminal decides whether or not to release the files back to the victim. Let
g denote the criminal’s choice, where
indicates return and
indicates destroy. The payoff of the victim is given by
For instance, the victims payoff is
if she gets her files back without paying the ransom (which could be equivalent to not being attacked) while her payoff is
if she pays the ransom and does not get her files back. The payoff of the criminal is given by
where
is the cost of returning files. For instance, the criminal’s profit is
r if the victim pays the ransom and the criminal does not return the files.
Let us briefly comment on the interpretation of the cost parameter
c. If the criminal can effortlessly return a victim access to her files,
, then it is a weakly dominant strategy for him to do so. This makes it is ‘easy’ for the criminal to build a reputation. In reality, however, we can expect that there are costs to returning access to files. These costs may include: checking the payment matches a particular victim, returning the key to that victim, and, perhaps most importantly, guiding the victim on how to decrypt their files and dealing with queries about files that fail to decrypt [
13]. This latter point is crucial in terms of reputation because giving back the private key is not enough—the files need to be successfully recovered by the victim in order that she would feel the ransom payment was honoured. Hence,
c is likely to be positive. This provides an incentive for the criminal to not return files.
In the following we assume that the above game is repeated indefinitely in periods
. Let
and
denote the respective valuation and choices in period
t. Given that victims are chosen randomly a victim will only ever be a victim in one period. Victims are assumed to be self-focused and so they ignore the externality effect that paying the ransom may have on future victims. Specifically, the payoff of the victim in period
t is
The criminal is forward-looking and discounts future payoffs with discount factor
. His aggregate payoff is thus
We assume that the objective of the victim in period t is to maximize and the objective of the criminal is to maximize . We also assume that both victims and criminal are risk neutral.
Whether the victim is willing to pay the ransom will depend on his beliefs about the likelihood of the criminal returning the files. Let
denote the perceived probability of the criminal returning the files in period
t if the ransom is paid. For simplicity we assume that the victim believes the probability of retrieving the files if the ransom is not paid is 0. Let
history at time
t be given by the vector
of past ransom demands, whether the ransom was paid, and whether files were returned. We will assume that beliefs
are a function of
and
.
3 Clearly, in reality, a victim would not have access to the complete history. Instead they would need to pick up snippets of information from personal and social networks, forums, search engines etc.
To look at how beliefs may be shaped it is useful to relate our model to that on reputation in repeated games. The basic model in this literature involves a long-lived player interacting with a sequence of short lived players [
25,
26,
27].
4 For instance, a monopolist interacting with a sequence of potential entrants [
30,
31]. The key question addressed in the literature is whether the long-lived player has an incentive to generate a reputation. This could be a monopolist generating a reputation for being tough against entrants or, in our case, a criminal generating a reputation for honouring ransom payments.
Models of reputation are driven by some level of informational asymmetry between the long-lived and short-lived players. One variant on the theme is a game of imperfect information and perfect recall in which the short-lived players do not know the payoff function of the long-lived player but can observe all actions. In our setting this can be equated with victims not knowing
c and/or
[
30]. Or it could be the short-run players put some positive probability the criminal is a ‘commitment type’ who will always honour ransom payments [
31,
32]. In either case beliefs
are shaped by history
because the past actions of the criminal reveal information about his type.
Throughout the following we take a partial equilibrium approach in which the criminal maximizes expected payoff taking as given the beliefs of victims. This allows us to abstract away from formally modelling incomplete information or equilibrium belief formation and focus on the incentives of the criminal. It also means we do not restrict to ‘rational’ victims. In an
Appendix A, however, we briefly consider equilibrium belief formation and Bayes Nash equilibrium.
3. Results
As a trivial benchmark case let us begin with the case of
independent beliefs in which
is independent of
for all
t. An assumption of independent beliefs is appropriate in a setting where there are many strands of ransomware which are indistinguishable, or treated as indistinguishable by victims. Hence, victims lump all ransomware attacks together and beliefs are based on the overall probability of getting files back. In this case the criminal that we are modelling in our game would have no (or very limited effect) on the beliefs of victims.
5 It is simple to show that the criminal’s optimal strategy is to never return files.
Proposition 1. In the case of independent beliefs, if it is optimal for the criminal to set for all t.
Proof. For any period t we can see that the victim will pay the ransom if and only if . Consider a specific period in which the ransom is paid. Given that for all is independent of , returning the files costs the criminal c and has no benefit. □
Proposition 1 encapsulates the basic intuition that if reputation is irrelevant then criminals have no incentive to return files. In this setting the only rational belief for victims is
. But, then victims are not willing to pay and so ransomware is not profitable. We can already see in Proposition 1 that reputation is vital if ransomware is to be a long term business model [
11]. In particular, the ransomware business model is dependent on beliefs,
, being somehow tied with history,
.
To appreciate the potential power of reputation let us consider another extreme. Suppose that we have
grim-trigger beliefs in which (1)
if
and
, (2)
otherwise. In this case, if the criminal once fails to return the files when a victim pays then no other victim will ever trust him in the future. If the criminal always return the files then initial beliefs are retained.
6 The following result shows that it can be optimal for the criminal to return files.
Proposition 2. In the case of grim-trigger beliefs it is optimal for the criminal to set when for all t if δ is sufficiently large.
Proof. Suppose that the criminal (a) charges a ransom
, where
and
, and (b) sets
if
, in all periods
t. Consider period
and suppose that the victim pays the ransom in this period. Should the criminal return the files? The expected future payoff of the criminal if he returns the files is
If the criminal does not return the files his future payoff is
. It is, therefore, optimal to return the files if
It is clear that . □
To illustrate Propositions 1 and 2 consider the linear distribution
. In the case of independent beliefs suppose beliefs are fixed
for some initial belief
. The expected profit of the criminal if he sets ransom
in each period
t is
Hence we get optimal ransom demand
Consider next grim-trigger beliefs with the same initial belief
. Suppose the criminal sets ransom
and always returns the files if the ransom is paid. His expected payoff is
Here we get optimal ransom demand
Note that the optimal ransom is higher in the case of grim-trigger beliefs because the criminal will pay the cost of returning the files. Returning the files is optimal (see the proof of Proposition 2) if
For plausible parameter values the value of is likely to be low. For instance, if and we have .
3.1. Sampling Recent Victims
Propositions 1 and 2 show that whether it is optimal for the criminal to return files will primarily depend on belief formation. For the remainder of the paper we consider a particular model of belief formation based on empirical frequencies. In motivating this approach we begin by recognizing that there is an extensive literature on learning in games [
33,
34]. It is widely recognized that beliefs typically do not obey Bayes rule (see Selten (1991) for an early, light-hearted take on the matter, with reference to models of reputation [
35]). Here we focus on a belief-based model of learning in which the victim’s beliefs are based on the past record of the criminal in returning files. Our approach is similar to that of Young (1993) [
34,
36] and consistent with beliefs being biased by event frequencies [
37].
Our model of belief formation can be explained as follows. Given period
and history
let
denote the subset of periods in which the ransom is paid. Let
n be an exogenous parameter that measures
sample size. If
then we assume
for some initial beliefs
. If
then denote by
the
n largest values in
, i.e.,
are the most recent
n periods in which the ransom was paid. We assume that
In interpretation, this means that beliefs are based on the proportion of times the criminal returned files the last
n times the ransom was paid. So, we can think of victims as sampling the last
n victims who paid the ransom.
7The following result is analogous to Proposition 2 in showing that it can be optimal for the criminal to return the files. This must be the case if sample size is small. The logic here is that it is ‘easy’ for the criminal to get a ‘bad reputation’ when the sample size is small, and once he has that reputation nobody ever pays the ransom. So, the better long term strategy is to pay the ransom.
Proposition 3. If the sample size is and δ is sufficiently large then it is optimal for the criminal to set when for all t.
Proof. In period
t we can see that the victim will pay the ransom if and only if
. Suppose that the victim pays the ransom in period
. If the criminal returns the files and continues with a strategy of charging
and returning files, then his expected payoff in subsequent periods is
Note that this equation takes account of the fact for all . If the criminal does not return the files his expected payoff is . This takes account of the fact that for all . It is, therefore, optimal to return the file if , where is as defined in the proof of Proposition 2. □
Our next result shows that at the opposite limit of a large n it is not optimal to return the files to every victim. In this case the large sample size means that the criminal can take the money and run some of the time without it fundamentally influencing his reputation.
Proposition 4. For any there exists such that if it is not optimal for the criminal to set when for all t.
Proof. We proceed by contradiction. Suppose that a victim in period
pays the ransom. Moreover, assume the criminal has a perfect record of returning files and so
. If the criminal returns the files then his expected payoff in future periods is at most
where
is the optimal ransom for
. Fix a particular realization of values
. Given this we can determine
and
. Suppose that there exists some period
at which point
n subsequent victims have paid the ransom. That is
.
Now suppose that the criminal does not return the files in period
but does continue to return the files to those who pay in all subsequent periods
. There will be at least
n periods in which we have beliefs
. In this case the victim will only pay if
. We set
. Consider again the realization of values
. We have fixed things so that
and
will remain unchanged. The only difference is the lower ransom. The ‘drop’ in payoff compared to
is, therefore,
The ‘gain’ in payoff compared to from not returning the files in period is c. For sufficiently large n we have . Hence the criminal can increase his payoff.
In the proceeding we assumed that there existed some period at which point n subsequent victims have paid the ransom. Potentially one can have a realization of values where this is not the case. Here, however, the drop in payoff from not returning the files is strictly less than (for ). We observe, therefore, that irrespective of the sequences of valuations the criminal earns a payoff above if he does not return the files in period . □
3.2. Simulation Results on Sample Size
Propositions 3 and 4 formally demonstrate that it may or may not be optimal for the criminal to return files depending on how sensitive victim beliefs are to the criminal’s actions. We considered, however, the relative extreme cases of
and
n large. To explore what happens in the middle ground we report the results of simulations in which we see how the profit of the criminal is influenced by
n. In the simulations we consider the linear distribution of valuations
.
8 We track the profits of the criminal over 1000 victims. Throughout we assume that victims start with the ‘optimistic’ initial belief
and then update beliefs according to Equation (
12). Each data point is the average of 1000 simulations.
We consider two variants on criminal strategy. Let us first explain our baseline
random model. This is characterized by an exogenous parameter
. For any period
t, if the victim in period
t pays the ransom then the criminal returns the files with probability
w. Moreover, the criminal sets ransom demand
which corresponds to the optimal ransom demand for beliefs
. So, in our baseline model the criminal will, over time, return the files
of the time.
Our baseline model is somewhat biased by the effect which drives Proposition 3. To appreciate why, suppose that there are n instances in a row where the criminal does not return the files. Then beliefs will be zero and no victim will pay the ransom. This means the ‘bad reputation’ sits forever. To control for this we consider a lower-bound model in which the criminal always guarantees that beliefs are at least w. Specifically, for any period t, if the victim in period t pays the ransom then (1) the criminal returns the files with probability w, unless (2) failure to return the files would result in beliefs falling below w, i.e., it would be the case that , in which case he returns the files, to make sure .
Consider first the case where the cost of returning files is
and the discount factor is
.
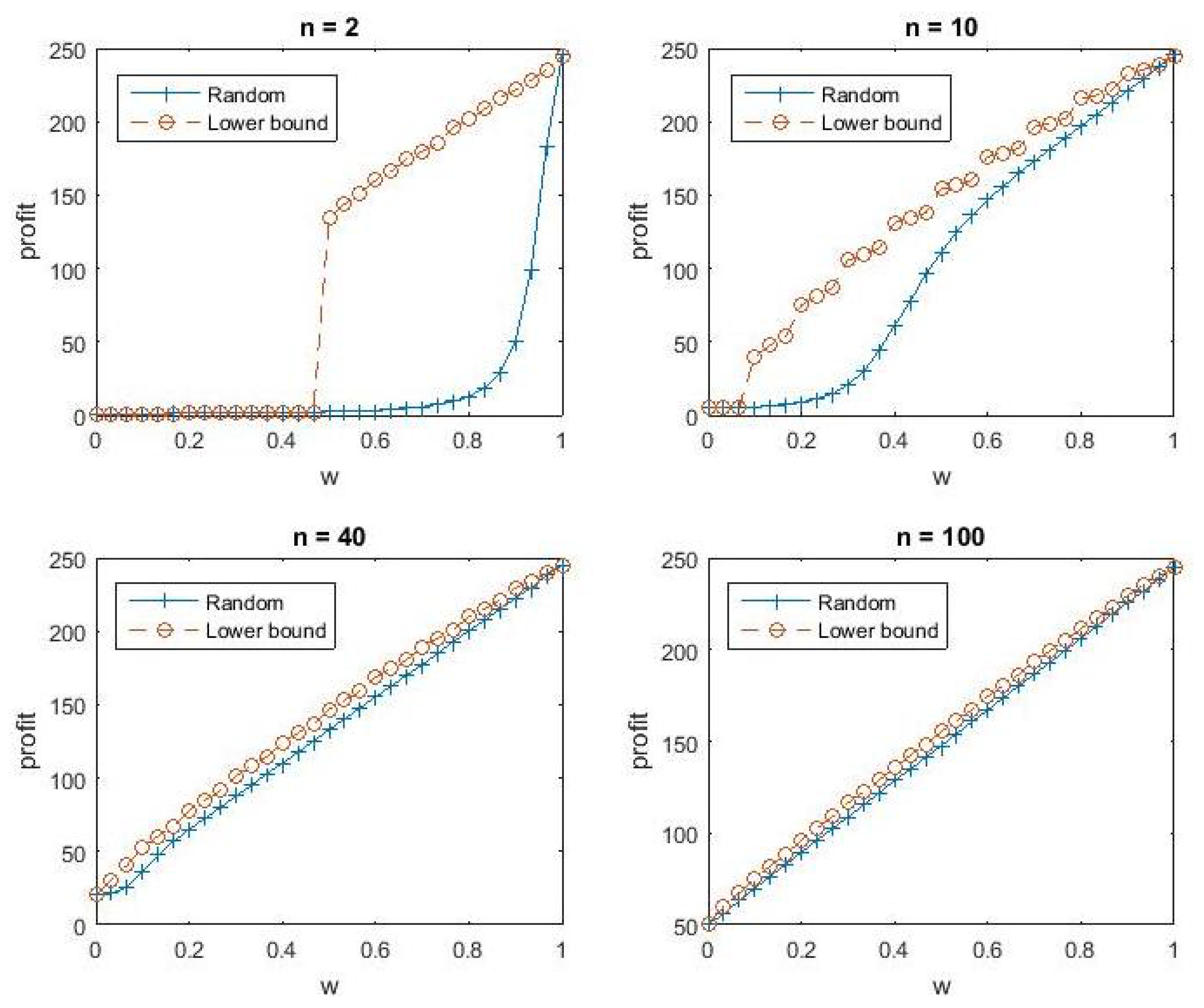
Figure 1 plots profit as a function of
w for four different values of
n. It is readily apparent that profit is increasing in
w. In other words the criminals profit is increasing in the likelihood of returning the files and the optimal strategy is to always return files to those that pay the ransom.
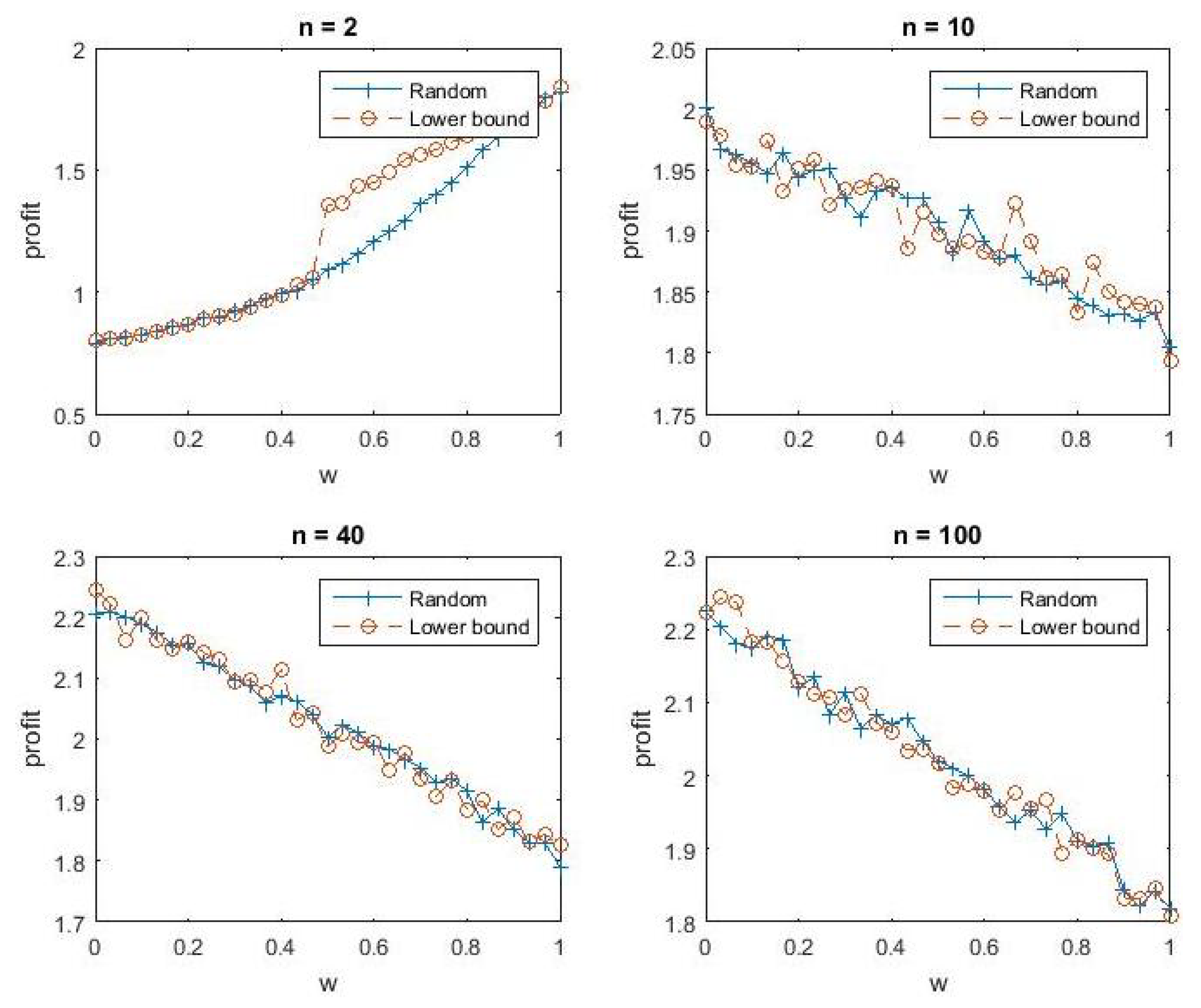
Figure 2 shows what happens if we increase the cost of returning files to
and lower the discount factor to
. Here we see that, with the exception of
, profits are highest when
and so the criminal’s optimal strategy is to not return files. Note, however, that this finding is critically dependent on two things: (1) a discount factor of
means the criminal is very much focused on the short term, and (2) it takes time for victims to update beliefs. So, the criminal essentially exploits victims during the time it takes them to collectively learn about his strategy. Clearly, this strategy is not consistent with a long term business model.
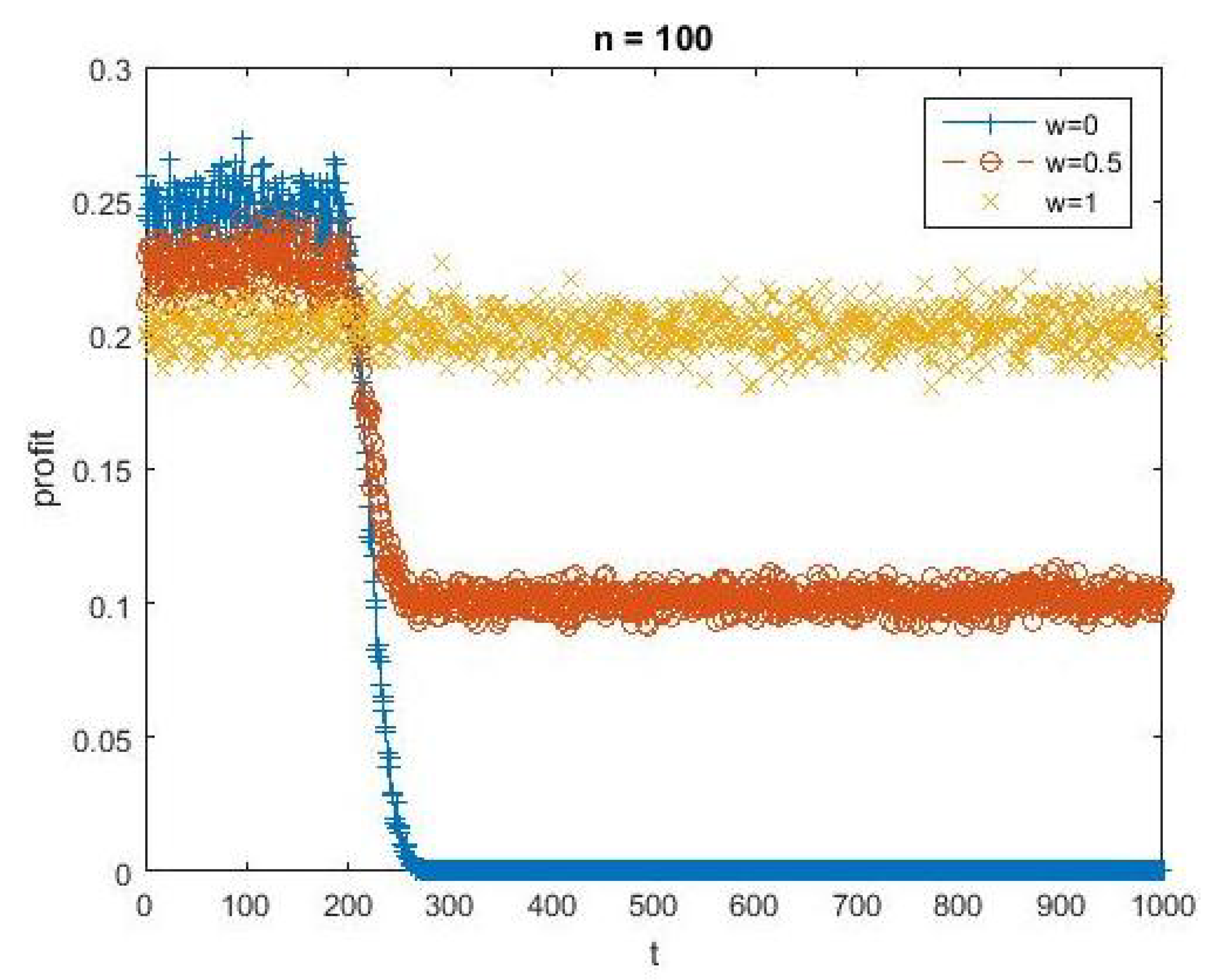
To illustrate the criminal’s trade-off in choosing between a high and low probability of returning files consider
Figure 3. This plots profit over time for three different values of
w when
and
. We can see that the strategy of never returning files
succeeds in the short run because it takes time for victims to update beliefs. But, over the long run the strategy of always returning files
is a clear winner.
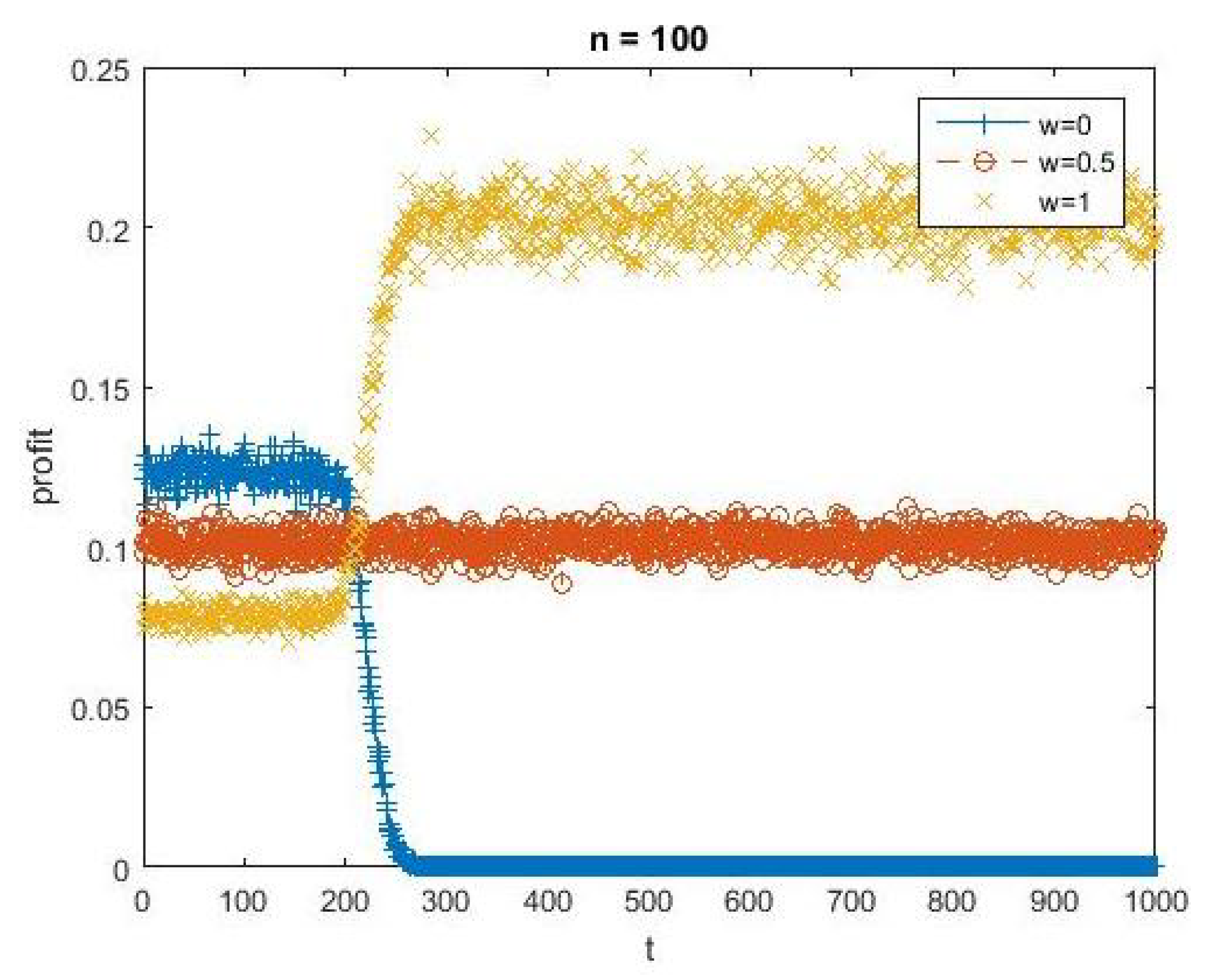
You might think the short term advantage of setting
stems from our assumption that victims are initially optimistic (with beliefs
). This, however, is not the key factor. To illustrate,
Figure 4 shows what happens when we set
. As you can see we get similar trade-offs across
w. The key factor driving the initial advantage of
is the time it takes for reputation to take hold. The smaller is
n the sooner reputations are formed and so the sooner profits are higher with
.
In summary, our simulations suggest that a criminal interested in maximizing overall profit will take a long term view and always return files to victims that pay. We observed no gains from a strategy that entails sometimes not returning the files. This suggests that Proposition 4 captures a very specific case. Only the criminal interested in short term gains (low discount factor) would optimally choose to not return files.
4. Conclusions
In this paper we have looked at the incentives for ransomware criminals to return files to victims. We have done so by studying a repeated game in which a criminal interacts with a new victim each period. A victim is assumed to form beliefs based on the past actions of the criminal. In simple settings we were able to obtain explicit results on when it is optimal for the criminal to always return the files and when it is not. We then used simulations to further our understanding around this issue.
To summarize and interpret our results first imagine a world in which there was only one ransomware criminal. In this setting the beliefs of victims will likely be shaped by the actions of the criminal. If so, the criminal will do best to always return the files. This results from two different factors (1) returning the files gives the criminal a ‘good reputation’, and (2) the criminal can benefit in the long term from that good reputation. Only the most short term of criminals would take the money and run. So, in this stylized setting incentives are clearly to return files.
In reality we know that there are hundreds, if not thousands, of competing ransomware strands. So, next consider a world in which there is a large number of ransomware strands and no distinction between them. Then it is difficult for the criminal to create a personalized reputation. Put another way, the reputation of the criminal is likely to be influenced by factors outside of his control. In this setting the optimal strategy is to not return the files. This, though, cannot succeed in the long run and ultimately would mean that ransomware has no viable future [
11]. In the short run, some victims will no doubt keep on paying the ransom in the ‘hope’ of getting their files back. Ultimately, however, the more news spreads that files are not returned the less trust there will be.
As we discussed in the introduction, evidence suggests that victims recover files around
of the time [
14]. This would suggest we are somewhere in between the two polar cases discussed above. Some ransomware criminals, we would suggest, are trying to create a good reputation for their ‘product’ to create a long term viable business model. Other criminals, by contrast, simply want to cash in on short term gains and have no incentive to honour ransom payments. Indeed, we observe fake ransomware that does not encrypt files at all [
6]. This melting pot of competing motives could influence the long-term evolution in ransomware in different ways.
If ransomware is to survive in the long term then the criminals behind a particular strand of ransomware, call it Locky, would want to separate their reputation from that of other strands of ransomware. In practical terms this means having a ‘brand’ that is recognized on search engines or forums that victims may consult after attack. It also means the criminals behind Locky would have an incentive to eliminate any competitors that may muddle their reputation. On the flip side, competitors would have an incentive to imitate Locky so as to free-ride on their good reputation. So, we could have a game of cat and mouse between competing criminal gangs.
From a law enforcement perspective things are somewhat complex. On the one hand if they interfere in the reputation of Locky then this would undermine the business model of Locky. For instance, law enforcement could frame things in a way that lowers victim’s beliefs about getting their files back (without, necessarily, explicit deception). This would, hopefully, have the long run effect of removing the criminal’s desire to continue with Locky. But, on the flip side, if Locky typically does return files then there is a short term welfare loss of discouraging victims from paying the ransom and getting their files back. So, there is a sense in which some victims have to sacrifice their own interests to undermine the long-term business model.
It is interesting that current advice tends to skim over the likelihood of getting files back. This is possibly because of a recognition that victims who are ‘desperate’ are going to be tempted to pay the ransom. Other reasons for not paying the ransom are that the victim may be targeted more in the future or may only get some of their files back before being asked for a larger ransom [
4]. In our model we have abstracted away from such issues but the basic insights from our paper still hold true. In particular, victims are likely to be influenced by beliefs, whether that be the probability of getting files back or the probability of the ransom increasing. The long term viability of ransomware relies on a good reputation.