Give and Let Give: Alternative Mechanisms Based on Voluntary Contributions †
Abstract
1. Introduction
2. An Interpolating Family of Mechanisms
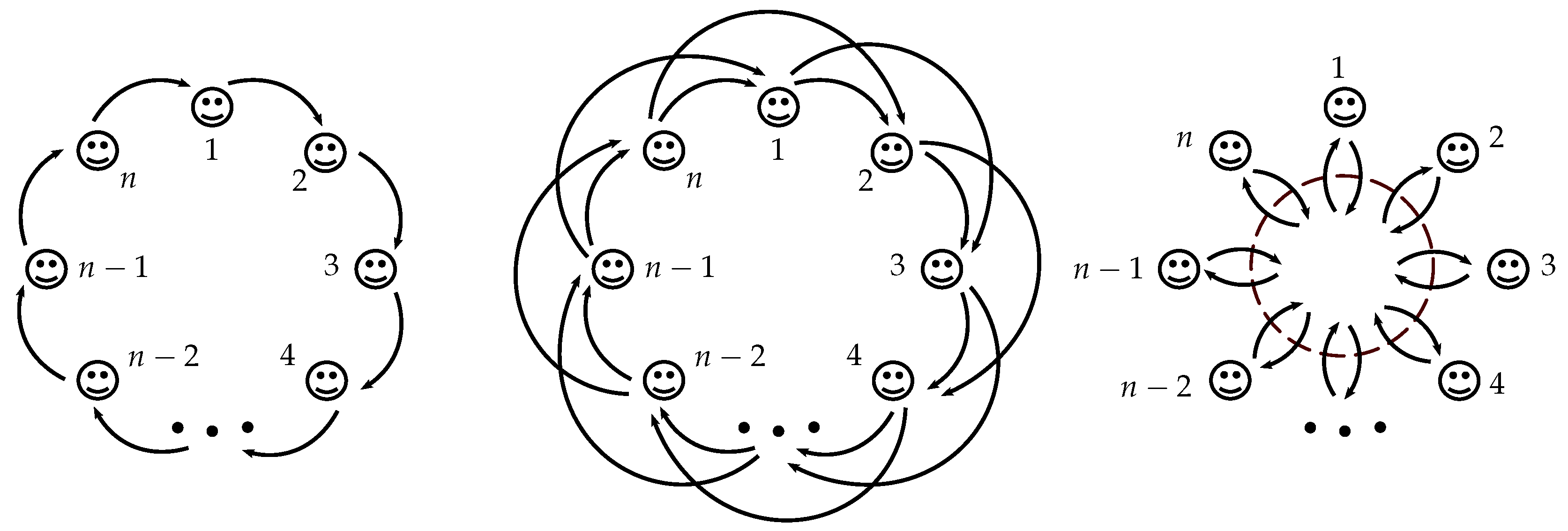
2.1. Giving Circle Mechanisms of Range m
2.2. Utility Functions
2.3. Pure-Strategy Nash Equilibria
- If for all i, thenis a Nash equilibrium. In the case of strict inequalities, this is the unique (pure strategy9) strict equilibrium. For , it is also the unique pure strategy equilibrium.
- If for all i, thenis a Nash equilibrium. In the case of strict inequalities, this is the unique (pure strategy) strict equilibrium. For , it is also the unique pure strategy equilibrium.
2.4. Interpolation
3. Choice of an Optimal Mechanism
3.1. Localized Bracketing
- If for all i, thenis the unique pure strategy Nash equilibrium.
- If for all i, thenis the unique pure strategy Nash equilibrium.
3.2. Optimal Mechanisms
4. Implications and Conclusions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix B. “Coincidental Coordination”
References
- Marwell, G.; Ames, R.E. Experiments on the Provision of Public Goods. I. Resources, Interest, Group Size, and the Free-Rider Problem. Am. J. Sociol. 1979, 84, 1335–1360. [Google Scholar] [CrossRef]
- Isaac, M.R.; McCue, K.F.; Plott, C.R. Public goods provision in an experimental environment. J. Public Econ. 1985, 26, 51–74. [Google Scholar] [CrossRef]
- Ledyard, J.O. Public Goods: A Survey of Experimental Research. In Handbook of Experimental Economics; Kagel, J.H., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 111–194. [Google Scholar]
- Chaudhuri, A. Sustaining cooperation in laboratory public goods experiments: a selective survey of the literature. Exp. Econ. 2011, 14, 47–83. [Google Scholar] [CrossRef]
- Groves, T.; Ledyard, J.O. Optimal Allocation of Public Goods: A Solution to the “Free Rider” Problem. Econometrica 1977, 45, 783–809. [Google Scholar] [CrossRef]
- Healy, P.J.; Jain, R. Generalized Groves–Ledyard mechanisms. Games Econ. Behav. 2017, 101, 204–217. [Google Scholar] [CrossRef]
- Fehr-Duda, H.; Fehr, E. Sustainability: Game human nature. Nat. News 2016, 530, 413. [Google Scholar] [CrossRef] [PubMed]
- Grech, P.; Nax, H.H. Nash Equilibria of dictator games: A new perspective. Preprint 2018. [Google Scholar] [CrossRef]
- Saijo, T. The Instability of the Voluntary Contribution Mechanism; Working Papers SDES-2014-3; Kochi University of Technology, School of Economics and Management: Kochi, Japan, 2014. [Google Scholar]
- Feng, J.; Saijo, T.; Shen, J.; Qin, X. Instability in the voluntary contribution mechanism with a quasi-linear payoff function: An experimental analysis. J. Behav. Exp. Econ. 2018, 72, 67–77. [Google Scholar] [CrossRef]
- Nordhaus, W. Climate Clubs: Overcoming Free-Riding in International Climate Policy. Am. Econ. Rev. 2015, 105, 1339–1370. [Google Scholar] [CrossRef]
- Isaac, R.M.; Walker, J.M. Group Size Effects in Public Goods Provision: The Voluntary Contributions Mechanism. Q. J. Econ. 1988, 103, 179–199. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | Broadly, one categorizes PGMs by linear, minimum, and maximum aggregation technologies, that is dependent on whether the resulting public good is determined by the average contribution, the lowest individual contribution, or the highest individual contribution. The different PGMs model different situations depending on whether it is the total effort or one of the extreme contributions that determines the societal benefit. The highest individual contribution, for example, may be relevant when members of a society (separately, yet bound by common destiny) attempt to solve a problem, while the total contribution may be more relevant for a pollution abatement situation (linear aggregation). |
| 4 | Indeed, the fact that many humans typically have other-regarding preferences is widely accepted [7] and often used to explain experimental LPGM data [3,4]. More surprising is the fact that there seems to be no analysis of the resulting consequences in terms of Nash equilibria of the game induced by the LPGM once this assumption is made. |
| 5 | The same effect, applying a similar reasoning to (“interactive”) dictator games, was found in [8]. The proof strategy given here is however different as we do not assume a “representative agent” as in that paper. |
| 6 | In the scholarly literature, LPGMs (and with some abuse of terminology, also linear “public goods games”) are often labeled as “voluntary contributions mechanisms” with linear aggregation technology. Given that all GCMs are also based on voluntary contributions, we avoid this alternative nomenclature here in order to prevent confusion. |
| 7 | To illustrate, imagine the two extreme mechanisms (with and ) were to be implemented in a church congregation. While the LPGM is akin to an alms basket being collected, potentially multiplied, and then shared equally amongst all, a GCM with involves envelopes of offerings (potentially multiplied and) being passed from each person to their next neighbor, say on the right. |
| 8 | Dictator loops have recently been found to occur in many dictator game experiments [8]. |
| 9 | While we are exclusively focusing on pure strategies in the present paper, recall that strict Nash equilibria are necessarily pure strategies. The qualifier in brackets is thus, strictly speaking, superfluous. |
| 10 | Recall that for , full-giving is a (weakly) dominant strategy for the LPGM even for narrowly selfish preferences. |
| 11 | The other extreme is somewhat more “incognito” in the existing literature, cf. Footnote 8. |
| 12 | See [12] for a related experimental analysis of the group size effect in public goods provisions. |
| 13 | In fact, since for , it holds that , for , it holds that if ; by Equation (A2), we have if ; and finally, for , we have . |
| 14 | A similar reasoning to the one in Footnote 13 shows that in fact, . |
| 15 | We caution the reader that, while related, this stability notion is not identical to trembling-hand perfection, as the latter relies on totally-mixed strategies. |
| Initial Individual Endowment | 1 | ||
|---|---|---|---|
| Individual outcome | |||
| maximal | |||
| minimal | 0 | ||
| Collective outcome | |||
| maximal | n | ||
| minimal | n | ||
| Equilibrium thresholds | zero giving | ||
| full-giving | |||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grech, P.D. Give and Let Give: Alternative Mechanisms Based on Voluntary Contributions. Games 2019, 10, 21. https://doi.org/10.3390/g10020021
Grech PD. Give and Let Give: Alternative Mechanisms Based on Voluntary Contributions. Games. 2019; 10(2):21. https://doi.org/10.3390/g10020021
Chicago/Turabian StyleGrech, Philip D. 2019. "Give and Let Give: Alternative Mechanisms Based on Voluntary Contributions" Games 10, no. 2: 21. https://doi.org/10.3390/g10020021
APA StyleGrech, P. D. (2019). Give and Let Give: Alternative Mechanisms Based on Voluntary Contributions. Games, 10(2), 21. https://doi.org/10.3390/g10020021




