Voting in Three-Alternative Committees: An Experiment

Abstract

We design an experiment to test how voters vote in a small committee election with three alternatives. Voters have common preferences that depend on an unknown state of nature. Each voter receives an imprecise private signal prior to the election and then casts a vote. The alternative with the most votes wins. We fix the number of voters in our experiment to be five and focus on differences in the information structure (prior and signal distributions). We test three different treatments (different prior and signal distributions) that pose different challenges for the voters. In one, simply voting for one’s signal is an equilibrium. In the other two, it is not. Despite the different levels of complexity for the voters, they come relatively close to the predicted strategies (that sometimes involve mixing). As a consequence, the efficiency of the decision is also relatively high and comes close to predicted levels. In one variation of the experiment, we calculate posterior beliefs for the subjects and post them. In another, we do not. Interestingly, the important findings do not change.

1. Introduction

Committees are an important staple of every level of decision making: From political institutions to any other type of public and private organizations. In our scenario—the Condorcet jury setting—the committee members (voters) have common interests that depend on an unknown state of nature. So, ex ante, the committee members are not sure which alternative is best. Committee members have prior beliefs about the probabilities of the different states of nature. Each committee member receives an imprecise, but informative, private signal about the state of nature prior to the election. They update their beliefs about the state of nature and cast a vote for one of the alternatives.

Can the committee efficiently elect the best alternative? Or would a dictator make a better choice? In most scenarios, more information is better than less. In our setting, however, voters also have to consider that they act in a game with multiple players. What if there is a conflict between information aggregation and strategic behavior of the voters?

The original Condorcet Jury Theorem (CJT) does not consider strategic behavior, but the recent previous literature does. The most relevant theoretical models for our experiment are Wit [1] and Feddersen and Pesendorfer [2] (among others) for two-alternative elections and Goertz [3] for three-alternative elections.1 Wit [1] and Feddersen and Pesendorfer [2] show that the equilibrium in two-alternative elections is unique and always efficient.2 Goertz [3] shows that in three-alternative elections, equilibria may no longer be unique and both efficient and inefficient equilibria may exist for the same committee. Equilibrium strategies are much harder to find and do not seem to have any intuitive properties.

Gerling et al. [4] and Palfrey [5] review most of the previous experimental literature on information aggregation in committees: Generally, in two-alternative elections, subjects tend to behave strategically; and since the CJT holds in equilibrium, the experimental outcomes are efficient.

Bouton et al. [6] and Bouton et al. [7] are the first to hint at the fact that experimental elections with three alternatives may be different in that respect, but their underlying model is not quite the same as ours and so their findings do not really answer our question. The attention of the former paper is on comparing the efficiency of approval voting versus the simple plurality rule and the latter investigates Duverger’s Law. In the common underlying model, there are three alternatives, but only two states of nature. The majority voters have only two possible types a and b and therefore consider only two possible strategies, voting for alternative A or B. The minority voters only vote for C. The strategic considerations of the voters in this model are more similar to those in a two-alternative election than to those in our election with three states of nature and no myopic minority voters.

Three-alternative elections have interesting twists that do not occur in two-alternative elections, and we would like to investigate how voters react to these. In the symmetric equilibrium of a two-alternative election, a voter with type/signal a is always at least as likely as a voter with signal b to vote for alternative A. Strategies follow a certain monotonicity, so that voters always either vote informatively for their signal or mix between the two alternatives. In three-alternative elections, one can investigate more complex information structures for which voting is less intuitive. There are equilibria in which voters have an incentive to vote against their own signal and vote for one or two of the other alternatives. There can be interesting tensions between posteriors and the efficient equilibrium strategy that do not exist in two-alternative elections. We investigate how voters react to these and how this impacts the efficiency of the decision. We essentially want to know whether a committee is still an efficient decision making vehicle when there are more than two alternatives and things get more complicated for the voters.

Experimentally, three-alternative elections pose yet another challenge. Goertz [3] shows that efficient equilibria exist. However, the proof is not constructive. Since strategies do not follow any nice properties, it is very hard to construct equilibria or find all the ones that exist for certain signal distributions. We chose three different signal distributions for our treatments and developed a numerical search algorithm to find the equilibria for our treatments. In treatment 1, informative voting (voting for one’s signal) is an equilibrium. In treatment 2, informative voting is not an equilibrium. One voter type mixes between all three alternatives, but there is no tension between predicted equilibrium strategies and the posteriors (see more detailed discussion below). In treatment 3, informative voting is not an equilibrium and there is a tension between predicted strategies and posteriors. So, the complexity for the voters increases from treatments 1–3.

Not surprisingly, subjects vote informatively when it is an equilibrium. But even in treatments 2 and 3, we find that voters’ behavior is very close to the predictions. As a consequence, efficiency is about as high as predicted. Following a large body of experimental literature on different Bayesian games, we calculate posterior probabilities of the different states of nature—given a subject’s signal—and post it on the computer screen for each subject before they have to cast a vote. However, we also ran a small number of sessions without posting posteriors to see whether this has any influence. We found no noteworthy difference in outcomes between sessions with and without posteriors, especially for efficiency.

In the following section, we present the theoretical model. We describe in a bit of detail how a rational voter votes in our scenario. We then present the experimental set-up, the results, and the conclusion.

2. Theoretical Background

2.1. Model

We get our theoretical predictions and the set up of the experiment from Goertz [3] which extends the previous models based on the Condorcet Jury Theorem (e.g., Wit [1] or Feddersen and Pesendorfer [2]) to three alternatives. We will keep this section brief and only highlight those aspects of the model that we need for the experiment.

Consider a committee with a finite and odd number $N\ge 3$ of voters. In all our sessions, we have $N=5$. The committee has to elect one of three alternatives from $\mathbf{K}=\{A,B,C\}$ with the simple plurality rule (one voter one vote). There are three states of nature $\{a,b,c\}=\mathbf{k}$ with prior probabilities ${\pi }_a,{\pi }_b,{\pi }_c>0$. Committee members have common, state-dependent preferences. In each state of nature, they prefer one of the three alternatives and are indifferent between the other two.

$$\begin{array}{ccc}\hfill u(X|x)& =& 1\forall X\in \mathbf{K},x\in \mathbf{k},\hfill \\ \hfill u(Y|x)& =& 0\forall Y\ne X\in \mathbf{K},x\in \mathbf{k}.\hfill \end{array}$$

Before the election, each voter receives a private signal about the state of nature that is independently drawn from a common distribution on $\{a,b,c\}=\mathbf{S}$. Denote the signal of voter i with $s_i\in \mathbf{S}$. Signals are informative but imprecise. Denote by ${\phi }_z(x)$ the probability of receiving signal x in state z. Signals are such that

$${\phi }_x(x)>{\phi }_x(y)+{\phi }_x(z)\forall x\in \mathbf{k},x\ne y\ne z\ne x\in \mathbf{S},$$

(1)

which implies that signal x occurs with a probability higher than $0.5$ in state x. This assumption is, among others, significant for the existence of an efficient equilibrium.

Committee members vote for one alternative in $\mathbf{K}$ or mix between different alternatives. Abstention is not an option. The alternative with most votes is elected. The following tie-breaking assumption applies: any tie involving alternative A is broken in favor of alternative A, and that a tie between alternatives B and C is broken in favor of alternative B.

The voting literature is typically interested in symmetric Bayesian Nash equilibria in which voters of the same type vote the same way. A voter’s type $t_i$ is defined as her private signal: $t_i=s_i$ and $\mathbf{T}=\mathbf{S}$. A strategy is a function $\sigma :\mathbf{T}\to \Delta (\mathbf{K})$, where ${\sigma }^X(t)$ is the probability that a committee member of type t chooses to vote for alternative X, and where ${\sum }_X{\sigma }^X(t)=1\forall t\in \mathbf{T}$. A strategy profile is responsive, if voters change their vote as a function of their private information with positive probability, i.e., if $\sigma (t_i)\ne \sigma (t_j)$ for at least two different $t_i,t_j\in \mathbf{T}$. The voting literature is usually interested in responsive equilibria, although it is always an equilibrium in these games if all voters vote (unresponsively) for the same alternative. A strategy profile is informative if all voters vote for their own type, i.e., ${\sigma }^X(x)=1$ for all $X\in \mathbf{K}$ and $x\in \mathbf{T}$. We occasionally use the informative voting strategy as a (naive) benchmark.

A strategy profile is efficient if the committee selects the correct alternative with a probability that is at least as high as the probability with which a single decision maker alone with one signal only would choose the correct alternative. Denote by $P_{\sigma zZ}^C$ the probability with which a committee correctly elects alternative Z in state z under strategy profile $\sigma$. The precise formulas can be found in the Appendix B. Ex-ante efficiency of a committee using strategy profile $\sigma$ can be calculated as $P_{\sigma }^C={\pi }_a{P}_{aA}^C+{\pi }_b{P}_{bB}^C+{\pi }_c{P}_{cC}^C$. The efficiency of a single decision maker is given by $P^{one}={\pi }_a{P}_{aA}^{one}+{\pi }_b{P}_{bB}^{one}+{\pi }_c{P}_{cC}^{one}$, where $P_{xX}^{one}={\pi }_x({\sum }_{y\in S}{\phi }_x(y){\sigma }_I^X(y))$ and ${\sigma }_I^X(y)$ is the probability that a single individual votes for alternative X given type y. A single individual always selects the alternative that is most likely given the posterior probabilities based on her type. Below we will indicate what ${\sigma }_I^X(y)$ is for our three treatments.3

Definition 1

(Efficient equilibrium). An equilibrium ${\sigma }_{*}$ for a committee characterized by $(\pi ,\phi )$ is efficient if $P_{{\sigma }^{*}}^C\ge P^{one}$.

Theoretically, one can only calculate ex-ante efficiencies. When we run our sessions, though, we can also compare ex-post efficiencies (i.e., the frequency with which the committee actually elected the correct alternative). Whenever it is possible, we use ex-post efficiencies rather than ex-ante ones. We call the ex-post efficiency “observed efficiency”.

In all our treatments, there exists an efficient equilibrium. On average, voters perform better than a single individual in all our sessions.

2.2. Voter Behavior

In this section, we briefly consider how a rational voter votes in this type of election. When comparing expected utilities of different ballots, voters need to consider only those events in which their vote changes the outcome of the election. These events are called pivotal events. In two-alternative elections, the only pivotal event is a tie between the two alternatives.4 In a three-alternative election, there are many more pivotal events, and the number of these events increases with the number of voters. Suppose, for example, that there are five voters, and that one of these voters considers voting for alternative A. Pivotal events occur if the other voters submit the following votes: $ABBC$ or $ABCC$. The pivotal events in three-alternative elections depend on the ballot that is considered and on the number of voters in the committee. Voters calculate the probabilities of all the pivotal events in which a vote for alternative Y changes the outcome of the election from X to Y in state z. We denote the sum of all these probabilities with $pi{v}_z^{YX}$. These probabilities are quite complex polynomials when there are more than two alternatives (see Appendix B).

Rational voters also consider the posterior probabilities of the different states of nature given their types. We denote with ${\pi }_z(t)$ the posterior probability of state z given a voter’s private type t. Now we can write the expected utility of considering a vote for alternative Y as

$$EU(Y|t)=-{\pi }_x(t)pi{v}_x^{YX}+{\pi }_y(t)pi{v}_y^{YX}+{\pi }_y(t)pi{v}_y^{YZ}-{\pi }_z(t)pi{v}_z^{YZ}.$$

(2)

If the voter is indeed most likely pivotal in state y, for example, then voting for Y is a good choice. If, however, the most likely pivotal event occurs in states x or z, then changing the outcome of the election to Y is a bad choice. The comparison of expected utilities depends on the precise interplay between pivotal and posterior probabilities.

On a sidenote, and since the comparison may interest the reader: in a two-alternative election, Equation (2) reduces to the first two terms. Without going into much detail, this implies that a voter with signal a, for example, is at least as likely to vote for alternative A as a voter with signal b. So, the prediction is that at most one voter type mixes and that either the other or both types vote informatively. Conceivably, this is not too hard for actual subjects to figure out either. It also implies that the equilibrium is unique and always efficient (e.g., Wit [1]), which is not at all the case in three-alternative elections.

3. Experimental Design and Predictions

3.1. Treatments

Table 1. Treatment design: priors and type Distributions.

Treatment	State	Priors	Type Distributions			Posteriors by Type
			a	b	c	a	b	c
1	a	$\frac{1}{3}$	$0.9$	$0.05$	$0.05$	0.9	0.05	0.05
	b	$\frac{1}{3}$	$0.05$	$0.9$	$0.05$	0.05	0.9	0.05
	c	$\frac{1}{3}$	$0.05$	$0.05$	$0.9$	0.05	0.05	0.9
2	a	$0.15$	$0.9$	$0.05$	$0.05$	0.284	0.029	0.029
	b	$0.425$	$0.4$	$0.55$	$0.05$	0.358	0.89	0.081
	c	$0.425$	$0.4$	$0.05$	$0.55$	0.358	0.081	0.89
3	a	$0.2$	$0.9$	$0.05$	$0.05$	0.36	0.04	0.04
	b	$0.4$	$0.4$	$0.55$	$0.05$	0.32	0.88	0.08
	c	$0.4$	$0.4$	$0.05$	$0.55$	0.32	0.08	0.88

shows our three treatments. $N=5$ for all treatments and sessions. Note that for the type distribution, the row entries add up to 1 (recall that a voter’s type is equal to the private signal). Consider treatment 2, for example. In state b, type a’s frequency is 0.4, type b’s 0.55, and type c’s 0.05. For the posterior probabilities, the column entries add up to 1. Consider treatment 2, for example. Given type a, for example, the posterior probabilities of states a, b, and c are 0.284, 0.358, and 0.358, respectively.

Our theoretical predictions for the treatments are in

Table 2. Predicted strategies by type: **analytical, ***numerical.

Treatment	Type	Prob. Voting for			${\mathit{P}}_{{\mathit{\sigma }}^{\mathit{I}}}^{\mathit{C}}$	${\mathit{P}}_{{\mathit{\sigma }}^{*}}^{\mathit{C}}$
		A	B	C
1 **	a	1	0	0	0.9945	0.9945
	b	0	1	0
	c	0	0	1
2 ***	a	0.379	0.235	0.386	0.6575	0.7817
	b	0	1	0
	c	0	0	1
3 ***	a	0.507	0.188	0.305	0.6775	0.7693
	b	0	1	0
	c	0	0	1

. McLennan [9] and Goertz [3] both assert that there exists an efficient equilibrium in our type of election. However, the proof in neither paper is constructive, at least not for all of our treatments. Treatment 1 is a symmetric committee. Informative voting is an equilibrium for a symmetric committee, and it is efficient (Goertz [3]). There is also another equilibrium (Goertz [3]): it is inefficient and has one of the types mixing between the two alternatives not indicated by her type (Theorems 2 and 3). This committee is a “knife-edge” committee in the sense that it is not stable to slight perturbations of the mixing probabilities or prior and type distributions. We therefore discarded it as a possible prediction for our experiment. We used numerical methods (a search algorithm) to verify that no other equilibria exist for treatment 1.5 For more details on our search algorithm, please refer to the Appendix A.

In treatments 2 and 3, informative voting was not an equilibrium. The search algorithm found the following equilibria: it returned unique responsive equilibria for treatments 2 and 3 that were also efficient. In both of these, type a voters mixed between all three alternatives while types b and c voted informatively.

The difference between treatments 2 and 3 lies in the information conveyed by the posterior and the pivotal probabilities for type a and whether the two types of information pointed in the same direction or not. In treatment 2, the posterior probabilities for a voter with type a no longer indicated strong evidence for state a. When considering voting for her type, type a also must take into account the pivotal probabilities. Those can be calculated using the formulas from the Appendix B. We only need to consider a few to see that voting for A was not necessarily a good choice: $pi{v}_a^{AB}=0.0135$, $pi{v}_a^{AC}=0.0135$, $pi{v}_b^{AB}=0.0726$, and $pi{v}_c^{AC}=0.0726$. A voter of type a would find herself most likely pivotal in states b or c when voting for A. So, voting exclusively for A was certainly not a good idea. Notice that both posterior probabilities and pivotal probabilities pointed away from voting for A exclusively. A naive voter using only posterior probabilities may vote for either B or C exclusively. A rational voter recognizes that she should mix between all three alternatives.

Treatment 3 was chosen such that posterior probabilities for a type a voter were “in favor” of voting for alternative A. When considering voting for her type, type a faced the same pivotal probabilities as in treatment 2, so a voter voting for A found herself most likely pivotal in states b and c.6 In this treatment, posterior probabilities and pivotal probabilities gave conflicting information and the differences in pivotal probabilities by far outweigh the differences in posterior probabilities. A naive voter using only posterior probabilities may vote for A exclusively in this treatment. Only a rational voter realized that pivotal probabilities need to be considered as well and that she should mix between all alternatives.

Table 2 also indicates the ex-ante efficiency of the decision under the predicted strategies, $P_{{\sigma }^{*}}^C$ (calculated using the formulas in the Appendix B). Since all voters had the same preferences, efficiency is a convenient measure of wellbeing of the voters. It measures how often the committee selects the correct alternative given a particular strategy profile. Since we occasionally used it as a naive benchmark, the table also indicates the efficiency of an informative voting profile (all voters voting for their type), denoted by $P_{{\sigma }_I}^C$.

3.2. Experimental Design

The experimental sessions were run at the Social Sciences Research Laboratory of the University of Saskatchewan, Saskatoon.7 Subjects were recruited from the undergraduate population through the participant pool of the lab and through class announcements and advertisements in various places. We ran nine sessions with a total of 106 subjects.

We chose a within-subject design: within one session, subjects went through all three treatments in different orders. The experiment was run on computer terminals in the laboratory. The experimental software was developed using zTree (Fischbacher [10]). First, a set of instructions was read aloud while participants read along. Instructions (see Appendix C) were handed out as hard copies so that participants were able to refer to them during the course of the session. Questions were answered, followed by two dry runs to familiarize the subjects with the software and the information presented on the various screens (see Appendix C).

Afterwards, subjects played 60 voting periods for cash. At the beginning of each voting period, subjects were randomly matched into different committees with five members each. Subjects knew that they were randomly matched at the beginning of each voting period and not likely to play with the same committee again. Since we typically over-recruited participants, some participants were randomly selected to be “inactive” during a particular voting period (with no information or feedback provided to them about the current period).

If a committee chose the correct alternative, each member received 100 experimental currency units (ECU). Otherwise, they received nothing. Each participant’s ECU balance at the end of the 60 periods was converted into CA$ at a rate of 200:1. In addition, subjects were paid a show-up fee of CA$ 6.

The Voting Task

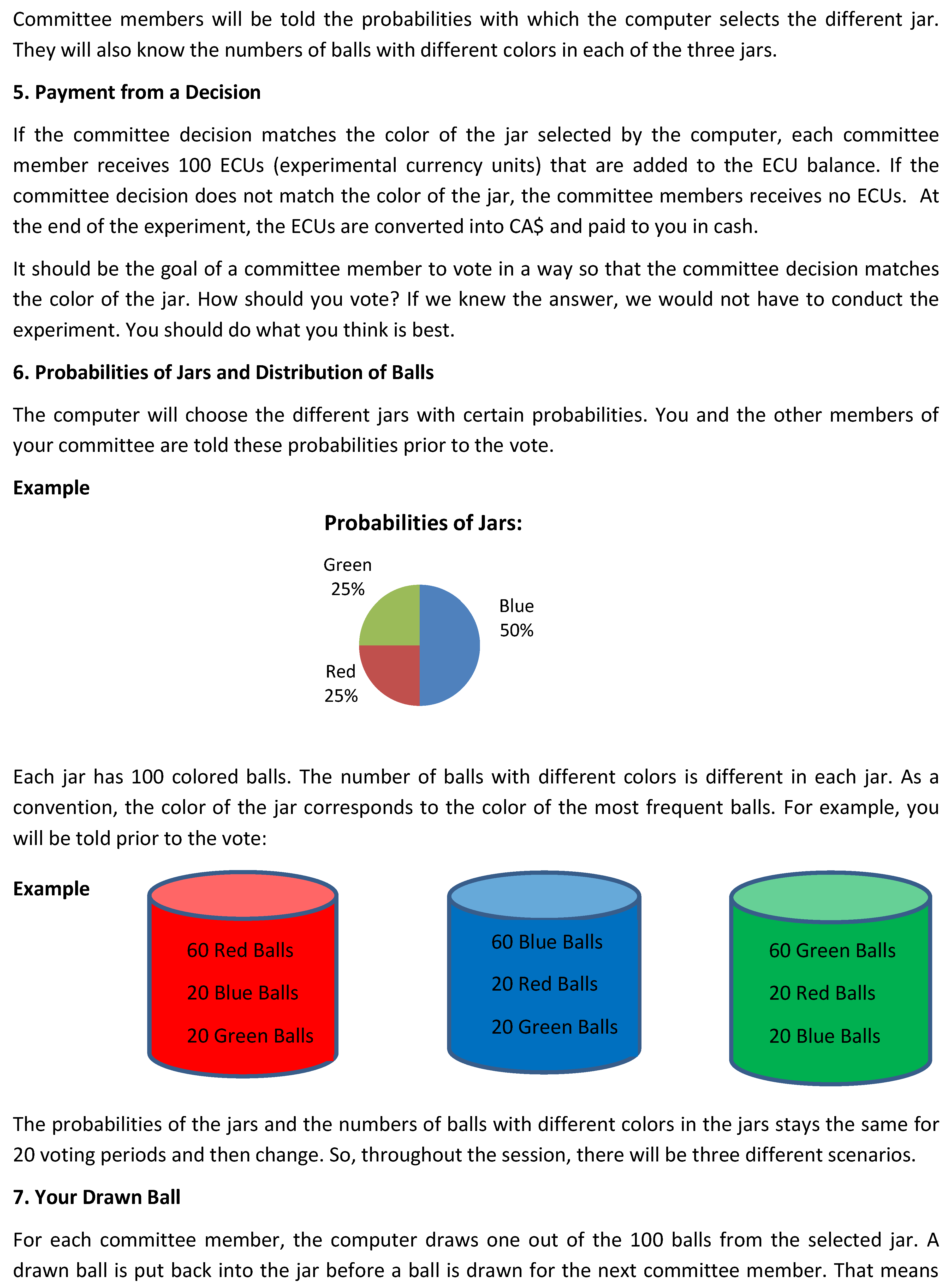
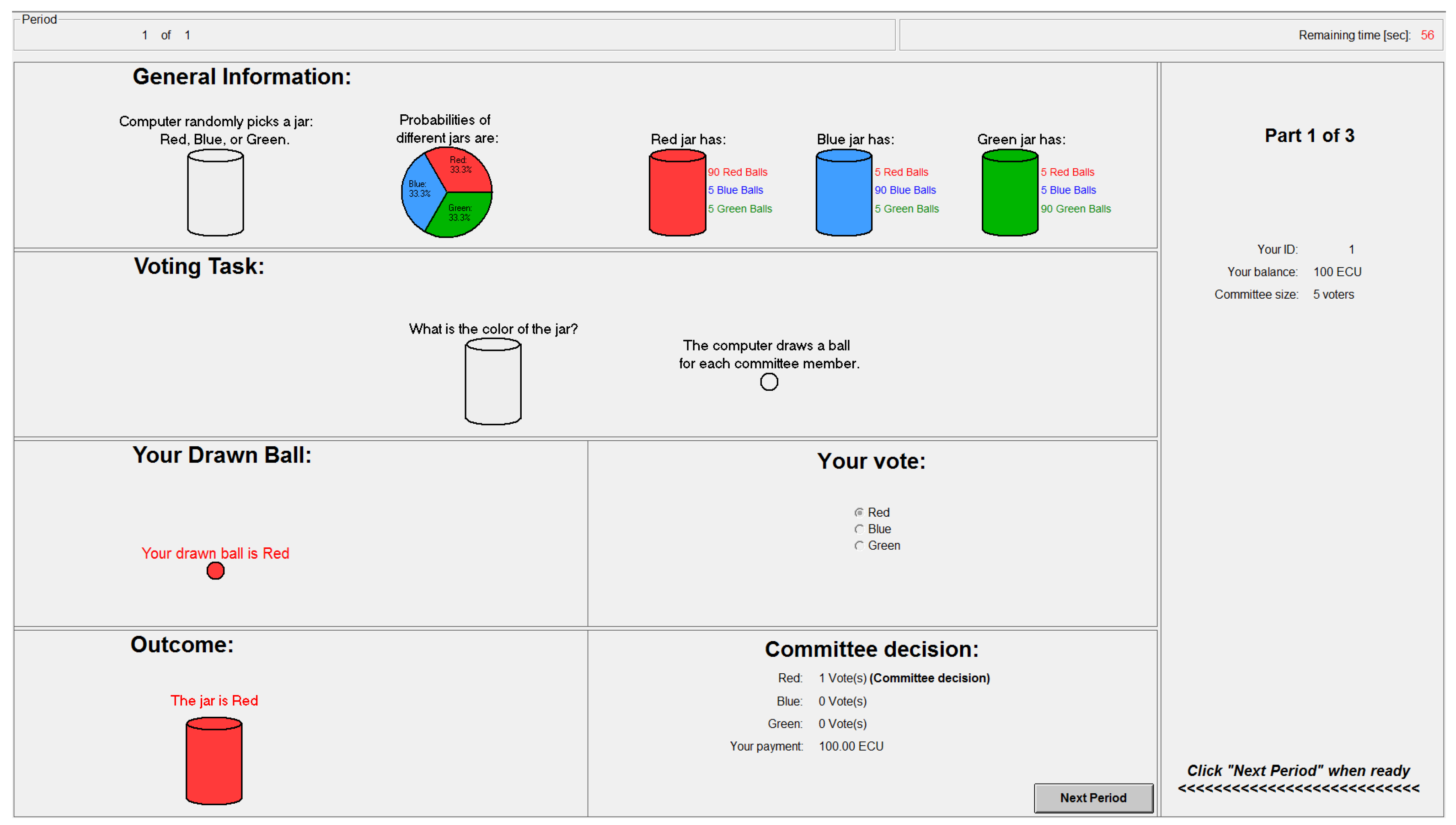
The voting task needed to be sufficiently abstract to avoid framing. We presented the task as follows (from the instructions): “there are three different jars with balls inside. Each jar has a different color: red, blue, or green. In each jar, there are 100 red, blue, and green balls, but the number of balls of different colors in each jar is different. For example, in the red jar, there will typically be more red balls than other balls... At the beginning of a voting period, the computer will randomly select one jar for each committee...If the committee decision matches the color of the jar selected by the computer, each committee member receives 100 ECUs.”

The prior and type distribution and the type of each committee member were represented as follows (from the instructions): “the computer will choose the different jars with certain probabilities. You and the other members of your committee are told these probabilities prior to the vote (probabilities are shown in pie charts). Each jar has 100 colored balls... For each committee member, the computer draws one out of the 100 balls from the selected jar. A drawn ball is put back into the jar before a ball is drawn for the next committee member... The color of your ball gives you a better idea about the likely color of the jar selected for your committee...”.

There is plenty of experimental evidence showing that subjects are generally not very good at calculating and using posterior probabilities (e.g., Charness and Levin [11]). To abstract from this known influence on voting behavior, the posterior probabilities of the different states were calculated for the committee member’s ball draw and presented in a simple pie chart (screen shots can be found in the Appendix C). The computer also indicated the posterior probabilities for all other possible ball draws to help subjects form beliefs about what others in their committee may do. Of course, they had no information about the actual colors of the balls drawn for the other committee members. In two of our sessions, we did not indicate posterior probabilities to the subjects. Surprisingly, the important findings did not change.

After 20 voting periods, we changed the treatment, so that each subject participated in each treatment. Between sessions, we also changed the order of the treatments to avoid order effects.

After each voting period, the committee members received feedback about the committee: the numbers of votes for each alternative, the committee decision, and their payment. Inactive committee members received no feedback.

4. Results

4.1. Basic Statistics

Table 3. Basic statistics.

Session	Order	Posteriors	Avg. Earnings	Subjects	No. of Committees per Period
1	1-2-3	Yes	25.75	10	2
2	1-2-3	Yes	15	9	1
3	1-2-3	Yes	24.83	15	3
4	2-1-3	Yes	26.25	10	2
5	3-2-1	Yes	25.75	10	2
6	1-2-3	Yes	20	12	2
7	3-1-2	Yes	23.67	15	3
8	1-2-3	No	21.25	12	2
9	1-2-3	No	18.85	13	2
Total			22.45 (avg.)	106	19

provides basic information about the experimental sessions.8 We conducted nine sessions which can be grouped into three waves. Sessions 1–3 had the same order of treatments (they were our pilot sessions). In sessions 4–7, we changed the order of the treatments to account for a possible order effect. Session 8 and 9 were used to test the effect of displaying posterior probabilities on the computer screens (we did not display posteriors in these sessions). We discuss the differences between sessions 1–7 and sessions 8–9 in more detail in a separate section below.

Average earnings ranged between CA$ 15 and CA$26.25 per sessions and excluded the show-up fee of CA$6. Differences in average earnings can in part be attributed to the fact that sessions had different numbers of subjects; some sessions had more, some had fewer inactive committee members who did not earn any profit in certain periods. Subjects in sessions with more inactive committee members earn less total profit. The number of five-voter committees operating simultaneously in each session is provided in the last column.

4.2. Results

As a first step, we want to investigate a really “naive” voting strategy: informative voting (i.e., naively voting for one’s signal or type). We already know from the previous literature that voters do not behave naively in two-alternative elections. But we want to verify if this is still true in the arguably more complex three-alternative elections.

Table 4. Frequencies of informative/naive voting by type and treatment.

Session	T1			T2			T3
Order of Play	a	b	c	a	b	c	a	b	c
1-2-3	1.00	0.977	0.929	0.234	0.982	0.882	0.53	0.961	1.00
1-2-3	1.00	0.969	1.00	0.233	1.00	1.00	0.933	1.00	0.968
1-2-3	0.976	0.991	0.91	0.298	1.00	0.964	0.719	0.986	0.987
2-1-3	0.984	0.947	1.00	0.194	1.00	0.98	0.596	1.00	0.982
3-2-1	1.00	1.00	0.986	0.365	0.907	0.94	0.747	0.96	0.982
1-2-3	1.00	0.988	1.00	0.265	1.00	1.00	0.707	1.00	1.00
3-1-2	0.939	0.895	0.944	0.229	0.923	0.986	0.503	0.902	0.857
1-2-3	0.917	0.89	0.913	0.281	1.00	1.00	0.563	1.00	1.00
1-2-3	0.96	0.973	1.00	0.292	1.00	0.972	0.541	1.00	1.00

shows the frequency of voting according to one’s type (informative voting) for each signal, treatment, and session. The ranking coincides with what would be expected of rational voters: All types should vote informatively in treatment 1, and types b and c should also do so in treatments 2 and 3. Voters of type a were predicted to vote more frequently for their type in treatment 3 than in treatment 2. This was exactly what we observe. Independent of the session (and therefore the order of play), the frequency of type a voting for alternative A changed between treatments. Type a subjects voted informatively with the highest frequency in treatment 1, followed by treatment 3, and with the lowest frequency in treatment 2. Notice also that the frequency of informative voting is quite close to 1 in treatment 1 for all types. Subjects understand that informative voting is the best choice in that treatment.

We can also conclude that type a voters do not use a naive voting strategy in treatments 2 and 3. Pair-wise comparison of the frequencies of type a’s informative voting between treatments were highly significant using a one-sided binomial test with sessions as the unit of observation.9 The frequency of informative voting did not change significantly in sessions 8 and 9 without posted posteriors (see more detailed discussion below).

As the next step, we investigated the complete voting strategy of each type of voter.

Table 5. Observed frequencies of voting by type (equilibrium predictions in brackets).

Type	T1			T2			T3
	A	B	C	A	B	C	A	B	C
a	0.97	0.017	0.013	0.267	0.399	0.334	0.626	0.175	0.199
	(1)	(0)	(0)	(0.379)	(0.235)	(0.386)	(0.507)	(0.188)	(0.305)
b	0.016	0.957	0.027	0.004	0.976	0.02	0.012	0.974	0.014
	(0)	(1)	(0)	(0)	(1)	(0)	(0)	(1)	(0)
c	0.018	0.023	0.959	0.002	0.03	0.968	0.004	0.027	0.969
	(0)	(0)	(1)	(0)	(0)	(1)	(0)	(0)	(1)

presents the average voting strategy of the subjects by type (frequencies of voting for the three different alternatives by type). As predicted, voters with types b and c voted informatively with a very high frequency (very close to 1) in all three treatments. Type a, on average, voted informatively in treatment 1 and mixed between all three alternatives in treatments 2 and 3.

For comparison, the table also shows the predicted mixing probabilities for rational voters (in brackets). Type a’s frequency of voting for the different alternatives changed qualitatively according to the equilibrium predictions in all three treatments. In fact, the frequencies were remarkably close to the predicted frequencies.10

The predicted strategies for type a in treatments 2 and 3 call for mixing between the three alternatives. On average, subjects do just that. One may wonder, however, whether this is just the result of taking an average over different subjects who each, individually, use different pure strategies. We checked individual voting behavior: voters of all types in treatment 1 and voters of types b and c mostly used pure (informative) strategies; voters of type a in treatments 2 and 3 do not.

Posterior Voting. How much of the observed behavior is influenced by the fact that posterior probabilities are posted? Do voters vote as indicated by the posterior probabilities (i.e., vote for the alternative that has the largest posterior probability given their signal)? In most of our cases, posterior voting coincided with informative/naive voting. So, whenever we can reject informative voting as an explanation of voting behavior, we can also reject posterior voting. There was only one case in which the two types of strategies differed: type a in treatment 2. Unfortunately, in that case, the prediction for posterior voting was not clear-cut. Given a voter’s type is a, states b and c were both the most likely states. So, a reasonable posterior voting strategy is any probability distribution over alternatives B and C, including voting exclusively for B or voting exclusively voting for C. Nevertheless, we do not believe that type a voters engaged in posterior voting in this case because they voted for alternative A with a relatively high probability as well. In addition, the important findings were similar in sessions with and without posted posteriors (see more detailed discussion below).

We also investigated how subjects fared in terms of efficiency.

Table 6. Efficiency.

Session	Order		T1	T2	T3
1	1-2-3		1	0.775	0.8
2	1-2-3		1	0.9	0.8
3	1-2-3		1	0.8	0.683
4	2-1-3		1	0.85	0.8
5	3-2-1		1	0.75	0.825
6	1-2-3		0.975	0.75	0.675
7	3-1-2		0.983	0.8	0.583
8 (no post.)	1–2–3		0.975	0.7	0.875
9 (no post.)	1–2–3		0.975	0.775	0.7
Total			0.989	0.782	0.734
		Single Decision Maker	0.9	0.6375	0.62
		Informative/naive Voting	0.989	0.703	0.679
		Equilibrium	0.989	0.799	0.763

shows the average efficiency of the subjects by treatments and compares it to several benchmarks. The first was the efficiency of a single decision maker. The second benchmark was the efficiency of the theoretically predicted equilibrium strategy profile. Since we used it as a naive benchmark, we also include the efficiency of an informative voting profile as another benchmark.

The equilibrium benchmark and the naive (informative) benchmark were calculated using the actual type draws from the experimental data. We obtained the informative benchmark by simply replacing the votes observed in the data with votes that correspond to the voters’ types and calculating the efficiency of the resulting outcomes. The equilibrium benchmark was calculated using simulations to get a relatively precise efficiency measure in the setting where players use mixed strategies. For each actual committee vote in the experimental data, we simulated 800 alternative votes based on the same type draws but employing the equilibrium mixed strategies. The single-individual benchmark was calculated as ${\sum }_{x\in k}{\pi }_x\left({\sum }_{y\in S}{\phi }_x\left(y\right){\sigma }_I^X\left(y\right)\right)$ where ${\sigma }_I^X\left(y\right)$ is the probability that a single individual votes for alternative X given type y. The single individual votes for the alternative that was most likely correct based on the posterior probabilities. So, in treatments 1 and 3, ${\sigma }_I^X(x)=1$ and ${\sigma }_I^X(y)=0$ for all types. In treatment 2, ${\sigma }_I^B(b)={\sigma }_I^C(c)=1$ and ${\sigma }_I^B(a)+{\sigma }_I^C(a)=1$. In the literature on small committees, a committee was considered efficient if it elected the correct alternative with a higher probability than a single individual alone. This was clearly true in all our cases.

Average efficiency was relatively high in all treatments—higher than the single-decision-maker and also (in treatments 2 and 3) higher than the informative-voting strategy profile. It was a bit lower than the equilibrium benchmark in treatments 2 and 3, which is not surprising given that average strategies were not quite the same as equilibrium strategies.

We verified some of the above observations with statistical tests. Efficiency was highest in treatment 1 (binomial test, p-value < 0.002).11 Consistent with the equilibrium, efficiency was higher in treatment 2 than in treatment 3, but the pattern cannot be confirmed statistically with sessions as the unit of observation. When we compared observed and predicted efficiency, we found that in treatment 1 observed efficiency was no lower than the equilibrium benchmark (binomial test, p-value < 0.05). In treatments 2 and 3, we found that they were not significantly different. Even though strategies were not quite as predicted, efficiency did not suffer. It was not significantly lower than it should have been if subjects played precisely the equilibrium strategies. That was quite reassuring for committees with uncertainty and maybe a bit surprising at first, given that subjects do not play precise equilibrium strategies.

Comparing efficiency to the naive informative-voting benchmark, we found—not surprisingly—that observed efficiency in treatment 1 was no lower than the benchmark (binomial test, p-value < 0.05). We also verified that observed efficiency in treatments 2 and 3 was higher than under the benchmark (p-value < 0.05 and $0.1$, respectively).

Table 7. Efficiency by state compared to benchmarks.

	T2			T3
	a	b	c	a	b	c
Observed	0.368	0.918	0.783	0.753	0.714	0.742
Equilibrium	0.445	0.856	0.867	0.652	0.755	0.823
Informative/Naive	0.982	0.643	0.664	0.987	0.543	0.65

displays the observed efficiencies by state for treatments 2 and 3 and compares them to the equilibrium benchmark and the informative/naive benchmark. In both treatments, observed efficiency was lower than predicted by the equilibrium in at least one state and higher in the other(s). In treatment 2, type a voters voted a bit too often for alternative B at the expense of alternatives A and C (see Table 5). So, we found a higher efficiency in state b and lower efficiencies in states a and c. In treatment 3, type a voters vote too often for alternative A (see Table 5). So, we get higher efficiency in state a, but lower efficiencies in states b and c.

4.3. Effect of Posting Posterior Probabilities

Given the importance of posterior probabilities in this setting, we investigate in this section whether any of the previous results are influenced by calculating and posting posterior probabilities for the subjects. In sessions 8 and 9, we posted prior and type distributions just as before, but omitted the posterior probabilities on the computer screens (see screenshots in the Appendix C). We repeated some of our analysis above while looking at sessions 1–7 and sessions 8 and 9 separately to see if there are any significant differences. We focused our analysis on the one voter type on which posting posteriors likely had the largest influence—type a—and on the efficiency of the voting decision.

Table 8. Informative/naive voting of type a.

	Treatments			Differences
	T1	T2	T3	T1–T3	T2–T3	T1–T2
No Posteriors	0.939	0.286	0.551	0.388	-0.265	0.653
Posteriors	0.98	0.262	0.647	0.333	-0.385	0.718
Combined	0.97	0.267	0.626	0.344	-0.359	0.703
No Post.- Post.	−0.041	0.024	−0.096

presents the frequency of informative/naive voting for type a with and without posteriors. The last three columns show the differences in frequencies between treatments, calculated separately for sessions with and without posteriors. The key takeaway from these results is that the treatment effects were consistent and similar in magnitude regardless of the information condition. Frequency rankings across treatments were the same for sessions with and without posteriors. The last row of the table shows the differences in frequencies between sessions with and without posteriors. These are the effects of omitting posterior information for each treatment. Relative to the treatment effects, omitting posterior probabilities had little effect on voting behavior.

To evaluate statistical significance of these differences, we estimated a logit model with subject and session random effects (a special case of a hierarchical/mixed-effects model):

• $y_{sij}^{k\ast }={\beta }_0+{\displaystyle \sum _{t=1}^2}{\delta }_{t}TREA{T}_t+{\displaystyle \sum _{t=1}^3}{\gamma }_{t}TREA{T}_t\times NOINFO+v_s+u_{si}+e_{sij}$,
• $y_{sij}^k=1$ if $y_{sij}^{k\ast }>0$ and 0 otherwise.

The dependent variable $y_{sij}^k$ is a dummy variable indicating a vote for alternative k (A, B, or C) in session s by subject i in period j. $TREA{T}_t$ are treatment dummies (treatment 3 dummy is omitted). $NOINFO$ is a dummy variable equal to 1 if posterior information is omitted, and equal to 0 otherwise. We also estimated an alternative specification with a dummy variable $INFO=1-NOINFO$ instead of $NOINFO$ to vary the base case. The model error consists of a session random effect $v_s$, a subject random effect $u_{si}$, and a random error $e_{sij}$. Inclusion of the random effects allows for non-independence of decisions by the same subject as well as within a session.

In this formulation, the sign and statistical significance of coefficients ${\delta }_t$ correspond to the differences between treatments reported in Table 8. The sign and statistical significance of coefficients ${\gamma }_t$ correspond to the differences between information conditions (posteriors or not) given in the last row of Table 8.

Table 9. Treatment and information (posting posteriors) effects on voting of type a.

	(1)	(2)	(3)	(4)	(5)	(6)
	Vote A	Vote A	Vote B	Vote B	Vote C	Vote C
TREAT1	3.7090 ${}^{***}$	2.9835 ${}^{***}$	−3.1215 ${}^{***}$	−1.9966 ${}^{***}$	−3.6967 ${}^{***}$	−3.1606 ${}^{***}$
	[0.3644]	[0.4088]	[0.4654]	[0.5205]	[0.5481]	[0.5724]
TREAT2	−2.0544 ${}^{***}$	−1.5798 ${}^{***}$	1.3900 ${}^{***}$	1.4305 ${}^{***}$	1.0990 ${}^{***}$	0.3836
	[0.1390]	[0.2605]	[0.1386]	[0.2760]	[0.1493]	[0.2611]
TREAT1 x NOINFO	−1.2132 ${}^{**}$		0.9496		1.2604
	[0.5991]		[0.7214]		[0.8438]
TREAT2 x NOINFO	−0.0132		−0.1348		0.0089
	[0.3766]		[0.3329]		[0.4125]
TREAT3 x NOINFO	−0.4877		−0.1753		0.7243 ${}^{*}$
	[0.3598]		[0.3609]		[0.4180]
TREAT1 x INFO		1.2132 ${}^{**}$		−0.9496		−1.2604
		[0.5991]		[0.7214]		[0.8438]
TREAT2 x INFO		0.0132		0.1348		−0.0089
		[0.3766]		[0.3329]		[0.4125]
TREAT3 x INFO		0.4877		0.1753		−0.7243 ${}^{*}$
		[0.3598]		[0.3609]		[0.4180]
Constant	0.7827 ${}^{***}$	0.2949	−1.8872 ${}^{***}$	−2.0625 ${}^{***}$	−2.0938 ${}^{***}$	−1.3695 ${}^{***}$
	[0.1746]	[0.3148]	[0.1735]	[0.3217]	[0.2123]	[0.3657]
Log likelihood	−1097.859	−1097.859	−998.330	−998.330	−920.495	−920.495
N	2443	2443	2443	2443	2443	2443

Standard errors in brackets. * $p<0.1$, ** $p<0.05$, *** $p<0.01$.

reports estimation results for informative/naive voting of type a (models (1) and (2)) as well as type a’s voting for the other alternatives (models (3)–(6)). Model (1) estimates of coefficients on $TREAT$ variables confirm that treatment differences (T1–T3 and T2–$T3$) in the “posteriors” row of Table 8 are highly statistically significant. The corresponding estimates in model (2) produce the same conclusion for the “no posteriors” row. Therefore, the treatment effects are statistically significant in both information conditions. Estimates of coefficients on the interaction terms in model (1) indicate that the effect of omitting posteriors information is not significant except in treatment 1. Informative/naive voting is the equilibrium strategy in treatment 1, and it is not clear why type a vote informatively less frequently without posteriors. Estimates of models (3)–(6) are also in line with predicted treatment effects on type a’s voting for B and C while showing essentially no impact of omitting posteriors.

We further investigated the impact of posterior information on efficiency.

Table 10. Efficiency.

	Treatments			Differences
	T1	T2	T3	T1–T3	T2–T3	T1–T2
No Posteriors	0.975	0.738	0.788	0.187	−0.050	0.237
Posteriors	0.993	0.793	0.720	0.273	0.073	0.200
Combined	0.989	0.782	0.734	0.255	0.048	0.207
No Post.- Post.	−0.018	−0.055	0.068

reports efficiency differences between treatments and information conditions. We again used a logit model to assess statistical significance of the differences:

• $y_{sj}^{*}={\beta }_0+{\displaystyle \sum _{t=1}^2}{\delta }_{t}TREA{T}_t+{\displaystyle \sum _{t=1}^3}{\gamma }_{t}TREA{T}_t\times NOINFO+v_s+e_{sj}$,
• $y_{sj}=1$ if $y_{sj}^{*}>0$ and 0 otherwise.

In this case, the dependent variable $y_{sj}$ is a dummy variable equal to 1 if a committee voted for the preferred (efficient) alternative in session s and election j, and 0 otherwise. The model includes session random effects $v_s$.

Table 11. Treatment and information effects (posting posteriors) on efficiency.

	(1)	(2)	(3)	(4)
	Efficient Outcome	Efficient Outcome	Efficient Outcome	Efficient Outcome
TREAT1	4.0605 ${}^{***}$	2.3543 ${}^{***}$	3.6595 ${}^{***}$	2.6314 ${}^{***}$
	[0.7211]	[0.7666]	[0.7237]	[0.7599]
TREAT2	0.4009 ${}^{**}$	−0.2771
	[0.1921]	[0.3733]
TREAT3			−0.4009 ${}^{**}$	0.2771
			[0.1921]	[0.3733]
TREAT1 x NOINFO	−1.3436		−1.3436
	[1.0096]		[1.0096]
TREAT2 x NOINFO	−0.3154		−0.3154
	[0.2967]		[0.2967]
TREAT3 x NOINFO	0.3626		0.3626
	[0.3069]		[0.3069]
TREAT1 x INFO		1.3436		1.3436
		[1.0096]		[1.0096]
TREAT2 x INFO		0.3154		0.3154
		[0.2967]		[0.2967]
TREAT3 x INFO		−0.3626		−0.3626
		[0.3069]		[0.3069]
Constant	0.9483 ${}^{***}$	1.3109 ${}^{***}$	1.3492 ${}^{***}$	1.0338 ${}^{***}$
	[0.1346]	[0.2767]	[0.1485]	[0.2577]
Log likelihood	−439.530	−439.530	−439.530	−439.530
N	1140	1140	1140	1140

Standard errors in brackets. * $p<0.1$, ** $p<0.05$, *** $p<0.01$.

reports estimation results of the stated model (model (1)), as well as models with $INFO$ dummy instead of $NOINFO$ (models (2) and (4)), and models that omit treatment 2 dummy instead of treatment 3 dummy (models (3) and (4)). Lack of significance of estimates on interaction terms indicates that we are unable to detect differences in efficiency as a result of omitting posteriors. At the same time, significant coefficients on $TREA{T}_1$ in all models indicate that the differences T1–$T3$ and T1–$T2$ are statistically significant with and without posteriors. The difference $T2$–$T3$ is statistically significant and has the correct sign with posteriors (coefficients on $TREA{T}_2$ in model (1)) but is not significant without posteriors (coefficients on $TREA{T}_2$ in model (2)).

5. Conclusions

Our findings suggest that small committees remain an efficient vehicle for information aggregation in elections with three alternatives—despite the fact that they are more complex for voters than two-alternative elections. Surprisingly, we also find that the important findings remain the same whether or not we calculate and post posterior probabilities for the subjects.

Our main focus lies on voter behavior and efficiency in three different treatments (signal distributions) that pose different strategic challenges. So, we chose treatments for which—according to our search algorithm—the responsive equilibrium is unique and efficient (except for treatment 1, for which an “unstable” knife-edge equilibrium also exists). We leave it to future research to investigate other treatments in which efficient and more “plausible” inefficient equilibria co-exist. It would be interesting to see whether voters continue coordinating on the efficient equilibria or whether they also coordinate on the inefficient ones. In this sense, three-alternative elections remain an interesting scenario to be investigated further (recall that in two-alternative elections, the committee equilibrium is always unique and efficient). Since general theoretical results remain elusive, our search algorithm can be a useful tool for constructing the desired treatments.