Voting in Three-Alternative Committees: An Experiment
Abstract
1. Introduction
2. Theoretical Background
2.1. Model
2.2. Voter Behavior
3. Experimental Design and Predictions
3.1. Treatments
3.2. Experimental Design
The Voting Task
4. Results
4.1. Basic Statistics
4.2. Results
4.3. Effect of Posting Posterior Probabilities
- ,
- if and 0 otherwise.
- ,
- if and 0 otherwise.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Numerical Search Algorithm
- The number of digits will always be limited.
- The choice of the acceptable difference in expected utilities needs to be specified ex-ante. Unfortunately, expected utilities may differ vastly for different s and this cannot be known ex-ante. So, if the acceptable difference is too small, the algorithm may miss certain equilibria. If it is too large, computational effort is not reduced. This problem remains, even if we use relative differences rather than absolute differences.
- Expected utilities may not change continuously. If the initial number of digits is not large enough, then expected utilities may never get close enough to qualify for a finer grid search. The inefficient equilibrium in Theorem 2 of Goertz [3] is an example.
Appendix B. Probability Formulas
Appendix B.1. Pivotal Probabilities
Appendix B.2. Committee Probabilities
Appendix C. Experimental Instructions and Screen Shots

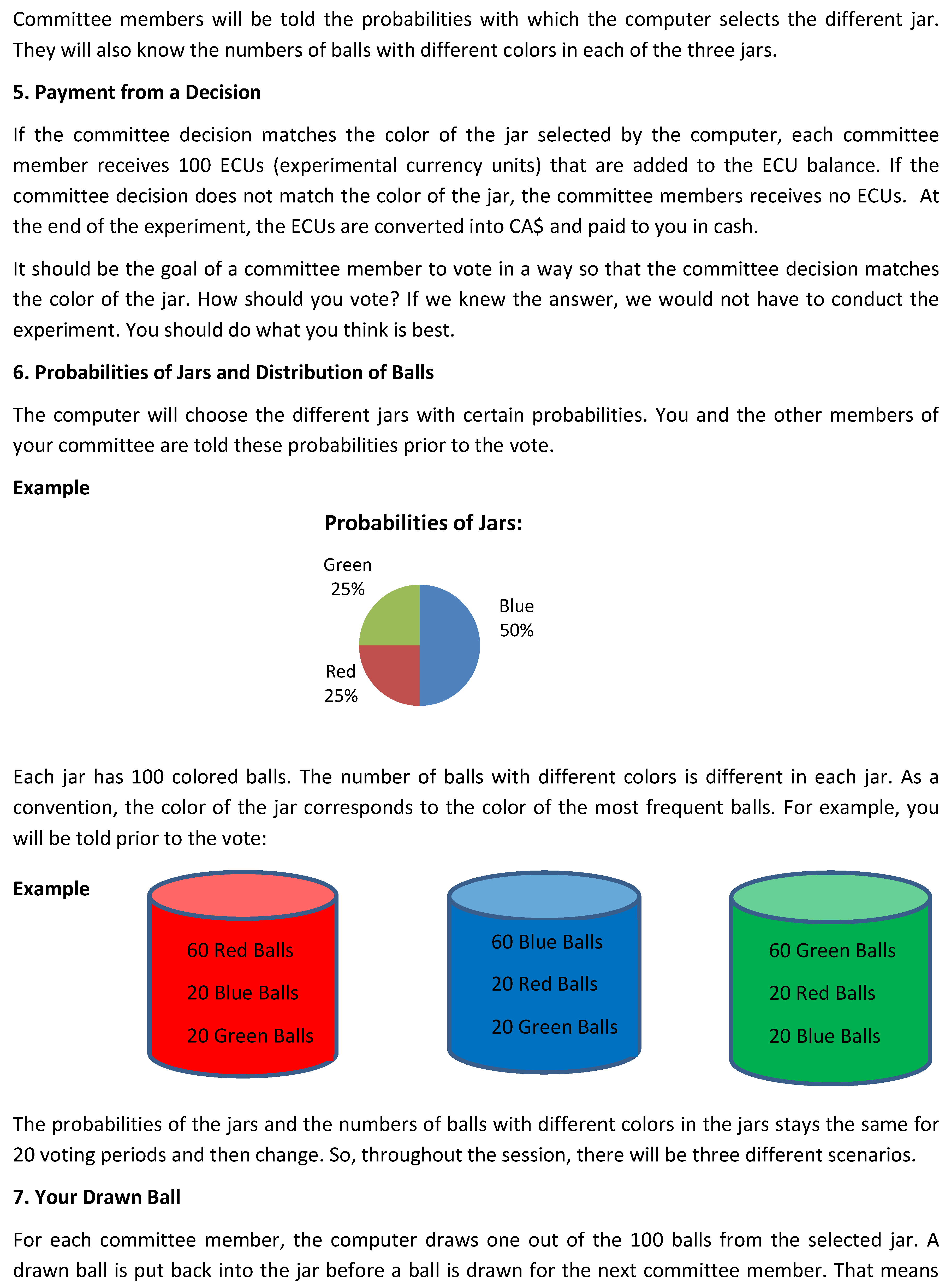



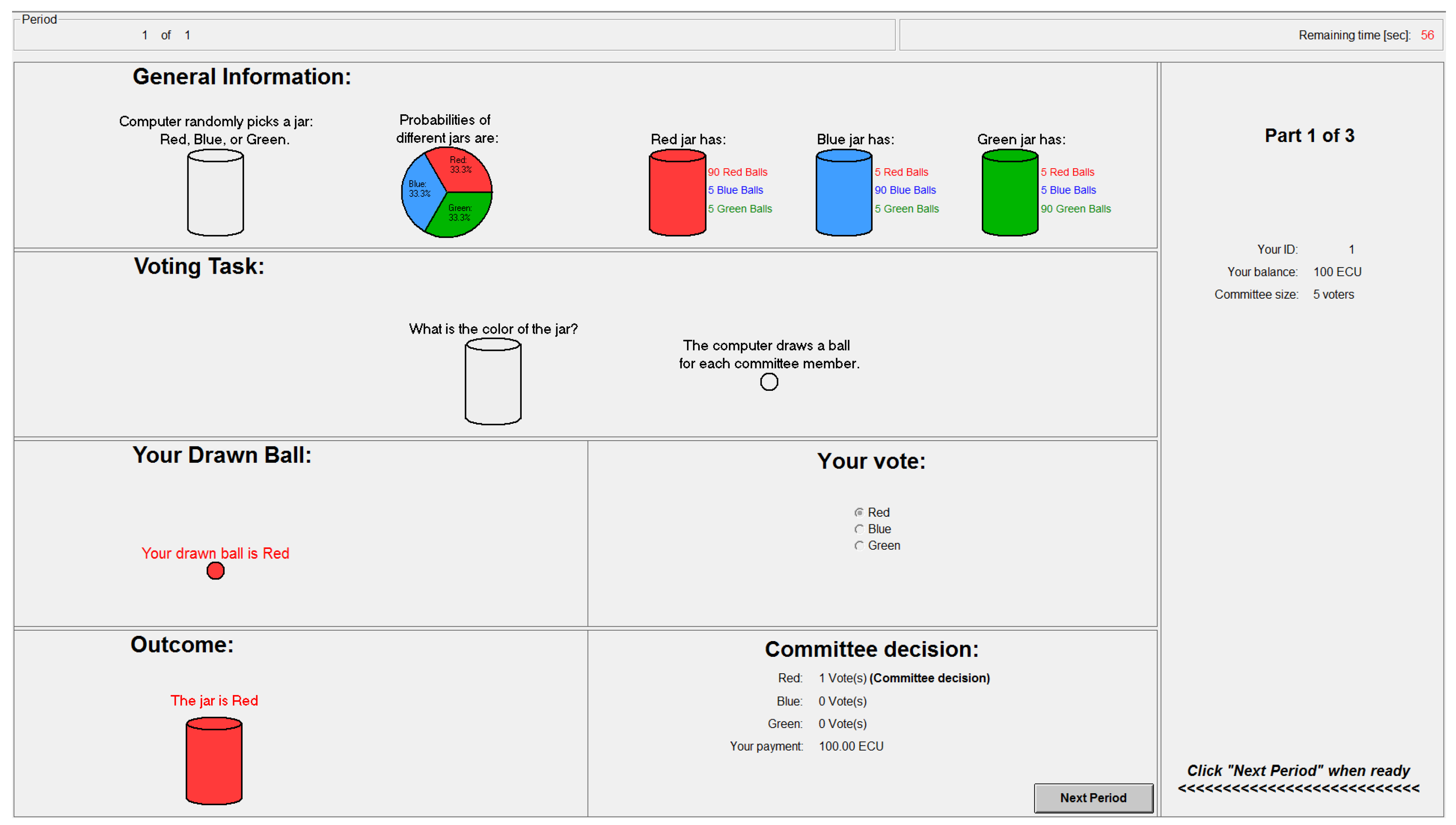
References
- Wit, J. Rational Choice and the Condorcet Jury Theorem. Games Econ. Behav. 1998, 22, 364–376. [Google Scholar] [CrossRef]
- Feddersen, T.; Pesendorfer, W. Convicting the Innocent: The Inferiority of Unanimous Jury Verdicts under Strategic Voting. Am. Political Sci. Rev. 1998, 92, 23–35. [Google Scholar] [CrossRef]
- Goertz, J.M. Inefficient Committees: Small Elections with Three Alternatives. Soc. Choice Welf. 2014, 43, 357–375. [Google Scholar] [CrossRef]
- Gerling, K.; Grüner, H.P.; Kiel, A.; Schulte, E. Information Acquisition and Decision Making in Committees: A Survey. Eur. J. Political Econ. 2005, 21, 563–597. [Google Scholar] [CrossRef]
- Palfrey, T.R. Experiments in Political Economy. In Handbook of Experimental Economics Vol. 2; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Bouton, L.; Castanheira, M.; Llorente-Saguer, A. Multicandidate Elections: Aggregate Uncertainty in the Laboratory. Games Econ. Behav. 2017, 101, 132–150. [Google Scholar] [CrossRef] [PubMed]
- Bouton, L.; Castanheira, M.; Llorente-Saguer, A. Divided Majority and Information Aggregation: Theory and Experiment. J. Public Econ. 2016, 134, 114–128. [Google Scholar] [CrossRef]
- Goertz, J.M.; Maniquet, F. On the Informational Efficiency of Simple Scoring Rules. J. Econ. Theory 2011, 146, 1464–1480. [Google Scholar] [CrossRef][Green Version]
- McLennan, A. Consequences of the Condorcet Jury Theorem for Beneficial Information Aggregation by Rational Agents. Am. Political Sci. Rev. 1998, 92, 413–418. [Google Scholar] [CrossRef]
- Fischbacher, U. zTree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Charness, G.; Levin, D. When Optimal Choices Feel Wrong; A Laboratory Study of Bayesian Updating, Complexity, and Affect. Am. Econ. Rev. 2005, 95, 1300–1309. [Google Scholar] [CrossRef]
| 1. | The original CJT considers only two alternatives, so most theoretical models keep that assumption. Goertz [3] restricts her attention to three alternatives. General results for any number of alternatives seem currently out of reach. |
| 2. | Note that there are several other papers that show the same in closely related models for two alternatives. There is also a large body of literature on large elections in which the number of voters is uncertain and converges to infinity. Those are not so closely related because the theoretical analysis is quite different (although the predictions tend to be similar). |
| 3. | For the sake of comparison: The efficiency benchmark is quite different in large elections. As , a limit equilibrium in a large election is efficient if it is true that for all alternatives X and states of nature x (n is the mean of random variable N). That implies that a limit equilibrium with as is only efficient if the correct alternative is chosen with probability 1 in each state of nature (e.g., Goertz and Maniquet [8]). In the literature, this definition is sometimes referred to as “full-information equivalence” because it requires the outcome of the election to be the same as it would be if all private signals were public information. For a large election, the law of large numbers implies that the state of nature can be inferred if all signals are publicly observable. |
| 4. | In most models of two-alternative elections, the number of voters is assumed to be odd. If it is even, then pivotal events are different from ties. |
| 5. | In this type of a voting game, it is always an equilibrium for all types to vote for the same alternative. Those are typically called unresponsive equilibria. The algorithm finds these as well. However, they are not particularly useful as predictions for experimental data because subjects never appear to use these types of strategies. |
| 6. | When type a considers voting for her type, pivotal probabilities were the same in treatments 2 and 3 because type distributions are the same in both treatments. Pivotal probabilities depend on the probabilities with which a random voter votes for a certain alternative, which are equal to type distributions when voters vote for their types. |
| 7. | Ethics approval was obtained from the Research Ethics Boards at the University of Guelph and the University of Saskatchewan, Saskatoon. |
| 8. | The data can be found as supplementary material. |
| 9. | Nine out of nine successes, , with the null of prob . Similar binomial tests were performed in other cases, unless otherwise stated. |
| 10. | Despite qualitative support for comparative statics, the results differ systematically from theoretical point predictions. In treatments 2 and 3, type a’s probability of voting for A, B, and C are different from the equilibrium mixed strategy (p-value < 0.002, except for B in treatment 3). |
| 11. | In binomial tests of comparison to benchmarks, we used session-level benchmark values rather than the overall benchmark averages reported in Table 6. |
| 12. | Although, even solving for may not be straightforward because the first order condition of is a polynomial of order which does not have a general solution for every N and may not even have a real root. |
| Treatment | State | Priors | Type Distributions | Posteriors by Type | ||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | |||
| 1 | a | 0.9 | 0.05 | 0.05 | ||||
| b | 0.05 | 0.9 | 0.05 | |||||
| c | 0.05 | 0.05 | 0.9 | |||||
| 2 | a | 0.284 | 0.029 | 0.029 | ||||
| b | 0.358 | 0.89 | 0.081 | |||||
| c | 0.358 | 0.081 | 0.89 | |||||
| 3 | a | 0.36 | 0.04 | 0.04 | ||||
| b | 0.32 | 0.88 | 0.08 | |||||
| c | 0.32 | 0.08 | 0.88 | |||||
| Treatment | Type | Prob. Voting for | ||||
|---|---|---|---|---|---|---|
| A | B | C | ||||
| 1 ** | a | 1 | 0 | 0 | 0.9945 | 0.9945 |
| b | 0 | 1 | 0 | |||
| c | 0 | 0 | 1 | |||
| 2 *** | a | 0.379 | 0.235 | 0.386 | 0.6575 | 0.7817 |
| b | 0 | 1 | 0 | |||
| c | 0 | 0 | 1 | |||
| 3 *** | a | 0.507 | 0.188 | 0.305 | 0.6775 | 0.7693 |
| b | 0 | 1 | 0 | |||
| c | 0 | 0 | 1 | |||
| Session | Order | Posteriors | Avg. Earnings | Subjects | No. of Committees per Period |
|---|---|---|---|---|---|
| 1 | 1-2-3 | Yes | 25.75 | 10 | 2 |
| 2 | 1-2-3 | Yes | 15 | 9 | 1 |
| 3 | 1-2-3 | Yes | 24.83 | 15 | 3 |
| 4 | 2-1-3 | Yes | 26.25 | 10 | 2 |
| 5 | 3-2-1 | Yes | 25.75 | 10 | 2 |
| 6 | 1-2-3 | Yes | 20 | 12 | 2 |
| 7 | 3-1-2 | Yes | 23.67 | 15 | 3 |
| 8 | 1-2-3 | No | 21.25 | 12 | 2 |
| 9 | 1-2-3 | No | 18.85 | 13 | 2 |
| Total | 22.45 (avg.) | 106 | 19 |
| Session | T1 | T2 | T3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Order of Play | a | b | c | a | b | c | a | b | c |
| 1-2-3 | 1.00 | 0.977 | 0.929 | 0.234 | 0.982 | 0.882 | 0.53 | 0.961 | 1.00 |
| 1-2-3 | 1.00 | 0.969 | 1.00 | 0.233 | 1.00 | 1.00 | 0.933 | 1.00 | 0.968 |
| 1-2-3 | 0.976 | 0.991 | 0.91 | 0.298 | 1.00 | 0.964 | 0.719 | 0.986 | 0.987 |
| 2-1-3 | 0.984 | 0.947 | 1.00 | 0.194 | 1.00 | 0.98 | 0.596 | 1.00 | 0.982 |
| 3-2-1 | 1.00 | 1.00 | 0.986 | 0.365 | 0.907 | 0.94 | 0.747 | 0.96 | 0.982 |
| 1-2-3 | 1.00 | 0.988 | 1.00 | 0.265 | 1.00 | 1.00 | 0.707 | 1.00 | 1.00 |
| 3-1-2 | 0.939 | 0.895 | 0.944 | 0.229 | 0.923 | 0.986 | 0.503 | 0.902 | 0.857 |
| 1-2-3 | 0.917 | 0.89 | 0.913 | 0.281 | 1.00 | 1.00 | 0.563 | 1.00 | 1.00 |
| 1-2-3 | 0.96 | 0.973 | 1.00 | 0.292 | 1.00 | 0.972 | 0.541 | 1.00 | 1.00 |
| Type | T1 | T2 | T3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | |
| a | 0.97 | 0.017 | 0.013 | 0.267 | 0.399 | 0.334 | 0.626 | 0.175 | 0.199 |
| (1) | (0) | (0) | (0.379) | (0.235) | (0.386) | (0.507) | (0.188) | (0.305) | |
| b | 0.016 | 0.957 | 0.027 | 0.004 | 0.976 | 0.02 | 0.012 | 0.974 | 0.014 |
| (0) | (1) | (0) | (0) | (1) | (0) | (0) | (1) | (0) | |
| c | 0.018 | 0.023 | 0.959 | 0.002 | 0.03 | 0.968 | 0.004 | 0.027 | 0.969 |
| (0) | (0) | (1) | (0) | (0) | (1) | (0) | (0) | (1) | |
| Session | Order | T1 | T2 | T3 | |
|---|---|---|---|---|---|
| 1 | 1-2-3 | 1 | 0.775 | 0.8 | |
| 2 | 1-2-3 | 1 | 0.9 | 0.8 | |
| 3 | 1-2-3 | 1 | 0.8 | 0.683 | |
| 4 | 2-1-3 | 1 | 0.85 | 0.8 | |
| 5 | 3-2-1 | 1 | 0.75 | 0.825 | |
| 6 | 1-2-3 | 0.975 | 0.75 | 0.675 | |
| 7 | 3-1-2 | 0.983 | 0.8 | 0.583 | |
| 8 (no post.) | 1–2–3 | 0.975 | 0.7 | 0.875 | |
| 9 (no post.) | 1–2–3 | 0.975 | 0.775 | 0.7 | |
| Total | 0.989 | 0.782 | 0.734 | ||
| Single Decision Maker | 0.9 | 0.6375 | 0.62 | ||
| Informative/naive Voting | 0.989 | 0.703 | 0.679 | ||
| Equilibrium | 0.989 | 0.799 | 0.763 |
| T2 | T3 | |||||
|---|---|---|---|---|---|---|
| a | b | c | a | b | c | |
| Observed | 0.368 | 0.918 | 0.783 | 0.753 | 0.714 | 0.742 |
| Equilibrium | 0.445 | 0.856 | 0.867 | 0.652 | 0.755 | 0.823 |
| Informative/Naive | 0.982 | 0.643 | 0.664 | 0.987 | 0.543 | 0.65 |
| Treatments | Differences | |||||
|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T1–T3 | T2–T3 | T1–T2 | |
| No Posteriors | 0.939 | 0.286 | 0.551 | 0.388 | -0.265 | 0.653 |
| Posteriors | 0.98 | 0.262 | 0.647 | 0.333 | -0.385 | 0.718 |
| Combined | 0.97 | 0.267 | 0.626 | 0.344 | -0.359 | 0.703 |
| No Post.- Post. | −0.041 | 0.024 | −0.096 | |||
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Vote A | Vote A | Vote B | Vote B | Vote C | Vote C | |
| TREAT1 | 3.7090 | 2.9835 | −3.1215 | −1.9966 | −3.6967 | −3.1606 |
| [0.3644] | [0.4088] | [0.4654] | [0.5205] | [0.5481] | [0.5724] | |
| TREAT2 | −2.0544 | −1.5798 | 1.3900 | 1.4305 | 1.0990 | 0.3836 |
| [0.1390] | [0.2605] | [0.1386] | [0.2760] | [0.1493] | [0.2611] | |
| TREAT1 x NOINFO | −1.2132 | 0.9496 | 1.2604 | |||
| [0.5991] | [0.7214] | [0.8438] | ||||
| TREAT2 x NOINFO | −0.0132 | −0.1348 | 0.0089 | |||
| [0.3766] | [0.3329] | [0.4125] | ||||
| TREAT3 x NOINFO | −0.4877 | −0.1753 | 0.7243 | |||
| [0.3598] | [0.3609] | [0.4180] | ||||
| TREAT1 x INFO | 1.2132 | −0.9496 | −1.2604 | |||
| [0.5991] | [0.7214] | [0.8438] | ||||
| TREAT2 x INFO | 0.0132 | 0.1348 | −0.0089 | |||
| [0.3766] | [0.3329] | [0.4125] | ||||
| TREAT3 x INFO | 0.4877 | 0.1753 | −0.7243 | |||
| [0.3598] | [0.3609] | [0.4180] | ||||
| Constant | 0.7827 | 0.2949 | −1.8872 | −2.0625 | −2.0938 | −1.3695 |
| [0.1746] | [0.3148] | [0.1735] | [0.3217] | [0.2123] | [0.3657] | |
| Log likelihood | −1097.859 | −1097.859 | −998.330 | −998.330 | −920.495 | −920.495 |
| N | 2443 | 2443 | 2443 | 2443 | 2443 | 2443 |
| Treatments | Differences | |||||
|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T1–T3 | T2–T3 | T1–T2 | |
| No Posteriors | 0.975 | 0.738 | 0.788 | 0.187 | −0.050 | 0.237 |
| Posteriors | 0.993 | 0.793 | 0.720 | 0.273 | 0.073 | 0.200 |
| Combined | 0.989 | 0.782 | 0.734 | 0.255 | 0.048 | 0.207 |
| No Post.- Post. | −0.018 | −0.055 | 0.068 | |||
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Efficient Outcome | Efficient Outcome | Efficient Outcome | Efficient Outcome | |
| TREAT1 | 4.0605 | 2.3543 | 3.6595 | 2.6314 |
| [0.7211] | [0.7666] | [0.7237] | [0.7599] | |
| TREAT2 | 0.4009 | −0.2771 | ||
| [0.1921] | [0.3733] | |||
| TREAT3 | −0.4009 | 0.2771 | ||
| [0.1921] | [0.3733] | |||
| TREAT1 x NOINFO | −1.3436 | −1.3436 | ||
| [1.0096] | [1.0096] | |||
| TREAT2 x NOINFO | −0.3154 | −0.3154 | ||
| [0.2967] | [0.2967] | |||
| TREAT3 x NOINFO | 0.3626 | 0.3626 | ||
| [0.3069] | [0.3069] | |||
| TREAT1 x INFO | 1.3436 | 1.3436 | ||
| [1.0096] | [1.0096] | |||
| TREAT2 x INFO | 0.3154 | 0.3154 | ||
| [0.2967] | [0.2967] | |||
| TREAT3 x INFO | −0.3626 | −0.3626 | ||
| [0.3069] | [0.3069] | |||
| Constant | 0.9483 | 1.3109 | 1.3492 | 1.0338 |
| [0.1346] | [0.2767] | [0.1485] | [0.2577] | |
| Log likelihood | −439.530 | −439.530 | −439.530 | −439.530 |
| N | 1140 | 1140 | 1140 | 1140 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goertz, J.M.M.; Chernomaz, K. Voting in Three-Alternative Committees: An Experiment. Games 2019, 10, 20. https://doi.org/10.3390/g10020020
Goertz JMM, Chernomaz K. Voting in Three-Alternative Committees: An Experiment. Games. 2019; 10(2):20. https://doi.org/10.3390/g10020020
Chicago/Turabian StyleGoertz, Johanna M.M., and Kirill Chernomaz. 2019. "Voting in Three-Alternative Committees: An Experiment" Games 10, no. 2: 20. https://doi.org/10.3390/g10020020
APA StyleGoertz, J. M. M., & Chernomaz, K. (2019). Voting in Three-Alternative Committees: An Experiment. Games, 10(2), 20. https://doi.org/10.3390/g10020020




