Example of a Finite Game with No Berge Equilibria at All

Abstract

The problem of the existence of Berge equilibria in the sense of Zhukovskii in normal-form finite games in pure and in mixed strategies is studied. The example of a three-player game that has Berge equilibrium neither in pure, nor in mixed strategies is given.

1. Introduction

The idea of a solution concept that today is usually called Berge equilibrium (in the sense of Zhukovskii) was launched by the French mathematician Claude Berge in his book Théorie générale des jeux à n personnes [1]. Unfortunately, this book remained virtually unnoticed in the English-speaking world. However, Berge’s book was translated into Russian in 1961, and maybe because the idea of Berge equilibrium fits very well with the most basic idea of communist ideology, it gained remarkable popularity in the former Soviet Union. In particular, numerous students from Arabic countries that studied there got acquainted with this idea, and after coming back from the Soviet Union, they continued studies on this valuable idea and returned it to the French- and English-speaking world1.

Actually, the idea of Berge equilibrium is in a sense opposite the idea of Nash equilibrium. While Nash equilibrium is based on egoism (each player aims to maximize his/her own payoff), Berge equilibrium is based on altruism (each player’s aim is to maximize the payoffs of all the other players, so when every player does so, everyone is better off). This explains why, in general, Berge equilibria yield higher payoffs to players than Nash equilibria.

However, it seems that Nash equilibria outperform Berge equilibria in one respect: the historic theorem stated in [4] assures that in any finite game, there exists at least one Nash equilibrium, in pure or mixed strategies. In the case of Berge equilibria, this problem is still a subject of debate. The aim of this paper is to give an example of a three-player game that has no Berge equilibria at all, neither in pure, nor in mixed strategies. The importance of this example follows from the following fact: According to the results of [2] extended to mixed strategies, in a finite two-player game, Nash equilibria in the original game and Berge equilibria in a game with interchanged payoffs are in a one-to-one correspondence. Therefore, due to the Nash theorem [4], every two-player finite game has at least one Berge equilibrium, in pure or mixed strategies. The problem of whether we should expect the same in games with a bigger number of players was posed as Open Problem No. 1 in [3]. Our counterexample shows that already among three-person games, there exist games with no Berge equilibria at all.

2. Basic Notions and Definitions

The noncooperative finite game in normal form is a triple:

$$G=⟨N,{\left(S_i\right)}_{i\in N},{\left(U_i\right)}_{i\in N}⟩,$$

(1)

where $N=\{1,\dots ,n\}$ denotes the set of players, $S_i$ is a finite set of pure strategies of a player i, and $U_i$ is a function from $S={\prod }_{i\in N}{S}_i$ in the set of real numbers that describes payoffs that are possible to obtain by player i. The mixed strategy of player i is identified with a probability distribution defined on the set $S_i$ of his/her pure strategies. The set of all mixed strategies of player i is denoted ${\tilde{S}}_i$. When at least one player chooses a “genuine mixed” (i.e., non-pure) strategy, payoffs are understood as suitable expected values, and the real-valued function they form, defined on $\tilde{S}={\prod }_{i\in N}{\tilde{S}}_i$, will be denoted ${\tilde{U}}_i$. We do not distinguish between a game and its mixed extension, and when we write strategy, we mean a general mixed strategy, with pure strategies being special cases of mixed ones. Let $\mathbf{s}=(s_1,\dots ,s_n)\in {\prod }_{i\in N}{\tilde{S}}_i$ be a strategy profile, then by ${\mathbf{s}}_{-i}$, we denote the incomplete strategy profile ${\mathbf{s}}_{-i}=(s_1,\dots s_{i-1},s_{i+1},\dots ,s_n)\in {\tilde{S}}_{-i}={\prod }_{j\ne i}{\tilde{S}}_j$. By a small abuse of symbols, we make an identification $(s_i,{\mathbf{s}}_{-i})=\mathbf{s}$.

Definition 1.

A strategy profile ${\mathbf{s}}^{*}=(s_1^{*},\dots ,s_n^{*})\in \tilde{S}$ is a Berge equilibrium (in the sense of Zhukovskii) of game G if:

$$\forall i\in N,\forall {\mathbf{s}}_{-i}\in {\tilde{S}}_{-i},{\tilde{U}}_i(s_i^{*},{\mathbf{s}}_{-i})\le {\tilde{U}}_i\left({\mathbf{s}}^{*}\right).$$

(2)

Let us compare this notion with the notion of Nash equilibrium:

Definition 2.

A strategy profile ${\mathbf{s}}^{*}=(s_1^{*},\dots ,s_n^{*})\in \tilde{S}$ is a Nash equilibrium of game G if:

$$\forall i\in N,\forall s_i\in {\tilde{S}}_i,{\tilde{U}}_i(s_i,{\mathbf{s}}_{-i}^{*})\le {\tilde{U}}_i\left({\mathbf{s}}^{*}\right).$$

(3)

In two-player or tree-player, two-strategy games, all Nash equilibria can be easily found as intersections of graphs of the best reply correspondences (see, for example, [5]). Musy et al. in the work [6] introduced an analogous notion of the best support correspondence, which enables one to find, at least in two-player or three-player, two-strategy games, all Berge equilibria. Although after a careful reading of their paper, it becomes clear that they deal with Berge equilibria in pure strategies only, their results can be in a straightforward way extended to mixed strategies. Therefore, we adopt the following definition that extends the original definition to mixed strategies [6].

Definition 3.

Let $i\in N$, $s_i\in {\tilde{S}}_i$. An incomplete strategy profile ${\overline{\mathbf{s}}}_{-i}\in {\tilde{S}}_{-i}$ is the best support to strategy $s_i$ if:

$$\forall {\mathbf{s}}_{-i}\in {\tilde{S}}_{-i}{\tilde{U}}_i(s_i,{\mathbf{s}}_{-i})\le {\tilde{U}}_i(s_i,{\overline{\mathbf{s}}}_{-i}).$$

(4)

It was noted in [6] that the best support correspondences can be used to reformulate the definition of Berge equilibrium in the same way as the best reply correspondences enable us to reformulate the definition of Nash equilibrium:

“A strategy profile is a Nash equilibrium if and only if each player’s strategy is a best reply to the co-players’ incomplete strategy profile, whereas a strategy profile is a Berge equilibrium if and only if co-payers’ incomplete strategy profile is a best support to each player’s strategy”.

It is straightforward to see that this refers also to Nash and Berge equilibria in mixed strategies.

3. Example of a Three-Player Game with No Berge Equilibria at All

Let us consider the following three-player game in which each of the players has two pure strategies. Pure strategies of the first, the second, and the third player are denoted $A_1,A_2$; $B_1,B_2$; $C_1,C_2$, respectively.

$$\begin{array}{ccc}& B_1\hfill & B_2\hfill \\ C_1:& \begin{array}{cc}\begin{array}{c}{A}_1\\ A_2\end{array}& \left(\begin{array}{cc}(2,1,0)& (1,1,1)\\ (2,0,1)& (1,0,2)\end{array}\right)\end{array}\end{array}\begin{array}{ccc}& B_1\hfill & B_2\hfill \\ C_1:& \begin{array}{cc}\begin{array}{c}{A}_1\\ A_2\end{array}& \left(\begin{array}{cc}(1,2,0)& (0,2,1)\\ (1,1,1)& (0,1,2)\end{array}\right)\end{array}\end{array}.$$

(5)

The left-hand matrix refers to the pure strategy $C_1$ of the third player, while the right-hand matrix refers to his/her pure strategy $C_2$. Let us note that this game is a very special one: None of the players has any possibility to influence their own payoff, no matter if they use any of their pure or mixed strategies. On the contrary, players’ payoffs depend exclusively on the choices of the remaining players.

This very special feature implies that any strategy profile of this game, consisting of strategies of any type, pure, genuine mixed, or both, is a (weak) Nash equilibrium. Moreover, since this game is a constant-sum game: increasing the payoff of one player inevitably leads to decreasing the payoffs of some, or all, other players, so any triple of payoffs yielded by any strategy profile is optimal in the Pareto sense. Therefore, neither the concept of Nash equilibrium, nor the concept of Pareto optimal results provides any hint to players about which strategies should be chosen. Sometimes, it is claimed (cf. [3]) that in such cases, the concept of Berge equilibrium could be of some help. Therefore, let us study Berge equilibria in this game.

One can easily check that the second and the third players’ best support to any of the first player’s (pure or mixed) strategies is a pair of pure strategies $(B_1,C_1)$; the first and the third players’ best support to any of the second player’s (pure or mixed) strategies is a pair of pure strategies $(A_1,C_2)$; and finally, the first and the second players’ best support to any of (pure or mixed) strategies of the third player is a pair of pure strategies $(A_2,B_2)$. More formally, let us denote by $p,q$, and r the probabilities with which the first, the second, and the third player choose, respectively, their first pure strategy. Denote by $b{s}_{-i}\left(s_i\right)$ the set of best supports ${\overline{\mathbf{s}}}_{-i}$ to strategy $s_i$. This means that if we plot graphs of the best support correspondences $b{s}_{-i}(·)$ as subsets of the three-dimensional unit cube ${[0,1]}^3$, these graphs form, respectively, edges $(p\in [0,1],1,1)$, $(1,q\in [0,1],0)$, and $(0,0,r\in [0,1\left]\right)$ of this cube. Their intersection is an empty set, so this game has no Berge equilibria, neither in pure, nor in mixed strategies (see Figure 1).

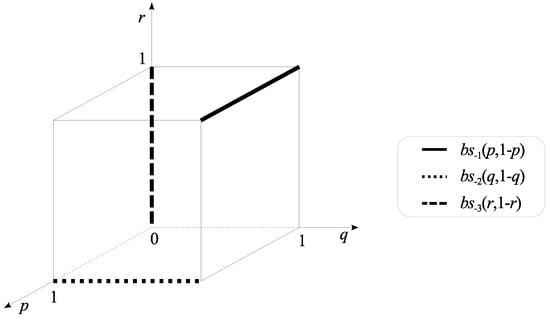
Figure 1. Best support correspondences $b{s}_i(·)$ corresponding to game (5).

Let us note that the game (5) was considered for the first time in an MSc. Thesis of P.Bytner [7], where he proved that this game has no Berge equilibria, neither in pure, nor in mixed strategies, using other methods. These methods will be described in a subsequent paper.

4. Summary

Our counterexample shows that already among three-player, two-strategy games, there are games with no Berge equilibria at all. Therefore, the problem of finding the conditions for the existence of Berge equilibrium beyond two-player games is an open one and is worth further studies.