Evolution of Cooperation in Public Goods Games with Stochastic Opting-Out
Abstract
1. Introduction
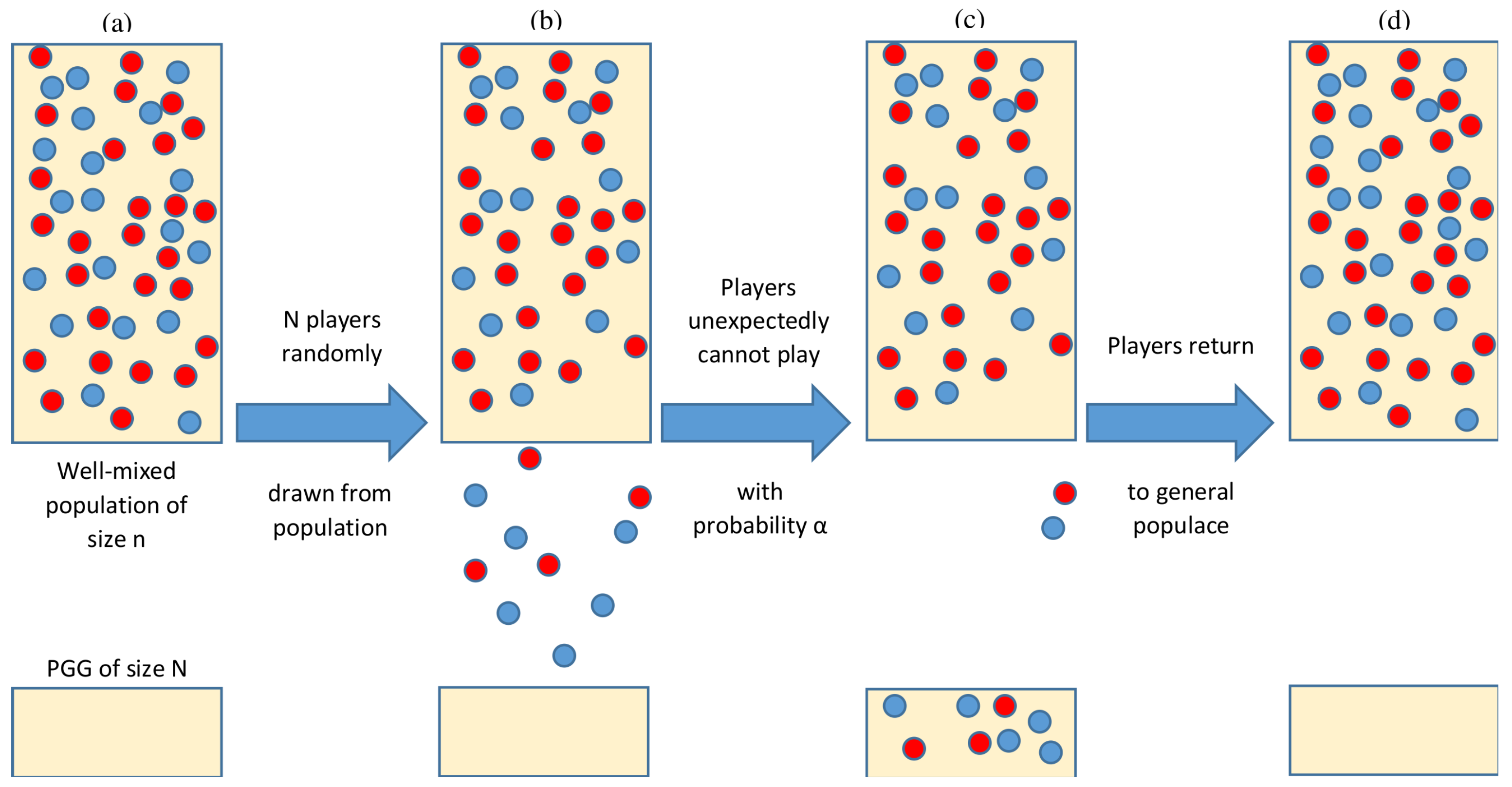
2. Model and Methods
3. Results
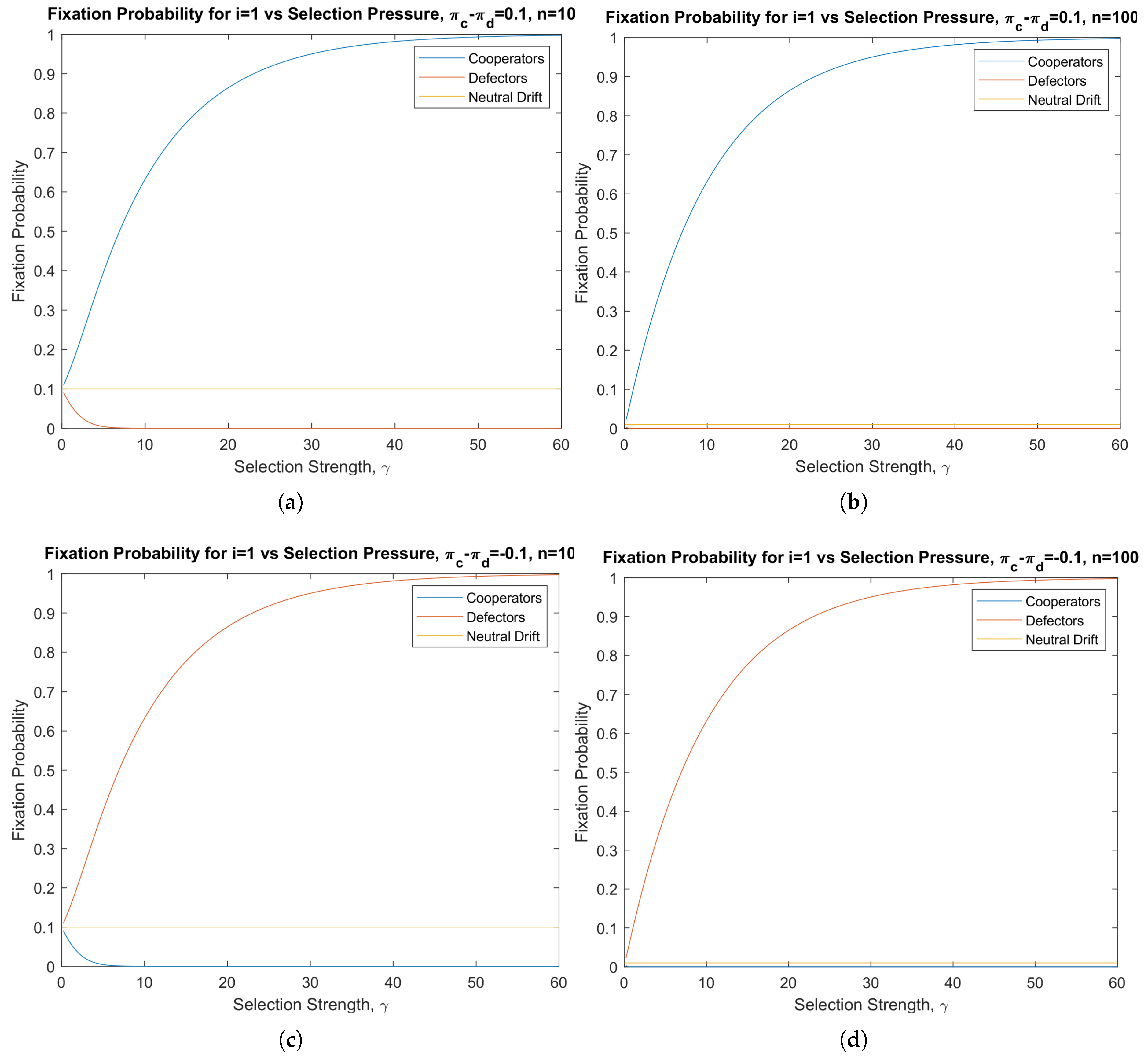
3.1. Pairwise Invasion Dynamics in Finite Populations
- Natural selection favors cooperation over defection , if ;
- Neutral evolution , if ;
- Natural selection favors defection over cooperation , if .
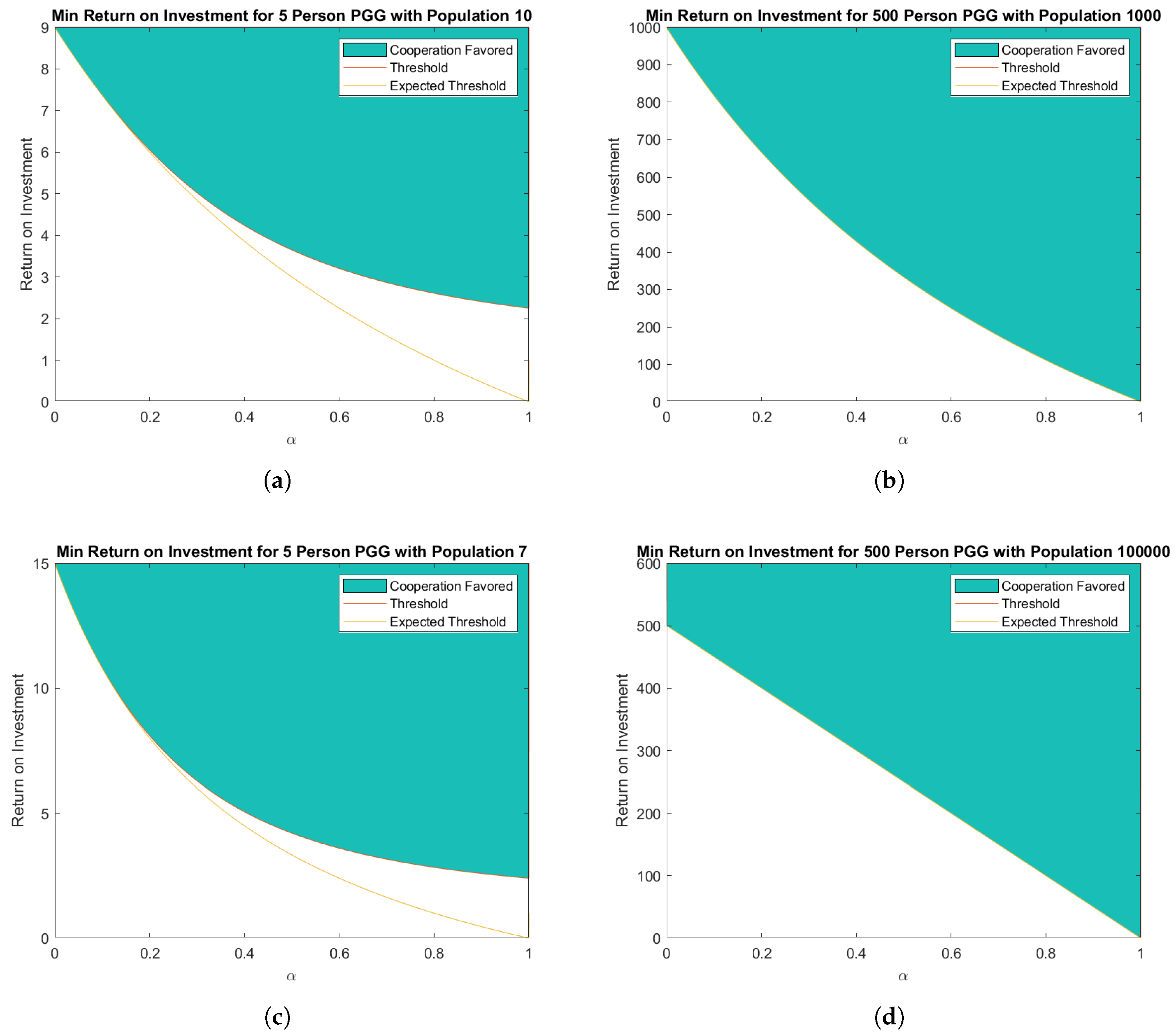
3.2. Approximations of the Critical Threshold for Natural Selection to Favor Cooperation
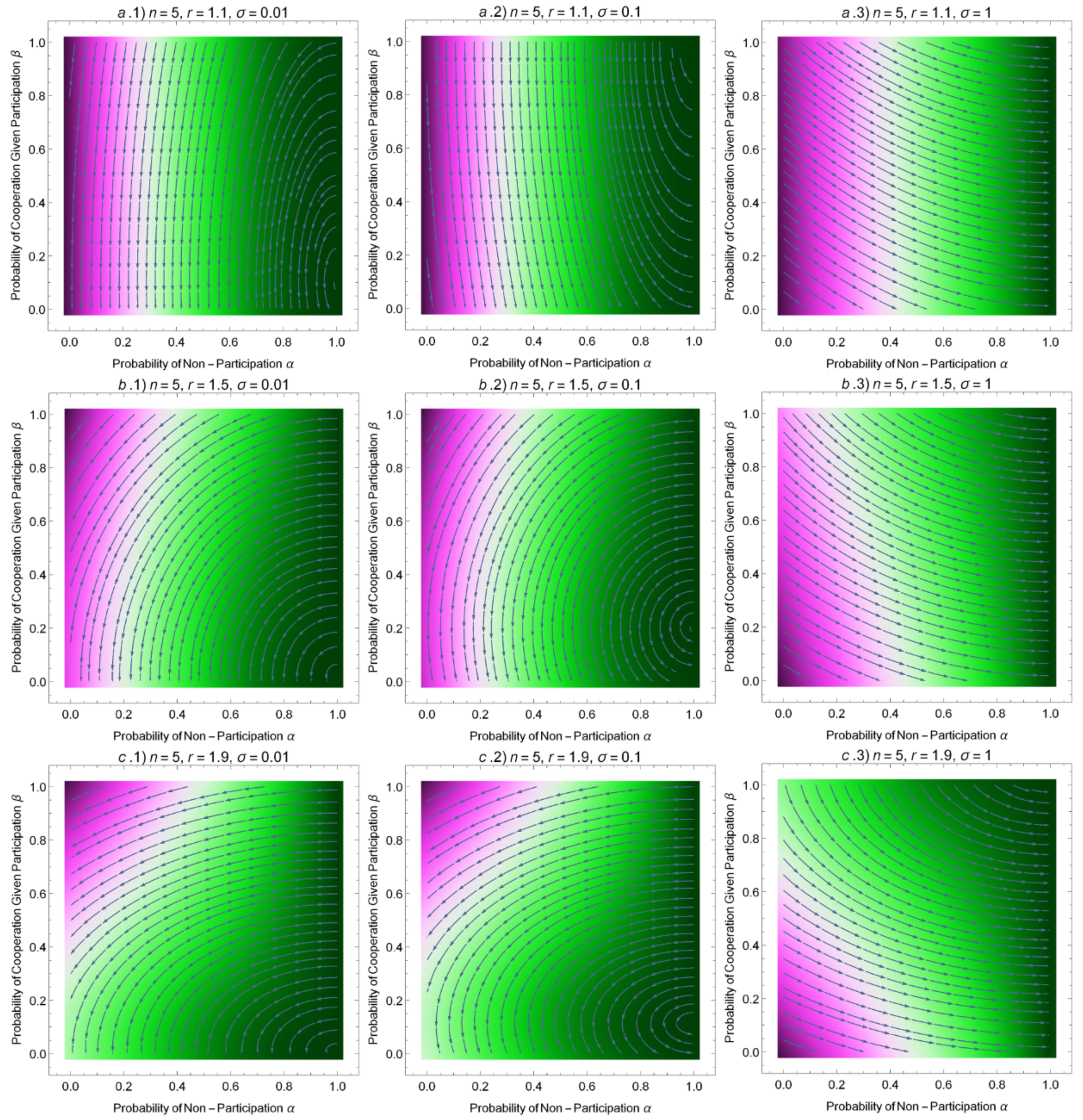
3.3. Adaptive Dynamics in Finite Populations
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of πd
Appendix B. Derivation of πc
Appendix C. Transition Matrix
Appendix D. Inequalities
Appendix D.1. Proof of (15)
Appendix D.2. Proof of (16)
Appendix D.3. Proof of (17)
Appendix D.4. Lemma 1:
Appendix D.5. Lemma 2:
Appendix D.6. Proof that as N/n → 0, R(α) > N(1 − α) ≈ Rexp (α)
Appendix D.7. Lemma 3: Behavior of R(α) as α → 0
Appendix E. Proof That R(α) Is Strictly Decreasing on [0, 1)
Proof S(αinv)U(α) > S(α)U(αinv) for αinv < α
Appendix F. Justification of Approximations
Appendix F.1. Approximation for R(α) as N → ∞,
Appendix F.2. Approximation for R(α) for n ≫ N ≫ 0
Appendix F.3. Approximation for R(α) as N → ∞
Appendix F.4. Approximation for R(α) as N/n → 0 and α → 1
Appendix G. Derivation of πy
References
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Hölldobler, B.; Wilson, E.O. The Superorganism: The Beauty, Elegance, and Strangeness of Insect Societies; WW Norton & Company: New York, NY, USA, 2009. [Google Scholar]
- Traulsen, A.; Nowak, M.A. Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. USA 2006, 103, 10952–10955. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.L. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Nadell, C.D.; Xavier, J.B.; Levin, S.A.; Foster, K.R. The evolution of quorum sensing in bacterial biofilms. PLoS Biol. 2008, 6, e14. [Google Scholar] [CrossRef] [PubMed]
- Goryunov, D. Nest-building in ants formica exsecta (hymenoptera, formicidae). Entomol. Rev. 2015, 95, 953–958. [Google Scholar] [CrossRef]
- Templeton, C.N.; Greene, E.; Davis, K. Allometry of alarm calls: Black-capped chickadees encode information about predator size. Science 2005, 308, 1934–1937. [Google Scholar] [CrossRef] [PubMed]
- Bailey, I.; Myatt, J.P.; Wilson, A.M. Group hunting within the carnivora: Physiological, cognitive and environmental influences on strategy and cooperation. Behav. Ecol. Sociobiol. 2013, 67, 1–17. [Google Scholar] [CrossRef]
- Melis, A.P.; Semmann, D. How is human cooperation different? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 2663–2674. [Google Scholar] [CrossRef]
- Wu, T.; Fu, F.; Zhang, Y.; Wang, L. The increased risk of joint venture promotes social cooperation. PLoS ONE 2013, 8, e63801. [Google Scholar] [CrossRef]
- Wang, J.; Fu, F.; Wu, T.; Wang, L. Emergence of social cooperation in threshold public goods games with collective risk. Phys. Rev. E 2009, 80, 016101. [Google Scholar] [CrossRef]
- Antal, T.; Ohtsuki, H.; Wakeley, J.; Taylor, P.D.; Nowak, M.A. Evolution of cooperation by phenotypic similarity. Proc. Natl. Acad. Sci. USA 2009, 106, 8597–8600. [Google Scholar] [CrossRef]
- Boyd, R.; Gintis, H.; Bowles, S. Coordinated punishment of defectors sustains cooperation and can proliferate when rare. Science 2010, 328, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Broom, M.; Rychtár, J. Game-Theoretical Models in Biology; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hauert, C.; Monte, S.D.; Hofbauer, J.; Sigmund, K. Replicator dynamics for optional public good games. J. Theor. Biol. 2002, 218, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Monte, S.D.; Hofbauer, J.; Sigmund, K. Volunteering as red queen mechanism for cooperation in public goods games. Science 2002, 296, 1129–1132. [Google Scholar] [CrossRef] [PubMed]
- Javarone, M.A. The host-pathogen game: An evolutionary approach to biological competitions. Front. Phys. 2016; 94, arXiv:1607–00998arXiv:1607.00998. [Google Scholar] [CrossRef]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Priklopil, T.; Chatterjee, K.; Nowak, M. Optional interactions and suspicious behaviour facilitates trustful cooperation in prisoners dilemma. J. Theor. Biol. 2017, 433, 64–72. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef]
- Hauert, C.; Miȩkisz, J. Effects of sampling interaction partners and competitors in evolutionary games. Phys. Rev. E 2018, 98, 052301. [Google Scholar] [CrossRef]
- Killingback, T.; Bieri, J.; Flatt, T. Evolution in group-structured populations can resolve the tragedy of the commons. Proc. R. Soc. Lond. B Biol. Sci. 2006, 273, 1477–1481. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Vasconcelos, V.V.; Santos, F.C.; Skyrms, B. Co-evolutionary dynamics of collective action with signaling for a quorum. PLoS Comput. Biol. 2015, 11, e1004101. [Google Scholar] [CrossRef]
- Sigmund, K.; Silva, H.D.; Traulsen, A.; Hauert, C. Social learning promotes institutions for governing the commons. Nature 2010, 466, 861. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Battiston, F.; Perc, M.; Latora, V. Determinants of public cooperation in multiplex networks. New J. Phys. 2017, 19, 073017. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Antisocial pool rewarding does not deter public cooperation. Proc. R. Soc. Lond. B Biol. Sci. 2015, 282, 20151975. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Perc, M. Conformity enhances network reciprocity in evolutionary social dilemmas. J. R. Soc. Interface 2015, 12, 20141299. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Fu, F.; Dou, P.; Wang, L. Social influence promotes cooperation in the public goods game. Phys. A Stat. Mech. Appl. 2014, 413, 86–93. [Google Scholar] [CrossRef]
- Wu, T.; Fu, F.; Wang, L. Moving away from nasty encounters enhances cooperation in ecological prisoner’s dilemma game. PLoS ONE 2011, 6, e27669. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Fu, F.; Zhang, Y.; Wang, L. Adaptive role switching promotes fairness in networked ultimatum game. Sci. Rep. 2013, 3, 1550. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502. [Google Scholar] [CrossRef]
- Broom, M.; Hadjichrysanthou, C.; Rychtář, J. Evolutionary games on graphs and the speed of the evolutionary process. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2010, 466, 1327–1346. [Google Scholar] [CrossRef]
- Chen, X.; Fu, F.; Wang, L. Influence of different initial distributions on robust cooperation in scale-free networks: A comparative study. Phys. Lett. A 2008, 372, 1161–1167. [Google Scholar] [CrossRef]
- Du, F.; Fu, F. Partner selection shapes the strategic and topological evolution of cooperation. Dyn. Games Appl. 2011, 1, 354. [Google Scholar] [CrossRef]
- Javarone, M.A. Statistical physics of the spatial prisoner’s dilemma with memory-aware agents. Eur. Phys. J. B 2016, 89, 42. [Google Scholar] [CrossRef]
- Javarone, M.A. Statistical Physics and Computational Methods for Evolutionary Game Theory; Springer: Berlin, Germany, 2018. [Google Scholar]
- Javarone, M.A.; Atzeni, A.E. The role of competitiveness in the prisoner’s dilemma. Comput. Soc. Netw. 2015, 2, 15. [Google Scholar] [CrossRef]
- Javarone, M.A.; Marinazzo, D. Evolutionary dynamics of group formation. PLoS ONE 2017, 12, e0187960. [Google Scholar] [CrossRef] [PubMed]
- Rychtár, J.; Stadler, B. Evolutionary dynamics on small-world networks. Int. J. Comput. Math. Sci. 2008, 2, 1–4. [Google Scholar]
- Schoenmakers, S.; Hilbe, C.; Blasius, B.; Traulsen, A. Sanctions as honest signals—The evolution of pool punishment by public sanctioning institutions. J. Theor. Biol. 2014, 356, 36–46. [Google Scholar] [CrossRef]
- Hauert, C.; Traulsen, A.; née Brandt, H.D.S.; Nowak, M.A.; Sigmund, K. Public goods with punishment and abstaining in finite and infinite populations. Biol. Theory 2008, 3, 114–122. [Google Scholar] [CrossRef]
- Traulsen, A.; Pacheco, J.M.; Nowak, M.A. Pairwise comparison and selection temperature in evolutionary game dynamics. J. Theor. Biol. 2007, 246, 522–529. [Google Scholar] [CrossRef]
- Imhof, L.A.; Nowak, M.A. Stochastic evolutionary dynamics of direct reciprocity. Proc. R. Soc. Lond. B Biol. Sci. 2010, 277, 463–468. [Google Scholar] [CrossRef]
- Isaac, R.M.; Walker, J.M. Group size effects in public goods provision: The voluntary contributions mechanism. Q. J. Econ. 1988, 103, 179–199. [Google Scholar] [CrossRef]
- Traulsen, A.; Hauert, C.; Silva, H.D.; Nowak, M.A.; Sigmund, K. Exploration dynamics in evolutionary games. Proc. Natl. Acad. Sci. USA 2009, 106, 709–712. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginsberg, A.G.; Fu, F. Evolution of Cooperation in Public Goods Games with Stochastic Opting-Out. Games 2019, 10, 1. https://doi.org/10.3390/g10010001
Ginsberg AG, Fu F. Evolution of Cooperation in Public Goods Games with Stochastic Opting-Out. Games. 2019; 10(1):1. https://doi.org/10.3390/g10010001
Chicago/Turabian StyleGinsberg, Alexander G., and Feng Fu. 2019. "Evolution of Cooperation in Public Goods Games with Stochastic Opting-Out" Games 10, no. 1: 1. https://doi.org/10.3390/g10010001
APA StyleGinsberg, A. G., & Fu, F. (2019). Evolution of Cooperation in Public Goods Games with Stochastic Opting-Out. Games, 10(1), 1. https://doi.org/10.3390/g10010001




