Abstract
I investigate how different dispersal patterns affect the evolution of cooperation in a spatially-structured population. I consider a finite fixed-size population of cooperators and free-riders residing on a one-dimensional lattice with periodic boundaries. Individuals interact via a multiplayer game, which is a version of a public goods game, and the population evolves via a Moran process. Individuals try to improve their interactions by evaluating the current state of the environment and moving to locations with better payoffs. I ran stochastic simulations of the evolution of this Markov process and found that if individuals disperse deterministically to locations with the best payoffs, then cooperation can still be maintained even in the worst-case scenarios, albeit at reduced levels compared to the better-case scenarios. This contrasts with an earlier investigation of probabilistic dispersal patterns, which resulted in the breakdown of cooperation in sparse populations with small interaction neighborhoods, a high mobility rate, and a large dispersal range.
1. Introduction
Cooperation abounds in nature and human society. Yet, naive mathematical models, such as the prisoner’s dilemma [1], demonstrate that cooperative behavior can be exploited: selfish individuals may enjoy benefits produced by cooperators while not incurring the cost of providing such benefits. It may seem that non-cooperators (often called defectors or free-riders) should therefore outcompete cooperators, and hence, understanding mechanisms that generate and maintain cooperation is one of the central problems in evolutionary biology [2].
Evolutionary game theory models [3,4,5] show that in infinite well-mixed populations, free-riders dominate cooperators. Real populations, however, are not usually well-mixed; an individual is more likely to interact with a certain subset of a population due to either spatial or social structure. This structure may allow cooperators to form clusters and to try to resist invasion by free-riders. It is therefore one of the key mechanisms enabling cooperation [6,7,8,9,10,11,12,13]. On the other hand, spatial structure may also inhibit cooperation when compared to the replicator dynamics [14]; comparison with random-matching models shows that spatial structure is still beneficial [15].
Additionally, individuals may move around looking for better neighborhoods and try to improve their interactions. Mobility has been incorporated into evolution-of-cooperation models in a variety of forms: individuals may (1) diffuse randomly [16,17,18,19,20,21], (2) move if they are unhappy with their current situation [22,23,24,25], and (3) utilize success-driven migration [26,27,28] when individuals sample alternative locations and decide where to move based on the knowledge obtained from these test interactions.
In this paper, I investigate how spatial structure and mobility affect the evolution of cooperation. I consider a finite fixed-size population of individuals, which are assigned the roles of either cooperator or free-rider. Individuals interact via a multiplayer game [29], and the population evolves via a birth-death Moran process [30]. The spatial structure in this model is represented by a one-dimensional lattice with periodic boundaries (a one-torus); individuals reside on the nodes of the lattice. Mobility is modeled via the success-driven migration approach: individuals evaluate the current state of the environment and move to locations within their dispersal range that provide better payoffs. In particular, this model can be described by a Markov process.
This paper represents an extension of an earlier investigation of the spatial structure and mobility in the context of the evolution of cooperation [28]. In [28], the probability that individuals moved to a new location was proportional to an increase in the payoff in that location compared to the current location. This modeling approach resulted in a generally negative effect of mobility on cooperation—sometimes to the point of the breakdown of cooperation—because free-riders joining a cluster of cooperators saw a much larger increase in the payoff compared to cooperators moving away from free-riders. It was conjectured in [28] that allowing individuals to move deterministically to locations with the best payoff may “level the playing field”: cooperators should find it easier to escape exploiting free-riders. In the current work, I test this conjecture by constructing and analyzing a model where individuals move deterministically, rather than probabilistically.
2. Methods
I adopt the basic individual-based model setup from [28]. A fixed-size population of N individuals resides on a 1-dimensional lattice with periodic boundaries with L nodes. Each individual possesses one of the two interactive traits: cooperator or free-rider. The individuals do not have “home locations”; each individual may occupy any node in the lattice. In particular, several individuals may reside in the same node at any given time. The individuals move around the lattice and play a multiplayer game, which is a version of a public goods game.
I created and simulated a stochastic process of the evolution of this population. The stochastic process is a Markov process with two types of events: reproduction and dispersal. There are two types of neighborhoods in the model: a neighborhood for strategic interactions, which determines with whom a given individual plays the multiplayer game, and a neighborhood for dispersal, which determines to what locations any given individual may move during a single dispersal event. These neighborhoods usually have different sizes, and hence, the two types of events take place on different spatial scales.
The strategic-interaction neighborhood of a lattice node is determined by the parameter D, the neighborhood radius. An individual plays the multiplayer game with everyone at a distance of at most D from the node of the individual. Therefore, each strategic-interaction neighborhood contains nodes in the lattice.
The dispersal neighborhood of a lattice node is determined by the parameter R, which corresponds to the dispersal range. An individual located at a given node in the lattice may move to any of the nodes at a distance of at most R from the node. Every node may be occupied by multiple individuals, so the individual may move to both occupied and unoccupied nodes. Hence, there are possible locations to choose from for a moving individual.
I will now explain in detail how the Markov process is implemented. In particular, I will emphasize how the current model differs from that in [28].
Reproduction is modeled as a birth-death Moran process. Each individual plays a round of a multiplayer game with all other individuals who are located in the given individual’s strategic-interaction neighborhood. All individuals in the neighborhood share equally the standing unit resource; cooperators pay a cost to provide benefits to all individuals in the neighborhood (neighbors). In our model, a cooperator pays a single cost to provide the same benefit to all neighbors. Biologically, we can interpret this behavior as sharing valuable information such as predator proximity [31]. Cooperators are the individuals who sacrifice part of their foraging ability to watch out for predators. They warn all individuals in the neighborhood if they spot a predator; these individuals receive the same benefit of the signal regardless of their number.
Let B be the benefit and C the cost of cooperation. The payoff of an individual is given by:
where and are the number of cooperators and free-riders, respectively, in the neighborhood of the individual , including the individual itself, and:
is the cost of providing the benefits of cooperation to the neighbors. The term represents the density-dependent competition for local resources. In particular, every free-rider present in the strategic-interaction neighborhood of an individual decreases the individual’s payoff.
At the initialization stage, each of the N individuals is randomly (with uniform probability) assigned a role of either cooperator or free-rider and a position in the lattice. All individuals play one round of the multiplayer game described above and obtain the associated payoffs. The Markov process proceeds in discrete time steps. The type of the next event—dispersal or reproduction—is determined randomly: the probability that the next event is dispersal is , where M is the mobility rate parameter.
If the next event is dispersal, then a randomly-chosen (with uniform probability) individual is given an opportunity to move to a different location. The individual “samples” all potential locations by temporarily moving to each of these locations (while all other individuals stay in their current positions), recording the corresponding payoffs, and chooses a new location. The cost of these test interactions is assumed to be negligible. In [28], the choice of a new location was probabilistic: an individual was more likely to move to locations that improved its payoff; the larger the improvement, the more likely the individual was to move to that specific location. In this paper, I implement two alternative dispersal algorithms:
- An individual considers all potential locations that offer the (same) maximum payoff and moves to one of these locations randomly with equal probability; I call this algorithm almost deterministic.
- An individual considers all potential locations that offer the (same) maximum payoff and moves to the closest such location; in case there is more than one such location (at most 2 in the 1-dimensional lattice), the individual chooses randomly between the two locations; I call this algorithm deterministic.
The reason for differentiating between almost deterministic and deterministic dispersal algorithms is that with the latter, free-riders would find it more difficult to penetrate into the center of a cooperating cluster. This makes it easier for clusters of cooperators to attempt to move away from free-riders. These two dispersal algorithms constitute the only difference of the current model from that in [28].
If the next event is reproduction, then all individuals play one round of the multiplayer game; the payoff of an individual , , is given by Equation (1). The payoffs from previous rounds of the game are not averaged or accumulated; only the last-round payoff contributes to reproduction. A “smoothing” function is then applied to the individual payoffs to obtain reproduction propensities:
This is done to allow individuals with negative payoffs or individuals outside large clusters of cooperators to reproduce. Once the reproduction propensities of all individuals are computed, one random individual is chosen for reproduction. The probability that this individual is is given by:
The offspring inherits the interactive strategy—cooperator or free-rider—of its parent and is placed in a random location in the strategic-interaction neighborhood of the parent. Finally, a randomly-chosen (with uniform probability) individual (except the newly-born one) is removed to maintain a constant population size. This realization of the Moran process is usually called BDB: an individual to give birth is chosen first; an individual to die is chosen next; and the individual’s fitness affects the birth process.
I ran each simulation until the Markov process reached one of its two absorbing states: all cooperators or all free-riders. For each combination of the model parameters, I averaged the results of 10,000 trials. The fraction of times the population evolves to cooperators only will be called the fixation probability of cooperators.
The number of trials—10,000—was chosen sufficiently large so that the variance of the simulated fixation probabilities would be sufficiently low. One can use the binomial distribution to estimate the variance of the simulated fixation probability of cooperators q as , where n is the number of trials. This expression attains its maximum value when , and hence, the standard deviation (the square root of the variance) does not exceed 0.005 when 10,000. It follows that the simulated fixation probability values are correct up to with a 95% confidence.
The parameters of the model are summarized in Table 1. Detailed justification of the choice of parameter values is given in [28]. Here, I just briefly mention the motivation behind the choice of the values of the benefit of cooperation parameter B. The values of B were defined as functions of C in such a way that the payoff of two neighboring cooperators did not depend on the value of C. The lowest value of B corresponds to the scenario when the payoff of cooperators in a cluster of exactly two cooperators coincides with the payoff of a lone free-rider; in this case, cooperators need to form clusters of a size of 3 or more to outcompete free-riders. The highest value of B ensures that the payoff of a lone cooperator is still lower than that of a lone free-rider for all values of C.

Table 1.
Summary of the parameters of the model.
3. Results
The effect of the spatial structure on the fixation probability of cooperators in the absence of dispersal () for this model was analyzed in [28]. These findings can be summarized as follows: cooperators do best in small strategic-interaction neighborhoods and higher population densities. In particular, for the smallest strategic-interaction neighborhood size (), highest population density (), and largest benefit-to-cost ratio ( and ), cooperators achieved a fixation probability close to one.
We note that even in the absence of strategic dispersal, there was inherent movement in the population due to the population dynamics. An individual to be replaced was chosen at random from the entire population, yet the offspring was placed in a neighborhood of the parent. Hence, the replacement events may change not only the interactive-trait composition, but also the spatial distribution of the population.
With the probabilistic dispersal model of [28], it turned out that increasing the mobility rate of the population did not help cooperators. Moreover, combining a high mobility rate () and a large dispersal neighborhood () with a sparse population, a small strategic-interaction neighborhood, and small benefit-to-cost ratios resulted in the breakdown of cooperation. It was conjectured that this happened because the probabilistic dispersal model made it much easier for free-riders to locate and exploit cooperating clusters (resulting in a large increase in fitness) than for cooperators to run away from free-riders (resulting in a small increase in fitness). Here, I test this conjecture by implementing two different dispersal models, both of which disregard the magnitude of the payoff gain in the individual movement decisions: an individual moves to a location with maximum payoff.
I analyze the results for almost deterministic and deterministic dispersal algorithms separately and then compare these two dispersal models with the probabilistic model considered in [28].
3.1. Almost Deterministic Dispersal
An increasing mobility rate, while keeping the dispersal range at its minimum value of , decreased the fixation probability of cooperators for small strategic-interaction neighborhoods (Figure 1). For medium and large strategic-interaction neighborhoods, mobility did not have any significant effect on the fixation probability of cooperators. These results are consistent with the outcomes of the probabilistic model in [28]. Introducing dispersal hurt cooperators in the case of small strategic-interaction neighborhoods because free-riders needed to move around the environment to be able to locate the compact cooperating clusters. With larger neighborhood sizes, free-riders may enjoy benefits provided by cooperators that are located farther away: there is less pressure for free-riders to locate cooperators. Hence, dispersal did not have a significant effect on the outcome of the evolution of the population in this case.
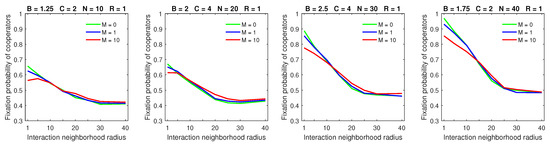
Figure 1.
Increasing the mobility rate does not help cooperators in the almost deterministic dispersal model, and it hurts cooperators when interaction neighborhoods are small.
Increasing the dispersal range decreased the fixation probability of cooperators for the mobility rate when the strategic-interaction neighborhoods were sufficiently small (Figure 2). Increasing the dispersal range for the mobility rate resulted in flattening of the fixation probability graphs (Figure 3). This effect is similar to the one observed in [28] for probabilistic dispersal. A larger dispersal range and higher mobility rate negate the advantage of compact cooperating clusters, and free-riders find it easier to locate and exploit such clusters. On the other hand, the breakdown of cooperation, which was possible for some parameter combinations in the probabilistic dispersal model, was no longer observed with almost deterministic dispersal.
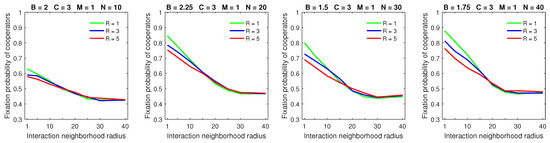
Figure 2.
Increasing the dispersal range for low mobility rate has a negative effect on the fixation probability of cooperators when the interaction neighborhoods are sufficiently small in the almost deterministic dispersal model.
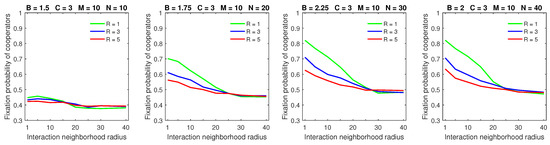
Figure 3.
Increasing the dispersal range for high mobility rate flattens the fixation probability curves in the almost deterministic dispersal model.
3.2. Deterministic Dispersal
Contrary to the probabilistic and almost deterministic dispersal cases, increasing the mobility rate, while keeping the minimum dispersal range (), had almost no negative effect on the fixation probability of cooperators in the deterministic dispersal model (Figure 4). The deterministic dispersal algorithm forces roaming free-riders to stop at the edges of cooperating clusters, hence making it easier for cooperators to move away from these free-riders.
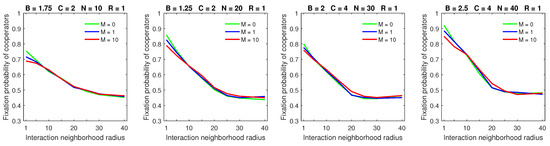
Figure 4.
Increasing the mobility rate has no effect on the fixation probability of cooperators in the deterministic dispersal model when the dispersal range is small except for very small interaction neighborhoods.
Increasing the dispersal range decreased the fixation probability of cooperators for low mobility rate when the strategic-interaction neighborhoods were sufficiently small (Figure 5); this is consistent with the probabilistic and almost deterministic cases. Increasing the dispersal range for high mobility rate resulted in a significantly lower fixation probability of cooperators for sufficiently large populations () and small-to-medium strategic-interaction neighborhoods (Figure 6). In contrast to the probabilistic and almost deterministic dispersal models, the flattening effect of a large dispersal range combined with high mobility rate was no longer observed with deterministic dispersal. Similar to the almost deterministic dispersal model, the breakdown of cooperation that was possible with probabilistic dispersal was no longer observed with deterministic dispersal.
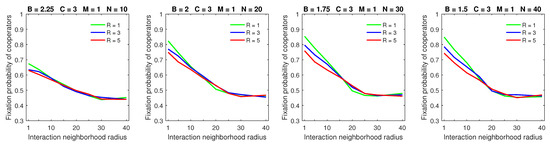
Figure 5.
Increasing the dispersal range for low mobility rate has a small negative effect on the fixation probability of cooperators when the interaction neighborhoods are sufficiently small in the deterministic dispersal model.
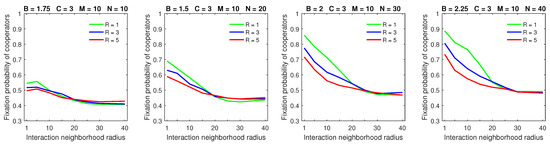
Figure 6.
Increasing the dispersal range for high mobility rate has a significant negative effect on the fixation probability of cooperators in sufficiently large populations with small-to-medium interaction neighborhoods in the deterministic dispersal model. The flattening effect is lower than in the probabilistic and almost deterministic dispersal models.
3.3. Comparison of Probabilistic, Almost Deterministic, and Deterministic Dispersal Models
All three dispersal models resulted in almost identical fixation probabilities of cooperators in populations with a low mobility rate () and small dispersal range (); see Figure 7. This happens because in this case, mobility had little effect on the fixation probability of cooperators.
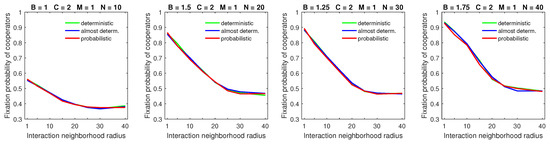
Figure 7.
Probabilistic, almost deterministic, and deterministic dispersal models result in almost identical fixation probabilities of cooperators when the mobility rate is low and the dispersal range is small. In all graphs, .
Increasing the mobility rate () demonstrated the visible advantage of the (almost) deterministic dispersal pattern over the probabilistic one for cooperators (Figure 8); the effect was more pronounced for a denser population. This is consistent with an earlier observation that increasing the mobility rate had little negative effect on the fixation probability of cooperators for deterministic dispersal when the dispersal range was small (cf. Figure 4).
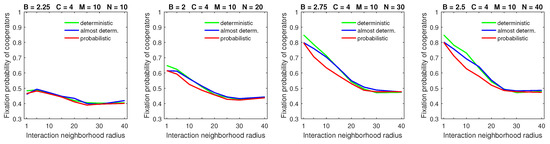
Figure 8.
The (almost) deterministic dispersal pattern results in higher fixation probabilities of cooperators compared to the probabilistic dispersal pattern when the mobility rate is high. The advantage of deterministic dispersal is greater for small interaction neighborhoods and dense populations. In all graphs, .
With probabilistic dispersal, where the propensity to move to a given location was proportional to the increase in payoff compared to the current location of an individual, free-riders were highly likely to move into a cluster of cooperators if it was within the dispersal range because joining such a cluster significantly increased the individual’s payoff. On the other hand, moving away from a free-rider resulted in marginal payoff improvement corresponding to the density-dependent competition for resources term . Consequently, increasing the mobility rate allowed free-riders to locate cooperators more efficiently, but cooperators found it difficult to move away from exploiting free-riders. The introduction of the deterministic dispersal, where individuals move to a location with the best payoff, allowed cooperators to move away from free-riders due to the competition for local resources more often; this made it harder for free-riders to keep exploiting cooperators compared to the probabilistic dispersal model.
Increasing the size of the dispersal neighborhood in populations with a low mobility rate demonstrated a small advantage of deterministic dispersal patterns over the probabilistic one for cooperators; see Figure 9 for and Figure 10 for . This is consistent with the overall principle that introducing mobility at a low rate does not effect a significant change in the fixation probabilities of cooperators. In this situation, different types of dispersal behavior are not going to produce significant variation in fixation probability.
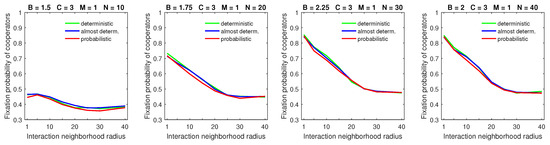
Figure 9.
Deterministic dispersal results in slightly higher fixation probabilities of cooperators for a low mobility rate and a medium dispersal range. In all graphs, .
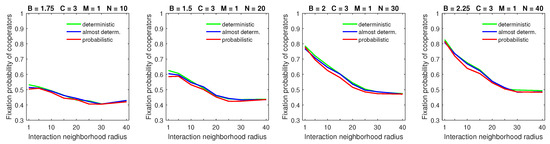
Figure 10.
Deterministic dispersal results in slightly higher fixation probabilities of cooperators for a low mobility rate and a large dispersal range. In all graphs, .
Increasing the dispersal range to in populations with a high mobility rate demonstrates the significant advantage of deterministic dispersal over the probabilistic one for cooperators in all but large strategic-interaction neighborhood cases (Figure 11). In this case, the probabilistic dispersal pattern was detrimental to cooperators [28] because increasing the dispersal neighborhood size helped free-riders locate cooperators. With deterministic dispersal, roaming free-riders were forced to stop at the edges of cooperating clusters. This gave cooperators opportunities to move away from exploiting free-riders, thus partially negating the improved searching capabilities of free-riders.
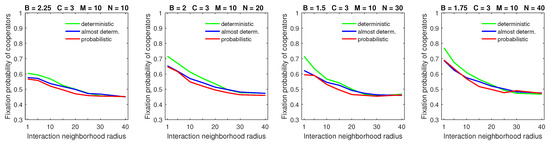
Figure 11.
Deterministic dispersal results in higher fixation probabilities of cooperators for a high mobility rate and a medium dispersal range. In all graphs, .
Similar observations apply to the large dispersal range in populations with a high mobility rate (Figure 12). Moreover, the “flattening” of the fixation probability curves, which was observed in the probabilistic dispersal model [28], is not present in the deterministic dispersal model. The flattening effect arose in the probabilistic dispersal model because a high mobility rate coupled with a large dispersal range negated the advantage of compact cooperating clusters, which were difficult for free-riders to locate. As was mentioned in the last paragraph, deterministically dispersing free-riders were forced to stop at the edges of cooperating clusters. This allowed cooperators to attempt to escape free-riders, which resulted in maintaining the advantage of small strategic-interaction neighborhoods for cooperators.
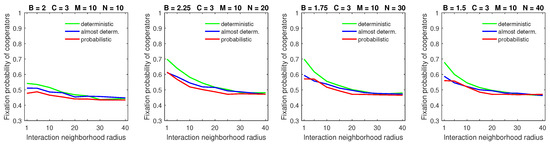
Figure 12.
Deterministic dispersal results in higher fixation probabilities of cooperators for a high mobility rate and large dispersal range. The flattening of the fixation probability curves’ effect, which was observed in the probabilistic dispersal case, is weaker in the deterministic dispersal model. In all graphs, .
Finally, the breakdown of cooperation, which occurred in the probabilistic model in sparse populations with a small benefit-to-cost ratio, small strategic-interaction neighborhoods, a high mobility rate, and large dispersal neighborhoods [28], was no longer observed with deterministic dispersal (Figure 13). By a “breakdown of cooperation”, I loosely mean the phenomenon when the fixation probability of cooperators drops sharply to its lowest levels (e.g., to about 0.3, as shown in the leftmost graph of Figure 13). Therefore, cooperation can still be maintained—albeit at reduced levels—even in the worst-case scenario with deterministic dispersal.
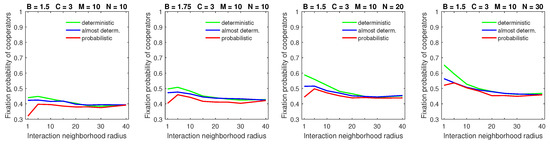
Figure 13.
Deterministic dispersal models avoid the breakdown of cooperation, which was observed in the probabilistic model for sparse populations with a small benefit-to-cost ratio, small interaction neighborhoods, a high mobility rate, and large dispersal neighborhoods. In all graphs, .
4. Discussion
I constructed and analyzed a stochastic model of the evolution of a spatially-structured fixed-size population of mobile cooperators and free-riders. Individuals reside on the nodes of a one-dimensional lattice with periodic boundaries (one-dimensional torus), and they interact with each other via a multiplayer game, which is a version of a public goods game where cooperators pay a fixed cost to produce benefits for all neighbors to share. Individuals disperse around the environment looking to improve their interactions: everyone prefers to be in the neighborhood of a cooperator and away from a free-rider.
A probabilistic dispersal pattern for this model was analyzed in [28]: the probability that an individual moved to a new location was proportional to the increase in the payoff in the new location compared to the payoff in the current location. This dispersal algorithm resulted in a disproportionate advantage to roaming free-riders: moving to the vicinity of a cooperator produced a much bigger gain in payoff than moving away from a free-rider. Hence, free-riders were more likely to find and exploit cooperators than cooperators to run away from free-riders. In particular, a breakdown of cooperation (i.e., a sharp decline in the fixation probability of cooperators to its lowest levels) occurred in sparse populations with a low benefit-to-cost ratio, small interaction neighborhoods, a high mobility rate, and large dispersal neighborhoods.
The purpose of this paper was to extend the model constructed in [28] and to investigate whether alternative dispersal patterns allowed maintenance of cooperation in all scenarios. It was conjectured in [28] that moving deterministically to the location (within the dispersal range) with the best payoff might allow cooperators to run away from free-riders more effectively. Since several locations within the dispersal neighborhood of an individual may provide the same maximum payoff, I considered two variants of deterministic dispersal: (1) individuals choose randomly among possible locations with the best payoff (I called this dispersal pattern almost deterministic); and (2) individuals move to the closest location with the best payoff; if there are two such locations, then the new location is chosen randomly among these two (I called this dispersal pattern deterministic).
I found that while deterministic dispersal patterns still did not help cooperators when the mobility rate of the population increased, they did result in higher fixation probabilities of cooperators compared to the probabilistic dispersal pattern across a variety of parameter combinations. Most importantly, the breakdown of cooperation, which was possible with probabilistic dispersal, was no longer observed with deterministic dispersal (Figure 13). This constitutes the main finding of this work.
This finding aligns philosophically with the investigation of the consequences of behavioral diversity on the evolution of cooperation presented in [32]. It was shown in [32] that limiting the strategic choice of individuals in a public goods game allowed cooperators to resist invasion by defectors. In the context of the model in [32], the strategic choice of an individual was the amount of the public good investment. In the context of the model analyzed in this paper, the strategic choice of an individual consisted of choosing a new location during dispersal. The deterministic dispersal pattern provided an individual with the simplest possible choice of at most two locations (with the best payoff). It turns out that it is this simplest behavioral pattern that resulted in the best outcome for cooperators in our model.
I would like to point out that the advantage of the simple deterministic dispersal pattern has been verified for the specific model (presented here) only. It still remains to be seen whether this observation can be generalized to other social dilemmas with various updating mechanisms. This is an interesting question to investigate, but it was beyond the scope of this project.
A natural extension of this research is to consider a similar model with different dispersal patterns on a two-dimensional lattice (the results for the two-dimensional case will be published elsewhere). Another potential extension of this model lies in the dispersal decision-making process. In the present setup, individuals base their decisions where (and whether) to move on the current state of the environment only; there is no individual bias to staying (possibly in certain specific locations) regardless of the potential interactions. It might be interesting to incorporate an inherent trait of an individual to stay in its current location into the dispersal decision-making process. This inherent trait (staying propensity) of an individual would be independent of its interactive role (cooperator or free-rider) in the multiplayer game. We may then study how varying staying propensities of cooperators and free-riders affects the fixation probability of cooperators; see [33] for a modeling approach of this kind.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Nowak, M. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nowak, M. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Nowak, M.; May, R. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Nowak, M.; Bonhoeffer, S.; May, R. Spatial games and the maintenance of cooperation. Proc. Natl. Acad. Sci. USA 1994, 91, 4877–4881. [Google Scholar] [CrossRef]
- Nakamaru, M.; Matsuda, H.; Iwasa, Y. The evolution of cooperation in a lattice-structured population. J. Theor. Biol. 1997, 184, 65–81. [Google Scholar] [CrossRef] [PubMed]
- Brauchli, K.; Killingback, T.; Doebeli, M. Evolution of cooperation in spatially structured populations. J. Theor. Biol. 1999, 200, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef]
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Roca, C.; Cuesta, J.; Sánchez, A. Effect of spatial structure on the evolution of cooperation. Phys. Rev. E 2009, 80, 046106. [Google Scholar] [CrossRef]
- Roca, C.; Cuesta, J.; Sánchez, A. Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 2009, 6, 208–249. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nat. Mater. 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Miekisz, J. Effects of sampling interaction partners and competitors in evolutionary games. Phys. Rev. E 2018, 98, 052301. [Google Scholar] [CrossRef]
- Vainstein, M.; Silva, A.T.C.; Arenzon, J. Does mobility decrease cooperation? J. Theor. Biol. 2007, 244, 722–728. [Google Scholar] [CrossRef] [PubMed]
- Sicardi, E.; Fort, H.; Vainstein, M.; Arenzon, J. Random mobility and spatial structure often enhance cooperation. J. Theor. Biol. 2009, 256, 240–246. [Google Scholar] [CrossRef] [PubMed]
- Gelimson, A.; Cremer, J.; Frey, E. Mobility, fitness collection, and the breakdown of cooperation. Phys. Rev. E 2013, 87, 042711. [Google Scholar] [CrossRef] [PubMed]
- Jia, N.; Ma, S. Evolution of cooperation in the snowdrift game among mobile players with random-pairing and reinforcement learning. Phys. A Stat. Mech. Appl. 2013, 392, 5700–5710. [Google Scholar] [CrossRef]
- Antonioni, A.; Sanchez, A.; Tomassini, M. Global information and mobility support coordination among humans. Sci. Rep. 2014, 4, 6458. [Google Scholar] [CrossRef]
- Tomassini, M.; Antonioni, A. Lévy flights and cooperation among mobile individuals. J. Theor. Biol. 2015, 364, 154–161. [Google Scholar] [CrossRef]
- Aktipis, C. Know when to walk away: Contingent movement and the evolution of cooperation. J. Theor. Biol. 2004, 231, 249–260. [Google Scholar] [CrossRef]
- Lin, H.; Yang, D.P.; Shuai, J. Cooperation among mobile individuals with payoff expectations in the spatial prisoner’s dilemma game. Chaos Solitons Fractals 2011, 44, 153–159. [Google Scholar] [CrossRef]
- Wu, T.; Fu, F.; Wang, L. Moving away from nasty encounters enhances cooperation in ecological prisoner’s dilemma game. PLoS ONE 2011, 6, e27669. [Google Scholar] [CrossRef]
- Cong, R.; Wu, B.; Qiu, Y.; Wang, L. Evolution of cooperation driven by reputation-based migration. PLoS ONE 2012, 7, e35776. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Yu, W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Natl. Acad. Sci. USA 2009, 106, 3680–3685. [Google Scholar] [CrossRef] [PubMed]
- Buesser, P.; Tomassini, M.; Antonioni, A. Opportunistic migration in spatial evolutionary games. Phys. Rev. E 2013, 88, 042806. [Google Scholar] [CrossRef] [PubMed]
- Erovenko, I.; Rychtář, J. The evolution of cooperation in 1-dimensional mobile populations. Far East J. Appl. Math. 2016, 95, 63–88. [Google Scholar] [CrossRef]
- Broom, M.; Rychtář, J. A general framework for analysing multiplayer games in networks using territorial interactions as a case study. J. Theor. Biol. 2012, 302, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, E.; Hauert, C.; Nowak, M. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Dugatkin, L. Principles of Animal Behavior, 3rd ed.; W. W. Norton & Company: New York, NY, USA, 2013. [Google Scholar]
- Stewart, A.; Parsons, T.; Plotkin, J. Evolutionary consequences of behavioral diversity. Proc. Natl. Acad. Sci. USA 2016, 113, E7003–E7009. [Google Scholar] [CrossRef] [PubMed]
- Pattni, K.; Broom, M.; Rychtář, J. Evolving multiplayer networks: Modelling the evolution of cooperation in a mobile population. Discret. Contin. Dyn. Syst. Ser. B 2018, 23, 1975–2004. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).