Inequality Aversion and Reciprocity in Moonlighting Games

Abstract

We study behavior in a moonlighting game with unequal initial endowments. In this game, predictions for second-mover behavior based on inequality aversion are in contrast to reciprocity. We find that inequality aversion explains only few observations. The comparison to a treatment with equal endowments supports the conclusion that behavior is better captured by intuitive notions of reciprocity than by inequality aversion. Extending the model by allowing for alternative reference points promises better performance, but leads to other problems. We conclude that the fact that inequality aversion often works as a good short-hand for reciprocity is driven by biased design choices.

1. Introduction

Models of inequality aversion, notably the Fehr-Schmidt model and the Bolton-Ockenfels model, have been able to organize experimental data from games involving interactions between players, such as results from ultimatum and gift-exchange games [1,2]. In contrast, they have not performed well in pure distribution experiments that were designed to test these and related models [3,4,5] (for an overview see [6]).

This does not, however, invalidate inequality aversion models. Still there is a possible way to account for both observations if we understand inequality aversion as a short-hand for reciprocity rather than as literal inequality aversion. This possible interpretation has already been put forward by Fehr and Schmidt [1]. Several studies compare a setting where reciprocity can matter (because a move by the player of interest is preceded by a meaningful move of the other player) with one where it cannot [7,8,9]. The results from these studies support the short-hand interpretation because inequality aversion works much better in the first than in the latter settings. In an alternative approach [10] punishment does not reduce inequality and hence inequality aversion drops out as a possible motive. Subjects still punish (though to a lesser degree), which suggests that reciprocity primarily drives punishment. [11] choose another approach by studying how responder behavior in an ultimatum game changes with the payoff that a third, passive, player receives in case of a rejection. This has little effect, i.e., rejections are unaffected by inequality aversion towards the third player. This suggests that rejections are driven by reciprocity. An exception is [12], which finds that whether the other player made a meaningful move before the player of interest, is irrelevant and therefore reciprocity is not supported. Inequality aversion, however, coincides here with maximin preferences (i.e., a desire to maximize the minimum payoff among those in the reference group) which has been suggested to play a major role in distribution games [3,4].

The starting point of this paper is the following crucial observation: The argument that inequality aversion can capture reciprocity rests on the implicit assumption that an action of the first mover perceived as kind leaves the second mover with a higher payoff than the first mover and an unkind action leaves the second mover with a lower payoff than the first mover. If this assumption holds, the second mover’s response reciprocating the first mover’s kindness or unkindness coincides with inequality aversion. In many experiments, such as trust and ultimatum games, this assumption appears to be naturally fulfilled. If the first mover has a windfall gain (such as in the ultimatum game), it does appear unkind not to share this equally. Or if both players have equal windfall gains (such as in the trust or investment game [13], transferring some of this to the other seems kind.

One can easily think, however, of many situations where inequality aversion and reciprocity will not coincide in the sense that common intuition would consider certain actions as reciprocal that are not in line with inequality aversion. These include poor pickpockets being punished or wealthy generous employers being rewarded with high efforts. Put differently, often equality of payoffs seems a plausible standard to decide whether actions are kind or unkind, but there are also situations where other considerations dominate.

This argument suggests that the success of the inequality aversion models could to a large degree be driven by a bias in experimental design choices that favor settings where the kind are “poor” and the unkind are “rich”. The question how far models of inequality aversion succeed in predicting experimental behavior is thus closely related to the question of how relevant and representative these designs are. They might be natural in the laboratory, where earnings are typically windfall gains and hence equal payoffs are, at least initially, a plausible benchmark for reciprocity. In contrast, they might not be particularly relevant if we want to use the models to explain behavior in field experiments or predict, for example, interactions between real employers and workers by incorporating inequality aversion in principal-agent models.

We test whether models of inequality aversion have any predictive power when the implicit assumption of coincidence of kindness with lower payoffs and unkindness with higher payoffs is not satisfied. To that aim we study behavior in a situation where there is an intuitively neutral action that can serve as an alternative benchmark to payoff equality against which to define kind and unkind actions. We then compare this to a setting where these benchmarks coincide. Specifically, we report on a one-shot experiment that varies the moonlighting game [14]. In one treatment, the action of the first mover to do nothing leaves payoffs roughly equal and hence reciprocating kindness (sending money) or unkindness (taking money) coincides with inequality aversion. In the other treatment even when taking money the first mover is worse off, such that, if this is perceived as unkind, reciprocating through punishment is in contrast to inequality aversion.

We find that while inequality aversion plays some role in moderating reciprocity, it has little explanatory power when it is inconsistent with reciprocity. Hence inequality aversion can help as a short-hand for reciprocity in games where both motives coincide, but outside this class of games it does not appear to yield good predictions. We discuss in the conclusions that simply re-defining the reference point is not a workable solution to reestablished the predictive power of inequality aversion models. We also discuss the implications for the applicability of inequality aversion models in the laboratory and beyond. While the focus of this study is on inequality aversion, we also consider whether models that explicitly incorporate reciprocity explain our data.

2. Experimental Design

We conducted two variants of the moonlighting game [14]. The moonlighting game is a two-player game where the first mover can either take money from the second mover or send some (which is then tripled). The second mover can punish the first mover or send him some money. Our design crucially deviates from the original moonlighting game in two respects. First, we employ the strategy method to obtain a complete schedule of responses from second movers. Second, in both of our treatments, the initial endowments are not perfectly equal. While they are almost equal in Treatment 1, initial endowments grossly favor the second mover in Treatment 2. The purpose of this treatment is to put inequality aversion in contrast to intuitive notions of reciprocity (see Section 3). Both treatments were run as one-shot experiments. 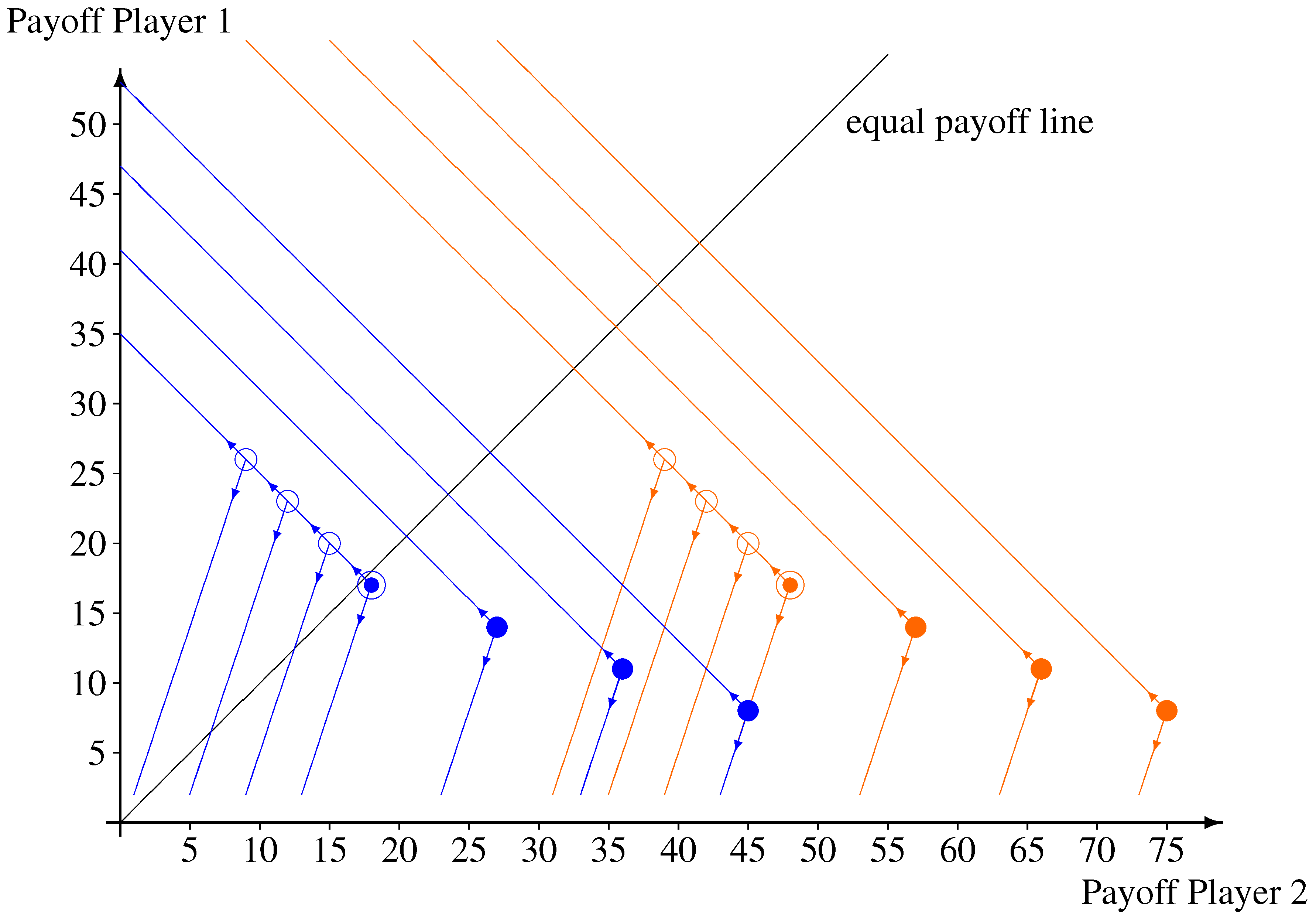Figure 1 gives a graphical representation of the strategy space.

Figure 1. Strategy space of the game (blue for Treatment 1 and orange for Treatment 2). The emphasized circles denote the status quo payoff distribution. Player 1 may move to another distribution by taking (empty circle of same color) or sending money (filled circle of same color). Player 2 may punish or reward by moving along the corresponding lines in the indicated directions.

Figure 1. Strategy space of the game (blue for Treatment 1 and orange for Treatment 2). The emphasized circles denote the status quo payoff distribution. Player 1 may move to another distribution by taking (empty circle of same color) or sending money (filled circle of same color). Player 2 may punish or reward by moving along the corresponding lines in the indicated directions.

Specifically, in Treatment 1 initial endowments are 17 Experimental Monetary Units (EMU) for Player 1 and 18 EMU for Player 2 (2 EMU = £1). We made the initial endowments in Treatment 1 slightly unequal in order to remove perfect equality as a focal point, while keeping the basic property intact that inequality aversion and reciprocity coincide. Player 1 could either take 9, 6, or 3 EMU from Player 2, take or send 0, or send 3, 6, or 9 EMU. If Player 1 sent any money to Player 2, the amount Player 2 received was tripled. Player 2 was asked to decide for all possible choices of Player 1 whether to send any money to Player 1 (which was not tripled) or to assign punishment points (labelled “reduction points” in the experimental instructions) to Player 1. Each punishment point cost 1 EMU to Player 2, but reduced the payoff of Player 1 by 3 EMU. The only restrictions placed on the amount that Player 2 could send or the punishment points he could assign were that they had to be integers and did not cause negative payoffs for either of the players.

Treatment 2 differed from Treatment 1 by a higher endowment of Player 2, namely 48 EMU. This implied that even if Player 1 took the maximum amount, 9 EMU, Player 2 would still have a substantially higher payoff (39 vs. 26), representing the idea of the poor pickpocket. As a result, if Player 1 takes something from Player 2, then inequality aversion and a notion of reciprocity that considers sending money as kind and taking money as unkind, suggest different actions. While reciprocity suggests to punish Player 1 (if the reciprocity motive is strong enough, otherwise do nothing), inequality aversion suggests to send some money to Player 1 even after he took something (if the motive is strong enough, otherwise do nothing). Since doing nothing is consistent with relatively weak forms of both inequality aversion and reciprocity, we need the comparison to Treatment 1 in order to assess the impact of inequality aversion by measuring how Player 2’s reaction to Player 1’s taking changes with different endowments.

We conducted six sessions (three for each treatment) with 16 subjects each (except for one session for Treatment 1 with just 14 subjects). Since the experiment was one-shot, we have 23, respectively 24, independent observations for each player role in each treatment. The experiments were conducted in the experimental laboratory at Royal Holloway in March 2005 and March 2006. The experiments were programmed and run in z-Tree [15]. Subjects were (mainly undergraduate) students from a variety of fields. All sessions took less than 45 minutes, including reading the instructions, filling out a questionnaire and receiving payment. Average payments were £ 9.13 in Treatment 1 and £ 15.91 in Treatment 2. The instructions are in the appendix.

3. Predictions

Our primary interest here is not to explicitly test any model of reciprocity but rather to study the performance of inequality aversion models when they are in contrast to intuitive notions of reciprocity. Nevertheless we want to briefly discuss different models and their predictions for our setup (see Table 1 for a summary).

Given the design of the experiment, doing nothing appears to be a natural candidate for a neutral action by the first mover in both treatments. Consequently sending money can be seen as kind and taking money as unkind. Following the same intuition, returning money is kind, while assigning punishment points is unkind. Our intuitive notion of reciprocity would thus imply that sending money is followed by weakly positive amounts of money being returned, whereas taking money is followed by assigning a weakly positive number of punishment points.

The predictions of models of inequality aversion for the second mover are straightforward. The second mover should send the first mover money only in situations where the first mover’s action leads the second mover to have more money than the first. The second mover should assign punishment points to the first mover only in situations where the first mover’s action leads the second mover to have less money than the first.

Applying reciprocity models such as those from Dufwenberg and Kirchsteiger [16] or Falk and Fischbacher [17] is not straightforward because this requires knowledge about beliefs, which we did not elicit. At least we can derive some general principles. Starting with the Dufwenberg-Kirchsteiger model, there is an equilibrium selection problem, typically including some implausible equilibria that include self-fulfilling prophecies of mutual hostility. For example, given two strongly reciprocal players, it can be an equilibrium that even if Player 2 would return significant amounts of money if Player 1 sent anything and would punish Player 1 if he took anything, Player 1 would choose to take money. This can be an equilibrium if Player 1 believes that Player 2 believes that Player 1 is very likely to take money. Then Player 2’s strategy is unkind, because the punishment of Player 1 after taking leaves Player 1 below his equitable payoff. In turn, Player 1 will take money just because punishment is costly for Player 2 as well (in addition to taking money directly harming Player 2). Thus the players can get stuck in a bad equilibrium because they expect negatively reciprocal reactions, even though they both know that Player 2 would have rewarded a kind action by Player 1. Changing the payoffs between our treatments can affect equilibrium selection and make such an equilibrium more likely in one treatment than the other. Whether this would drive any treatment differences seems difficult to assess without eliciting beliefs. Leaving such equilibria aside, we can derive some general insights.

First, given that assigning punishment points is inefficient, the equitable payoff (which is determined as the average between the maximum feasible and the minimum resulting from feasible efficient strategies) for Player 1 will result if Player 2 sends half her money to Player 1. Thus, any return of less than half her capital (after any of Player 1’s choices) is actually unkind. Given the higher endowment in Treatment 2, this increases the requirements on a return for qualifying as kind. This in turn has two implications. On the one hand, this means that in a “kind” equilibrium of the asymmetric treatment, the amount returned will be higher than in a kind equilibrium of the symmetric treatment. On the other hand, as this makes being kind more expensive for Player 2, a kind equilibrium should become less likely.

The second general insight is that given the way the equitable payoff is determined, doing nothing is not necessarily Player 1’s neutral action. Depending on Player 1’s belief about Player 2’s response, it can involve sending or taking money. For example, if Player 1 believes Player 2 will never take any action, Player 1 sending 3 will lead to Player 2 receiving her equitable payoff. Alternatively, if Player 2 always returns $2/3$ of the surplus gained, but never punishes, then doing nothing becomes the neutral action, whereas if she returns $8/9$ of the surplus, then the neutral action becomes taking 3. Thus the Dufwenberg-Kirchsteiger model can, but does not have to agree with our intuitive notion that for Player 1 sending is always kind and taking is always unkind.

As a third insight, considering “unkind” equilibria, given that Player 2 could send a lot more in Treatment 2, any assignment of a given number of punishment points is relatively more unkind in the asymmetric Treatment 2 than in the symmetric Treatment 1. Therefore, if Person 2 wants to reciprocate unkindness, punishing is more attractive (i.e., the utility component obtained for punishing is larger). Thus for actions perceived as unkind, we should see Player 2 punishing more in Treatment 2 than in Treatment 1, though what is perceived as unkind may change. An interesting observation in this context is that because punishment is costly, if an action is punished, it actually becomes more unkind. Thus small differences in beliefs can have large effects, as punishment becomes self-enforcing. On the other hand, given that Player 2 is less likely to return anything in Treatment 2 than in Treatment 1 but if she does, returns more, the action of Player 1 leading to the equitable payoff for Player 2 can move up or down. Hence, it is not obvious which actions do get punished.

The linearity of the utility function in both own payoff and the reciprocity component has further, somewhat implausible implications, specifically that in an “unkind” equilibrium, Player 2 would always assign the maximum permissible punishment points, whereas in a “kind” equilibrium, Player 2 would send her whole capital to Player 1 (if Player 2 perceives Player 1’s move as kind and cares enough about positive reciprocity she wants to be as kind as possible). In equilibrium this actually eliminates the kindness of Player 1’s move (whatever that move was) and thus undermines the equilibrium itself. The specific functional form thus makes “kind” equilibria impossible in our setting.

For the Falk-Fischbacher model we can also draw some qualitative predictions. In this model, kindness is assessed by comparing the payoffs of the two players. In Treatment 2, Player 2 is always better off than Player 1 unless she sends a non-trivial amount to Player 1. Thus in Treatment 2, even if Player 1 takes money, his action is considered kind. Thus, a reciprocal Player 2 should reward Player 1. Rewarding Player 1 constitutes choosing an action that increases the payoff of Player 1 compared to what Player 1 expected. Thus punishment is consistent with equilibrium only if Player 1 actually expects to be punished more harshly. In that case, however, Player 1 should not have chosen to take in the first place. Thus Player 2 should infer from seeing Player 1 taking that Player 1 expects not to be punished and should not punish. Thus, in Treatment 2 we should not see any punishment by Player 2.

In general, the model by Falk and Fischbacher implies that any given send or take action by Player 1 is considered kinder in Treatment 2 than in Treatment 1. Thus we should see kinder reactions by Player 2. However, the kindness of Player 2 depends on the expectations of Player 1 (or more precisely on Player 2’s second-order belief regarding Player 1’s expectation). This means that “kinder” actions do not necessarily imply higher transfers (or lower punishments), but they do under the plausible assumption that Player 1 expects to be treated better or equal in Treatment 2 than in Treatment 1. Thus, under reasonable assumptions regarding beliefs, we should expect higher transfers and lower punishment in Treatment 2 compared to Treatment 1, and in particular punishment should not occur at all in Treatment 2.

Our intuitive notion of reciprocity is better captured by the approach to reciprocity taken in the model by Cox, Friedman, and Sadiraj [18]. Their model of reciprocity captures the idea that Player 2 will be more altruistic towards Player 1 if Player 1 has been more generous towards Player 2. Hence, this model incorporates reciprocity by allowing for preferences over distributions to change depending on others’ actions. Specifically, facing the same opportunity set G, Player 2 will choose a kinder action towards Player 1 if it is preceded by an action of Player 1 that increased the maximum possible payoff to Player 2 than if it is preceded by an action that reduced the maximum possible payoff to Player 2. Furthermore, their Axiom S considers the status quo. It implies that facing a given opportunity set G as the status quo, Player 2 will be more altruistic towards Player 1 if the action by Player 1 changed the situation to favor Player 2 relative to the status quo. Similarly, Player 2 will be less altruistic towards Player 1 if the action by Player 1 made Player 2 worse off than the status quo.

In our experiment, the initial endowments are a plausible candidate for the status quo (the experimental instructions explicitly referred to these as initial endowments that could be changed by Player 1 by sending or taking). Therefore, for comparable opportunity sets that Player 2 faces in Treatment 2 after Player 1 has taken money and in Treatment 1 after Player 1 has sent money, Player 2 should act less altruistically towards Player 1 in Treatment 2 than in Treatment 1. The Cox-Friedman-Sadiraj model also predicts that following the same action by Player 1, Player 2 will be (weakly) more altruistic in Treatment 2 than in Treatment 1, because players’ preferences are increasingly benevolent in their income.

Table 1. Summary of key predictions by the different models.

Model	Prediction
Inequality aversion	T1: Player 2 does not punish after Player 1 has sent and does not sent after Player 1 has taken. T2: Player 2 does not punish after any action of Player 1.
Fehr-Schmidt	T1, T2: Player 2 either equalizes payoffs or does nothing.
Naive reciprocity	T1, T2: Player 2 does not punish after Player 1 has sent and does not send after Player 1 has taken.
Dufwenberg-Kirchsteiger general	Kind equilibrium: Player 2’s sent amount in T2 > T1, but sending is less likely. Unkind equilibrium: Player 2’s punishment in T2 > T1.
Dufwenberg-Kirchsteiger linear	See above, but only extreme amounts should be observed (sending all or punish the maximum).
Falk-Fischbacher	T2: No punishment should be observed. Under reasonable assumptions Player 2’s sent amount in T2 > T1.
Cox-Friedman-Sadiraj	Player 2’s sent amount in T2 ≥ T1 and Player 2’s punishment in T2 ≤ T1. For similar budget sets Player 2’s sent amount in T1 > T2 and Player 2’s punishment in T2 > T1.

Table 1. Summary of key predictions by the different models.

Model	Prediction
Inequality aversion	T1: Player 2 does not punish after Player 1 has sent and does not sent after Player 1 has taken. T2: Player 2 does not punish after any action of Player 1.
Fehr-Schmidt	T1, T2: Player 2 either equalizes payoffs or does nothing.
Naive reciprocity	T1, T2: Player 2 does not punish after Player 1 has sent and does not send after Player 1 has taken.
Dufwenberg-Kirchsteiger general	Kind equilibrium: Player 2’s sent amount in T2 > T1, but sending is less likely. Unkind equilibrium: Player 2’s punishment in T2 > T1.
Dufwenberg-Kirchsteiger linear	See above, but only extreme amounts should be observed (sending all or punish the maximum).
Falk-Fischbacher	T2: No punishment should be observed. Under reasonable assumptions Player 2’s sent amount in T2 > T1.
Cox-Friedman-Sadiraj	Player 2’s sent amount in T2 ≥ T1 and Player 2’s punishment in T2 ≤ T1. For similar budget sets Player 2’s sent amount in T1 > T2 and Player 2’s punishment in T2 > T1.

4. Results

4.1. Overview

In the following we compare the data from Treatments 1 and 2 (see Table 2 and Table 3, respectively). The most interesting part of the data is obviously the behavior of Player 2 after Player 1 has taken money in Treatment 2. In this case the predictions of inequality aversion and our intuitive notion of reciprocity differ. Out of 24 Players 2 in Treatment 2, 12 never take action after Player 1 has taken money, seven punish all acts of taking, Subject 83 only punishes taking 9, Subjects 73 and 85 send money after all acts of taking. Subject 93 shows a somewhat inconsistent pattern. (This may be partly due to errors, as this subject actually stated in a post-experimental questionnaire to have assigned punishment points after Player 1 taking and sending money back after Player 1 sending). Finally, Subject 59 appears to be confused. (In the questionnaire, she replies to the question “Please explain how you made your choice!” plainly with “random”.) For the significance levels we report below, it does not make a difference whether we exclude this subject from the analysis or not.

For comparison, in Treatment 1, 14 of the 23 Players 2 never take action after Player 1 takes and eight punish all acts of taking. Subject 21 punishes taking 9 or 6 EMU, but sends 3 EMU after Player 1 has taken 3 EMU. (This might also be a mistake given that she took no action if Player 1 took nothing).

Table 2. Player 2 behavior in the Moonlighting-game with almost equal endowments (Treatment 1). DecTx and DecSy are the decisions of Player 2 after Player 1 has taken x EMU or sent y EMU, respectively, where sending y implies gains of 3y for Player 2. A positive value indicates the number of EMU sent back, a negative value the number of reduction points assigned, where each reduction point costs 3 EMU to player 1.

Treatment 1
Subject(s)	DecT9	DecT6	DecT3	DecT0	DecS3	DecS6	DecS9
3,7,9,27,31,33,37,43,45	0	0	0	0	0	0	0
1	0	0	0	–3	0	0	0
5	0	0	0	0	5	10	15
11	–8	–6	–3	0	0	0	0
13	–8	–4	–3	–1	3	6	9
15	–5	–4	–3	2	3	5	8
17	0	0	0	0	3	3	3
19	0	0	0	0	3	0	0
21	–3	–3	3	0	3	6	9
23	–6	–4	–2	0	1	3	5
25	0	0	0	0	3	6	9
29	–3	–2	–1	0	0	0	0
35,41	–3	–2	–1	0	3	6	9
39	–4	–3	–2	0	6	9	12

Table 2. Player 2 behavior in the Moonlighting-game with almost equal endowments (Treatment 1). DecTx and DecSy are the decisions of Player 2 after Player 1 has taken x EMU or sent y EMU, respectively, where sending y implies gains of 3y for Player 2. A positive value indicates the number of EMU sent back, a negative value the number of reduction points assigned, where each reduction point costs 3 EMU to player 1.

Treatment 1
Subject(s)	DecT9	DecT6	DecT3	DecT0	DecS3	DecS6	DecS9
3,7,9,27,31,33,37,43,45	0	0	0	0	0	0	0
1	0	0	0	–3	0	0	0
5	0	0	0	0	5	10	15
11	–8	–6	–3	0	0	0	0
13	–8	–4	–3	–1	3	6	9
15	–5	–4	–3	2	3	5	8
17	0	0	0	0	3	3	3
19	0	0	0	0	3	0	0
21	–3	–3	3	0	3	6	9
23	–6	–4	–2	0	1	3	5
25	0	0	0	0	3	6	9
29	–3	–2	–1	0	0	0	0
35,41	–3	–2	–1	0	3	6	9
39	–4	–3	–2	0	6	9	12

Thus when inequality aversion and reciprocity coincide, as they do in Treatment 1 after Player 1 has taken money and in most of the literature, the results are very favorable for inequality aversion. Eight subjects clearly support it, 14 at least do not reject it and the one inconsistent choice is quite possibly an error. This corresponds to the classical results where inequality aversion organizes the data well. In contrast, in Treatment 2, among the 12 subjects that choose inconsistently with payoff maximization after Player 1 has taken money, eight act clearly in contrast to inequality aversion, but in line with reciprocity. Only two subjects are unambiguously inequality averse. Incidentally, the behavior of the inequality averse Subject 73 is not consistent with any functional form of inequality aversion. Both her payoff and the inequality are larger and the payoff of Player 1 is smaller, after she sends 11 if Player 1 has sent 9 (p2: 64, p1: 19) than before she sends anything if Player 1 has taken 9 (p2: 39, p1: 26). Hence a distributional model that is consistent with her sending anything if Player 1 has taken 9 (which she does) would imply that she sends substantially more than 11 if Player 1 has sent 9. Subject 85 might have wanted to equalize payoffs, but gets the math wrong by sending an amount equal to the difference and hence inverting the inequality in each case. (This subject indeed states in the post-experimental questionnaire “my calculations were wrong”.)

Table 3. Player 2 behavior in the Moonlighting-game with unequal endowments (Treatment 2). DecTx and DecSy are the decisions of Player 2 after Player 1 has taken x EMU or sent y EMU, respectively, where sending y implies gains of 3y for Player 2. A positive value indicates the number of EMU sent back, a negative value the number of reduction points assigned, where each reduction point costs 3 EMU to player 1. Subject 59 is apparently confused.

Treatment 2
Subject(s)	DecT9	DecT6	DecT3	DecT0	DecS3	DecS6	DecS9
51,55,57,63,65,67,69,71,81,95	0	0	0	0	0	0	0
53	0	0	0	0	5	10	15
59	7	–2	–4	2	–3	6	5
61	–2	–1	–1	0	0	1	1
73	5	6	7	8	9	10	11
75	–8	–6	–3	0	–3	–3	3
77	0	0	0	0	1	2	3
79	–8	–7	–6	15	22	27	33
83	–2	0	0	0	1	2	3
85	13	19	25	31	43	55	67
87	–8	–7	–6	0	12	15	18
89	–3	–2	–1	0	3	6	9
91	–3	–3	–3	0	0	0	0
93	–1	–2	1	0	3	2	–2
97	–5	–4	–3	–2	5	8	10

Table 3. Player 2 behavior in the Moonlighting-game with unequal endowments (Treatment 2). DecTx and DecSy are the decisions of Player 2 after Player 1 has taken x EMU or sent y EMU, respectively, where sending y implies gains of 3y for Player 2. A positive value indicates the number of EMU sent back, a negative value the number of reduction points assigned, where each reduction point costs 3 EMU to player 1. Subject 59 is apparently confused.

Treatment 2
Subject(s)	DecT9	DecT6	DecT3	DecT0	DecS3	DecS6	DecS9
51,55,57,63,65,67,69,71,81,95	0	0	0	0	0	0	0
53	0	0	0	0	5	10	15
59	7	–2	–4	2	–3	6	5
61	–2	–1	–1	0	0	1	1
73	5	6	7	8	9	10	11
75	–8	–6	–3	0	–3	–3	3
77	0	0	0	0	1	2	3
79	–8	–7	–6	15	22	27	33
83	–2	0	0	0	1	2	3
85	13	19	25	31	43	55	67
87	–8	–7	–6	0	12	15	18
89	–3	–2	–1	0	3	6	9
91	–3	–3	–3	0	0	0	0
93	–1	–2	1	0	3	2	–2
97	–5	–4	–3	–2	5	8	10

Note that our design does not artificially minimize the significance of inequality. In Treatment 2, if Player 1 takes 3, 6 or even 9 EMU, the inequality is still substantial (45 vs. 20, 42 vs. 23, or 39 vs. 26) and the instructions showed this distribution in a table, but only two Players 2 consistently transferred money to Player 1 in these situations.

We summarize these observations as:

• Result 1: If inequality aversion and reciprocity agree, after Player 1 has taken money in Treatment 1, most of the behavior is consistent. If inequality aversion and reciprocity predict different behavior, after Player 1 has taken money in Treatment 2, most of the observed non-selfish behavior is inconsistent with inequality aversion.

Concerning the behavior after Player 1 has sent money to Player 2, both inequality aversion and our intuitive notion of reciprocity predict that Player 2 will send something back. According to inequality aversion, the amount sent back should be higher in Treatment 2, given the larger inequality. More precisely, the linear Fehr-Schmidt model would suggest that the amount sent back should either be zero or equalize payoffs, so in Treatment 2, the positive returns should be larger. Alternative models of inequality aversion that would be consistent with returns that reduce, but do not fully eliminate inequality need to be concave in own payoff or convex in inequality. Either of these properties also implies larger returns in Treatment 2 than in Treatment 1 for equal amounts sent.

The results show little support. In Treatments 1 and 2, 12 out of 23 Players 2 and 11 out of 24 Players 2, respectively, never take action after Player 1 has sent something. In Treatment 1, the remaining 11 Players 2 send back money, but only Subjects 5 and 39 send more than Player 1 has sent, while still not enough to equalize payoffs. In Treatment 2, where we would expect Player 2 to send back more, only 10 Players 2 regularly send money back, but Subject 75, in stark contrast to inequality aversion, punishes even after 3 and 6 have been sent and sends money back only after 9 have been sent. (That Subject 93 punishes after Player 1 sends 9 is probably again an error and the patterns for Subject 59 again suggests confusion.) The average amount sent back is, as would be predicted by inequality aversion, higher in Treatment 2, but this is exclusively due to Subject 79, who indeed equalizes payoffs, and Subject 85, who apparently wants to do the same. Interestingly, while Subject 79 is perfectly in line with inequality aversion as long as Player 1 has not taken any money, he punishes Player 1 by the maximal allowable amount if she takes, clearly inconsistent with inequality aversion.

• Result 2: Even when Player 2 sends money to Player 1, this is almost never eliminating inequality.

4.2. Statistical Tests for the Role of Inequality Aversion

To test whether the degree of inequality has any impact for a given choice of Player 1, we conduct Mann-Whitney tests comparing the reaction of Players 2 for each of the possible choices of Player 1. For none of them the choice by Player 2 differs significantly between treatments ($p>0.1$ in all cases), most importantly for none of the taking actions of Player 1 does the behavior of Players 2 differ between treatments. This result suggests that there is no significant effect of the degree of inequality for a given behavior of Player 1 on the behavior of Player 2. As noted above, under reasonable assumptions the Falk-Fischbacher model predicts as well, following the same action by Player 1, kinder behavior in Treatment 2 than in Treatment 1. This prediction does not find significant support in our data. Interestingly, the only comparison where we get anywhere near significance is after Player 1 has neither send nor taken. If doing nothing is perceived as neutral, then reciprocity would not yield a clear prediction to reward or punish and thus equality concerns may more strongly come into play. The observed difference is, however, rather small and significant only with a stretch ($p<0.1$ in a one-tailed Mann-Whitney test).

• Result 3: Across treatments, if the actions by Player 1 are the same but the resulting inequality differs, the reactions by Player 2 do not differ significantly.

4.3. Statistical Tests for the Role of Intuitive Notions of Reciprocity

In order to test whether our intuitive notion of reciprocity, i.e., whether Player 1 has sent or taken, has a significant impact for a given degree of inequality, we compare the results in Treatment 2 after Player 1 has taken 3, 6, or 9 EMU with those in Treatment 1 after Player 1 has sent 3 EMU. In the latter case, the absolute payoff difference between Player 2 and Player 1, $(27-14)$, is the same as in Treatment 2 after Player 1 has taken 9 EMU $(39-26)$. Moreover the relative payoffs $(27:14)$ are roughly $2:1$, as they are after Player 1 has taken 6 EMU in Treatment 2 $(42:23)$. In addition, after Player 1 has taken 3 in Treatment 2, Player 2 is substantially better off than after Player 1 has sent 3 in Treatment 1 (45 vs. 27). Player 1 is however only slightly better off (20 vs. 14), so that most plausible forms of altruistic utility functions (e.g., $U=m{y}^{\varphi }$, with m “my payoff” and y “your payoff”) would predict (weakly) higher returns in Treatment 2 than in Treatment 1 if reciprocity does not matter. Hence depending on the specific functional form that inequality aversion, or more generally altruism towards the less well-off, takes, we would expect Player 2’s action after “send 3” in Treatment 1 to be similar to (or even to be less generous than) the action taken after “take 9”, “take 6”, or “take 3” in Treatment 2. In particular, with the linear Fehr-Schmidt model, choices should be exactly equal after “send 3” in Treatment 1 and “take 9” in Treatment 2. (They should also be exactly equal after “send 6” in Treatment 1 and “take 3” in Treatment 2 as these both lead to an inequality of 25.) In contrast, if Players 2 are driven by reciprocity, we would expect them to return money after “send 3” in Treatment 1, but punish in Treatment 2 after Player 1 has taken money.

The data clearly support that reciprocity matters. Indeed, in Treatment 1, “send 3” is followed in 11 out of 23 cases by sending money and in no case by punishment, whereas in Treatment 2 “take 9”, “take 6”, and “take 3” are followed in 8 to 9 cases by punishment and only in 2 to 3 cases by sending money. This difference in behavior is significant ($p<0.01$ in all cases, Mann-Whitney). And more generally, in both treatments, as long as second movers take any action, they typically follow Player 1 sending by returning money and Player 1 taking by punishment. Indeed, comparing Player 2’s behavior after any sending action in Treatment 1 with that after any taking action in Treatment 2 yields a significant difference at $p<0.01$ (Mann-Whitney) for any such pair-wise comparison.

• Result 4: Across treatments, if the actions by Player 1 are different but the resulting inequality is the same, the reactions by Player 2 differ significantly, in line with reciprocity.

4.4. Considering Predictions by the Reciprocity Models

While the results of our experiments are thus supportive of our simple intuitive notion of reciprocity, they are, however, hardly in line with qualitative predictions based on the Dufwenberg-Kirchsteiger model. For example, punishment is rarely at the maximum permissible level. It is reasonably frequently at the maximum after Player 1 has taken 9 (5 out of 17 cases), but only two subjects, 79 and 87, punish at the maximal permissible level after Player 1 has taken 3 or 6. Moreover, the amount sent is never at the maximum allowed level. Indeed, Players 2 never send as much that they are worse off than Player 1, showing that while inequality aversion may be a poor model to explain behavior in our experiment, equality matters in the sense that altruism rarely extends to the point of self-sacrifice to benefit the rich (the only exception is Subject 85, who inverses the inequality but states to have miscalculated). Thus, the rather implausible predictions based on the linearity in the various utility components in Dufwenberg and Kirchsteiger are clearly rejected.

Furthermore, the cut-off between Player 1’s actions that trigger positive returns and those that trigger punishment is for most second movers the action of taking nothing, which is not inconsistent with the Dufwenberg-Kirchsteiger model, but better captured by the Cox-Friedman-Sadiraj because changing the status quo in favor of Player 2 generally attracts rewards and changing the status quo harming Player 2 generally attracts punishments: for 13 among the 16 subjects (17 if the confused subject is included) who both punish and reward, Player 1 taking no action marks a turning point. We also note that the punishment by Players 2 in Treatment 2 that we do observe contradicts the qualitative prediction of the Falk-Fischbacher model that punishment should not occur, whereas the fact that punishment is not stronger in Treatment 2 than in Treatment 1 contradicts another of the qualitative predictions of the Dufwenberg-Kirchsteiger model.

• Result 5: The qualitative predictions derived for the Dufwenberg-Kirchsteiger and Falk-Fischbacher models are not supported.

4.5. Behavior of Player 1

Concerning the behavior of Player 1, if inequality aversion drives subjects’ behavior, we would expect them to take more in Treatment 2 where taking will reduce inequality if it is not punished. (The prediction will thus ultimately depend on the beliefs of subjects in the role of Player 1, which we did not elicit.) While there is a small difference in the predicted direction because a higher share of Players 1 take the maximum permitted 9 EMU (12 in Treatment 2 vs. eight in Treatment 1), the overall difference in Player 1 behavior is quantitatively very small (the average transfer from Player 1 to Player 2 is $-3$ in Treatment 1 and $-3.63$ in Treatment 2) and not significant according to a Mann-Whitney test ($p>0.5$). More specifically, in Treatment 2, 15 Players 1 take money from Player 2, seven Players 1 send 3 or 6 EMU and two neither take nor send. In Treatment 1, 13 Players 1 take money from Player 2, again seven Players 1 send money (only one the maximum of 9 EMU) and three neither take nor send. We note that while taking more is in line with inequality aversion, it is also in line with selfishness if Players 1 correctly anticipate that Players 2 are more lenient in Treatment 2. Moreover, given actual Player 2 behavior, taking 9 is maximizing expected payoffs for Player 1 in both treatments. Finally, the fact that an equal number of first movers send money in both treatments does not support the qualitative prediction from the Dufwenberg-Kirchsteiger model that kind equilibria should be less likely in Treatment 2.

• Result 6: Player 1 behavior differs very little across treatments, in contrast to the predictions of inequality aversion.

5. Discussion and Concluding Remarks

The experiment we report on deviates from the typical experimental design choices where reciprocity, when it matters, coincides with inequality aversion. Our systematic variation shows that, as in previous experiments, inequality aversion does quite well when it is in line with reciprocity, but it has little explanatory power when it contradicts reciprocity. When comparing the two treatments after the same action of Player 1, reciprocal Players 2 only consider the effect of Player 1’s action on their payoff but not the resulting payoff distribution. Therefore reciprocal Players 2 should react in the same manner in both treatments while inequality averse Players 2 should react differently. The results for the Players 2 in this case differ slightly, but insignificantly. In contrast, in situations where different actions of Player 1 lead to comparable levels of inequality, reciprocity implies different actions of Player 2 but not inequality aversion. For this case the difference in the data is highly significant. This suggest that the behavior of Players 2 in our experiment is more strongly guided by reciprocity than by equality concerns.

Our results strengthen those of [9] who compare in a moonlighting game treatments where the first mover is free to make a choice with another treatment where instead a random device determines his move. They find that in the first treatment, where reciprocity matters and is in line with inequality aversion, rewards and punishment by the second mover are substantially larger than in the second treatment, where they can be driven inequality aversion alone. This shows that inequality aversion yields a better prediction when it is in line with reciprocity. Our results go beyond this conclusion by showing that if reciprocity is not eliminated as a motivation but is in contrast to inequality aversion, then it dominates and inequality aversion does not organize the data well.

Previous experiments (e.g., [4]) have shown that subjects rarely punish richer players that have not misbehaved. The current study shows that they rather frequently punish poorer players who have misbehaved. Thus at least in the realm of harming behavior, whether the other player has previously been kind or unkind appears to be of more importance than payoff comparisons. We note that in our experiment, the predictions of our simple concept of reciprocity and inequality aversion differ only for the case if Player 1 misbehaves. We thus essentially test negative reciprocity against advantageous inequality aversion. This might bias our design in favor of reciprocity, because negative reciprocity appears to be a more robust phenomenon than positive reciprocity, while the Fehr-Schmidt model assumes aversion towards disadvantage inequality to be stronger than towards advantageous inequality.

Since we did not elicit beliefs, we could only make limited predictions for the reciprocity models of Dufwenberg-Kirchsteiger and Falk-Fischbacher. Most of these are not supported, so the observed behavior is overall not captured well by these models.

The Cox-Friedman-Sadiraj model [18] captures the impact of reciprocity in our experiment quite well, because it assigns an important role to the impact that the first mover’s action had on the second mover and to the status quo. Indeed, the two comparisons discussed above suggest that whether the first mover has helped or harmed the second mover plays a very important role, and apparently more so than inequality. We note that our experiments were not designed to test the Cox-Friedman-Sadiraj model, because they were already run in 2005 and 2006. Our experiments are structurally well suited to test this model, but the parameters are not perfect. Ideally the second mover would face the same budget set in the asymmetric treatment after a first mover’s taking action as in the symmetric treatment after a first mover’s sending action (and for completeness, in a possible third treatment after a neutral status quo-preserving action of neither sending nor taking). Then one could directly compare the responses to these different actions across treatments (that all imply the same budget set for the second mover) and any differences could be attributed to the effects of the first mover’s action leaving the status quo unchanged or changing it to the benefit or the harm of the second mover.

Our results support that inequality aversion models can serve as an easy to apply short-hand version for reciprocity when the perceived neutral action (neither kind nor unkind), implies equal payoffs. However, when there is a suggestive alternative neutral action, such as doing nothing in our Treatment 2, so that taking money appears to be clearly unkind and sending money appears to be clearly kind, inequality aversion models largely fail. Thus literal inequality aversion seems to be of minor importance when reciprocity can matter and only serves as short-hand when they do agree.

One could consider extensions of inequality aversion models that take an alternative reference point as “equitable”, such as the one implied by Player 1 taking no action. For example, in Treatment 2, one could apply the Fehr-Schmidt model after subtracting from each payoff the payoff that would result from Player 1 taking the identified neutral action.

There are a number of problems with such an approach. First, it would suggest that behavior between our two treatments do not differ at all, but we find some minor differences. In particular, three subjects show signs of literal inequality aversion in Treatment 2, Subject 73 who also sends money to Player 1 after he has taken money, Subject 79 who, as long as Player 1 does not take anything, is equalizing payoffs and Subject 85 who apparently wants to equalize payoffs. This behavior could be taken into account by allowing for heterogeneity of reference points among individuals, but that would make the model untestable. Fitting heterogenous reference points allows to capture any behavior that satisfies certain consistency requirements within the model.

Second, and strengthening the first problem, the choice of the neutral action is not always as straightforward as in our design. Here taking money has an obvious negative flavor (even in spite of Player 1 being poorer in Treatment 2), while sending is obviously friendly. Identifying a neutral action may not always be that easy. For example, what is a neutral wage in a gift-exchange game, in particular if the equilibrium wage for selfish players is positive but small?

Finally, the perceived neutral action is certainly affected by the labelling of actions. For example, consider an experiment corresponding to our Treatment 2, but with the endowment for Player 1 increased by 9 EMU, the endowment for Player 2 decreased by 9 EMU and Player 1 restricted to sending between 0 and 18 EMU to Player 2, where anything beyond 9 EMU will be tripled. This is exactly the same game, but since the term “take money” has been eliminated, those actions that correspond to taking money in our treatment will most likely not be perceived as hostile and we would expect substantially different behavior. Even an extended Fehr-Schmidt model, however, if it is supposed to retain general applicability, should be independent of labelling. If the labels assigned to actions matter, this would also contradict approaches that model reciprocity directly such as Dufwenberg-Kirchsteiger, where the evaluation of behavior as kind or unkind only depends on the range of outcomes that the possible choices have. What is labelled as the neutral action could only serve as an equilibrium selection device by impacting on beliefs. In contrast, the Cox-Friedman-Sadiraj model predicts that labels would matter, because it matters how the first mover changes the payoffs relative to the status quo.

A possible route to take the dependence of the neutral action on the labelling into account would be to consider initial endowments as entitlements and take these as the neutral payoff allocation, evaluating the kindness of actions by how they influence payoffs in relation to these endowments. This approach leads to other contradictions. In the ultimatum game, initial endowments are unequal, but these do not seem to be taken as acceptable and leaving them unchanged is not perceived as a neutral action, but an unkind one. In games like the ultimatum game, equal payoffs appear to be the standard against which actions are measured as kind or unkind. And while in our experiment, an action that does not affect current payoffs is apparently considered neutral by most subjects (the payoffs resulting in this case being considered as entitlements), this is not the case in the ultimatum game for most people (where the pie to be split is not considered an entitlement of the proposer).

To conclude, the present experiment does not invalidate inequality aversion as a useful as-if model for reciprocal behavior that might otherwise be difficult to capture in explicit models of reciprocity. Indeed, behavior in Treatment 1 is to some degree in line with inequality aversion models. Our results, however, strengthen previous results that suggest that literal inequality aversion is of little importance. They also highlight that the success of the models in explaining previous experimental results may have been to a considerable degree a consequence of a bias in experimental design choices, namely those where equal payoffs are intuitively a focal point for neutral actions. This suggests boundaries to the applicability of inequality aversion and implies that special care should be taken when applying it to novel problems where this condition might not hold, in particular to settings outside the laboratory.