The Insider-Outsider Model Reexamined

Abstract

In this note we introduce different levels of decay in the Goyal, Galeotti and Kamphorst (GGK) insider-outsider model of network formation. First, we deal with situations where the amount of decay is sufficiently low to avoid superfluous connections in strict Nash networks and we examine the architectures of strict Nash networks. We show that centrality and small diameter are robust features of strict Nash networks. Then, we study the Nash and efficient networks when the decay vanishes.

1. Introduction

Social networks play a vital role in the diffusion of information across society in setting as diverse as referral networks for jobs (Granovetter, 1974) and assessing quality of products ranging from cars to computers (Rogers an Kincaid, 1981). The role played by networks has led researchers to develop theories of network formation. Several models have been proposed which address different types of network situations.

Our paper deals with the two-way flow connections model introduced by Bala and Goyal (2000a). In this model a player i can access a player j directly by forming a costly link with j. Moreover, through her link with j, player i accesses other players that player j is accessing on her own. Finally the link formed by player i creates a similar flow of information to player j, and hence the name two-way flow model. A phone call is a typical example given to illustrate this type of situation.

In the basic two-way flow model of Bala and Goyal (2000a), the transmission of information between two players is independent of the distance between these players in the network, that is there is no decay. Moreover, players are homogeneous, that is each player i benefits identically from accessing other players and all the costs associated with the setting of links do not depend on the identity of the initiator and the receiver of the link. In this context, Bala and Goyal (2000a) find that the set of equilibrium networks is very small, i.e., only the empty network and the inward-pointing star (a star network where the player at the center forms all the links) can be strict Nash networks.

Now in many situations they are delays as well as lowering of quality, when information is transmitted through a series of agents, making decay a significant factor. Moreover individuals are often heterogeneous. For instance some of them may be more interesting in a particular issue and therefore better informed which makes them more valuable as contacts.

In this paper, we focus on the impact of the introduction of both decay and players heterogeneity on the architectures of networks that will be formed in equilibrium. We ask what are the predictable patterns of networks that will emerge when players have the opportunity to set links between each other, in presence of decay in the flow of resources and players heterogeneity.1

Our paper revisits the insider-outsider model introduced by GGK (2006) and refines some of their results. The authors introduce heterogeneity of players in the two-way flow model of Bala and Goyal (2000a). More precisely, they assume that players belong to different groups and costs of forming links within groups is lower than costs of forming inter-groups links. The model is called the insider-outsider model in their paper. GGK (2006) first consider the transmission of value to be independent of the length of the paths between players, that is there is no decay. Then they introduce a small amount of decay into their framework to test the robustness of their findings.2 They show that for very small amount of decay and for intermediate costs of intra-groups and inter-groups links3, the empty network and the interlinked periphery-sponsored stars network are the only strict Nash networks. Note that a interlinked periphery-sponsored stars network satisfies two conditions. First, in each group there exists a player, called the center player, such that all other players of the group, called the periphery players, form a link with the center player. Second, there exists a player belonging to one group who forms a link with the center player of the other group.

In the paper we elaborate on the insider-outsider model introduced by GGK (2006) concerning decay in two directions. First, we deal with situations where the amount of decay is sufficiently low to avoid superfluous links in strict Nash networks and we examine the architectures of strict Nash networks. We show that in this situation the set of non-empty strict Nash networks is larger than in GGK (2006). It includes three other types of architectures in addition to interlinked periphery-sponsored stars networks. It is interesting to note that all these architectures share similar structural properties, namely small diameter and high asymmetries in centrality of players, since these properties are also features of equilibrium networks in the homogeneous model of Bala and Goyal (2000a) and the insider-outsider model without decay of GGK (2006). Second, we refine the result of GGK (2006) by assuming that the decay is sufficiently close to 1. More precisely, the class of interlinked periphery-sponsored stars networks, that the authors show as the unique non-empty strict Nash network contains two types of architectures. In the first one, the inter-groups link is sponsored by the center of a star, while in the second one this link is sponsored by a periphery player. We show that if the amount of decay is very low, then the second type of architecture cannot be strict Nash networks. So only the first type of architecture can be non-empty strict Nash networks. This result is important since it shows that strict Nash networks are also efficient networks when the amount of decay is low enough.4

The rest of the paper is organized as follows. In Section 2, we present the framework of our model. Section 3 addresses the results that we obtain and Section 4 concludes.

2. Model Setup

We consider a society in which individuals are divided into pre-specified groups and costs of forming links within the groups are lower as compared to costs of forming inter-groups links. To simplify, we assume that there are only 2 groups. Let $N^t=\{1^t,2^t,\dots ,{\overline{n}}^t\}$ be the set of players belonging to group t, $t\in \{0,1\}$. The set of players is $N=N^0\cup N^1$. As in GGK (2006), we assume that $|N^0|=|N^1|=\overline{n}\ge 4$.5 In the following we will assume that players who belong to the same group are similar and players who belong to different groups are different. In this paper the fact that two players are similar will allow them to have relationships which are less costly than the relationships between two players who are different. Indeed, if two players are similar they can communicate quickly (they speak the same language), while if two players are different (they speak different languages) the communication takes time and is most costly.

Each player $i\in N$ is assumed to possess some information of value to other players. She can augment her information by communicating with other people. This communication is made possible via pair-wise links. A strategy of player $i^t\in N^t$, $t\in \{0,1\}$, is a vector $g_{i^t}=(g_{i^t,1^t},\dots ,g_{i^t,{(i-1)}^t},g_{i^t,{(i+1)}^t},\dots ,$$g_{i^t,{\overline{n}}^t},$$g_{i^t,1^{1-t}},\dots ,g_{i^t,{\overline{n}}^{1-t}})$, where $g_{i,j}\in \{0,1\}$ for each player $j\in N$. We say that player i has formed a link with player j in g iff $g_{i,j}=1$. We assume throughout the paper that the link $g_{i,j}=1$ allows both players i and j to access each other’s information. The set of strategies of player i is denoted by ${\mathcal{G}}_i$. The set $\mathcal{G}={\mathcal{G}}_1\times \dots \times {\mathcal{G}}_n$ is the set of pure strategies of all players. A strategy profile $g=(g_1,\dots ,g_n)$ can be represented as a directed network. We use $g+g_{i,j}$ ($g-g_{i,j}$) to refer to the network obtained when the link $g_{i,j}=1$ is added (removed) from g. Given a network $g\in \mathcal{G}$, let $g_{-i}$ denote the network obtained when all of player i’s links are removed from g. Let ${\overline{g}}_{i,j}=max\{g_{i,j},g_{j,i}\}$. For a network g, a chain between player k and player j, $j\ne k$ , is a finite sequence $j_0,j_1,\dots ,j_m$ of distinct players such that ${\overline{g}}_{j_{\ell },j_{\ell +1}}=1$ and $j_0=j$, $j_m=k$. The distance $d(i,j;g)$ between i and j in g is given by the number of links in the shortest chain between i and j (if there is no chain between two players i and j in g we set $d(i,j;g)=\infty$). The diameter of a network g is $D(g)={max}_{i,j\in N}\left\{d(i,j;g)\right\}$. Let $M^t(g)=\{(i^t,j^t)\in N^t\times N^t\backslash \left\{i\right\}\mid d(i^t,j^t;g)\ge d(i^{\prime },j^{\prime };g)\text{for}\text{all}(i^{\prime },j^{\prime })\in N^t\times N^t\}$ be the couples of players who belong to the group $N^t$ that are at maximal distance in g. A network g is minimal if $g_{i,j}=0$ whenever there is a chain between i and j in $g-g_{i,j}$. A network g is connected if $D(g)\ne \infty$. Moreover we say that a group of players $N^t$, $t\in \{0,1\}$, is connected in g if for any two players $i,j\in N^t$$d(i,j;g)\ne \infty$. A network g is minimally connected if it is connected and minimal. The subnetwork $g(N^t)$, $t\in \{0,1\}$, of g is a network which consists of the players in $N^t$ and such that $g{(N^t)}_{i,j}=g_{i,j}$ for all $i,j\in N^t$. Finally, we say that a player i is an end player if ${\overline{g}}_{i,j}=1$ for one player $j\in N\backslash \left\{i\right\}$, and ${\overline{g}}_{i,k}=0$ for all players $k\in N\backslash \{i,j\}$.

We now define five networks architectures that play a role in our results. A periphery-sponsored star (PSS) is a network g in which there exists a center player, $i_c(g)$, such that $g_{j,i_c(g)}=1$ for all $j\in N\backslash \left\{i_c(g)\right\}$, and there are no other links. A center interlinked periphery-sponsored stars (CIPSS) is a network g in which $g(N^t)$ is a PSS for each $t\in \{0,1\}$ and there is a link between the two centers. A non center interlinked periphery-sponsored stars (NCIPSS) is a network in which $g(N^t)$ is a PSS for each $t\in \{0,1\}$, and a non center player of a PSS forms a link with the center player of the other PSS. It is worth noting that CIPSS and NCIPSS are not treated as distinct architectures in GGK (2006), since the authors called both these architectures interlinked periphery-sponsored stars. A mixed star (MS) is similar to a PSS except that there is a unique player called $j_p(g)\ne i_c(g)$ such that $g_{i_c(g),j_p(g)}=1$ instead of $g_{j_p(g),i_c(g)}=1$. A interlinked mixed stars network (IMS) is a network in which $g(N^t)$ is a MS, $g(N^{1-t})$ is a PSS, and $j_p(g(N^t))$ forms a link with $i_c(g(N^{1-t}))$. A distance 3 interlinked periphery-sponsored stars network (D3PSS) is a network such that $g(N^{1-t})$ is a PSS, and there are two players in $N^t$, say $i_2^t$ and $i_3^t$, such that $g(N^t\backslash \left\{i_3^t\right\})$ is a PSS, $g_{i_3^t,i_c(g(N^{1-t}))}=1$ and $g_{i_2^t,i_3^t}=1$. Figure 1 below depicts these architectures. In this figure, players in group $N^0$ are denoted by 0 and players in group $N^1$ are denoted by 1. In the following, we denote the set of networks which consists of all PSS, all CIPSS, all NCIPSS, all IMS, and all D3PSS, by $\mathcal{A}$ .

Figure 1. Networks architectures.

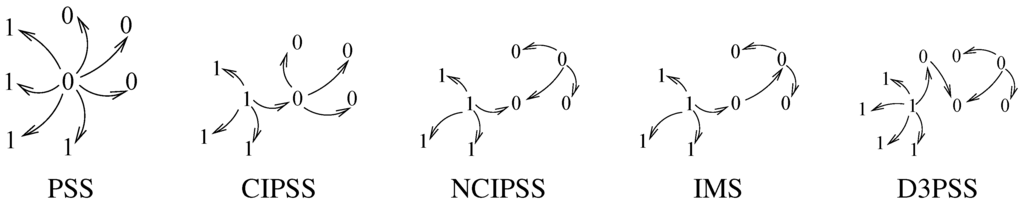
Figure 1. Networks architectures.

To complete the definition of a normal-form game of network formation, we specify the payoffs. Let $c_L$ ($c_H$) be the costs incurred by a player $i\in N^t$, $t\in \{0,1\}$, when she forms a link with a player $j\in N^t$ ($j\in N^{1-t}$). We assume that $c_H>c_L>0$. Let $\delta \in \left(0,1\right)$ be the value of the decay parameter. Define $N_i(g)=\{j\in N\backslash \left\{i\right\}\mid \text{there}\text{is}\text{a}\text{chain}\text{between}i\text{and}j\text{in}g\}$ as the set of players who are observed by player i in the network g. The payoff obtained by player $i^t\in N^t$, $t\in \{0,1\}$, in a network g is given by:

$${\Pi }_{i^t}(g)=\sum _{j\in N_{i^t}(g)}{\delta }^{d(i^t,j;g)}-\left(\sum _{j\in N^t}{g}_{i^t,j}{c}_L+\sum _{j\in N^{1-t}}{g}_{i^t,j}{c}_H\right)$$

Note that this payoff function is identical to the one in GGK (2006) in their insider-outsider model with decay. In this payoff function we take into account the three following assumptions: (i) the value that player i obtains from player j does not depend on the group of j, (ii) the value that player i obtains from player j depends on the distance between i and j, and (iii) the cost that player i incurs for a link with player j depends on whether i and j belong to the same group or not.

The strategy $g_i$ is said to be a best response of player i to the network $g_{-i}$ if:

$${\Pi }_i(g_i+g_{-i})\ge {\Pi }_i(g_i^{\prime }+g_{-i}),\text{for}\text{all}{g}_i^{\prime }\in {\mathcal{G}}_i$$

The set of all of player i’s best responses to $g_{-i}$ is denoted by $\mathcal{B}{\mathcal{R}}_i(g_{-i})$. A network g is said to be a Nash network if $g_i\in \mathcal{B}{\mathcal{R}}_i(g_{-i})$ for each player $i\in N$. We define a strict best response and a strict Nash network by replacing ‘≥’ with ‘>’. The set of non-empty strict Nash networks is denoted by $SNN$.

A network g is said to be an efficient network if it maximizes the total payoffs of players, that is ${\sum }_{i=1}^n{\Pi }_i(g)\ge {\sum }_{i=1}^n{\Pi }_i(g^{\prime })$, for all $g^{\prime }\in \mathcal{G}$.

3. Results

Let $\underline{\delta }(n)$ be the value of the decay parameter such that a non-empty strict Nash network is minimal.6 We are interested by the second point of Proposition 4.3 of GGK (pg.365, 2006) where the authors choose $c_L$ such that $c_L>1>\delta$. We will show that if $c_L>1$, then it is possible to obtain a more precise characterization of strict Nash networks than the one proposed by GGK. It is worth noting that if $c_L>\delta$, then each end player sponsors her link in a strict Nash network. We now present a technical remark which is useful in several proofs.

Remark 1 

(R1) If $i_1^t,i_2^t,i_3^t\in N^t$, $t\in \{0,1\}$, $g_{i_1^t,i_2^t}={\overline{g}}_{i_2^t,i_3^t}=1$ and ${\sum }_{\ell \in N}{\overline{g}}_{i_2^t,\ell }=2$, then $g\notin SNN$.

Indeed, if player $i_1^t$ replaces the link $g_{i_1^t,i_2^t}$ by the link $g_{i_1^t,i_3^t}$, then $i_1^t$ obtains a payoff greater or equal to the payoff she obtains in g.

The proposition that follows shows that a non-empty strict Nash network is minimally connected.

We first present a lemma that is used in the proposition. The proof of this lemma is put in Appendix.

Lemma 1 

Let $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Suppose $g\in SNN$ in which there are four players $i,j,i^{\prime },j^{\prime }\in N$, such that $g_{i,j}=g_{i^{\prime },j^{\prime }}=1$. If there is a chain between i and $i^{\prime }$ which goes through players j and $j^{\prime }$, then $i,j\in N^t$ and $i^{\prime },j^{\prime }\in N^{1-t}$, $t\in \{0,1\}$.

Proposition 1 

Suppose $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. A non-empty strict Nash network is minimally connected.

Proof 

Let $N_{+}^t(g)=\{i^t\in N^t\mid {\sum }_{j\in N\backslash \left\{i^t\right\}}{g}_{i^t,j}=0\}$ be the set of players in $N^t$ who form no links with any player, and let $N_{N^t}(g)=\{i^t\in N^t\mid \exists j^{1-t}\in N^{1-t},g_{j^{1-t},i^t}=1\}$ be the set of players in $N^t$ who received a link from a player in $N^{1-t}$. Suppose $\delta >\underline{\delta }(n)$ and $g\in SNN$. It follows that g is minimal. We now show that if $c_H<\delta +(\overline{n}-1){\delta }^2$, then g is connected.

First we show that if player $i^t\in N^t$ has formed a link, then all players in $N^t$ must observe her. To introduce a contradiction, assume that there exist in g two players, $i^t,j^t\in N^t$, $t\in \{0,1\}$, and a player $k\in N\backslash \{i,j\}$, such that $i^t\notin N_{j^t}(g)$ and $g_{i^t,k}=1$. Since $i^t\notin N_{j^t}(g)$ and $i^t$ plays a strict best response, we have by linearity of the payoff function: ${\Pi }_{j^t}(g+g_{j^t,k})-{\Pi }_{j^t}(g)>{\Pi }_{i^t}(g)-{\Pi }_{i^t}(g-g_{i^t,k})>0$. Hence player $j^t$ does not play a strict best response in g. Therefore, $g\notin SNN$, a contradiction. It follows that either no player has formed a link in $N^t$, $t\in \{0,1\}$, or there exists a chain between all players who belong to $N^t$. Formally, for each $t\in \{0,1\}$, we have either $N_{+}^t(g)=N^t$ or $N^t$ is connected in g.

We now use this result to show that g is connected. We consider two cases.

• Suppose $N_{N^t}(g)=\varnothing$ and $N_{N^{1-t}}(g)=\varnothing$, that is there are no links between the two groups. We will show in the following that such a situation cannot happen.
  First, since g is non-empty, we cannot have simultaneously $N_{+}^t(g)=N^t$ and $N_{+}^{1-t}(g)=N^{1-t}$. Suppose that $N_{+}^t(g)\ne N^t$, for one $t\in \{0,1\}$. In that case, we know from the point above that $N^t$ is connected.
  Second, we show in two steps that $N^t$ constitutes a PSS. We begin to show that if $(i^t,j^t)\in M^t(g)$, then $d(i^t,j^t;g)=2$. To introduce a contradiction, suppose that $d(i^t,j^t;g)>2$. In that case there exist two distinct players $i_1^t,j_1^t$ such that ${\overline{g}}_{i^t,i_1^t}={\overline{g}}_{j^t,j_1^t}=1$. We have: (i) $g_{i^t,i_1^t}=$$g_{j^t,j_1^t}=1$ since $c_L>\delta$, (ii) there is a chain between $i^t$ and $j^t$ which goes through $i_1^t$ and $j_1^t$, (iii) players $i^t$, $j^t$, $i_1^t$, and $j_1^t$ belong to $N^t$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1. A contradiction. Thus we can conclude that $g(N^t)$ constitutes a star. In this star, each end player sponsors her link with the center, since $\delta <c_L$. So $g(N^t)$ constitutes a PSS.
  Third, we show that $N_{N^t}(g)\ne \varnothing$. Indeed, since $c_H<\delta +(\overline{n}-1){\delta }^2$, a player $i\in N^{1-t}$ strictly gains by forming a link with the center of the PSS formed by the group $N^t$. It follows that $N_{N^t}(g)\ne \varnothing$, which contradicts the assumption $N_{N^t}(g)=\varnothing$.
• Suppose $N_{N^t}(g)\ne \varnothing$ or $N_{N^{1-t}}(g)\ne \varnothing$ in g. We assume wlog that there are players $i^t\in N^t$ and $j^{1-t}\in N^{1-t}$ such that $g_{i^t,j1-t}=1$. Since a player in $N^t$ has formed a link, $N^t$ is connected. We now show that g is connected. To introduce a contradiction suppose g is not connected. In that case there exists a player $k^{1-t}\in N^{1-t}$ such that $j^{1-t}\notin N_{k^{1-t}}(g)$. We have: ${\Pi }_{k^{1-t}}(g+g_{k^{1-t},j^{1-t}})-{\Pi }_{k^{1-t}}(g)>{\Pi }_{i^t}(g)-{\Pi }_{i^t}(g-g_{i^t,j^{1-t}})>0$ since $c_H>c_L$ and player $k^{1-t}$ obtains more resources due to the link with $j^{1-t}$ than $i^t$ through her link with $j^{1-t}$. It follows that $k^{1-t}$ does not play a strict best response, a contradiction. Thus we conclude that g is connected.

The previous proposition means that in a non-empty strict Nash network, each player i obtains some resources of all other players. Obviously, each player i does not obtain all the resources of other players because of the decay.

The proposition that follows deals with the diameter of non-empty strict Nash networks. We first present a lemma that is used in the proposition. This lemma shows that if there are several links between players of different groups in a strict Nash network, then there is a group, say $N^t$, such that $\overline{n}-1$ players in $N^t$ are not directly linked with players who belong to $N^{1-t}$.

Lemma 2 

Let $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Suppose $i\in N^t$ and $j\in N^{1-t}$. If $g\in SNN$ and ${\overline{g}}_{i,j}=1$, then ${\sum }_{\ell \in N^t\backslash \left\{i\right\},{\ell }^{\prime }\in N^{1-t}}{\overline{g}}_{\ell ,{\ell }^{\prime }}=0$ or ${\sum }_{\ell \in N^{1-t}\backslash \left\{j\right\},{\ell }^{\prime }\in N^t}{\overline{g}}_{\ell ,{\ell }^{\prime }}=0$.

The proof of the lemma is put in Appendix.

Proposition 2 

Suppose $\delta \in (\underline{\delta }(n),1)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Let $g\in SNN$.

1. 

If g contains one inter-groups link: $g_{i_{*}^t,j_{*}^{1-t}}=1$ with $i_{*}^t\in N^t$ and $j_{*}^{1-t}\in N^{1-t}$, then $D(g(N^t))\le 3$ and $D(g(N^{1-t}))=2$, for $t\in \{0,1\}$.

2. 

If g contains several inter-groups links between the two groups, then $D(g(N))=2$.

Proof 

Suppose $\delta \in (\underline{\delta }(n),1)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. We know from Proposition 1 that a non-empty strict Nash network is minimally connected. We prove successively the two parts of the proposition.

• Let $g\in SNN$, with only one inter-groups link. We assume that this link is formed by $i_{*}^t\in N^t$ with $i_{*}^{1-t}\in N^{1-t}$, that is $g_{i_{*}^t,i_{*}^{1-t}}=1$.
  First, we show that $D(g(N^t))<4$. To introduce a contradiction, we assume that there are $i^t,j^t\in N^t$ such that $D(g(N^t))\ge 4$. There are two cases.
  (a) Let $(i_0^t,j_0^t)\in M^t(g)$, with $i_0^t,j_0^t\in N^t\backslash \left\{i_{*}^t\right\}$. There are players $i_1^t,j_1^t\in N^t$ such that ${\overline{g}}_{i_0^t,i_1^t}={\overline{g}}_{j_0^t,j_1^t}=1$. In that case: (i) we have $g_{i_0^t,i_1^t}=g_{j_0^t,j_1^t}=1$ since $\delta <c_L$, (ii) there exists a chain between players $i_0^t$ and $j_0^t$ which contains players $i_1^t$ and $j_1^t$, and (iii) $i_0^t,i_1^t,j_0^t,j_1^t\in N^t$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1. A contradiction.
  (b) Suppose now that if $(i^t,j^t)\in M^t(g)$, then either $i^t=i_{*}^t$, or $j=i_{*}^t$. In other words, the player $i_{*}^t$ who has formed a link with a player in $N^{1-t}$, is always one of the two players at maximal distance in $g(N^t)$. In the following we deal with $(i_{*}^t,j^t)\in M^t(g)$. Note first that since $j^t$ is an end player and $\delta <c_L$, $j^t$ has formed a link with a player, say $j_1^t$, who belongs to the chain between $i_{*}^t$ and $j^t$ in g. There are two cases.
  (b1) Suppose player $i_{*}^t$ has formed a link in g with a player, say $i_1^t\in N^t$, who belongs to the chain between $i_{*}^t$ and $j^t$. In such a case we have (i) $g_{i_{*}^t,i_1^t}=g_{j^t,j_1^t}=1$, (ii) there is a chain between players $i_{*}^t$ and $j^t$ which contains players $i_1^t$ and $j_1^t$, and (iii) $i_{*}^t,i_1^t,j^t,j_1^t\in N^t$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1. A contradiction.
  (b2) Suppose player $i_{*}^t$ has formed no links in g with a player who belongs to the chain between $i_{*}^t$ and $j^t$. In that case, there is a player, say $i_1^t\in N^t$, who has formed the link with $i_{*}^t$ and belongs to the chain between $i_{*}^t$ and $j^t$.
  We show that the link $g_{i_1^t,i_{*}^t}=1$ is the only link player $i_1^t$ has formed in g. Indeed, suppose $i_1^t$ has formed a link with a player say $i_k^t\ne i_{*}^t$. Suppose $i_k^t$ does not belong to the chain between $i_1^t$ and $j^t$. We have $(k^t,j^t)\in M^t(g)$ and by point (a) we know that g is not strict Nash. Suppose now that $i_k^t$ belongs to the chain between $i_1^t$ and $j^t$. We have (i) $g_{i_1^t,i_k^t}=g_{j^t,j_1^t}=1$, (ii) there is a chain between $i_1^t$ and $j^t$ which contains players $i_k^t$ and $j_1^t$, and (iii) $i_1^t,i_k^t,j_1^t,j^t\in N^t$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1.
  Since the link $g_{i_1^t,i_{*}^t}=1$ is the only link that player $i_1^t$ has formed in g, it follows that there is a player $i_2^t$ who belongs to the chain between $i_{*}^t$ and $j^t$ such that $g_{i_2^t,i_1^t}=1$. However in this situation player $i_2^t$ does not play a strict best response, by (R1). Consequently $g\notin SNN$. A contradiction.
  Second we show that $D(g(N^{1-t}))=2$. Using arguments similar to those for $N^t$ it is easy to see that $D(g(N^{1-t}))<4$. We now show that $D(g(N^{1-t}))<3$. To introduce a contradiction suppose that $D(g(N^{1-t}))=3$. We divide the proof into two cases.
  (a) Suppose there are $(i^{1-t},j^{1-t})\in M^{1-t}(g)$ such that $i^{1-t},j^{1-t}\in N^{1-t}\backslash \left\{i_{*}^{1-t}\right\}$. So there are players $i_1^{1-t},j_1^{1-t}\in N^{1-t}$ such that ${\overline{g}}_{i^{1-t},i_1^{1-t}}={\overline{g}}_{j^{1-t},j_1^{1-t}}=1$. In that case: (i) we have $g_{i^{1-t},i_1^{1-t}}=g_{j^{1-t},j_1^{1-t}}=1$ since $\delta <c_L$, (ii) there is a chain between $i^{1-t}$ and $j^{1-t}$ which contains players $i_1^{1-t}$ and $j_1^{1-t}$, and (iii) we have $i^{1-t},j^{1-t},i_1^{1-t},j_1^{1-t}\in N^{1-t}$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1.
  (b) Suppose now that if $(i^{1-t},j^{1-t})\in M^{1-t}(g)$, then either $i=i_{*}^{1-t}$, or $j=i_{*}^{1-t}$. In the following we deal with $(i_{*}^{1-t},j^{1-t})\in M^{1-t}(g)$. Since $j^{1-t}$ is an end player, she has formed a link with a player $j_1^{1-t}\in N^{1-t}$ who belongs to the chain between $i_{*}^t$ and $j^{1-t}$. In such a case we have (i) $g_{i_{*}^t,i_{*}^{1-t}}=g_{j^{1-t}{j}_1^{1-t}}=1$, (ii) there exists a chain between players $i_{*}^t$ and $j^{1-t}$ which contains players $i_{*}^{1-t}$ and $j_1^{1-t}$, and (iii) $i_{*}^t\in N^t$, and $i_{*}^{1-t},j^{1-t},j_1^{1-t}\in N^{1-t}$. When (i) and (ii) are valid, it is not possible for (iii) to be valid simultaneously by Lemma 1.
  The conclusion follows.
• We now consider a minimally connected strict Nash network g in which there are more than one inter-groups link. The arguments which allow to obtain the contradiction in this part are very similar to the arguments used in the previous part. Therefore we briefly show the way to use Lemma 1 in the proof. We know from Lemma 2 that there exists one player who belongs to one group, say $i_{*}^t\in N^t$, such that $i_{*}^t$ is involved in all the inter-groups links.
  We first deal with players in $N^{1-t}$ and show that ${\overline{g}}_{i_{*}^t,i^{1-t}}=1$ for all $i^{1-t}\in N^{1-t}$. Let $B\subset N^{1-t}$ be the set of players $i^{1-t}\in N^{1-t}$ such that ${\overline{g}}_{i_{*}^t,i^{1-t}}=1$ . By assumption we have $\left|B\right|\ge 2$. Moreover we know that we have ${\overline{g}}_{i^t,i^{1-t}}=0$ for all $(i^t,i^{1-t})\in N^t\backslash \left\{i_{*}^t\right\}\times N^t$.
  To introduce a contradiction, we suppose that $B\ne N^{1-t}$. Since g is connected there are players $j^{1-t},k^{1-t}\in B$ and a player $i^{1-t}\in N^{1-t}$ such that ${\overline{g}}_{i^{1-t},k^{1-t}}=1$. Let ${\ell }^{1-t}\in N^{1-t}$ be an end player such that $k^{1-t}$ belongs to the chain between $i_{*}^t$ and ${\ell }^{1-t}$. By construction there is a player ${\ell }_1^{1-t}\in N^{1-t}$ such that ${\overline{g}}_{{\ell }_1^{1-t},{\ell }_1^{1-t}}=1$. Note that we can have ${\ell }_1^{1-t}=k^{1-t}$ and ${\ell }^{1-t}=i^{1-t}$. Moreover, since $\delta <c_L$, we have $g_{{\ell }^{1-t},{\ell }_1^{1-t}}=1$.
  Either $j^{1-t}$ is an end player, and $g_{j^{1-t},i_{*}^t}=1$ since $\delta <c_L$, or there exists an end player ${\ell }_j^{1-t}\in N^{1-t}\backslash \left\{j^{1-t}\right\}$ such that ${\ell }_j^{1-t}\in N_{j^{1-t}}(g-{\overline{g}}_{i_{*}^t,j^{1-t}})$. In the second case by construction and since $\delta <c_L$, we have $g_{{\ell }_j^{1-t},m^{1-t}}=1$ for one player $m^{1-t}\in N^{1-t}$.
  If $j^{1-t}$ is an end player, then Lemma 1 is contradicted for players $i_{*}^t,j^{1-t},{\ell }_1^{1-t},{\ell }^{1-t}$ and g cannot be a strict Nash network. If $j^{1-t}$ is not an end player, then Lemma 1 is contradicted for players ${\ell }_j^{1-t},m^{1-t},{\ell }_1^{1-t},{\ell }^{1-t}$ and g cannot be a strict Nash network. It follows that $B=N^{1-t}$. It is worth noting that $g_{i^{1-t},i_{*}^t}=1$ for all $i^{1-t}\in N^{1-t}$ since $\delta <c_H$.
  We now deal with players in $N^t$ and show that ${\overline{g}}_{i_{*}^t,i}=1$ for all $i\in N^t$. To introduce a contradiction, suppose there is an end player $k^t\in N^t,k^t\ne i_{*}^t$, such that ${\overline{g}}_{i_{*}^t,k^t}=0$. Since g is connected and $\delta <c_L$ there is a player $j^t\in N^t\backslash \{k^t,i_{*}^t\}$ such that $g_{k^t,j^t}=1$. In that case Lemma 1 is contradicted for players $k^t,j^t,i_{*}^t,i^{1-t}$$\in N^{1-t}$, since $g_{i^{1-t},i_{*}^{1-t}}=1$. Therefore g is not a strict Nash network. The result follows.
  To conclude, since ${\overline{g}}_{i_{*}^t,i}=1$ for all $i\in N$ we have $D(g(N))=2$.

It follows from the previous proposition that the maximal diameter of strict Nash networks is equal to five. It is worth noting that small diameter also characterizes non-empty strict Nash networks in the model with no decay of GGK (2006). The proposition that follows gives an exact characterization of strict Nash networks. We first present two lemmas that are used in the proposition. The proofs of these lemmas are put in Appendix.

Lemma 3 

Suppose $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Suppose g is a non-empty strict Nash network and there is only one inter-groups link.

1. 

If there is $t\in \{0,1\}$ such that $D(g(N^t))=3$, then g is a D3PSS.

2. 

If for each $t\in \{0,1\}$ we have $D(g(N^t))=2$, then g is a CIPSS, a NCIPSS or a IMS .

Lemma 4 

Suppose $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Suppose g is a strict Nash network and there are several inter-groups links. Then g is a PSS.

Proposition 3 

Suppose $\delta >\underline{\delta }(n)$ and $c_H<\delta +(\overline{n}-1){\delta }^2$. Then, $SNN\subset \mathcal{A}$. Moreover, there exists $\overline{\delta }$ such that for any $\delta \in (\overline{\delta },1)$, CIPSS are the only networks in $SNN$.

Proof 

Suppose $\delta >\underline{\delta }(n)$, and $c_H<\delta +(\overline{n}-1){\delta }^2$. Lemmas 3 and 4 establish that $SNN\subset \mathcal{A}$. Concerning the second part of the proposition, GGK (2006, Proposition 4.3 part (2a), pg.365) showed that for δ sufficiently close to 1, only interlinked periphery-sponsored stars networks can be candidates as strict Nash networks.

It is easy to check that in a CIPSS, g, no player has an incentive to change her strategy when δ is sufficiently close to 1. Therefore, $g\in SNN$.

We now show that if δ is sufficiently close to 1, then a NCIPSS cannot be strict Nash. Indeed, suppose a NCIPSS, g, in which players $i_c^t\in N^t$ and $i_c^{1-t}\in N^{1-t}$ are respectively the centers of the stars formed with players in $N^t$ and $N^{1-t}$. Let player ${\ell }_{*}^t\in N^t$ be the player such that $g_{{\ell }_{*}^t,i_c^t}=g_{{\ell }_{*}^t,i_c^{1-t}}=1$. Let $i_0^t\in N^t\backslash \{{\ell }_{*}^t,i_c^t\}$, be a periphery player. If $i_0^t$ deletes her link with $i_c^t$ and forms a link with ${\ell }_{*}^t$, then the change in $i_0^t$’s payoffs is ${\Pi }_{i_0^t}(g-g_{i_0^t,i_c^t}+g_{i_0^t,{\ell }_{*}^t})-{\Pi }_{i_0^t}(g)=-{\delta }^2(\overline{n}-4-(2\overline{n}-5)\delta +(\overline{n}-1){\delta }^2)$. Consequently, for any $\delta \in \left(\frac{\overline{n}-4}{\overline{n}-1},1\right)$, we have ${\Pi }_{i_0^t}(g-g_{i_0^t,i_c^t}+g_{i_0^t,{\ell }_{*}^t})-{\Pi }_{i_0^t}(g)>0$, and $g\notin SNN$. The result follows.

It follows from the previous proposition that in all non-empty strict Nash architectures few players play a key role in the flow of resources. More precisely, we can distinguish two types of players, end players and non-end players. If one player of the first type is deleted, then only her own resources will not be accessed by other players. This is very different for the second type of players. As an illustration suppose a population with 100 players, that contains two groups, denoted by $N^0,N^1$, of 50 players each. We know from Proposition 3 that there are only at most 4 players who are not end players in a non-empty strict Nash network. Suppose we delete one of these players, say $i\in N^t$, $t\in \{0,1\}$. Then this will prevent players of group $N^{1-t}$ the access to resources of at least 47 players of the group $N^t$. In that sense, non end players have a significant role in the flow of resources in the network, by contrast with end players. It is worth noting that asymmetries in players centrality also characterizes non-empty strict Nash networks in the model with no decay of GGK (2006).

We now give an example of parameter values such that all networks $g\in \mathcal{A}$ are strict Nash networks.

Example 1 

Suppose $n=120,\delta =0.94,c_L=40,c_H=45$. It can be checked that non minimal networks cannot be strict Nash. Moreover, it can be checked that all networks $g\in \mathcal{A}$ are strict Nash networks.

We now show that for the same range of costs as in Proposition 3, if the decay parameter is sufficiently close to 1, then CIPSS are efficient networks.

Proposition 4 

Suppose $c_H<\delta +(\overline{n}-1){\delta }^2$. Then there exists $\widehat{\delta }$ such that for any $\delta \in (\widehat{\delta },1)$, CIPSS are efficient networks.

Proof 

Let g be an efficient network. First, we show that there exists $\widehat{\delta }$ sufficiently close to 1 such that there is at most one link between players in $N^t$ and players in $N^{1-t}$ in g. Suppose that there is no decay, that is $\delta =1$. In that case, we are in the situation studied by GGK (2006, p.369). Consequently, (a) each component part of an efficient network is minimal; (b) if g is non-empty and efficient, then it is either minimally connected with 1 inter-groups link and $2(\overline{n}-1)$ intra-groups links or partially connected with each group generating a minimal connected component. Since $c_H<\delta +(\overline{n}-1){\delta }^2$, g is connected by Proposition 1. The above observations hold when $\widehat{\delta }$ is sufficiently close to 1. Suppose now that $\delta <1$. To introduce a contradiction, suppose that there are two links between players $i\in N^t$ and players $j\in N^{1-t}$ in g. If one of these links is replaced by a link between two players who belong to the same group, then the difference in total cost is $c_H-c_L$, and the difference in the total gross payoff cannot exceed $4{\overline{n}}^2({\delta }^n-\delta )$. Clearly for all $c_H>c_L$, there is $\widehat{\delta }$ sufficiently close to 1 such that $\widehat{\delta }-{\widehat{\delta }}^n<(c_H-c_L)/(4{\overline{n}}^2)$. Second, we show that CIPSS are efficient networks. We know that an efficient network is minimally connected and contains one link between the two groups. Let E be the set of minimally connected networks which contain one link between the two groups. E is the set of networks candidate to be efficient. All the networks in E contain the same number of links. Consequently, we do not need to take into account total cost of setting links in networks $g^{\prime }\in E$, but only the gross total payoff: ${\sum }_{i\in N}{\sum }_{j\in N_i(g^{\prime })}{\delta }^{d(i,j;g^{\prime })}$. Only the distance between the players plays a role in this function. Let $Dis(k;g)=\{(i,j)\in N\times N\mid d(i,j;g)=k\}$. We have:

$$\sum _{i\in N}\sum _{j\in N_i(g^{\prime })}{\delta }^{d(i,j;g^{\prime })}=\sum _{k\in \{0,\dots ,2\overline{n}-1\}}\left|Dis(k;g^{\prime })\right|{\delta }^k$$

Since each $g^{\prime }\in E$ is minimally connected, it contains $2\overline{n}-1$ links. It follows that in each $g^{\prime }\in E$ we have $|Dis(1;g^{\prime })|=2(2\overline{n}-1)$. We know that in $g^{\prime }\in E$ there is at most one link between players in $N^t$ and players in $N^{1-t}$. Let this link be between $i_{*}^t\in N^t$ and $i_{*}^{1-t}\in N^{1-t}$. In that case, all players $j^t\in N^t\backslash \left\{i_{*}^t\right\}$ cannot be at distance 2 of players $j^{1-t}\in N^{1-t}\backslash \left\{i_{*}^{1-t}\right\}$. Consequently, for any $g^{\prime }\in E$, $|Dis(2;g^{\prime })|\le 2\overline{n}\times (2\overline{n}-1)-2(2\overline{n}-1)-2{(\overline{n}-1)}^2=2\overline{n}(\overline{n}-1)$, where $2\overline{n}\times (2\overline{n}-1)$ is the total number of couples, $2(2\overline{n}-1)$ is the number of couples at distance 1, and $2{(\overline{n}-1)}^2$ is the number of other couples which cannot be at distance 2. In CIPSS networks there are $2\overline{n}(\overline{n}-1)$ couples of players who belong to $Dis(2;g^{\prime })$. Since all couples which do not belong to $Dis(1;g^{\prime })\cup Dis(2;g^{\prime })$ belong to $Dis(3;g^{\prime })$ in a CIPSS, the result follows.

Recall that the class of interlinked periphery-sponsored stars networks that GGK (2006) find as the unique non-empty strict Nash networks, contains two types of architectures, namely CIPSS and NCIPSS. It is easy to see why NCIPSS are less efficient than CIPSS. Indeed, recall that in NCIPSS there exists a link between a periphery player, say $i_{*}^t\in N^0$, and the center player of the star formed by the other group, say $i_{*}^{1-t}\in N^1$. Suppose that this link is replaced by a link between the two center players, $i_{*}^{1-t}\in N^1$ and say $i_0\in N^0$. It is easy to see that the loss of the total value obtained by $i_{*}^t$ is the same as the additional value obtained by $i_0$, while the total value obtained by each player $i\in N\backslash \{i_0,i_{*}^t\}$ increases. Therefore our result shows that if δ is high enough, then non-empty strict Nash networks are also efficient networks.

4. Conclusion

Heterogeneity of players and imperfect transitivity of information flows are central features of economic and social networks. In this note we re-examine the insider-outsider model of GGK (2006) which takes these features into account, by allowing for different degrees of decay in information flows. We refine the results of GGK (2006) paper for the case decay is low and costs of intra-group and inter-group links are intermediate. We find new strict Nash architectures for higher values of decay. It is interesting to note that all these architectures have small diameter and high asymmetries with regard to centrality of players, since these properties are also features of equilibrium networks in the GGK (2006) insider-outsider model with no decay. We also refine the results of GGK (2006) insider-outsider model when δ is sufficiently close to 1. We show for this case that only one type of interlinked periphery-sponsored stars networks can be strict Nash networks. It follows from this result that equilibrium networks are also efficient networks when δ is sufficiently close to 1.

In this note, we restrict our study to situations in which there are only two groups of players. Future research may consider introducing a higher number of groups in the model to examine the robustness of our finding concerning centrality and diameters of strict Nash networks as well as the compatibility between strict Nash and efficient networks.