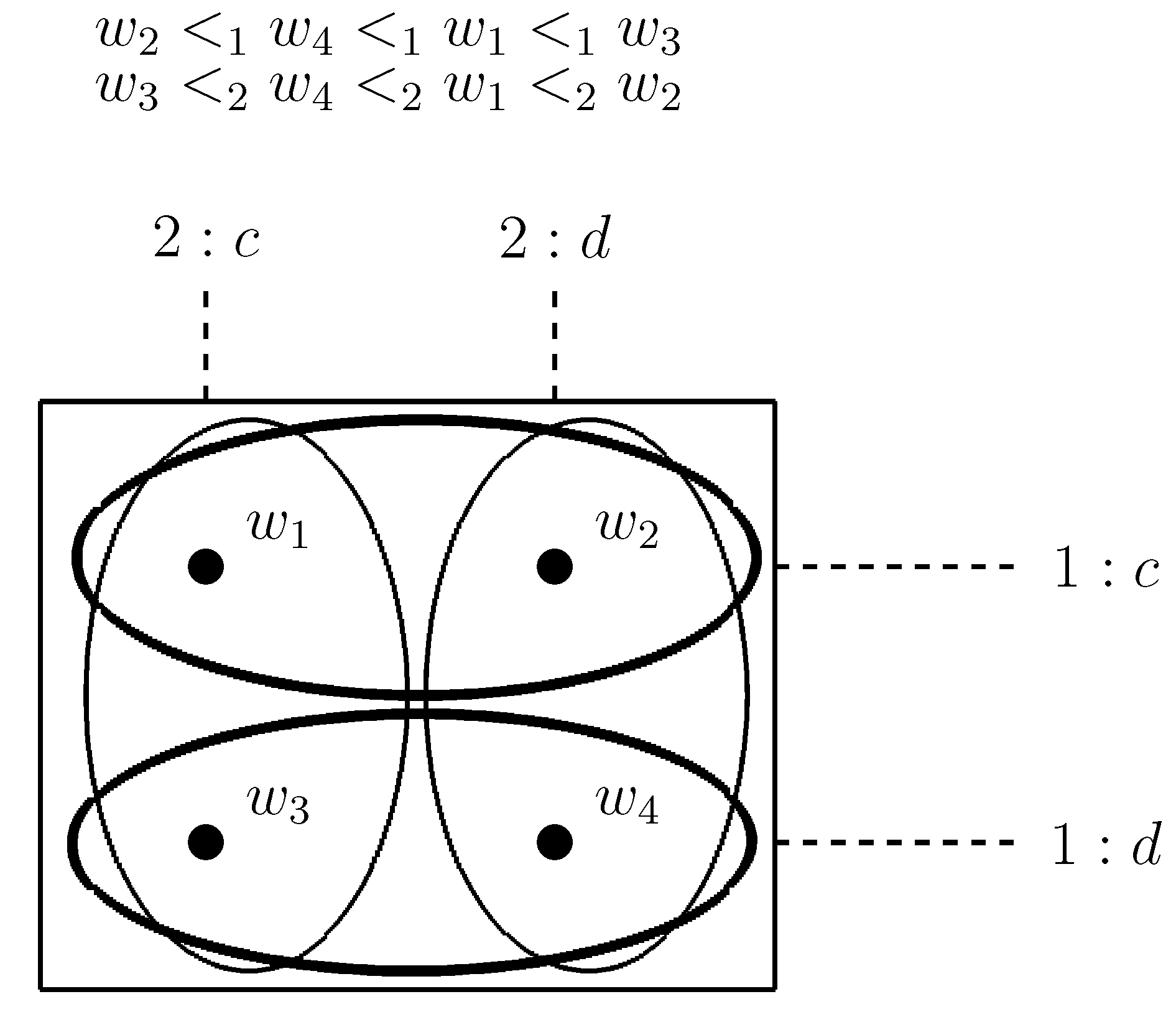A. ANNEX: Proofs of Some Theorems
A.1. Proof of Theorems 1 and 3
is determined by the class of -models. is determined by the class of -models.
Proof. We only provide a sketch of the proof of Theorem 3. The proof of Theorem 1 is a straightforward adaptation of the proof of Theorem 3. It is sufficient to remove the constraint (S6) from the following definition 3.
It is straightforward to show that all axioms in
Figure 2 are valid and that the rules of inference preserve validity in the class of
-models. The other part of the proof is shown using two major steps.
Step 1. We provide an alternative semantics for in terms of standard Kripke models whose semantic conditions correspond one-to-one to the axioms in Table 2. The definition of Kripke -models is the following one.
Definition 3 (Kripke
-model)
Kripke -models are tuples where:W is a nonempty set of possible worlds or states;
∼ is an equivalence relation on W;
maps every joint action to a transition relation between possible worlds such that:- S1
if and only if, for every ,
- S2
if then ,
- S3
,
- S4
if then or ,
- S5
if for every there is such that and then there is a v such that and ;
- S6
if and and , then ;
maps every agent i to an equivalence relation on W such that:- S6
if , then if and only if ,
- S7
if then ;
maps every agent i to a reflexive, transitive relation on W such that:- S8
if then ,
- S9
if and then or ;
is a valuation function.
Truth conditions of
formulas in Kripke
-models are again standard for atomic formulas and the Boolean operators. The truth conditions for Boolean operators and for operators
,
and
are the ones of
Section 2.2. The truth condition for operators
are:
It is a routine task to prove that the axiomatic system of the logic
given in Table 2 is sound and complete with respect to this class of Kripke
-models via the Sahlqvist theorem, cf. [
44, Th.2.42]. Indeed all axioms in Table 2 are in the so-called Sahlqvist class [
45]. Thus, they are all expressible as first-order conditions on Kripke models and are complete with respect to the defined model classes.
Step 2. The second step shows that the semantics in terms of -models of Definition 2 and the semantics in terms of Kripke -models of Definition 3 are equivalent. As the logic is sound and complete for the class of Kripke -models and is sound for the class of -models, we have that for every formula φ, if φ is valid in the class of Kripke -models then φ is valid in the class of -models. Consequently, for every formula φ, if φ is satisfiable in the class of -models then φ is satisfiable in the class of Kripke -models. Therefore, in this second step we just need to show that for every formula φ, if φ is satisfiable in the class of Kripke -models then φ is satisfiable in the class of -models.
Suppose
φ is satisfiable in the class of Kripke
-models. This means that there is a Kripke
-model
and world
w such that
. We can now build a
-model
which satisfies
φ. The model
is defined as follows:
;
for every and , if and only if ;
for every , ;
for every , ;
.
By induction on the structure of
φ, it is just a trivial exercise to show that we have
.
A.2. Proof of Theorem 2
Proof. Let us start to prove that the satisfiability problem of
is EXPTIME-hard when
. Let us consider two distinct agents
. Let us consider a modal formula
φ made of operators
,
and
. It is easy to check that the following two statements are equivalent:
So we have a reduction from the satisfiability problem of
to the satisfiability problem of S5
plus universal modality
.
But the satisfiability problem of S5
plus the universal modality
is EXPTIME-hard as it is the case for the satisfiability problem of K plus the universal modality [
46]. Indeed, we can reduce the satisfiability problem of S5
plus the universal modality
to the satisfiability problem of K plus the universal modality by translating a formula of K plus the universal modality into S5
plus universal modality. Let
x be an extra proposition. The translation works as follows:
where is the K-operator;
where is the K-operator;
for all , where is the universal operator.
And
φ is satisfiable in K plus universal modality iff
is satisfiable in S5
plus the universal modality. So
is EXPTIME-hard.
Now let us prove that the satisfiability problem of
is NEXPTIME. We are going to prove that we can make a filtration of any
model, preserving both the semantic constraints of Definition 1 and the truth of formulas (see [
47] for a general introduction to the filtration method in modal logic). Let us consider a
-model
where we suppose ∼ to be the universal modality, without loss of generality. As usual, we consider a formula
φ, the set
of all subformulas of
φ and the equivalence relation ≡ over
W defined by
iff for all
,
iff
. We note
the equivalence class of ≡ containing
w. Let us define
by:
;
;
;
iff for all formulas , iff and ;
iff for all formulas , implies ;
.
We leave the reader checking that
is well-defined,
satisfies the constraints of Definition 1 and that if
then
.
This filtration implies that if a formula
φ is satisfiable, then it is satisfiable in a model of size
where
is the length of the formula
φ. A possible algorithm for solving the satisfiability of
φ may be as follows:
Guess non-deterministically a -model whose size is bounded by where π only gives truthness of propositions occurring in φ;
Guess non-deterministically a world w of M;
Check if .
This algorithm non-deterministically runs in exponential time. So the satisfiability problem of
is in NEXPTIME.
A.3. Proof of Theorem 4
Proof. The satisfiability problem of
is clearly NP-hard because it is a conservative extension of the classical propositional logic whose satisfiability problem in NP-complete (Cook’s Theorem [
20]).
Now let us prove it is in NP. Clearly if a formula
φ is
-satisfiable, there exists a
-model
whose size is bounded by
. Here is an non-deterministic algorithm to check if a given formula
φ is satisfiable:
Guess non-deterministically a -model whose size is bounded by where π only gives truthness of propositions occurring in φ;
Guess non-deterministically a world w of M;
Check if .
This algorithm non-deterministically runs in polynomial time. So the satisfiability problem of is in NP.
A.4. Proof of Theorem 5a
For all , we have:
Lemma 1.
Proof. ;
from Active;
by 1. and Boolean principles;
by Boolean principles;
if
by Aware;
by 4. and Boolean principles;
if ; by Single;
if
by Necessitation of from 6;
if
by Axiom K for plus ModusPonens from 7;
by Boolean principles from 8.
by 2, 3, 5 and 9.
Now let us prove Theorem 5a. We give here a version of the proof that uses Axioms K, T, 4 and 5 for epistemic modal operators.
Proof. by Definition of ;
by Axiom 5 for ;
by Axiom 4 for plus Boolean principles;
by 1, 2, 3 and Boolean principles;
by modal logic K principles;
by Lemma 1;
by 4, 5, 6 and Boolean principles;
by modal logic K principles;
by 7 and 8;
by Axiom T of ;
by 9 and 10.
We give another version of the proof of Theorem 5a that uses Axioms K, T and 5 for epistemic modal operators and introspection over preferences “”.
Proof. by Definition of ;
by Axiom 5 for ;
by 1 and 2;
by modal logic K principles;
by Lemma 1;
by 2, 4, 5 and Boolean principles;
by modal logic K principles;
by Lemma 1 (or introspection over preferences);
by 8 and 9;
by Axiom T of ;
by 10 and 11.
A.5. Proof of Theorem 6
For all , we have:
Proof. if
by Single;
if
by necessitation of ;
if
by 2, axiom K of plus ModusPonens;
if
by 3 and Boolean principles;
by axiom T of S5Ki.
if
by JonitAct;
for
by 5 and 6;
by Boolean principles and 7;
by Boolean principle “”;
by distributivity of ∧ over ;
by 4 plus Boolean principles;
by Axiom T of ;
by 12 and Boolean principles;
by 8, 9, 10, 11 and 13;
by 14 and Boolean principles.
A.6. Proof of Theorem 7
For all ,
Proof.
Lemma 2.
Proof. The proof of the lemma consists in proving by induction on n that and . We leave the proof of these two -theorems based on Lemma 1 to the reader.
Here we prove .
by Axiom JointAct
by Axiom T of ;
if
By 1, 2, axiom T for and Boolean principles;
by CompleteInfo or (Lemma 1 considered as axioms plus axiom T for );
by Axiom T for ;
by 4, 5 and Boolean principles;
by Boolean principles;
if
by 3, 6, 7 and Boolean principles;
by 8 and Boolean principles.
let and let us prove that if the theorem 7 is true for all then it is true for .
by Axiom T for plus Boolean principles;
by induction;
by Definition of and Boolean principles;
by 1, 2, 3;
;
by Boolean principles
if
by JointAct, definition of and Boolean principles;
by distributivity of ∧ over ;
by modal logic K principle “” ;
by induction;
by necessitation rule on 9;
by modal logic K principles applied on 10;
by Lemma
A.6;
from 8, 11 and 12;
by 13 and Boolean principles;
by Boolean principles;
if
by 5, 6, 7, 14, 15;
if
by 4 and 16;
by 17.
A.7. Proof of Theorem 8
Consider an arbitrary -model , a world w in M and such that for all positive integers n we have . Then, there is a model such that for all positive integers n we have .
Proof. The proof is based on the following Lemma 3.
Lemma 3. For all , we have In other words, player i’s strategy a survives after n rounds of IDSDS if and only if, a survives after rounds of IDSDS and in the subgame of depth n, for every alternative strategy b of i, there is a joint action of the other agents that survives after rounds of IDSDS such that playing a while the others play is for i at least as good as playing b while the others play .
Lemma 3 ensures that the definition of
can be rewritten in the following shorter equivalent form:
Let us consider w such that for all positive integers n, . We can now show how to build the accessibility relations of the model in such a way that for all positive integers n. The construction goes as follows.
For all positive integers n, let be the subset of all joint actions such that . As , we have . Let us define . As Δ is finite, there exists a positive integer such that and for all positive integers , . Let Ω be the set of all worlds u such that and such that there exists such that . Note that .
For all
, we define
as follows:
Now, let us prove that for all , for all , we have . Let be such that . As , we have . By Lemma 3, it implies that for all , there exists such that and . But by definition of , we have equivalence between and . So for all , we have . As for all we have , we obtain for all positive integers n.
A.8. Proof of Theorem 9
If M is a model then is a model.
Proof. It is just a routine to verify that and every are equivalence relations, every is reflexive and transitive, and the model satisfies the semantic constraints C1, C4, C5 and C6.
Let us prove that satisfies constraints C2 and C3.
We first prove that satisfies constraint C2. We introduce the following useful notation. Suppose . Then, iff there is such that .
Now, suppose for every there is such that and . It follows that for every there is such that and . The latter implies that there is v such that and (by the semantic constraint C2). Now, suppose for all if then . It follows that: there is and such that and . The latter implies that there is and such that and for all , . We conclude that there is no such that which leads to a contradiction.
We now consider constraint C3. Suppose and . It follows that and which implies , because M satisfies constraint C3. The latter implies . Now, suppose and . It follows that and which implies , because M satisfies constraint C3. The latter implies .
A.9. Proof of Theorem 10
Proof. The proofs of
R1-
R6 go as in Dynamic Epistemic Logic (DEL) (see [
10]). We here prove
R7.
,
IFF if then ,
IFF if then (by Axiom Def|δC|),
IFF if then or ,
IFF if then, if then ,
IFF if then, ,
IFF if then, ,
IFF if .
A.10. Proof of Theorem 11
The logic is completely axiomatized by the axioms and inference rules of together with the schemata of Theorem 10.
Proof. By means of the principles R1-R7 in Theorem 10, it is straightforward to prove that for every formula there is an equivalent formula. In fact, each reduction axiom R2-R7, when applied from the left to the right by means of the rule of replacement of proved equivalence, yields a simpler formula, where “simpler” roughly speaking means that the dynamic operator is pushed inwards. Once the dynamic operator attains an atom it is eliminated by the equivalence R1. Hence, the completeness of is a straightforward consequence of Theorem 1.
A.11. Proof of Theorem 12
For all , for all , .
Lemma 4. .
Proof. by Active;
by 1 and T for and Boolean principles;
by Active;
by 3;
by 2 and 4;
by Definition and Boolean principles;
by 6 and Boolean principles to propagate ;
for all ;
by 7 and Boolean principles (induction on n);
if
by Boolean principles and because is transitive (as , all sequence are such that there exists such that );
by Definition of and Boolean principles;
by 8, 9, 10;
by 11 and Boolean principles;
by 5 and 12;
by 13 and Boolean principle.
Lemma 5. .
Proof. We prove it by induction. Let us consider the case where by convention.
by Definition of and Boolean principles;
by Lemma 4 and Boolean principles;
by 1 and Boolean principles;
by 2 and 3;
by 1 and Boolean principles;
by 4 and Boolean principles;
by Boolean principles and Indep;
by Proposition 2 and K() principles;
by definitions of , , JointAct and Boolean principles;
by R2. and R7.
;
by Boolean principles;
by Boolean principles and 10;
.
by R2. and R4.;
by 5, 6, 7, 8, 9, 11, 12, 13.
by 13, 12;
;
by Definition of and Boolean principles;
by 16, modal logic K() principles and Boolean principles;
by ;
by 15, 17, 18;
by 14 and 19.
Now let us consider the inductive case.
by Definition of ;
by Boolean principles and rules R2. and R3. (we can distribute over Boolean connectives);
by Boolean principles and Axiom R2., R3., R4. and R6.;
by induction and 3;
by Boolean principles (we remove the multiple “”);
by 1, 2, 4, 5.
Now let us finish the proof:
by definition of and Boolean principles;
by 1 and Boolean principles (induction on n);
by Boolean principles (see definition of );
by rule R7.;
by 3, 4, Lemma 5, R2. and R3.;
by induction with 5;
by rule R2. and R3.;
by 7 and induction;
by R2., R4. and T for and Boolean principles;
by Lemma 5 and induction;
by 2, 3, 6;
by 8, 9, 10;
by 11 and 12.
A.12. Proof of Theorem 13.
For all , .
Proof. By Theorem 7, Theorem 12 and Boolean principles.
A.13. Proof of Theorem 14
The satisfiability problem of a given formula φ in a -model is PSPACE-hard.
Proof. Let us prove that that the satisfiability problem of
is PSPACE-hard. Let
i be an agent. Let us consider a formula
φ written only with atomic propositions and with modal operators
and
. We have equivalence between:
φ is satisfiable in a -model;
φ is satisfiable in a model of the logic S5 (i.e. the fusion of the logic S5 for and S5 for ).
Hence, we have reduced the satisfiability problem of a given formula
φ in a
-model to the satisfiability problem of a given formula
φ of S5
which is PSPACE-hard. So the satisfiability problem of a given formula
φ in a
-model is PSPACE-hard.
A.14. Proof of Theorem 15
If and then the satisfiability problem of a given formula φ in a -model is NP-complete.
If or the satisfiability problem of a given formula φ in a -model is PSPACE-complete.
Proof. We give here some hint for the proof. When there is only one agent and
then the games are trivial and reduced to singletons. In these settings, a
-frame
is such that ∼ and
for each agent
i are equal to the relation
. So the modal operators
and
are superfluous. The operator
can be treated as a proposition. Hence the logic is similar to the logic S5 which is NP. This is the main argument why when there is only one agent and
the logic
is NP. NP-hardness is granted because
is a conservative extension of Classical Propositional Logic.
Now let us prove that the satisfiability problem of a given formula
φ in a
-model is PSPACE-hard in other cases. First let us consider the case where
. Let us consider two distinct agents
i,
. Let
φ be a formula written only with atomic propositions and with epistemic modal operators
and
. We have equivalence between:
φ is satisfiable in a -model;
φ is satisfiable in the logic S5 (i.e., the fusion of the logic S5 for and S5 for ).
The direction
is straightforward and is already true with the assumption of the Axiom CompleteInfo. The direction
comes from the fact that the Constraint
C4 (corresponding to the Axiom CompleteInfo) has disappeared. So we can easily transform a model of the epistemic modal logic into a
-model. Note that in the case of the logic
, the direction
is not true anymore. Indeed, it is not possible to transform a model of S5
with more than
worlds into a
-model. Hence, we have reduced the satisfiability problem of a given formula
φ in a
-model into the satisfiability problem of a given formula
ψ of S5
which is PSPACE-hard. So the satisfiability problem of a given formula
φ in a
-model is PSPACE-hard.
Now let us the consider the case where
and
. Let
a and
b be two distinct actions. We prove that we can reduce the satisfiability problem of a given formula
φ in a
-model to the satisfiability problem of K. Here is a possible translation:
where is the K-operator;
where is the K-operator;
for all propositions p;
for all propositions p.
And
φ is satisfiable in K iff
is satisfiable in
. Hence, the logic
is also PSPACE-hard in this case.
Now we are going to prove that the satisfiability problem of
is PSPACE. We do not give all the details but we give the idea for a tableau method [
21] for the logic
. The tableau method is a non-deterministic procedure. The creation of a model proceeds as follows:
We start the procedure by guessing a “grid”, that is to say an equivalence class for the relation ∼ of maximal size and also its preference relation as in the algorithm of Theorem 2. We also choose non-deterministically a world w in this class.
We adapt the classical tableau method rules for the epistemic modal logic [
21], that is to say:
- −
Suppose that a world w contains a formula of the form . Then we propagate the formula ψ in all nodes v such that .
- −
Suppose that a world w contains a formula of the form . Then we create an equivalence class for ∼, we choose a point v such that in this equivalence class and we propagate ψ in v.
Suppose that a node w contains a formula . Then we propagate the formula ψ in all nodes v such that ;
Suppose that a node w contains a formula . Then we choose non-deterministically a world v such that and we propagate ψ in v.
Suppose that a node w contains a formula . Then we propagate the formula ψ in all nodes v such that ;
Suppose that a node w contains a formula . Then we choose non-deterministically a world v such that and we propagate ψ in v.
During the construction, we explore the structure in depth first so that we only need to have one branch in memory at each step. Thus, the algorithm is a non-deterministic procedure that uses only a polynomial amount of memory. So the satisfiability problem of
is in NPSPACE. According the Savitch’s theorem [
48], it is in PSPACE.
A.15. Proof of Theorem 16
For every and for every , if and only if .
Proof. (⇒) We first prove the left-to-right direction. Suppose that and . The latter means that for every there is such that .
The latter means that for every
there is
such that:
there is such that and
for all if and and then there is such that and .
Consider an arbitrary
. It follows that there is an element
δ of Δ which satisfies the previous conditions A and B. By definition of
and
we have that: if there is
such that
then there is
such that
. Therefore, from item A, we conclude:
- C.
there is such that .
Take two arbitrary worlds and suppose that and and . By definition of , we have and . Consider now the following three cases.
CASE 1. Suppose . Then, by definition of , we have that and . Therefore, from item B, it follows that there is such that and . From the latter, by definition of , we conclude that there is such that and .
CASE 2. Suppose that and that there is such that and . From the former, by definition of , it follows that . From the latter, by definition of , it follows that there is such that and . Therefore, we have that there is such that and .
CASE 3. Suppose that and that there is no such that and . From the former, by definition of , it follows that . From the latter, by definition of (and the fact that ), it follows that there is such that and and . Therefore, we have that there is such that and .
From the previous three cases, it follows that:
- D.
for all if and and then there is such that and .
From the items C and D we conclude that .
(⇐) Let us prove the right-to-left direction. Suppose that and . The latter means that for every there is such that .
The latter means that for every
there is
such that:
- E.
there is such that and
- F.
for all if and and then there is such that and .
Consider an arbitrary
. It follows that there is an element
δ of Δ which satisfies the previous conditions E and F. By definition of
and
we have that: if there is
such that
then there is
such that
. Therefore, from item E, we conclude:
- G.
there is such that .
Take two arbitrary worlds and suppose that and and . By Definition of , and we have and and . Thus, by the previous item F, there is such that and . But as we have . Thus and .
It follows that:
- H.
for all if and and then there is such that and .
From the items G and H we conclude that .
A.16. Proof of Corollary 1
For every , for every and for every , we have if and only if .
Proof. Define a world v to be C-reachable from world w in n steps (with ), and note this , if and only if there exist worlds such that and and for all , there exists such that . Define . We have if and only if for all .
By definition of , we have for all . Therefore, if and only if for all .
Moreover, according to Theorem 16, for every we have if and only if . Therefore, we have that for all if and only if for all .
It follows that, if and only if .