Coordination and Cooperation Problems in Network Good Production
Abstract
:1. Introduction
2. The General Model and the Computerized Game Version
2.1. The General Model

2.2. The Computerized Game Version Used in the Experiment
| Scenario Number | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| costs = 10; | costs = 30; | costs = 50; | costs = 10; | costs = 30; | costs = 50; |
| info | info | info | no info | no info | no info | |
| costs = 50; | costs = 30; | costs = 10; | costs = 50; | costs = 30; | costs = 10; |
| info | info | info | no info | no info | no info | |
| costs = 10; | costs = 30; | costs = 50; | costs = 10; | costs = 30; | costs = 50; |
| no info | no info | no info | info | info | info | |
| costs = 50; | costs = 30; | costs = 10; | costs = 50; | costs = 30; | costs = 10; |
| no info | no info | no info | info | info | info | |
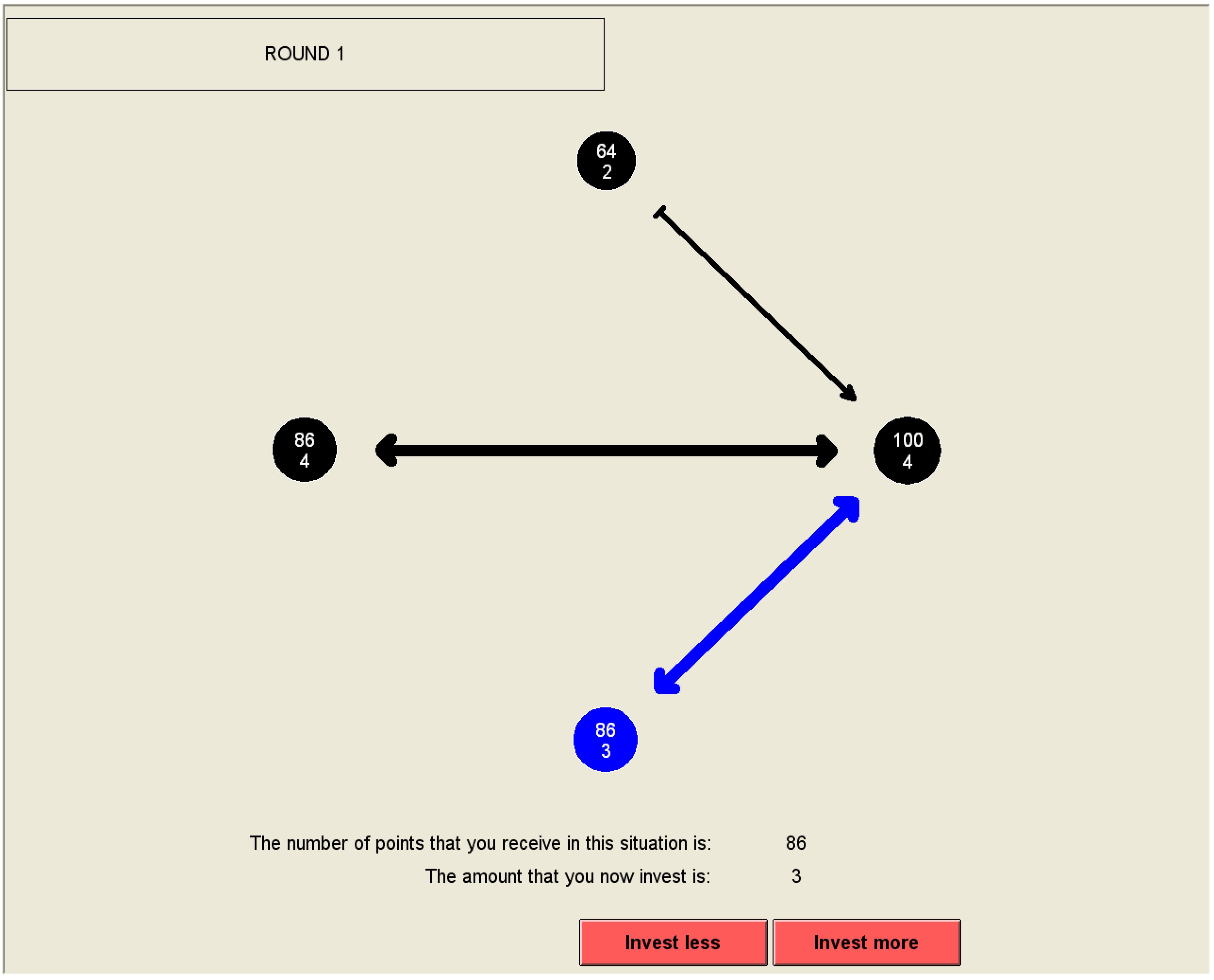
3. Predicting the Outcomes in the Experiment
3.1. Investments and Payoffs for a Given Network
3.2. Combining Link Decisions and Investments
| α = 48, β = 16 λ = 2, n = 4 | Investments | Payoffs | ||||||||||
| No cost | Low cost | Intermediate cost | High cost | |||||||||
| c = 0 | c = 10 | c = 30 | c = 50 | |||||||||
| Networks | Nash | SO | Nash | SO | Nash | SO | Nash | SO | Nash | SO | ||
| Empty |  | η = 0 | 3 | 3 | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 72 |
| 2 dyads |  | η = 1 | 4 | 4 | 96 | 96 | 86 | 86 | 66 | 66 | 46 | 46 |
| 2-star |  | ηi = 0 | 3 | 3 | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 72 |
| ηi = 1 | 4 | 4 | 96 | 104 | 86 | 94 | 66 | 76 | 46 | 54 | ||
| ηi = 2 | 4 | 5 | 128 | 120 | 108 | 100 | 68 | 60 | 28 | 20 | ||
| Line |  | ηi = 1 | 4 | 4 | 96 | 104 | 86 | 94 | 66 | 74 | 46 | 54 |
| ηi = 2 | 4 | 5 | 128 | 130 | 108 | 120 | 68 | 70 | 28 | 30 | ||
| Triangle |  | ηi = 0 | 3 | 3 | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 72 |
| ηi = 2 | 4 | 6 | 128 | 144 | 108 | 124 | 68 | 84 | 28 | 44 | ||
| 3-star |  | ηi = 1 | 4 | 5 | 104 | 112 | 94 | 102 | 74 | 82 | 54 | 62 |
| ηi = 3 | 5 | 7 | 160 | 144 | 130 | 114 | 70 | 54 | 10 | -6 | ||
| Square |  | η = 2 | 4 | 6 | 128 | 144 | 108 | 124 | 68 | 84 | 28 | 44 |
| Stem |  | ηi = 1 | 4 | 5 | 104 | 110 | 94 | 100 | 74 | 80 | 54 | 60 |
| ηi = 2 | 4 | 6 | 144 | 156 | 124 | 136 | 84 | 96 | 44 | 56 | ||
| ηi = 3 | 5 | 7 | 160 | 182 | 130 | 152 | 70 | 92 | 10 | 32 | ||
| D-Box |  | ηi = 2 | 4 | 8 | 144 | 160 | 124 | 140 | 84 | 100 | 44 | 60 |
| ηi = 3 | 5 | 9 | 170 | 234 | 140 | 204 | 80 | 144 | 20 | 84 | ||
| Complete |  | η = 3 | 5 | 12 | 190 | 288 | 160 | 258 | 100 | 198 | 40 | 138 |
- (i)
- s* is a Nash equilibrium and
- (ii)
- Πi(, g+ij) > Πi(x*, g) implies Πj(, g+ij) < Πj(x*, g) for all i, j ϵ N where are the Nash investments for the network g+ij.
4. Experimental Design
4.1. Data Collection
4.2. Procedure
5. Descriptive Results
| c = 10 | c = 30 | c = 50 | All link costs | ||||||||||||||||||||||||
| Network | Info | No info | Total | Info | No info | Total | Info | No info | Total | Info | No info | Total | |||||||||||||||
| Empty |  | 0 | 0 | 0 | 46 | 49 | 95 | 195 | 192 | 387 | 241 | 241 | 482 | ||||||||||||||
| Dyad |  | 0 | 0 | 0 | 9 | 12 | 21 | 10 | 13 | 23 | 19 | 25 | 44 | ||||||||||||||
| 2 dyads |  | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||||||||||||||
| 2-star |  | 0 | 0 | 0 | 4 | 5 | 9 | 1 | 1 | 2 | 5 | 6 | 11 | ||||||||||||||
| Line |  | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 2 | ||||||||||||||
| Triangle |  | 1 | 0 | 1 | 5 | 7 | 12 | 1 | 3 | 4 | 7 | 10 | 17 | ||||||||||||||
| 3-star |  | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | ||||||||||||||
| Square |  | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| Stem |  | 4 | 3 | 7 | 8 | 4 | 12 | 0 | 0 | 0 | 12 | 7 | 19 | ||||||||||||||
| D-Box |  | 8 | 5 | 13 | 21 | 16 | 37 | 0 | 0 | 0 | 29 | 21 | 50 | ||||||||||||||
| Complete |  | 199 | 192 | 391 | 118 | 115 | 233 | 5 | 1 | 6 | 322 | 308 | 630 | ||||||||||||||
| Total | 212 | 200 | 412 | 212 | 209 | 421 | 212 | 212 | 424 | 636 | 621 | 1,257 | |||||||||||||||
| c = 10 | c = 30 | c = 50 | All link costs | |||||||||||||||||||
| Network | Invest. | Info | No Info | Total | Info | No Info | Total | Info | No info | Total | Info | No Info | Total | |||||||||
| Empty | Nash | 0 | 0 | 0 | 43 | 46 | 89 | 191 | 185 | 376 | 234 | 231 | 465 | |||||||||
| Coop | - | - | - | - | - | - | - | - | - | - | - | - | ||||||||||
| Rest | 0 | 0 | 0 | 3 | 3 | 6 | 4 | 7 | 11 | 7 | 10 | 17 | ||||||||||
| Total | 0 | 0 | 0 | 46 | 49 | 95 | 195 | 192 | 387 | 241 | 241 | 482 | ||||||||||
| Other | Nash | 3 | 2 | 5 | 26 | 33 | 59 | 5 | 8 | 13 | 34 | 43 | 77 | |||||||||
| Coop | 2 | 0 | 2 | 12 | 1 | 13 | 1 | 0 | 1 | 15 | 1 | 16 | ||||||||||
| Rest | 8 | 6 | 14 | 10 | 11 | 21 | 6 | 11 | 17 | 24 | 28 | 52 | ||||||||||
| Total | 13 | 8 | 21 | 48 | 45 | 93 | 12 | 19 | 31 | 73 | 72 | 145 | ||||||||||
| Complete | Nash | 136 | 149 | 285 | 81 | 89 | 170 | 0 | 0 | 0 | 217 | 238 | 455 | |||||||||
| Coop | 33 | 8 | 41 | 22 | 11 | 33 | 5 | 0 | 5 | 60 | 19 | 79 | ||||||||||
| Rest | 30 | 35 | 65 | 15 | 15 | 30 | 0 | 1 | 1 | 45 | 51 | 96 | ||||||||||
| Total | 199 | 192 | 391 | 118 | 115 | 233 | 5 | 1 | 6 | 322 | 308 | 630 | ||||||||||
| Total | Nash | 139 | 151 | 290 | 150 | 168 | 318 | 196 | 193 | 389 | 485 | 512 | 997 | |||||||||
| Coop | 35 | 8 | 43 | 34 | 12 | 46 | 6 | 0 | 6 | 75 | 20 | 95 | ||||||||||
| Rest | 38 | 41 | 79 | 28 | 29 | 57 | 10 | 19 | 29 | 76 | 89 | 165 | ||||||||||
| Total | 212 | 200 | 412 | 212 | 209 | 421 | 212 | 212 | 424 | 636 | 621 | 1,257 | ||||||||||
6. Analyses
6.1. Analysis Strategy
6.2. Results
| Model 0a | Model 1b | Model 2c | ||||||||||||||||||||||||||||||
| Coeff. | S.E. | p | Coeff. | S.E. | p | Coeff. | S.E. | p | ||||||||||||||||||||||||
| Nash investment | 1.344 | .117 | .000 | 3.309 | .311 | .000 | 3.785 | .516 | .000 | |||||||||||||||||||||||
| Complete network | 2.332 | .338 | .000 | 3.357 | .666 | .000 | ||||||||||||||||||||||||||
| Other network | 1.386 | .298 | .000 | 2.951 | .564 | .000 | ||||||||||||||||||||||||||
| Nash × Complete | –2.353 | .343 | .000 | –2.738 | .545 | .000 | ||||||||||||||||||||||||||
| Nash × Other | –3.185 | .375 | .000 | –3.519 | .533 | .000 | ||||||||||||||||||||||||||
| Complete × costs = 10 | 18.525 | .693 | .000 | |||||||||||||||||||||||||||||
| Other × costs = 10 | 16.495 | .738 | .000 | |||||||||||||||||||||||||||||
| Complete × costs = 50 | –5.228 | .592 | .000 | |||||||||||||||||||||||||||||
| Other × costs = 50 | –2.772 | .400 | .000 | |||||||||||||||||||||||||||||
| Nash × costs = 10 | –.137 | .141 | .332 | |||||||||||||||||||||||||||||
| Nash × costs = 50 | –.567 | .496 | .253 | |||||||||||||||||||||||||||||
| Number of groups | 1,257 | 1,257 | ||||||||||||||||||||||||||||||
| Log Likelihood | –1,756 | –1,189 | ||||||||||||||||||||||||||||||
| Model 3a | Model 4b | |||||||
| Coeff. | S.E. | p | Coeff. | S.E. | p | |||
| Complete network | .879 | .285 | .002 | –.464 | .627 | .459 | ||
| Other network | –.114 | .243 | .639 | –.544 | .388 | .162 | ||
| Complete × Sophistication (0–1) | 2.236 | 1.298 | .085 | |||||
| Other × Sophistication (0–1) | 2.191 | 1.480 | .139 | |||||
| Complete × Round (0–7) | .301 | .098 | .002 | |||||
| Other × Round (0–7) | .057 | .082 | .483 | |||||
| Complete × Low/High | .678 | .634 | .284 | |||||
| Other × Low/High | .510 | .503 | .311 | |||||
| Complete × Information | .051 | .395 | .897 | |||||
| Other × Information | .109 | .224 | .625 | |||||
| Number of groups | 400 | 400 | ||||||
| Log Likelihood | –673 | –649 | ||||||
| Model 5a | Model 6b | |||||||
| Coeff. | S.E. | p | Coeff. | S.E. | p | |||
| Cooperation | –1.904 | .222 | .000 | –3.620 | .586 | .000 | ||
| Rest | –1.740 | .170 | .000 | –1.321 | .223 | .000 | ||
| Cooperation × costs = 10 | .027 | .196 | .892 | –.003 | .221 | .990 | ||
| Rest × costs = 10 | .433 | .192 | .024 | .421 | .184 | .022 | ||
| Cooperation × costs = 50 | –2.221 | .641 | .001 | –2.309 | .621 | .000 | ||
| Rest × costs = 50 | –1.041 | .366 | .004 | –1.038 | .363 | .004 | ||
| Cooperation × Information | 1.389 | .299 | .000 | |||||
| Rest × Information | –.086 | .205 | .675 | |||||
| Cooperation × Sophistication (0–1) | 1.853 | 1.316 | .159 | |||||
| Rest × Sophistication (0–1) | .147 | .887 | .868 | |||||
| Cooperation × Round (0–23) | .064 | .029 | .028 | |||||
| Rest × Round (0–23) | –.035 | .020 | .072 | |||||
| Number of groups | 1,200 | 1,200 | ||||||
| Log Likelihood | –730 | –697 | ||||||
7. Conclusion and Discussion
Acknowledgements
References
- Olson, M. The Logic of Collective Action; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Taylor, M. The Possibility of Cooperation; Cambridge University Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Bramoullé, Y.; Kranton, R. Public goods in networks. J. Econ. Theory 2007, 135, 478–494. [Google Scholar]
- Ballester, C.; Calvó-Armengol, A.; Zenou, Y. Who’s who in networks? Wanted: The key player. Econometrica 2006, 74, 1403–1417. [Google Scholar]
- Hardin, R. Collective Action; Johns Hopkins University Press: Baltimore, MD, USA, 1982. [Google Scholar]
- Heckathorn, D.D. Dynamics and dilemmas of collective action. Am. Sociol. Rev. 1996, 61, 250–277. [Google Scholar]
- Coleman, J.S. Foundations of Social Theory; Belknap Press of Harvard University Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Raub, W.; Weesie, J. Reputation and efficiency in social interactions: An example of network effects. Am. J. Sociol. 1990, 96, 626–654. [Google Scholar]
- Gould, R.V. Collective action and network structure. Am. Sociol. Rev. 1993, 58, 182–196. [Google Scholar]
- Marwell, G.; Oliver, P. The Critical Mass in Collective Action: A Micro-Social Theory; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Flache, A. The Double Edge of Networks; Thesis Publishers: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Chwe, M.S. Structure and strategy in collective action. Am. J. Sociol. 1999, 105, 128–156. [Google Scholar]
- Jackson, M.O.; Watts, A. On the formation of interaction networks in social coordination games. Games Econ. Behav. 2002, 41, 265–291. [Google Scholar]
- Eguíluz, V.M.; Zimmerman, M.G.; Cela-Conde, C.J.; San Miguel, M. Cooperation and the emergence of role differentiation in the dynamics of social networks. Am. J. Sociol. 2005, 110, 977–1008. [Google Scholar]
- Goyal, S.; Vega-Redondo, F. Network formation and social coordination. Games Econ. Behav. 2005, 50, 178–207. [Google Scholar]
- Ule, A. Exclusion and cooperation in networks. Ph.D Thesis, Tinbergen Institute, Rotterdam, The Netherlands, 2005. [Google Scholar]
- Berninghaus, S.K.; Vogt, B. Network formation in symmetric 2 × 2 games. Homo Oeconomicus 2006, 23, 421–466. [Google Scholar]
- Takács, K.; Janky, B. Smiling contributions: Social control in a public goods game with network decline. Physica A 2007, 378, 76–82. [Google Scholar]
- Buskens, V.; Corten, R.; Weesie, J. Consent or conflict: Coevolution of coordination and networks. J. Peace Res. 2008, 45, 205–222. [Google Scholar]
- Corten, R.; Buskens, V. Co-evolution of conventions and networks: An experimental study. Soc. Networks 2010, 32, 4–15. [Google Scholar]
- Galeotti, A.; Goyal, S. The law of the few. Am. Econ. Rev. 2010. (Forthcoming). [Google Scholar]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar]
- Berninghaus, S.K.; Ehrhart, K.-M.; Ott, M. Myopically Forward-Looking Agents in a Network Formation Game: Theory and Experimental Evidence; SFB 504 Discussion Paper Series No. 08–02; 2008; University of Mannheim: Mannheim, Germany. [Google Scholar]
- Berninghaus, S.K.; Ehrhart, K.-M.; Ott, M. A network experiment in continuous time: The influence of link costs. Exp. Econ. 2006, 9, 237–251. [Google Scholar]
- Calvo-Armengol, A. Job contact networks. J. Econ. Theory 2004, 115, 191–206. [Google Scholar]
- Goyal, S.; Joshi, S. Unequal connections. Int. J. Game Theory 2006, 34, 319–349. [Google Scholar]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar]
- Selten, R. Evolution, learning, and economic behavior. Games Econ. Behav. 1991, 3, 3–24. [Google Scholar]
- Camerer, C.F.; Ho, T.-H.; Chong, J.-K. Sophisticated experience-weighted attraction learning and strategic teaching in repeated games. J. Econ. Theory 2002, 104, 137–188. [Google Scholar]
- Greiner, B. The Online Recruitment System ORSEE 2.0: A Guide for the Organization of Experiments in Economics. Working Paper Series in Economics 10; University of Cologne: Cologne, Germany, 2004. [Google Scholar]
- Nagel, R. A review of beauty contest games. In Games and Human Behavior: Essays in Honor of Amnon Rapoport; Budescu, D., Erev, I., Zwick, R., Eds.; Erlbaum: Hillsdale, NJ, USA, 1999; pp. 391–410. [Google Scholar]
- Camerer, C.F.; Ho, T.-H.; Chong, J.-K. A cognitive hierarchy model of games. Q. J. Econ. 2004, 119, 861–898. [Google Scholar]
- McFadden, D. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: New York, NY, USA, 1973; pp. 105–142. [Google Scholar]
- Scott Long, J. Regression Models for Categorical and Limited Dependent Variables; Sage Publications: Thousand Oaks, CA, USA, 1997. [Google Scholar]
- Cameron, A.C.; Gelbach, J.B.; Miller, D.L. Robust Inference with Multi-Way Clustering; Working paper; University of California: Davis, CA, USA.
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Knigge, A.; Buskens, V. Coordination and Cooperation Problems in Network Good Production. Games 2010, 1, 357-380. https://doi.org/10.3390/g1040357
Knigge A, Buskens V. Coordination and Cooperation Problems in Network Good Production. Games. 2010; 1(4):357-380. https://doi.org/10.3390/g1040357
Chicago/Turabian StyleKnigge, Antonie, and Vincent Buskens. 2010. "Coordination and Cooperation Problems in Network Good Production" Games 1, no. 4: 357-380. https://doi.org/10.3390/g1040357
APA StyleKnigge, A., & Buskens, V. (2010). Coordination and Cooperation Problems in Network Good Production. Games, 1(4), 357-380. https://doi.org/10.3390/g1040357




