The ‘Hawk-Dove’ Game and the Speed of the Evolutionary Process in Small Heterogeneous Populations
Abstract
:1. Introduction
2. Data Collection
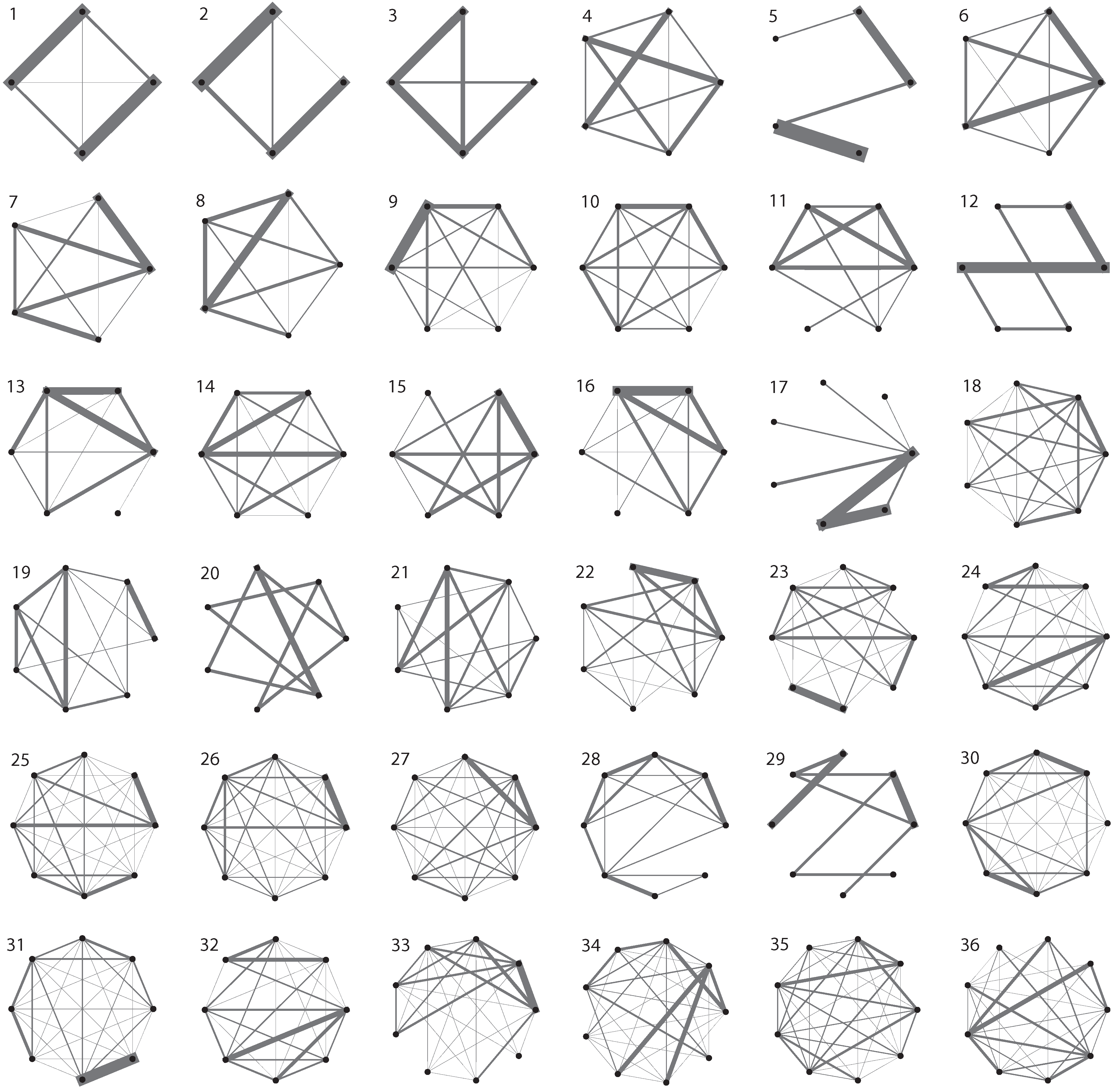

3. Evolutionary Dynamics
- (1)
- Each vertex plays with every of its neighbours one round of a Hawk-Dove game with the payoff matrix of equ. 2.
- (2)
- The fitness of a vertex is calculated as the sum of its payoffs from these games plus a background fitness value.
- (3)
- A vertex is chosen for reproduction with a probability proportional to its fitness.
- (4)
- A neighbour of the reproducing vertex is chosen with a probability proportional to the edge weight and replaced by a clone of the reproducing vertex.
4. Results
4.1. Fixed Fitness Case
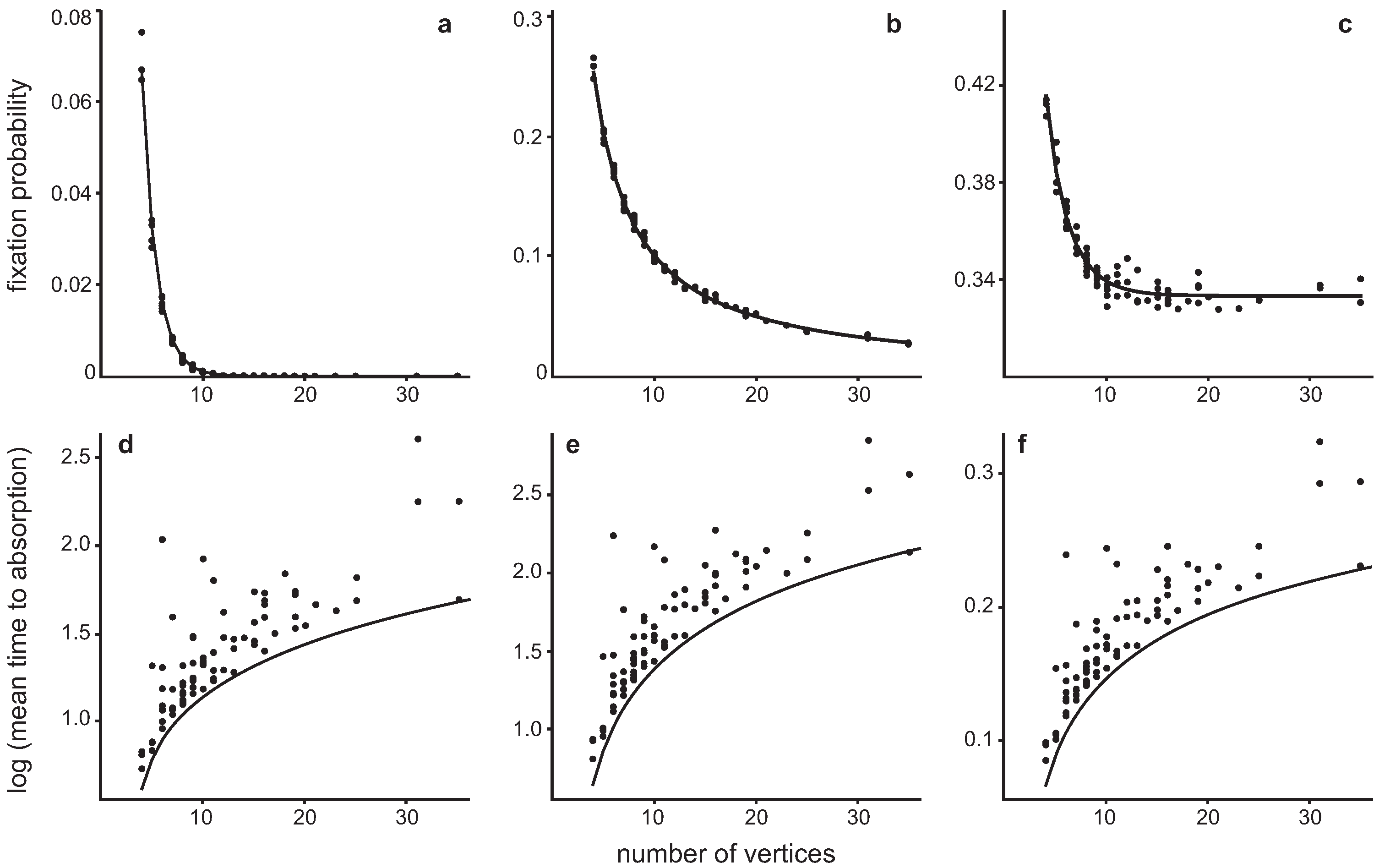
4.2. Invasion of a single Hawk in a population of Doves
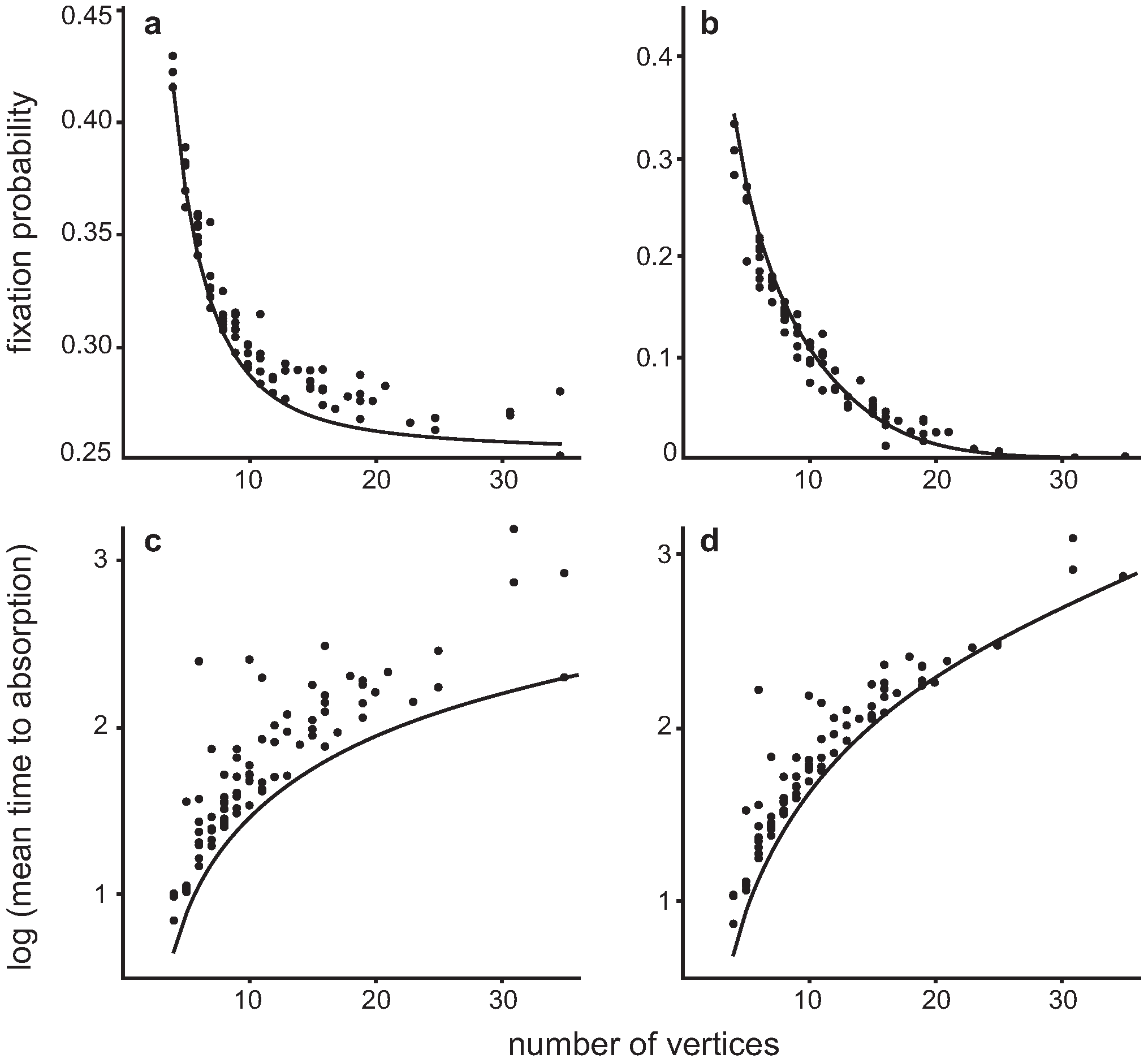
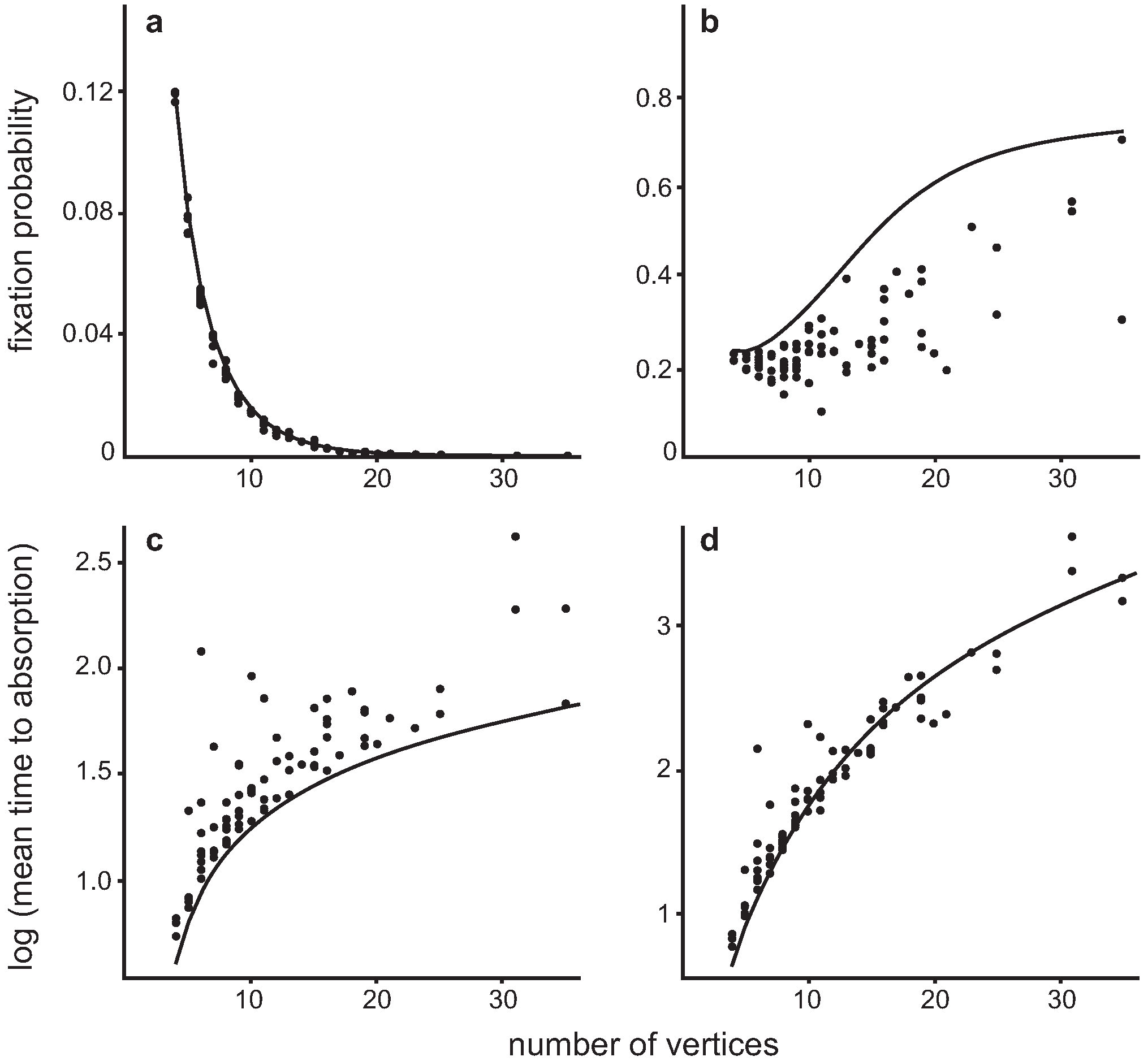
4.3. Invasion of a single Dove in a population of Hawks
4.4. Vertex degree and strength variance
| Full model (vard+vars +vard vars) R2 | F vard | P vard | F vars | P vars | Reduced model (vard) R2 | |
|---|---|---|---|---|---|---|
| Fixed r = 0.5 | 0.75 | 255.0 | *** | 2.5 | ns | 0.73 |
| Fixed r = 1.0 | 0.72 | 196.3 | *** | 0.0 | ns | 0.72 |
| Fixed r = 1.5 | 0.76 | 242.3 | *** | 0.2 | ns | 0.76 |
| Hawk C = 2 | 0.74 | 223.2 | *** | 0.1 | ns | 0.74 |
| Hawk C = 13 | 0.72 | 200.0 | *** | 1.7 | ns | 0.71 |
| Dove C = 2 | 0.75 | 227.1 | *** | 1.5 | ns | 0.73 |
| Dove C = 13 | 0.72 | 196.9 | *** | 0.3 | ns | 0.72 |
5. Discussion
Acknowledgements
References and Notes
- von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Maynard Smith, J. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Maynard Smith, J.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar]
- Hamilton, W.D. The genetical evolution of social behaviour I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Sandholm, W.H. Population Games and Evolutionary Dynamic; MIT Press: Cambridge, USA, in press.
- Gintis, H. Game Theory Evolving; Princeton University Press: Princeton, USA, 2000. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar]
- Nowak, M.A. Evolutionary Dynamics; Belknap Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Traulsen, A.; Claussen, J.C.; Hauert, C. Coevolutionary dynamics: from finite to infinite populations. Phys. Rev. Lett. 2005, 95, 238701. [Google Scholar] [CrossRef]
- Ewens, W.J. Mathematical Population Genetics; Springer: New York, USA, 1979. [Google Scholar]
- Nowak, M.A.; Sigmund, K. Evolutionary dynamics of biological games. Science 2004, 303, 793–799. [Google Scholar]
- Moran, P.A.P. Random processes in genetics. Math. Proc. Cam. Philos. Soc. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Moran, P.A.P. The Statistical Processes of Evolutionary Theory; Clarendon: Oxford, UK, 1962. [Google Scholar]
- Ridley, M. Evolution; Blackwell Publishing: Malden, USA, 2004. [Google Scholar]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar]
- Nowak, M.A.; Bonhoeffer, S.; May, R.M. More spatial games. Int. J. Bifurcation Chaos 1994, 4, 33–56. [Google Scholar] [CrossRef]
- Nakamura, M.; Matsuda, H.; Iwasa, Y. The evolution of cooperation in a lattice structured population. J. Theor. Biol. 1997, 184, 65–81. [Google Scholar]
- Nakamura, M.; Nogami, H.; Iwasa, Y. Score-dependent fertility model for the evolution of cooperation in a lattice. J. Evol. Biol. 1998, 194, 101–124. [Google Scholar]
- Lindgren, K.; Nordahl, M.G. Evolutionary dynamics of spatial games. Physica D 1994, 75, 292–309. [Google Scholar]
- Killingback, T.; Doebeli, M. Spatial evolutionary game theory: hawks and doves revisited. Proc. R. Soc. B-Biol. Sci. 1996, 263, 1135–1144. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar]
- Lieberman, E.; Hauert, C.; Nowak, M.A. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar]
- Whigham, P.A.; Dick, G.C.; Spencer, H.G. Genetic drift on networks: Ploidy and the time to fixation. Theor. Popul. Biol. 2008, 74, 283–290. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar]
- Ohtsuki, H.; Nowak, M.A. The replicator equation on graphs. J. Theor. Biol. 2006, 243, 86–97. [Google Scholar]
- Ohtsuki, H.; Nowak, M.A. Direct reciprocity on graphs. J. Theor. Biol. 2007, 247, 462–470. [Google Scholar]
- Abramson, G.; Kuperman, M. Social games in a social network. Phys. Rev. E 2001, 63, 030901. [Google Scholar]
- Taylor, P.D.; Day, T.; Wild, G. Evolution of cooperation in a finite homogenous graph. Nature 2007, 447, 469–472. [Google Scholar]
- Broom, M.; Rychtar, J. An analysis of the fixation probability of a mutant on special classes of non-directed graphs. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2008, 464, 2609–2627. [Google Scholar] [CrossRef]
- Voelkl, B.; Kasper, C. Social structure of primate interaction networks facilitates the emergence of cooperation. Biol. Lett. 2009, 5, 462–464. [Google Scholar]
- Kun, A.; Scheuring, I. Evolution of cooperation on dynamical graphs. Biosystems 2009, 96, 65–68. [Google Scholar]
- Noë, R.; Université Strasbourg, Strasbourg, FR. Personal communication, 2009.
- Karlin, S.; Taylor, H.M. A First Course in Stochastic Processes; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Antal, T.; Scheuring, I. Fixation of strategies for an evolutionary game in finite populations. Bull. Math. Biol. 2006, 68, 1923–1944. [Google Scholar] [CrossRef]
- Broom, M.; Hadjichrysanthou, C.; Rychtar, J. Evolutionary games and the speed of the evolutionary process. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2010, 466, 1327–1346. [Google Scholar] [CrossRef]
- Voelkl, B.; Kasper, C. Grooming reciprocation in primates. to be submitted for publication.
- Fruteau, C.; Voelkl, B.; van Damme, E.; Noë, R. Supply and demand determine the market value of food providers in vervet monkeys. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 12007–12012. [Google Scholar] [CrossRef]
- Troisi, A.; Schino, G.; Aureli, F. Allogrooming and interindividual proximity in two species of macaques (Macaca fascicularis and M. nemestrina). Behaviour 1989, 111, 196–207. [Google Scholar]
- Arnold, K.; Whiten, A. Grooming interactions among the chimpanzees of the Budongo Forest, Uganda: Test of five explanatory models. Behaviour 2003, 140, 519–552. [Google Scholar]
- Kasper, C.; Voelkl, B. A social network analysis of primate groups. Primates 2009, 50, 343–356. [Google Scholar]
- Traulsen, A.; Hauert, C. Stochastic evolutionary game dynamics. In Reviews of Nonlinear Dynamic Complexity; Schuster, H-G, Ed.; Wiley: New York, USA, 200; Volume 2, pp. 25–62. [Google Scholar]
- Broom, M.; Rychtar, J.; Stadler, B. Evolutionary dynamics on small-order graphs. J. Interdiscip. Math. 2009, 12, 129–140. [Google Scholar] [CrossRef]
- Snijders, T.A.B. The degree variance: An index of graph heterogeneity. Soc. Networks 1981, 3, 163–174. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Voelkl, B. The ‘Hawk-Dove’ Game and the Speed of the Evolutionary Process in Small Heterogeneous Populations. Games 2010, 1, 103-116. https://doi.org/10.3390/g1020103
Voelkl B. The ‘Hawk-Dove’ Game and the Speed of the Evolutionary Process in Small Heterogeneous Populations. Games. 2010; 1(2):103-116. https://doi.org/10.3390/g1020103
Chicago/Turabian StyleVoelkl, Bernhard. 2010. "The ‘Hawk-Dove’ Game and the Speed of the Evolutionary Process in Small Heterogeneous Populations" Games 1, no. 2: 103-116. https://doi.org/10.3390/g1020103
APA StyleVoelkl, B. (2010). The ‘Hawk-Dove’ Game and the Speed of the Evolutionary Process in Small Heterogeneous Populations. Games, 1(2), 103-116. https://doi.org/10.3390/g1020103





