A Comparative Review of Quantum Neural Networks and Classical Machine Learning for Cardiovascular Disease Risk Prediction

Abstract

Cardiac risk prediction is critical for the early detection and prevention of cardiovascular diseases, a leading global cause of mortality. In response to the growing volume and complexity of healthcare data, there has been increasing reliance on computational approaches to enhance clinical decision-making and improve early detection of cardiac risks. Although classical machine learning techniques have demonstrated strong performance in cardiovascular disease prediction, their efficiency and scalability are increasingly challenged by high-dimensional and large-scale medical datasets. Emerging advances in quantum computing have introduced quantum machine learning (QML) as a promising alternative, offering novel computational paradigms with the potential to outperform classical methods in terms of speed and problem-solving capability. This review analyzed twelve studies, evaluating data types, quantum architecture, performance metrics, and comparative efficacy against classical machine learning models. Our findings indicate that QNNs show promise for enhanced predictive accuracy and computational efficiency. However, significant challenges in scalability, noise resilience, and clinical integration persist. The translation of quantum advantage into clinical practice necessitates further validation on large-scale with diverse datasets.

1. Introduction

Cardiovascular diseases (CVDs) are the leading cause of death worldwide. According to the World Health Organization, approximately 19.8 million people died in 2022 due to CVDs, accounting for nearly 32% of all global deaths. More than three-quarters of CVD deaths occurred in low- and middle-income countries, where healthcare systems are often underdeveloped and lack the sophisticated infrastructure for early diagnosis and effective treatment service. Detecting cardiovascular diseases at an early stage is critical in reducing mortality rates and improving patients’ lives through timely medical intervention [1].

Over the years, developed countries have witnessed a decline in CVD-related deaths. This is largely attributed to advancements in healthcare systems and the adoption of advanced technological and clinical innovations. Recently, we witnessed an exponential increase in the availability of healthcare data. Many hospitals and clinics have begun integrating information systems to manage patient records and provide assistance to medical professionals. However, these systems are still underutilized when it comes to clinical decision-making, despite the rapid progress in computing and machine learning [2].

Consequently, there is a growing demand for trustworthy and efficient healthcare systems to support medical decision-making. While classical machine learning models have significantly achieved this, they are challenged as the complexity and volume of healthcare data continue to grow. Therefore, there is a need for even more powerful and efficient solutions. Quantum computing has emerged as a promising technology, with the potential to revolutionize predictive analytics by offering new ways to process and analyze massive datasets [3,4].

With the ongoing development of quantum hardware, quantum machine learning (QML) offers significant advantages in computational speed and problem-solving capabilities. For certain complex problems, quantum algorithms are expected to provide exponential speedups compared with their classical counterparts. This could drastically reduce computational time for tasks that currently take years, compressing them into minutes or just seconds [5]. Such a transformative leap would be particularly impactful in critical domains like cardiac risk prediction, where the real-time analysis of massive, high-dimensional datasets is essential for clinical decision-making and personalized medicine [6].

Given the growing interest in the field of predicated CVDs, this study aims to present a comprehensive literature review on cardiac risk prediction, benchmarking classical machine learning against quantum machine learning approaches. Through this analysis, researchers and practitioners will gain insight into current techniques with existing limitations and opportunities for future development.

The remainder of this paper is structured as follows: Section 2 provides background on cardiovascular diseases and associated risk factors. Section 3 overviews the fundamentals of quantum computing and quantum machine learning. Section 4 presents state-of-the-art techniques. In Section 5, the research methodology is discussed. Section 6 summarizes the key findings in the results. Section 7 identifies the significance of this work. Finally, Section 8 outlines conclusions and future work.

2. Cardiovascular Diseases (CVDs)

At the beginning of the 20th century, cardiovascular disease (CVD) was responsible for less than 10% of global mortality. However, by the end of the century, CVD had emerged as a leading cause of death, indicating it would surpass infectious diseases to become the foremost cause of death and disability worldwide. CVD affects many lives and often remains a silent, creeping threat. Cardiovascular disease (CVD) fundamentally attacks the circulatory system: the vital network of arteries, veins, and capillaries that nourish the heart, the brain, and every part of the body. When these vessels become narrowed, stiffened, or blocked, their crucial function of oxygen and nutrient delivery is severely compromised [7].

Cardiovascular disease encompasses a range of conditions affecting the heart and blood vessels, each presenting unique symptoms and risks.

2.1. CVD Key Types

1.

Coronary Artery Disease (CAD)

Coronary Artery Disease (CAD) silently restricts blood and oxygen flow to the heart, causing symptoms like chest pain, shortness of breath, and nausea. Over time, this damage can weaken the heart muscle, leading to heart failure, where the heart can no longer pump effectively [8].

As shown in Figure 1, restricted blood flow resulting from arterial blockage can lead to ischemia and increase the risk of myocardial infarction, emphasizing the critical need for early diagnosis and intervention in CAD.

2.

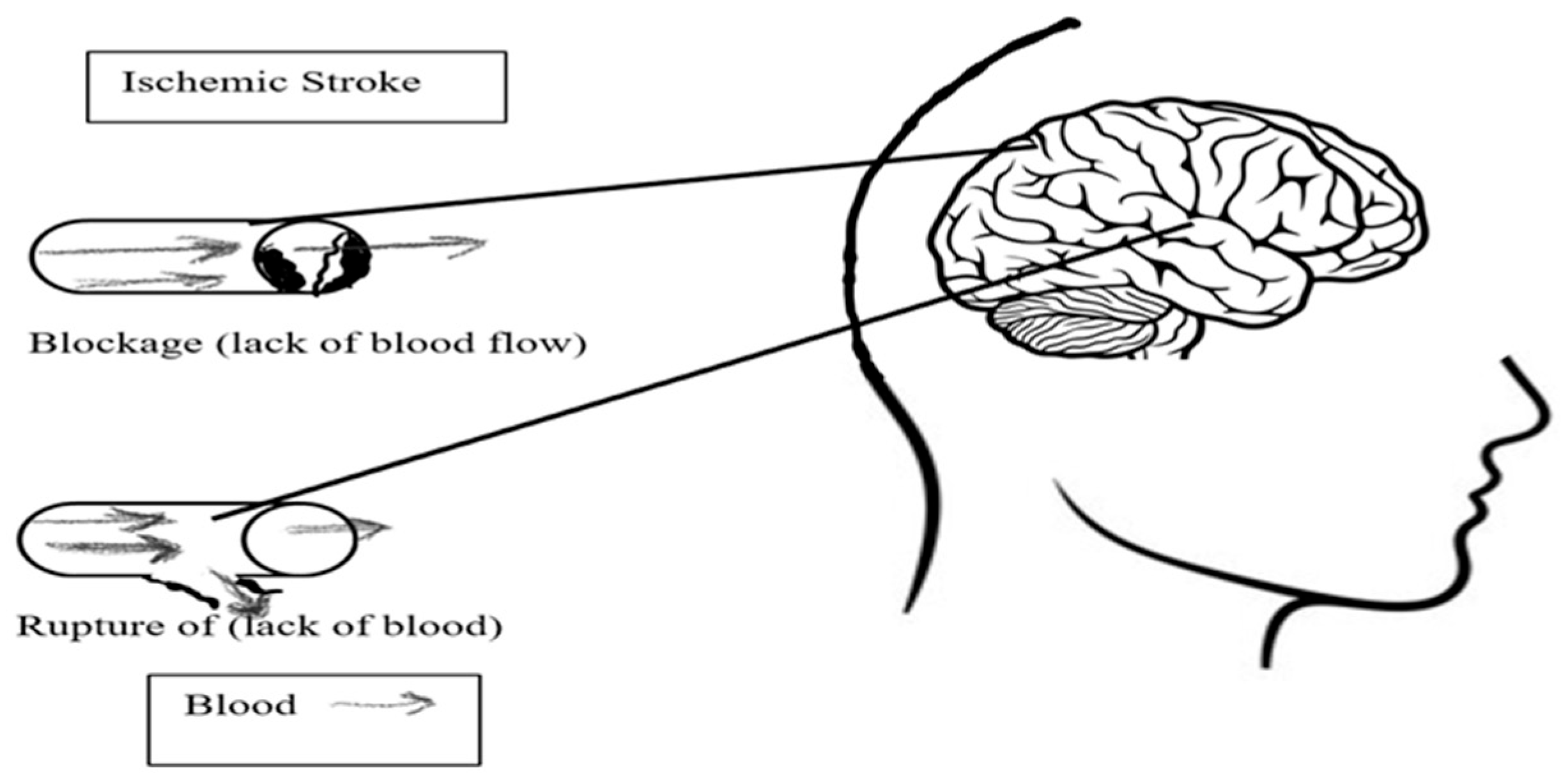
Cerebrovascular Disease

This disease impacts the brain’s blood arteries and brain’s blood supply. The relevant factors consist of strokes and blood clots. Symptoms can manifest sudden hemiplegia, or hemiparesis; difficulty speaking; and severe headaches. It is imperative that anyone exhibiting symptoms of one of these gets immediate medical assistance [9].

Figure 2 highlights the two main stroke types: ischemic, where a blockage obstructs blood flow to the brain, and hemorrhagic, where a ruptured vessel leaks blood into the brain tissue. Accurately distinguishing stroke types is essential for timely diagnosis and intervention, which reduces brain damage and improves patient outcomes [10].

3.

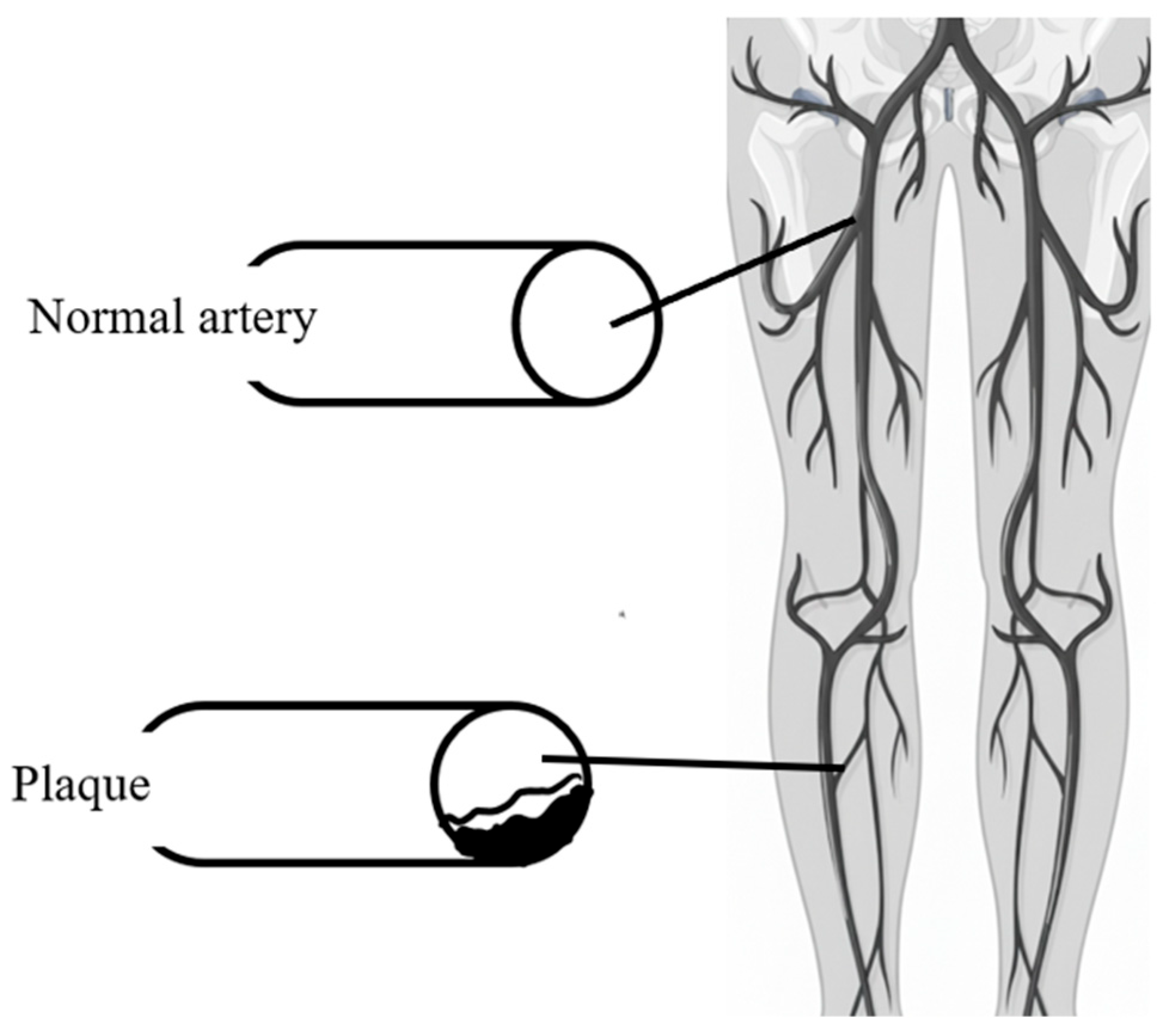
Peripheral Artery Disease (PAD)

When blood flow is restricted to the legs and arms and affects the blood vessels in the arms and legs, peripheral artery disease rises. This causes pain during physical activities, numbness, and weakness in the limbs; hair loss in the weak areas of the legs or arms is also a strong symptom [11].

Figure 3 demonstrates a comparison between a normal artery and an atherosclerotic artery within the lower limbs. The normal artery features a smooth, unobstructed lumen that allows adequate blood flow to the surrounding tissues. In contrast, the atherosclerotic artery shows significant plaque buildup along the arterial wall, which narrows the lumen and restricts blood flow [11].

4.

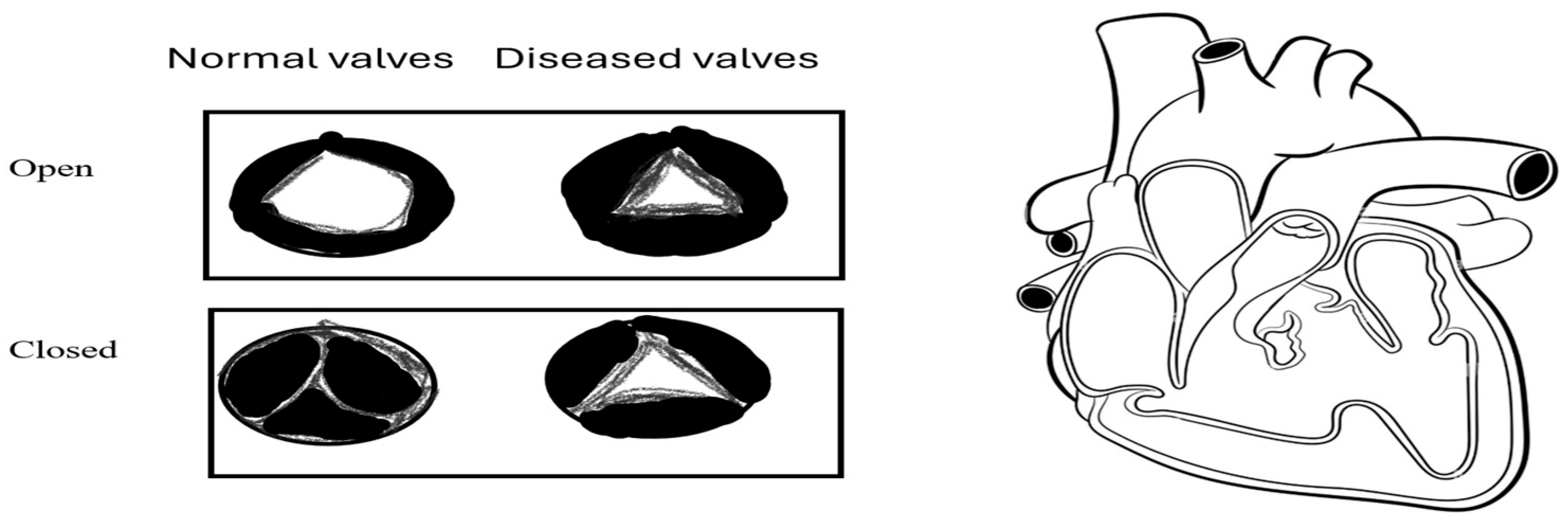
Rheumatic Heart Disease (RHD)

Rheumatic Heart Disease results from heart and valve damage caused by a past streptococcal infection (rheumatic fever). It manifests through severe symptoms like breathlessness and swelling in the limbs or abdomen, illustrating how an infection can trigger permanent cardiac failure [12,13].

Figure 4 visually represents how Rheumatic Heart Disease (RHD) causes structural damage to heart valves, impairing the heart’s ability to pump blood effectively due to changes in the structure of the valves.

5.

Congenital Heart Disease (CHD)

Congenital heart disease (CHD) is heart defects present at birth. CHD is the most prevalent form of significant congenital malformations, impacting around 1% of live births globally. CHDs disrupt blood flow in the heart and can lead to complications like heart failure, stroke, and sudden death. Although often fatal in the past, advancements in medical care have significantly improved survival rates [14,15].

6.

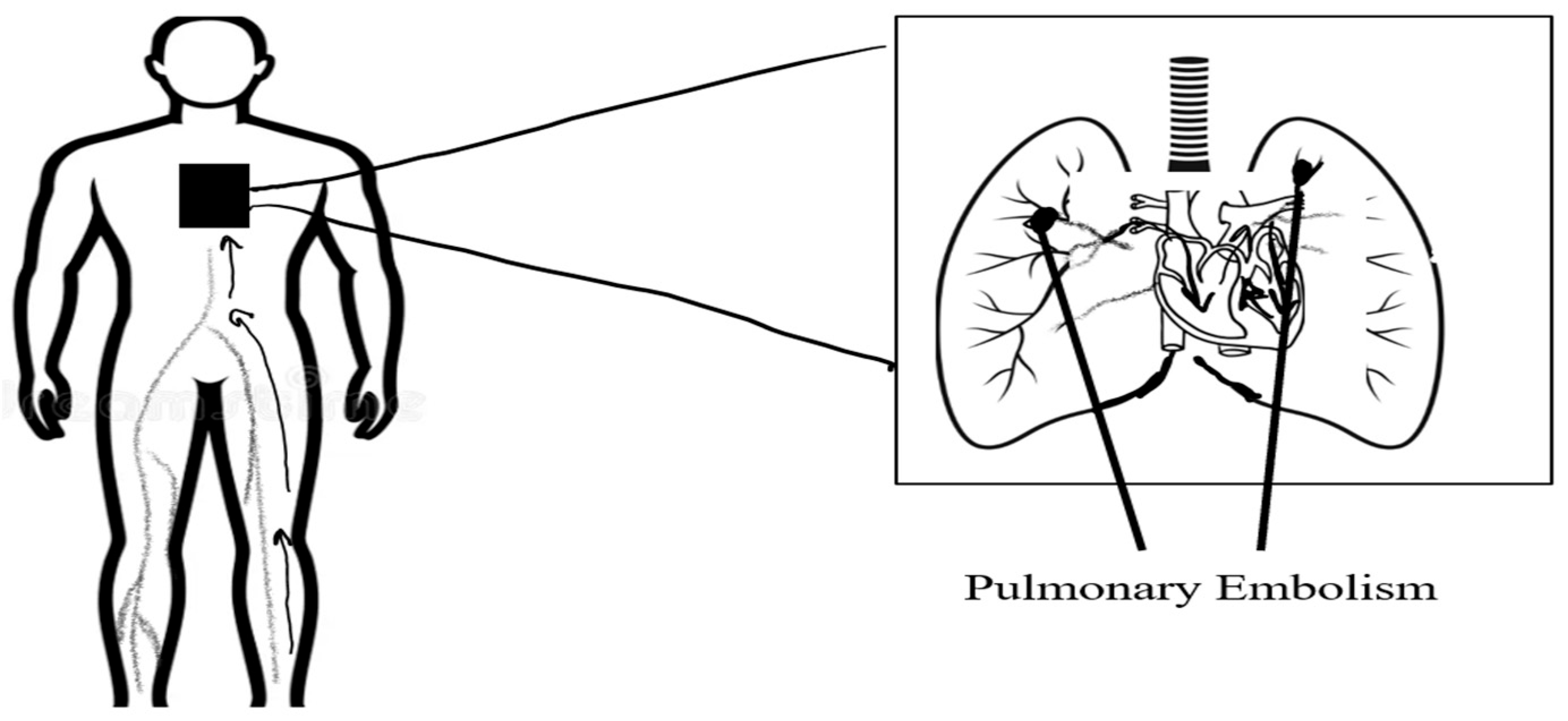
Pulmonary Embolism (PE)

Pulmonary embolism (PE) is a serious condition in which a blood clot obstructs a major lung artery, often originating from deep vein thrombosis (DVT) in the lower extremities. PE is a major cause of illness and death, impacting 39 to 115 individuals per 100,000 annually [16]. Globally, it is the third leading cause of death from cardiovascular disease after coronary artery disease and stroke [17].

Figure 5 shows how PE affects blood circulation. Normally, blood flows from the right side of the heart to the lungs for oxygenation, then returns to the left side to supply the body. PE occurs when a blood clot obstructs this flow, potentially leading to serious and life-threatening complications, with the severity depending on the clot’s size and the number of affected vessels [18].

Pulmonary embolism (PE) leads to sudden shortness of breath, chest pain, and coughing up blood, requiring immediate treatment. Blockages that affect blood flow to the heart or brain can cause heart attacks and strokes, with fatty deposits in arteries a common cause [18,19].

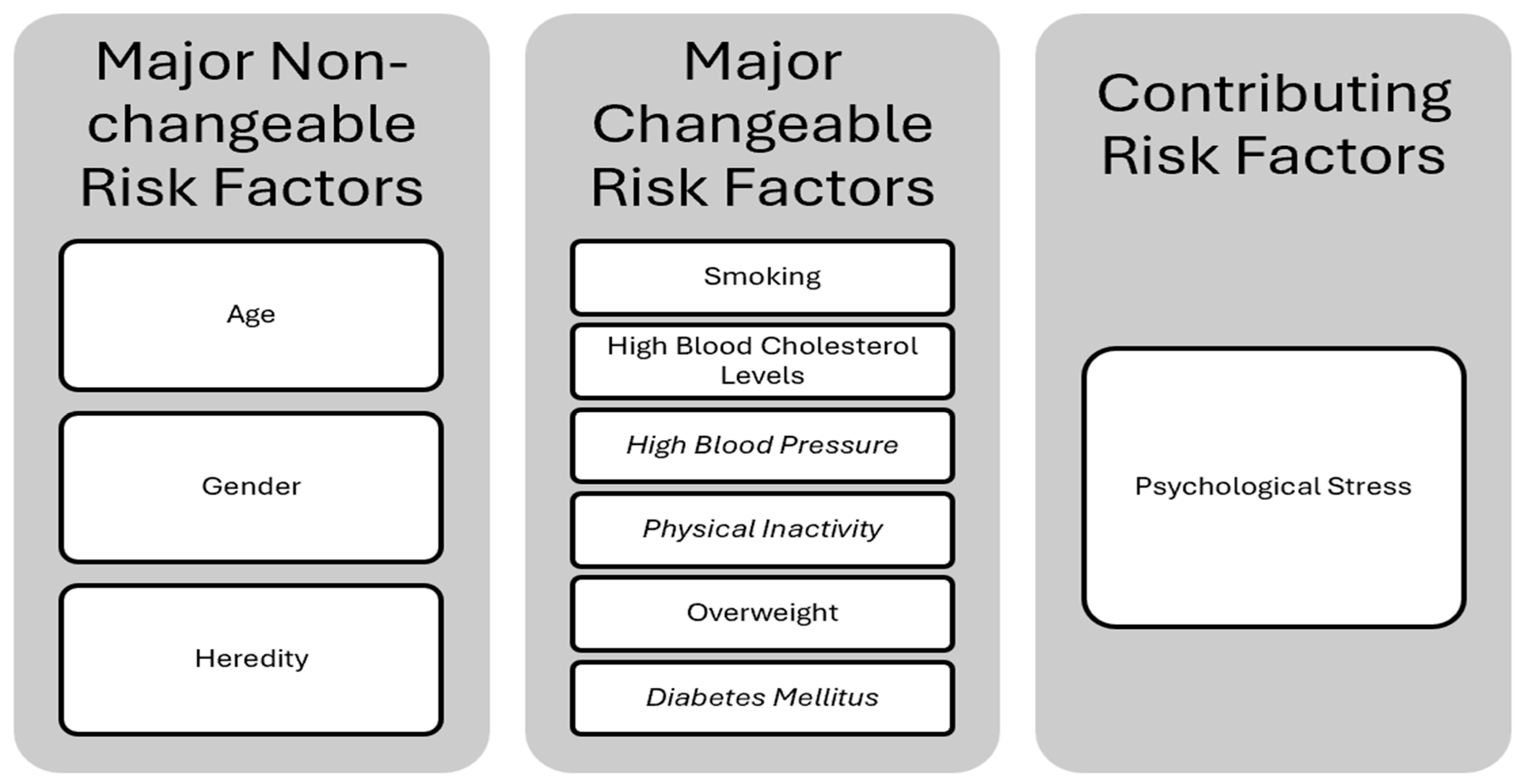
2.2. CVD Risk Factors

We can categorize the risks into three groups, major non-changeable risk factors, major changeable risk factors, and contributing risk factors, as follows:

2.2.1. Major Non-Changeable Risk Factors

Age

Cardiovascular diseases become significantly more frequent with advanced age. Notably, over 80% of deaths from coronary disease occur in people older than 65 years old.

Gender

Female hormones offer a cardiovascular protective effect, keeping clinical coronary disease rare in premenopausal women. While risk increases after menopause, these cardiovascular death rates remain lower than men’s.

Heredity (Family History and Race)

Heredity dictates cardiovascular risk through early-onset heart disease in close family members and significant racial disparities. Individuals of South Asian or African descent face higher risks that persist regardless of lifestyle or environmental factors.

Fixed factors such as age, gender, and heredity determine baseline cardiovascular risk. Since these cannot be changed, it is essential to manage modifiable lifestyle factors aggressively to reduce overall risk [19].

2.2.2. Major Changeable Risk Factors

Smoking

Smoking significantly increases cardiovascular risk and can double or triple cardiac mortality due to the harmful effects of nicotine, carbon monoxide, and tar. It contributes to heart disease by causing vascular spasms, reducing protective HDL cholesterol, and promoting blood clot formation [19].

High Blood Cholesterol Levels (Hypercholesterolemia)

Cholesterol is an essential structural component produced by the liver. Its effect on health depends on whether it is carried by Low-Density Lipoproteins (LDLs), which increase risk, or High-Density Lipoproteins (HDLs), which are protective. Managing these levels through primary and secondary prevention is crucial to reducing the risk of coronary disease and heart attacks [19].

High Blood Pressure (Arterial Hypertension)

Hypertension is a major cardiovascular risk factor that accelerates atherosclerosis and leads to heart muscle hypertrophy, increasing the risk of heart failure and multi-organ damage. Effective blood pressure management is essential for prevention and can lower the risk of stroke by 40% and coronary disease by 25% [19].

Physical Inactivity

Physical inactivity is a major health risk, contributing to cardiovascular disease and conditions like diabetes. Engaging in regular physical activity is highly protective. It reduces cardiovascular mortality by up to 35% by normalizing blood pressure and improving sugar levels [19].

Overweight (Obesity)

Obesity is a complex public health crisis, driven by genetics and lifestyle, that directly strains the heart and triggers chronic inflammation and vascular damage. It often acts as a “risk multiplier” by causing hypertension and diabetes, significantly elevating the likelihood of stroke and heart failure [19].

Diabetes Mellitus

Diabetes mellitus is a serious metabolic disorder that can increase cardiovascular mortality by up to five times and cause silent heart attacks due to nerve damage. Early screening after age 40 is important, as diabetes worsens other risk factors, such as hypertension, and greatly increases the risk of stroke and heart disease [19].

2.2.3. Contributing Risk Factors

Psychological Stress

Psychological stress, acute or chronic, is a major cardiovascular risk factor that can trigger heart attacks and strokes and accelerate damage from other risks. It harms heart health through emotional outbursts, job strain, and depression, making mental well-being essential for heart disease prevention [19,20]. Figure 6 below divides risk factors for cardiovascular disease (CVD) into three categories. Major non-changeable risk factors are inherent and cannot be modified. Conversely, major changeable risk factors represent behaviors or conditions that can be managed or altered to significantly reduce risk, alongside other contributing risk factors like psychological stress.

Heart disease remains a critical global health concern. Traditional diagnostic reliance on patient history, physical examination, and symptoms often suffers from inaccuracy and high resource demands. Machine learning (ML) offers a promising solution to this challenge. By efficiently applying algorithms to clinical datasets, ML enables the automated extraction of meaningful insights, significantly improving the prediction and diagnostic accuracy of heart disease [21].

While current ML algorithms significantly improve efficiency and insight extraction from clinical datasets, the sheer scale and complexity of advanced medical analysis may eventually exceed classical computing limits. To tackle the most computationally demanding challenges in personalized medicine, researchers are now exploring the potential of quantum computing [22].

3. Quantum Computing (QC)

Quantum computing (QC) is a transformative field that arises from the intersection of quantum mechanics, physics, and mathematics with computer science. It enables the solution of complex problems at speeds beyond the reach of classical computers, marking a fundamental paradigm shift in computational methods. This innovative approach has attracted significant attention for its potential to revolutionize the handling of computationally intensive challenges [23,24].

The quantum computing market is witnessing significant growth and investment. After being valued at USD 10.13 billion in 2022, it is projected to reach approximately USD 125 billion by 2030. This remarkable expansion is driven by the rising demand for high-performance computing and technology’s diverse applications across various industries, including petroleum, financial services, and aviation [25].

This section aims to introduce principles of quantum computing.

3.1. Principles of Quantum Computing

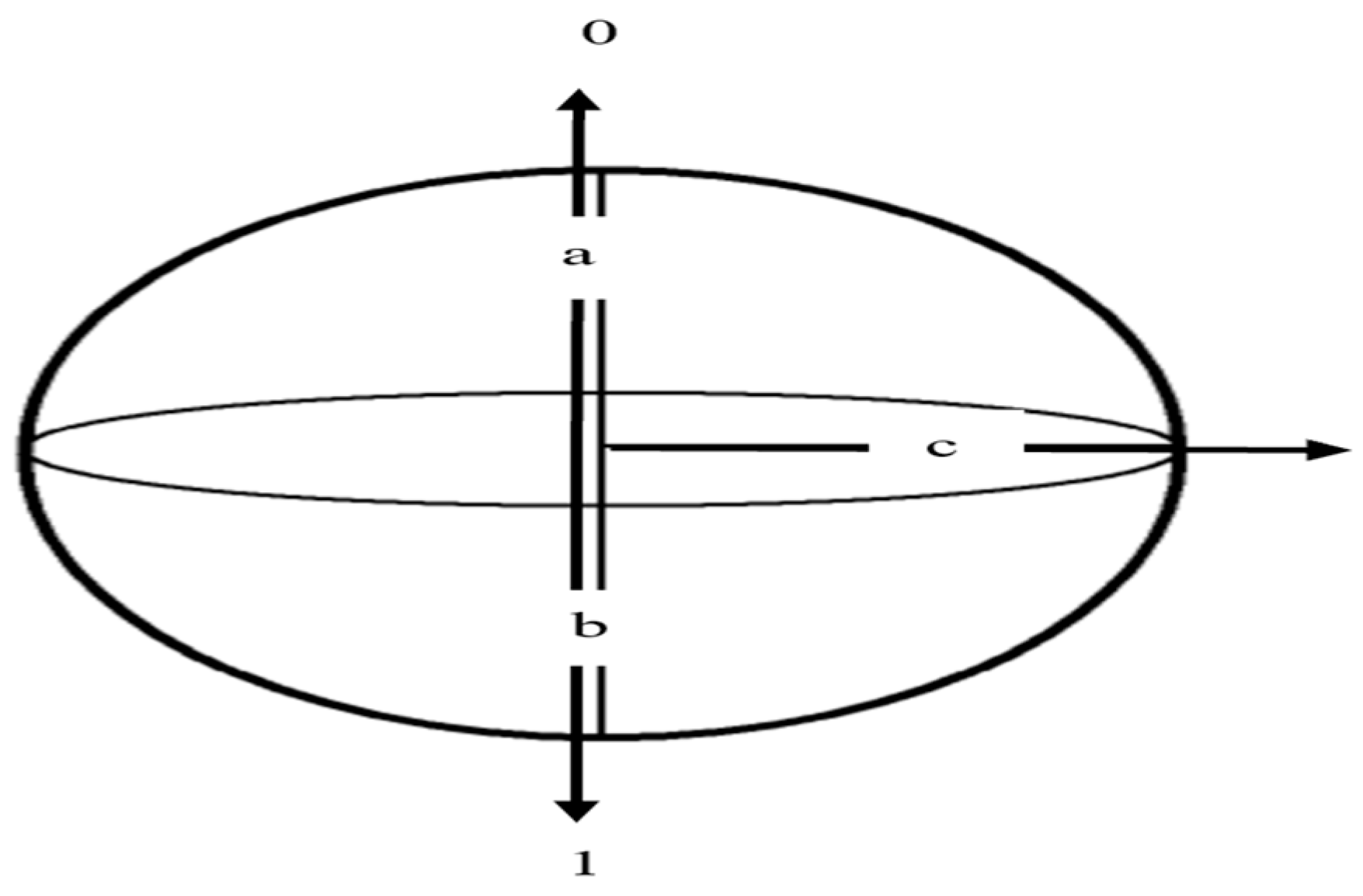
3.1.1. Qubits and Quantum States

While the fundamental unit of information in classical computing is the bit, which functions as a binary element restricted to representing a single value at any given time, 0 or 1, the quantum bit (qubit) utilizes superposition by existing in either of 0,1 or an intermediate state, represented as a linear combination of the 0 and 1 states as follows:

$$|\psi ⟩=\alpha \mid 0⟩+\beta \mid 1⟩$$

(1)

where $|\psi ⟩$ is the quantum state of the qubit and $\alpha$ and $\beta$ are complex coefficients (amplitudes) that describe the probability amplitudes of the states $\mid 0⟩$ and $\mid 1⟩$, respectively. These coefficients satisfy the normalization condition of Equation (2):

$${\mid \alpha \mid }^2+{\mid \beta \mid }^2=1$$

(2)

The qubit’s state, as formulated by Equation (1), is a unit vector within a two-dimensional complex vector space known as Hilbert space.

Figure 7 shows the Bloch sphere, a standard visualization tool in quantum computing, to illustrate the possible states of a single qubit. The poles represent the classical basis states: $\mid 0⟩$at the North Pole (a) and $\mid 1⟩$ at the South Pole (b). A qubit can exist in a superposition of these states, represented by any point on the surface of the sphere, such as the example shown in (c) [23,24,26].

3.1.2. Superposition

This is a unique quantum property that allows a qubit to exist in multiple states simultaneously. It enables quantum computers to handle multiple data states at once, existing in a linear combination of all possible states simultaneously, and a single system of N qubits can effectively represent $2^N$ classical states. This capability allows for parallel processing, significantly enhancing computational power, and allows quantum computers to solve complex problems far more efficiently than classical ones. This advantage is particularly significant for optimization, cryptography and the accurate simulation of other complex quantum systems in chemistry and materials science [23,24,26].

3.1.3. Entanglement

Entanglement means the ability of the quantum state of one qubit to become inseparably linked to the state of another, irrespective of the physical distance separating them. This correlation ensures that measuring the state of one qubit instantly determines the state of its entangled partner.

Unlike in a classical computer, where increasing the bits will increase the complexity of the computing power, in quantum computing, entanglement properties change this behavior. Therefore, more qubits can cause its computing power to be exponentially fast. This can be done by expressing the states as a sum, or superposition, of products of states. Quantum models leverage those relationships to find solutions to complex problems. Entanglement allows quantum systems to store and process complex data correlations, enabling powerful computational strategies that are physically impossible in classical [24,27].

3.1.4. Quantum Gates

Analogous to how classical logic gates manipulate bits, quantum gates serve as the fundamental operators used to manipulate qubits. Quantum gates apply unitary transformations to the qubit state vector within Hilbert space. These linear operations precisely modify the amplitude (absolute values of $\mathsf{\alpha }$ and $\mathsf{\beta }$, which control the measurement outcome probabilities). Also, they affect the phase (angles on $\mathsf{\alpha }$ and $\mathsf{\beta }$, which affect how qubits interact with each other) while guaranteeing the preservation of quantum information.

Quantum logic gates must satisfy the condition of unitarity. A unitary matrix satisfies the condition of Equation (3):

$$U^{†}U=U{U}^{†}=I$$

(3)

where $U$ is the gate matrix, $U^{†}$ is the conjugate transpose of $U$, and $I$ is the identity matrix. This is needed to ensure that the gate transformation:

• Preserves the inner product as a guarantee that the total probability of all possible outcomes remains normalized to one;
• Is reversible, since every unitary operation has an inverse equal to its conjugate transpose;
• Is represented by a unitary matrix allowing for precise mathematical characterization and physical implementation.

Common examples of quantum gates include the Hadamard gate (H), which maps a computational basis state to an equal superposition of |0> and |1> [27,28].

Quantum gates are building blocks for quantum circuits, manipulating qubits to perform calculations. These gates facilitate operations that take advantage of the unique properties of quantum states.

3.1.5. Measurement

Qubits exist in multiple states simultaneously: not just the classical 0 and 1, but any linear combination of both. Until the qubit is measured, it remains in this intermediate state.

Upon measurement, the qubit probabilistically collapses to one of the basis states; the probability of measuring $\mid 0⟩$ is ${\alpha }^2$, and the probability of measuring $\mid 1⟩$ is ${\beta }^2$ [24,26].

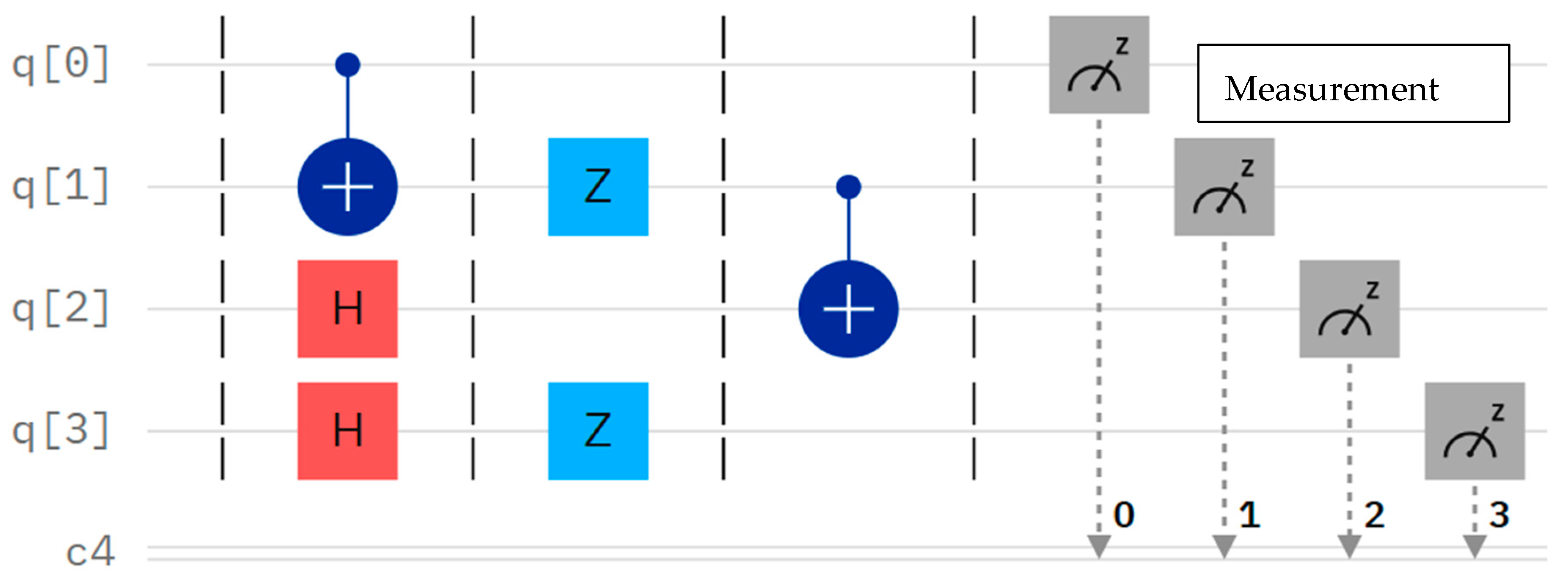
3.1.6. Quantum Circuits

The quantum circuit model serves as the foundational framework for quantum computation, consisting of a systematic arrangement of three primary components. First, qubits function as the basic units of information, capable of existing in a superposition of basis states. Second, quantum gates are unitary operations that manipulate these qubits; these gates can act on single qubits or facilitate the entanglement of multiple qubits. Finally, measurement operations are typically applied at the conclusion of the circuit to extract classical information, collapsing the quantum state into one of the basis states. This computational flow is usually represented diagrammatically, utilizing horizontal lines to indicate qubits and boxes or symbols to denote the sequence of gates applied from left to right, providing a visual and intuitive way to track the transformation of quantum information, as in Figure 8:

Figure 8 illustrates the architecture of a quantum circuit that manipulates four qubits. The circuit employs various single-qubit gates, including the Hadamard gates (H) and flip gates (z), alongside the two-qubit CNOT Gate (), which is crucial for inducing entanglement. Finally, a measurement operation is performed on the first qubit (q0), collapsing its quantum state to extract the classical information [24,26].

3.2. Quantum Neural Networks (QNNs)

A Quantum Neural Network (QNN) is a type of machine learning model that uses quantum principles such as entanglement and superposition to perform computations. It uses parametrized quantum circuits that encode classical data into quantum states, process it with trainable quantum gates, and extract classical information by measurement.

It has the potential to outperform classical neural networks. Various models for designing and implementing a Quantum Neural Network have been introduced. Most research in the field of Quantum Neural Networks has focused on translating classical neural network components into quantum components. This is not always possible due to the absence of quantum equivalents for certain classical components, such as non-linear activation functions. The definition of a QNN is not a unified conclusion in academic circles [29,30,31].

3.3. Challenges in QC

Initial efforts in quantum computing development were met with unexpected complexity, resulting in a phase of disappointment. While developers have aimed to create machines with ultimate capacities of millions of qubits, initial experiments involving only a few qubits have exposed unforeseen noise challenges. Enhancing the reliability of quantum computing is essential while current quantum computers work in Noisy Intermediate-Scale Quantum (NISQ) and suffer from the following issues:

3.3.1. Quantum Decoherence and Noise

The paramount obstacle is the environmental sensitivity of the qubit. Its susceptibility to noise, temperature, and magnetic fields leads directly to decoherence, reflecting significant loss of information and resulting computational errors. Managing these effects requires physical isolation and error-correction techniques, which are inherently challenging to implement [24,32].

3.3.2. Quantum Error Correction

Qubits are vulnerable to complex errors such as phase flips, in contrast to the discrete bit-flips encountered in classical systems. Moreover, the quantum properties of superposition and entanglement make error correction especially challenging.

Current research focuses on developing fault-tolerant quantum processors and advanced error-correction algorithms. These efforts ultimately aim to achieve reliable quantum processors with tens of thousands of qubits: a significant milestone that has not yet been reached [33,34].

3.3.3. Hardware Scalability

As the number of qubits increases, the difficulty of controlling them grows exponentially. Research findings indicate that running Quantum Neural Networks (QNNs) on current quantum hardware leads to significant performance degradation. This limitation, coupled with persistent scalability challenges, has restricted the applicability of QNNs to large datasets and complex real-world problems [35,36].

The field of quantum computing has made notable progress, shifting from theoretical concepts to real-world applications. Recent advances in processing power and computational accuracy are laying the foundation for future breakthroughs in large-scale quantum computing [33].

4. State of the Art

The heart serves as the body’s primary pump, and its proper operation is essential for general health. When it malfunctions, it can result in severe issues throughout the body. Recently, machine learning has emerged as a transformative tool in cardiology, significantly enhancing the prediction and diagnosis of heart conditions. By analyzing vast amounts of patient data, these algorithms can identify subtle patterns that traditional methods often overlook. This facilitates earlier detection of diseases and enables the development of more customized treatment approaches [37].

This section presents a comparative analysis of established classical machine learning techniques and emerging Quantum Neural Networks (QNNs) regarding their performance in heart risk prediction that utilized heart disease from the UCI database [38].

Classical machine learning (ML) techniques, which include algorithms like Support Vector Machines (SVMs), Random Forests (RF), and Logistic Regression (LR), have long formed the foundation of predictive models in clinical medicine. The performance of these models with the UCI Heart Disease Dataset is serving as a widely adopted standard benchmark for this research. The following studies highlight the latest findings on the performance of these classical machine learning approaches for heart disease prediction.

Harshit Jindal et al. [39] (2020) applied three machine learning algorithms, Logistic Regression, K-Nearest Neighbor (KNN), and Random Forest, to predict heart disease using the UCI dataset. While KNN achieved the highest individual accuracy, of 88.52%, the combined use of all three algorithms resulted in an overall accuracy of 87.5%, which enhanced the performance of Logistic Regression and Random Forest compared with when used individually. That study demonstrated that integrating multiple algorithms can improve the robustness and reliability of heart disease prediction models.

Karna Vishnu Vardhana Reddy et al. [40] (2021) examined the performance of various machine learning classifiers using the optimal attribute set identified through the Correlation-based Feature Selection (CFS) technique for heart disease risk prediction. The authors evaluated sets of classifiers, with the main four classifiers being Naive Bayes, Logistic Regression, Sequential Minimal Optimization (SMO), and K-Nearest Neighbors (KNNs), to assess the impact of feature optimization on predictive performance. The results revealed that the Naive Bayes classifier achieved the highest overall accuracy, of 84.15%, with a sensitivity of 84.2%, precision of 84.3%, and an F1-Score of 84.1%, demonstrating strong and balanced classification capability. Logistic Regression and SMO also produced competitive results, attaining accuracy of 83.17% and 83.83%, respectively, while KNNs recorded a relatively lower accuracy of 78.87%.

Bharti et al. [41] (2021) developed a framework for heart disease detection using a combination of classical machine learning and Deep Learning techniques. Their study utilized the UCI Cleveland Heart Disease Dataset and evaluated multiple classical models, including Random Forest, Logistic Regression, Naive Bayes, and Support Vector Machine (SVM), alongside Deep Learning approaches. Among the classical models, the Random Forest classifier achieved the highest accuracy, of approximately 88%, while the remaining models produced slightly lower accuracy values. The Deep Learning component was evaluated using three different configurations, achieving accuracies of 76.7%, 81.9%, and 94.2%, respectively.

A study by Ed-Daoudy et al. [42] (2023) analyzed six machine learning classifiers (Naive Bayes, Support Vector Machine, Multi-Layer Perceptron, Decision Tree, Logistic Regression, and Random Forest) using the UCI heart disease database. The dataset was randomly split with a seed, using 70% of the data for training and 30% for testing. The results established Random Forest as the top-performing model, achieving the highest F1-Score, of 87.64%, and accuracy, of 87.50%. Logistic Regression followed closely with excellent performance consistency, with an F1-Score of 86.96% and identical precision and sensitivity values of 86.96%. For minimizing false alarms, both the Naive Bayes and Decision Tree models offered the most reliable positive predictions, registering the highest precision at 89.13%. Conversely, the Multi-Layer Perceptron model lagged, showing the lowest performance across the board, with an F1-Score of only 80.90%.

Khadijah Alfadli, et al. (2023) [43] conducted a comprehensive comparative study on classical and modern machine learning (ML) algorithms for heart disease prediction using the UCI Heart Disease Dataset. That study categorized ML techniques into two main groups: classical models, such as K-Nearest Neighbor (KNN), Support Vector Machine (SVM), Naive Bayes (NB), Logistic Regression (LR), Gaussian Process (GP), Decision Tree (DT), and Random Forest (RF), and modern Deep Learning models, including Artificial Neural Networks (ANNs) such as the Multi-Layer Perceptron (MLP) and Recurrent Neural Network (RNN). The researchers also utilized the five best-performing ML models to create an Ensemble Model. Their experiments demonstrated that both categories performed effectively, with the SVM and hybrid Ensemble Models achieving the highest accuracy, of 83.15%, followed closely by MLP (82.61%), RNN (80.98%), GP (80.43%), and LR (80.43%). In terms of recall and precision, SVM achieved 87.25% and 83.18%, respectively, while the Ensemble Model obtained a balanced performance with 86% recall, 83.97% precision, and an F1-Score of 84.95%. That study concluded that while individual classifiers like SVM and MLP exhibit strong predictive ability, combining multiple high-performing models into an ensemble framework results in superior overall performance and robustness. This approach supports the principle that ensemble methods leverage the complementary strengths of different algorithms to achieve higher accuracy and better generalization in cardiovascular disease prediction.

Ram Kumar et al. [44] (2024) have presented a recent comparison: “Investigations on Cardiovascular Diseases and Predicting Using Machine Learning Algorithms”. It demonstrates the performance of different machine learning models (KNN, SVM, ANN, and CNN)—applied to the Cleveland Heart Disease Dataset. The Convolutional Neural Network (CNN) achieved the best overall performance, with an accuracy of 83.61% and a high F1-Score of 85.2%, indicating a strong balance between precision and recall. While the KNN model achieved relatively high recall (91.7%), its lower accuracy (66.7%) reflects limitations in overall predictive reliability. Similarly, SVM and ANN showed moderate results, with accuracies of 74.2% and 70.08%, respectively. These findings highlight that Deep Learning architectures such as CNNs are more effective in capturing complex, non-linear relationships within medical datasets, thereby offering improved precision and robustness for automated cardiovascular disease prediction.

Nurliana Nasution et al. (2025) [45] evaluated the performance of four machine learning algorithms—Logistic Regression, Random Forest, Support Vector Machine (SVM), and K-Nearest Neighbors (KNNs)—using the UCI Heart Disease dataset to identify effective models for heart disease prediction. That study assessed these algorithms both with and without feature selection techniques, specifically Chi-Square and Mutual Information. Without feature selection, Random Forest achieved the highest accuracy, of 89.7%, followed by SVM with 87.0%, KNNs with 84.8%, and Logistic Regression with 84.2%. The authors found that feature selection did not significantly improve model performance, as the dataset’s original features were already highly relevant to heart disease prediction.

Table 1. Comparative performance of classical machine learning models in cardiovascular disease prediction.

Ref.	Study	Model	Accuracy	Sensitivity (Recall)	Precision	F1-Score
[39]	Heart Disease Prediction Using Machine Learning Algorithms	Logistic Regression, K-Nearest Neighbors and Random Forest Classifiers	87.5%	NA	NA	NA
[39]	Heart Disease Prediction Using Machine Learning Algorithms	K-Nearest Neighbors (KNNs)	88.52%	NA	NA	NA
[40]	Heart Disease Risk Prediction Using Machine Learning Classifiers with Attribute Evaluators	Naive Bayes	84.15%	84.2%	84.3%	84.1%
[40]	Heart Disease Risk Prediction Using Machine Learning Classifiers with Attribute Evaluators	Logistic Regression	83.17%	83.2%	83.2%	83.1%
[40]	Heart Disease Risk Prediction Using Machine Learning Classifiers with Attribute Evaluators	Sequential Minimal Optimization	83.83%	83.8%	83. %	83.8%
[40]	Heart Disease Risk Prediction Using Machine Learning Classifiers with Attribute Evaluators	K-Nearest Neighbors (KNNs)	78.87%	78.9%	78.9%	78.8%
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	Logistic Regression	83.3%	86.3%	NA	NA
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	K-Nearest Neighbors	84.8%	85%	NA	NA
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	Support Vector Machine (SVM)	83.2%	78.2%	NA	NA
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	Random Forest	80.3%	78.2%	NA	NA
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	Decision Tree	82.3%	78.5%	NA	NA
[41]	Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning	Deep Learning (Feature Selection and Outlier Detection)	94.2%	82.3%	NA	NA
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Naive Bayes	84.09%	82.00%	89.13%	85.42%
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Support Vector Machine (SVM)	85.23%	83.33%	88.89%	86.02%
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Multi-Layer Perceptron	80.68%	83.72%	78.26%	80.90%
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Decision Tree	82.95%	80.39%	89.13%	84.54%
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Logistic Regression	86.36%	86.96%	86.96%	86.96%
[42]	A Scalable and Real-Time System for Disease Prediction Using Big Data Processing	Random Forest	87.50%	86.67%	88.64%	87.64%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	Support Vector Machine (SVM)	83.15%	87.25%	83.18%	85.17%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	ANN: Multi-Layer Perceptron (MLP)	82.61%	85.29%	83.65%	84.47%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	ANN: Recurrent Neural Network (RNN)	80.98%	82.35%	83.17%	82.76%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	Gaussian Process (GP)	80.43%	85.29%	80.56%	82.86%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	Logistic Regression: LR	80.43%	83.33%	81.73%	82.52%
[43]	Feature-Limited Prediction on the UCI Heart Disease Dataset	Hybrid: Ensemble Model	83.15%	86%	83.97%	84.95%
[44]	Investigations on Cardiovascular Diseases and Predicting Using Machine Learning Algorithms	K-Nearest Neighbor (KNN)	66.7%	91.7%	88.8%	90.2%
[44]	Investigations on Cardiovascular Diseases and Predicting Using Machine Learning Algorithms	Support Vector Machine (SVM, Linear Kernel)	74.2%	85%	74%	79.1%
[44]	Investigations on Cardiovascular Diseases and Predicting Using Machine Learning Algorithms	Artificial Neural Network (ANN)	70%	84.2%	77.0%	80.4%
[44]	Investigations on Cardiovascular Diseases and Predicting Using Machine Learning Algorithms	Convolutional Neural Network (CNN)	83.61%	97%	76%	85.2%
[45]	Predicting Heart Disease Using Machine Learning: An Evaluation of Logistic Regression, Random Forest, SVM, and KNN Models on the UCI Heart Disease Dataset	Random Forest (RF)	89.7%	NA	NA	NA
[45]	Predicting Heart Disease Using Machine Learning: An Evaluation of Logistic Regression, Random Forest, SVM, and KNN Models on the UCI Heart Disease Dataset	Support Vector Machine (SVM)	87.0%	NA	NA	NA
[45]	Predicting Heart Disease Using Machine Learning: An Evaluation of Logistic Regression, Random Forest, SVM, and KNN Models on the UCI Heart Disease Dataset	Logistic Regression (LR)	84.2%	NA	NA	NA

summarizes the performance of these studies.

In Table 1, the comparative analyses confirm that classical machine learning (ML) techniques exhibit strong and reliable performance in heart risk prediction, particularly when validated against benchmark datasets such as the UCI Heart Disease Dataset. These models can achieve high accuracy, making them effective tools for current clinical decision support. However, as medical data becomes increasingly vast, complex, and high-dimensional, the need for techniques capable of efficiently handling such a scale becomes evident. This trend motivates the exploration of novel computational paradigms, such as Quantum Neural Networks (QNNs), that offer the potential for exponential computational power to uncover deeper predictive insights from the rapidly expanding landscape of healthcare data.

Quantum computing, unlike classical computing, is a comparatively new development. It first surfaced in science fiction in the late 1970s. Richard Feynman is recognized as the originator of the idea of a quantum computer in 1981. He put forth the argument that quantum computers may effectively model quantum processes, consequently avoiding the exponential resource needs of classical computers [24].

The following section will discuss key research that implements and trains various QNN architectures using the UCI Heart Disease Dataset. These models, including the Hybrid Quantum Neural Network (HQNN) and the Instance Quantum Deep Learning (IQDL) model, were executed and evaluated on quantum simulators.

Hanif Heidari and Gerhard Hellstern (2022) [46] proposed a hybrid quantum classification framework for early heart disease prediction, combining quantum and classical computational paradigms to enhance predictive performance. That study evaluated two models, the Quantum Neural Network and the Random Forest Quantum Neural Network, on the UCI Cleveland and Statlog Heart Disease Datasets. Here, we focus on the performance of the QNN model on the UCI Cleveland dataset. It was tested across different numbers of qubits and layers using 10-fold cross-validation to ensure robustness. The best configuration, consisting of three qubits and three layers, achieved an impressive accuracy of approximately 91.7–96.4%, outperforming other parameter combinations. That study highlights notable improvements in classification accuracy and robustness compared with traditional machine learning methods.

Heidari et al. (2022) [47] applied Hybrid Quantum–Classical Neural Network (HQNN) and Hybrid Quantum Random Forest (HQRF) models on the UCI Cleveland Heart Disease Dataset and also evaluated the models on the Statlog Heart Disease Dataset. In that study, we were interested in the performance of the HQNN on the UCI Cleveland dataset. In comparison with alternative combinations, an HQNN with three layers and three qubits obtained a maximum AUC of 96.43%., demonstrating a significant improvement over classical.

Abdulsalam et al. (2023) [48] compared the performance of various quantum models, including the Quantum Support Vector Classifier (QSVC), Quantum Neural Network (QNN), and Variational Quantum Classifier (VQC), against classical machine learning classifiers such as the Support Vector Machine (SVM) and Artificial Neural Network (ANN). The results indicated that the quantum models outperformed their classical counterparts. In this context, the QNN achieved an accuracy of 86.84%, demonstrating its potential effectiveness in heart disease prediction.

Alsubai et al. (2023) [49] discovered the effectiveness of Quantum Neural Network (QNN) in quantum machine learning (QML) and Quantum Deep Learning (QDL) models for heart failure detection using the UCI Cleveland Heart Disease Dataset. In their study, the QML approach was implemented through a quantum circuit that encoded medical features into a hybrid quantum–classical framework using parameterized rotation and entanglement gates. This model achieved a promising accuracy of 83.6%, showing the potential of quantum model performance. The authors introduced QDL architecture composed of multiple stacked quantum circuit layers. The QDL model significantly outperformed both traditional machine learning techniques and the single-layer QML model, with an accuracy of 98%.

Nouf et al. (2024) [50] conducted a comprehensive analysis of optimization strategies in quantum machine learning (QML) to enhance the predictive efficiency of quantum-based models. Utilizing the Cleveland Heart Disease Dataset in a Quantum Neural Network (QNN), the authors compared three optimizers: COBYLA, L-BFGS-B, and ADAM. The experimental results emphasized the influence of optimizer selection on QML performance, indicating that the COBYLA algorithm achieved superior outcomes, with a predictive accuracy of 92%. Furthermore, COBYLA demonstrated remarkable computational efficiency, requiring only one minute of training compared with six and ten minutes for L-BFGS-B and ADAM, which attained accuracies of 89% and 52%, respectively. These findings highlight the importance of tailored optimization techniques in improving the scalability and robustness of quantum learning frameworks for biomedical prediction tasks.

Darolia et al. (2024) [51] proposed a hybrid approach for cardiovascular disease prediction that integrates Quantum Neural Networks (QNNs) with Long Short-Term Memory (LSTM) networks and compared their results with different classifiers. Here, the focus is on the proposed model and the QNN model. The QNN combined with LSTM is enhanced by a self-improved Aquila optimization algorithm for feature selection. The model achieved an accuracy of 95.54%, outperforming the QNN alone, which achieved 90.7%. These findings indicate that the integration of quantum computing techniques with LSTM networks, along with optimized feature selection, can significantly improve predictive accuracy and reliability compared with traditional machine learning methods, making this approach a promising tool for early and precise cardiovascular disease detection.

Table 2. Comparative performance metrics for quantum and hybrid quantum machine learning models.

Ref.	Study	Model	Accuracy	Sensitivity (Recall)	Precision	F1-Score
[46]	Early Heart Disease Prediction Using Hybrid Quantum Classification	QNN in Quantum Deep Learning (DL) Model	91.7~96.4%	NA	NA	NA
[47]	Heart Disease Detection using Quantum Computing and Partitioned Random Forest Methods	Hybrid Quantum–Classical Neural Network (HQNN)	96.43%	NA	NA	NA
[48]	Explainable Heart Disease Prediction Using Ensemble Quantum Machine Learning Approach	QNN in Quantum Machine Learning (QML)	86.84%	86%	88%	87%
[49]	Heart Failure Detection Using Instance Quantum Circuit Approach and Traditional Predictive Analysis	QNN in Quantum Machine Learning (QML)	84%	84%	83%	84%
[49]	Heart Failure Detection Using Instance Quantum Circuit Approach and Traditional Predictive Analysis	QNN in Quantum Deep Learning (DL) Model	98%	98%	98%	98%
[50]	Optimization Strategies in Quantum Machine Learning: A Performance Analysis	QNN with COBYLA Optimizer	92%	89%	97%	93%
[50]	Optimization Strategies in Quantum Machine Learning: A Performance Analysis	QNN with L-BFGS-B Optimizer	89%	86%	94%	90%
[50]	Optimization Strategies in Quantum Machine Learning: A Performance Analysis	QNN with ADAM Optimizer	52%	53%	97%	68%
[51]	Enhanced Cardiovascular Disease Prediction Through Self-Improved Aquila Optimized Feature Selection in Quantum Neural Network and LSTM Model	Quantum Neural Networks (QNNs)	90.79%	93.28%	92.58%	92.93%
[51]	Enhanced Cardiovascular Disease Prediction Through Self-Improved Aquila Optimized Feature Selection in Quantum Neural Network and LSTM Model	Quantum Neural Networks (QNN) with Long Short-Term Memory (LSTM) Networks	95.5%	95.87%	96%	96.94%

summarizes comparative studies.

The reviewed studies confirm that classical machine learning (ML) techniques have demonstrated consistently strong performance in predicting heart disease using the UCI Cleveland dataset, typically achieving accuracy values ranging between 78% and 89%. Deep learning approaches have shown the capability to extract more complex data representations, with some architectures achieving accuracy of up to 94%. However, recent advancements in Quantum Neural Network (QNN)-based models have revealed promising improvements, with several studies reporting accuracy values exceeding 90% and, in some cases, reaching up to 98%. These findings highlight a growing trend in leveraging quantum-based computation as a complementary alternative to classical learning, especially in complex medical prediction problems. While classical ML remains strong and well-established, quantum-enhanced models demonstrate the potential to offer superior predictive capability and improved generalization, particularly when integrated in hybrid architectures or optimized appropriately for parameter selection.

5. Research Methodology

The comparative review presented here synthesizes findings from twelve academic studies [39,40,41,42,43,44,45,46,47,48,49,50,51] to evaluate the performance of classical and quantum-enhanced machine learning models for heart disease prediction.

5.1. Dataset

The thematic scope was limited to cardiovascular disease (CVD) and heart disease risk prediction, with particular emphasis on studies employing the UCI Heart Disease Dataset, primarily the Cleveland version, establishing it as the standard benchmark [38]. This consistency is crucial, as it allows for a direct, fair comparison of model performance across different computational paradigms, including classical machine learning (ML), Deep Learning (DL), Quantum Neural Networks (QNNs), and hybrid architectures. Studies were systematically selected within the 2020–2025 timeframe to prioritize current research trends while excluding those involving general healthcare or non-cardiac conditions, as well as studies published before 2020. The technical assessment required high-fidelity computational environments, such as quantum simulators like Qiskit and PennyLane, and real quantum hardware. Purely theoretical models without experimental or simulated validation were excluded. Only peer-reviewed journals, conference proceedings, and verified technical preprints (e.g., arXiv) were considered to ensure data quality and academic rigor.

5.2. Classical Machine Learning (ML) Methods

The classical machine learning of this review includes:

Traditional Classifiers: Logistic Regression (LR), K-Nearest Neighbors (KNNs), Support Vector Machines (SVMs), Random Forest (RF), Decision Tree (DT), and Naive Bayes;

Deep Learning (DL) Architectures: Convolutional Neural Networks (CNNs), Artificial Neural Networks (ANNs), Multi-Layer Perceptrons (MLPs), and Recurrent Neural Networks (RNNs);

Ensemble and Feature Engineering: Several studies investigated the impact of combining multiple algorithms (Ensemble Models) and using techniques like Correlation-based Feature Selection (CFS) to optimize the input feature set.

5.3. Quantum Neural Network (QNN) Methods

The emerging quantum segment focuses on Variational Quantum Circuits (VQCs), which function as QNNs, and hybrid architecture:

QNN Models: Quantum Support Vector Classifier (QSVC), Variational Quantum Classifier (VQC), Hybrid Quantum Neural Network (HQNN), Hybrid Random Forest Quantum (HQRF), and QNN on Quantum Deep Learning (QDL);

Quantum Execution: All QNN models discussed were executed and evaluated on quantum simulators, reflecting the current state of NISQ (Noisy Intermediate-Scale Quantum) technology. Utilizing simulation environments enables controlled experimentation on circuit construction, qubit scalability, and parameter optimization without being restricted by the noise and instability of present-day physical quantum hardware [52].

Optimization Analysis: One key study [51] specifically analyzed the role of optimizers (COBYLA, L-BFGS-B, ADAM) on QNN training: a crucial component of the current hybrid quantum–classical paradigm.

5.4. Evaluation Metrics

Model performance across all studies was primarily assessed using standard classification metrics: accuracy, sensitivity (recall), precision, and F1-Score. These metrics are directly derived from the confusion matrix, which summarizes a model’s predictions by categorizing outcomes into four components: true positives (TPs), True Negatives (TNs), False Positives (FPs), and false negatives (FNs). Together, these measures provide a comprehensive understanding of a model’s predictive capability, highlighting both its correctness and its ability to distinguish between classes effectively.

5.4.1. Accuracy

This measures the proportion of total predictions (both positive and negative) that the model classified correctly.

$$Accurasy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(4)

5.4.2. Sensitivity (Recall)

Sensitivity (recall) is known as the true positive rate. It measures the model’s ability to correctly identify actual positive cases. This metric is important in medical diagnosis (such as heart disease prediction), where failing to detect a positive case as a false negative can lead to severe clinical consequences.

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(5)

5.4.3. Precision

This measures the true positive predictions. It reflects how often the model is correct when it predicts a case as positive.

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(6)

5.4.4. F1-Score

This measures both precision and recall, which provide a single score that shows both metrics. It is particularly useful for evaluating models with imbalanced datasets, where high accuracy might be misleading.

$$F1-Score=2 \ast {\displaystyle \frac{Precision\ast Recall}{Precision+Recall}}$$

(7)

In most cases, the highest reported accuracy is used as the primary comparison indicator, since several studies either do not report all performance metrics consistently or do not provide sufficient information to calculate the remaining measures accurately [53,54].

6. Results and Comparative Performance Analysis

This study identified twelve relevant studies that examined the use of benchmarks of classical and quantum-enhanced models for heart disease detection in the UCI dataset, highlighting a trend toward superior predictive capability with emerging quantum methods.

6.1. Performance of Classical Machine Learning Models

Classical ML techniques established a robust baseline, with the highest performance generally achieved by sophisticated Deep Learning and Ensemble Models.

6.1.1. Traditional Classifiers

These demonstrated strong, reliable results, achieving a wide range of performance metrics. Specifically:

• An accuracy range between 66.7% and 89.7% [44,45].
• Sensitivity (recall) ranging from 78.2% up to 97% [41,42,43,44].
• Precision in the range of 74% to 89.13% [42,43,44].
• An F1-Score ranging from 78.2 to 90.2% [40,41,42,43,44].

The following section will discuss the specific performance characteristics of each traditional classifier in detail.

• Random Forest (RF) and Decision Tree (DT)

These classifiers were consistently among the top performers; RF achieved the highest individual accuracy among the traditional models, at 89.7% [45]. It also performed exceptionally in another study, achieving 87.50% accuracy and the high F1-Score for that study, at 87.64% [42], demonstrating excellent balance between precision and recall. In the same study [42], DT achieved an accuracy of 82.95% and a high precision of 89.13%, showing its effectiveness in minimizing false alarms.

• K-Nearest Neighbors (KNNs)

KNNs showed highly variable results, suggesting its performance is highly sensitive to the dataset split or specific feature engineering used.

In [39], KNNs achieved accuracy of 88.5% as its strongest reported performance. In [44], the accuracy dropped significantly, to 66.7%. The same model achieved the highest sensitivity (recall), of 91.7%, and a very high F1-Score of 90.2%. This indicates that the model in this case was highly effective in identifying true positive cases but struggled substantially with correctly classifying negative cases, which explains the lower accuracy. Studies [40,41] reported mid-range KNN performance, with accuracy values of 78.87% and 84.8%, respectively.

These findings collectively demonstrate that the performance of KNNs on heart disease detection is highly dependent on dataset preprocessing, hyperparameter tuning, and feature selection methods.

• Support Vector Machine (SVM)

The SVM demonstrated consistently strong performance across studies. The highest accuracy achieved was 87% in [45]. In [42], the SVM achieved 85.23% accuracy with an F1-Score of 86.02%, indicating good balance across evaluation metrics. The SVM in this study did not overfit toward either detecting too many positive cases with high false alarms nor under-detecting actual positive patients. In [43], the SVM recorded a high sensitivity of 87.25% and an F1-Score of 85.17%. This confirms its effectiveness in correctly identifying positive heart disease cases.

These results imply that the SVM maintains reliable predictive capability, particularly when appropriate kernel functions or optimization strategies are used.

• Logistic Regression (LR)

Logistic Regression showed consistent performance across the reviewed studies, generally achieving accuracy values in the range of 80–84%, as reported in [40,42,45]. In its strongest reported result, LR achieved 86.36% accuracy, with identical precision and sensitivity (recall) values of 86.96%, resulting in a perfectly matched F1-Score of 86.96% [44]. This uniformity across metrics indicates that Logistic Regression was able to classify both positive and negative cases in a well-balanced manner, with minimal trade-off between detecting true positive patients and avoiding false negative outcomes.

• Naive Bayes

Naive Bayes demonstrated consistent results across the reviewed studies with an accuracy of 84% [40,42]. It achieved the highest reported precision, of 89.13%, in a comprehensive comparative study [42], reflecting strong reliability in its positive predictions. NB recorded its strongest balanced performance in a study utilizing Correlation-based Feature Selection (CFS), achieving 84.15% accuracy along with high sensitivity at 84.2%, precision of 84.3%, and an F1-Score of 84.1% [40]. These findings indicate that Naive Bayes performs particularly well when irrelevant or noisy features are reduced, highlighting the algorithm’s sensitivity to optimized feature sets.

6.1.2. Deep Learning

The DL models exhibited variable performances, indicating high sensitivity to architecture and configuration, but ultimately achieved the highest accuracy of the classical group.

• Deep Learning (DL)

The Deep Learning component achieved its highest accuracy, of 94.2%, in study [42]. This result was obtained using the third model version, which incorporated feature selection and outlier detection. The architecture consisted of three dense layers with 128, 64, and 32 units, respectively. The dropout hyperparameters were set to 0.2 in the first stage and 0.1 in the second stage.

• Convolutional Neural Network (CNN)

The Convolutional Neural Network (CNN) in [44] achieved an accuracy of 83.61% and recorded the highest sensitivity (recall) among all models at 97%. Although its precision was lower, at 76%, the resulting F1-Score of 85.2% indicates strong capability in minimizing false negative predictions.

• Artificial Neural Network (ANN)

  ○

  General ANN

The Artificial Neural Network (ANN) showed the lowest performance listed for DL, at 70% accuracy, in [44]. The ANN maintained a competitive recall of 84.2% and an F1-Score of 80.4%. This indicates that although the ANN struggled to correctly classify all samples overall, it was still relatively effective at detecting most positive heart disease cases.

• Multi-Layer Perceptron (MLP) and Recurrent Neural Network (RNN)

These foundational Artificial Neural Network (ANN) models showed stable and balanced results. The MLP achieved an accuracy of 82.61% and a strong F1-Score of 84.47% [44]. The RNN recorded lower performance, with an accuracy of 80.98% and an F1-Score of 82.76% [43]. MLP and RNN Deep Learning architectures provide reliable, mid-range predictive performance.

This comparative review has established a robust performance for heart disease prediction in the UCI dataset using classical machine learning. The most reliable classifiers, Random Forest and Logistic Regression, achieved strong accuracy, while highly specialized models like the Convolutional Neural Network (CNN) achieved high sensitivity. The maximum overall classical accuracy was achieved by sophisticated Deep Learning (DL) configurations.

This analysis confirms the high potential of optimized classical methods, setting a clear, high benchmark that next-generation computational models must surpass to demonstrate a practical advantage in processing complex healthcare data.

6.2. Performance of Quantum Neural Network (QNN) Models

The studies that reviewed QNN architecture executed quantum simulators. This consistently surpasses the peak performance of classical machine learning methods on the UCI Heart Disease Dataset. The results are categorized by the complexity of quantum architecture and different optimization strategies.

6.2.1. Deep Quantum Learning

The most optimistic results were achieved by Quantum Deep Learning (QDL) models, demonstrating the power of quantum circuits.

• QNN in Quantum Deep Learning (DL): This model achieved the highest performance across all reviewed studies, reporting a perfect 98% across accuracy, sensitivity, precision, and F1-Score in [50]. This result is highly significant, as it shows that a multi-layered quantum approach can achieve near-perfect classification, exceeding classical accuracy. Additionally, it showed high promise, with accuracy ranging from 91.7% to 96.4% in early comparative work [46].

6.2.2. Quantum Machine Learning

• Quantum Neural Network

These baseline results demonstrate the competitive performance of single-layer quantum architectures for heart disease prediction. A basic-instance quantum machine learning (QML) model [49] showed robust, balanced metrics, achieving 84% accuracy and an 84% F1-Score. In [48], QNN surpassed this slightly by an accuracy of 86.84%, a strong F1-Score of 87%, sensitivity of 86%, and precision of 88%. It reflected balance and super performance that exceeded the performance of many optimized classical machine learning approaches without requiring complex Deep Learning architectures.

The study in [50] showed the significant effect of the optimizer on the performance of the QNN. The QNN achieved its peak single-layer result of 92% accuracy using the COBYLA optimizer. However, QNN standard optimizers like ADAM resulted in catastrophic failure by only 52% accuracy. This implies that a proper optimization selection is essential for exploiting the QNN’s predictive potential.

6.2.3. Hybridization Techniques

Hybrid QNN models immediately demonstrated high promise, with initial results showing performance ranging from 91.7% to 96.4% accuracy in [46]. More sophisticated integration in [51] provided a maximized predictive reliability. It implemented Quantum Neural Networks (QNNs) with Long Short-Term Memory (LSTM) networks with performance of a 95.5% accuracy and a 96.94% F1-Score. This strongly confirms the benefit of Hybridization Techniques in maximizing predictive reliability.

6.3. Analysis Summary

Evaluations of classical machine learning models in studies [39,40,41,42,43,44,45] have established a baseline for cardiovascular disease (CVD) prediction performance. These models, predominantly assessed using the UCI Heart Disease Dataset, report accuracy rates ranging from 78.87% [40] to 94.2% [45]. Among traditional classifiers, the Random Forest (RF) algorithm consistently demonstrates strong performance, achieving 89.7% accuracy in study [46] and 87.5% in study [42].

Although studies [42,44] used the Multi-Layer Perceptron (MLP) and Convolutional Neural Networks (CNNs) to improve results, performance was still limited by polynomial time and space scaling. As clinical datasets increase in size and complexity, computational overhead grows quadratically or cubically, which restricts real-time diagnostic delivery unless significant hardware parallelization is used.

Analysis of Quantum Neural Network (QNN) models shows a significant potential for quantum advantage in heart disease detection. The multi-layered Quantum Deep Learning (QDL) architecture consistently achieves accuracy that surpasses the classical UCI benchmark. This superior performance, with accuracy rates reaching up to 98%, is facilitated by the preservation of quantum superposition and the utilization of unitary gates in accordance with entanglement principles [49]. Additionally, the selection of appropriate optimizers further enhances performance [50].

The superior performance of Quantum Neural Networks (QNNs) observed in this review, notably in studies [47,49,51], is not merely a numerical improvement but is rooted in the unique representational capacity of quantum mechanics. Unlike classical algorithms such as Support Vector Machines or Random Forests [42,45], which are limited by kernel functions, QNNs utilize Quantum Feature Mapping. This allows clinical data to be projected into an exponentially large Hilbert space, where complex, non-linear correlations between heart disease risk factors become linearly separable.

In terms of computational time efficiency, study [49] demonstrates that quantum-based machine learning (ML) and Deep Learning (DL) approaches enhance system performance by substantially reducing runtime complexity. That study reports a theoretical runtime complexity of O (log n), which facilitates faster processing of complex diagnostic tasks. Study [50] corroborates these results, noting execution times as brief as one minute when employing the COBYLA optimizer. Collectively, these findings indicate that Quantum Neural Networks (QNNs) improve predictive accuracy and deliver the throughput required for real-time clinical integration.

Memory efficiency is critical for the clinical viability of quantum architecture, as it is determined by hardware overhead and the specific constraints of quantum information processing. Study [46] demonstrates that network inputs are qubits, which must adhere to the principles of superposition and quantum entanglement. For an N-dimensional cardiovascular dataset, amplitude encoding requires at least ${log}_2$ N qubits, highlighting the substantial hardware requirements for high-dimensional quantum states. Notably, a single qubit, when combined with robust classical optimization, can address general optimization problems of any dimensionality. This hybrid approach substantially reduces space complexity and mitigates memory limitations by representing complex cardiovascular data with minimal hardware requirements [46].

A significant limitation of the high performance reported in these studies is that the results were obtained solely within simulated quantum environments. These outcomes should be assessed in light of the existing limitations of physical quantum hardware. In contrast to classical processors, which demonstrate high reliability, current Noisy Intermediate-Scale Quantum (NISQ) devices are subject to gate errors and decoherence. These physical phenomena can substantially reduce theoretical accuracy when moving from noise-free simulation to practical hardware implementation [33,34,47].

7. Significance of This Work

While numerous studies have examined machine learning techniques for CVD risk prediction [40,41,44], few have provided a comprehensive comparison between classical and quantum approaches. This manuscript systematically reviews and contrasts these methodologies to clarify the distinct advantages and challenges of Quantum Neural Networks (QNNs), offering actionable insights for researchers and clinicians. Our findings highlight the necessity for further investigation into scalable quantum machine learning, supported by the promising performance metrics observed in current quantum machine learning.

A notable finding of this review is the lack of standardized reporting on computational efficiency across the selected studies. While predictive accuracy is consistently documented, explicit metrics for training time, circuit depth, and execution overhead are often omitted. This gap is significant, as the clinical viability of quantum machine learning depends not only on diagnostic precision but also on the ability to provide timely results in resource-constrained medical environments. Future research must prioritize benchmarking algorithmic latency alongside accuracy to bridge the gap between experimental simulation and practical healthcare deployment.

8. Conclusions

Heart disease is one of the leading causes of death worldwide, highlighting the need for better management methods. Today, machine learning techniques are widely used to study medical data and detect hidden patterns, which can improve the diagnosis and treatment of heart disease. These methods support more accurate decisions in healthcare.

Several reviewed studies highlight clear trends in the performance of classical machine learning and Deep Learning models for heart disease prediction, particularly in the UCI Cleveland dataset. However, recent advancements indicate that Quantum Neural Networks (QNNs) have introduced a next-generation computational paradigm with the potential to surpass current classical and Deep Learning limitations. Although QNN evaluations are still conducted on quantum simulators, the current results already show superior generalization capability and stronger accuracy behavior, indicating a promising future direction. We plan to extend our comparative analysis between Quantum Neural Networks (QNNs) and classical machine learning models to include diverse datasets beyond the UCI Heart Disease repository and explore their application in other relevant fields.