An Optimal Stacked Ensemble Deep Learning Model for Predicting Time-Series Data Using a Genetic Algorithm—An Application for Aerosol Particle Number Concentrations
Abstract
1. Introduction
- Improving the forecasting accuracy for atmospheric time-series data based on the ensemble technique of different RNN methods, where each method makes the prediction with different time-lag value.
- Automatic identification of time-lag for the RNN using a heuristic algorithm, which searches for the optimal (or near optimal) solution.
- A parallel implementation of the proposed model was applied in order to enhance its performance in terms of computation time without losing the accuracy or reliability.
2. Materials and Methods
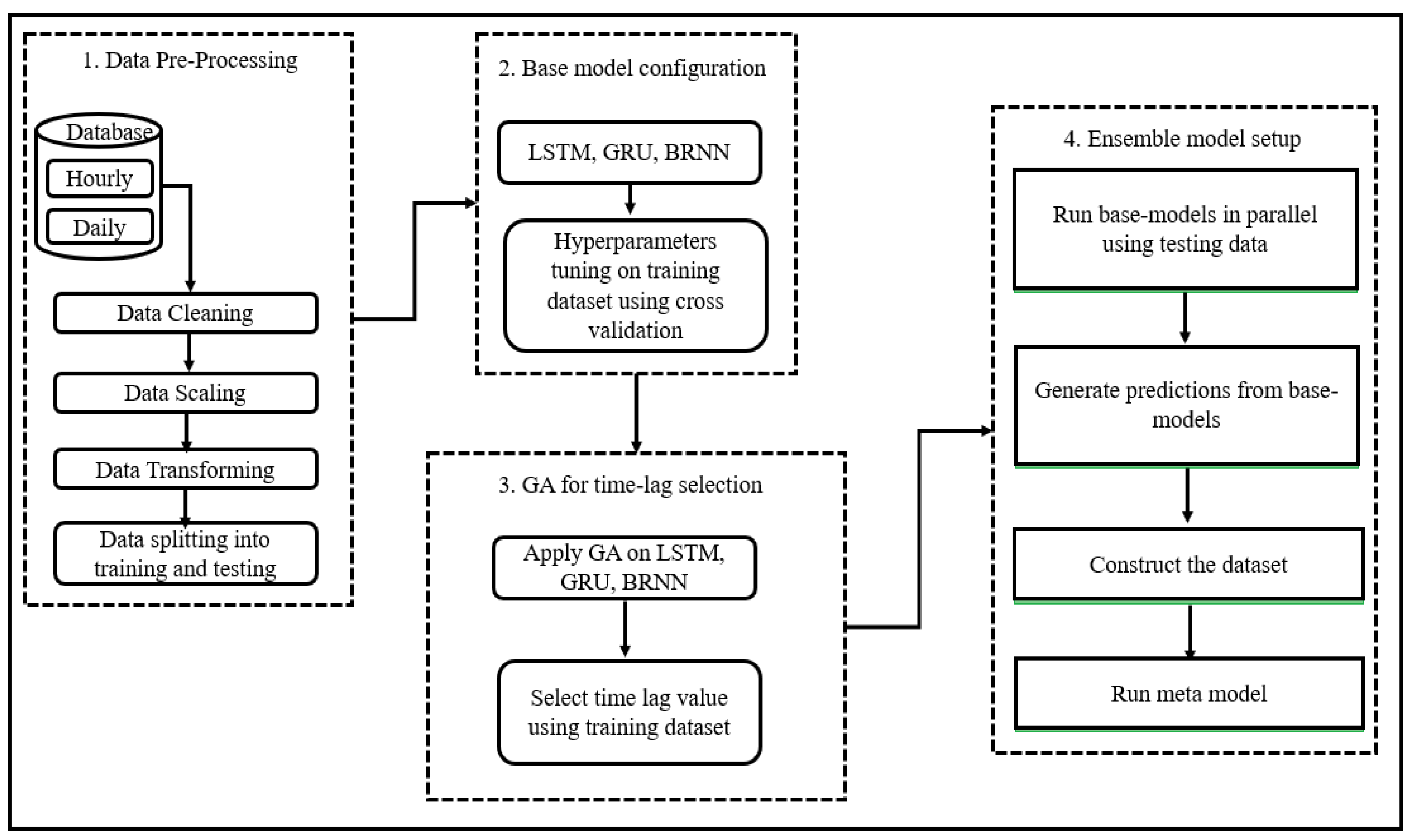
2.1. Database, Handling, and Preprocessing
- Checking: The database contained some missing data due to technical and instrumental issues. These missing values were replaced using the imputation method through interpolation. Each database became consistent with the expected number of records.
- Scaling: The processed database was normalized because it is preferred to train the model with data values which fall within the same range as the activation function used in the model training. So, the scaling factor is dependent on the activation function. In this case, the data were scaled between 0 and 1 to transform it within the range of the neural network activation function.
- Transformation: The data were transformed from a time-series form to a supervised form. The supervised data contained a sample with input and output components. The input component was a number of prior observations (defined by time-lag value). The output component contained the observation to be forecasted. In another words, the input was the observations from previous time steps, and the output was the observation of the current time step. The observation of the current time step became the input for the next time step, and so on.
2.2. Model Setup
- Because it is a time-series forecasting problem, the prediction process can be accomplished using time-series methods such as RNN, which is able to capture temporal dependencies between data to produce more accurate results. Other methods can be used, such as Artificial Neural Network (ANN) and Bayesian Optimization methods, but these methods may cause overfitting as the time-lag feature is not taken into account. In the time-series data, the proper selection of time-lag value can reduce dimensionality of the non-linear data and avoid overfitting.
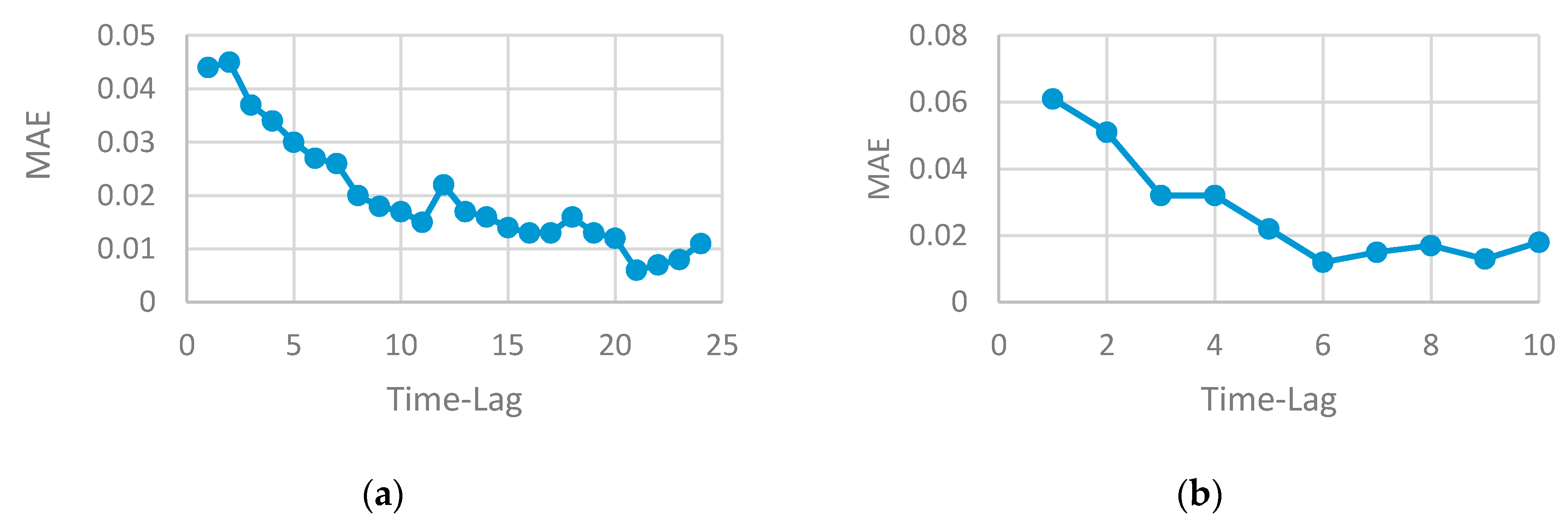
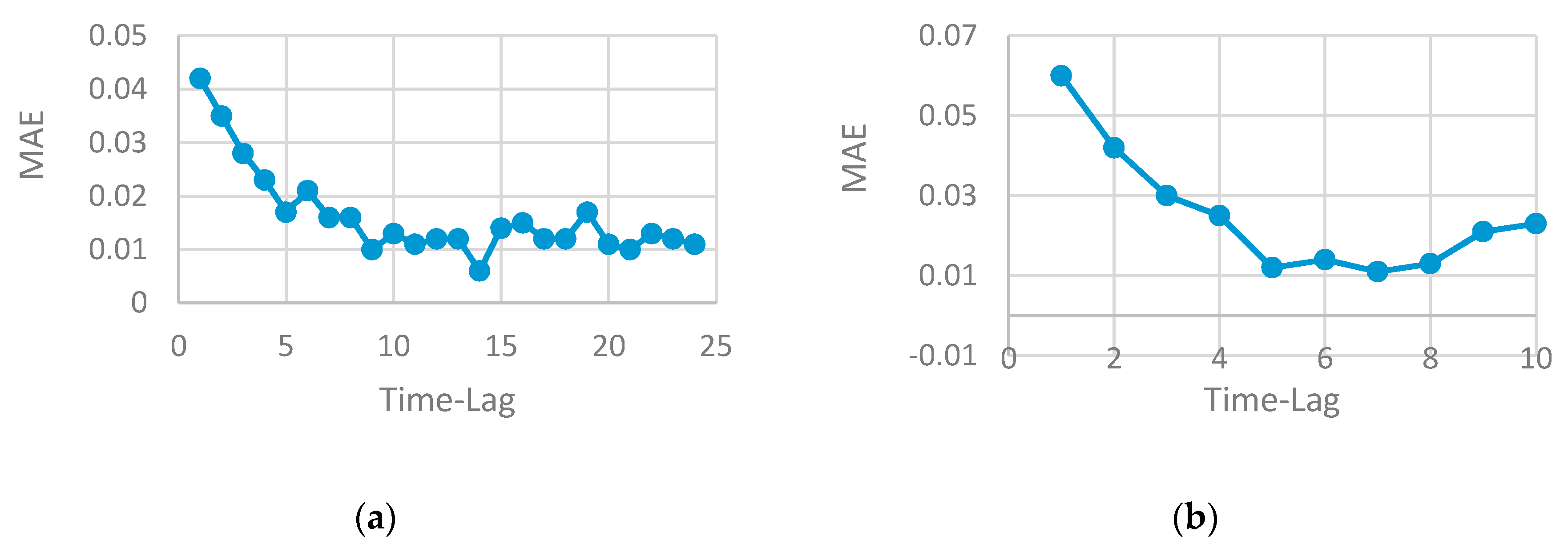
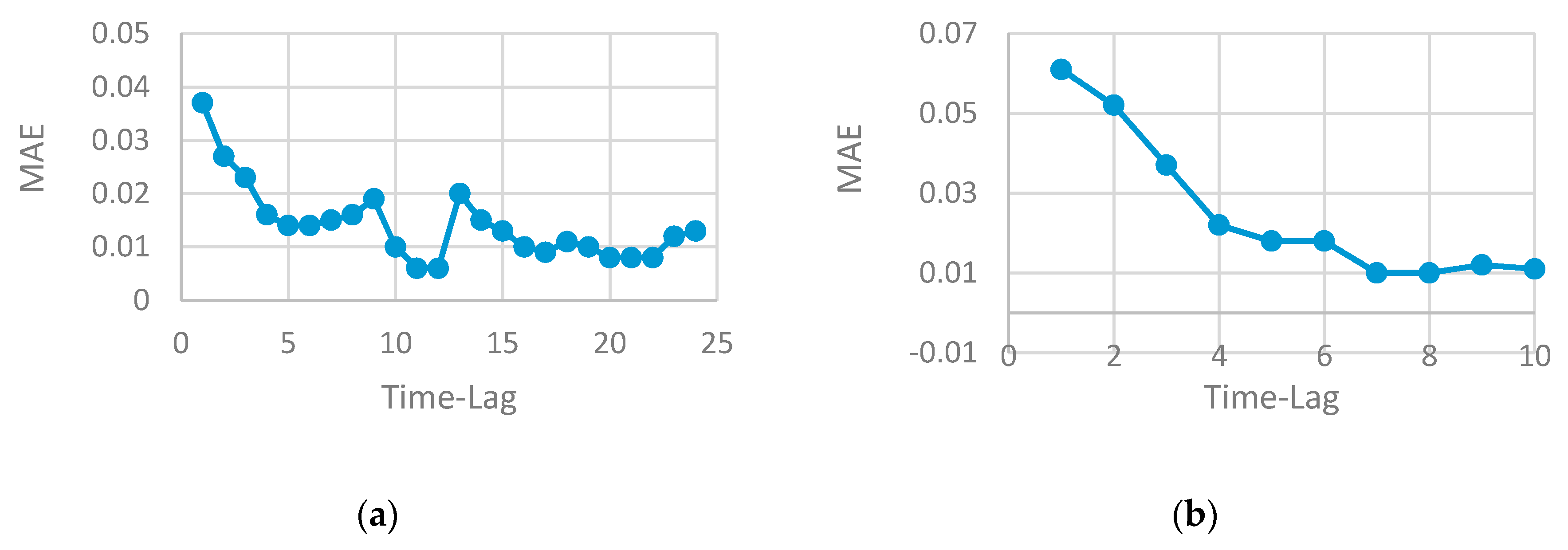
- The proper selection of time-lag can improve model performance and generate a more accurate result. The time-series data can be viewed as a set of equal chunks where the records of each chunk are correlated and consistent. Finding the number of records at each chunk represents time-lag value, which is a difficult problem to solve and requires the running of several experiments to search for the best value that may generate the best prediction accuracy. Repeating this process has a high computational cost and consumes the resources. Using a heuristic algorithm to solve search problems is highly preferable by researchers as it can find the optimal solution (or near optimal) in a reasonable time with less computational cost. GA is used in this paper to enable us to find the optimal time-lag and prevent overfitting, increase model accuracy and generate the prediction with less computational cost compared to other heuristic algorithms.
- More accurate results can be achieved through the use of ensemble technique, which combines the result of each single model to improve accuracy. The prediction result of ensemble method is usually better than the prediction of a single model. Heterogeneous ensemble learning is used in this paper, as different base models are used with different hyperparameter tuning.
- Robust and strong;
- Non-deterministic algorithm and can be used for a variety of problems;
- Works with the string-coded of the variables rather than the variable itself, so the coding discretizes the search space even if the function might be continuous;
- An optimal solution could be generated by GA as it works with more than one solution (population).
- Initial population: A binary vector randomly initialized the use of the uniform distribution defining initial solution. The population size was set to have 50 possible solutions.
- Selection: Select the parents from population with the best fitness value.
- Crossover: Exchange the variables between selected parents to generate new offspring. One-point crossover was used for that.
- Mutation: A binary bit flip with probability of 0.1 was applied to the solution pool by randomly swapping bits to achieve diversity on the solutions.
- Fitness function: MAE was used to evaluate solution.
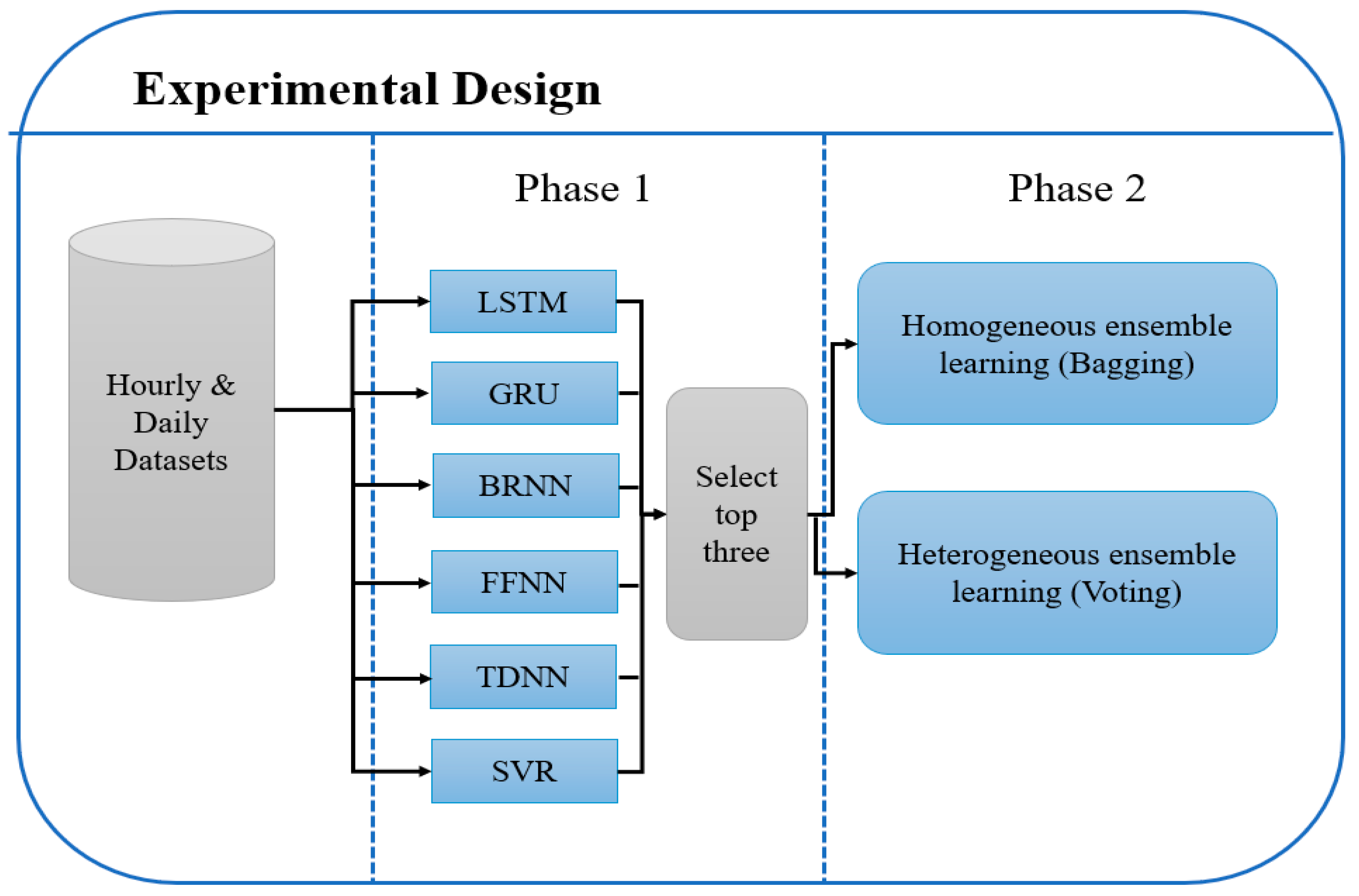
- Level 0 (base models): Used three models (LSTM, GRU and BRNN) with selected time-lag value proposed by GA. The testing database was divided into 5 folds that were disjointed and of equal size. One fold remained aside, while others were used to train each model. The prediction was then made using holdout fold. More robust results are generated for each model.
- Level 1 (meta model): Took the output from level 0 as an input to a single model called a meta-learner to produce the prediction output. A new training database was constructed from the predictions of sub-models where the first column contained predictions generated by LSTM. The second column contained predictions generated by GRU; the third column contained predictions generated by BRNN; and the last column contained the actual expected output. This way, a new stacked database was constructed. A ML algorithm is then used to learn how to best combine the prediction of sub-models. It is the meta-learner that uses a new stacked dataset for training.
2.3. Computation Setup and Platform
3. Results and Discussion
3.1. RNN Models—Evaluation and Performance
- The performance of any neural network depends on the parameters tuning. The good selection of each parameter (such as the number of neurons, the number of layers, the number of time-lag, etc.) can either increase or decrease accuracy. Finding the optimal selection of network parameters is an NP problem that requires repeating the experiment by changing one parameter while keeping the other fixed. Determining the set of parameters that influence the network performance depends on the problem domain and the type of data. In this paper, time-series data are used where the RNN method is well-suited to be applied. The number of lags is a very effective parameter that can increase or decrease the model accuracy. The use of a heuristic algorithm in the proposed work searched for the best value of the time-lag to be chosen for each network architecture. This selection guarantees the use of the best value, that produces a robust model and enhances accuracy.
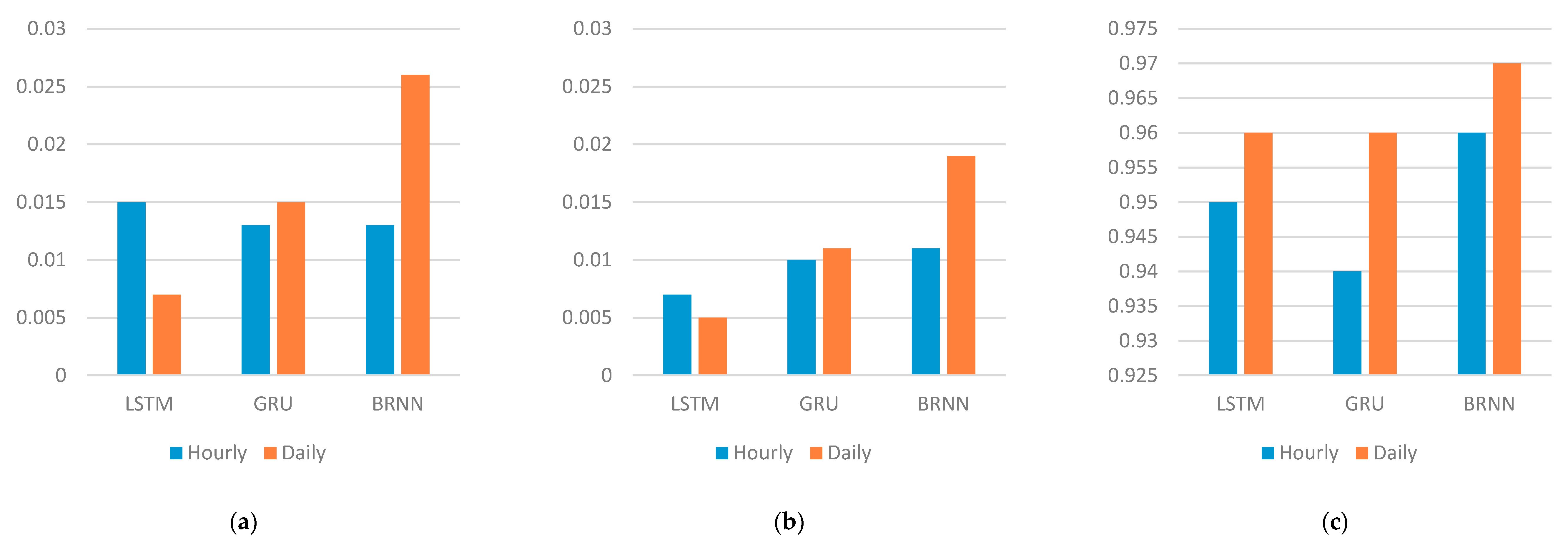
- A recurrent neural network is the best method to be used to design a predictive model for time-series data. Many variants of RNN have been developed in the literature where each version has its advantages and disadvantages. The three selected RNN methods used in this paper are LSTM, GRU and BRNN. Three models are designed using each method. The results can be summarized as follows:
- (a)
- LSTM model is accurate, robust and efficient. For a large amount of data, LSTM needs more time to generate an accurate prediction.
- (b)
- GRU is simpler than LSTM. On the other hand, it is less accurate, although the time needed to run a GRU model is less than the LSTM running time.
- (c)
- BRNN is accurate and robust, but it needs much time to produce a prediction on account of its backward and forward architecture.
- The number of the time-lag has a great effect on the algorithm performance for time-series data. Increasing the time-lag value (window size) increases the running time of the model.
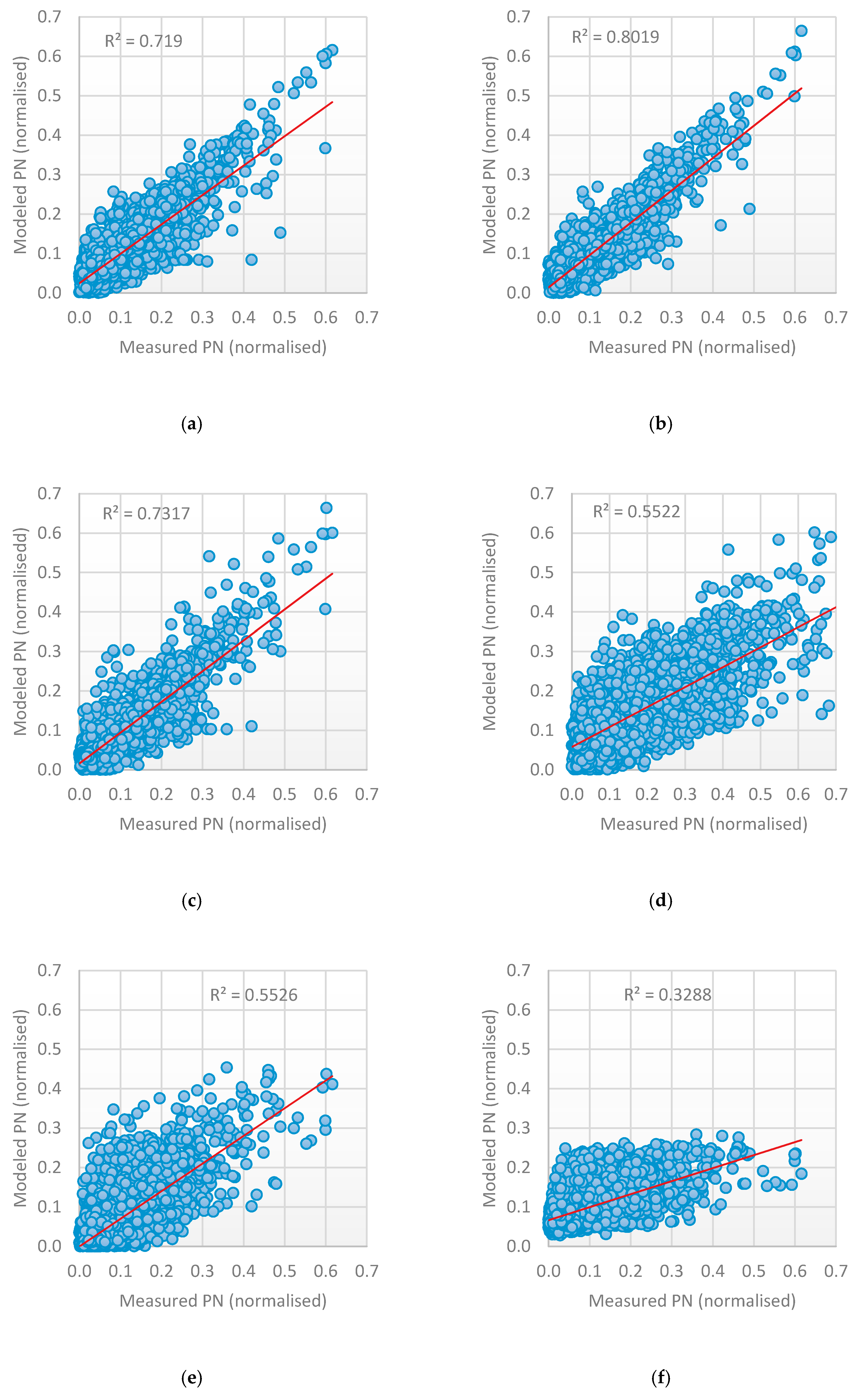
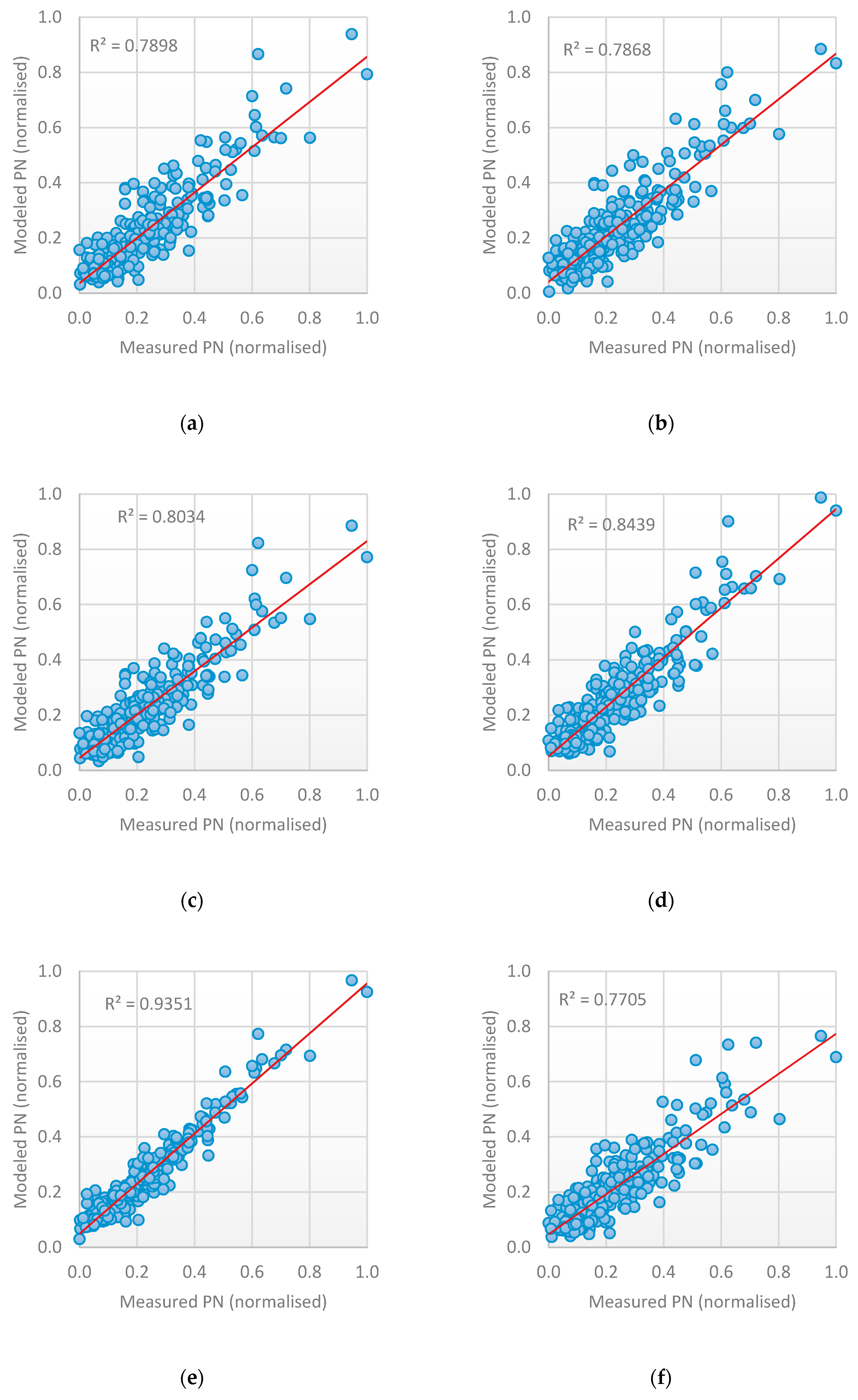
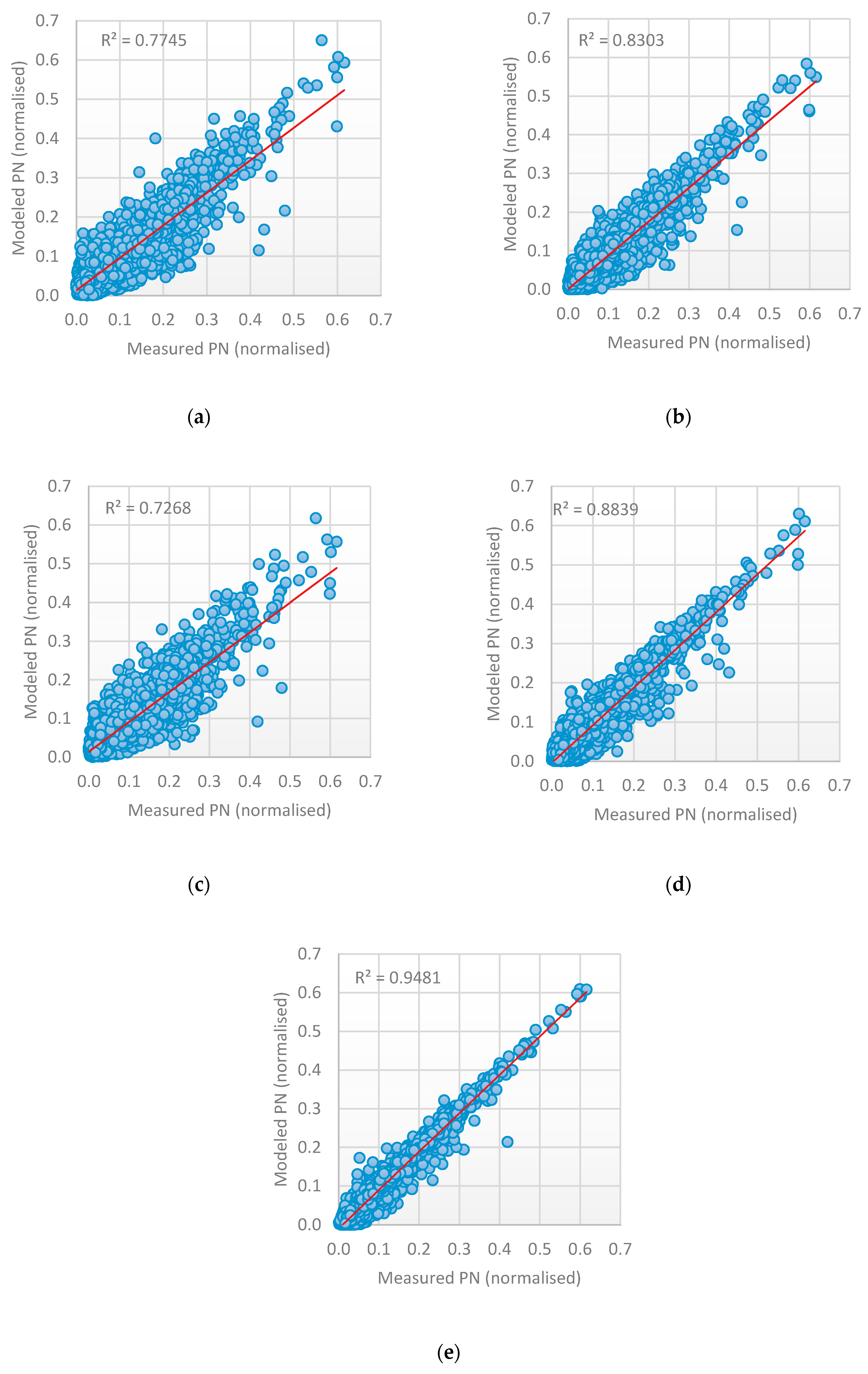
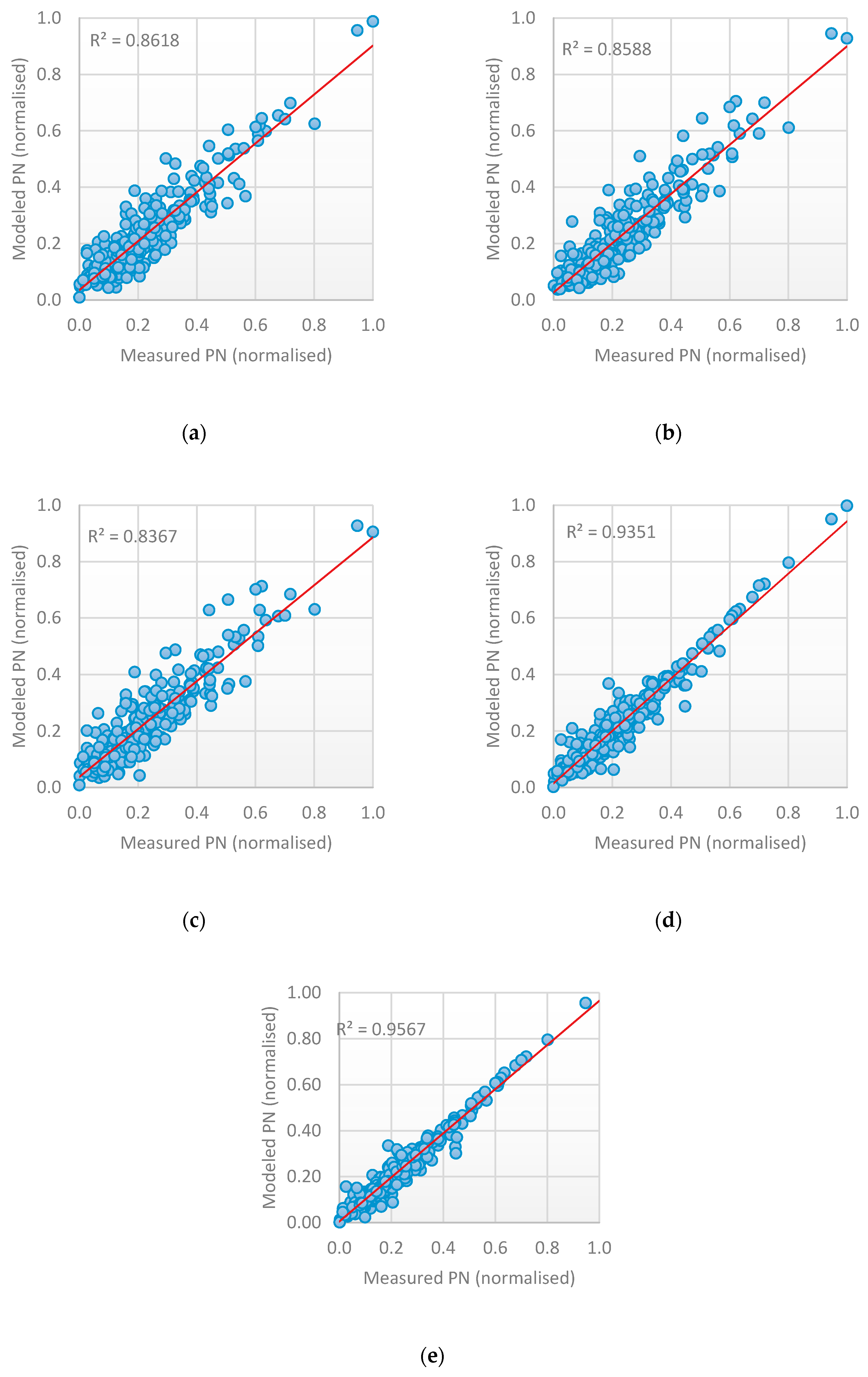
- An improvement in the prediction accuracy can be achieved by combination of the result of each method to produce a final one. This is achieved by designing stacked heterogenous ensemble learning that combines the output of each RNN method and uses a new learner to generate the final output. The ensemble learning technique improves accuracy, and the parallel implementation reduces running time. Having three base-learners with a different time-lag number and different architecture reduced error generalization and overfitting, and increased diversity, as shown in Table 5.
- The parallel implementation of ensemble method enhances model performance, by reducing time needed to make the prediction.
3.2. Comparison with Other and Previous Methods
4. Conclusions
- An improvement in the prediction model can be achieved by including more data with different features, such as the use of air quality image data. A combination between Convolutional Neural Network and Recurrent Neural Network can provide a more robust and high precision predictive model.
- Parallelize neural network models by dividing the single neural network algorithm into tasks where each task can be run in a single core. The running time of the neural network can be reduced, and the performance will be enhanced in terms of speedup.
- Various optimization parameters can be tested and investigated to improve accuracy such as the learning function and network structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Recurrent Neural Network (RNN)
- Missing data and outliers. For example, some statistical models (e.g., Support Vector Machine (SVM)) are sensitive to missing data and the forecasting accuracy is affected.
- Assumptions of linear relationship, which cannot deal with complex nonlinear relationships. For example, the ARIMA model can only describe the linear relationship between variables.
- Number of variables in the regression equation. For example, the prediction accuracy of a regression model depends on the number of dependent variables. Increasing the number of variables improves the accuracy but increases the computation time.
Appendix A.1. Long-Short Term Memory (LSTM)
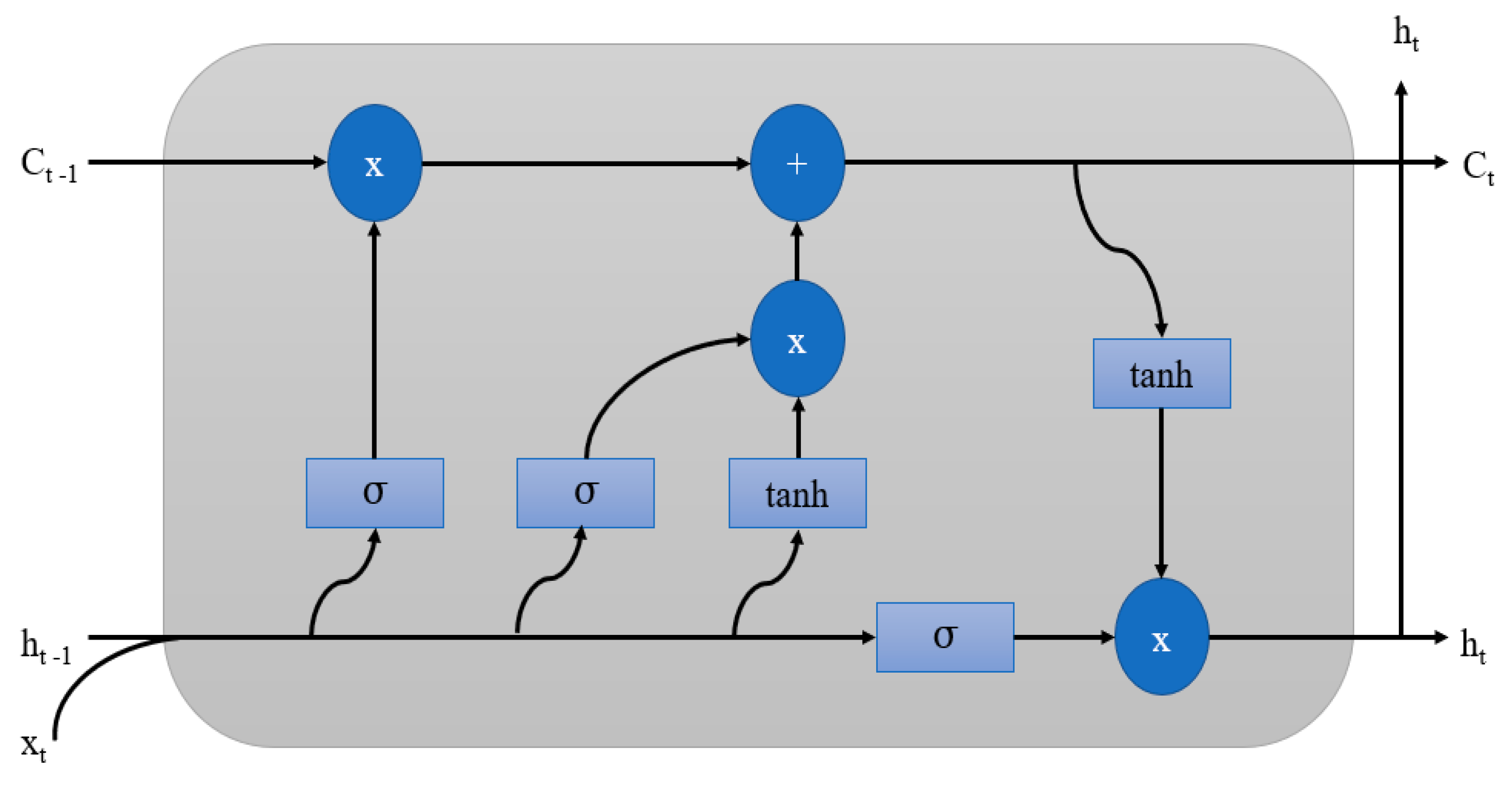
Appendix A.2. Gated Recurrent Networks (GRU)
Appendix A.3. Bi-Directional Recurrent Neural Networks (BRNN)

Appendix A.4. Ensemble Learner Algorithm
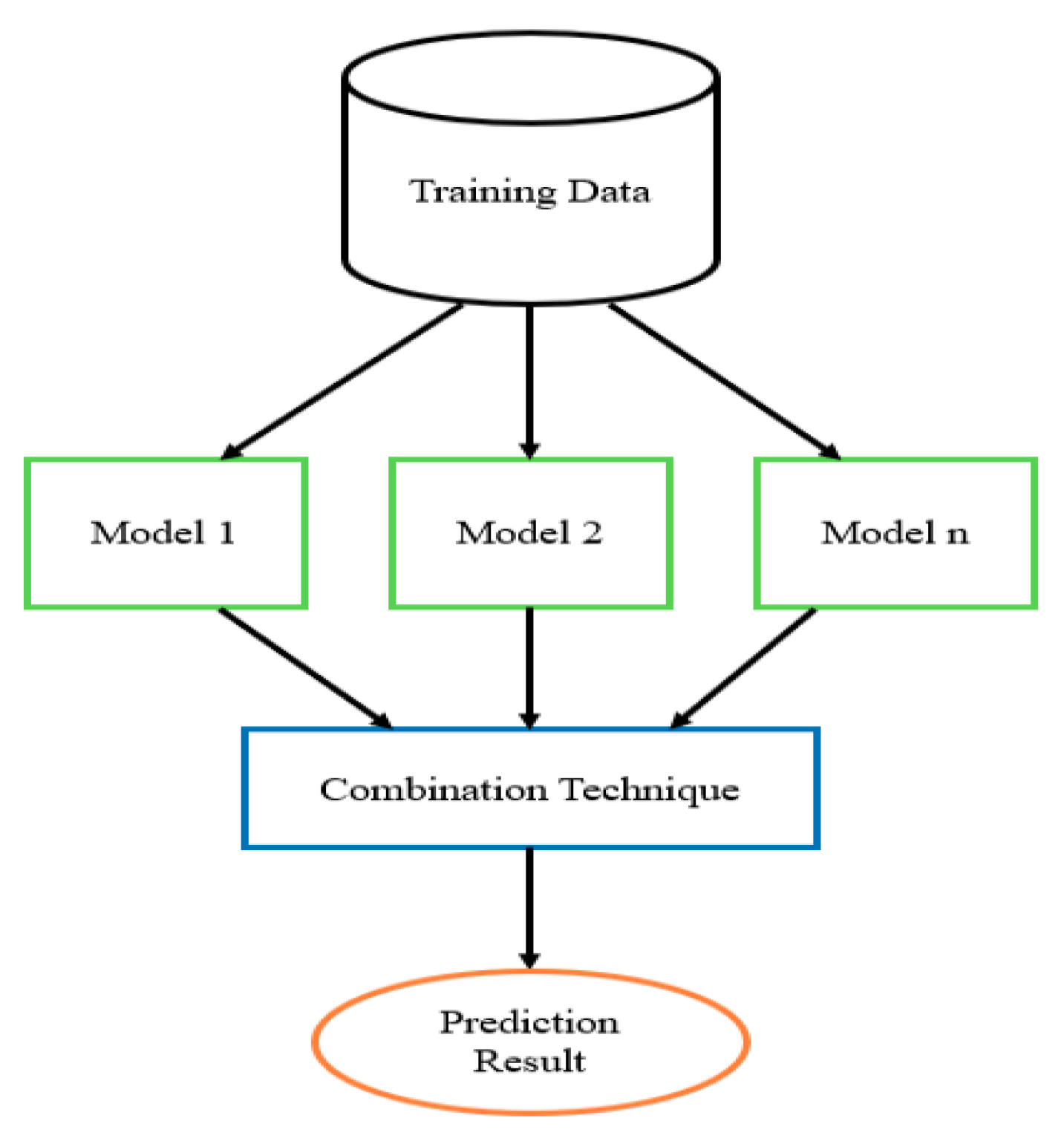
- The Training Data (i.e., problem database);
- Ensemble Models (i.e., NN methods used as a base learner);
- Combination Techniques (i.e., the way to produce the final prediction).
- Training Data: The base learner models used in the ensemble method can be trained with the same problem database, or each model can be trained with a subset database that is different from the subset used with other learners. The k-fold cross validation method can be used to divide the database into samples where each base learner uses one sample for training. It is preferred that each base learner generates a result with a low correlation with results generated by other base learners to achieve a generalization in the model performance. Based on this, using different samples to train each base learner is preferred when constructing the ensemble model.
- Ensemble Models: Selecting base learners that contribute to the ensemble architecture depends on the problem domain. In time-series data, RNN and its variants can be used to construct the ensemble model. The tuning of each base learner model becomes a challenge that influences its performance. When the ensemble model is constructed using the same kind of learning algorithm as for base learners (for example, a neural network), then it is called a homogeneous ensemble. If it is made up of more than one different learning algorithm, it is called heterogeneous [53]. When training the base learner models used in the ensemble design, each base learner model will have an error value that reflects its prediction accuracy. It is recommended to use models that result in a low correlation of error made by each model. This implies the tuning of each model with a different value of parameters.
- Combination Techniques: At the end of training, the results are combined to produce the final prediction. There are many ways to do this:
- Bagging: Dividing the database into samples where each one is fed to one base learner model. The final prediction is estimated by finding the average of each base learner model prediction. There are different bagging models, including Bagged Decision Tree, Random Forest and Extra Trees.
- Boosting: Building a chain of base learner models where each one attempts to fix the error of the model that proceeds it. Common boosting models include AdaBoost and Stochastic Gradient Boosting.
- Voting: Building an ensemble model with more than one base learner with some statistics (such as mean) to combine the final prediction.
Appendix A.5. Genetic Algorithm (GA)
- Initial population;
- Fitness function;
- Selection;
- Crossover;
- Mutation.
References
- Chung, H.; Shin, K.-S. Genetic Algorithm-Optimized Long Short-Term Memory Network for Stock Market Prediction. Sustainability 2018, 10, 3765. [Google Scholar] [CrossRef]
- Bui, C.; Pham, N.; Vo, A.; Tran, A.; Nguyen, A.; Le, T. Time Series Forecasting for Healthcare Diagnosis and Prognostics with the Focus on Cardiovascular Diseases. In Proceedings of the Precision Medicine Powered by pHealth and Connected Health, Ho Chi Minh, Vietnam, 18–21 November 2017; Springer Science and Business Media LLC: Singapore, 2017; Volume 63, pp. 809–818. [Google Scholar]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Mills, A.R.; Harrison, R.F.; Fleming, P.J. Gas turbine engine prognostics using Bayesian hierarchical models: A variational approach. Mech. Syst. Signal Process. 2016, 70, 120–140. [Google Scholar] [CrossRef]
- Chen, W.-C.; Chen, W.-H.; Yang, S.-Y. A Big Data and Time Series Analysis Technology-Based Multi-Agent System for Smart Tourism. Appl. Sci. 2018, 8, 947. [Google Scholar] [CrossRef]
- Murat, M.; Malinowska, I.; Gos, M.; Krzyszczak, J. Forecasting daily meteorological time series using ARIMA and regression models. Int. Agrophysics 2018, 32, 253–264. [Google Scholar] [CrossRef]
- Salcedo, R.L.; Alvim-Ferraz, M.C.; Alves, C.A.; Martins, F.G. Time-series analysis of air pollution data. Atmos. Environ. 1999, 33, 2361–2372. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, H.; Zhao, Z.; Xiang, X.; Li, M.; Juan, J.; Song, J.; Cao, Y.; Wang, X.; Chen, L.; et al. Association between ambient air pollution and daily hospital admissions for ischemic stroke: A nationwide time-series analysis. PLoS Med. 2018, 15, e1002668. [Google Scholar] [CrossRef]
- Stieb, D.M.; Szyszkowicz, M.; Rowe, B.H.; Leech, J.A. Air pollution and emergency department visits for cardiac and respiratory conditions: A multi-city time-series analysis. Environ. Health 2009, 8, 25. [Google Scholar] [CrossRef]
- Ravindra, K.; Rattan, P.; Mor, S.; Aggarwal, A.N. Generalized additive models: Building evidence of air pollution, climate change and human health. Environ. Int. 2019, 132, 104987. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Junninen, H.; Aalto, P.P.; Kulmala, M.; Laurson, L.; Foster, A.S. Predicting atmospheric particle formation days by Bayesian classification of the time series features. Tellus B Chem. Phys. Meteorol. 2018, 70, 1–10. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Dada, L.; Alghamdi, M.A.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Hussein, T. Mutual Information Input Selector and Probabilistic Machine Learning Utilisation for Air Pollution Proxies. Appl. Sci. 2019, 9, 4475. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Wraith, D.; Boor, B.E.; Hussein, T. Bayesian Proxy Modelling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models. Appl. Sci. 2019, 9, 4976. [Google Scholar] [CrossRef]
- Bai, L.; Wang, J.; Ma, X.; Lu, H. Air Pollution Forecasts: An Overview. Int. J. Environ. Res. Public Health 2018, 15, 780. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.F.; Mallard, J.W. Contributions of Natural Emissions to Ozone and PM2.5as Simulated by the Community Multiscale Air Quality (CMAQ) Model. Environ. Sci. Technol. 2011, 45, 4817–4823. [Google Scholar] [CrossRef] [PubMed]
- Borrego, C.; Monteiro, A.; Ferreira, J.; Miranda, A.I.; Costa, A.M.; Carvalho, A.C.; Lopes, M. Procedures for estimation of modelling uncertainty in air quality assessment. Environ. Int. 2008, 34, 613–620. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Motlagh, N.H.; Fung, P.L.; Lu, D.; Timonen, H.; Kuula, J.; Niemi, J.V.; Tarkoma, S.; Petaja, T.; Kulmala, M.; et al. Intelligent Calibration and Virtual Sensing for Integrated Low-Cost Air Quality Sensors. IEEE Sens. J. 2020, 20, 13638–13652. [Google Scholar] [CrossRef]
- Zaidan, M.; Surakhi, O.; Fung, P.L.; Hussein, T. Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters. Sensors 2020, 20, 2876. [Google Scholar] [CrossRef]
- Cabaneros, S.M.; Calautit, J.K.; Hughes, B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019, 119, 285–304. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed]
- Hussein, T.; Atashi, N.; Sogacheva, L.; Hakala, S.; Dada, L.; Petäjä, T.; Kulmala, M. Characterization of Urban New Particle Formation in Amman—Jordan. Atmosphere 2020, 11, 79. [Google Scholar] [CrossRef]
- Hussein, T.; Dada, L.; Hakala, S.; Petäjä, T.; Kulmala, M. Urban Aerosol Particle Size Characterization in Eastern Mediterranean Conditions. Atmosphere 2019, 10, 710. [Google Scholar] [CrossRef]
- Balaguer-Ballester, E.; i Valls, G.C.; Carrasco-Rodriguez, J.; Soria-Olivas, E.; Del Valle-Tascon, S. Effective 1-day ahead prediction of hourly surface ozone concentrations in eastern Spain using linear models and neural networks. Ecol. Model. 2002, 156, 27–41. [Google Scholar] [CrossRef]
- Li, G.; Alnuweiri, H.; Wu, Y.; Li, H. Acceleration of back propagation through initial weight pre-training with delta rule. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2002; pp. 580–585. [Google Scholar]
- Idrissi, J.; Hassan, R.; Youssef, G.; Mohamed, E. Genetic Algorithm for Neural Network Architecture Optimization. In Proceedings of the 3rd International Conference of Logistics Operations Management (GOL), Fez, Morocco, 23–25 May 2016. [Google Scholar]
- Lim, S.P.; Haron, H. Performance comparison of Genetic Algorithm, Differential Evolution and Particle Swarm Optimization towards benchmark functions. In Proceedings of the 2013 IEEE Conference on Open Systems (ICOS), Kuching, Malaysia, 2–4 December 2013; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2013; pp. 41–46. [Google Scholar]
- Ashari, I.A.; Muslim, M.A.; Alamsyah, A. Comparison Performance of Genetic Algorithm and Ant Colony Optimization in Course Scheduling Optimizing. Sci. J. Inform. 2016, 3, 149–158. [Google Scholar] [CrossRef]
- Tarafdar, A.; Shahi, N.C. Application and comparison of genetic and mathematical optimizers for freeze-drying of mushrooms. J. Food Sci. Technol. 2018, 55, 2945–2954. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Chen, N. A comparison of three heuristic optimization algorithms for solving the multi-objective land allocation (MOLA) problem. Ann. GIS 2018, 24, 19–31. [Google Scholar] [CrossRef]
- Sachdeva, J.; Kumar, V.; Gupta, I.; Khandelwal, N.; Ahuja, C.K. Multiclass Brain Tumor Classification Using GA-SVM. In Proceedings of the 2011 Developments in E-systems Engineering, Dubai, UAE, 6–8 December 2011; pp. 182–187. [Google Scholar] [CrossRef]
- Fu, H.; Li, Z.; Li, G.; Jin, X.; Zhu, P. Modelling and controlling of engineering ship based on genetic algorithm. In Proceedings of the International Conference on Modelling, Identification & Control (ICMIC), Wuhan, China, 24–26 June 2012; pp. 394–398. [Google Scholar]
- Foschini, L.; Tortonesi, M. Adaptive and business-driven service placement in federated Cloud computing environments. In Proceedings of the 2013 IFIP/IEEE International Symposium on Integrated Network Management (IM 2013), Ghent, Belgium, 27–31 May 2013; pp. 1245–1251. [Google Scholar]
- Khuntia, A.; Choudhury, B.; Biswal, B.; Dash, K. A heuristics based multi-robot task allocation. In Proceedings of the 2011 IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, Kerala, India, 22–24 September 2011; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2011; pp. 407–410. [Google Scholar]
- Alam, T.; Qamar, S.; Dixit, A.; Benaida, M. Genetic Algorithm: Reviews, Implementations, and Applications. Preprints 2020, 2020060028. [Google Scholar] [CrossRef]
- Tabassum, M.; Mathew, K. A Genetic Algorithm Analysis towards Optimization Solutions. Int. J. Digit. Inf. Wirel. Commun. 2014, 4, 124–142. [Google Scholar] [CrossRef]
- Khairalla, M.A.; Ning, X.; Al-Jallad, N.T.; El-Faroug, M.O. Short-Term Forecasting for Energy Consumption through Stacking Heterogeneous Ensemble Learning Model. Energies 2018, 11, 1605. [Google Scholar] [CrossRef]
- Siwek, K.; Osowski, S. Improving the accuracy of prediction pf PM10 pollution by the wavelet transformation and an ensemble of neural predictors. Eng. Appl. Artif. Intell. 2012, 25, 1246–1258. [Google Scholar] [CrossRef]
- Tan, K.K.; Le, N.Q.K.; Yeh, H.-Y.; Chua, M.C.H. Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties. Cells 2019, 8, 767. [Google Scholar] [CrossRef]
- Xie, Q.; Cheng, G.; Xu, X.; Zhao, Z. Research Based on Stock Predicting Model of Neural Networks Ensemble Learning. In Proceedings of the MATEC Web of Conferences, Shanghai, China, 12–14 October 2018; EDP Sciences: Ulis, France, 2018; Volume 232, p. 02029. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Zhang, G.P. Neural Networks for Time-Series Forecasting. In Handbook of Natural Computing; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; pp. 461–477. [Google Scholar]
- Mikolov, T.; Karafia’t, M.; Burget, L.; Cernocky, J.; Khudanpur, S. Recurrent neural network based language model. In Proceedings of the Interspeech 2010 11th Annual Conference of the International Speech, Makuhari, Chiba, Japan, 26–30 September 2010. [Google Scholar]
- Mikolov, T.; Joulin, A.; Chopra, S.; Mathieu, M.; Ranzato, M. Learning Longer Memory in Recurrent Neural Networks. 2014. Available online: https://arxiv.org/abs/1412.7753 (accessed on 4 November 2020).
- Wang, J.; Hu, F.; Li, L. Deep Bi-directional Long Short-Term Memory Model for Short-Term Traffic Flow Prediction. Lect. Notes Comput. Sci. 2017, 9, 306–316. [Google Scholar] [CrossRef]
- Why Are Deep Neural Networks Hard to Train? 2018. Available online: http://neuralnetworksanddeeplearning.com/chap5.html (accessed on 3 November 2020).
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. 2014. Available online: https://arxiv.org/abs/1412.3555 (accessed on 4 November 2020).
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches. In Proceedings of the SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 25 October 2014; Association for Computational Linguistics (ACL): Stroudsburg, PA, USA, 2014. [Google Scholar]
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Peimankar, A.; Weddell, S.J.; Jalal, T.; Lapthorn, A.C. Evolutionary multi-objective fault diagnosis of power transformers. Swarm Evol. Comput. 2017, 36, 62–75. [Google Scholar] [CrossRef]
- Naftaly, U.; Intrator, N.; Horn, D. Optimal ensemble averaging of neural networks. Netw. Comput. Neural Syst. 1997, 8, 283–296. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Canova, F.F.; Laurson, L.; Foster, A.S. Mixture of Clustered Bayesian Neural Networks for Modeling Friction Processes at the Nanoscale. J. Chem. Theory Comput. 2016, 13, 3–8. [Google Scholar] [CrossRef]
- Surakhi, O.; Serhan, S.; Salah, I. On the Ensemble of Recurrent Neural Network for Air Pollution Forecasting: Issues and Challenges. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 512–526. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
- Pearl, J. Heuristics: Intelligent Search Strategies for Computer Problem Solving; Addison-Wesley: Boston, MA, USA, 1984; p. 3. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, Machine Learning; Addison Wesley Longman: Reading, UK, 1989. [Google Scholar]
| Serial Number | Software Package | Toolbox | Usage |
|---|---|---|---|
| 1 | Pandas | Read_csv | Read the file of type csv |
| 2 | Numpy | Array | Create an array data type |
| 3 | Matplotlib | Pyplot | Create a figure |
| 4 | sklearn.preprocessing | MinMaxScaler | Scales data to a given range |
| 5 | Time | Time | Finds current time |
| 6 | Keras.models | Sequential | Implement a sequential (not parallel) model |
| 7 | Keras.layers | Dense LSTM | Implement a fully connected layer Implement LSTM cell blocks |
| 8 | kernel_initializer | Normal | Initialize network weights |
| 9 | sklearn.metrics | r2_score mean_absolute_error | Evaluate R-squared Evaluate mean absolute error |
| 10 | Multiprocessing | Process | Divide work between multiple processes |
| 11 | GA | Genetic algorithm | Implements genetic algorithm operations |
| Tuned Parameter | Optimal Value/Hourly | Optimal Value/Daily |
|---|---|---|
| Number of hidden layers | 3 | 3 |
| Number of neurons at each layer | 150, 100, 50 | 150, 100, 50 |
| Number of epochs | 4000 | 4000 |
| Learning rate | 0.001 | 0.01 |
| Batch size | 126 | 48 |
| Long-Short Term Memory (LSTM) | Gated Recurrent Networks (GRU) | Bi-Directional Recurrent Neural Networks (BRNN) | ||||
|---|---|---|---|---|---|---|
| Time-Lag | Run Time | Time-Lag | Run Time | Time-Lag | Run Time | |
| Hourly | 21 | 76.8 | 14 | 53.05 | 11 | 89.3 |
| Daily | 6 | 2.29 | 7 | 2.53 | 10 | 2.92 |
| LSTM | GRU | BRNN | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | Time-Lag | RMSE | MAE | R2 | Time-Lag | RMSE | MAE | R2 | Time-Lag | |
| Hourly | 0.015 | 0.007 | 0.95 | 21 | 0.013 | 0.010 | 0.94 | 14 | 0.013 | 0.011 | 0.96 | 11 |
| Daily | 0.007 | 0.005 | 0.96 | 6 | 0.015 | 0.011 | 0.96 | 7 | 0.026 | 0.019 | 0.97 | 10 |
| Model | Hourly | Daily | ||||
|---|---|---|---|---|---|---|
| Accuracy | Variance | Run Time | Accuracy | Variance | Run Time | |
| Long-Short Term Memory (LSTM) | 95.1% | 0.00476 | 76.866 | 91.3% | 0.0214 | 2.292 |
| Gated Recurrent Networks (GRU) | 94.2% | 0.00459 | 53.058 | 86.5% | 0.0275 | 2.531 |
| Bi-Directional Recurrent Neural Networks (BRNN) | 93.7% | 0.00512 | 89.409 | 88.1% | 0.0232 | 2.929 |
| Ensemble | 97.1% | 0.00402 | 27.082 | 92.8% | 0.0213 | 1.103 |
| Model | Hourly | Daily | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
| Artificial Neural Networks (ANN) | 0.086 | 0.035 | 0.78 | 0.049 | 0.052 | 0.43 |
| Long-Short Term Memory (LSTM) | 0.037 | 0.028 | 0.71 | 0.076 | 0.057 | 0.79 |
| Gated Recurrent Networks (GRU) | 0.058 | 0.041 | 0.80 | 0.077 | 0.058 | 0.78 |
| Bi-Directional Recurrent Neural Networks (BRNN) | 0.037 | 0.027 | 0.73 | 0.046 | 0.033 | 0.80 |
| Model | Hourly | Daily | ||||
|---|---|---|---|---|---|---|
| RMS | MAE | R2 | RMSE | MAE | R2 | |
| Long-Short Term Memory (LSTM) | 0.037 | 0.028 | 0.71 | 0.076 | 0.057 | 0.79 |
| Gated Recurrent Networks (GRU) | 0.058 | 0.041 | 0.80 | 0.077 | 0.058 | 0.78 |
| Bi-Directional Recurrent Neural Networks (BRNN) | 0.037 | 0.027 | 0.73 | 0.046 | 0.033 | 0.80 |
| Feed-forward Neural Networks (FFNN) | 0.078 | 0.055 | 0.55 | 0.071 | 0.54 | 0.84 |
| Time Delay Neural Networks (TDNN) | 0.061 | 0.041 | 0.55 | 0.086 | 0.063 | 0.93 |
| Support Vector Regression (SVR) | 0.18 | 0.63 | 0.32 | 0.1 | 0.071 | 0.77 |
| Model | Hourly | Daily | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
| Bagging-Feed-forward Neural Networks | 0.048 | 0.036 | 0.77 | 0.062 | 0.046 | 0.86 |
| Bagging-Time Delay Neural Networks | 0.041 | 0.025 | 0.83 | 0.062 | 0.047 | 0.86 |
| Bagging-Support Vector Regression | 0.08 | 0.30 | 0.72 | 0.067 | 0.051 | 0.83 |
| Voting -Long-Short Term Memory, Gated Recurrent Networks, Bi-Directional Recurrent Neural Networks | 0.026 | 0.019 | 0.88 | 0.042 | 0.030 | 0.93 |
| Stacking -Time Delay Neural Networks, Feed-forward Neural Networks, Bi-Directional Recurrent Neural Networks | 0.019 | 0.014 | 0.94 | 0.035 | 0.024 | 0.95 |
| Related Works | Ensemble Method | Application Domain | Results |
|---|---|---|---|
| Khairalla et al. [36] | Stacking heterogeneous ensemble | Energy consumption | 91.24% |
| Siwek and Osowski [37] | The multilayer perceptron, Elman network, radial base function and support vector machine | Air pollution | 92% |
| Tan, et al. [38] | Recurrent Neural Networks | Enhancer classification | 75.5% |
| Qi, et al. [39] | Long-Short Term Memory | Chinese Stock Market prediction | 58.8% |
| The proposed ensemble model | Long-Short Term Memory, Gated Recurrent Networks and Bi-Directional Recurrent Neural Networks | Air pollution | 97.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surakhi, O.M.; Zaidan, M.A.; Serhan, S.; Salah, I.; Hussein, T. An Optimal Stacked Ensemble Deep Learning Model for Predicting Time-Series Data Using a Genetic Algorithm—An Application for Aerosol Particle Number Concentrations. Computers 2020, 9, 89. https://doi.org/10.3390/computers9040089
Surakhi OM, Zaidan MA, Serhan S, Salah I, Hussein T. An Optimal Stacked Ensemble Deep Learning Model for Predicting Time-Series Data Using a Genetic Algorithm—An Application for Aerosol Particle Number Concentrations. Computers. 2020; 9(4):89. https://doi.org/10.3390/computers9040089
Chicago/Turabian StyleSurakhi, Ola M., Martha Arbayani Zaidan, Sami Serhan, Imad Salah, and Tareq Hussein. 2020. "An Optimal Stacked Ensemble Deep Learning Model for Predicting Time-Series Data Using a Genetic Algorithm—An Application for Aerosol Particle Number Concentrations" Computers 9, no. 4: 89. https://doi.org/10.3390/computers9040089
APA StyleSurakhi, O. M., Zaidan, M. A., Serhan, S., Salah, I., & Hussein, T. (2020). An Optimal Stacked Ensemble Deep Learning Model for Predicting Time-Series Data Using a Genetic Algorithm—An Application for Aerosol Particle Number Concentrations. Computers, 9(4), 89. https://doi.org/10.3390/computers9040089





