1. Introduction
Today, we can almost say that robots are used in all areas of human life. From the military, industrial and even domestic fields, robots are deployed in all those fields, and these deployments continue to increase every day. These robots are different from each other, depending on the fields in which they are used and their tasks to be performed. These differences can be described by their shape, size and performance, among other traits. Some of them are statics and others are dynamics. One can meet these dynamic robots, especially in public areas such as at airports, in hotels, in hospitals and even in public transportation stations. Mobile robots are a kind of robot which helps human beings to be more efficient and productive in daily life activities.
In addition, the motion of these robots is a difficult task to perform, because they should avoid some obstacles along the road to their destination. Performing object avoidance when moving from one position to another is a complex and composite task for mobile robots, since this task involves scanning the surrounding environment, detection of obstacles, path planning and navigation to the desired destination and dock to achieve a specific task, such as auto-recharging their batteries when needed. Usually, many of these obstacles are static, but often some of them can be dynamic. In this case, the complexity level of a robot’s navigation task is increased. As such, it is useful to make these robots more accurate. Knowing that a simple error of a mobile robot can lead to collisions and financial losses, the mobile robots need more space for free movement in their navigation times. Thus, it is essential to make the mobile robots operate appropriately to maximize space utilization and prevent accidents. Doing so will save financial loses to both the robot’s developers (companies) and its users (customers).
Actually, to be more economic in the field of robotics, micro-electromechanical sensors (MEMSs) are a good solution to replace the existing expensive and huge sensors used in mobile robots. These MEMSs are embedded in almost all modern edge devices. In this context, the authors of [
1,
2,
3] used acoustic signals to develop lightweight health monitoring AI systems. The developed technologies, based on edge devices with a bi-level optimization approach, can be used efficiently in on-board diagnostics (OBD) and smartphones. A basic platform for the design of a lightweight AI system is provided, which utilizes its built-in microphone for the health monitoring of agriculture machines. The adopted strategies considerably reduce the bulky data transmission on the Internet. Therefore, they provide very lightweight and economic artificial neural networks (ANNs), which are innovative frameworks and consist of a new roadmap to develop autonomous agriculture machines.
Additionally, several approaches are developed under different modeling assumptions to improve the robots’ navigation information. For example, to name a few in the motion planning problem, one can refer to [
4,
5,
6]. We also have the connectivity graphs, which are used to offer multipath possibility to the robots. Several studies are done to find the optimal shortest path among these multipaths for the robots so that an active simultaneous localization and mapping (SLAM) framework is developed in [
7], which exploits a graph structure in order to improve the exploration time and accuracy. This framework is helped by an online algorithm based on least squares optimization for compensating the most common sources of errors, allowing the robot to reconstruct a more accurate graph. James et al. [
8] also present four methods to adjust the connectivity of a networked system. To do so, a basic algorithm to track a desired connectivity profile through the addition and deletion of a sequence of single connections between two unmanned aerial vehicles (UAV) is developed.
The cell decomposition method consists of a kind of connectivity graph by dividing each dimension of the space into multiple parts. As the resulting path does not satisfy non-holonomic constraints, C. Zhang et al. [
9] proposed trajectory planning and tracking for autonomous vehicles, based on a state lattice and model predictive control. To find feasible continuous plans, D. Zeng et al. [
10] employed smooth cubic curvature polynomials in their investigation to ensure algorithm completeness and pick out the best trajectory, taking smoothness, comfort and economy into account. In the field of mobile robotics, navigation is an essential task classified into global navigation and local navigation. In global navigation, many methods have been developed such as those in [
11,
12]. To complete these, the authors of [
13,
14] discussed and developed some popular methods used in the local navigation class. Various researchers solved their navigation problems by successfully using the above two classes of navigation methods.
To further improve the accuracy of the motion information of robots, many filtering approaches exist and continue to be developed in the literature. Many applications are using the unscented Kalman filter (UKF) in various domains nowadays, ranging from target tracking [
15] to multi-sensor fusion [
16,
17]. Another form of sensor fusion research to improve the performance of existing mobile robots is found in [
18], where two methods (Dempster–Shafer theory and Kalman filtering) are used to integrate a global positioning system (GPS) and an inertial measurement unit (IMU), and the obtained results allowed for selecting the most accurate method for robot localization at an appropriate cost. In addition to completing the governing equations of the robot, the authors implemented a proportional–derivative controller to control and evaluate the kinematic and localization algorithms of the robot.
A similar work is [
19], in which the encoder, compass, IMU and GPS measurements are used in combination with extended Kalman filter (EKF) to study and discuss the localization and navigation algorithms of the mobile robots. In this study, the proposed method contains three main approaches. In each of them, the method combines the robot controller with the measurements of the considered approach using sensor fusion, which combines the on-board sensor and GPS measurements through EKF. The three approaches were verified in a simulation, and the performance of the proposed algorithms was demonstrated when a fault in the encoder was considered. In the same field of research, two filtering approaches had been used by the authors of [
20] to analyze the localization performance of SLAM (SLAM with a linear Kalman filter (KF) and SLAM with EKF). The simulation results of the proposed SLAM-based algorithms were evaluated and compared, and the results outperformed other algorithms regarding SLAM. In addition to presenting good accuracy, the proposed SLAM algorithms also gave a sensible computational complication.
Other examples of SLAM research can be found in [
21], where an overview of the existing SLAM approaches is presented, with a focus on novel hybridized light detection and ranging (LiDAR) camera solutions. The authors first presented a short theory behind the SLAM process, concerning current, state-of-the-art LiDAR camera solutions. Then, they discussed visual SLAM with a monocular and stereo camera, as well as modern red green blue-depth (RGB-D) and event cameras. Therefore, all of the above research allows us to deepen our understanding regarding SLAM and its contributions to the artificial intelligence built in mobile robots. Three main contributions are done in this research paper:
First, a new navigation algorithm, based on IR sensors for mobile robots, is created and named the novel IR navigation algorithm (NIRNA). This algorithm facilitates the robot’s navigation to dock to the charger in the docking station.
The second contribution consists of integrating NIRNA into an odometric system to build an Odom-NIRNA navigation system. This system greatly increases the quality of the classical odometer data.
The navigation systems of the inertial navigation system (INS), Odom-NIRNA and the KF-based estimation system are combined to develop a new estimation approach, based on a hybridization technique named hierarchical infrared navigational algorithm hybridization (HIRNAH), to improve the accuracy of the current estimation systems for four-wheeled mobile robot (4-WMR) localization.
The build for HIRNAH is based on the principle of Kalman filters (KFs) for nonlinear systems, such as UKFs. This technique is a tight hybridization technique, which contains three hierarchical levels and thus provided a better robot state estimation. In the proposed system, each navigation system processes separately the robot state information and then, based on these results, the errors in the robot state are calculated. These state errors and the localization data from the RPLIDAR-A3 scanner (measurement unit) are used as inputs into the system filtering module (SFM) to produce the estimated errors of the robot state. Based on the obtained estimated errors, the robot’s optimal state estimation is calculated, which is much more accurate than the robot’s state estimation from some previous research.
The remainder of the paper is structured as follows:
Section 2 describes the experimental configurations (parameters, setup and implementation) based on a real robot, while
Section 3 is devoted to presenting the results and discussion of the experiments (statistical evaluation analysis and comparison of results). The future works then end this section.
Section 4 describes the HIRNAH system proposed to improve the location of the robot in detail. Finally, the conclusion is presented in
Section 5.
3. Comparison Analysis and Statistical Evaluation of the Results
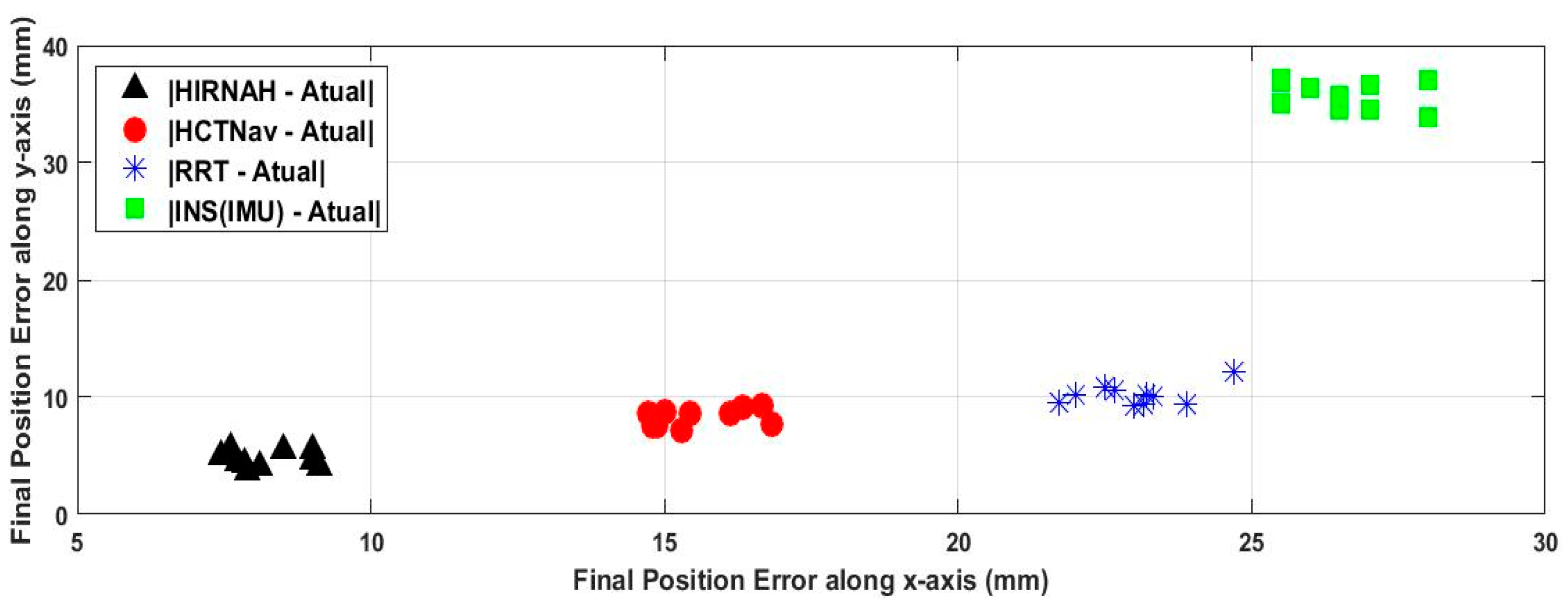
The produced errors of the position and orientation are presented in
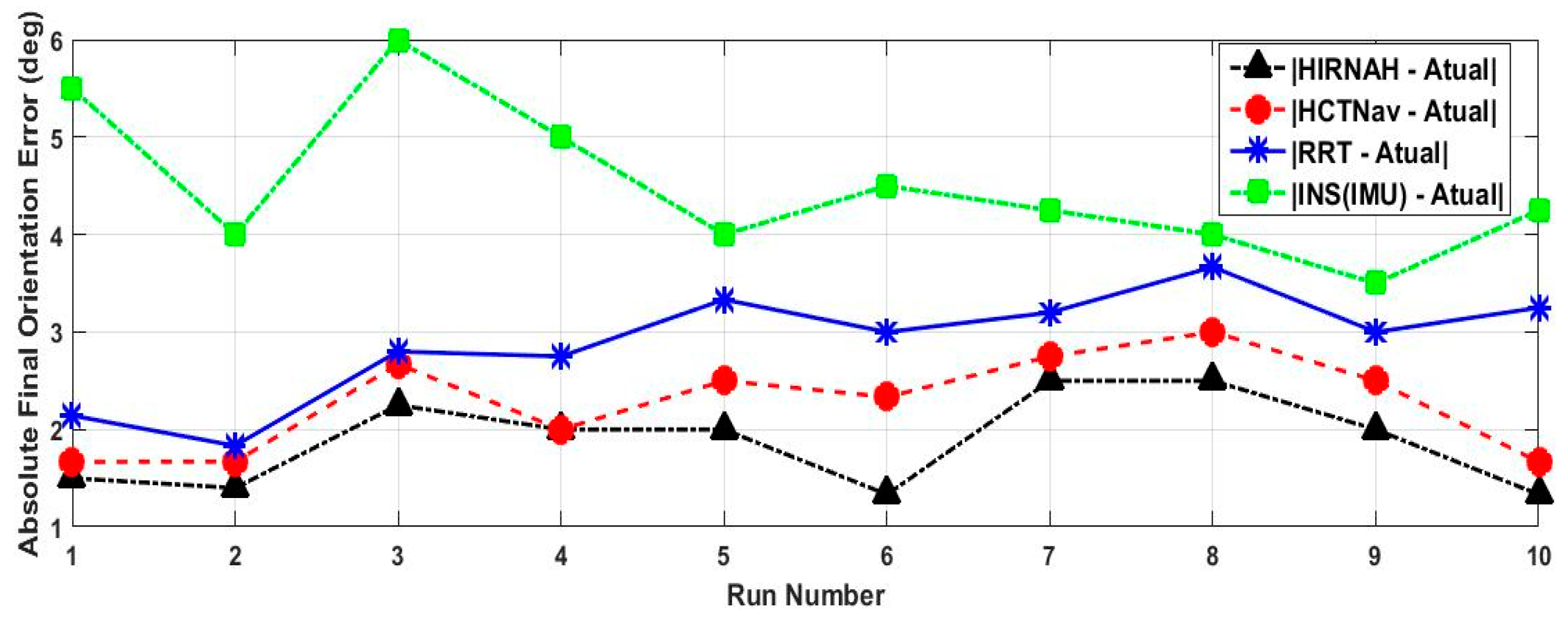
Figure 6 and
Figure 7, while the statistical analysis based on mean square error (MSE) are presented in
Table 3 below.
In these experimentation tests, the robot’s travel path consisted of reaching the charger from the RDP by implementing successively the system based on NIRNA, HCTNav, RRT and INS (IMU) and then comparing the results. Implementing the system based on NIRNA, HCTNav or RRT consisted of successfully using as a navigation algorithm in the Odom-NIRNA module (see
Figure 8) NIRNA, HCTNav or RRT. While implementing INS (IMU), the system was helped by camera data for navigation. The robot at the RDP facing the charger began to find the shortest path to the charger using the system.
From
Figure 6 and
Figure 7 and
Table 3, one can see that HIRNAH (the system when using NIRNA) provided more accurate positions and orientations, which was better than the system results when HCTNav, RRT or INS (IMU) were considered. In
Figure 6, ten runs in each performance measurement of the robot’s final poses are shown. In this figure, HIRNAH was the best with the lowest errors on average along the x-axis (8.22 mm) and along the y-axis (4.64 mm), followed successively by HCTNav and RRT. For HCTNav, the average errors along the x-axis and y-axis were 15.60 mm and 8.31 mm, respectively. That was slightly better than those of RRT, which were 23.02 mm and 10.20 mm, respectively. Finally, the worst-case performance measurement was given by INS(IMU), with the more erroneous information, on average, 26.55 mm errors along the x-axis and 35.8 mm errors along the y-axis. In
Figure 7, one can notice that HIRNAH presents the best performance measurement (in terms of the robot’s orientation errors for ten runs) with the lowest curve, followed successively by the curves for HCTNav, RRT and INS (IMU).
Throughout the ten experimental runs, HIRNAH provided less errors than the other performance measurements, except in run number four, where HIRNAH and HCTNav had the same errors. This is an exception which doesn’t appear often; otherwise (if it appears several times) it means the above supremacy of HIRNAH can be reversed under some conditions. Finally, the worst-case orientation errors of the robot were provided when the system used INS (IMU) in standalone mode.
Moreover, a statistical analysis based on the mean square error (MSE) metric was also done to evaluate the performance of our proposed method. The MSE values for the different estimation methods used are summarized in
Table 3. Recall that a low MSE implies high confidence for the localization and states estimation methods. From these results in
Table 3, the proposed HIRNAH method presents the most accurate results when compared with the others (HCTNav, RRT and INS (IMU)) used in this research. The large values of the MSE for INS (IMU) were due to its accumulated drifts during a long period of operation in the computation of the state variables. When HCTNav is considered, low MSE values were provided, compared with those of RRT and INS (IMU). This describes the effectiveness of this navigation algorithm. For RRT, the random choice of the next node made it perform worse, with somewhat high MSE values. Finally, HIRNAH provided smaller (and therefore more precise) values in terms of MSE along the three parameters of the robot state variables, thanks to the low noise associated with the robot’s pose when using NIRNA and given the history of measurements that can affect the accuracy of the robot’s state. Therefore, the proposed HIRNAH method, which uses a filtering technique and NIRNA, can significantly reduce the MSE of the robot state.
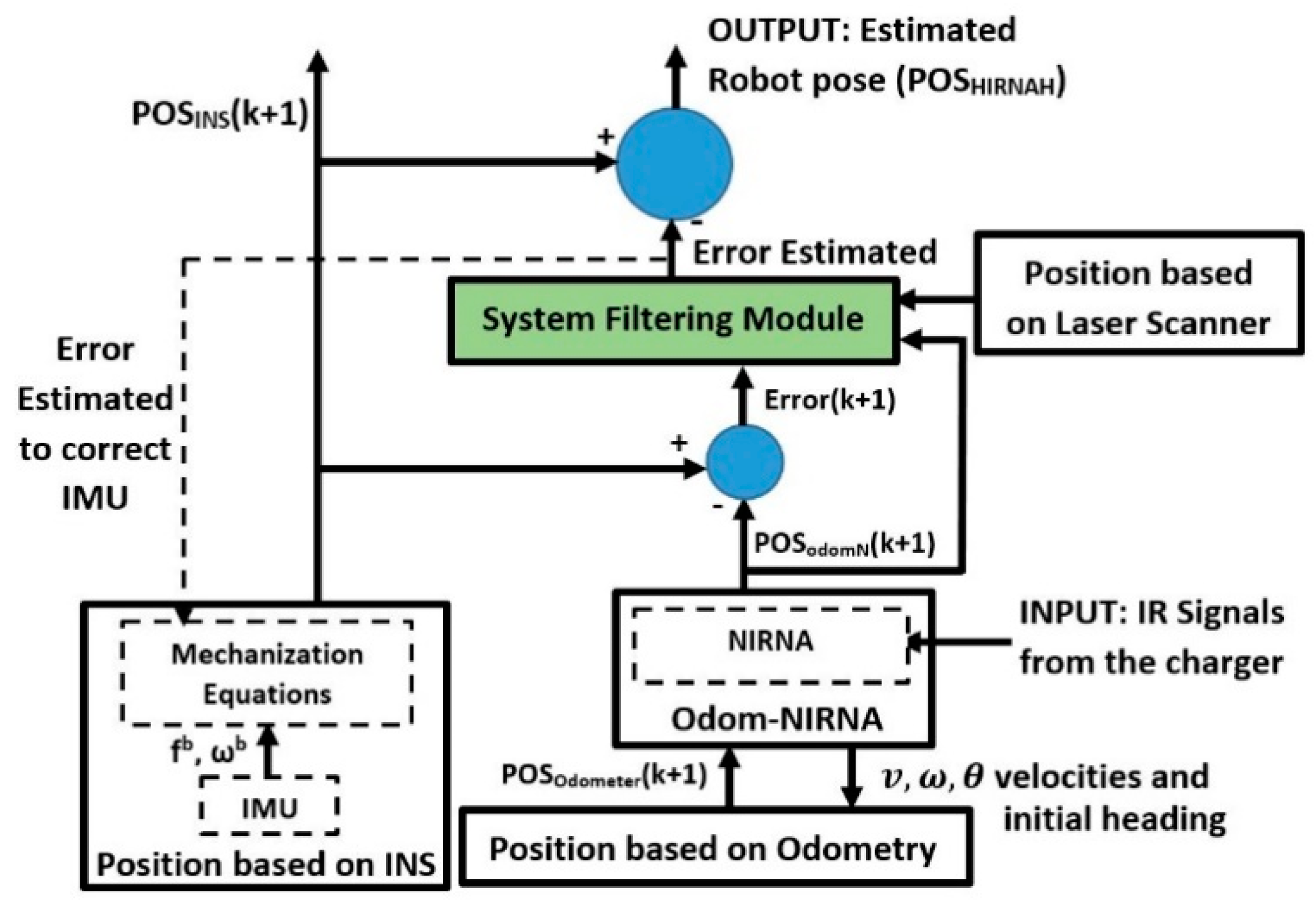
4. Hierarchical Infrared Navigational Algorithm Hybridization (HIRNAH)
The HIRNAH system presented in this paper contains two navigation systems (one Odom-NIRNA and one INS) and an RPLIDAR-A3 scanner as an observation measurement unit (module). Below in
Figure 8, the block scheme of the HIRNAH architecture is shown. These two navigation systems are combined to profit from their complementation. From the first navigational system, NIRNA and Odometer are handled together in order to produce the first navigational data, while in the second navigational system, an INS using an IMU provides the second navigation data. These navigational data are used to compute the robot state error, called error. This error, in addition to the Odom-NIRNA data (
POSOdomN) and the localization data from the RPLIDAR-A3 scanner (measurement unit), are used as inputs for the SFM to calculate the state estimated errors of the robot. These estimated errors in turn are used to compute the current optimal estimated state of the robot (
POSHIRNAH) and to correct the INS mechanization equations for the next loop. Independently, the system provides the INS navigation data (
POSINS(k+1)).
Let us consider a 4-WMR with the inertial reference frame
and robot body frame
. In the Cartesian coordinate system and inertial frame, our robot’s pose is expressed by
. The robot body frame
is selected so that x is forward and y is lateral, with the origin located at the robot’s kinematics center. The inertial reference frame
is stationary and attached to the initial position of the robot. Thus, by applying a UKF as a localization algorithm for a 4-WMR, the state variables considered are for its pose
, which can be defined as
In the rest of this paper, the state variable will be represented by for simplicity reasons.
4.1. Position Based on Odom-NIRNA
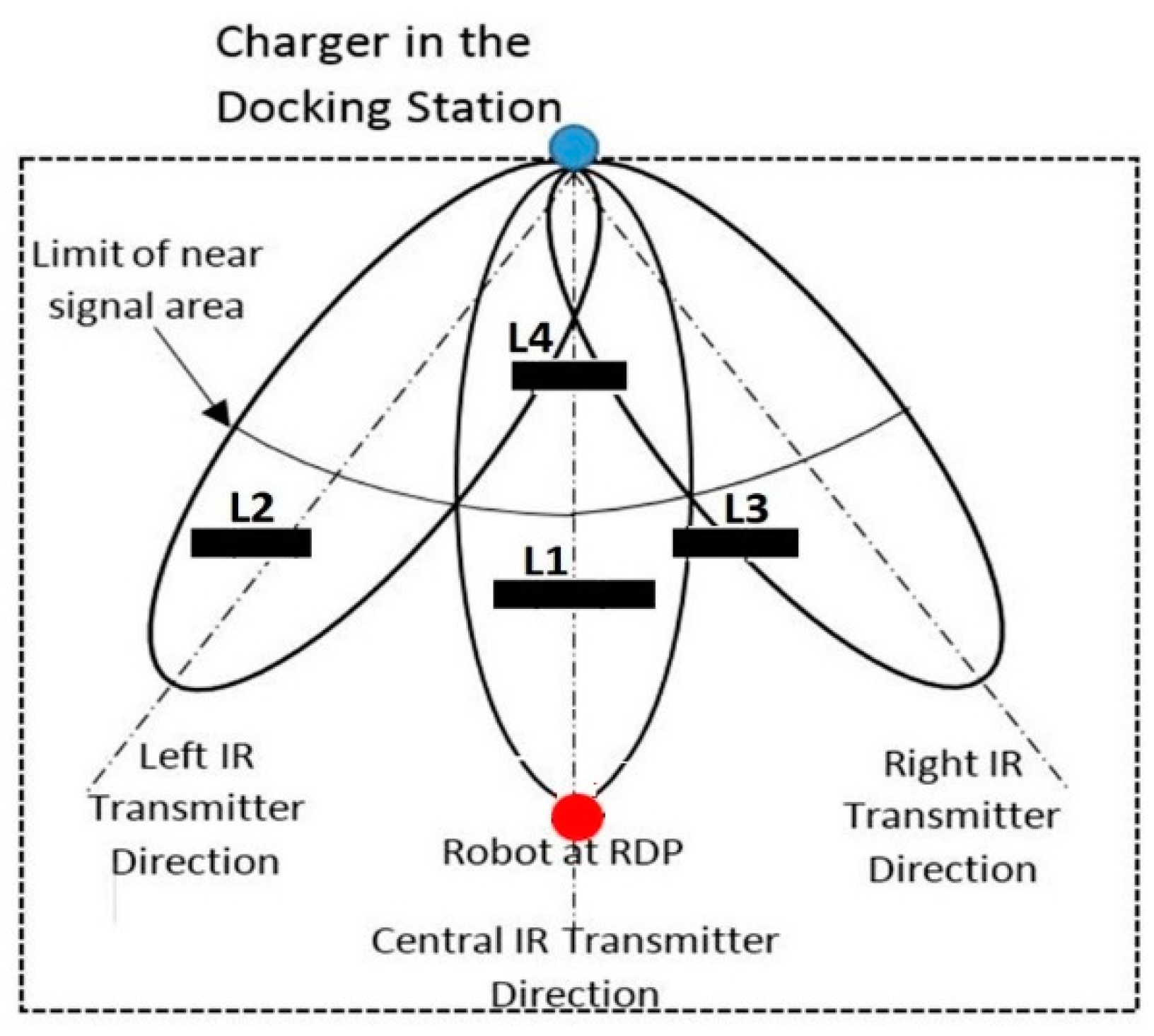
4.1.1. Novel Infrared Navigational Algorithm (NIRNA)
The new docking strategy, named the novel infrared navigation algorithm (NIRNA), aims to navigate the autonomous robots to a specific place (here a docking station). Its controller’s operating principle is summarized below in Algorithm 2. The novelty lies in the structure and the positioning of the IR sensors in both the charger and the charge controller on the robot. The final pose (
xR, yR, θR) and connection status (CFlag) are the algorithm outputs, and a detailed description is given in [
23]. In this paper, NIRNA is embedded into the odometer technology, and then the differential drive model [
24] is adopted to estimate the kinematic model of the robot.
| Algorithm 2. Controller of Novel Infrared Navigational Algorithm (NIRNA) |
| Input: 6 broadcast IR signals from the three IRTs of the charger |
| Output: direction//direction can be left, right, ahead and back |
| 1: while (1) |
| 2: looking for the 6 broadcast IR signals from charger |
| 3: if Any signals Received then |
| 4: Identify Signal sources and Signal level |
| 5: if Obstacle in front of the Robot then |
| 6: Calculate Distance between Robot and the Obstacle |
| 7: Choose direction, to bypass the Obstacle |
| 8: Return direction = left or right or back, |
| 9: else//go ahead at more 1 m by following the received IR Signal |
| 10: Return direction = ahead, |
| 11: end if |
| 12: else goto line 5 |
| 13: end if |
| 14: end while |
4.1.2. Odom-NIRNA Based Localization
For localization purposes, a mobile robot has to know its current location and orientation so that it can easily move from its current location to a destination. In the literature, there are many localization techniques with respect to mobile robots. Dead reckoning is one of them, which is more popularly used by scientific researchers. Thus, in this paper, we used the dead reckoning model, as applied in [
23], as our research method for robot location. The selected velocities
,
(linear and angular) and the orientation
by NIRNA are used to calculate the output (position vector) of the Odom-NIRNA navigation system, denoted OdomN. Algorithm 1 above illustrates the working principle of Odom-NIRNA. The robot’s Cartesian position is specified by the vector
, and its orientation is defined by
. Using the two coordinate frames (inertial reference frame
and robot body frame
) during mobile robot motion, with respect to the inertial reference frame, the position vector
is updated based on
, which is the position vector from the odometer
.
By adding the increments (travel distance () and change in angle ()) of the robot from a known position (starting point), one can get its estimated pose .
At time
, the estimated robot configuration is given by the following:
In the absence of wheel slippage and backlash, using the velocity data (linear and angular) of the robot, in addition to the odometric prediction above (commonly referred to as dead reckoning), good accuracy can be obtained on the location of the robot.
4.2. Position Based on INS (Inertial Measurement Units-Based Localization)
The INS (IMU) system can be used in two modes: standalone and cooperative. When used in standalone mode, it can be helped by a camera to navigate the robot to its charger. In cooperative mode, it will be used with the Odom-NIRNA system to determine robot state errors. The inertial measurement units (IMUs) play an important role in the INS to determine the position and orientation of the vehicles (robots here). This device is frequently used in robotics to help the robots in their navigation process. Usually, it contains many sensors such as accelerometers, gyroscopes and so on. The results (the linear acceleration and the velocity) produced by an accelerometer for mobile robots are affected by significant noise and accumulated drifts. The orientation obtained from a gyroscope contains some temporal drift and bias, which are the main source of gyroscope’s errors. To overcome this unbounded error, several data fusion techniques have been developed [
25,
26,
27]. Therefore, fusion (of both an accelerometer and gyroscope sensor) into a single device (IMU) is suitable to determine the pose of an object and to make up for the weakness of one over the other. In this paper, our used IMU is a 6-Degree of Freedom (DoF) accelerometer and gyroscope used to determine the pose estimation of our robot, as done in [
23].
The measurements of the rotational rate from the gyroscope (in our used IMU) have to be integrated to yield the orientation. This is represented by
where
is the robot’s heading rate based on the IMU’s reading,
is the robot’s actual heading rate,
is the IMU bias drift error and
is the associated white noise. The value of
is obtained by integrating
Equation (4) below presents the robot’s actual orientation based on the IMU reading:
In the inertial reference frame, based on the readings of the accelerometer data from the IMU model used, the position of the robot
is estimated by
where the robot velocity in the robot body frame is
, with
as the robot’s linear velocity and
as its angular velocity.
In the Cartesian coordinate system, Equation (5) is rewritten to
4.3. Position Based on RPLIDAR-A3 Scanner
The sensor measurements considered in this section were provided by an RPLIDAR-A3 scanner, similar to the approaches adopted in [
28,
29,
30]. It was positioned on the robot at height
(46 cm) above the ground and with the tilt control fixated at
= 9°. Recall that, in the Cartesian coordinate system and in the inertial frame, our robot’s position is expressed by
. 𝑁 landmarks at known positions
,
i = 1, …, 𝑁 are considered in the robot’s navigation space. We assumed to be zero, for simplicity, the uncertainties associated with landmark locations. During the robot’s motion, at each time step, the distance
d and the relative angle
to one or more landmarks were observed. That means, with RPLIDAR-A3 scan readings given in the plane of the RPLIDAR-A3 scanner, each RPLIDAR-A3 scan
comprises a set of distance readings
, i ∈ [1, 𝑁] and the angles
∈ [−90°, 90°] associated with these. The observation model provides a mechanism for computing the expected values of observations from the sensors, given the knowledge of the robot’s navigation space (location of the charger and all the landmarks) and an estimate of the robot’s location. In the frame of the RPLIDAR-A3 scanner, the scans
are represented in polar coordinates. Through the sensors mounted on the robot, at each time step
k + 1, both the distance and the relative angle to the landmarks were observed, and the observation model is given by
where
and
are zero-mean Gaussian observation noises and
.
To get the Cartesian coordinates of a measurement in the robot fixed frame, the following mapping transformation
→
(
,, ), as shown in Equation (8), can be applied, where
denotes the robot position related to the landmark
i using the measurement model of an RPLIDAR-A3 scanner:
As our robot’s navigation space is a flat environment and its body frame in consideration is a two-dimensional frame {
}, the
coordinate was set to be zero and replaced by
, the related angle between the robot and the landmark
i for analysis simplicity. In the same body frame, the RPLIDAR-A3 scan measurement angle
was zero forward and positive to the left. In this context, Equation (8) can be rewritten and represented below by Equation (9):
4.4. System Filtering Module
In order to estimate the errors of the robot state, the following standard discrete time equations can be used to represent the system, with the system model represented abstractly as
f and the measurement model represented abstractly as
h (be they linear or non-linear):
where
E is the system state,
q is the process noise,
n is the observation noise,
u1 is the exogenous input to the state transition function,
u2 is the exogenous input to the state observation function and
Z is the noisy observation of the system.
This SFM aims to smooth the location of the robot. To do so, the considered state variable of the robot is the error term (E) between Equations (2) and (6), which is found by subtracting from .
The adopted process model is presented below by Equation (11), which is a recursive equation deducted from Equations (2) and (6):
where
is a 3 × 3 identity matrix,
and
is a 3 × 3 rotational cosine matrix related to the control unit of the system and defined by
The state variable of our system is defined by Equation (13):
The first step of the UKF implementation is the state vector augmentation. Thus, the
n-dimension state vector
of the system needs to be restructured and augmented with
q-term process noise. That is presented below in Equation (14):
where
qk−1 is the augmented part and the dimension of the augmented state vector is
na =
n +
q. The process model can be rewritten as a function of
to calculate the a priori state estimate:
where the modeled part of the predefined data differences is represented by
while the augmented part is
, a zero mean white noise.
Here, we only consider the system input error while neglecting the system model error.
Thus, the augmented a priori state estimate and its covariance matrix are restructured as
where
and
are the covariance matrices of the state variable
and the process noise
, respectively.
The observation model used here, called the output function or errors estimated, is represented below by Equation (17):
The procedure and implementation of the UKF algorithm adopted here is same as that given in [
20]. By merging the INS’s belief
with the probability of making exactly that observation
, the robot corrects its posture. That is
, represented in Equation (18) by
where
is the corrected pose using HIRNAH along the corresponding axis.
5. Conclusions
A new HIRNAH system for mobile robot state estimation and localization has been constructed in this research paper. Based on sensor fusion through a tight hybridization technique, the built system contains three hierarchical levels. Two navigation systems (Odometer and INS) and a sensor measurement module (an RPLIDAR-A3 scanner) cooperated to achieve this HIRNAH system. The information from the two navigation systems (INS(IMU) and Odom-NIRNA) are used to estimate the robot’s state errors. These errors are entered into the SFM with the sensor measurement (RPLIDAR-A3 scanner) data to produce estimated errors and smooth the robot pose provided by the INS(IMU) system in order to produce the robot’s final pose of the entire system. The Odom-NIRNA system is built based on integrating a new navigation algorithm NIRNA and odometry to improve the classical odometry navigation data.
In this research, simulations were conducted in order to validate the applicability of the proposed system. Based on the results from these simulations, a real system was built and used to experiment on a real robot in our laboratory. The experiment results show that HIRNAH outperforms all the performance measurements used in this research, such as HCTNav, RRT and INS(IMU). This means that the odometry integrated with NIRNA can be used to provide a more accurate estimation of the location information (position and orientation) for a 4-WMR.
In our future work, we plan to improve the proposed method by taking into account another scenario, including more landmarks and some dynamic objects. In addition, as we only tested the proposed method on a robot using a single IRR, there is further need to extend the number of IRRs to three (left IRR, central IRR and right IRR) and perform more evaluations of our built HIRNAH system. Another extension possibility will be to increase the number of runs in the experiments to at least a hundred times, and perhaps with other filtering techniques.