A Unified Methodology for Heartbeats Detection in Seismocardiogram and Ballistocardiogram Signals
Abstract
1. Introduction
- The development of a common methodology for the analysis and segmentation of both SCG and BCG waveforms. This is an element of novelty, allowing to treat SCG and BCG waveform segmentation under a unified framework. Higher level models dealing with single SCG/BCG heartbeats could thus benefit from this common extraction routine.
- Rigorous evaluation of the proposed methodology on a pool of four independent datasets, featuring different measurement setups and time resolutions. This allows to better assess the robustness and generality of the methodology, over a wide set of operating conditions. Results show good heartbeat detection scores, in terms of sensibility and precision. Also, temporal annotation of inter-beat intervals exhibit low RMSE and MAE errors. Such results are shown to be comparable to and improve over related and recent literature.
2. Methods
2.1. Related Works
2.2. Datasets Description and Preprocessing
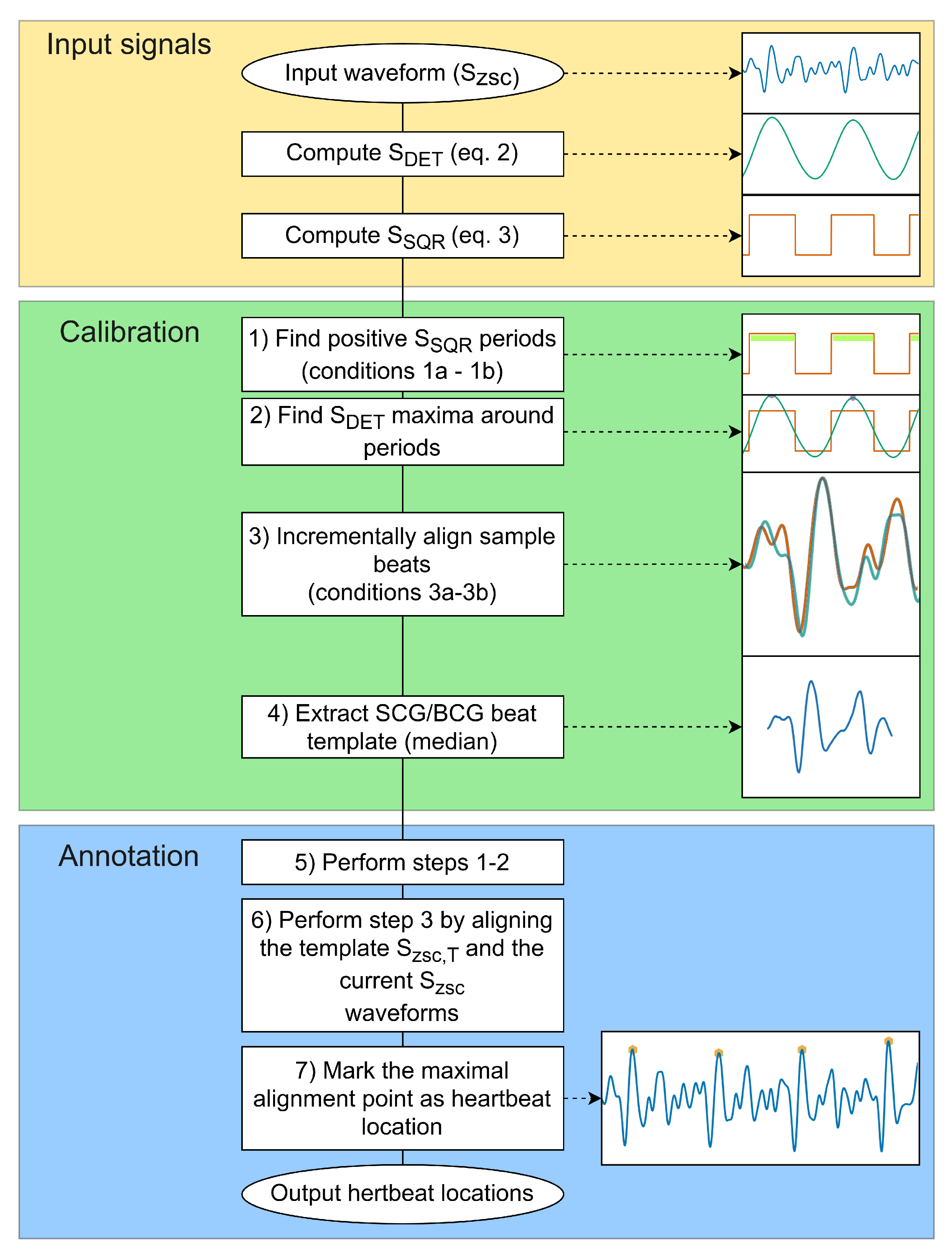
2.3. Proposed Methodology for Unsupervised Heartbeat Detection and Annotation
| Algorithm 1 Detection of heartbeat events. |
Inputs:
Begin:
Return time instants of heartbeats |
3. Results and Discussion
3.1. Performance Metrics and Evaluation Procedures
- Sensitivity, i.e., percentage of correctly identified reference points: ;
- Precision, i.e., percentage of TP in all detected points: .
- Root Mean Squared Error (RMSE), RMSE=;
- Mean Absolute Error (MAE), MAE=.
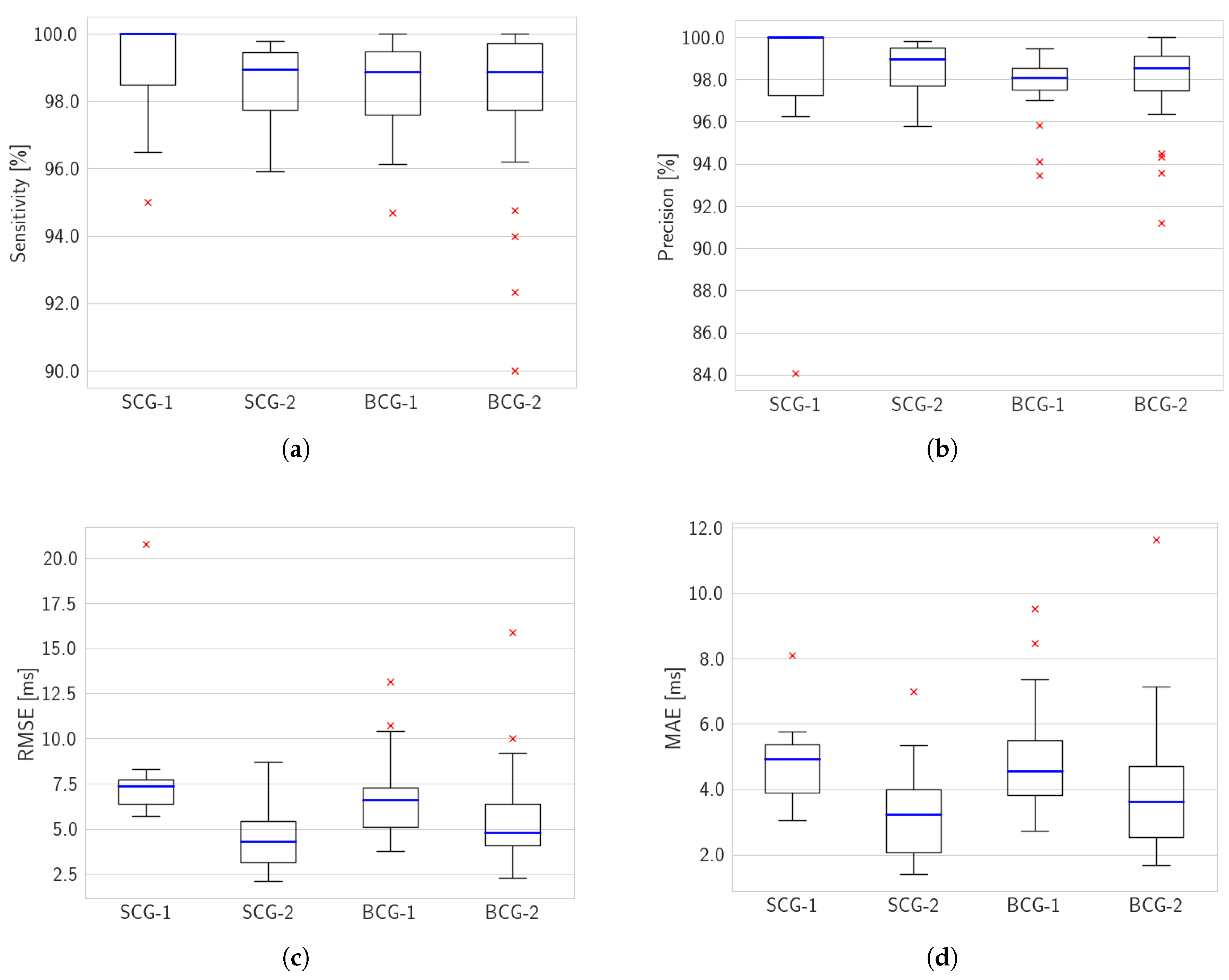
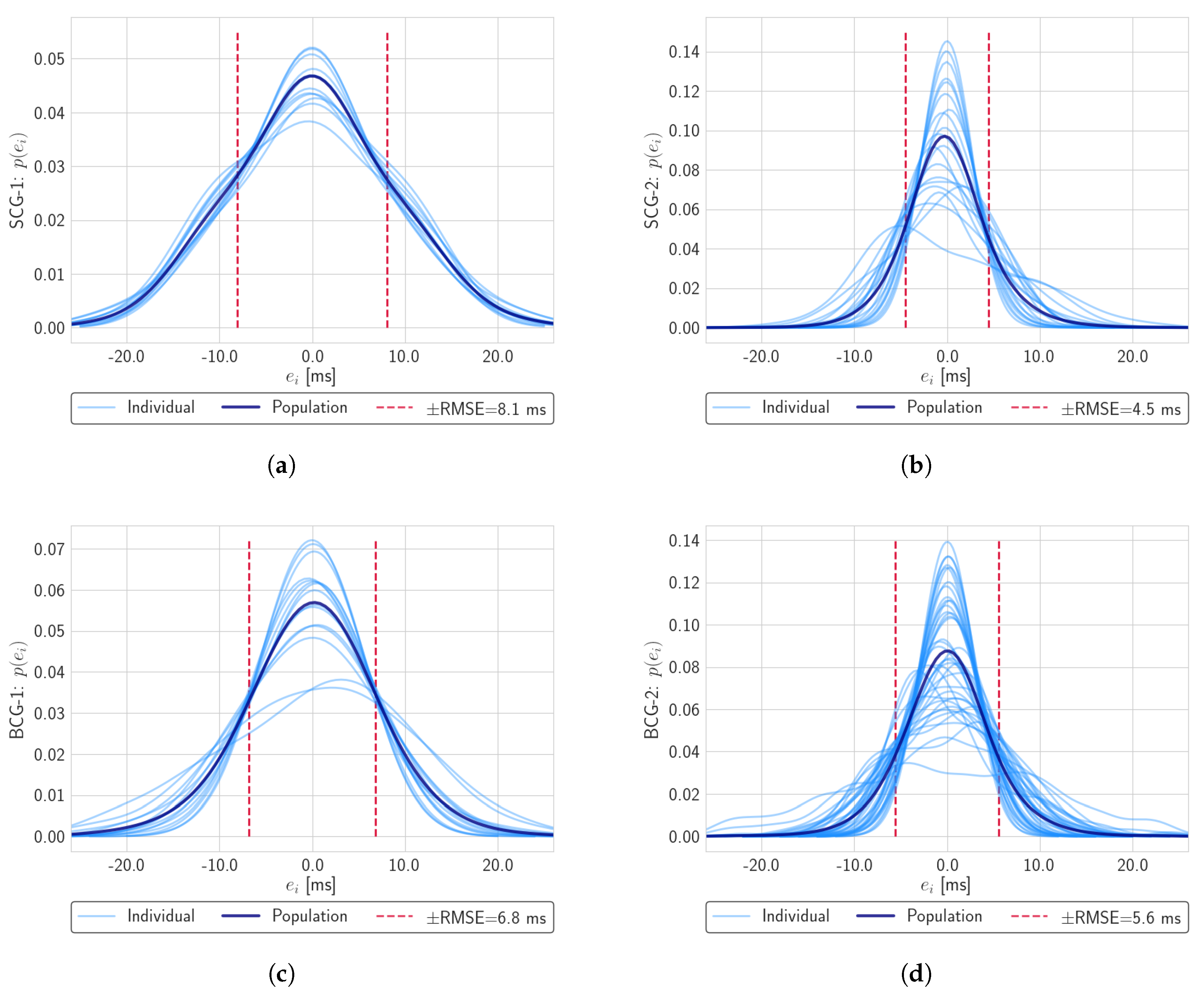
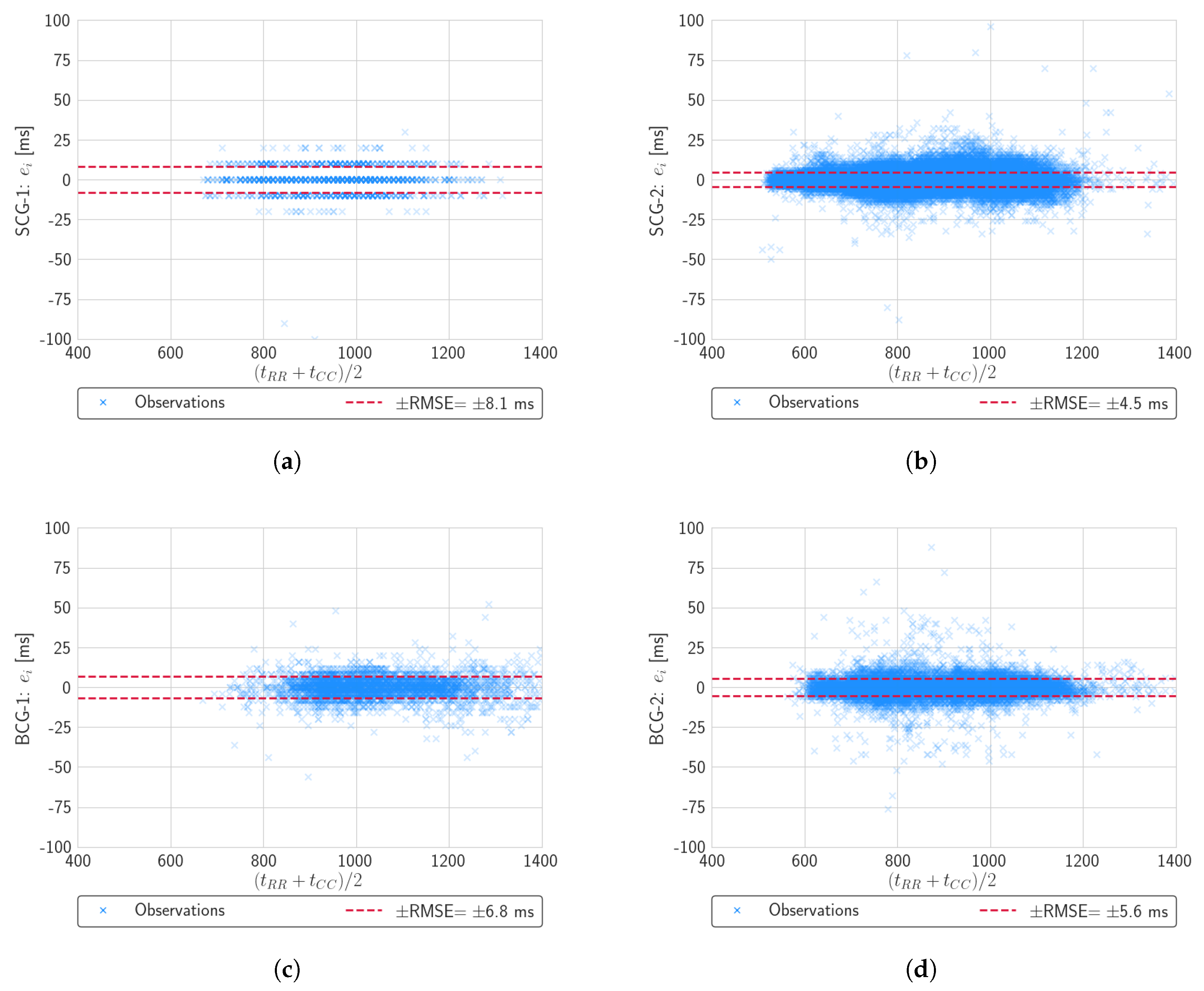
3.2. Performance Results
3.3. Discussion
- Kruskal–Wallis test, a non-parametric method to asses whether scores from each dataset all belong to the same distribution. In case the test is significant, it is possible to reject such null hypothesis.
- Mann–Whitney U test, similar to Kruskal–Wallis, but applied to just two populations.
Comparison with Related Literature
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guerra, C.; Bianchi, V.; Grossi, F.; Mora, N.; Losardo, A.; Matrella, G.; De Munari, I.; Ciampolini, P. The HELICOPTER Project: A Heterogeneous Sensor Network Suitable for Behavioral Monitoring. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer International Publishing: Cham, Switzerland, 2015; Volume 9455, pp. 152–163. [Google Scholar] [CrossRef]
- Mora, N.; Matrella, G.; Ciampolini, P. Cloud-Based Behavioral Monitoring in Smart Homes. Sensors 2018, 18, 1951. [Google Scholar] [CrossRef] [PubMed]
- Debes, C.; Merentitis, A.; Sukhanov, S.; Niessen, M.; Frangiadakis, N.; Bauer, A. Monitoring Activities of Daily Living in Smart Homes: Understanding human behavior. IEEE Signal Process. Mag. 2016, 33, 81–94. [Google Scholar] [CrossRef]
- Ho, D.K. Voice-controlled virtual assistants for the older people with visual impairment. Eye 2018, 32, 53–54. [Google Scholar] [CrossRef] [PubMed]
- Mora, N.; De Munari, I.; Ciampolini, P. Subject-independent, SSVEP-based BCI: Trading off among accuracy, responsiveness and complexity. In Proceedings of the 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, France, 22–24 April 2015; pp. 146–149. [Google Scholar] [CrossRef]
- Mora, N.; Bianchi, V.; De Munari, I.; Ciampolini, P. A low cost brain computer interface platform for AAL applications. Assist. Technol. Res. Ser. 2013, 33, 946–952. [Google Scholar] [CrossRef]
- Mora, N.; De Munari, I.; Ciampolini, P. Improving BCI Usability as HCI in Ambient Assisted Living System Control. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer International Publishing: Cham, Switzerland, 2015; Volume 9183, pp. 293–303. [Google Scholar] [CrossRef]
- Eerikäinen, L.M.; Bonomi, A.G.; Schipper, F.; Dekker, L.; Vullings, R.; De Morree, H.M.; Aarts, R.M. How Accurately Can We Detect Atrial Fibrillation Using Photoplethysmography Data Measured in Daily Life? Comput. Cardiol. 2019. [Google Scholar] [CrossRef]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and Seismocardiography: A Review of Recent Advances. IEEE J. Biomed. Health Inform. 2015, 19, 1414–1427. [Google Scholar] [CrossRef]
- Kortelainen, J.M.; Van Gils, M.; Parkka, J. Multichannel bed pressure sensor for sleep monitoring. In Computing in Cardiology; IEEE: New York, NY, USA, 2012. [Google Scholar]
- Wang, X. Relation of chaos activity characteristics of the cardiac system with the evolution of species. Chin. Sci. Bull. 2002, 47, 2042. [Google Scholar] [CrossRef]
- Wang, X.; Luo, C. Researches on chaos phenomenon of EEG dynamics model. Appl. Math. Comput. 2006, 183, 30–41. [Google Scholar] [CrossRef]
- Wang, X.; Luo, C.; Meng, J. Nonlinear dynamic research on EEG signals in HAI experiment. Appl. Math. Comput. 2009, 207, 63–74. [Google Scholar] [CrossRef]
- Mincholé, A.; Rodriguez, B. Artificial intelligence for the electrocardiogram. Nat. Med. 2019, 25, 22–23. [Google Scholar] [CrossRef]
- Sadek, I.; Biswas, J.; Abdulrazak, B. Ballistocardiogram signal processing: A review. Health Inf. Sci. Syst. 2019, 7, 10. [Google Scholar] [CrossRef] [PubMed]
- Taebi, A.; Solar, B.; Bomar, A.; Sandler, R.; Mansy, H. Recent Advances in Seismocardiography. Vibration 2019, 2, 64–86. [Google Scholar] [CrossRef]
- Inan, O.T.; Baran Pouyan, M.; Javaid, A.Q.; Dowling, S.; Etemadi, M.; Dorier, A.; Heller, J.A.; Bicen, A.O.; Roy, S.; De Marco, T.; et al. Novel Wearable Seismocardiography and Machine Learning Algorithms Can Assess Clinical Status of Heart Failure Patients. Circ. Heart Fail. 2018, 11. [Google Scholar] [CrossRef] [PubMed]
- Mora, N.; Cocconcelli, F.; Matrella, G.; Ciampolini, P. Detection and Analysis of Heartbeats in Seismocardiogram Signals. Sensors 2020, 20, 1670. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, BME-32, 230–236. [Google Scholar] [CrossRef]
- Kim, C.S.; Ober, S.L.; McMurtry, M.S.; Finegan, B.A.; Inan, O.T.; Mukkamala, R.; Hahn, J.O. Ballistocardiogram: Mechanism and Potential for Unobtrusive Cardiovascular Health Monitoring. Sci. Rep. 2016, 6, 31297. [Google Scholar] [CrossRef]
- Shafiq, G.; Tatinati, S.; Ang, W.T.; Veluvolu, K.C. Automatic Identification of Systolic Time Intervals in Seismocardiogram. Sci. Rep. 2016, 6, 37524. [Google Scholar] [CrossRef]
- Starr, I. The relation of the ballistocardiogram to cardiac function. Am. J. Cardiol. 1958, 2, 737–747. [Google Scholar] [CrossRef]
- Salerno, D.M.; Zanetti, J. Seismocardiography: A new technique for recording cardiac vibrations. Concept, method, and initial observations. J. Cardiovasc. Technol. 1990, 9, 111–118. [Google Scholar]
- Zanetti, J.; Salerno, D. Seismocardiography: A technique for recording precordial acceleration. In Computer-Based Medical Systems, Proceedings of the Fourth Annual IEEE Symposium, Baltimore, MD, USA, 12–14 May 1991; IEEE Comput. Soc. Press: Washington, DC, USA, 1991; pp. 4–9. [Google Scholar] [CrossRef]
- Di Rienzo, M.; Vaini, E.; Castiglioni, P.; Lombardi, P.; Meriggi, P.; Rizzo, F. A textile-based wearable system for the prolonged assessment of cardiac mechanics in daily life. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 6896–6898. [Google Scholar] [CrossRef]
- Jafari Tadi, M.; Lehtonen, E.; Saraste, A.; Tuominen, J.; Koskinen, J.; Teräs, M.; Airaksinen, J.; Pänkäälä, M.; Koivisto, T. Gyrocardiography: A New Non-invasive Monitoring Method for the Assessment of Cardiac Mechanics and the Estimation of Hemodynamic Variables. Sci. Rep. 2017, 7, 6823. [Google Scholar] [CrossRef]
- Yang, C.; Tang, S.; Tavassolian, N. Utilizing Gyroscopes Towards the Automatic Annotation of Seismocardiograms. IEEE Sens. J. 2017, 17, 2129–2136. [Google Scholar] [CrossRef]
- Kaisti, M.; Tadi, M.J.; Lahdenoja, O.; Hurnanen, T.; Saraste, A.; Pankaala, M.; Koivisto, T. Stand-Alone Heartbeat Detection in Multidimensional Mechanocardiograms. IEEE Sens. J. 2019, 19, 234–242. [Google Scholar] [CrossRef]
- Jeger-Madiot, N.; Gateau, J.; Fink, M.; Ing, R.K. Non-contact and through-clothing measurement of the heart rate using ultrasound vibrocardiography. Med. Eng. Phys. 2017, 50, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Yang, F.; Tian, Y.; Jing, X.; Wang, J. Contact-free Measurement of Heart Rate Variability via a Microwave Sensor. Sensors 2009, 9, 9572–9581. [Google Scholar] [CrossRef]
- Tu, J.; Lin, J. Fast Acquisition of Heart Rate in Noncontact Vital Sign Radar Measurement Using Time-Window-Variation Technique. IEEE Trans. Instrum. Meas. 2016, 65, 112–122. [Google Scholar] [CrossRef]
- Yao, Y.; Shin, S.; Mousavi, A.; Kim, C.S.; Xu, L.; Mukkamala, R.; Hahn, J.O. Unobtrusive Estimation of Cardiovascular Parameters with Limb Ballistocardiography. Sensors 2019, 19, 2922. [Google Scholar] [CrossRef]
- Yousefian, P.; Shin, S.; Mousavi, A.; Kim, C.S.; Mukkamala, R.; Jang, D.G.; Ko, B.H.; Lee, J.; Kwon, U.K.; Kim, Y.H.; et al. The Potential of Wearable Limb Ballistocardiogram in Blood Pressure Monitoring via Pulse Transit Time. Sci. Rep. 2019, 9, 10666. [Google Scholar] [CrossRef]
- Shao, D.; Tsow, F.; Liu, C.; Yang, Y.; Tao, N. Simultaneous Monitoring of Ballistocardiogram and Photoplethysmogram Using a Camera. IEEE Trans. Biomed. Eng. 2017, 64, 1003–1010. [Google Scholar] [CrossRef]
- Lee, H.; Cho, A.; Lee, S.; Whang, M. Vision-Based Measurement of Heart Rate from Ballistocardiographic Head Movements Using Unsupervised Clustering. Sensors 2019, 19, 3263. [Google Scholar] [CrossRef]
- Lydon, K.; Bo, Y.S.; Rosales, L.; Enayati, M.; Ho, K.C.; Rantz, M.; Skubic, M. Robust heartbeat detection from in-home ballistocardiogram signals of older adults using a bed sensor. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 7175–7179. [Google Scholar] [CrossRef]
- Koivistoinen, T.; Junnila, S.; Varri, A.; Koobi, T. A new method for measuring the ballistocardiogram using EMFi sensors in a normal chair. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 3, pp. 2026–2029. [Google Scholar] [CrossRef]
- González-Landaeta, R.; Casas, O.; Pallàs-Areny, R. Heart rate detection from an electronic weighing scale. Physiol. Meas. 2008, 29, 979–988. [Google Scholar] [CrossRef]
- Su, J.; Zhu, X.; Zhang, X.; Tang, J.; Liu, L. Ballistocardiogram Measurement System Using Three Load-Cell Sensors Platform in Chair. In Proceedings of the 2009 2nd International Conference on Biomedical Engineering and Informatics, Tianjin, China, 17–19 October 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, C.; Carek, A.M.; Inan, O.T.; Mukkamala, R.; Hahn, J. Ballistocardiogram-Based Approach to Cuffless Blood Pressure Monitoring: Proof of Concept and Potential Challenges. IEEE Trans. Biomed. Eng. 2018, 65, 2384–2391. [Google Scholar] [CrossRef] [PubMed]
- Meriheinä, U. BCG Measurements in Beds; Technical Report; Murata Electronics: Nagaokakyo, Japan, 2019. [Google Scholar]
- Sørensen, K.; Schmidt, S.E.; Jensen, A.S.; Søgaard, P.; Struijk, J.J. Definition of Fiducial Points in the Normal Seismocardiogram. Sci. Rep. 2018, 8, 15455. [Google Scholar] [CrossRef] [PubMed]
- Hurnanen, T.; Lehtonen, E.; Tadi, M.J.; Kuusela, T.; Kiviniemi, T.; Saraste, A.; Vasankari, T.; Airaksinen, J.; Koivisto, T.; Pankaala, M. Automated Detection of Atrial Fibrillation Based on Time–Frequency Analysis of Seismocardiograms. IEEE J. Biomed. Health Inform. 2017, 21, 1233–1241. [Google Scholar] [CrossRef] [PubMed]
- Bruser, C.; Diesel, J.; Zink, M.D.H.; Winter, S.; Schauerte, P.; Leonhardt, S. Automatic Detection of Atrial Fibrillation in Cardiac Vibration Signals. IEEE J. Biomed. Health Inform. 2013, 17, 162–171. [Google Scholar] [CrossRef] [PubMed]
- Sundar, A.; Pahwa, V. Evaluating the Performance of State of the Art Algorithms for Enhancement of Seismocardiogram Signals. In Proceedings of the First International Conference on Intelligent Computing and Communication; Mandal, J.K., Satapathy, S.C., Sanyal, M.K., Bhateja, V., Eds.; Springer: Singapore, 2017; pp. 37–45. [Google Scholar]
- Javaid, A.Q.; Ashouri, H.; Dorier, A.; Etemadi, M.; Heller, J.A.; Roy, S.; Inan, O.T. Quantifying and Reducing Motion Artifacts in Wearable Seismocardiogram Measurements During Walking to Assess Left Ventricular Health. IEEE Trans. Biomed. Eng. 2017, 64, 1277–1286. [Google Scholar] [CrossRef]
- Khosrow-Khavar, F.; Tavakolian, K.; Blaber, A.; Menon, C. Automatic and Robust Delineation of the Fiducial Points of the Seismocardiogram Signal for Noninvasive Estimation of Cardiac Time Intervals. IEEE Trans. Biomed. Eng. 2017, 64, 1701–1710. [Google Scholar] [CrossRef]
- Zakeri, V.; Akhbardeh, A.; Alamdari, N.; Fazel-Rezai, R.; Paukkunen, M.; Tavakolian, K. Analyzing Seismocardiogram Cycles to Identify the Respiratory Phases. IEEE Trans. Biomed. Eng. 2017, 64, 1786–1792. [Google Scholar] [CrossRef]
- Guidoboni, G.; Sala, L.; Enayati, M.; Sacco, R.; Szopos, M.; Keller, J.M.; Popescu, M.; Despins, L.; Huxley, V.H.; Skubic, M. Cardiovascular Function and Ballistocardiogram: A Relationship Interpreted via Mathematical Modeling. IEEE Trans. Biomed. Eng. 2019, 66, 2906–2917. [Google Scholar] [CrossRef]
- Javaid, A.Q.; Wiens, A.D.; Fesmire, N.F.; Weitnauer, M.A.; Inan, O.T. Quantifying and Reducing Posture-Dependent Distortion in Ballistocardiogram Measurements. IEEE J. Biomed. Health Inform. 2015, 19, 1549–1556. [Google Scholar] [CrossRef]
- Yao, Y.; Ghasemi, Z.; Shandhi, M.M.H.; Ashouri, H.; Xu, L.; Mukkamala, R.; Inan, O.T.; Hahn, J.O. Mitigation of Instrument-Dependent Variability in Ballistocardiogram Morphology: Case Study on Force Plate and Customized Weighing Scale. IEEE J. Biomed. Health Inform. 2020, 24, 69–78. [Google Scholar] [CrossRef]
- Suliman, A.; Carlson, C.; Warren, S.; Thompson, D. Performance Evaluation of Processing Methods for Ballistocardiogram Peak Detection. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 502–505. [Google Scholar] [CrossRef]
- Lee, W.; Yoon, H.; Han, C.; Joo, K.; Park, K. Physiological Signal Monitoring Bed for Infants Based on Load-Cell Sensors. Sensors 2016, 16, 409. [Google Scholar] [CrossRef] [PubMed]
- Brüser, C.; Winter, S.; Leonhardt, S. Robust inter-beat interval estimation in cardiac vibration signals. Physiol. Meas. 2013, 34, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Sadek, I.; Biswas, J.; Abdulrazak, B.; Haihong, Z.; Mokhtari, M. Continuous and unconstrained vital signs monitoring with ballistocardiogram sensors in headrest position. In Proceedings of the 2017 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Orland, FL, USA, 16–19 February 2017; pp. 289–292. [Google Scholar] [CrossRef]
- Cocconcelli, F.; Mora, N.; Matrella, G.; Ciampolini, P. Seismocardiography-based detection of heartbeats for continuous monitoring of vital signs. In Proceedings of the 2019 11th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 18–20 September 2019; pp. 53–58. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, M.A.; Argelagos-Palau, A.; Fernandez-Chimeno, M.; Ramos-Castro, J. A comparison of heartbeat detectors for the seismocardiogram. In Computing in Cardiology; IEEE: New York, NY, USA, 2013. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet. Circulation 2000, 101. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, T.; Sharma, L.N.; Bhuyan, M.K. Automatic Detection of Aortic Valve Opening using Seismocardiography in Healthy Individuals. IEEE J. Biomed. Health Inform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Luu, L.; Dinh, A. Using Moving Average Method to Recognize Systole and Diastole on Seismocardiogram without ECG Signal. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 3796–3799. [Google Scholar] [CrossRef]
- Khosrow-khavar, F.; Tavakolian, K.; Menon, C. Moving toward automatic and standalone delineation of seismocardiogram signal. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 7163–7166. [Google Scholar] [CrossRef]
- Laurin, A.; Khosrow-Khavar, F.; Blaber, A.P.; Tavakolian, K. Accurate and consistent automatic seismocardiogram annotation without concurrent ECG. Physiol. Meas. 2016, 37, 1588–1604. [Google Scholar] [CrossRef]
- Landreani, F.; Golier, D.; Hossein, A.; Rabineau, J.; Van de Borne, P.; Caiani, E.; Migeotte, P.F. Heartbeat Detection Using Three-Axial Seismocardiogram Acquired by Mobile Phone. In Proceedings of the 2018 Computing in Cardiology Conference (CinC), Maastricht, Netherlands, 23–26 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Thakkar, H.K.; Sahoo, P.K. Towards Automatic and Fast Annotation of Seismocardiogram Signals Using Machine Learning. IEEE Sens. J. 2020, 20, 2578–2589. [Google Scholar] [CrossRef]
- Paalasmaa, J.; Toivonen, H.; Partinen, M. Adaptive Heartbeat Modeling for Beat-to-Beat Heart Rate Measurement in Ballistocardiograms. IEEE J. Biomed. Health Inform. 2015, 19, 1945–1952. [Google Scholar] [CrossRef]
- Yu, Y.; Bruser, C.; Pietrzyk, U.; Leonhardt, S.; van Waase, S.; Schiek, M. Model-Based Verification of a Non-Linear Separation Scheme for Ballistocardiography. IEEE J. Biomed. Health Inform. 2014, 18, 174–182. [Google Scholar] [CrossRef]
- He, Z.; Wang, M.; Xie, Q.; Wang, G.; Zhao, Y.; Lian, Y.; Meng, B.; Peng, Z. A Heart Rate Measurement System Based on Ballistocardiogram for Smart Furniture. In Proceedings of the 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Chengdu, China, 26–30 October 2018; pp. 151–154. [Google Scholar] [CrossRef]
- Alvarado-Serrano, C.; Luna-Lozano, P.S.; Pallàs-Areny, R. An algorithm for beat-to-beat heart rate detection from the BCG based on the continuous spline wavelet transform. Biomed. Signal Process. Control. 2016, 27, 96–102. [Google Scholar] [CrossRef]
- Nurmi, S.; Saaresranta, T.; Koivisto, T.; Meriheinä, U.; Palva, L. Validation of an Accelerometer Based BCG Method for Sleep Analysis; Technical Report; Aalto University: Espoo, Finland, 2016. [Google Scholar]
- Wang, X.; Meng, J. A 2-D ECG compression algorithm based on wavelet transform and vector quantization. Digit. Signal Process. 2008, 18, 179–188. [Google Scholar] [CrossRef]
- Wang, X.; Meng, J. Wavelet-based hybrid ECG compression technique. Analog. Integr. Circuits Signal Process. 2009, 59, 301–308. [Google Scholar] [CrossRef]
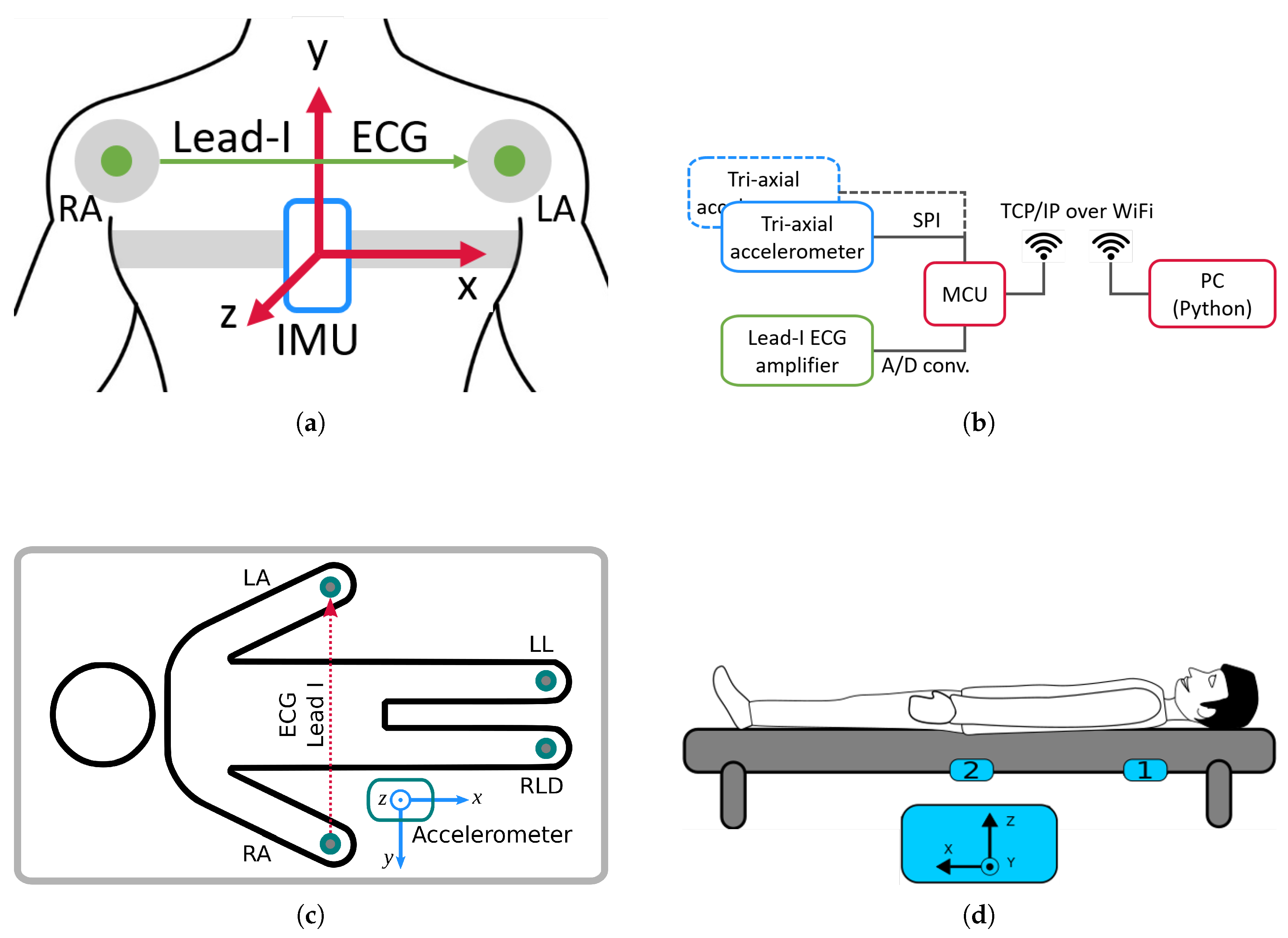

| ID | Nrec | Fs | Brief Description |
|---|---|---|---|
| SCG-1 | 13 | 100 Hz | Custom SCG dataset of sitting subjects |
| SCG-2 | 20 | 500 Hz | CEBS database: SCG of lying subjects |
| BCG-1 | 18 | 250 Hz | Custom BCG dataset: bed frame 1 |
| BCG-2 | 42 | 500 Hz | Custom BCG dataset: bed frame 2, three lying position per subject |
| Dataset | Sensitivity (%) | Precision (%) | RMSE (ms) | MAE (ms) |
|---|---|---|---|---|
| SCG-1 | ||||
| mean | 98.9 | 97.9 | 8.1 | 4.8 |
| 10th LPP | 96.2 | 96.3 | 8.2 | 5.7 |
| SCG-2 | ||||
| mean | 98.5 | 98.6 | 4.5 | 3.3 |
| 10th LPP | 97.0 | 97.2 | 6.1 | 4.8 |
| BCG-1 | ||||
| mean | 98.4 | 97.6 | 6.8 | 5.0 |
| 10th LPP | 96.7 | 95.0 | 10.6 | 7.9 |
| BCG-2 | ||||
| mean | 98.9 | 98.5 | 4.8 | 3.6 |
| 10th LPP | 96.2 | 96.4 | 8.8 | 5.9 |
| Sensitivity | 0.9057 | ||
| Precision | 0.9677 | ||
| RMSE | 0.7842 | ||
| MAE | 0.5213 |
| Sensitivity | 0.6290 | ||
| Precision | 0.0663 | ||
| RMSE | 0.0003 | * | ** |
| MAE | 0.0036 | * | ** |
| Metric | Dataset a | Dataset b | |||
|---|---|---|---|---|---|
| Sensitivity | SCG-1 | SCG-2 | 0.1526 | ||
| SCG-1 | BCG-1 | 0.2031 | |||
| SCG-1 | BCG-2 | 0.1630 | |||
| SCG-2 | BCG-1 | 0.4683 | |||
| SCG-2 | BCG-2 | 0.4447 | |||
| BCG-1 | BCG-2 | 0.4268 | |||
| Precision | SCG-1 | SCG-2 | 0.1514 | ||
| SCG-1 | BCG-1 | 0.0534 | |||
| SCG-1 | BCG-2 | 0.0634 | |||
| SCG-2 | BCG-1 | 0.0514 | |||
| SCG-2 | BCG-2 | 0.1591 | |||
| BCG-1 | BCG-2 | 0.1507 | |||
| RMSE | SCG-1 | SCG-2 | 0.0006 | * | ** |
| SCG-1 | BCG-1 | 0.1422 | |||
| SCG-1 | BCG-2 | 0.0083 | * | ** | |
| SCG-2 | BCG-1 | 0.0117 | * | ||
| SCG-2 | BCG-2 | 0.0686 | |||
| BCG-1 | BCG-2 | 0.0502 | |||
| MAE | SCG-1 | SCG-2 | 0.0121 | * | |
| SCG-1 | BCG-1 | 0.4762 | |||
| SCG-1 | BCG-2 | 0.0273 | * | ||
| SCG-2 | BCG-1 | 0.0117 | * | ||
| SCG-2 | BCG-2 | 0.1501 | |||
| BCG-1 | BCG-2 | 0.0331 | * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mora, N.; Cocconcelli, F.; Matrella, G.; Ciampolini, P. A Unified Methodology for Heartbeats Detection in Seismocardiogram and Ballistocardiogram Signals. Computers 2020, 9, 41. https://doi.org/10.3390/computers9020041
Mora N, Cocconcelli F, Matrella G, Ciampolini P. A Unified Methodology for Heartbeats Detection in Seismocardiogram and Ballistocardiogram Signals. Computers. 2020; 9(2):41. https://doi.org/10.3390/computers9020041
Chicago/Turabian StyleMora, Niccolò, Federico Cocconcelli, Guido Matrella, and Paolo Ciampolini. 2020. "A Unified Methodology for Heartbeats Detection in Seismocardiogram and Ballistocardiogram Signals" Computers 9, no. 2: 41. https://doi.org/10.3390/computers9020041
APA StyleMora, N., Cocconcelli, F., Matrella, G., & Ciampolini, P. (2020). A Unified Methodology for Heartbeats Detection in Seismocardiogram and Ballistocardiogram Signals. Computers, 9(2), 41. https://doi.org/10.3390/computers9020041






