Evaluation of Features in Detection of Dislike Responses to Audio–Visual Stimuli from EEG Signals
Abstract
1. Introduction
2. Materials and Methods
- (i)
- frequency decomposition with DFT, such as the PSD (Section 2.2.1), Logarithmic Energy (LogE) (Section 2.2.2), and Linear Frequency Cepstral Coefficients (LFCC) (Section 2.2.3),
- (ii)
- DWT-based decomposition with four different wavelet functions, such as Daubechies of order 4 and 32, Coiflets of order 5 and Symmlets of order 8 (Section 2.2.4).
2.1. Preprocessing of the EEG Signal
2.2. Feature Extraction
2.2.1. Power Spectral Density
2.2.2. Logarithmic Energy
2.2.3. Linear Frequency Cepstral Coefficients
2.2.4. Discrete Wavelet Transform Based Features
2.3. Dataset
2.4. Experimental Protocol
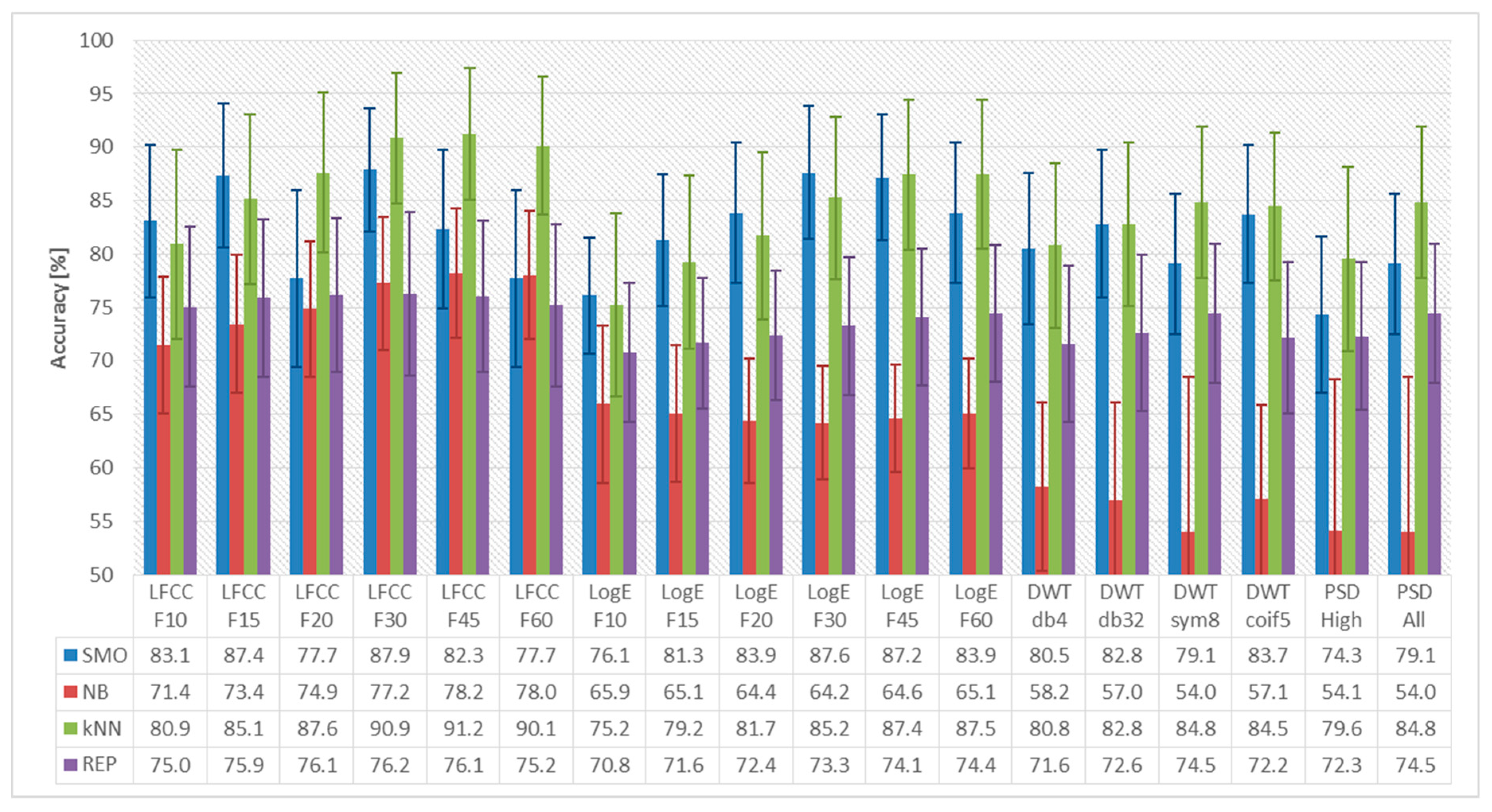
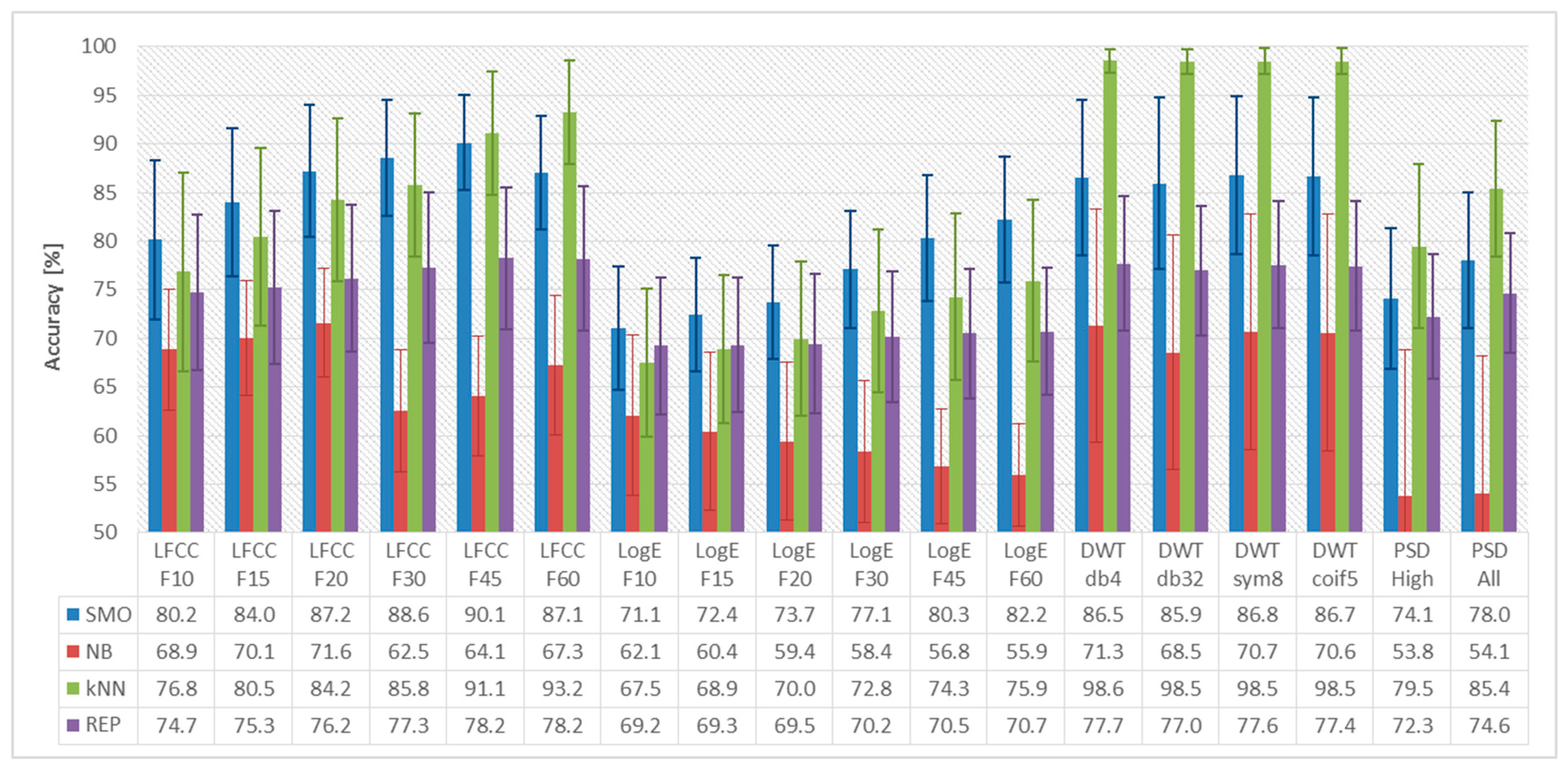
3. Evaluation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. DEAP: A database for emotion analysis using physiological signals. IEEE Trans. Affect. Comput. 2011, 3, 18–31. [Google Scholar] [CrossRef]
- Koelstra, S.; Mühl, C.; Patras, I. EEG analysis for implicit tagging of video data. In Proceedings of the 2009 3rd International Conference on Affective Computing and Intelligent Interaction and Workshops, Amsterdam, The Netherlands, 10–12 September 2009; pp. 1–6. [Google Scholar]
- Koelstra, S.; Yazdani, A.; Soleymani, M.; Mühl, C.; Lee, J.S.; Nijholt, A.; Pun, T.; Ebrahimi, T.; Patras, I. Single trial classification of EEG and peripheral physiological signals for recognition of emotions induced by music videos. In Proceedings of the International Conference on Brain Informatics, Toronto, ON, Canada, 28–30 August 2010; pp. 89–100. [Google Scholar]
- Koelstra, S.; Patras, I. Fusion of facial expressions and EEG for implicit affective tagging. Image Vis. Comput. 2013, 31, 164–174. [Google Scholar] [CrossRef]
- Kroupi, E.; Yazdani, A.; Ebrahimi, T. EEG correlates of different emotional states elicited during watching music videos. In Proceedings of the International Conference on Affective Computing and Intelligent Interaction, Memphis, TN, USA, 9–12 October 2011; pp. 457–466. [Google Scholar]
- Berridge, K.; Winkielman, P. What is an unconscious emotion? (The case for unconscious “liking”). Cognit. Emotion 2003, 17, 181–211. [Google Scholar] [CrossRef] [PubMed]
- Mehrabian, A. Basic Dimensions for a General Psychological Theory: Implications for Personality, Social, Environmental, and Developmental Studies; Oelgeschlager, Gunn & Hain: Cambridge, MA, USA, 1980. [Google Scholar]
- Jenke, R.; Peer, A.; Buss, M. Feature extraction and selection for emotion recognition from EEG. IEEE Trans. Affect. Comput. 2014, 5, 327–339. [Google Scholar] [CrossRef]
- Zheng, W.L.; Zhu, J.Y.; Lu, B.L. Identifying stable patterns over time for emotion recognition from EEG. IEEE Trans. Affect. Comput. 2017, 10, 417–429. [Google Scholar] [CrossRef]
- Li, M.; Lu, B.L. Emotion classification based on gamma-band EEG. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 1223–1226. [Google Scholar]
- Güntekin, B.; Başar, E. Event-related beta oscillations are affected by emotional eliciting stimuli. Neurosci. Lett. 2010, 483, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Martini, N.; Menicucci, D.; Sebastiani, L.; Bedini, R.; Pingitore, A.; Vanello, N.; Milanesi, M.; Landini, L.; Gemignani, A. The dynamics of EEG gamma responses to unpleasant visual stimuli: From local activity to functional connectivity. NeuroImage 2012, 60, 922–932. [Google Scholar] [CrossRef] [PubMed]
- Lange, C.G.; James, W. The Emotions; Williams & Wilkins Co.: Philadelphia, PA, USA, 1922. [Google Scholar]
- Cannon, W.B. The James-Lange theory of emotions: A critical examination and an alternative theory. Am. J. Psychol. 1927, 39, 106–124. [Google Scholar] [CrossRef]
- Sternberg, R.J. Psychology: In Search of the Human Mind; Wadsworth Publishing: Belmont, CA, USA, 2001. [Google Scholar]
- Schachter, S. The interaction of cognitive and physiological determinants of emotional state. In Advances in Experimental Social Psychology; Academic Press: Cambridge, MA, USA, 1964; pp. 49–80. [Google Scholar]
- Liu, Y.; Fu, Q.; Fu, X. The interaction between cognition and emotion. Chin. Sci. Bull. 2009, 54, 4102. [Google Scholar] [CrossRef]
- Lazarus, R.S. Progress on a cognitive-motivational-relational theory of emotion. Am. Psychol. 1991, 46, 819. [Google Scholar] [CrossRef] [PubMed]
- Meyer, L.B. Emotion and Meaning in Music; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Oliver, M.B.; Hartmann, T. Exploring the role of meaningful experiences in users’ appreciation of “good movies”. Projections 2010, 4, 128–150. [Google Scholar] [CrossRef]
- Yazdani, A.; Lee, J.S.; Vesin, J.M.; Ebrahimi, T. Affect recognition based on physiological changes during the watching of music videos. ACM Trans. Interact. Intell. Syst. 2012, 2, 1–26. [Google Scholar] [CrossRef]
- Hadjidimitriou, S.K.; Hadjileontiadis, L.J. Toward an EEG-based recognition of music liking using time-frequency analysis. IEEE Trans. Biomed. Eng. 2012, 59, 3498–3510. [Google Scholar] [CrossRef] [PubMed]
- Bastos-Filho, T.F.; Ferreira, A.; Atencio, A.C.; Arjunan, S.; Kumar, D. Evaluation of feature extraction techniques in emotional state recognition. In Proceedings of the 2012 4th International Conference on Intelligent Human Computer Interaction (IHCI), Kharagpur, India, 27–29 December 2012; pp. 1–6. [Google Scholar]
- Nie, D.; Wang, X.W.; Shi, L.C.; Lu, B.L. EEG-based emotion recognition during watching movies. In Proceedings of the 2011 5th International IEEE/EMBS Conference on Neural Engineering, Cancun, Mexico, 27 April–1 May 2011; pp. 667–670. [Google Scholar]
- Al-Nafjan, A.; Hosny, M.; Al-Wabil, A.; Al-Ohali, Y. Classification of human emotions from electroencephalogram (EEG) signal using deep neural network. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 419–425. [Google Scholar] [CrossRef]
- Bos, D.O. EEG-based emotion recognition. Influ. Visual Audit. Stimuli. 2006, 56, 1–7. [Google Scholar]
- Brown, L.; Grundlehner, B.; Penders, J. Towards wireless emotional valence detection from EEG. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 2188–2191. [Google Scholar]
- Li, X.; Zhang, P.; Song, D.; Yu, G.; Hou, Y.; Hu, B. EEG based emotion identification using unsupervised deep feature learning. In Proceedings of the SIGIR2015 Workshop on Neuro-Physiological Methods in IR Research, Santiago, Chile, 13 August 2015. [Google Scholar]
- Murugappan, M.; Juhari, M.R.; Nagarajan, R.; Yaacob, S. An Investigation on visual and audiovisual stimulus based emotion recognition using EEG. Int. J. Med. Eng. Inform. 2009, 1, 342. [Google Scholar] [CrossRef]
- Murugappan, M. Human emotion classification using wavelet transform and KNN. In Proceedings of the 2011 International Conference on Pattern Analysis and Intelligence Robotics, Kuala Lump, Malaysia, 28–29 June 2011; pp. 148–153. [Google Scholar]
- Rached, T.S.; Perkusich, A. Emotion recognition based on brain-computer interface systems. In Brain-Computer Interface Systems-Recent Progress and Future Prospects; InTech: Rijeka, Croatia, 2013; pp. 253–270. [Google Scholar]
- Yohanes, R.E.; Ser, W.; Huang, G.B. Discrete Wavelet Transform coefficients for emotion recognition from EEG signals. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 2251–2254. [Google Scholar]
- Feradov, F. Study of the Quality of Linear Frequency Cepstral Coefficients for Automated Recognition of Negative Emotional States from EEG Signals; Volume G: Medicine, Pharmacy and Dental Medicine; Researcher’s Union: Plovdiv, Bulgaria, 2016. [Google Scholar]
- Liu, N.; Fang, Y.; Li, L.; Hou, L.; Yang, F.; Guo, Y. Multiple feature fusion for automatic emotion recognition using EEG signals. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 896–900. [Google Scholar]
- Wahab, A.; Kamaruddin, N.; Palaniappan, L.K.; Li, M.; Khosrowabadi, R. EEG signals for emotion recognition. J. Comput. Methods Sci. Eng. 2010, 10, 1–11. [Google Scholar] [CrossRef]
- Othman, M.; Wahab, A.; Karim, I.; Dzulkifli, M.A.; Alshaikli, I.F.T. EEG emotion recognition based on the dimensional models of emotions. Procedia-Soc. Behav. Sci. 2013, 97, 30–37. [Google Scholar] [CrossRef]
- Othman, M.; Wahab, A.; Khosrowabadi, R. MFCC for robust emotion detection using EEG. In Proceedings of the 2009 IEEE 9th Malaysia International Conference on Communications (MICC), Kuala Lumpur, Malaysia, 14–17 December 2009; pp. 98–101. [Google Scholar]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Liu, C.-L. A Tutorial of the Wavelet Transform; NTUEE: Taipei, Taiwan, 2010. [Google Scholar]
- Bradley, M.M.; Lang, P.J. Measuring emotion: The self-assessment manikin and the semantic differential. J. Behav. Ther. Exp. Psychiatry 1994, 25, 49–59. [Google Scholar] [CrossRef]
- Feradov, F.; Mporas, I.; Ganchev, T. Evaluation of Cepstral Coefficients as Features in EEG-based Recognition of Emotional States. In Proceedings of the International Conference on Intelligent Information Technologies for Industry, Varna, Bulgaria, 14–16 September 2017; pp. 504–511. [Google Scholar]
- Witten, I.H.; Frank, E. Data mining: Practical machine learning tools and techniques with Java implementations. ACM Sigmod Record 2002, 31, 76–77. [Google Scholar] [CrossRef]
| Author(s) | Features | Classifier | Accuracy |
|---|---|---|---|
| Bastos-Filho et al. [23] | Signal statistics, PSD and HOC * | kNN | 70.1% |
| Nie et al. [24] | Spectral Log. Energy of different frequency bands | SVM | 87.5% |
| Al-Nafjan et al. [25] | PSD, frontal asymmetry features * | DNN | 7.513 (MSE) |
| Bos [26] | Alpha and Beta bands, ratios and power | FDA | 92.3% |
| Brown et al. [27] | Alfa power ratio features, Beta power features | QDC, SVM, kNN | 82.0% (3-class) 85.0% (2-class) |
| Li et al. [28] | PSD of different bands of DBN features * | SVM | 66.9% |
| Murugappan [29] | DWT (db4, db8, sym8, coif5) to calculate St. Dev, Power and Entropy | kNN | 82.9% |
| Murugappan et al. [30] | DWT (db4) to calculate statistical features of alpha band | MLP-BP NN | 66.7% |
| Rached et al. [31] | DWT (db4) to calculate theta and alpha energy and entropy * | NN | 95.6% |
| Yohanes et al. [32] | DWT coefficients for different wavelets (coif., db, sym.) | ELM, SVM | 89.3% |
| Feradov [33] | Log. Energy and LFCC * | SVM | 75.7% |
| Liu et al. [34] | LFCC * | kNN | 90.9% |
| Wahab et al. [35] | Statistical time domain features/ MFCC | RVM, SVM, MLP, DT, BN, EFuNN | 97.8% |
| Othman et al. [36] | MFCC, KDE | MLP NN | 0.05 (MSE) |
| Othman et al. [37] | MFCC | MLP NN | 90% |
| # | Subject ID | Dislikes in (%) | # | Subject ID | Dislikes in (%) |
|---|---|---|---|---|---|
| 1 | P2 | 30.0% | 13 | P20 | 22.5% |
| 2 | P4 | 40.0% | 14 | P21 | 70.0% |
| 3 | P5 | 27.5% | 15 | P22 | 67.5% |
| 4 | P6 | 20.0% | 16 | P23 | 42.5% |
| 5 | P11 | 45.0% | 17 | P24 | 20.0% |
| 6 | P12 | 40.0% | 18 | P25 | 32.5% |
| 7 | P13 | 22.5% | 19 | P26 | 22.5% |
| 8 | P14 | 22.5% | 20 | P28 | 32.5% |
| 9 | P15 | 27.5% | 21 | P29 | 35.0% |
| 10 | P16 | 55.0% | 22 | P30 | 45.0% |
| 11 | P17 | 27.5% | 23 | P31 | 22.5% |
| 12 | P19 | 27.5% | 24 | P32 | 45.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feradov, F.; Mporas, I.; Ganchev, T. Evaluation of Features in Detection of Dislike Responses to Audio–Visual Stimuli from EEG Signals. Computers 2020, 9, 33. https://doi.org/10.3390/computers9020033
Feradov F, Mporas I, Ganchev T. Evaluation of Features in Detection of Dislike Responses to Audio–Visual Stimuli from EEG Signals. Computers. 2020; 9(2):33. https://doi.org/10.3390/computers9020033
Chicago/Turabian StyleFeradov, Firgan, Iosif Mporas, and Todor Ganchev. 2020. "Evaluation of Features in Detection of Dislike Responses to Audio–Visual Stimuli from EEG Signals" Computers 9, no. 2: 33. https://doi.org/10.3390/computers9020033
APA StyleFeradov, F., Mporas, I., & Ganchev, T. (2020). Evaluation of Features in Detection of Dislike Responses to Audio–Visual Stimuli from EEG Signals. Computers, 9(2), 33. https://doi.org/10.3390/computers9020033






